Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A novel one-dimensional chain built of vanadyl ions and pyrazine-2,5-dicarboxylate†
Marianne
Lankelma
a,
Jeroen
de Boer
a,
Marilena
Ferbinteanu
b,
André Luis
Dantas Ramos
ad,
Radu
Tanasa
c,
Gadi
Rothenberg
a and
Stefania
Tanase
*a
aVan't Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: s.grecea@uva.nl; Web: http://hims.uva.nl/hcsc
bFaculty of Chemistry, Inorganic Chemistry Department, University of Bucharest, Dumbrava Rosie 23, Bucharest 020462, Romania
cDepartment of Physics & CARPATH, “Alexandru Ioan Cuza” University of Iasi, Boulevard Carol I, no. 11, Iasi 700506, Romania
dEnvironmental Engineering Department, Federal University of Sergipe (UFS), Aracaju, SE, Brazil
First published on 11th May 2015
Abstract
We present a new coordination polymer, {[VO(pzdc)(H2O)2] H2O}n, built from vanadyl and pyrazine-2,5-dicarboxylate (pzdc) ions. It consists of a one-dimensional chain of vanadyl ions linked by pzdc ions. The carboxylate groups show monodentate coordination, while the pyrazine ring is present both in non-coordinated and coordinated modes. This novel structure is stabilized by an intricate network of hydrogen bonds. The material is highly robust, and thermally stable up to 400 K. It is also antiferromagnetic, with a maximum magnetic susceptibility at ca. 50 K. The orbital shape and population analysis by means of DFT analysis confirm the π-acceptor role of the aromatic nitrogen function of the ligand, while the oxygen-based moieties (carboxylates from pzdc, the aqua ligands and oxo from V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group) behave as normal donors. Charting the density flow related with significant transitions computed by time-dependent DFT, we determined the ligand-to-metal charge transfer processes. The topology of the chain complex implies two different types of connecting bridges. Using Broken Symmetry DFT modelling gives evidence for two different exchange coupling mechanisms between the vanadyl ions along each of these two molecular bridges. One is strongly antiferromagnetic, practically reducing the chain to ‘vanadyl dimers’. The other is almost uncoupled, due to the large distance between the vanadyl ions.
O group) behave as normal donors. Charting the density flow related with significant transitions computed by time-dependent DFT, we determined the ligand-to-metal charge transfer processes. The topology of the chain complex implies two different types of connecting bridges. Using Broken Symmetry DFT modelling gives evidence for two different exchange coupling mechanisms between the vanadyl ions along each of these two molecular bridges. One is strongly antiferromagnetic, practically reducing the chain to ‘vanadyl dimers’. The other is almost uncoupled, due to the large distance between the vanadyl ions.
Introduction
Vanadium compounds are widely studied in chemistry and applied in industry. They are studied for their redox chemistry, which enables a variety of applications in oxidation catalysis,1–3,4 including its largest application in sulfuric acid synthesis.2,5–8 Among these, epoxidation of aliphatic or cycloalkenes is highly relevant because it is a straightforward route for producing various chemicals.1–3 However, such reactions are mainly performed in homogeneous media, making the catalyst recycle impossible. Consequently, efforts have been made for embedding vanadium ions in highly stable metal–organic frameworks (MOFs) which may be used as heterogeneous catalysts to possibly overcome this problem.9,10One interesting emerging area is the synthesis of vanadium-based metal–organic frameworks (V-MOFs). These are rare compared with MOFs of other transition metals.9,10 This is likely due to the rich solution chemistry of vanadium which gives various species under different conditions. MIL-47 is the first V-MOF obtained in the hydrothermal reaction of VCl3 with terephtalic.11 It has a large specific surface area, but shows high sensitivity to air. Removing the guest molecules by calcination in air induces VIII to VIV oxidation.12 Few other V-MOFs were obtained under similar conditions. All of them are made using polycarboxylate ligands, such as 1,4-benzenedicarboxylic acid,13–16 isophthalic acid,15 trimesic acid,17 1,2,4,5-benzene-tetracarboxylic acid,18 2,5-dimethylterephtalic acid,19 biphenyl-4,4′-dicarboxylic acid,20 2,6-naphtalene-dicarboxylic acid,21 1,4-naphtalenedicarboxylic acid22 and 2,5-dihydroxyterephtalic acid.22
Extending our recent material design strategies23–25 to V-MOFs, we discovered a new coordination polymer built of vanadyl and pyrazine-2,5-dicarboxylate (pzdc) ions, {[VO(pzdc)(H2O)2] H2O}2n. Here we discuss its synthesis, structural aspects and magnetic properties. There are a few vanadyl chain compounds of vanadium-phosphate type which are relevant to catalytic applications.26–30 Examples of carboxylate-bridged vanadyl chains are scarce, and they include formate,31 acetate,32,33 glycolate32,33 and benzoate34 as bridges. Theoretical calculations have suggested that the band gap in such systems may be tuned from semiconducting to metallic states, broadening the application possibilities of hybrid inorganic–organic compounds.35
Experimental
Materials and instrumentation
Hydrothermal syntheses were carried out in Teflon-capped borosilicate tubes placed in a VWR VENTI-Line oven. Microscopic analysis was performed on a Euromex Holland microscope. Infrared spectra (4000–300 cm−1, resol. 0.5 cm−1) were recorded on a Varian 660 FTIR spectrometer equipped with a Gladi ATR device, using the reflectance technique. Ligand field spectra were obtained on a Perkin-Elmer Lambda 900 spectrophotometer using the diffuse reflectance technique and MgO as a reference. X-ray powder diffraction patterns were recorded on a bench Rigaku MiniFlexII diffractometer. Thermogravimetric analysis (TGA) was performed with Netzsch STA 449 F3 Jupiter in the temperature range of 25–800 °C under an argon atmosphere (flow of 40 cm3 min−1) at a heating rate of 5 °C min−1. The temperature dependent magnetic susceptibility measurements in the 1.8–300 K range were recorded on a Quantum Design MPMS-5 5T SQUID magnetometer. Data were corrected for the magnetization of the sample holder and for diamagnetic contributions, which were estimated from the Pascal constants. Unless stated otherwise, all chemicals are commercially available (Aldrich, >99% pure) and were used as received.Procedure for synthesis of the one-dimensional vanadium coordination polymer
Vanadyl sulphate (160 mg, 0.636 mmol), pyrazine-2,5-dicarboxylic acid (156 mg, 0.773 mmol) and deionized water (15 mL) are reacted at 120 °C for 24 h. The brown-reddish crystals formed were collected by filtration and washed with water and acetone respectively. Yield: 120 mg (66%). C12H16N4O16V2 (574.16 g mol−1) C, H, N analysis (%) calcd C 25.10, H 2.81, N 9.76; found C 25.33, H 2.89, N 9.98. IR (ν, cm−1): 3443 (w), 3300 (w), 3135 (w), 2907 (vw), 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 847 (w), 1680 (w), 1612 (s), 1484 (m), 1388 (m), 1310 (s), 1272 (w), 1165 (s), 1040 (m), 976 (s), 930 (m), 832 (m), 757 (m), 728 (m), 661 (m), 499 (w), 597 (m), 521 (s); UV-Vis (λmax, nm): 225 (π–π*), 279 (π–π*), 464 (LMCT), 800 (d–d).
847 (w), 1680 (w), 1612 (s), 1484 (m), 1388 (m), 1310 (s), 1272 (w), 1165 (s), 1040 (m), 976 (s), 930 (m), 832 (m), 757 (m), 728 (m), 661 (m), 499 (w), 597 (m), 521 (s); UV-Vis (λmax, nm): 225 (π–π*), 279 (π–π*), 464 (LMCT), 800 (d–d).
Structure determination and refinement
Intensity data for a single crystal of {[VO(pzdc)(H2O)2] H2O}n were collected using Mo Ka radiation (λ = 0.71073 λ) on a Rigaku CCD diffractometer. The intensity data were corrected for Lorentz and polarization effects, for absorption (Ψ-scan absorption correction) and extinction. The structures were solved by Patterson methods. Several programs were used for data reduction, structure solution and structure refinement. Refinement of F2 was done against all reflections. The weighted R factor, wR, and goodness of fit S are based on F2. Conventional R factors are based on F, with F set to zero for negative F2. All non-hydrogen atoms were refined with anisotropic displacement parameters. All hydrogens were placed at calculated positions and were refined riding on the parent atoms. Crystallographic data have been registered at the Cambridge Structural Data Base as CCDC-943141.Electronic structure calculations
The Density Functional Theory (DFT) calculations were carried out, at experimental geometry, with the Amsterdam Density Functional (ADF) code36–39 using the Becke–Perdew (BP86) functional40–42 and the triple-zeta-polarization (TZP) basis set from the ADF library.Results and discussion
The reaction of vanadyl sulphate and pyrazine-2,5-dicarboxylic acid under hydrothermal conditions gives brown-reddish crystals of the one-dimensional {[VO(pzdc)(H2O)2] H2O}n. A series of control experiments confirmed that single crystals of {[VO(pzdc)(H2O)2] H2O}n are also formed when performing the hydrothermal synthesis using vanadium(III) chloride or vanadyl sulphate as the vanadium source, as well as with hydroquinone or pyrazole-2,5-dicarboxylic acid as co-ligands. These results show the high stability of this unidimensional polymer.The FTIR spectrum of {[VO(pzdc)(H2O)2] H2O}n has a strong band at 976 cm−1, characteristic of the vanadyl group ν(V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). The bands centered at 521 cm−1 and 597 cm−1 are due to ν(V–O).34 Similarly, the two distinct bands at 3443 and 3300 cm−1, assigned to ν(O–H), are in agreement with the presence of both coordinated and non-coordinated water molecules. The characteristic bands of the ligand are observed in the low−frequency range of 1600–600 cm−1. The νasym(COO−) is located at 1612 cm−1 and νsym(COO−) at 1388 cm−1, leading to a difference of 224 cm−1.34 This indicates a monodentate coordination of the carboxylate group in agreement with the XRD structure described below. The UV-Vis spectrum shows d1 configuration features, corresponding to a distorted octahedral geometry. Thermogravimetric analysis showed that the compound is stable up to 125 °C. A weight loss of 18.3% is observed between 125 °C and 300 °C (see Fig. S3† for details). This corresponds to the removal of both coordinated and non-coordinated water molecules (calc. 18.1%). The weight loss of 6.6% observed between 200 °C and 300 °C is typical for vanadyl compounds containing water molecules coordinated at equatorial positions.43 The weight loss above 380 °C is due to the decomposition of the organic ligand. The thermal stability of 1D carboxylate-bridged vanadyl systems is rarely discussed in the literature. The only exception is the vanadyl benzoate chain which is stable up to 300 °C.34
O). The bands centered at 521 cm−1 and 597 cm−1 are due to ν(V–O).34 Similarly, the two distinct bands at 3443 and 3300 cm−1, assigned to ν(O–H), are in agreement with the presence of both coordinated and non-coordinated water molecules. The characteristic bands of the ligand are observed in the low−frequency range of 1600–600 cm−1. The νasym(COO−) is located at 1612 cm−1 and νsym(COO−) at 1388 cm−1, leading to a difference of 224 cm−1.34 This indicates a monodentate coordination of the carboxylate group in agreement with the XRD structure described below. The UV-Vis spectrum shows d1 configuration features, corresponding to a distorted octahedral geometry. Thermogravimetric analysis showed that the compound is stable up to 125 °C. A weight loss of 18.3% is observed between 125 °C and 300 °C (see Fig. S3† for details). This corresponds to the removal of both coordinated and non-coordinated water molecules (calc. 18.1%). The weight loss of 6.6% observed between 200 °C and 300 °C is typical for vanadyl compounds containing water molecules coordinated at equatorial positions.43 The weight loss above 380 °C is due to the decomposition of the organic ligand. The thermal stability of 1D carboxylate-bridged vanadyl systems is rarely discussed in the literature. The only exception is the vanadyl benzoate chain which is stable up to 300 °C.34
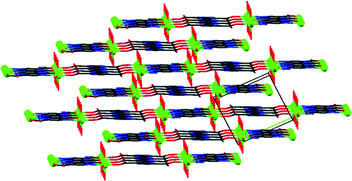
The X-ray structural analysis revealed that the brown-reddish compound crystallizes in the orthorhombic system, space group Pna21. Table 1 summarizes relevant bond distances and angles. Fig. 1 shows that {[VO(pzdc)(H2O)2] 2H2O}n is a chain of vanadyl ions linked by pyrazine-2,5-dicarboxylate. The ligand binds to V4+ in two distinct modes: bidentate by means of two carboxylate oxygens and tetradentate by means of two carboxylate oxygens and two nitrogen atoms from the pyrazine ring. The V⋯V separation is 7.068 Å through the tetradentate ligand and 11.097 Å through the bidentate ligand. The length of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond (V1–O2 = 1.598(2) Å) is on the lower side compared to the reported values for vanadyl compounds.24,44 This value and the relatively high V
O bond (V1–O2 = 1.598(2) Å) is on the lower side compared to the reported values for vanadyl compounds.24,44 This value and the relatively high V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequency (976 cm−1) indicates a strong V
O stretching frequency (976 cm−1) indicates a strong V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. The coordination geometry of the vanadium is distorted octahedral. This is indicated by the displacement of the vanadium atom from the equatorial plain (O3, N1, O6, O1) towards the oxido group (ΔD = 0.282 Å) and the elongation of the bond trans to the oxido group (ΔL = 0.158 Å). These values are comparable to the usual values found for vanadyl complexes of carboxylate ligands.43,45 The crystallographic data are included in the ESI.†
O bond. The coordination geometry of the vanadium is distorted octahedral. This is indicated by the displacement of the vanadium atom from the equatorial plain (O3, N1, O6, O1) towards the oxido group (ΔD = 0.282 Å) and the elongation of the bond trans to the oxido group (ΔL = 0.158 Å). These values are comparable to the usual values found for vanadyl complexes of carboxylate ligands.43,45 The crystallographic data are included in the ESI.†
 | ||
| Fig. 1 The 1D chain of {[VO(pzdc)(H2O)2]·H2O}n. Hydrogen atoms and lattice water molecules were omitted for clarity. | ||
| V1–O1 (water) | 2.0413(18) | O1–V1–O2 | 95.55(9) |
| V1–O2 (oxido) | 1.598(2) | O1–V1–O3 | 165.69(9) |
| V1–O3 (water) | 2.0411(19) | O1–V1–O4 | 82.03(8) |
| V1–O4 (axial carboxylate) | 2.1299(18) | O1–V1–O6 | 88.67(8) |
| V1–O6 (equat carboxylate) | 1.9716(17) | O1–V1–N1 | 89.54(7) |
| V1–N1 (pyrazine) | 2.1580(17) | O2–V1–O3 | 98.59(9) |
| O2–V1–O4 | 165.47(7) | ||
| O2–V1–O6 | 106.13(8) | ||
| O2–V1–N1 | 91.18(9) | ||
| O3–V1–O4 | 83.73(8) | ||
| O3–V1–O6 | 89.51(8) | ||
| O3–V1–N1 | 87.98(7) | ||
| O4–V1–O6 | 88.18(7) | ||
| O4–V1–N1 | 74.52(8) |
Several reports7,46,47 showed that octahedral vanadyl complexes containing both N- and O-donor ligands often prefer the N-donor in trans position with respect to the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. However, this new compound is different, as the carboxylate oxygen is bound at the axial position. The binding of the N-donor at the equatorial position can be explained by considering the π(aromatic) character of the nitrogen donor atom and the perpendicular orientation of the pyrazine ring with respect to the V
O bond. However, this new compound is different, as the carboxylate oxygen is bound at the axial position. The binding of the N-donor at the equatorial position can be explained by considering the π(aromatic) character of the nitrogen donor atom and the perpendicular orientation of the pyrazine ring with respect to the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. In this orientation, the donating nitrogen p orbital can only interact with the best π donor orbitals on vanadium, e.g. dxz and dyz.
O bond. In this orientation, the donating nitrogen p orbital can only interact with the best π donor orbitals on vanadium, e.g. dxz and dyz.
The molecular structure is stabilized by an intricate network of hydrogen bonds (see details in Table S2 in ESI†). The oxido group (O2), the coordinated (O1 and O3) and non-coordinated water (O8) molecules, coordinated (O4) and non-coordinated (O7) carboxylate oxygens as well as the non-coordinated pyrazine nitrogen (N2) are involved in hydrogen bonding. The non-coordinated water molecule is bound to four different chains. The oxido group is hydrogen bonded to the coordinated water molecule of a neighbouring chain (Fig. 2).
A brief evaluation of the coordination features of the vanadium ion is realized analyzing, qualitatively, the single occupied molecular orbital (SOMO) resulting from restricted Density Functional Theory (DFT) calculations. The shape is roughly the same, irrespective of the functional definition (e.g. BP86 vs. B3LYP).48 This function offers the non-trivial information about the balance of coordination effects.
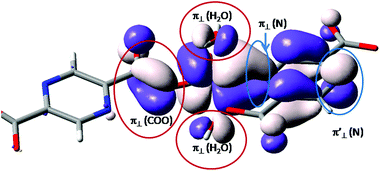
In the molecular orbital (MO) theory of ligand field effects, the donation is seen as yielding antibonding components. The predominant d-type atomic components point to lobes of the ligands having the opposite sign of the wave function. This pattern is observed (see Fig. 3) for the oxygen coordinating atoms, labeled as π⊥ (H2O) and π⊥ (COO) for the aqua and carboxylate ligands. The subscript ⊥ suggests that the π-type orbitals are perpendicular to the molecular plane of the ligand. These components fall in an antibonding relationship with the d-type atomic orbital component of the central ion. In contrast, the nitrogen component, belonging to the pyrazine moiety, follows a bonding-type overlap. The lobes of d(π) and π(N) components have the same sign, being therefore coalesced in a common surface which determines the elongated aspect of the d-function in the direction of pyrazine ligand. This suggests a back-donation feature of the pyrazine moiety. The corresponding nitrogen function is also seen at the other end of the ligand, labeled π′⊥ (N). At this margin, in the idealized model, the metal ion is removed and the p(π) orbital of the nitrogen in the aromatic system is freely visible. If we conventionally take the z axis along the [V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+ unit, then the d-type component can be assigned as a xy function. In the given SOMO axial ligands, namely the oxygen from the vanadyl group and the opposite carboxyl group do not have contributions since this would demand a δ type overlap, which is chemically unavailable. The oxygen ligand is not visible in Fig. 3, but the axial carboxyl can be observed as “clean” from orbital contributions.
O]2+ unit, then the d-type component can be assigned as a xy function. In the given SOMO axial ligands, namely the oxygen from the vanadyl group and the opposite carboxyl group do not have contributions since this would demand a δ type overlap, which is chemically unavailable. The oxygen ligand is not visible in Fig. 3, but the axial carboxyl can be observed as “clean” from orbital contributions.
The Natural Bond Orbital (NBO)49 provides, among other valuable data, the Wiberg bond index.50 This is found to be equal to 2.13 for the vanadyl moiety and confirms the formal double bond inside this unit. The other coordination contacts show subunitary values, indicating the partial covalent nature of the regular coordination. Thus, the Wiberg index for the coordination contact between vanadium and the oxygen atoms of the aqua ligands is about 0.36. The oxygen from carboxylate trans to the vanadyl group has a Wiberg index of 0.38, while the one in trans to the nitrogen is 0.57. The nitrogen shows a 0.45 value. If we assimilate the bond index with the strength of coordination, the vanadyl oxygen is a very strong donor, while the aqua groups are the weakest ligands. One carboxyl shows a surprising coordination strength (sustained also by the shorter bond observed in XRD) while another one is relatively weak. We interpret this as a sort of trans effect, a kind of push–pull effect on the O–V–N trans axis. It is driven by the alleged acceptor effect of the aromatic nitrogen, that strengthens the donor action of the opposite oxygen atom. The bond order of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit is due to relatively high d components in orbitals belonging to the doubly occupied MOs, carrying σ and π in-phase d–p overlap. The electron population arrived at by this effect on the vanadium atom, formally an excess with respect to the d1 nominal configuration of V4+, is partly passed by back donation action towards the nitrogen group.
O unit is due to relatively high d components in orbitals belonging to the doubly occupied MOs, carrying σ and π in-phase d–p overlap. The electron population arrived at by this effect on the vanadium atom, formally an excess with respect to the d1 nominal configuration of V4+, is partly passed by back donation action towards the nitrogen group.
Other information can be drawn from the population analysis, under the provision that this is prone to certain conventions. Thus, the Mulliken analysis (which has the drawback of sharing equally the overlap population between atoms with different electronegativities) provides an atomic charge of about +1.4, sensibly lower than the formal V4+ oxidation state. It is due to a population of about 3.4 electrons on the d shell of vanadium. An interesting alternate view is provided by the Hirshfeld population analysis.51 This is based on a reference consisting of conventional partition of the molecule on fragments. These are computed as a preamble to the molecular calculation, in a manner in which their overlapping is first not allowed. Then, after the full calculation, the density found at a given point is shared between fragments proportionally to their contribution resulting in a non-interacting regime at the same coordinate. Thus, if for the vanadyl part the V(4+) and O(2−) fragments are taken, the Hirshfeld analysis yields a 2.93 charge on vanadium and −1.33 on oxygen, somewhat close to the formal oxidation states. Taking the [VO]2+ as a preamble fragment, its post-computational charge is about +1.5.
A further analysis is realized by the TD-DFT (time dependent DFT) calculations.52 This is a facile procedure that provides spectral information. The calculation is based on unrestricted DFT calculations, since the restricted formalism does not work properly in combination with the TD approach. The TD-DFT does not account for all excited states, being confined to one-particle promotion effects. The charge transfer processes are well accounted and also particular cases of d–d transitions, such as the formal d1 systems, where we deal with one-electron transitions, are well suited. The calculation provides the position and intensity of the transitions that can be further assimilated with the respective peaks and surfaces of Gaussian profiles.
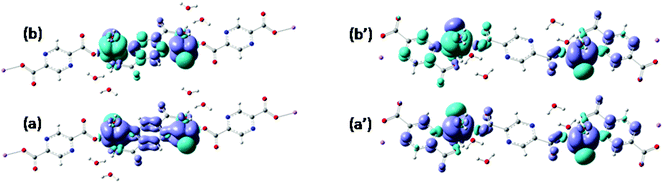
Assuming Gaussian profiles with arbitrary bandwidths and the surface equal to the computed intensity, a qualitative account of the spectrum is realized (see Fig. 4). The spectrum simulated as a superposition of broad Gaussian signals is similar to the experimental profile (except an overall blue-shift of about 100 nm) for the four visually distinct convoluted bands. The simulation with narrow components illustrates the multitude of transitions engulfed in the observed bands. The main contributors to the lowest band (with a peak at about 800 nm in experimental data and at 700 in the simulated global profile) are analyzed with the help of density difference maps shown in Fig. 5. Thus, by mapping the total density of the system in a given i-th excited state, ρi, and denoting by ρ0 the ground state distribution, the difference ρi − ρi0, gives information about the density flow in the given TD-DFT transition. Fig. 5 shows a charge transfer from the carboxylate donor group towards the two π* components of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit. The carboxylate charge depletion is almost identical in the two cases. The π* components look like the (a)≅π*(y) and (b)≅π*(x) components made by the respective V(yz)–O(py) and V(xz)–O(px) antibonding components (as the orbital sign is not visible, the lobes of the assigned V
O unit. The carboxylate charge depletion is almost identical in the two cases. The π* components look like the (a)≅π*(y) and (b)≅π*(x) components made by the respective V(yz)–O(py) and V(xz)–O(px) antibonding components (as the orbital sign is not visible, the lobes of the assigned V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety have the same color). Clearly, one distinguishes the four-lobe pattern of the d component from vanadium and the two-lobe p type one from the oxygen.
O moiety have the same color). Clearly, one distinguishes the four-lobe pattern of the d component from vanadium and the two-lobe p type one from the oxygen.
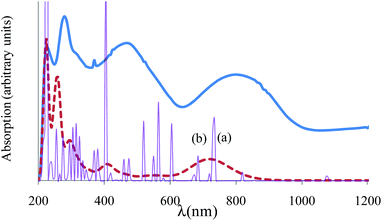 | ||
| Fig. 4 Experimental vs. computed absorption spectrum of {[VO(pzdc)(H2O)2] 2H2O}2n. The experimental is given in a thick continuous line. The computed TD-DFT spectrum, simulated with a common bandwidth of 1000 cm−1 for each transition is shown by a dashed line, incorporating the convolution of all the transition components. The thin line with sharp peaks corresponds to the TD-DFT spectrum taken with 50 cm−1 bandwidths, underlining the position and intensities of individual transitions. The peaks labelled (a) and (b) correspond to the labelling from Fig. 5 analysed as charge transfer flow. | ||
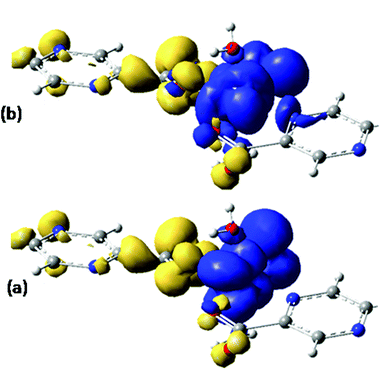 | ||
| Fig. 5 Difference density maps (excited state minus ground state) for the first two intense transitions (see Fig. 4) centered around 700 nm. The dark (blue) colored areas correspond to accumulation of density while the light (yellow) ones to depletion areas. The transition can be conceived as charge displacement from light to dark colored zones, i.e. as ligand-to-metal charge transfer (LMCT) between carboxylate and VO2+ groups. | ||
The d–d transitions are intermixed with other charge transition processes, with the less intense transitions located between 400 and 600 nm in the simulated spectrum. Probably, these form the right side slope of the band centered at 500 nm in the experimental profile.
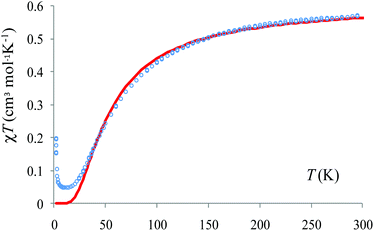
These calculations also offer useful hints with respect to the magnetic property analysis. The temperature-dependent magnetic susceptibility measurements are given in Fig. S4.† The Broken-Symmetry (BS) approach, in conjunction with unrestricted DFT calculations is a convenient approach, particularly in the case of dimers. The DFT is basically a single-determinant method and cannot be used to account literally for the spin coupled states. In general, these are multi-determinant combinations, resulting from the spin-flip algebra. However, the BS route offers information about the coupling constants. The BS configuration, obtained by reverting the spin density at one site of a dimer, is not a real state, but it is a numerical experiment that provides the coupling constant. The high spin (HS) state, triplet in our case, admits a good representation in the DFT frame since it has a single determinant nature (the sole configuration with spin up in the non-degenerate orbital scheme).
The chain contains two types of bridges: one having a shorter V⋯V distance and a long range interaction mediated by the nitrogen and carboxylate coordination functions; the other with more distant V⋯V interactions and bridging made only by the carboxylate moieties of the given ligand. These two types of interactions were mimicked taking two dimers with the appropriate bridging mode. The BS-DFT calculations are performed collecting the converged total bonding energies, E, and the 〈S2〉 expectation values from the output of the calculations on the HS and BS states. Taking the spin Hamiltonian of the dimer in the following form:
| Ĥ = −2JŜ1Ŝ2 | (1) |
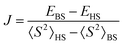 | (2) |
For a dimer made of two 1/2 spins, the 〈S2〉HS quantity is almost 2, close to the nominal S(S + 1) value with S = 1. Note that deviations may be due to the fact that unrestricted DFT does not provide rigorous eigenvalues of the spin module. In the case of BS, the state must have 〈S2〉BS ≈ 1, not zero, as for S = 0. The closeness of 〈S2〉 to the respective 2 and 1 values is a certification that the calculations are correct (Fig. 6).
Using the B3LYP functional,40,55 as implemented in ADF, we obtain for the first dimer, with shorter inter-center distance, a value of J = −46.3 cm−1. The other bridge has a much smaller absolute value J = −0.18 cm−1. However, the absolute magnitudes depend strongly on the choice of the functional. For instance, the BP86 or LDA functionals yield larger antiferromagnetic coupling for the first type of dimer, but also retrieve the sensibly smaller strength of the second one. Therefore, the mutual comparison of the two units can be taken as qualitatively valid information. At the same time, the weaker interaction along the second type of bridge can be intuitively accepted. The picture of SOMO from Fig. 3 offers a hint: From the side of the ligand that leads to a carboxylate-only bridge, the ligand does not show components from the body of pyrazine skeleton. This suggests that the communication of the d-type spins is not mediated via the bridge orbitals. In turn, the nitrogen coordinated side shows a contribution of the whole pyrazine moiety. A reasonable super-exchange way is available. The same information is obtained from the spin density maps in Fig. 6. The first dimer has contributions of the bridging ligand, while the second one suggests an interrupted spin communication over the pyrazine bridge and consequently a smaller absolute coupling.
The calculations offer a useful hint: the slope between 50 and 150 K can be assigned to the predominant antiferromagnetic coupling along the tetradentate pyrazine dicarboxylate bridge. There is a very weak antiferromagnetic coupling for the other dimer, namely the bidentate pyrazine dicarboxylate bridge. However, DFT can overestimate the antiferromagnetism and, assuming the action of a certain error shift, the situation may be in fact a small ferromagnetism on the weakly coupled dimer, against a predominant strong antiferromagnetism on the other. Under this assumption (taking only the T > 10 K part of the χMT vs. T curve) we estimate that J = −33.2 cm−1, a value close to the B3LYP estimation. The weak antiferromagnetic coupling is also suggested by the Curie–Weiss fitting of the data above 100 K: χM = C/(T − θ) with C = 0.426 cm3 K mol−1 and θ = −26.3 K (Fig. 7).
Since B3LYP is a hybrid method, containing a pure DFT part mixed with a percent of Hartree–Fock (HF) exchange, we can tune the portion of this last contribution. The regular DFT contains a HF = 20% ratio. Enhancing this to HF = 30%, 40% and 50%, we respectively obtain the −27.86, −21.66, −20.93 values for the J coupling parameters. Accounting for numerical uncertainties from both computational and experimental evaluation (confined to a dimer model), we see the qualitative match in accounting the range of the coupling. The same applies for the relative comparison of the two types of bridging, namely strong antiferro via nitrogen contact and very weak, either ferro or antiferro, over the oxygen-only based bridging.
Conclusions
Reacting vanadyl sulphate and pyrazine-2,5-dicarboxylic acid under hydrothermal conditions gives a brown-reddish crystalline material, {[VO(pzdc)(H2O)2] H2O}n. This unexpected material is stabilized by a network of hydrogen bonds, and is stable up to 400 K. The chain has alternating bridging types, due to different ends of the ligand having respective different coupling constants, a dominant antiferromagnetic interaction and a weak one, with a possible ferromagnetic nature. DFT calculations allowed a semi-quantitative analysis of the properties and drawing the qualitative mechanisms. In this way, the coordination bonding regime was established, showing that the oxygen donors have donating properties while the aromatic amines show π-acceptor back bonding features.Acknowledgements
ALDR thanks the CAPES Foundation for a Senior Fellowship under the “Science without Borders” program. MF acknowledges support from PNII UEFISCDI PCCE 9/2010 and UB/2014 research grants. This work is part of the Research Priority Area Sustainable Chemistry of the UvA, http://suschem.uva.nl.Notes and references
- J. A. L. da Silva, J. J. R. Frausto da Silva and A. J. L. Pombeiro, Coord. Chem. Rev., 2013, 257, 2388–2400 CrossRef CAS.
- G. Licini, V. Conte, A. Coletti, M. Mba and C. Zonta, Coord. Chem. Rev., 2011, 255, 2345–2357 CrossRef CAS.
- A. G. J. Ligtenbarg, R. Hage and B. L. Feringa, Coord. Chem. Rev., 2003, 237, 89–101 CrossRef CAS.
- G. Rothenberg and J. H. Clark, Org. Process Res. Dev., 2000, 4, 270–274 CrossRef CAS.
- J. C. Volta, C. R. Acad. Sci., Ser. IIc: Chim., 2000, 3, 717–723 CrossRef CAS.
- V. Conte, A. Coletti, B. Floris, G. Licini and C. Zonta, Coord. Chem. Rev., 2011, 255, 2165–2177 CrossRef CAS.
- M. R. Maurya, A. Kumar, M. Ebel and D. Rehder, Inorg. Chem., 2006, 45, 5924–5937 CrossRef CAS PubMed.
- I. E. Wachs, Dalton Trans., 2013, 42, 11762–11769 RSC.
- A. L. Dantas Ramos, S. Tanase and G. Rothenberg, Quim. Nova, 2014, 37, 123–133 CrossRef.
- P. Van der Voort, K. Leus, Y.-Y. Liu, M. Vandichel, V. Van Speybroeck, M. Waroquier and S. Biswas, New J. Chem., 2014, 38, 1853–1867 RSC.
- K. Barthelet, J. Marrot, D. Riou and G. Ferey, Angew. Chem., Int. Ed., 2002, 41, 281–284 CrossRef CAS.
- H. Leclerc, T. Devic, S. Devautour-Vinot, P. Bazin, N. Audebrand, G. Ferey, M. Daturi, A. Vimont and G. Clet, J. Phys. Chem. C, 2011, 115, 19828–19840 CAS.
- K. Barthelet, K. Adil, F. Millange, C. Serre, D. Riou and G. Ferey, J. Mater. Chem., 2003, 13, 2208–2212 RSC.
- K. Barthelet, J. Marrot, G. Ferey and D. Riou, Chem. Commun., 2004, 520–521 RSC.
- K. Barthelet, D. Riou and G. Ferey, Chem. Commun., 2002, 1492–1493 RSC.
- F. Carson, J. Su, A. E. Platero-Prats, W. Wan, Y. Yun, L. Samain and X. Zou, Cryst. Growth Des., 2013, 13, 5036–5044 CAS.
- A. Lieb, H. Leclerc, T. Devic, C. Serre, I. Margiolaki, F. Mahjoubi, J. S. Lee, A. Vimont, M. Daturi and J.-S. Chang, Microporous Mesoporous Mater., 2012, 157, 18–23 CrossRef CAS.
- K. Barthelet, D. Riou, M. Nogues and G. Ferey, Inorg. Chem., 2003, 42, 1739–1743 CrossRef CAS PubMed.
- A. Phan, A. U. Czaja, F. Gandara, C. B. Knobler and O. M. Yaghi, Inorg. Chem., 2011, 50, 7388–7390 CrossRef CAS PubMed.
- Y.-Y. Liu, S. Couck, M. Vandichel, M. Grzywa, K. Leus, S. Biswas, D. Vollmer, J. Gascon, F. Kapteijn, J. F. M. Denayer, M. Waroquier, V. Van Speybroeck and P. Van der Voort, Inorg. Chem., 2013, 52, 113–120 CrossRef CAS PubMed.
- Y.-Y. Liu, K. Leus, M. Grzywa, D. Weinberger, K. Strubbe, H. Vrielinck, R. Van Deun, D. Volkmer, V. Van Speybroeck and P. Van der Voort, Eur. J. Inorg. Chem., 2012, 2819–2827 CrossRef CAS.
- A. Centrone, T. Harada, S. Speakman and T. A. Hatton, Small, 2010, 6, 1598–1602 CrossRef CAS PubMed.
- R. Plessius, R. Kromhout, A. L. Dantas Ramos, M. Ferbinteanu, M. C. Mittelmeijer-Hazeleger, R. Krishna, G. Rothenberg and S. Tanase, Chem. – Eur. J., 2014, 20, 7922–7925 CrossRef CAS PubMed.
- S. Tanase, M. C. Mittelmeijer-Hazeleger, G. Rothenberg, C. Mathoniere, V. Jubera, J. M. M. Smits and R. de Gelder, J. Mater. Chem., 2011, 21, 15544–15551 RSC.
- S. Tanase, F. Prins, J. M. M. Smits and R. de Gelder, CrystEngComm, 2006, 8, 863–865 RSC.
- M.-J. Cheng, R. J. Nielsen, J. Tahir-Kheli and W. A. Goddard III, Phys. Chem. Chem. Phys., 2011, 13, 9831–9838 RSC.
- R. C. Haushalter, Q. Chen, T. V. Soghomonian, J. Zubieta and C. J. Oconnor, J. Solid State Chem., 1994, 108, 128–133 CrossRef CAS.
- S. Petit, S. A. Borshch and V. Robert, J. Am. Chem. Soc., 2002, 124, 1744–1749 CrossRef CAS.
- R. E. Sykora, K. M. Ok, P. S. Halasyamani, D. M. Wells and T. E. Albrecht-Schmitt, Chem. Mater., 2002, 14, 2741–2749 CrossRef CAS.
- S. L. Wang and W. J. Tsai, J. Solid State Chem., 1996, 122, 36–40 CrossRef CAS.
- T. R. Gilson, I. M. Thompostlethwaite and M. Webster, J. Chem. Soc., Dalton Trans., 1986, 895–897 RSC.
- H.-J. Koo and M.-H. Whangbo, Solid State Sci., 2010, 12, 685–690 CrossRef CAS.
- C. Weeks, Y. N. Song, M. Suzuki, N. A. Chernova, P. Y. Zavalij and M. S. Whittingham, J. Mater. Chem., 2003, 13, 1420–1423 RSC.
- I. Djerdj, M. Cao, X. Rocquefelte, R. Cerny, Z. Jaglicic, D. Arcon, A. Potocnik, F. Gozzo and M. Niederberger, Chem. Mater., 2009, 21, 3356–3369 CrossRef CAS.
- T. Tachikawa, J. R. Choi, M. Fujitsuka and T. Majima, J. Phys. Chem. C, 2008, 112, 14090–14101 CAS.
- ADF2008.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available from: http://www.scm.com Search PubMed.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- S. J. A. van Gisbergen, C. F. Guerra and E. J. Baerends, Abstr. Papers Am. Chem. Soc., 2001, 221, U401–U401 Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 34, 7406–7406 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822–8824 CrossRef.
- S. Cevik, B. Sasmaz, M. Poyraz, M. Sari and O. Buyukgungor, J. Chem. Crystallogr., 2011, 41, 796–800 CrossRef CAS.
- T. Mukherjee, J. C. Pessoa, A. Kumar and A. R. Sarkar, Inorg. Chem., 2011, 50, 4349–4361 CrossRef CAS PubMed.
- T. S. Smith, C. A. Root, J. W. Kampf, P. G. Rasmussen and V. L. Pecoraro, J. Am. Chem. Soc., 2000, 122, 767–775 CrossRef CAS.
- S. S. Amin, K. Cryer, B. Y. Zhang, S. K. Dutta, S. S. Eaton, O. P. Anderson, S. M. Miller, B. A. Reul, S. M. Brichard and D. C. Crans, Inorg. Chem., 2000, 39, 406–416 CrossRef CAS.
- C. Yuan, L. Lu, X. Gao, Y. Wu, M. Guo, Y. Li, X. Fu and M. Zhu, J. Biol. Inorg. Chem., 2009, 14, 841–851 CrossRef CAS PubMed.
- M. J. Louwerse and G. Rothenberg, Phys. Rev. B: Condens. Matter, 2012, 85 Search PubMed.
- F. Weinhold and C. Landis, Valency and Bonding. A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, Cambridge, 2005 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- H. Nagao, M. Nishino, Y. Shigeta, T. Soda, Y. Kitagawa, T. Onishi, Y. Yoshioka and K. Yamaguchi, Coord. Chem. Rev., 2000, 198, 265–295 CrossRef CAS.
- T. Onishi, Y. Takano, Y. Kitagawa, T. Kawakami, Y. Yoshioka and K. Yamaguchi, Polyhedron, 2001, 20, 1177–1184 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: IR, UV-Vis, TGA, temperature-dependent magnetic susceptibility and crystallographic data. CCDC 943141. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt01628b |
| This journal is © The Royal Society of Chemistry 2015 |