Open Access Article
Open Access ArticleAmbivalent binding between a radical-based pincer ligand and iron†
Katie L. M.
Harriman
ab,
Alicea A.
Leitch
ab,
Sebastian A.
Stoian
c,
Fatemah
Habib
ab,
Jared L.
Kneebone
d,
Serge I.
Gorelsky
ab,
Ilia
Korobkov
ab,
Serge
Desgreniers
e,
Michael L.
Neidig
d,
Stephen
Hill
cf,
Muralee
Murugesu
*ab and
Jaclyn L.
Brusso
*ab
aDepartment of Chemistry, University of Ottawa, Ottawa, Ontario K1N 6N5, Canada. E-mail: jbrusso@uottawa.ca; m.murugesu@uottawa.ca
bCentre for Catalysis Research and Innovation, University of Ottawa, Ottawa, Ontario K1N 6N5, Canada
cNational High Magnetic Field Laboratory, Florida State University, Tallahassee, Florida 32310, USA
dDepartment of Chemistry, University of Rochester, Rochester, New York 14627, USA
eDepartment of Physics, University of Ottawa, Ottawa, Onatrio K1N 6N5, Canada
fDepartment of Physics, Florida State University, Tallahassee, Florida 32306, USA
First published on 7th May 2015
Abstract
A complex exhibiting valence delocalization was prepared from 3,5-bis(2-pyridyl)-1,2,4,6-thiatriazinyl (Py2TTA˙), an inherently redox active pincer-type ligand, coordinated to iron (Fe(Py2TTA)Cl2 (1)). Complex 1 can be prepared via two routes, either from the reaction of the neutral radical with FeCl2 or by treatment of the anionic ligand (Py2TTA−) with FeCl3, demonstrating its unique redox behaviour. Electrochemical studies, solution absorption and solid-state diffuse reflectance measurements along with X-ray crystallography were carried out to elucidate the molecular and solid-state properties. Temperature- and field-dependent Mössbauer spectroscopy coupled with magnetic measurements revealed that 1 exhibits an isolated S = 5/2 ground spin state for which the low-temperature magnetic behaviour is dominated by exchange interactions between neighbouring molecules. This ground state is rationalized on the basis of DFT calculations that predict the presence of strong electronic interactions between the redox active ligand and metal. This interaction leads to the delocalization of β electron density over the two redox active centres and highlights the difficulty in assigning formal charges to 1.
Introduction
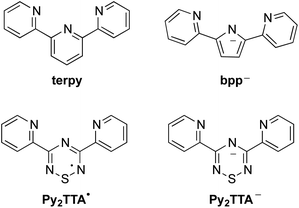
Ligand design and coordination chemistry go hand in hand. While many ligand architectures have been developed, examples of tunable, multidentate, open-shell systems are much more rare. The preparation and implementation of such ligands has significant potential in a diverse range of applications, from functional materials to catalysis.1–12 To date, one of the most widely studied ligand systems is 2,2′;6′,2′′-terpyridine (terpy, Chart 1), whose tridentate chelating environment allows for coordination to a variety of metal ions with a wide range of geometries, many of which have found application in, for example, catalysis, gas adsorption, magnetic materials, organic electronics, biomedical applications, etc.13–15 While terpy is known to be a redox active ligand, stabilizing the anionic terpy radical by itself is not possible and requires metal coordination to be isolated.16–18 Thus, the development of an inherently redox active non-innocent terpy analogue, in which the coordination environment is maintained, is an attractive design strategy as it is expected to enable a tunable pincer ligand system where the various oxidation states can be achieved prior to coordination. Such ligand design is appealing for a variety of applications from catalyst design and development to molecular magnets and switches, while affording properties not available to simple terpy based complexes.1,3,5,11,19 For example, replacing the central pyridine ring with a redox active neutral radical facilitates the development of mixed-valence compounds, a topic central to the search for highly conducting materials.20–22 In that regard, a number of research groups have focused on developing terpy analogues in order to enhance its redox properties. The general approach has been to replace the peripheral pyridine rings with nitrogen rich functional groups, or to attach radical pendant groups to the central pyridine ring at the 2, 4 and/or 6 positions.23–27 Although this has afforded ligands that offer improved redox activity compared to terpy, their application remains limited due to reduction potentials, solubility and stability of the isolated metal complexes. Alternatively, an inherently redox active structural mimic of terpy may be achieved by exchanging the three carbon atoms within the central pyridyl ring with the N–S–N fragment leading to 3,5-bis(2-pyridyl)-1,2,4,6-thiatriazinyl (Py2TTA˙), a neutral seven π-electron ring system flanked by two pyridyl groups.28 Not only does this ligand design maintain the topology of terpy, but it also affords ambiguity in regards to oxidation states as both the anionic and neutral states are isolatable.29 In other words, Py2TTA enables coordination of the neutral radical (Py2TTA˙) in a manner comparable to terpy, as well as the anionic form (Py2TTA−), which is similar to the monoanionic 2,5-bis(2-pyridyl)pyrrolide (bpp) ligand. While bpp has been recognized as an anionic analogue of terpy, this ligand system is relatively underdeveloped compared to the ubiquitous application of terpy ligands in coordination chemistry.30–34 This may be attributed to the slight differences between the binding pockets of terpy vs.bpp, which can lead to alternative coordination environments (e.g., twisted bridging mode affording multi-nuclear metal complexes, head-to-head coordination dimer) in addition to the expected chelating tridentate binding mode.30In the case of Py2TTA, since both the neutral and anionic states are isolatable without coordination, this enables one to probe the reactivity and redox properties of the ligand through treatment with redox active metals. It is anticipated that having two redox active moieties in close proximity would enable electron transfer, which may result in strong electronic interaction between the redox active sites such that delocalization can occur. In such systems it is expected that assigning conventional oxidation states to the metal ion would be difficult due to the electron delocalization. Intermediate oxidation states and unusual physical properties are therefore anticipated due to the redox relationship. As exemplified in Fig. 1, a redox active ligand coordinated to high-spin Fe could achieve an S = 5/2 ground state through either FeII–L0, where L0 is a neutral radical, or FeIII–L−1, with a closed-shell anionic description of the ligand. In such situations, the beta electron can transfer between the ligand and the metal thus resulting in a complex S = 5/2 system.
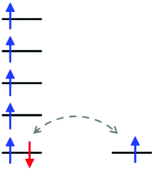 | ||
| Fig. 1 Schematic representation of the ambivalent nature of the single d-orbital based β-electron (highlighted in red) for a high spin iron complex resulting in an S = 5/2 ground spin state. | ||
Intrigued by the potential of Py2TTA˙ to exhibit strong electronic interactions with redox active first row transition metals (namely iron), we have begun to explore its coordination chemistry. To that end, we herein present the synthesis, electronic and solid-state properties of Py2TTA˙, a pincer-type tridentate ligand, and its coordination complex with iron (Fe(Py2TTA)Cl2 (1)). Based on these studies, not only does coordination to iron stabilize Py2TTA˙ with respect to dimerization, but strong delocalized electronic interactions are also exhibited between the non-innocent redox active ligand and the iron centre. As such, 1 can be classified as an S = 5/2 system in which unambiguous assignment of the formal oxidation states between the ligand and metal is difficult. The uniqueness of 1 is exemplified further by its preparation via treatment of FeII with the neutral radical Py2TTA˙ as well as through the reaction between FeIII and Py2TTAH.
Results and discussion
Synthesis
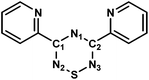
Although Py2TTA˙ can be prepared in situ via oxidation of Py2TTAH with half an equivalent of iodine in the presence of base (e.g., 4-dimethylaminopyridine (DMAP)),28 isolating the radical in the solid state following this route proved to be problematic leading to intractable mixtures. This challenge was overcome by changing the oxidant to N-chlorosuccinimide (NCS), affording Py2TTA˙ as a microcrystalline copper coloured solid (Scheme 1).29 Purification can be accomplished by sublimation under vacuum or recrystallization in hot acetonitrile (MeCN). Based on single crystal X-ray analysis, Py2TTA˙ self-associates in the solid state to form a sulphur–sulphur bridged co-facial dimer.29 Such structural features have also been reported for other TTA derivatives.35,36 Although dimerization occurs, stabilization of the radical may be accomplished through metal coordination, as has been shown to work with other radical based ligand systems.37,38 The coordinating ability of Py2TTA˙ with redox active metal centres was, therefore, investigated. To that end, a solution of FeCl2 in degassed MeCN was layered over a solution of Py2TTA˙ in degassed chloroform (CHCl3) under an inert environment. After three days, Fe(Py2TTA)Cl2 (1) crystallized out of solution as dark green-brown blocks suitable for X-ray analysis. Alternatively, 1 can be generated using much less stringent conditions, simply by layering a solution of Py2TTAH in N,N-dimethylformamide (DMF) under a solution of FeCl3 in methanol at RT in air. After three days, 1 crystallized out as dark green-brown blocks suitable for single crystal X-ray analysis. At first, this was surprising due to the redox chemistry that must be taking place as the same product, Fe(Py2TTA)Cl2, is formed from treatment of FeII with the neutral radical Py2TTA˙ as well as the reaction between FeIII and Py2TTAH. If the oxidation state of iron in the final product is +3, this would require reduction of the radical ligand by FeII in the first reaction. If, however, the product is a FeII complex, FeIII must oxidize Py2TTA−. Nonetheless, regardless of the oxidation states in Fe(Py2TTA)Cl2, it is apparent that formation of complex 1 proceeds through a unique redox reaction. Moreover, this procedure establishes a much more simple and robust route to generate coordination complexes with the neutral radical Py2TTA˙, which does not require generation of the radical prior to coordination or the use of air/moisture sensitive reactions.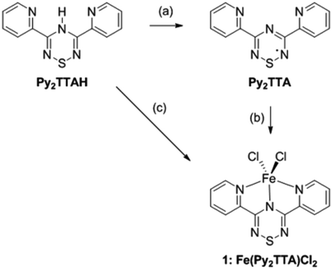 | ||
| Scheme 1 Synthesis of the radical ligand (Py2TTA˙) and Fe(Py2TTA)Cl2 (1). Reagents and conditions: (a) NCS, DMAP, MeCN, RT; (b) FeCl2, CHCl3/MeCN, RT; (c) FeCl3, DMF/MeOH, RT. | ||
Electrochemical studies
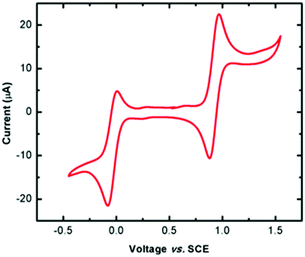
The redox behaviour of complex 1 was probed by cyclic voltammetry using a non-coordinating solvent (dichloromethane; DCM), revealing two quasi-reversible redox processes at 0.923 V and −0.037 V (vs. SCE, Fig. 2). Although electrochemical studies could not be carried out on the radical ligand due to its limited solubility and stability in solution, the more anodic peak is attributed to the Py2TTA 0/+1 process, as similar results have been reported for other thiatriazinyl (TTA) radicals studied under the same conditions (i.e., DCM, Bu4NPF6 electrolyte).39 The redox couple at −0.037 V, by contrast, is more anodically shifted than the −1/0 processes reported for TTA radicals, even those with strongly electron withdrawing substituents.39 This redox couple is therefore attributed to the FeII/FeIII process, which is consistent with similar iron complexes, even though the potential for this couple can vary widely depending on the ligand system. Furthermore, rigorously degased solvents (i.e., freeze–pump–thaw) are necessary due to the potential for oxidation of the TTA ligand in solution. This results in an additional peak at 0.272 V resulting from the formation of Fe(Py2TTAO)Cl2 (see ESI Fig. S1 and S2†).UV-vis spectroscopy
To elucidate the electronic structure of complex 1, solution absorption and solid state diffuse reflectance spectroscopic studies were carried out in the range of 200–1200 nm. Since spectroscopic studies could not be carried out on the radical ligand due to its limited solubility and stability towards oxidation, Py2TTAH was investigated for comparative purposes. Molar absorptivity values are provided in the ESI Fig. S3 and Table S1.† These studies, presented in Fig. 3, demonstrate complex 1 absorbs in the high energy region (235 and 272 nm), which may be attributed to ligand based transitions (cf. 235 nm and 261 nm for Py2TTAH). As well, a series of less intense bands in the visible region (e.g., 300–400 nm) characteristic of metal centred d–d transitions are observed. The absorption profile for compound 1 also reveals broad and relatively intense low energy transitions observed at 500–1100 nm. Since near-IR bands are often observed in coordination complexes of paramagnetic ligands,40 this suggests Py2TTA may be open-shell (i.e., a neutral radical) thus requiring the metal centre to be FeII. The diffuse reflectance measurements are in good agreement with the solution based absorption profiles. In addition to broadening of the peaks, the solid-state measurements were associated with a red-shift. Notably, the near-IR band in the solid-state revealed a narrowing of the peak window in comparison to the solution measurements, presumably due to crystal packing effects.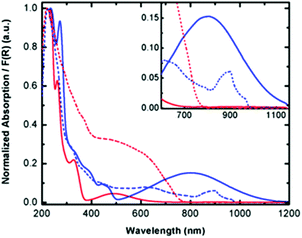 | ||
| Fig. 3 Solution absorption (solid lines) and solid-state diffuse reflectance (dashed lines) spectra for Py2TTAH (red) and Fe(Py2TTA)Cl2 (blue). | ||
Structural studies of Fe(Py2TTA)Cl2 (1)
Complex 1 crystallizes in the orthorhombic space group Pnma; two views of the asymmetric unit with atom labelling are shown in Fig. 4.‡ In 1, the metal centre adopts a five coordinate coordination arrangement with the metal centre residing within the plane of the tridentate Py2TTA ligand. The remaining metal coordination environment is filled by two Cl anions above and below the molecular framework. Thus the molecule adopts an overall C2v symmetry. Interestingly, in the Py2TTA dimer, the pyridyl substituents exhibit a slight propeller-like distortion with respect to the central TTA ring, whereas when coordinated to iron they become co-planar. This may be attributed to the influence of the iron centre on the ligand or, perhaps more likely, is a result of the crystallographic space group and the consequence of the molecule being situated on a mirror plane. Nonetheless, Py2TTA acts a pincer-type tridentate ligand leading to a coordination geometry that may be described as an intermediate between bipyramidal and square base pyramid. This coordination environment is similar to that reported for other five coordinate dichloride FeII and FeIII complexes with pincer ligands.41–43 Based on charge balance, there are two possible oxidation state assignments; FeIII coordinated to anionic Py2TTA−, or FeII coordinated to Py2TTA˙, a neutral radical ligand. Comparing the C–N bond lengths within the TTA fragment of 1 to that of Py2TTA and Py2TTAH (Table 1), it would appear the ligand is anti-aromatic indicative of anionic character. Similar trends have also been reported for other TTA derivatives with varying oxidation states.35 However, the planarity of the ligand, coupled with the absorption profile (vide supra) is suggestive of FeII coordinated to a neutral open shell Py2TTA˙ ligand. Thus based on the single crystal X-ray data, it is difficult to pinpoint whether complex 1 is FeII or FeIII. Considering the Fe–N bond lengths, the two corresponding to the pyridyl rings are essentially equivalent and are consistent with what is commonly observed for Fe–N bonds in terpy systems.18,44–46 The other, which represents the interaction between iron and the nitrogen on the TTA ring, is shorter than average, indicative of π-bonding interactions.16,17 This observation is supported by DFT calculations in which significant π-orbital overlap between the metal centre and the nitrogen atom of the TTA ring is present in the HOMO (vide infra). These findings are indicative of strong interactions between the redox active centres resulting in delocalization of electron density and difficulty in assigning formal charges.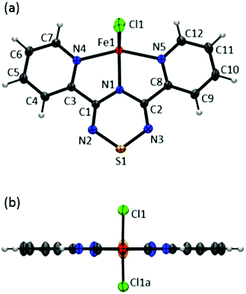 | ||
| Fig. 4 ORTEP drawings (50% thermal ellipsoids) of Fe(Py2TTA)Cl2 viewed from (a) above and (b) side of the molecular framework. | ||
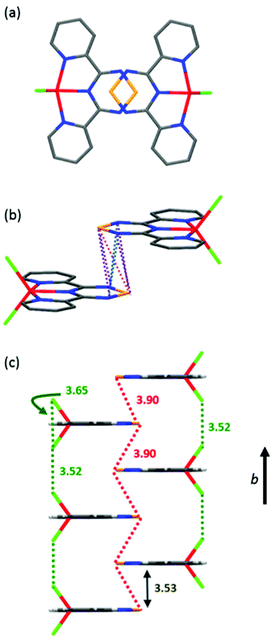
In the solid-state, complex 1 is highly ordered consisting of layers of discrete molecules interacting in a head-to-tail fashion along the a-axis, which alternate along the c-axis (Fig. 5, S4 and S5†). Looking along the b-axis, the TTA fragment of one Py2TTA ligand overlaps with another on the next layer such that a number of close intermolecular contacts exist (S1⋯S1′ = 3.90 Å; S1⋯N2′ = 3.90 Å; S1⋯N3′ = 3.86 Å; N2⋯N3′ = 3.61 Å), as highlighted in Fig. 5, S6 and S7.† Interestingly, the molecules of alternating layers along b are superimposed. This leads to interactions between the chloride ion of one molecule with another two layers away of 3.52 Å, which is in good agreement with the sum of the van der Waals radii.47 Thus, within the packing motif of complex 1, there are two dominant structural features, ligand–ligand and halogen–halogen.
Magnetic properties
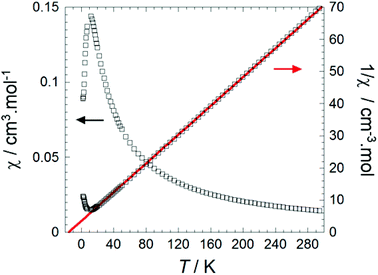
In order to probe the magnetic properties of 1, dc magnetic susceptibility was investigated under a 1000 Oe field in the temperature range 1.8–300 K, see Fig. 6 and S8.† At room temperature the χT value of 4.25 cm3 K mol−1 for Fe(Py2TTA)Cl2 is close to the expected value for an S = 5/2 species (4.376 cm3 K mol−1), consistent with an anionic ligand coordinated to a ferric ion (i.e., FeIIIL−1). However, the possibility of a strongly coupled metal ion to a radical ligand, as in the case of FeIIL0, cannot be ruled out as it would also lead to a S = 5/2 system given that ferromagnetic interactions would be effective at room temperature, as supported by spin density calculations (vide infra).The inverse susceptibility is linear from room temperature all the way down to well below 50 K, obeying a Curie–Weiss law, 1/χ = (T − θw)/C, with a negative Weiss constant θw = −14 K, indicating dominant intermolecular antiferromagnetic interactions. Meanwhile, the slope of the 1/χ vs. T plot gives a Curie constant of C = 4.43 cm3 K mol−1, again confirming the S = 5/2 molecular spin state. Deviations from a Curie–Weiss law below ∼12 K suggest the onset of long-range antiferromagnetic order, although this trend (sharp decrease in χ) could also be due to spin–orbit anisotropy (i.e., zero-field splitting). Nevertheless, the significant Weiss constant and low-temperature Mössbauer data (vide infra) seem to suggest appreciable molecular spin–spin correlations (i.e., ordering) below 15 K. Potential intermolecular exchange pathways are shown in Fig. 5 and can be rationalized on the basis of broken symmetry DFT calculations (vide infra).
Mössbauer spectroscopy
To investigate the electronic structure, field- and temperature-dependent 57Fe Mössbauer spectroscopic studies were carried out on 1. Inspection of Fig. 7 and S9–S11† shows that the zero-field Mössbauer spectra recorded for a finely ground sample of 1 above 15 K consist of quadrupole doublets characterized by an isomer shift δ = 0.41(1) mm s−1 and a quadrupole splitting ΔEQ = 1.04(4) mm s−1. Although, these values are rather typical of high-spin FeIII our DFT calculations for 1 (vide infra) not only reproduce well these values but also predict the presence of a large degree of spin- and valence-delocalization between the two redox sites of the molecule.48,49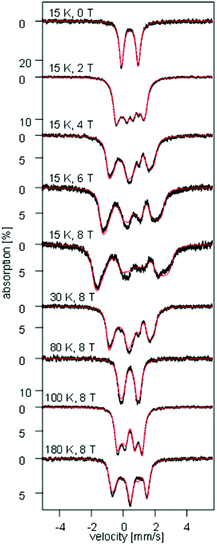 | ||
| Fig. 7 Field- and temperature-dependent Mössbauer spectra recorded for a ground solid sample of 1. The solid red lines overlaying the experimental data are simulations obtained using eqn (1a)–(c) and the parameters listed in Table 2. | ||
Analysis of the magnetic susceptibility data suggests the onset of a magnetically ordered phase below 15 K. This is corroborated by the hyperfine structure observed in the field-dependent 4.2 K Mössbauer spectra (see Fig. S10†). Inspection of Fig. S9† shows that increasing the temperature from 4.2 to 15 K leads to an increase in the relaxation rate of the electronic spin from slow to fast, when compared with the nuclear Larmor precession frequency, presumably concomitant with a transition from an ordered to a paramagnetic phase. Consequently, the field-dependent spectra recorded above 15 K can be approximated within the framework of a simple paramagnetic spin-Hamiltonian involving two antiferromagnetically coupled S = 5/2 entities, as described by eqn (1a)–(c).
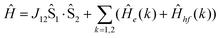 | (1a) |
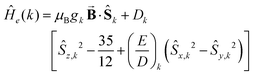 | (1b) |
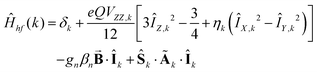 | (1c) |
The quantities in eqn (1a)–(c) have their usual meaning, 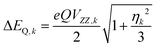 and
and 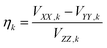 . For these spectra the magnitude of the observed magnetic hyperfine splitting is determined by an effective field that arises from the vector sum of the applied and internal fields,
. For these spectra the magnitude of the observed magnetic hyperfine splitting is determined by an effective field that arises from the vector sum of the applied and internal fields,  . The internal field is determined by the product of the thermally averaged spin expectation value with a hyperfine coupling constant,
. The internal field is determined by the product of the thermally averaged spin expectation value with a hyperfine coupling constant, 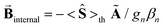 .50
.50
At high temperatures, a Curie-like behaviour (i.e., 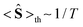 ) is expected. As such, the hyperfine splitting of the 8 T spectra in the 150–180 K range is dominated by the nuclear Zeeman and nuclear quadrupole interactions. Moreover, both the magnetic anisotropy (zero-field splitting, ZFS) of the local iron sites and the intermolecular exchange interactions have a negligible effect at these temperatures. Analysis of these spectra demonstrate that ΔEQ < 0 and the electric field gradient (EFG) asymmetry parameter is η = 0.5(3). At lower temperatures, knowledge of the EFG tensor enables quantification of the magnitude of the ZFS, the intermolecular coupling, J12, and the local hyperfine coupling tensor A. Simulations suggest that not only does the S = 5/2 ground state of 1 exhibit a relatively small ZFS, but they also indicate a hyperfine coupling tensor A with small anisotropy. These simulations clearly demonstrate that, above 15 K, the supramolecular exchange interactions between near-neighbour molecules are antiferromagnetic (see ESI†). Parameters obtained from the best simulations (red solid lines in Fig. 7) using eqn (1a)–(c) are listed in Table 2.
) is expected. As such, the hyperfine splitting of the 8 T spectra in the 150–180 K range is dominated by the nuclear Zeeman and nuclear quadrupole interactions. Moreover, both the magnetic anisotropy (zero-field splitting, ZFS) of the local iron sites and the intermolecular exchange interactions have a negligible effect at these temperatures. Analysis of these spectra demonstrate that ΔEQ < 0 and the electric field gradient (EFG) asymmetry parameter is η = 0.5(3). At lower temperatures, knowledge of the EFG tensor enables quantification of the magnitude of the ZFS, the intermolecular coupling, J12, and the local hyperfine coupling tensor A. Simulations suggest that not only does the S = 5/2 ground state of 1 exhibit a relatively small ZFS, but they also indicate a hyperfine coupling tensor A with small anisotropy. These simulations clearly demonstrate that, above 15 K, the supramolecular exchange interactions between near-neighbour molecules are antiferromagnetic (see ESI†). Parameters obtained from the best simulations (red solid lines in Fig. 7) using eqn (1a)–(c) are listed in Table 2.
| S 1,2 | J 12 [cm−1] | D 1,2 [cm−1] | (E/D)1,2 | g 1,2 | δ 1,2 [mm s−1] | ΔEQ1,2a [mm s−1] | η 1,2 | A x1,2/gnβn [T] | A y1,2/gnβn [T] | A z1,2/gnβn [T] | A iso1,2/gnβn [T] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The ZFS and EFG tensors are rotated with respect to the local A tensors using a standard set of Euler rotations such that α = β = 90° and γ = 0°. | |||||||||||
| 5/2 | 2.7(4) | 0.6(4) | 0.05(5) | 2.00 | 0.41(1) | −1.04(4) | 0.5(3) | −22(1) | −21(1) | −20(1) | −21(1) |
Computational studies
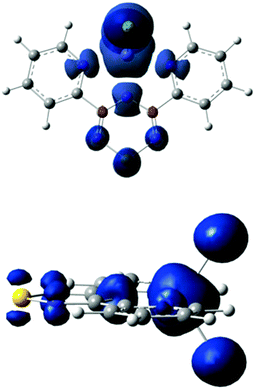
Density functional theory (DFT) calculations were performed using the Gaussian 09 program employing the spin-unrestricted method at the PBEPBE/TZVP and B3LYP/6-311G level of theory. Optimization of the electronic state with a spin of 5/2 in the gas phase results in an energy minimum with C2V symmetry. The spin density distribution of the electronic state is shown in Fig. 8. The Mulliken population analysis (MPA)-derived spin densities for the iron and chlorine atoms are 3.93(4.10) and 0.28(0.23) a.u., respectively, and 0.51(0.44) a.u. for Py2TTA; the aforementioned values were obtained using the PBEPBE/TZVP (B3LYP/6-311G) functional/basis set combinations. The nitrogen and sulphur atoms of Py2TTA carry a spin density in the range of 0.06(0.04)–0.14(0.16) a.u. The natural population analysis (NPA)-derived spin densities obtained using PBEPBE/TZVP exhibit similar values for the iron and chlorine atoms of 3.77 and 0.30 a.u., and a value of 0.62 a.u. for Py2TTA. Interestingly, the theoretically predicted values (B3LYP/6-311G) of the zero-field Mössbauer parameters δ = 0.40 mm s−1, ΔEQ = −0.94 mm s−1 and η = 0.4 compare extremely well with those observed experimentally (vide supra). Although these values are typical of high-spin FeIII sites, the theoretically predicted charge and spin density distributions imply that the valence description of the ground electronic states of the complex is in fact between FeII–L0, with a neutral radical, and FeIII–L−1, with the closed-shell anionic description of the ligand. This observation suggests that the predicted spin densities result from the single β electron of the formal FeII site being delocalized over the two redox active sites of 1. Since this itinerant electron maintains its spin during transfer between the two redox centres it enforces a parallel alignment of the local spins. Whereas, in the absence of valence delocalization, strong antiferromagnetic direct exchange interactions would be expected between the local spins of the FeII and the neutral radical ligand.51–54 Parallel analysis of the magnetic susceptibility data and field-dependent Mössbauer spectra reveal appreciable magnetic exchange interactions between near-neighbour molecules in 1. In order to explore the origin of these interactions, a series of broken – symmetry calculations have been performed on supramolecular dimer moieties that comprise distinct molecules of the same unit cell. These calculations suggest that the strongest intermolecular interactions are antiferromagnetic and that they occur along the stacking b-axis, as expected from the large number of short intermolecular contacts present in the solid-state (see ESI†).Conclusions
We have isolated Fe(Py2TTA)Cl2, a distinctive complex exhibiting valence delocalization between a non-innocent pincer-type radical ligand and redox active metal ion. Interestingly, 1 can be prepared via two routes; either through treatment of FeII with the neutral radical Py2TTA˙, or the reaction between FeIII and Py2TTAH, highlighting the versatility of this system. This unique behaviour is attributed to the redox compatibility between the non-innocent ligand and iron. Based on spectroscopic, structural, computational and magnetic analysis, this distinctive system exhibits strong electronic interactions between the ligand and metal, which leads to delocalization of electron density resulting in an S = 5/2 complex. While the Mössbauer and magnetic parameters may seem indicative of high-spin FeIII, DFT calculations not only reproduce those values quite well but they also predict the presence of a large degree of spin- and valence-delocalization between the two redox sites of 1. Thus, assignment of formal oxidation states is difficult due to ambiguity of the ligand–metal interactions.In summary, we established a simple and efficient synthetic route to create coordination complexes with Py2TTA˙, which do not require generation of the radical prior to coordination. This facilitates further exploration of metal complexes with Py2TTA˙ to probe the tunability of this ligand topography and tap into the ambiguity of the redox relationship. Such a unique system opens exciting avenues. In comparison to terpy, Py2TTA provides the same coordination environment yet greater versatility by virtue of its redox flexibility.
Acknowledgements
The authors thank the University of Ottawa, the Canadian Foundation for Innovation (CFI) and NSERC (Discovery and RTI grants, Vanier Graduate Scholarship) for their financial support. SH acknowledges the support of the NSF (DMR-1309463). Part of this work was performed at NHMFL, which is supported by the NSF (DMR-1157490) and the State of Florida. SAS is an NHMFL Jack E. Crow postdoctoral fellow. The Mössbauer spectrometer was purchased using the NHMFL User Collaboration Grant Program (UCGP-5064) awarded to Dr Andrzej Ozarowski.Notes and references
- I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303–349 RSC.
- A. F. Heyduk, R. A. Zarkesh and A. I. Nguyen, Inorg. Chem., 2011, 50, 9849–9863 CrossRef CAS PubMed.
- R. G. Hicks, Nat. Chem., 2011, 3, 189–191 CrossRef CAS PubMed.
- R. G. Hicks, Stable Radicals: Fundamentals and Applied Aspects of Odd-Electron Compounds, John Wiley & Sons, Ltd., Wiltshire, 2010 Search PubMed.
- K. E. Preuss, Dalton Trans., 2007, 2357–2369 RSC.
- W. Kaim and B. Schwederski, Coord. Chem. Rev., 2010, 254, 1580–1588 CrossRef CAS.
- W. I. Dzik, J. I. van der Vlugt, J. N. H. Reek and B. de Bruin, Angew. Chem., Int. Ed., 2011, 50, 3356–3358 CrossRef CAS PubMed.
- V. Lyaskovskyy and B. de Bruin, ACS Catal., 2012, 2, 270–279 CrossRef CAS.
- K. Searles, A. K. Das, R. W. Buell, M. Pink, C.-H. Chen, K. Pal, D. G. Morgan, D. J. Mindiola and K. G. Caulton, Inorg. Chem., 2013, 52, 5611–5619 CrossRef CAS PubMed.
- S. Fortier, J. J. Le Roy, C.-H. Chen, V. Vieru, M. Murugesu, L. F. Chibotaru, D. J. Mindiola and K. G. Caulton, J. Am. Chem. Soc., 2013, 135, 14670–14678 CrossRef CAS PubMed.
- C. Y. Ang, R. T. Boeré, L. Y. Goh, L. L. Koh, S. L. Kuan, G. K. Tan and X. Yu, Chem. Commun., 2006, 4735–4737 RSC.
- C. Y. Ang, S. L. Kuan, G. K. Tan, L. Y. Goh, T. L. Roemmele, X. Yu and R. T. Boeré, Can. J. Chem., 2015, 93, 181–195 CrossRef CAS.
- E. C. Constable, Chem. Soc. Rev., 2007, 36, 246–253 RSC.
- E. A. Medlycott and G. S. Hanan, Chem. Soc. Rev., 2005, 34, 133–142 RSC.
- R. Shunmugam, G. J. Gabriel, K. A. Aamer and G. N. Tew, Macromol. Rapid Commun., 2010, 31, 784–793 CrossRef CAS PubMed.
- J. A. Bailey, M. G. Hill, R. E. Marsh, V. M. Miskowski, W. P. Schaefer and H. B. Gray, Inorg. Chem., 1995, 34, 4591–4599 CrossRef CAS.
- G. D. Jones, J. L. Martin, C. McFarland, O. R. Allen, R. E. Hall, A. D. Haley, R. J. Brandon, T. Konovalova, P. J. Desrochers, P. Pulay and D. A. Vicic, J. Am. Chem. Soc., 2006, 128, 13175–13183 CrossRef CAS PubMed.
- J. England, C. C. Scarborough, T. Weyhermueller, S. Sproules and K. Wieghardt, Eur. J. Inorg. Chem., 2012, 4605–4621 CrossRef CAS.
- M. Sorai, Y. Nakazawa, M. Nakano and Y. Miyazaki, Chem. Rev., 2013, 113, PR41–PR122 CrossRef PubMed.
- K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655–2685 CrossRef CAS PubMed.
- A. Kobayashi and H. Kitagawa, J. Am. Chem. Soc., 2006, 128, 12066–12067 CrossRef CAS PubMed.
- N. Kojima and N. Matsushita, Coord. Chem. Rev., 2000, 198, 251–263 CrossRef CAS.
- C. R. Benson, A. K. Hui, K. Parimal, B. J. Cook, C.-H. Chen, R. L. Lord, A. H. Flood and K. G. Caulton, Dalton Trans., 2014, 43, 6513–6524 RSC.
- A. K. Hui, R. L. Lord and K. G. Caulton, Dalton Trans., 2014, 43, 7958–7963 RSC.
- P. Ghosh, S. Samanta, S. K. Roy, S. Demeshko, F. Meyer and S. Goswami, Inorg. Chem., 2014, 53, 4678–4686 CrossRef CAS PubMed.
- L. Hu, W. Liu, C.-H. Li, X.-H. Zhou and J.-L. Zuo, Eur. J. Inorg. Chem., 2013, 2013, 6037–6048 CrossRef CAS.
- C. Stroh, P. Turek, P. Rabu and R. Ziessel, Inorg. Chem., 2001, 40, 5334–5342 CrossRef CAS PubMed.
- A. A. Leitch, I. Korobkov, A. Assoud and J. L. Brusso, Chem. Commun., 2014, 50, 4934–4936 RSC.
- N. J. Yutronkie, A. A. Leitch, I. Korobkov and J. L. Brusso, Cryst. Growth Des., 2015, 15, 2524–2532 CAS.
- X.-H. Hu, Y. Liang, C. Li and X.-Y. Yi, Dalton Trans., 2014, 43, 2458–2464 RSC.
- M. S. Alam, M. Stocker, K. Gieb, P. Mueller, M. Haryono, K. Student and A. Grohmann, Angew. Chem., Int. Ed., 2010, 49, 1159–1163 CrossRef CAS PubMed.
- J. W. Ciszek, Z. K. Keane, L. Cheng, M. P. Stewart, L. H. Yu, D. Natelson and J. M. Tour, J. Am. Chem. Soc., 2006, 128, 3179–3189 CrossRef CAS PubMed.
- L. M. Yan and J. M. Seminario, J. Phys. Chem. A, 2005, 109, 6628–6633 CrossRef CAS PubMed.
- G. H. Imler, Z. Lu, K. A. Kistler, P. J. Carroll, B. B. Wayland and M. J. Zdilla, Inorg. Chem., 2012, 51, 10122–10128 CrossRef CAS PubMed.
- R. T. Boeré, A. W. Cordes, P. J. Hayes, R. T. Oakley, R. W. Reed and W. T. Pennington, Inorg. Chem., 1986, 25, 2445–2450 CrossRef.
- R. T. Boeré, T. L. Roemmele and X. Yu, Inorg. Chem., 2011, 50, 5123–5136 CrossRef PubMed.
- K. Ouch, M. S. Mashuta and C. A. Grapperhaus, Inorg. Chem., 2011, 50, 9904–9914 CrossRef CAS PubMed.
- N. G. R. Hearns, R. Clérac, M. Jennings and K. E. Preuss, Dalton Trans., 2009, 3193–3203 RSC.
- R. T. Boeré and T. L. Roemmele, Coord. Chem. Rev., 2000, 210, 369–445 CrossRef.
- T. Kurahashi and H. Fujii, J. Am. Chem. Soc., 2011, 133, 8307–8316 CrossRef CAS PubMed.
- J. L. Wong, R. H. Sanchez, J. G. Logan, R. A. Zarkesh, J. W. Ziller and A. F. Heyduk, Chem. Sci., 2013, 4, 1906–1910 RSC.
- S. C. Bart, K. Chlopek, E. Bill, M. W. Bouwkamp, E. Lobkovsky, F. Neese, K. Wieghardt and P. J. Chirik, J. Am. Chem. Soc., 2006, 128, 13901–13912 CrossRef CAS PubMed.
- B. L. Small, M. Brookhart and A. M. A. Bennett, J. Am. Chem. Soc., 1998, 120, 4049–4050 CrossRef CAS.
- A. M. Tondreau, C. C. H. Atienza, J. M. Darmon, C. Milsmann, H. M. Hoyt, K. J. Weller, S. A. Nye, K. M. Lewis, J. Boyer, J. G. P. Delis, E. Lobkovsky and P. J. Chirik, Organometallics, 2012, 31, 4886–4893 CrossRef CAS.
- S. A. Cotton, V. Franckevicius and J. Fawcett, Polyhedron, 2002, 21, 2055–2061 CrossRef CAS.
- Y. Nakayama, Y. Baba, H. Yasuda, K. Kawakita and N. Ueyama, Macromolecules, 2003, 36, 7953–7958 CrossRef CAS.
- T. G. Wright and W. H. Breckenridge, J. Phys. Chem. A, 2010, 114, 3182–3189 CrossRef CAS PubMed.
- P. Gütlich, E. Bill and A. X. Trautwein, in Mössbauer Spectroscopy and Transition Metal Chemistry. Fundamentals and Applications, Springer-Verlag, Berlin, Heidelberg, 2011 Search PubMed.
- L. R. Widger, Y. Jiang, M. A. Siegler, D. Kumar, R. Latifi, S. P. de Visser, G. N. L. Jameson and D. P. Goldberg, Inorg. Chem., 2013, 52, 10467–10480 CrossRef CAS PubMed.
- E. Münck and B. H. Huyn, in ESR and NMR of Paramagnetic Species in Biological and Related Systems, ed. I. D. Bertini and R. S. Drago, Reidel Publishing Company, Holland, 1979, pp. 275–288 Search PubMed.
- M. Drillon, G. Pourroy and J. Darriet, Chem. Phys., 1984, 88, 27–37 CrossRef CAS.
- G. Blondin and J. J. Girerd, Chem. Rev., 1990, 90, 1359–1376 CrossRef CAS.
- J. J. Borras-Almenar, E. Coronado, S. M. Ostrovsky, A. V. Palii and B. S. Tsukerblat, Chem. Phys., 1999, 240, 149–161 CrossRef CAS.
- B. Bechlars, D. M. D'Alessandro, D. M. Jenkins, A. T. Iavarone, S. D. Glover, C. P. Kubiak and J. R. Long, Nat. Chem., 2010, 2, 362–368 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic procedures, electrochemistry, UV-visible, Mössbauer, Raman spectroscopy, crystallography, computational studies, and magnetic measurements. CCDC 1021206. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt01374g |
‡ Crystal data at 200(2) K for C12H8Cl2FeN5S, M = 381.04, orthorhombic, a = 13.7473(4) Å, b = 7.1687(2) Å, c = 14.4831(3) Å, α = 90°, β = 90°, γ = 90°, V = 1427.31(6) Å3, space group Pnma, Z = 4, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203 reflections measured, 1890 unique (Rint = 0.0181). The final wR(F2) was 0.0590 (all data). 203 reflections measured, 1890 unique (Rint = 0.0181). The final wR(F2) was 0.0590 (all data). |
| This journal is © The Royal Society of Chemistry 2015 |