3d single-ion magnets

Abstract

One of the determining factors in whether single-molecule magnets (SMMs) may be used as the smallest component of data storage, is the size of the barrier to reversal of the magnetisation, U_eff. This physical quantity depends on the magnitude of the magnetic anisotropy of a complex and the size of its spin ground state. In recent years, there has been a growing focus on maximising the anisotropy generated for a single 3d transition metal (TM) ion, by an appropriate ligand field, as a means of achieving higher barriers. Because the magnetic properties of these compounds arise from a single ion in a ligand field, they are often referred to as single-ion magnets (SIMs). Here, the synthetic chemist has a significant role to play, both in the design of ligands to enforce propitious splitting of the 3d orbitals and in the judicious choice of TM ion. Since the publication of the first 3d-based SIM, which was based on Fe(II), many other contributions have been made to this field, using different first row TM ions, and exploring varied coordination environments for the paramagnetic ions.

---

Gavin A. Craig

Gavin A. Craig graduated with an MSci (Hons.) in Chemistry from the University of Glasgow in 2008. Under the supervision of Guillem Aromí at the Universitat de Barcelona, he obtained an MSc (2010) and then a PhD (2013) working in the field of spin crossover. During his doctoral studies he undertook several placements in the group of Azzedine Bousseksou at the LCC in Toulouse. Since November 2013 he is a Post-Doctoral Research Associate in the group of Mark Murrie in the School of Chemistry at the University of Glasgow, studying the effect of pressure on molecular magnetic materials.

Mark Murrie

Mark Murrie received his PhD from the University of Manchester in 1997 under the supervision of Professor Dave Garner FRS and Professor David Collison. Following postdoctoral positions at the University of Edinburgh, with Professor Richard Winpenny and at the University of Bern in Switzerland, with Professor Hans Güdel, he joined the School of Chemistry at the University of Glasgow in 2003, where he is now Reader. His current research interests are in the synthesis & characterisation of molecular magnets and magnetic nanoparticles and the application of high pressure science to magnetic systems.

---

Key learning points

(1) Slow relaxation of the magnetisation arises from a single 3d ion under an appropriate ligand field.

(2) Slow relaxation in single-ion magnets (SIMs) can be observed, and energy barriers measured, using alternating current (ac) susceptibility measurements.

(3) Quantum tunnelling of the magnetisation (QTM) may lead to no out-of-phase component of the dynamic magnetic susceptibility being observed. It may be possible to hinder the QTM by applying an additional external dc field.

(4) Design principles based on the 3d ion used, coordination number, and ligand field generated to target and attain SIM behaviour.

1. Introduction

If a single molecule could be used to encode binary information, then vast increases in data storage density could be achieved with respect to traditional media. The exploration of this possibility for the compound [Mn₁₂O₁₂(OAc)₁₆(H₂O)₄]·2AcOH·4H₂O (Mn₁₂ac) led to the establishment of a new class of materials called single-molecule magnets (SMMs).¹ Mn₁₂ac has a preferential direction for the resultant magnetisation that arises from the precession of the spin in a magnetic field, caused by the anisotropy associated with the metal ions in the complex. At low temperature, by flipping the orientation of the field, this preferential direction can be reversed; that is, switched from lying along the z-axis, to lying along the −z-axis. Crucially, magnetisation in either direction is retained when the field is removed. Therefore, it can be imagined that “1” in binary coding could be assigned to the magnetisation along the +z direction, and “0” to the magnetisation along the −z direction.

Since then this field, which has more generally studied molecular nanomagnets, has undergone several developments. Often, this has involved looking at the potential of molecular nanomagnets to fulfil applications in areas such as quantum computing or magnetic refrigeration, as well as how to deposit these molecules on surfaces.² On a synthetic level, it has also led to the study of the one-dimensional analogues of SMMs, known as single-chain magnets (SCMs).^3,4 Another synthetic strategy has been the use of a single ion to develop monometallic SMMs, an approach which first used lanthanide ions.⁵

In this Tutorial Review, we will focus on the relatively recent approach to obtain SMMs whose magnetic properties arise from a single first row transition metal (TM) ion in a suitable ligand field that creates magnetic anisotropy. In the literature, these are often referred to as either single-ion magnets (SIMs) or mononuclear SMMs, neither of which are perfect descriptors. Monometallic SMM is probably better but herein, we have chosen to use the SIM acronym rather than e.g. MSMM, which is more awkward. In Section 2, we briefly describe how slow relaxation of the magnetisation may arise, how it is observed, and why SIMs have become a focus of attention. Section 3 highlights some of the different strategies employed to induce a large magnetic anisotropy using a single 3d ion.

2. Single-molecule magnets: towards monometallic complexes

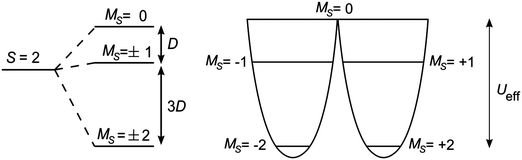
For a single-molecule magnet to function effectively as a means of data storage, there must be a barrier to the re-orientation of the molecule's magnetisation, to prevent a loss of information. The origin of the barrier lies in magnetic anisotropy. When the spin ground state of a molecule is S > 1/2, then zero-field splitting (ZFS) may arise if the symmetry is lower than cubic. The symmetry lowering may lead to the separation of excited states, which can then mix through spin–orbit coupling. The Hamiltonian associated with ZFS can be expressed as:

Ĥ = D[Ŝ²_z − S(S + 1)/3] + E(Ŝ²_x − Ŝ²_y) (1)

where D is the axial ZFS parameter, E is the rhombic or transverse ZFS parameter, and Ŝ is the spin projection along a given axis.⁶ The effect of a negative axial ZFS on an S = 2 state is shown in Fig. 1. Here, the M_S sublevel with the greatest magnetic moment is that of lowest energy, and the molecule is referred to as possessing easy-axis anisotropy. The M_S label indicates that orbital angular momentum in a given compound is largely quenched. Where the effects of orbital angular momentum are more significant, the sublevels are labelled M_J, where J denotes the total angular momentum (vide infra). However, use of the M_S notation is still applied in many such cases, in particular where D is reported. For an integer spin system, easy-axis anisotropy is essential for the type of bi-stability shown in Fig. 1. The inclusion of a non-zero E term removes the degeneracy of the ±M_S levels in zero field for an integer spin system, unlike for a half-integer spin system.¹ The barrier U_eff to loss of magnetisation, is given by:

U_eff = |D|·S² (2a)

or

|D|·(S² − ¼) (2b)

where S denotes the spin ground state of the molecule ((2a) is for integer spin systems, (2b) for half-integer). The maximum theoretical value of U_eff assumes that a species reverses the magnetisation direction by climbing over the top of the double well shown in Fig. 1.

Fig. 1 (left) Splitting of an S = 2 state into its constituent M_S levels, induced by negative axial ZFS. (right) A view of the double-well thus generated, with the barrier to relaxation shown as U_eff.

2.1 Measurement of the barrier to relaxation

The barrier to relaxation in SMMs is usually determined by alternating current (ac) susceptibility measurements. Under these conditions, the magnetic susceptibility of a compound consists of two components, corresponding to a real (in-phase) contribution, χ_M′, and an imaginary (out-of-phase) contribution, χ_M′′, which depend on the angular frequency with which the magnetic field oscillates.¹ The inability of the magnetisation to follow the progressively faster switching field causes a decrease of the in-phase component and an increase of the out-of-phase component. The out-of-phase component will reach a maximum in χ_M′′ before decreasing again with the highest frequencies of switching fields. At this maximum, the angular frequency (ω) can be related to the relaxation time, τ, through:

ωτ = 2πντ = 1 (3)

This relaxation may occur through several possible processes.⁷ Quantum tunnelling of the magnetisation (QTM) allows the spin to flip by tunnelling from an M_S state on one side of the barrier to a resonant M_S state on the other side; for example, from the M_S = +2 level to the M_S = −2 level in Fig. 1.⁸ When QTM is particularly efficient, the barrier may be bypassed completely, and no signal in the out-of-phase susceptibility will be observed. QTM can arise from lower than ideal symmetry in a molecule, which induces a transverse component (E and/or allowed higher order terms) to the anisotropy. The relationship between symmetry and the presence of transverse anisotropy, which dramatically reduces U_eff, is one of the driving forces behind attempts to control the topology of single-molecule magnets.⁹ Alternatively, the relaxation can be phonon-assisted in either a two phonon process (Orbach, Raman) or a one phonon process (direct). Orbach processes involve absorption of a phonon causing excitation to a real state, before emission of a phonon and relaxation. A Raman process sees the absorption of a phonon causing the excitation of a spin to an imaginary level, before relaxation and emission of a phonon. A direct process involves the spin of the molecule flipping with emission of a phonon.

By scanning the frequency to measure the dynamic susceptibility at several different temperatures, the relationship between τ and T may be determined through an Arrhenius plot of ln(τ) vs. 1/T. At higher temperatures, a linear fit will normally be possible, corresponding to eqn (4)

ln τ = ln τ₀ + U_eff/k_BT (4)

and thus U_eff may be derived from the gradient of the Arrhenius plot, where τ₀ is the microscopic attempt time, i.e. the relaxation attempt time for reversal at T = ∞ (or it may be considered as (1/τ₀) which corresponds to the intrinsic relaxation rate, with units of s⁻¹: see ref. 36), and k_B is the Boltzmann constant.¹⁰ The τ₀ value for Mn₁₂ac is ∼10⁻⁷ s and this is typical for SMMs, although values from ∼10⁻⁶ to ∼10⁻¹¹ s are commonly reported. This case corresponds to Orbach relaxation, because U_eff is related to the energy difference between real states. Raman or direct processes will be manifested through curvature of the plot, indicating more complex relationships between the relaxation time and the barrier to relaxation, because they have different temperature dependencies. Direct processes show a very slight temperature dependence in an Arrhenius plot, while Raman processes may be thought of as intermediate between Orbach and direct processes. Such a case is illustrated in Fig. 2, for the compound Na[(tpa^t-Bu)Fe]·THF (vide infra).¹¹

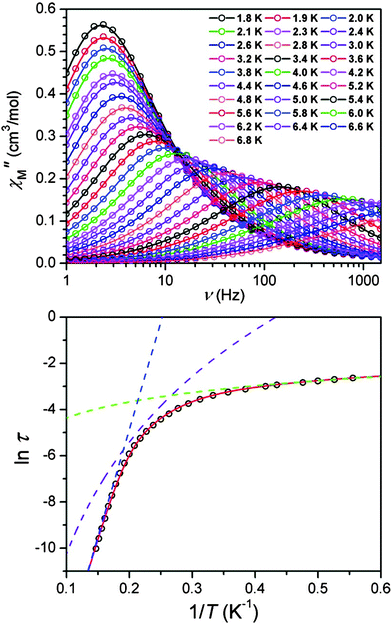Fig. 2 Top: variable-frequency out-of-phase ac susceptibility data for Na[(tpa^t-Bu)Fe]·THF, under a 1500 Oe dc field at various temperatures. Bottom: Arrhenius plot constructed from data. Dashed lines represent data fits to an Orbach (blue), Raman (purple), and direct (green) process. The solid red line represents a fit to the three processes simultaneously. Reprinted with permission from ref. 11. Copyright (2010) American Chemical Society.

2.2 Increasing U_eff

The relationship between the barrier to relaxation of the magnetisation and the ground spin state S led to a vast effort towards building the compounds with the highest possible nuclearity, in an attempt to maximise U_eff.² However, the stumbling block encountered was that D was found to be inversely proportional to S².¹² Therefore, incorporating large numbers of paramagnetic transition metal ions in a compound may be antagonistic to generating a large magnetic anisotropy. Often, this is because the anisotropy axis for a given ion within a polymetallic complex is not aligned with that of another ion within the same complex, leading to a diminished overall anisotropy.¹³ By employing a single ion, this scenario would be avoided, but leads to a clear limiting factor: M_S can only ever be as large as the maximum spin of the single ion. The challenge thus presented is how to achieve the greatest possible anisotropy, given by D, and so attain larger barriers for the relaxation of the magnetisation.

The discussion in Section 2 described situations where M_S states are split by ZFS. In the majority of these cases, first order orbital angular momentum is quenched. The axial anisotropy that arises is due to second order spin–orbit coupling, which admixes relevant excited states into the ground state. The large first order orbital angular momentum in the lanthanides has already led to many studies of monometallic 4f single-molecule magnets.² Therefore, many of the examples described below seek coordination environments in which first order orbital angular momentum is largely unquenched, potentially leading to much higher barriers.

3. 3d single-ion magnets

The first example of a monometallic 3d SMM was the high spin Fe(II) compound K[(tpa^Mes)Fe] (1, H₃tpa^Mes = Tris((5-mesityl-1H-pyrrol-2-yl)methyl)amine).¹⁴ The Fe(II) ion lies in a trigonal pyramidal geometry, with an N₄ coordination sphere (Fig. 3). The bulky ligand promotes the unusual geometry around the metal centre by impeding access to the second axial site. The orbital splitting thus induced generates a large magnetic anisotropy due to the unequal occupation of the 1e orbitals shown in Fig. 3, which leads to unquenched orbital angular momentum. The non-superposition of the variable field magnetisation measurements confirms that a large axial zero-field splitting is attained, with fits of the data yielding D = −39.6 cm⁻¹, together with a small rhombic contribution, E = −0.4 cm⁻¹. This rhombic contribution arises from a small structural distortion around the Fe(II) ion, which lowers the three-fold symmetry.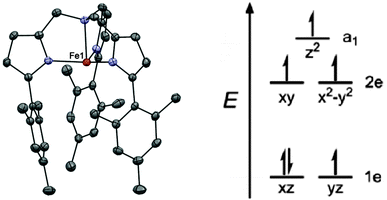

Fig. 3 (left) A view of the anion [(tpa^Mes)Fe]⁻; Fe, red; N, blue; and C, grey. (right) A simplified view of the orbital splitting. Reprinted with permission from ref. 14. Copyright (2010) American Chemical Society.

No out-of-phase signal for the magnetic susceptibility could be detected in the absence of an applied dc field, which was attributed to efficient QTM. To lower the rate of tunnelling, a dc field of 1500 Oe was applied during the alternating current (ac) susceptibility measurements leading to maxima in χ′′. While the value of D extracted from the fits of the static magnetic properties may have suggested a very large barrier (U = S²·|D| = 4 × 39.6 = 158 cm⁻¹), the effective barrier, U_eff = 42 cm⁻¹, derived from the Arrhenius plot was much lower due to tunnelling processes.

Subsequently, 1 was used as a platform to develop compounds in which other sterically demanding derivatives of tpa enforced similar geometries upon Fe(II) (see Table 1, compounds 2 and 3).¹¹ Compound 2 is the only analogue to have crystallographically imposed three-fold symmetry and it shows the highest barrier. Since the study of this family of high spin Fe(II) compounds, comparable strategies have been used for other first row transition metals. As will be shown, many of these complexes share some features with 1–3, such as low coordination numbers and unusual geometries, and efficient QTM in the absence of an applied dc field.

Table 1 Compilation of the compounds discussed in this review

Compound	U eff/cm^−1 (applied field/Oe)	τ 0/s	Ref.
Mn(III)
Ph4P[Mn(opbaCl2)(py)2] (4)	12.6 (1000)	1.2 × 10^−7	15
[Mn(5-TMAM(R)-salmen)(H2O)Co(CN)6]·7H2O·MeCN (5)	11.5 (4500)	2.9 × 10^−7	16
[Mn((OPPh2)2N)3] (6)	8.3 (2250)	0.5 × 10^−7	17
Fe(I)
[K(crypt-222)][Fe(C(SiMe3)3)2] (7)	226 (0)	1.3 × 10^−9	19, 20
[(cAAC)2Fe][B(C6F5)4] (9)	<20 (3000)	—	21
(cAAC)2FeCl (10)	22.4 (500)	7.0 × 10^−8	21
Fe(II)
K[(tpa^Mes)Fe] (1)	42 (1500)	2.0 × 10^−9	14
Na[(tpa^t-Bu)Fe] (2)	65 (1500)	6.7 × 10^−11	11
Na[(tpa^Ph)Fe] (3)	25 (1500)	—	11
[Fe(C(SiMe3)3)2] (8)	146 (500)	4 × 10^−9	18, 20
Fe[N(SiMe3)(Dipp)]2 (11)	181 (500)	1 × 10^−11	18
Fe[N(H)Ar′]2 (12)	109 (1800)	5 × 10^−9	18
Fe[N(H)Ar*]2 (13)	104 (875)	4 × 10^−8	18
Fe(OAr′)2 (14)	43 (2500)	3 × 10^−7	18
Fe[N(H)Ar^#]2 (15)	—	—	18
[Fe(N(SiMe3)2)2(PCy3)] (16)	29.2/16 (600)	6.0 × 10^−7/1.6 × 10^−6	22, 23
[^5CpFe(C6H3iPr3-2,6)] (20)	28.0 (750)/99.7 (2500)	6.0 × 10^−6/7.8 × 10^−9	24
[Fe(1-ptz)6](BF4)2 (21)	15 (2000)	4.2 × 10^−8	25
PhB(MesIm)3Fe-N=PPh3 (22)	15 (1000)	8.7 × 10^−7	27
Fe(III)
[(PNP)FeCl2] (23)	32 (0)	2 × 10^−8	28
Co(II)
[Li(15-crown-5)][Co(N(SiMe3)2)3] (17)	16.1 (800)	3.5 × 10^−7	22
[Co(N(SiMe3)2)2(THF)] (18)	18.1 (600)	9.3 × 10^−8	22
[Co(N(SiMe3)2)2(PCy3)] (19)	19.1 (750)	3.0 × 10^−7	22
[(ArN=CMe)2(NPh)]Co(NCS)2 (24)	11.1 (2000)	3.6 × 10^−6	30
[(ArN=CPh)2(NPh)]Co(NCS)2 (25)	16.7/17.4 (2000)	5.1 × 10^−7/1.6 × 10^−6	30
[Co(terpy)Cl2] (26)	19.5 (600)/2.8 (5600)	1.1 × 10^−6/7.4 × 10^−2	31
[Co(terpy)(NCS)2] (27)	11.8 (600)/2.1 (5600)	5.9 × 10^−6/0.11	31
[Co(P(S)([N(CH3)N=CHC3N2H3]3))](NO3)2 (28)	23 (2000)	4 × 10^−6	32
K(Co(N[CH2C(O)NC(CH3)3]3)) (29)	8.7 (1500)	8 × 10^−6	32
cis-[Co(dmphen)2(NCS)2]·0.25EtOH (30)	16.2 (1000)	4 × 10^−7	33
[(L)4Co^III2Co^II(H2O)2](NO3)4·6H2O (31)	5.6 (1000)	1.0 × 10^−5	34
[(3G)CoCl](CF3SO3) (32)	24 (1500)	1.9 × 10^−9	35
[dmphCoBr2] (33)	22.9 (1000)	3.7 × 10^−10	37
[Co(L)(OAc)Y(NO3)2] (34)	15.7 (1000)	8.9 × 10^−7	38
[Co(acac)2(H2O)2] (35)	∼16 (various)	—	39
[Co(abpt)2(tcm)2] (36)	59.9 (3000)	1.4 × 10^−9	40
[Co(12C4)2](I3)2(12C4) (37)	17 (500)	1.5 × 10^−6	41
[Co(L^1)2] (38, L^1 = 2-(4,5-diphenyl-1H-imidazol-2-yl)phenol)	34.1 (400)/61.9 (1000)	7.5 × 10^−8/1.0 × 10^−10	45
[Co(L^3)2] (39, L^3 = 2-(4,5-diphenyl-1H-imidazol-2-yl)-6-methoxyphenol)	29.2 (400)/43.8 (1000)	1.4 × 10^−7/2.6 × 10^−9	45
Co(hpbdti)2 (40)	39.4/29.7/10.6 (2000)	1.3 × 10^−8/5.4 × 10^−7/1.3 × 10^−5	46
[Co(PPh3)2Br2] (41)	27.8 (1000)	5.9 × 10^−11	42
[Co(PPh3)2Cl2] (42)	25.8 (1000)	1.2 × 10^−9	44
[Co(DPEphos)Cl2] (43)	24.3 (1000)	2.1 × 10^−10	44
[Co(Xantphos)Cl2] (44)	20.8 (1000)	6.0 × 10^−9	44
(Ph4P)2[Co(OPh)4]·CH3CN (45)	21.1 (1400)	7 × 10^−10	43
K(Ph4P)[Co(OPh)4] (46a)	Required dilution, see 46b	—	43
K(Ph4P)[Co0.06Zn0.94(OPh)4] (46b)	34.0 (0)	1.0 × 10^−9	43
(Ph4P)2[Co(SPh)4] (47)	21.1 (0)	1.0 × 10^−6	43, 47
(Ph4P)2[Co(SePh)4] (48)	19.1 (0)	3 × 10^−6	43
(Ph4P)2[Co(C3S5)2] (49)	33.9 (0)	4.5 × 10^−6	48
(HNEt3)(Co^IICo^III3L6) (50)	75.8 (0)	1 × 10^−7	49
[Co^IIICo^II(LH2)2(Cl)(H2O)](H2O)4 (51)	7.9 (1000)	6.1 × 10^−6	50
[Co^IIICo^II(LH2)2(Br)(H2O)](H2O)4 (52)	14.5 (1000)	1.0 × 10^−6	50
Ni(I)
[Ni(6-Mes)2]Br (53)	11.8 (600)	4.6 × 10^−6	51

---

3.1 Mn(III)

Mn(III) has been widely used in the field of molecular nanomagnets. For the d⁴ Mn(III) ion, the Jahn–Teller effect leads to a tetragonal distortion away from O_h symmetry towards D_4h, most commonly an elongation along the z-axis. This splits the ⁵E ground state and mixing of the ⁵B₁ state with excited states, through second order spin–orbit coupling, gives rise to the zero-field splitting where D is almost always negative in a tetragonally elongated environment.

The most comprehensive study of a monometallic Mn(III) SMM so far was performed by Vallejo and co-workers on the complex Ph₄P[Mn(opbaCl₂)(py)₂] (4, where H₄opbaCl₂ = N,N′-3,4-dichloro-o-phenylenebis(oxamic acid)).¹⁵ This compound contains an axially elongated Mn(III) ion, with a mixed N₂O₂ donor set in the equatorial positions, provided by the ligand, and two axial N atoms provided by pyridine molecules (Fig. 4). The coordination of the ligand forms three chelate rings that impose a distortion around the metal centre.

Fig. 4 A view of the complex [Mn(opbaCl₂)(py)₂]⁻. Mn, lilac; N, blue; O, red; C, grey; Cl, green.

A high-field EPR (HFEPR) powder study was performed yielding a value for the ZFS of D = −3.421(2) cm⁻¹ and a transverse component E of −0.152(2) cm⁻¹. The axial magnetic anisotropy was shown by complete active space (CAS) calculations to be mainly due to second order spin–orbit coupling, with D_SOC = −2.97 cm⁻¹ and a smaller spin–spin contribution. Maxima in the out-of-phase ac susceptibility were seen on the application of a dc field of 1000 Oe, and the Arrhenius plot gave U_eff = 12.6 cm⁻¹ (Fig. 5(a)). Measurement of a single crystal using a micro-SQUID (Fig. 5(b)) reveals closed hysteresis loops at zero field, due to the fast QTM, consistent with the absence of χ′′ signals in zero dc field.

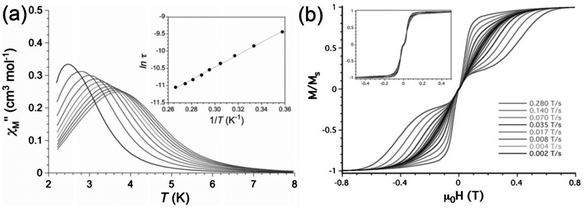Fig. 5 (a) Temperature dependence of χ′′ under a dc field of 1000 Oe, and (inset) the derived Arrhenius plot for compound Ph₄P[Mn(opbaCl₂)(py)₂]. (b) Sweep rate dependence of the normalised magnetisation, as measured at 0.5 K and (inset) at 0.03 K. Reprinted with permission from ref. 15. Copyright (2013) Wiley-VCH.

The barrier to relaxation observed for 4 is of the same order of magnitude as that found for the other examples of Mn(III)-based SIMs in the literature. The dimetallic complex [Mn(5-TMAM(R)-salmen)(H₂O)Co(CN)₆]·7H₂O·MeCN 5, 5-TMAM(R)-salmen = (R)-N,N′-(1-methylethylene)bis(5-trimethylammoniomethylsalicylideneiminate), which contains a diamagnetic Co(III) ion, was shown to have an axial ZFS of D = −3.3 cm⁻¹, by fitting the isofield magnetisation curves.¹⁶ Despite displaying a small frequency dependence for χ′ and χ′′ in zero applied dc field, maxima in the out-of-phase component were not observed, even on application of a dc field of 4500 Oe. Fits of the dynamic susceptibility data yielded an effective barrier U_eff = 9.3 or 11.5 cm⁻¹ (for zero field and 4500 Oe, respectively). A slightly lower barrier (U_eff = 8 cm⁻¹, under a field of 2250 Oe) was determined for the monometallic complex [Mn(OPPh₂)₂N₃] (6).¹⁷

3.2 Fe(I)

The rather low values of D found for the six-coordinate Mn(III) containing compounds are due to the large energy gap between the ground state and excited states. The magnitude of D is inversely proportional to the gap between ground and excited states, and also depends upon which d orbitals are involved (the interested reader can find this point illustrated in Fig. 2 of ref. 32). The relatively strong crystal field arising from coordinative saturation can be reduced by lowering the coordination number. This allows better mixing with excited states and often an almost unquenched orbital angular momentum than can produce large increases in the magnetic anisotropy. The two-coordinate linear Fe(I) complex [K(crypt-222)][Fe(C(SiMe₃)₃)₂] (7), can be synthesised by single electron reduction of the neutral Fe(II)-based SIM¹⁸ [Fe(C(SiMe₃)₃)₂] (8) with KC₈ (Fig. 6).¹⁹ The Fe(I) oxidation state was unequivocally established using Mössbauer spectroscopy. Fe(I) has a half-integer spin of S = 3/2. According to Kramers′ theorem, QTM should be minimised in such half-integer systems, which should show slow relaxation of the magnetisation, even in the absence of an applied dc field. Ab initio calculations confirmed the success of the strategy in reducing the ligand field around the metal centre, as well as indicating large energy splittings of the M_J sublevels, which should lead to a significant energy barrier.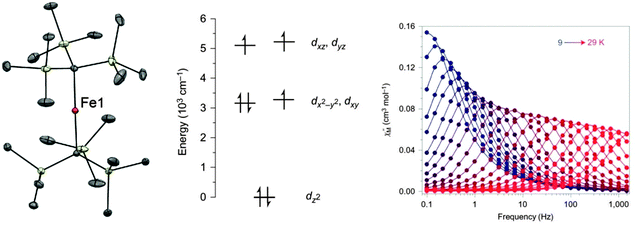

Fig. 6 (left) A view of the anion [Fe(C(SiMe₃)₃)₂]⁻; Fe, orange; C, grey; Si, pale yellow. (middle) A view of the energies of the 3d orbitals in 7. (right) Dynamic magnetic susceptibility data for 7, measured under zero applied field. Reprinted with permission from ref. 19. Copyright (2013) Nature Chemistry, Macmillan Publishers Ltd.

Frequency-dependence of the out-of-phase susceptibility was observed without the need for an applied field (Fig. 6). In fact, the barrier to relaxation in 7 is U_eff = 226 cm⁻¹, which is the highest value recorded to date for monometallic 3d SMMs. This barrier was derived from the linear region of the Arrhenius plot between 29 and 20 K. Below 20 K, the Arrhenius plot curves, as the relaxation deviates from an Orbach mechanism. Intermolecular dipolar interactions may aid QTM in these types of complexes, so dynamic susceptibility measurements were performed on a frozen solution to reduce the interactions. Dilution had previously been shown as an effective means of mitigating tunneling in the case of the compound (Ph₄P)₂[Co(SPh)₄] (47, vide infra). The resulting plot deviated to a lesser extent from Arrhenius behaviour, but still displayed curvature, which could arise from lower than axial symmetry around the Fe(I) ion, permitting mixing of the M_J states. In a subsequent work Mössbauer spectroscopy was used to extend the high temperature range over which the relaxation could be measured.²⁰ Interestingly, above 50 K on the timescale of the experiment, 7 appears to follow an Arrhenius law associated with a larger effective barrier (420 cm⁻¹) than in the range 9 to 50 K. This barrier is close to the energy difference between the M_J = ±7/2 and M_J = ±3/2 levels, derived from theoretical calculations.

However, the strategy of using Fe(I) in linear environments is not a guarantee of large barriers to relaxation. In the compound [(cAAC)₂Fe][B(C₆F₅)₄] (9, where cAAC = a cyclic alkyl(amino) carbene), the barrier was found to be U_eff < 20 cm⁻¹ under a field of 3000 Oe.²¹ Compared to 7, compound 9 has a different electronic structure, with additional π-bonding interactions. Theoretical studies suggest that the carbene π_z orbitals reduce the axial nature of the ground state doublet. Compound 9 can be synthesised from the trigonal Fe(I) complex (cAAC)₂FeCl (10), which has an easy-plane anisotropy (vide infra) and a barrier of 22.4 cm⁻¹ in an applied field of 500 Oe.

3.3 Other examples containing Fe(II)

As mentioned above, compound 7 is derived from the neutral Fe(II) SIM complex [Fe(C(SiMe₃)₃)₂] (8). This system was described as part of a family of two-coordinate Fe(II) complexes which present either a strictly linear geometry, as in the cases of 8, Fe[N(SiMe₃)(Dipp)]₂ (11, Dipp = C₆H₃-2,6-Prⁱ₂), Fe[N(H)Ar′]₂ (12, Ar′ = C₆H₃-2,6-(C₆H₃-2,6-Prⁱ₂)₂), Fe[N(H)Ar*]₂ (13, Ar* = C₆H₃-2,6-(C₆H₂-2,4,6-Prⁱ₃)₂), and Fe(OAr′)₂ (14), or a bent geometry, as found for Fe[N(H)Ar^#]₂ (15, L–Fe–L = 140.9°, Ar^# = C₆H₃-2,6-(C₆H₂-2,4,6-Me₃)₂).¹⁸ With the exception of compound 15, for which only the onset of slow magnetic relaxation was observed under an applied dc field, maxima in the out-of-phase component under different field strengths allowed Arrhenius plots to be derived for compounds 8 and 11–14. These plots were found to be significantly curved, which is attributed to the applied field inhibiting QTM while at the same time promoting direct relaxation processes.

This methodology of unsaturated coordination environments is the most common method of achieving high anisotropy for Fe(II). To this end, three trigonal planar Fe(II) compounds were prepared as part of a comparative study with their Co(II) analogues. However only one of the ferrous compounds, [Fe(N(SiMe₃)₂)₂(PCy₃)] (16, where Cy = cyclohexyl) displayed slow relaxation of the magnetisation, while all three Co(II) compounds did (17–19, Table 1) and all four compounds were studied under applied dc fields.²² Complex 16 had been previously reported,²³ and in both cases its dynamic magnetic properties were studied. Somewhat unusually, the barriers reported for the same compound differ in the two papers, as recognised by the authors of the later work. In the 2011 paper, the barrier was calculated as 29.2 cm⁻¹, while the more recent paper found a value of 16.0 cm⁻¹, both determined in an applied dc field of 600 Oe. The reason is unclear, but this does highlight the importance of reporting exactly how the barrier is determined.

Two different barriers were found for the same compound [⁵CpFe(C₆H₃iPr₃-2,6)] (20) under different fields.²⁴ Compound 20 can be prepared from the reaction of the diamagnetic complex [⁵CpFeBr(dme)] (⁵Cp = pentaisopropylcyclopentadienide, dme = 1,2-dimethoxyethane) with 2,6-diisopropylphenylmagnesium bromide in THF. Fits of the reduced magnetisation data for 20 give D = −51.4 cm⁻¹ and E = −0.3 cm⁻¹. Under an applied field, the ac susceptibility measurements revealed two types of relaxation process. The first, observed under a field of 750 Oe, process I was assigned to direct relaxation between the M_S = ±2 states of the S = 2 ground state. The second, slower process II (under a field of 2500 Oe) was ascribed to a phonon-induced excitation to the M_S = ±1 levels prior to relaxation. Accordingly, process I had a lower barrier (28.0 cm⁻¹) than process II (99.6 cm⁻¹).

In some of the cases already described, the importance of the symmetry around the central metal ion is apparent and this is also crucial for the compound [Fe(1-ptz)₆](BF₄)₂ (21), where 1-ptz = 1-propyltetrazole (Fig. 7).²⁵ Complex 21 is a classic spin crossover (SCO) compound which was the first system to be reversibly photo-switched from the diamagnetic low spin (LS) to the paramagnetic high spin (HS) form in the solid state.²⁶ Extensive crystallographic studies have shown that the symmetry of 21 is intimately related to how the compound is thermally treated. Slow cooling of the compound causes it to undergo a phase transition with a loss of symmetry, while flash cooling causes 21 to retain its high temperature space group (R3̄) with the now LS Fe(II) lying in a D_3d local symmetry. Irradiation of this LS high symmetry form of 21 gives access to a HS high symmetry phase, where the local symmetry of the Fe(II) ions gives rise to an axial magnetic anisotropy: HFEPR data gives D = −14.8 cm⁻¹, together with a transverse component of E = −0.95 cm⁻¹. The barrier to relaxation of the magnetisation under an applied dc field of 2000 Oe, is 15 cm⁻¹. The ability to turn the SIM behaviour on and off by photo-switching between the HS and LS states, together with the possible states within the HS form render 21 a tristable system (|0〉, |−2〉, |+2〉) (Fig. 7).

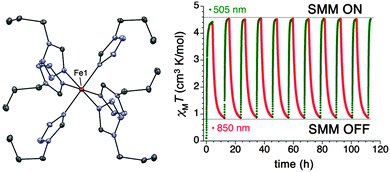Fig. 7 (left) A view of the cation [Fe(1-ptz)₆]²⁺, Fe, orange; N, blue; C, grey. (right) Photo-excitation cycles of the high symmetry form of 21, represented as the variation in χT with time. Reprinted with permission from ref. 25. Copyright (2013) American Chemical Society.

Another example of an SCO compound that shows slow relaxation of the magnetisation is PhB(MesIm)₃Fe-N=PPh₃ (22) (MesIm = mesitylimidazole).²⁷ Unlike 21, here the Fe(II) centre is four-coordinate and displays a pseudo three-fold symmetry around the metal ion. Photo-excitation of the LS state at low temperatures allows the meta-stable HS state to be generated. Under an applied dc field of 1000 Oe, a frequency dependence in χ′′ could be observed, and the fit of the Arrhenius plot yielded a barrier to relaxation of 15 cm⁻¹. While the relaxation barriers for compounds 21 and 22 are significantly lower than those found for Co(II) complexes (vide infra), both systems are fascinating for illustrating the overlap between molecular nanomagnets and SCO compounds.

3.4 Fe(III)

Partial SCO was observed in the only existing SIM containing Fe(III), [(PNP)FeCl₂] (23, PNP = N[2-P(CHMe₂)₂-4-methylphenyl]₂⁻), where the Fe(III) is in a distorted 5-coordinate environment.²⁸ At temperatures above 80 K, 23 is found in the HS S = 5/2 state, as evidenced by the dc magnetic measurements, and also by an extensive variable temperature crystallographic study. Below 80 K, 23 is found in an intermediate S = 3/2 spin state. Ac susceptibility measurements reveal that 23 is the first (and to date, only) example of a monometallic Fe(III) complex to display slow relaxation of the magnetisation, even in the absence of dc field, with a barrier of 36 cm⁻¹.

3.5 Co(II)

The promise of Co(II) for use in polymetallic SMMs has been previously highlighted, with a particular emphasis placed on the effects of the molecular shape, size and symmetry.²⁹ One of the first examples of a monometallic Co(II) SIM takes advantage of the first order spin–orbit coupling displayed by the d⁷ ion when it lies just above the basal plane of a square-based pyramid. In the compounds [(ArN=CMe)₂(NPh)]Co(NCS)₂ (24, (ArN=CMe)₂(NPh) = 2,6-bis(1-[(2,6-diisopropylphenyl)imino]ethyl)pyridine) and [(ArN=CPh)₂(NPh)]Co(NCS)₂ (25, (ArN=CPh)₂(NPh) = 2,6-bis(1-[(2,6-diisopropylphenyl)imino]benzyl)pyridine), the neutral bis(imino)pyridine ligands coordinate to the metal centre in three of its equatorial positions and the two monodentate thiocyanate ligands fill an axial and equatorial position.³⁰ Due to the steric constraints of the pincer ligands, the transition metal sits above the basal plane of the pyramid. In the regular geometry, in which the metal ion lies in the basal plane of the pyramid, the degenerate d_xz and d_yz orbitals are fully occupied, while in the distorted environment they are unequally occupied, giving rise to an appreciable magnetic anisotropy (Fig. 8).

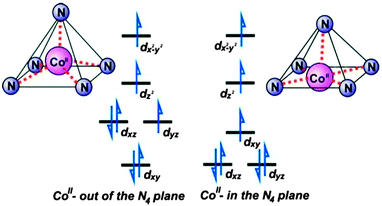Fig. 8 A simplified scheme illustrating the relative energies of the d-orbitals in a distorted square-based pyramid (left) and ideal square-based pyramid (right). Reprinted with permission from ref. 30. Copyright (2011) American Chemical Society.

The static magnetic properties reveal intermolecular ferromagnetic interactions between molecules of 25 at low temperature. To disrupt these contacts, 25 was dissolved in THF and the magnetic measurements repeated. As expected, χ_MT was seen to decrease at low temperature, as was the case for compound 24. The barrier to relaxation recorded for the solid state and frozen solution dynamic magnetic experiments performed on 25 was similar (16.7 and 17.4 cm⁻¹, respectively, under a dc field of 2000 Oe), while 24 displayed a smaller barrier of 11.1 cm⁻¹ (also at 2000 Oe). In the compound [Co(terpy)Cl₂] (26), the basal plane of the pyramid is formed by one Cl⁻ ion and the three donor N-atoms of the terpyridine ligand, with the metal ion also sitting just above this plane.³¹ The coordination sphere is therefore different compared to those of 24 and 25, leading to a different d-orbital splitting. In [Co(terpy)(NCS)₂] (27), the thiocyanate ligands both point out of the plane defined by the coordination of terpy to the metal ion. Through ac susceptibility measurements under two different fields, two different relaxation processes – fast and slow – could be observed for compounds 26 and 27, with barriers (fast/slow) of 19.5/2.8 cm⁻¹ and 11.8/2.1 cm⁻¹, respectively.

A wider theoretical study of how variations in coordination geometry can lead to magnetic anisotropy in first row transition metals has been carried out.³² Using CASSCF calculations, it can be shown how D may be expected to vary with the number of d-electrons and the symmetry around the metal ion. Using this predictive strategy, two systems from the literature were identified that ought to show high magnetic anisotropy, [Co(P(S)([N(CH₃)N=CHC₃N₂H₃]₃))](NO₃)₂ (28) and K(Co(N[CH₂C(O)NC(CH₃)₃]₃)) (29). Compound 28 (Fig. 9) was predicted to have a large negative value of D, which was found to be −72 cm⁻¹ based on the temperature and field-dependence of the magnetisation. Under a field of 2000 Oe, one clearly resolved temperature dependent maximum in χ′′ could be observed, with a barrier of U_eff = 23 cm⁻¹. For 29, the barrier at 1500 Oe was observed to be 8.7 cm⁻¹, and the anisotropy derived from the magnetisation measurements was consistent with theoretical calculations, with D = +16 cm⁻¹.

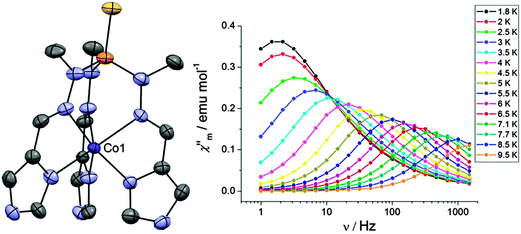Fig. 9 (left) A view of the cation [Co(P(S)([N(CH₃)N=CHC₃N₂H₃]₃))]²⁺; Co, purple; N, blue; P, orange; S, yellow; C, grey. (right) Frequency dependence of χ′′ under a dc field of 2000 Oe. Reprinted with permission from ref. 32. Copyright (2013) American Chemical Society.

Positive D values leading to SMM-like behaviour in monometallic Co(II) complexes is not uncommon, despite the perception that this might prevent slow relaxation processes.³³ The first example of a hexa-coordinate Co(II) SIM, the compound cis-[Co(dmphen)₂(NCS)₂]·0.25EtOH (30, dmphen = 2,9-dimethyl-1,10-phenanthroline) displays slow relaxation of the magnetisation with U_eff = 17.0 cm⁻¹ under a dc field of 1000 Oe, with D = +98 cm⁻¹. The slow relaxation is a result of a transverse anisotropy (xy plane). Under these conditions, the magnetisation would have a preferred orientation in the xy plane, either along the x- or the y-axis, rather than along the z-axis. The barrier to reorientation in the opposite direction along the same axis would then be governed by the parameter E. Through the relation U_eff ∼ 2E, a theoretical barrier of 16.8 cm⁻¹ was determined, based on the value of E = +8.4 cm⁻¹ obtained from low temperature magnetisation data. This was also the explanation put forward for the compound [(L)₄Co^III₂Co^II(H₂O)₂](NO₃)₄·6H₂O (31) (where L is a carbohydrazide derivative).³⁴

An alternative explanation of how positive axial anisotropy can result in slow relaxation of the magnetisation has been proposed for the pseudotetrahedral Co(II) complex [(3G)CoCl](CF₃SO₃) (32, where 3G = 1,1,1-tris-[2N-(1,1,3,3-tetramethylguanidino)methyl]ethane).³⁵ For 32, slow magnetic relaxation was observed with a barrier of 24 cm⁻¹ under a dc field of 1500 Oe, and EPR determined D = +12.7 cm⁻¹ and E = 1.2 cm⁻¹. Here it is proposed that relaxation from the M_S = +1/2 to the M_S = −1/2 level is slowed by a phonon bottleneck,³⁶ such that relaxation involves excitation to the higher lying M_S = ±3/2 levels. From the EPR and magnetisation data, an energy gap of the order of 24 cm⁻¹ was found to separate the M_S = ±1/2 levels from the higher lying M_S = ±3/2 levels, consistent with the barrier determined from the dynamic susceptibility measurements. A similar situation was found for the compound [dmphCoBr₂] (33, dmph = 2,9-dimethyl-1,10-phenanthroline).³⁷ The easy-plane anisotropy in this compound, with D = +11.68 cm⁻¹ and E = −2.60 cm⁻¹, yielded U_eff = 22.9 cm⁻¹ (under a field of 1000 Oe).

A phonon bottleneck has been ruled out for the compound [Co(L)(OAc)Y(NO₃)₂] (34, where LH₂ = N,N′,N′′-trimethyl-N,N′′-bis(2-hydroxy-3-methoxy-5-methylbenzyl)-diethylenetriamine) (Fig. 10).³⁸ Here, the magnetic anisotropy is of an easy-plane nature, with D = +47 cm⁻¹ and E = 1.6 cm⁻¹. Inelastic neutron scattering (INS) revealed an excitation with an associated energy of 95.2 cm⁻¹, corresponding to the energy gap (= 2D) between the M_S = ±3/2 and M_S = ±1/2 levels. Dilution experiments with the purely diamagnetic species [Zn(L)(OAc)Y(NO₃)₂] did not cause any increase in the relaxation, suggesting that a phonon bottleneck is not at the root of the observed barrier. The determined barrier of U_eff = 15.7 cm⁻¹, was far lower than the energy gap between the M_S = ±3/2 and M_S = ±1/2 doublets. In fact, fits of the Arrhenius plot to a T⁻ⁿ law indicate that an optical acoustic Raman process is a viable proposal for the relaxation mechanism, mixed with direct processes.

Fig. 10 (left) A view of [Co(L)(OAc)Y(NO₃)₂] (34); Co, purple; Y, pale blue; C, grey; O, red; N, blue. (right) A simplified representation of the energy levels in 34. Reprinted with permission from ref. 38. Copyright (2013) Wiley-VCH.

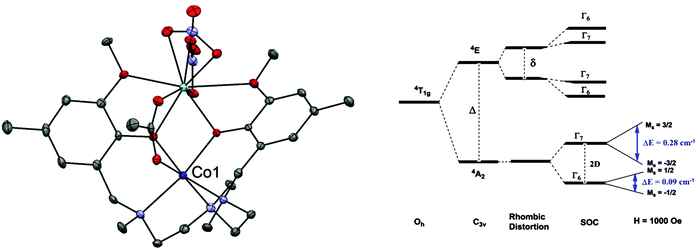
The most concerted effort to clarify how and why slow magnetic relaxation occurs in complexes with an easy plane anisotropy has been carried out on the hexa-coordinate Co(II) complex [Co(acac)₂(H₂O)₂] (35, acac = acetylacetonate).³⁹ The dynamic ac susceptibility can be accounted for with a linear fit to an Arrhenius plot, suggesting a thermally-activated Orbach process at higher temperatures. At lower temperatures, Raman and direct processes are responsible for the relaxation. Because Orbach processes proceed through phonon-induced transitions to higher energy states, their associated energy barrier should reflect this and be of the order of 2D, which in this case would imply a barrier of around 130 cm⁻¹. However, the barrier to thermal relaxation was found to be ∼16 cm⁻¹.

Formally, direct phonon-induced transitions between the two states that describe the low temperature electronic states of Co(II), shown in Fig. 11 as |Φ〉 and |Ψ〉, are forbidden. In theory, this leaves two-phonon Orbach and Raman relaxation processes available, with the proviso that ZFS is often far larger than the available thermal energies at low temperatures, hindering Orbach-driven relaxation. However, this clear-cut two level description is not entirely accurate (Fig. 11(a)). Hyperfine interactions with the nuclear spin of the Co(II) ion (I = 7/2) broaden these two levels into a manifold in which some phonon-induced transitions are permitted (Fig. 11(b)). The application of an external magnetic field exacerbates this splitting, and confers upon each state a measureable magnetic moment (Fig. 11(c)). Finally, an interaction between the nuclear spin and molecular vibrations in the lattice allow phonon-induced transitions between different nuclear spin states (Fig. 11(d)). The combination of these perturbations allows slow relaxation in Co(II) ions with easy plane anisotropy to be observed at low magnetic fields. Hence, it is proposed that hyperfine interactions should be minimised to limit the relaxation pathways available to a SIM. In fact, the low coordinate Fe(I) compound 7, which has the highest barrier found for a transition metal SIM fits with this strategy. The highest barrier for a Co(II) SIM with easy plane anisotropy was reported for the octahedral Co(II) complex [Co(abpt)₂(tcm)₂] (36), where abpt = 4-amino-3,5-bis(2-pyridyl)-1,2,4-triazole and tcm = tricyanomethanide, which displays a barrier of U_eff = 59.9 cm⁻¹ for an applied field of 3000 Oe, and D = +55 cm⁻¹ and E/D = 0.27.⁴⁰

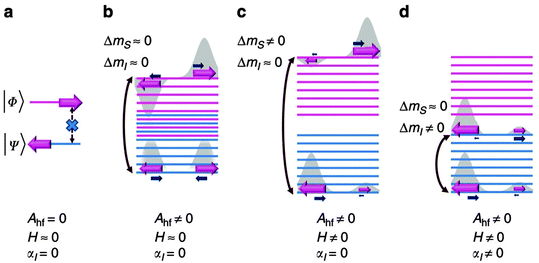Fig. 11 (top) A schematic view of the energy levels in the Kramers ion Co(II) with positive axial anisotropy. A_hf = hyperfine coupling; H = an applied magnetic field; α_l = lattice-phonon interactions. See text for details. Reprinted with permission from ref. 39. Copyright (2014) Nature Communications, Macmillan Publishers Ltd.

However, the majority of Co(II)-based SIMs display negative D values. In the cobalt(II)-12-crown-4 (12C4) complex [Co(12C4)₂](I₃)₂(12C4) (37) (Fig. 12) the Co(II) ion is coordinated by four oxygen atoms from the two crown molecules, leading to a distorted square anti-prismatic geometry.⁴¹ Density functional theory (DFT) calculations show that the partially filled d_xz and d_yz orbitals are almost degenerate. This gives rise to a low-lying excited state and coupling with the ground state can give rise to a large axial anisotropy.

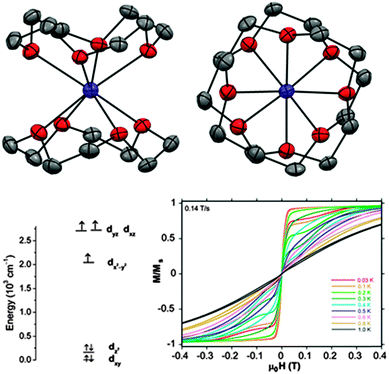Fig. 12 (top) A view of the cation [Co(12C4)₂]²⁺; Co, purple; O, red; C, grey. (bottom, left) d-orbital energy diagram derived from DFT calculations. (bottom, right) Field dependence of the normalised magnetisation of 37. Reprinted with permission from ref. 41. Copyright (2014) American Chemical Society.

Through fits of the dc susceptibility measurements, values of D = −37.6 cm⁻¹ and E = 0.1 cm⁻¹ were obtained. HFEPR studies showed the compound to be nearly “silent”. This was attributed to a combination of only the ±3/2 doublet being populated at low temperatures together with a large, negative D causing a large energy gap to the ±1/2 doublet. Simulations put a lower limit on this axial anisotropy of |D| > 20 cm⁻¹ and further theoretical calculations also confirm the large, negative D value. Suppression of QTM using an applied dc field of 500 Oe allows the observation of an out-of-phase signal in the ac susceptibility measurements, with an associated barrier to relaxation of 17.0 cm⁻¹.

Of the variety of coordination environments that have been employed to try to induce slow magnetic relaxation in Co(II) complexes, the most successful is tetrahedral or pseudo-tetrahedral, as in the case of 32, and 38–48 (see Table 1).^42–47 The value of D can be increased by increasing the softness of the donor atom in a family of compounds based on the complex anion [Co(EPh)₄]²⁻ (E = O, S, Se): (Ph₄P)₂[Co(OPh)₄]·CH₃CN (45), K(Ph₄P)[Co(OPh)₄] (46), (Ph₄P)₂[Co(SPh)₄] (47), (Ph₄P)₂[Co(SePh)₄] (48). However, it does not necessarily follow that the relaxation barrier increases in line with increasing D, and the reported barriers all lie in the range 19–34 cm⁻¹.^43,47 Similarly, the tetragonally-elongated pseudotetrahedral Co(II) compound (Ph₄P)₂[Co(C₃S₅)₂] (49) (C₃S₅²⁻ = 4,5-dimercapto-1,3-dithiole-2-thione) displays a large magnetic anisotropy, leading to a barrier of U_eff = 33.9 cm⁻¹ in the absence of an applied dc field.⁴⁸

Although compounds 46–49 display slow relaxation of the magnetisation without an applied dc field, this phenomenon is still rather rare for 3d SIMs. (HNEt₃)(Co^IICo^III₃L₆) (50, where H₂L = R-4-bromo-2-((2-hydroxy-1-phenylethylimino)methyl)phenol) displays zero-field slow magnetic relaxation.⁴⁹ The coordination environment around the Co(II) ion is twisted away from octahedral towards D₃ symmetry. The effect of the coordination geometry on the energies of the d-orbitals is shown in Fig. 13, consistent with the presence of significant unquenched orbital angular momentum. Fits of the magnetisation data give D = −115 cm⁻¹ and E = 2.8 cm⁻¹. The strong axial anisotropy leads to slow relaxation of the magnetisation, with a barrier of U_eff = 75.8 cm⁻¹. It is suggested that having the central Co(II) ion surrounded by three diamagnetic Co(III) ions helps to isolate the d⁷ centre, enhancing the SIM behaviour. A similar point was made for [Co^IIICo^II(LH₂)₂(X)(H₂O)](H₂O)₄ (51, X = Cl; 52, X = Br, LH₄ = 2-[((2-hydroxy-3-methoxyphenyl)methylene)amino]-2-(hydroxymethyl)-1,3-propanediol) where the presence of the diamagnetic Co(III) ion aids the observation of SIM behaviour, by reducing Co(II)⋯Co(II) intermolecular interactions.⁵⁰

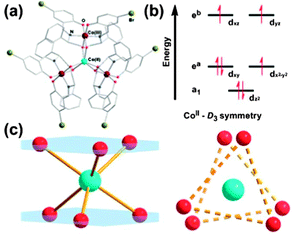Fig. 13 (a) A view of the cation in 50. (b) Approximate energy splittings of the d orbitals in D₃ symmetry. (c) A view of the coordination sphere and geometry around the Co(II) ion. Reprinted with permission from ref. 49. Copyright (2013) Royal Society of Chemistry.

3.6 Ni(I)

The only example of SIM behaviour described to date involving Ni(I) is for the linear, two-coordinate geometry, similar to that of 7. In [Ni(6-Mes)₂]Br (53) (6-Mes = 1,3-bis(2,4,6-trimethylphenyl)-3,4,5,6-tetrahydropyrimidin-2-ylidene), the mesityl groups of the bulky aromatic ligand are sufficient to block the equatorial sites on the Ni(I) ion, leading to the low coordination number.⁵¹ The geometry is found to be nearly linear, with a C–Ni–C angle of 179.27(13)°. The dc magnetic measurements show that the room temperature value of χT (1.12 cm³ mol⁻¹ K) is well above that expected for an S = 1/2 ion (0.375 cm³ mol⁻¹ K), indicative of the presence of unquenched orbital momentum. An applied field is required to observe slow magnetic relaxation, the barrier for which was determined as 11.8 cm⁻¹, based on the linear region of the Arrhenius plot.

3.7 Ni(II)

Despite promising studies that have shown very large magnetic anisotropy in several Ni(II) complexes, as of yet there has been no experimental demonstration of slow relaxation of the magnetisation in monometallic Ni(II) compounds. For example, in the trigonal bipyramidal compound [Ni(Me₆tren)Cl](ClO₄) (54), D is estimated to be between −120 and −180 cm⁻¹ and E = 1.6 cm⁻¹ from HFEPR measurements.⁵²

4. Conclusions and outlook

In the relatively short time in which they have been studied, 3d SIMs or monometallic SMMs have already yielded some fascinating results and possibilities. Amongst these, the linear Fe(I) compound 7 stands out, both for the huge barrier to relaxation of the magnetisation observed and also for the synthetic challenge such a compound represents. The ability to switch on slow relaxation of the magnetisation in the SCO compounds 21 and 22 also raises the question of how many “dormant” SIMs could be found in photo-switchable SCO complexes.

Attempts to understand the slow magnetic relaxation in Kramers ions with positive axial anisotropy have outlined the importance of physical considerations beyond the symmetry around a 3d ion, such as the importance of hyperfine interactions. Control of the relaxation pathways available to a single-ion magnet should allow for improvement in performance as a potential data carrier. The physics of these compounds and how this relates to other possible applications for nanomagnets, such as quantum computing, still has wide scope for exploration. This point was addressed for compound 49, which was shown to have a large axial anisotropy that enabled slow relaxation of the magnetisation to be observed. On the other hand, this anisotropy was so large that 49 was found to be EPR-silent, rendering it ineffective for use in quantum computing, for which EPR would need to be used to observe and address spin transitions.

The chemical synthesis of these compounds presents a huge opportunity. If factors such as nuclear spin, symmetry around the metal ion, and modification of ligands are taken into account, then there are clearly a large number of experimental parameters to be tuned and explored. The d⁸ ion Ni(II), for example, remains an extremely promising candidate, given the huge magnetic anisotropy already displayed in several compounds.

Acknowledgements

The UK Engineering and Physical Sciences Research Council are thanked for financial support (grant ref. EP/K033662/1).

References

1. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, OUP, 2006.
2. All of these advances are touched upon in: Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer-Verlag, Berlin, 2014.
3. H. Miyasaka, M. Julve, M. Yamashita and R. Clérac, Inorg. Chem., 2009, 48, 3420.
4. L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750.
5. H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1.
6. J. Ribas Gispert, Coordination Chemistry, Wiley-VCH, Weinheim, 2008.
7. R. L. Carlin, Magnetochemistry, Springer, Berlin, 1986.
8. D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268.
9. K. S. Pedersen, J. Bendix and R. Clerac, Chem. Commun., 2014, 50, 4396.
10. Molecular Magnets: Physics and Applications, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer-Verlag, Berlin, 2014.
11. W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115.
12. O. Waldmann, Inorg. Chem., 2007, 46, 10035.
13. P. Parois, S. A. Moggach, J. Sánchez-Benítez, K. V. Kamenev, A. R. Lennie, J. E. Warren, E. K. Brechin, S. Parsons and M. Murrie, Chem. Commun., 2010, 46, 1881.
14. D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224.
15. J. Vallejo, A. Pascual-Álvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075.
16. R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300.
17. A. Grigoropoulos, M. Pissas, P. Papatolis, V. Psycharis, P. Kyritsis and Y. Sanakis, Inorg. Chem., 2013, 52, 12869.
18. J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125.
19. J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577.
20. J. M. Zadrozny, D. J. Xiao, J. R. Long, M. Atanasov, F. Neese, F. Grandjean and G. J. Long, Inorg. Chem., 2013, 52, 13123.
21. P. P. Samuel, K. C. Mondal, N. Amin Sk, H. W. Roesky, E. Carl, R. Neufeld, D. Stalke, S. Demeshko, F. Meyer, L. Ungur, L. F. Chibotaru, J. Christian, V. Ramachandran, J. van Tol and N. S. Dalal, J. Am. Chem. Soc., 2014, 136, 11964.
22. A. Eichhöfer, Y. Lan, V. Mereacre, T. Bodenstein and F. Weigend, Inorg. Chem., 2014, 53, 1962.
23. P.-H. Lin, N. C. Smythe, S. I. Gorelsky, S. Maguire, N. J. Henson, I. Korobkov, B. L. Scott, J. C. Gordon, R. T. Baker and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 15806.
24. D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, Chem. – Eur. J., 2011, 17, 4700.
25. X. Feng, C. Mathonière, I.-R. Jeon, M. Rouzières, A. Ozarowski, M. L. Aubrey, M. I. Gonzalez, R. Clérac and J. R. Long, J. Am. Chem. Soc., 2013, 135, 15880.
26. A. Hauser, Chem. Phys. Lett., 1986, 124, 543.
27. C. Mathonière, H.-J. Lin, D. Siretanu, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2013, 135, 19083.
28. S. Mossin, B. L. Tran, D. Adhikari, M. Pink, F. W. Heinemann, J. Sutter, R. K. Szilagyi, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2012, 134, 13651.
29. M. Murrie, Chem. Soc. Rev., 2010, 39, 1986.
30. T. Jurca, A. Farghal, P.-H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814.
31. F. Habib, O. R. Luca, V. Vieru, M. Shiddiq, I. Korobkov, S. I. Gorelsky, M. K. Takase, L. F. Chibotaru, S. Hill, R. H. Crabtree and M. Murugesu, Angew. Chem., Int. Ed., 2013, 52, 11290.
32. S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010.
33. J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, J. Am. Chem. Soc., 2012, 134, 15704.
34. D. Wu, X. Zhang, P. Huang, W. Huang, M. Ruan and Z. W. Ouyang, Inorg. Chem., 2013, 52, 10976.
35. J. M. Zadrozny, J. Liu, N. A. Piro, C. J. Chang, S. Hill and J. R. Long, Chem. Commun., 2012, 48, 3927.
36. A more detailed discussion and description of phonon bottlenecks and their effects can be found in: R. Schenker, M. N. Leuenberger, G. Chaboussant, D. Loss and H. U. Güdel, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184403.
37. W. Huang, T. Liu, D. Wu, J. Cheng, Z. W. Ouyang and C. Duan, Dalton Trans., 2013, 42, 15326.
38. E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130.
39. S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300.
40. R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Inorg. Chem., 2014, 53, 5896.
41. L. Chen, J. Wang, J.-M. Wei, W. Wernsdorfer, X.-T. Chen, Y.-Q. Zhang, Y. Song and Z.-L. Xue, J. Am. Chem. Soc., 2014, 136, 12213.
42. R. Boča, J. Miklovič and J. Titiš, Inorg. Chem., 2014, 53, 2367.
43. J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209.
44. F. Yang, Q. Zhou, Y. Zhang, G. Zeng, G. Li, Z. Shi, B. Wang and S. Feng, Chem. Commun., 2013, 49, 5289.
45. A. Buchholz, A. O. Eseola and W. Plass, C. R. Chim., 2012, 15, 929.
46. D.-K. Cao, J.-Q. Feng, M. Ren, Y.-W. Gu, Y. Song and M. D. Ward, Chem. Commun., 2013, 49, 8863.
47. J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732.
48. M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716.
49. Y. Y. Zhu, C. Cui, Y. Q. Zhang, J. H. Jia, X. Guo, C. Gao, K. Qian, S. D. Jiang, B. W. Wang, Z. M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802.
50. V. Chandrasekhar, A. Dey, A. J. Mota and E. Colacio, Inorg. Chem., 2013, 52, 4554.
51. R. C. Poulten, M. J. Page, A. G. Algarra, J. J. Le Roy, I. López, E. Carter, A. Llobet, S. A. Macgregor, M. F. Mahon, D. M. Murphy, M. Murugesu and M. K. Whittlesey, J. Am. Chem. Soc., 2013, 135, 13640.
52. R. Ruamps, R. Maurice, L. Batchelor, M. Boggio-Pasqua, R. Guillot, A. L. Barra, J. Liu, E.-E. Bendeif, S. Pillet, S. Hill, T. Mallah and N. Guihéry, J. Am. Chem. Soc., 2013, 135, 3017.

---