Positional recurrence maps, a powerful tool to de-correlate static and dynamical disorder in distribution maps from molecular dynamics simulations: the case of Nd₂NiO_4+d

Abstract

In order to investigate the on-site motion of the diffusive species in crystalline solids, we have implemented a code to perform a time-summation of displacements of specific atoms, involving symmetry and adapted projections. The resulting 2D maps have been called ‘positional recurrence maps’ (PRM). Only displacements are considered, instead of positions, so static deformations are filtered out. In this paper we present the PRM method and show the type of information on the dynamics of selected atoms that can be obtained. We take, as an example, the Nd₂NiO_4+d system in which we were able to characterize in detail the effects of the dynamical delocalization of the apical oxygen.

---

Introduction

Oxygen ion conducting materials have been thoroughly investigated in the past decades.^1–4 The property of oxygen ion conduction, meaning the current flow induced by the diffusion of oxide ions through the crystal, is of particular interest for technological devices and in particular for electrodes in solid oxide fuel cell (SOFC).^5–8

In order to design optimal oxygen ion conducting materials, the microscopic mechanism of diffusion must be elucidated both in terms of the displacement pattern of an oxide ion from one site of the crystal lattice to another and in terms of the driving force, i.e. where ions recover energy to diffuse. The fact that the crystal should contain connected and partially-occupied oxygen sites restricts the list of the potential candidates to a few families of structures: the fluorite-type oxides, the perovskite-related oxides and the K₂NiF₄-type oxides.

A diffusion mechanism describes the energy required by an ion to migrate in the crystal, which is a microscopic description of macroscopic diffusion coefficients. In this respect, due to their double negative charges and large ionic radius of 1.4 Å, the mobility of oxide ions would seem, at first sight, to be unlikely. The migration of an oxide ion is generally attributed to a thermally-activated hopping process, with typical migration energies lower than 1 eV. Therefore, high temperatures have to be considered in order to reach suitable values of ionic conductivity.

However, recent studies have shown that a few materials of the Brownmillerite-type and of the K₂NiF₄-type show significant and highly anisotropic oxygen mobility even close to room-temperature.^9–11 Such anomalous diffusion cannot be explained by thermally-activated, stochastic oxygen hopping, usually described with an Arrhenius law.

In the Brownmillerite system, a phonon-assisted diffusion mechanism was proposed, implying a coupling of diffusion events with specific low-energy lattice dynamics.¹² Only recently, a similar scenario, where lattice dynamics triggers low temperature oxygen diffusion, has been revealed in the case of the K₂NiF₄-type materials.¹³

In these works and in many others dealing with high temperature, thermally activated oxygen ion diffusion, molecular dynamics (MD) simulations played a major role in elucidating the specific migration paths of diffusing species and in clarifying the underlying mechanism.^14–18

A variety of useful information concerning atomic motion, diffusion pathways, diffusion constants (or at least the statistics of diffusion events) and lattice dynamics, can be extracted from MD trajectories. However, while the diffusion events can easily be seen in a global time-summation of the trajectory, as available in many MD analysis codes (for example LAMP and nMoldyn), we did not find any software to visualise and analyse the on-site motion of the diffusive species, meaning with site occupation in space and time of an atom respect to its equilibrium position.

For this reason, we have implemented a MATLAB¹⁹ code to perform the time-summation of specific atoms and their corresponding displacements, involving symmetry and adapted projections, to provide 2D maps that are visually similar to density maps. To avoid any confusion with the ‘nuclear density map’ from diffraction, which usually refers to the reverse Fourier transform of elastic coherent scattering, we will use the term ‘positional recurrence maps’ (PRM) for the present representations, which also integrates the inelastic scattering. With the PRM method, as implemented by us, only displacements are considered instead of positions and so static deformations are removed.

Filtering out static deformations, as typically found in complex structures with split site positions with respect to a high-symmetry structure, is particularly useful in system where dynamic motion is believed to play a major role on the physical property of interest, as in the present case for ionic conductivity.

We take as an example the Nd₂NiO_4+d system in which, thanks to the use of PRM, we were able to characterize in detail the effects of dynamical delocalization of apical oxygen and how their modifications correlate with the real changes in lattice dynamics measured in inelastic neutron scattering experiments.¹³

In this particular system, and as in most non-stoichiometric ionic conductors, diffusive atoms sit in disordered positions with respect to high-symmetry structures. The ability to isolate dynamical motion from average occupation probabilities is thus essential to properly estimate the effective atomic motion and its role in the microscopic mechanism of diffusion.

In this work, we present in detail the mathematics behind the PRM method and show how the relevant information on the dynamics of selected atoms that can be obtained: (i) the minimal MD simulation time required by an atom to explore all the space around its equilibrium position; (ii) the minimal MD time required to see a diffusion event and the time required to explore all diffusive channels; (iii) the effect of temperature and lattice parameters on the allowed displacement directions and on the maximum distance that an atom can reach; (iv) the effect of stoichiometry on the on-site atom dynamics.

Theoretical method

We performed ab initio DFT MD calculations using the VASP code.^20,21 The calculations have been performed in the NVT ensemble in a 40 ps time window for an approximately regular supercell containing 112, 114, and 232 atoms for oxygen excess contents d = 0, d = 0.125 and d = 0.25, respectively. Projected augmented wave (PAW) potentials were chosen for the ionic core–valence electron interactions and the Perdew, Burke, and Ernzerhof (PBE) scheme for the generalized gradient approximation (GGA) was used for the exchange–correlation potential.

We performed spin-polarized calculations on the low-temperature, tetragonal phase of stoichiometric Nd₂NiO_4.0 with collinear magnetism on Ni ions only. For Nd, a simplified pseudopotential with frozen 4f orbitals has been used. For more detailed information about simulations please refers to ref. 13. The most important parameter used for the MD simulations are reported in the ESI† (Table S1 for Nd₂NiO₄ and Table S2 for Nd₂NiO_4+d).

The construction process of a PRM is based on the cumulative sum in time of the nuclear trajectories, considering atomic displacements instead of atomic positions, as described in eqn (1).

With n(x,y,z)_j,T the positional recurrence map of atoms j limited in time to the integrated simulation time T, p_j(x_t,y_t,z_t) the atomic position of atom j at step t, p_j(x_CoM,y_CoM,z_CoM) its center-of-mass (CoM) position. In our case the structure has been optimized before the molecular dynamics, hence

p_j (x_CoM, y_CoM, z_CoM) = p_j (x_t=0, y_t=0, z_t=0) (2)

Point group symmetry is added through i operations, where Aⁱ corresponds to the i symmetry equivalence, while the B_j vectors are used to sum equivalent atoms. The additional vectors C_j can be added to transform the displacement space back to Cartesian space. In the PRM method, any non equivalent atom of the structure can be visualised. The PRM method can easily reveal the shift of the mean atomic positions away from the equilibrium site in the form of a splitting in the PRM density. Considering a 40 ps long MD simulation, a tetragonal supercell and apical oxygen as the selected atoms, eqn (1) becomes:

With Aⁱ

The best way to visualise the PRM analysis is to plot a 2D map in a specific plane of the unit cell where the most of the effects are expected. A complete (or partial) projection of n(x,y,z)_j,T along the direction orthogonal to the selected plane is then performed.

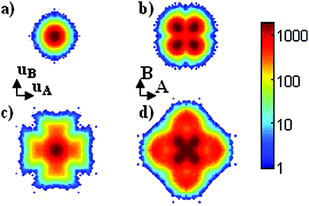
To illustrate the difference between the center-of-mass origin and the Cartesian origin, simulations of tetragonal Nd₂NiO_4.0 with optimized lattice parameters and with a reduced c-axis have been performed. 2D maps of the apical oxygen atoms in Cartesian space and in displacement space (PRM) have been extracted and are shown in Fig. 1. Since the atomic position of the apical oxygen atom is of the type (x,x,z), a splitting is expected into four lobes in the [110] direction from (0,0,z) in the Cartesian projection. The simulations with the reduced c-axis length gives a structure with constrained amplitude of motion, i.e. small vibration around the equilibrium position, and the static splitting of the atomic positions is effectively observed in Fig. 1b. On the contrary, in the PRM, the centre-of-mass positions (x,x,z) are re-centred at (0,0,z) and a single spot defining the constrained motion is observed in Fig. 1a.

Fig. 1 (a and c) PRM projected on (u_A, u_B) plane and (b and d) Cartesian position projected on (a and b) plane of apical oxygen atoms of Nd₂NiO_4.0 from molecular dynamics simulations at 310 K. (a and b) Structural model with slightly compressed c-axis parameter, and (c and d) optimized c-axis parameter in. The colour scale is logarithmic and white corresponds to zero background, blue to one count, with respect to the integration unit box of volume d³r = 5.45 × 10⁻⁵ ų.

For larger amplitude of motion, as in the case of simulations with optimal c-axis parameter, the PRM maps give a straightforward visualization of the atomic displacement pattern, i.e. dynamics. Fig. 1c shows that the atomic motions are clearly along [100] and [010]. On the contrary, using the simple projection of atomic positions, a more confused picture is obtained, as shown in the Cartesian projection of Fig. 1d. The PRM method is thus useful to reveal the dynamics of specific atoms without the effects of static disorder.

The code is available in the ESI† for the Nd₂NiO_4+d case. The PRM approach is easily transferable to any system with an orthogonal structure (α = β = γ = 90°) and it has been tested on K₂NiF₄ systems and on perovskite and perovskite-related systems, i.e. already exploitable in the fields of ionic conductors, HT superconductors, Mott insulators and multiferroics.

Results and discussion

MD simulations (up to 40 ps) have been carried out on the Nd₂NiO_4+d for d = 0, 0.125, 0.25 and at temperatures of 150, 230, 310, 670, 1070 K. As an example, a random step of the MD is shown in Fig. 2, where we can see the presence of several, interstitial oxygen atoms and their first neighbour apical oxygen, but also the presence of metastable positions defining distorted polyhedra (orange pyramids in Fig. 2) and oxygen in transient positions in between apical and interstitial sites. Simulations clearly show that diffusion events have occurred, but no detailed information about how each atom displaces about its equilibrium position is evident. Furthermore, in the time integral there is no clear indication if the atoms have had enough time to explore phase space. It should be confirmed that the simulation is long enough to satisfy the ergodic hypothesis, i.e. to be able to assume that the average of a process parameter over time and the average over the statistical ensemble are the same. Only in this case, the evolution of a single MD simulation may be used to determine macroscopic, thermodynamic properties.

Fig. 2 Random step of the MD calculation on the (2√2, 2√2, 1) supercell of Nd₂NiO_4.25 at T = 310 K. NiO₆ polyhedra are depicted in blue, while square-pyramid NiO₅ polyhedra are in orange. Excess oxygen atom in an interstitial site is in red and bound to its four apical oxygen neighbours. Apical-interstitial oxygen pair in saddle state is in orange and bound to its first neighbour nickel atom.

PRM can easily address these issues by looking directly at the phase space of a particle. The effect of simulation time on PRM of oxygen apical atoms of Nd₂NiO_4.25 is shown in Fig. 3. The time label corresponds to the upper limit of the cumulative sum over the apical oxygen trajectories. Starting from t = 0 the oxygen atoms displace and explore the space around their equilibrium position. Depending on the structure, a specific atom needs a minimum amount of time to explore all the phase space around equilibrium depending on parameters like the potential stiffness and the complexity of neighbouring shells. For the apical oxygen in Nd₂NiO_4.25 at least 20 ps of MD are needed to explore the whole space around equilibrium position – it is only after 20 ps that the intensity map in the area inside a displacement radius of 1 Å from the centre of mass does not change any more.

Fig. 3 PRM of apical oxygen atoms of Nd₂NiO_4.25 in function of MD time evolution at 310 K. Each PRM is cut in space to the conventional F-cell (black border). The colour scale is logarithmic and white corresponds to zero background, blue to one count, with respect to the integration unit box of volume d³r = 1.08 × 10⁻⁴ ų. The time label corresponds to the upper limit of the cumulative sum over the apical oxygen atom trajectories.

In the non-stoichiometric cases, as for Nd₂NiO_4.25, diffusion events can be also observed where the mobile oxygen is the apical oxygen jumping along [110] to the nearest, vacant interstitial site. In this case, 40 ps is necessary to have unchanged intensity in the map in the zones beyond a displacement radius of 1 Å from the centre of mass (see Fig. 3).

PRM are also useful to reveal displacement patterns and their modifications, i.e. activation of different dynamics, as a function of external parameters, namely stoichiometry d and temperature. Fig. 4 shows the PRM of apical oxygens from 40 ps MD simulations for Nd₂NiO_4.0, Nd₂NiO_4.125 and Nd₂NiO_4.25 at five different temperatures: 150, 230 K (LT), 310 K (RT), 670, 1070 K (HT).

Fig. 4 PRM of apical oxygen atoms from molecular dynamics at T = 150, 230, 310, 670 and 1070 K, of Nd₂NiO_4.0, Nd₂NiO_4.125 and Nd₂NiO_4.25. Each PRM is cut in space to the conventional F-cell (black border). The colour scale is logarithmic and white corresponds to zero background, blue to one count, with respect to the integration unit box of volume d³r = 5.45 × 10⁻⁵ ų for d = 0, d³r = 5.33 × 10⁻⁵ ų for d = 0.10 and d³r = 1.08 × 10⁻⁴ ų for d = 0.25.

In the stoichiometric Nd₂NiO_4.0 case, the PRM at room temperature (310 K or RT) shows a cross shape with preferred displacements in the [010] direction, which is expected since the low temperature orthorhombic phase (LTO) has its tilt pattern along [010]. At low temperature (150 K, 230 K or LT) the apical oxygen PRM is completely isotropic, which means that the apical oxygen is rigidly held within the NiO₆ octahedron. At high temperature (670 K, 1070 K or HT), a change is observed in the displacement from the [010] to the [110] direction, due to the activation of the [110] tilt mode.

In the most-oxidized Nd₂NiO_4.25 case, the PRM of apical oxygen at LT shows [110] delocalization. This comes from the first neighbour interaction of NiO₆ and interstitial oxygen atoms. In this rigid case, much of the freedom of the NiO₆ octahedron is pinned by the interstitial oxygen. At RT the second neighbour interaction disappears and the [110] pathway is enabled. At HT the apical oxygen density shows an even broader [110] delocalization.

In the intermediate Nd₂NiO_4.125 case, the PRM pattern of the apical oxygen atom at RT shows both [010] and [110] delocalization. This is consistent with the quarter filling of interstitial sites by excess oxygen atoms for d = 0.125, which means that, assuming only the first shell of O_int neighbours is strained, about 75% of apical oxygen atoms have ‘normal’ dynamics and contribute to [010] delocalization, and 25% of them experience a [110] deformation, which thus activates the [110] delocalization. At LT a similar PRM is observed, but with fewer [010] displacements and more pronounced [110] delocalization. In this rigid regime, every NiO₆ octahedron is strongly dependent on its neighbours, which means that the [110] strained apical oxygen drives the free apical oxygen from [010] to [110]. At HT, the octahedra become less constrained, which leads to a renewed [010] delocalization, a strong [110] delocalization from interstitial oxygen, and an easy diffusion between apical and interstitial sites.

At the high-temperature limit of 1070 K, the patterns look almost isotropic. Such behaviour means that the apical oxygens are freed from the octahedron and behave independently, which is consistent with the HT, average structural representation and the incoherent diffusion model. We note that, even at high temperature, no diffusion events are observed for the Nd₂NiO_4.0 model.

PRM can be obtained for any non equivalent atom in the structure and, for the case under discussion, it is interesting to map the displacement pattern of excess oxygen atoms initially located in interstitial sites.

Fig. 5 shows the PRM of interstitial oxygen for the Nd₂NiO_4.125 and the Nd₂NiO_4.25 and for the three temperatures, T = 310, 670 and 1070 K. The Nd₂NiO_4.125 analysis complements in a straightforward way the previous results (see Fig. 4 and connected discussion). A well-defined interstitial site is present for which the phase space explored does not change with temperature. Diffusion events are present at each temperature, revealed by the population of former interstitial sites in the apical sites. With increasing temperature, a second, more distant site is occupied (see Fig. 5b and c). This means that at RT, the interstitial oxygen can diffuse only to the apical oxygen that the [110] octahedron tilt scheme has brought close and thus that diffusion is linked to the dynamics of the lattice. At HT interstitial oxygen has enough thermal energy to diffuse to any possible next neighbour, apical oxygen site.

Fig. 5 PRM of interstitial oxygen atoms from molecular dynamics on (a–c) Nd₂NiO_4.125, and (d–f) Nd₂NiO_4.25. (a and d) refers to T = 310 K, (b and e) to T = 670 K, and (c and f) to T = 1070 K. Each PRM is cut in space to the conventional F-cell (black border). The colour scale is logarithmic and white corresponds to zero background, blue to one count, with respect to the integration unit box of volume d³r = 5.33 × 10⁻⁵ ų for d = 0.10 and d³r = 1.08 × 10⁻⁴ ų for d = 0.25.

The Nd₂NiO_4.25 scenario is more complex, but still in agreement with the description of the apical oxygen PRM (see Fig. 4 and connected discussion). At RT there is a complex swinging behaviour of the excess oxygen in the interstitial sites towards the apical sites (see Fig. 5d). At intermediate temperature, T = 670 K (see Fig. 5e), the phase space of oxygen diffusing to apical site is completely defined, while the outer spots in non-defined sites are meta-stable positions as the oxygen has not had enough time to move further. Indeed at high-temperature (see Fig. 5d) a pattern is observed which is very similar to the one of the apical oxygen atoms, yet less pronounced in intensity due to the lower statistics (there is much less excess oxygen than apical oxygen). At any temperature, the delocalization pattern is more complex and the sites better defined after diffusion in the Nd₂NiO_4.25 case than in the Nd₂NiO_4.125. This means that the inclusion of a high amount of excess oxygen starts to sterically constrain the available diffusion paths, as the defective clusters overlap, which leads to energetically unfavorable configurations. The agreement between the two, related PRM representations confirms that, at HT, 40 ps simulations are long enough to let apical or interstitial oxygen have time to completely explore the phase space up to next neighbour positions.

The simulations reported here are in good agreement with experimental results obtained for the apical oxygen displacement factors from neutron single crystal diffraction data for Nd₂NiO_4.25 and its Pr-based homologous at different temperatures.²² Large displacement amplitudes along [110] have been shown to be present already at ambient temperature, while the potential develops with an anharmonic behaviour for O_ap and the Pr atoms, making the Pr₂O₂ layer a dynamically activated interface for easy oxygen diffusion. While the information on dynamics is not easy to extract from diffraction studies, the experimental results are in good agreement with simulations of Nd₂NiO_4.25. This suggests that the large displacement amplitudes found experimentally for the apical oxygen atoms in Nd₂NiO_4.25 and Pr₂NiO_4.25 have a pronounced dynamical contribution. Nd₂NiO_4.25 and Pr₂NiO_4.25 are special cases with respect to homologous K₂NiF₄-type oxides, as they can uptake a significant amount of extra oxygen atoms and consequently produce large displacements. The dynamical origin of oxygen atom delocalization is thus an important factor for easy oxygen diffusion between apical and interstitial sites down to ambient temperature. Indeed the same magnitude of displacement amplitudes are found for example in La₂CoO_4+d, but only at much higher temperatures.²³

Conclusions

We have performed MD simulations on Nd₂NiO_4+d with different stoichiometries with the aim of understanding their lattice dynamics. We have derived position recurrence maps (PRM) as an efficient way to visualize the on-site motion of the diffusive species, meaning the occupation in space and time of an atom with respect to its site.

Since reliable MD simulations are dependent on the simulation time, satisfactory comparisons on similar systems are possible only if simulation times are long enough. The PRM method is a simple way to map the on-site phase space of a specific non equivalent atom in the structure. This also determines the minimal time of a MD run that is required to satisfy the ergodic hypothesis.

PRM reveals the dynamics of specific atoms and the effects of parameters like stoichiometry and temperature. From the results on Nd₂NiO_4+d systems, we have found that, for d = 0, the low temperature structure forbids any diffusion events on a 40 ps timescale and freezes the NiO₆ octahedron in its contracted tilt pattern, with a strong localization of the apical oxygen atom. High temperatures enable the delocalization of the apical oxygen and thus the free rotations of the NiO₆ octahedra. The change of dynamics from [010] to [110] direction favours apical oxygen diffusion.

Considering the effect of d, excess oxygen in interstitial sites activates the [110] dynamics of apical oxygen atoms. At RT the interstitial oxygen can diffuse only to the apical oxygen that the [110] octahedron tilt scheme brings closer and therefore that diffusion is linked to the specific lattice dynamics.

At HT, interstitial oxygen has enough thermal energy to diffuse to any possible next neighbourhood apical oxygen site. At 1070 K, the patterns look almost isotropic, meaning that the apical oxygen atoms are freed from the octahedra and behave independently; this corresponds well to the HT average representation and to the incoherent diffusion model. We note that, even at high temperature, no diffusion events are observed for the Nd₂NiO_4.0 model.

Acknowledgements

We acknowledge the computing time given on the ILL cluster.

References

1. A. J. Jacobson, Chem. Mater., 2010, 22, 660–674.
2. A. Orera and P. R. Slater, Chem. Mater., 2010, 22, 675–690.
3. J. W. Fergus, J. Power Sources, 2006, 162, 30–40.
4. N. P. Brandon, S. Skinner and B. C. H. Steele, Annu. Rev. Mater. Res., 2003, 33, 183–213.
5. A. Chroneos, B. Yildiz, A. Tarancon, D. Parfitt and J. A. Kilner, Energy Environ. Sci., 2011, 4, 2774–2789.
6. K. T. Lee, H. S. Yoon and E. D. Wachsman, J. Mater. Res., 2012, 27, 2063–2078.
7. F. Chauveau, J. Mougin, J. M. Bassat, F. Mauvy and J. C. Grenier, J. Power Sources, 2010, 195, 744–749.
8. A. Yamada, Y. Suzuki, K. Saka, M. Uehara, D. Mori, R. Kanno, T. Kiguchi, F. Mauvy and J. C. Grenier, Adv. Mater., 2008, 20, 4124–4128.
9. S. Inoue, M. Kawai, N. Ichikawa, H. Kageyama, W. Paulus and Y. Shimakawa, Nat. Chem., 2010, 2, 213–217.
10. A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, J. Mater. Chem., 2010, 20, 266–270.
11. J. M. Bassat, M. Burriel, O. Wahyudi, R. Castaing, M. Ceretti, P. Veber, I. Weill, A. Villesuzanne, J. C. Grenier, W. Paulus and J. A. Kilner, J. Phys. Chem. C, 2013, 117, 26466–26472.
12. W. Paulus, H. Schober, S. Eibl, M. Johnson, T. Berthier, O. Hernandez, M. Ceretti, M. Plazanet, K. Conder and C. Lamberti, J. Am. Chem. Soc., 2008, 130, 16080–16085.
13. A. Perrichon, A. Piovano, M. Boehm, M. Zbiri, M. Johnson, H. Schober, M. Ceretti and W. Paulus, J. Phys. Chem. C, 2015, 119, 1557–1564.
14. A. Villesuzanne, W. Paulus, A. Cousson, S. Hosoya, L. Le Dreau, O. Hernandez, C. Prestipino, M. I. Houchati and J. Schefer, J. Solid State Electrochem., 2011, 15, 357–366.
15. C. Tealdi, C. Ferrara, P. Mustarelli and M. S. Islam, J. Mater. Chem., 2012, 22, 8969–8975.
16. D. Parfitt, A. Chroneos, J. A. Kilner and R. W. Grimes, Phys. Chem. Chem. Phys., 2010, 12, 6834–6836.
17. E. N. Naumovich and V. V. Kharton, Theochem-J. Mol. Struct., 2010, 946, 57–64.
18. A. Kushima, D. Parfitt, A. Chroneos, B. Yildiz, J. A. Kilner and R. W. Grimes, Phys. Chem. Chem. Phys., 2010, 13, 2242–2249.
19. MATLAB R2015b, The MathWorks, Inc., Natick, MA, United States.
20. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 48, 13115–13118.
21. G. Kresse and J. Furthmuller, Phys. Rev. B, 1996, 54, 11169–11186.
22. M. Ceretti, O. Wahyudi, A. Cousson, A. Villesuzanne, M. Meven, B. Pedersen, J. M. Bassat and W. Paulus, J. Mater. Chem. A, 2015, 3, 21140–21148.
23. L. LeDreau, C. Prestipino, O. Hernandez, J. Schefer, G. Vaughan, S. Paofai, J. Manuel Perez-Mato, S. Hosoya and W. Paulus, Inorg. Chem., 2012, 51, 9789–9798.

---

Footnote

† Electronic supplementary information (ESI) available: DFT simulation parameters, position recurrence map code. See DOI: 10.1039/c5cp06464c

---