The role of copper in the thermal conductivity of thermoelectric oxychalcogenides: do lone pairs matter?

Abstract

Understanding the underlying mechanisms that suppress thermal conduction in solids is of paramount importance for the targeted design of materials for thermal management and thermoelectric energy conversion applications. Bismuth copper oxychalcogenides, BiOCuQ (Q = Se, Te), are highly crystalline thermoelectric materials with an unusually low lattice thermal conductivity of ∼0.5 Wm⁻¹ K⁻¹, a value normally found in amorphous materials. Here we unveil the origin of the unusual thermal transport properties of these phases. First principles calculations of the vibrational properties combined with analysis of in-situ neutron diffraction data, demonstrate that weak bonding of copper atoms within the structure leads to an unexpected vibrational mode at low frequencies, which is likely to be a major contributor to the low thermal conductivity of these materials. In addition, we show that anharmonicity and the large Grüneisen parameter in these oxychalcogenides are mainly related to the low frequency copper vibrations, rather than to the Bi³⁺ lone pairs.

---

Introduction

Declining stocks of fossil fuels and concerns over CO₂ gas emissions pose a major challenge to society, which motivates the search for alternative energy generation technologies, including those for energy recovery. Thermoelectric power generation from waste heat offers one possible solution to the problem of increasing energy efficiency using existing energy-generation technologies. To enable widespread implementation of thermoelectric energy recovery, significant improvements in the performance of thermoelectric materials, which is related to a figure of merit, ZT = S²σT/κ (where S, σ and κ are the Seebeck coefficient, electrical and thermal conductivities respectively),¹ are required. High ZT necessitates coexistence of high electrical conductivity and low thermal conductivity, an extremely unusual combination of properties. For this reason, understanding phonon transport in thermoelectric materials with ultralow thermal conductivities, such as Cu₁₂Sb₄S₁₃ and Cu₃SbSe₃,^2,3 is attracting considerable interest.

Bismuth copper oxychalcogenides, formulated as BiOCuQ or BiCuQO (Q = Se, Te) have been recently identified as promising thermoelectric materials.^4,5 Aliovalent doping at the bismuth site can enhance their power factor and results in remarkable thermoelectric performances.^6,7 High values of ZT have been obtained by doping with Sr²⁺, Ca²⁺ and Pb²⁺,^5–7 while ZT = 1.4 has been achieved through texturing.⁸ The outstanding performance of these materials arises from their intrinsically low lattice thermal conductivity, whose origin remains unclear, despite recent studies of the phonon density of states of the oxyselenide.^9,10 Previous experimental studies have suggested that low thermal conduction is due to the presence of the Bi³⁺ lone pair,¹¹ which can reduce the lattice thermal conductivity due to bond anharmonicity.¹² Here we will show, however, that anharmonicity is primarily linked to an unexpected copper vibrational mode; a feature that may lead to a new approach for the design of thermoelectric materials with enhanced ZT.

Experimental

Synthesis

Stoichiometric mixtures of Cu, Bi, Bi₂O₃ and a chalcogen (S, Se or Te) were ground prior to being sealed into evacuated fused silica tubes (∼10⁻⁴ Torr). For the reaction producing BiOCuS, the sealed tube was first heated at 1 K min⁻¹ up to 673 K, and maintained at that temperature for 48 hours. After cooling the tube to room temperature, the sample was ground, pressed into a pellet and sealed into an evacuated silica tube for a second firing at 873 K for 48 hours. For BiOCuSe, the sealed tube was first heated at 623 K for 20 hours and then up to 773 K for 10 hours, using a 2 K min⁻¹ ramp rate. After grinding and resealing the sample into a carbon-coated silica tube, it was heated at 873 K for 7 hours. For BiOCuTe, the tube was first heated up to 623 K with a ramp rate of 1 K min⁻¹. After 24 hours, the temperature was increased to 773 K, and the silica tube maintained at that temperature for 48 hours. After cooling, the sample was ground and sealed into an evacuated silica tube again for a final firing at 773 K for 72 hours. The quality of each sample was initially assessed using powder X-ray diffraction, which indicated that each sample consisted of highly-crystalline BiOCuQ (Q = S, Se, Te). For thermal transport measurements, the powders were hot pressed into well-densified pellets (∼95% of theoretical density), under a N₂ flow. The following conditions were used: for BiOCuS, 823 K and 130 bar for 10 min; for BiOCuSe, 853 K and 50 bar for 30 min; for BiOCuTe, 773 K and 50 bar for 30 min.

Powder neutron diffraction

Neutron diffraction data for powdered samples of BiOCuQ were collected on the POLARIS diffractometer at the ISIS facility, Rutherford Appleton Laboratory. Approximately 3 g of each powdered sample was contained in an evacuated and sealed high-purity boron-free silica ampoule. The ampoule was contained in a vanadium can held inside a furnace evacuated to a pressure <10⁻⁴ Torr. Time-of-flight data were collected on heating from ambient temperature to 673 K, at the following temperatures: 293, 373, 473, 573, 623 and 673 K. Each dataset was collected for ∼300 μA h proton beam current on the ISIS neutron target (approximately 2 hours duration). Data reduction and file output was carried out using the Mantid¹³ software package. Normalised diffraction patterns from the Polaris backscattering, 90° and low angle detector banks (average 2θ = 146.7°, 92.6° and 52.2° respectively) were used simultaneously in Rietveld refinements carried out using the GSAS package.¹⁴ Final observed, calculated and difference profiles, together with final refined parameters, and selected bond distances and angles can be found in the ESI.† The following expression, which corresponds to the Einstein model of a harmonic oscillator,¹⁵ has been used to determine the Einstein temperature of the copper atoms:

U_iso = h²T/(mk_Bθ_E²4π²)

where h and k_B are the Plank and Boltzmann constants, m is the mass and θ_E is the Einstein temperature of the oscillator. The Einstein temperature can be determined from the slope of U_iso(T). The vibrational frequency is related to θ_E by ν = k_Bθ_E/h. The Debye temperature of the stiff network formed by Bi, O and Q can be determined using the following expression:¹⁵

U_iso = [3h²/mk_Bθ_D²4π²]T

where θ_D is the Debye temperature. The average velocity of sound in the Debye model is given by:
where n is the number of atoms per unit volume.

Thermal conductivity measurements

Thermal diffusivity measurements were carried out on 12.7 mm diameter hot-pressed pellets over the temperature range 300 ≤ T/K ≤ 573 using a Netzsch LFA 447 instrument. This instrument determines the thermal diffusivity (α) and the heat capacity (C_p) of the sample. The thermal conductivity (κ) is calculated from the relationship: κ = αC_pρ, where ρ is the sample density. For the determination of the heat capacity, a reference material, Pyroceram™ 9606, was used. The density of each sample was determined using the Archimedes method.

Calculations

Vibrational properties have been obtained by using density functional perturbation theory (DFPT)¹⁶ as implemented in the Quantum Espresso (QE) package.¹⁷ The experimental unit cell parameters (determined at 293 K using neutron diffraction data) were used as input. The calculation has been performed by using a set of ultrasoft pseudopotentials¹⁸ with the PBEsol exchange–correlation functional.¹⁹ The kinetic energy cutoff and the charge density cutoff are set to be 40 Ry and 200 Ry, respectively. An 8 × 8 × 4 k-point mesh is used to sample the Brillouin zone. The dynamical matrix has been constructed on a 4 × 4 × 2 q-point mesh and subsequently interpolated onto a finer mesh (24 × 24 × 12) to generate the vibrational density of states (VDOS). The mode-resolved Grüneisen parameter is computed using
and evaluating the fractional contribution of the jth atom in the unit cell to the sth mode at a sampling point q. Total energy response to atomic displacements was determined by shifting the ions along inequivalent tetragonal directions and computing the energy of the new configuration. The maps explore a range of displacements up to 0.4 Å.

Results and discussion

Three sets of experimental observations are especially relevant: (1) the total thermal conductivity of BiOCuQ (Fig. 1) is dominated by the lattice component, shows the 1/T dependence expected for crystalline solids at temperatures above the Debye temperature, and falls from the oxysulfide to the oxytelluride, following the normal trend of decreasing thermal conductivity with increasing atomic mass. (2) Measurements of the elastic properties of BiOCuSe indicate that this material has a low Young's modulus (76.5 GPa at 300 K) suggesting weak bonding, and a high Grüneisen parameter of ∼1.5,¹² which is indicative of bond anharmonicity. (3) Powder neutron diffraction data on BiOCuQ (ESI†), collected as a function of temperature, indicate that the BiOCuQ structure (Fig. 1) is retained over this temperature range. These data also reveal striking differences in the magnitude of the atomic displacement parameter (ADP). In particular, the ADP for copper, which does not show any significant anisotropy, is considerably larger than those of the remaining crystallographic sites. Although all ADPs increase linearly with temperature, the copper ADP increases at a faster rate (Fig. 1c). In sharp contrast to Cu_2−xSe or Cu₃SbSe₃, in which mobile copper atoms are not constrained to their equilibrium positions within the structure and can move to neighbouring sites,^3,20,21 examination of the difference Fourier maps for BiOCuQ at high temperatures indicate that copper atoms remain in their crystallographic site, and there is no evidence of structural disorder. This is confirmed by measurements of ionic conductivity in BiOCuSe, which has been found to be negligible,²² and indicates that the unusual thermal transport behaviour of BiOCuQ cannot be attributed to a liquid or part-liquid like state of the copper sublattice. This is highly significant for thermoelectric applications, given the detrimental effect of ion migration that irreversibly damages the legs of thermoelectric devices.²³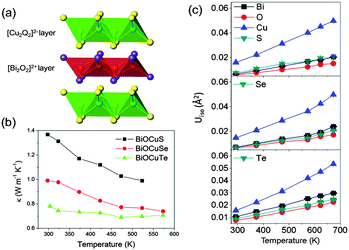

Fig. 1 (a) Polyhedral view of the crystal structure of BiOCuQ; (b) total thermal conductivity as a function of temperature; (c) ADPs for BiOCuQ as a function of temperature.

In order to elucidate the origin of the low thermal conductivity, phonon vibrations for BiOCuQ (Fig. 2) were computed using first principles calculations. The main feature, common to all three compositions, is the presence of a very low frequency manifold of optic modes centred at ca. 60 cm⁻¹ (Fig. 3 and ESI†). Low frequency optic modes are known to exist in low-thermal-conductivity materials containing heavy ions.^24,25 However, in BiOCuQ those vibrations have a large and unexpected copper contribution to the phonon DOS, which outweighs that of the heavier Bi atom, as it is six times larger than that of Bi in BiOCuS, three times larger in BiOCuSe, and twice in BiOCuTe (ESI†). The position of this low frequency optic manifold is in excellent agreement with the neutron data analysis. Assuming that copper behaves as a localised Einstein harmonic oscillator, the Einstein temperature, θ_E, can be determined from the slope of a plot of U_isovs. temperature (Table 1). The determined θ_E corresponds to a frequency of ca. 60 cm⁻¹, in very good agreement with our computed values. By assuming that Bi, O and Q atoms constitute a stiff network, the average mass and U_iso for those atoms can be used to estimate the Debye temperature, θ_D (Table 1). These estimates are in excellent agreement with the values computed within the quasi-harmonic approximation, and also agree with the limited literature data available (θ_D = 245 K for BiOCuSe).²⁶ The average velocity of sound estimated from θ_D is also in good agreement with measurements (2170 ms⁻¹ for BiOCuSe¹²).

Table 1 Einstein (θ_E) and Debye (θ_D) temperatures, together with the average velocity of sound (v_s) and the frequency of the localised copper mode (ν_Cu), determined from analysis of neutron diffraction data. Values in parenthesis are θ_D computed from first-principle calculations

Material	θ E/K	ν Cu/cm^−1	θ D/K	v s/ms^−1
BiOCuS	93	65	230 (231)	2100
BiOCuSe	95	66	210 (211)	2000
BiOCuTe	89	62	170 (196)	1700

---

Fig. 2 (a) Phonon dispersion curves for BiOCuQ. Key: black solid line: BiOCuS; red dashed line: BiOCuSe; green dash-dot line: BiOCuTe. The inset (b) shows the total energy response to the compression of Cu–S, La–O, and Bi–O bonds in BiOCuS and LaOCuS.

Fig. 3 (a) Total vibrational DOS of BiOCuSe projected on each element. (b) Mode-resolved Grüneisen parameter versus mode frequency for BiOCuQ with Q = S (black), Se (red), Te (green). Phonon frequencies were computed using the experimentally determined structures at 293 K.

In order to evaluate the role of copper in the reduction of the lattice thermal conductivity, we computed the mode-resolved Grüneisen parameter and projected it onto the atoms (Table 2). Contrary to previous work which attributed the large Grüneisen parameter to the presence of the Bi³⁺ lone pair,¹² our results clearly indicate that the major contributors are copper and chalcogen, while the bismuth contribution is always small. The largest Grüneisen parameters at low frequency are found for BiOCuS and BiOCuSe (Fig. 3b), but the copper contribution for BiOCuTe is still comparatively high. This finding supports the existence of a copper rattling mode in BiOCuQ. At the root of this rattling mode is weak Cu–Q bonding, as evidenced by a number of findings: (1) the Cu–Q distances in BiOCuQ are longer than those reported for other compounds containing Cu⁺ in a tetrahedral coordination. For instance, the Cu–Se distance in CuGaSe₂ is 2.385(1) Å,²⁷ significantly shorter than the value of 2.5143(3) Å found for BiOCuSe (ESI†). This is consistent with the observation that empirical bond valence sums for BiOCuQ are too small and appear to underestimate the oxidation state of copper, hence suggesting that bonds are weaker. (2) Although BiOCuQ are layered compounds without cages, the θ_E of ca. 90 K for copper (Table 1) is comparable to that previously found (79 K) for the rattler atom located in the oversized cages of the skutterudite LaFe₄Sb₁₂.¹⁵ (3) Calculations of the fitted total energy response to deformation of the Cu–Q bond (Fig. 2b) indicate that this bond is soft, and that the total energy is minimally affected by Cu–S bond compression up to 0.3 Å (approximately 12% of the bond length). The weak bonding of the copper atoms may be related to the close structural relationship between the [Cu₂Q₂]²⁻ slabs found in these materials and the superionic conductor Cu_2−xSe, which also exhibits a low thermal conductivity.²⁰ The Cu⁺ diffusion path in Cu_2−xSe involves octahedral sites²⁸ which are absent in the [Cu₂Q₂]²⁻ slabs of BiOCuQ. Hence the weak copper bonding in BiOCuQ may be related to a suppressed ionic conduction, owing to the absence of a suitable diffusion path for copper ions.

Table 2 Grüneisen parameters projected on the atoms. Values are computed using a finite difference formula using the phonon frequencies determined from the experimental lattice parameters at 293 K and at 673 K. Last column gives the total Grüneisen parameter per unit cell (2 formula units)

ndsp;	La/Bi	O	Cu	Q	TOT
LaOCuS	0.13	0.16	0.37	0.34	2.00
LaOCuSe	0.15	0.17	0.40	0.27	1.98
BiOCuS	0.18	0.22	0.43	0.48	2.62
BiOCuSe	0.19	0.22	0.45	0.31	2.34
BiOCuTe	0.19	0.25	0.31	0.25	2.00

---

Although the thermoelectric properties of the analogous rare-earth oxychalcogenides have not been extensively investigated, it is known that the total thermal conductivity increases on replacing bismuth by a rare-earth element (e.g. κ(LaOCuS) = 2.3 W m⁻¹ K⁻¹; κ(LaOCuSe) = 2.1 Wm⁻¹ K⁻¹ at room temperature).^29,30 Replacement of La by Bi causes an increase in the distortion of the [Cu₂Q₂]²⁻ and the [Bi₂O₂]²⁺ layers.³¹ Previous theoretical work indicates that the 6s² lone pair in Bi³⁺ is stereochemically active, and the increased distortion of the [Bi₂O₂]²⁺ layers has been attributed to bonding interactions between O 2p and Bi 6s states.³² In order to extricate the bismuth contribution to the thermal conductivity reduction from that of copper, we have also analysed the vibrational properties of LaOCuQ. Our results show that the low frequency region is still dominated by copper modes as in BiOCuQ, and that the lanthanum vibrational modes are shifted to higher frequencies and overlap less with the copper modes (ESI†), when compared to BiOCuQ. This indicates that the change in atomic mass is at the origin of the variation in thermal conductivity associated with the Bi/La substitution. Calculations of the deformation energy indicate that both Bi–O and La–O bonds are reasonably stiff when compared to Cu–Q bonds (Fig. 2b), and the mode resolved Grüneisen parameter indicates that in all cases Cu and the chalcogen are the major contributors to anharmonicity.

The effects associated with the bismuth site may be, however, indirect.² If the bismuth lone pair is indeed stereochemically active, the Coulomb interaction could couple the copper rattling with the bismuth displacement. The direct observation of a lone pair in the electronic structure is dubious,³³ and this concept often translates into hybridization between O 2p and Bi 6s states, which has been observed in the projected density of states (PDOS).³² In addition, the PDOS of BiOCuS indicates cross gap hybridation involving Bi 6p and O 2p as well as Cu and S p states (the second being larger). By contrast, in LaCuOS cross gap hybridization associated with La and O is negligible whereas it remains large for the Cu–S layer. A deviation of the Born effective charges from their nominal value is also a characteristic signature of stereochemically active ions. Those effects may lead to vibronic interactions, which involve the coupling of electronic and vibrational effects, and justify the increased anharmonicity, which will be associated with cross gap hybridization. Calculated Born effective charges (ESI†), show larger deviations from nominal values in BiCuOS with respect to LaCuOS, confirming that the lone pair in BiOCuQ is stereochemically active.

To further assess the possible Bi–Cu and La–Cu interplay in the anharmonicity, we studied the total energy response to atomic displacements. These maps (Fig. 4 and ESI†) represent the energy landscape associated with the simultaneous displacement of Bi/La and Cu ions. When cooperative distortions are favored the total energy change is small or negative, but as shown in Fig. 4, the Bi/La displacements are independent from the Cu displacements. These maps also provide further evidence that the energy landscape for the copper vibrations is very flat. The results presented here are in sharp contrast with the recent report of Cu–Sb bond length fluctuations in the tetrahedrite Cu₁₂Sb₄S₁₃, in which low lattice thermal conductivity has been linked to an anharmonic rattling mode of copper, which is assisted by the lone pairs in the antimony atoms.² This clear difference between Cu₁₂Sb₄S₁₃ and BiOCuQ might be related to the layered structure of BiOCuQ, in which Bi and Cu are segregated into different layers (Fig. 1a).

Fig. 4 Total energy response to atomic displacements of Bi and Cu in BiCuOS. The displacements were done along inequivalent tetragonal directions: (a) Bi along x and Cu along x, (b) Bi along z and Cu along x, (c) Bi along +z and Cu along +z, and (d) Bi along −z and Cu along +z.

Conclusions

Using a combination of theoretical calculations and neutron diffraction experiments, we have shown that the presence of a localised low-energy vibrational mode on the copper, rather than the presence of the Bi³⁺ lone pair, is the fundamental mechanism leading to low thermal conductivity in these oxychalcogenides. This localised mode, which occurs in layered materials containing no cages, is a consequence of weak copper bonding. These oxychalcogenides could be described as incipient ionic conductors, in which copper mobility may be suppressed due to the absence of a suitable diffusion path. For decades, the search for novel thermoelectrics has been based on rattling mechanisms associated with heavy elements in cages (e.g. skutterudites, clathrates). We have provided compelling qualitative and quantitative evidence that layered compounds, with no cages, may exhibit a similar rattling behavior, arising from suppressed ionic conduction. This mechanism for the reduction of lattice thermal conductivity, which has been identified here for the first time, offers an alternative approach for the design of thermoelectric materials with ZT > 1.

Acknowledgements

This work was supported by funding of a PhD studentship (S. D. N. L.) by the Energy Technology Partnership and European Thermodynamics Ltd. The authors also thank the ISIS Facility and STFC (Science and Technology Facilities Council) for the neutron beam time allocation, and the Royal Society for an International Exchange Grant. This work was partially supported by Solvay Special Chemicals. R. A. R. A. O, D. W. and M. F. thank the High Performance Computing Center at Michigan State University. M. F. acknowledges collaboration with the AFLOW Consortium (http://www.aflowlib.org) under the sponsorship of DOD-ONR (N000141310635).

Notes and references

1. D. M. Rowe, Thermoelectrics Handbook: Macro to Nano, ed. D. M. Rowe, CRC Press, Boca Raton FL, 2006.
2. W. Lai, Y. Wang, D. T Morelli and X. Lu, Adv. Funct. Mater., 2015, 25, 3648.
3. W. Qiu, L. Xi, P. Wei, X. Ke, J. Yang and W. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15031.
4. P. Vaqueiro, G. Guelou, M. Stec, E. Guilmeau and A. V. Powell, J. Mater. Chem. A, 2013, 1, 520.
5. L. D. Zhao, D. Berardan, Y. L. Pei, C. Byl, L. Pinsard-Gaudart and N. Dragoe, Appl. Phys. Lett., 2010, 97, 092118.
6. F. Li, T.-R. Wei, F. Kang and J.-F. Li, J. Mater. Chem. A, 2013, 1, 11942.
7. S. D. N. Luu and P. Vaqueiro, J. Mater. Chem. A, 2013, 1, 12270.
8. J. Sui, J. Li, J. He, Y.-L. Pei, D. Berardan, H. Wu, N. Dragoe, W. Cai and L. D. Zhao, Energy Environ. Sci., 2013, 6, 2916.
9. S. K. Saha, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 041202(R).
10. J. Ding, B. Xu, Y. Lin, C. Nan and W. Liu, New J. Phys., 2015, 17, 083012.
11. M. D. Nielsen, V. Ozolins and J. P. Heremans, Energy Environ. Sci., 2013, 6, 570.
12. Y.-L. Pei, J. He, J. F. Li, F. Li, Q. Liu, W. Pan, C. Barreteau, D. Berardan, N. Dragoe and L. D. Zhao, NPG Asia Mater., 2013, 5, e47.
13. Details of the Mantid open source framework supporting high-performance computing to manipulate and analyse neutron and muon scattering data may be found at http://dx.doi.org/10.5286/SOFTWARE/MANTID.
14. A. C. Larson and R. B. von Dreele, General Structure Analysis System, Los Alamos Laboratory, 1994, Report LAUR 85-748.
15. B. C. Sales, D. G. Mandrus and B. C. Chakoumakos, Semicond. Semimetals, 2001, 70, 1.
16. S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515.
17. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni and D. Ceresoli, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
18. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
19. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446.
20. H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher and T. Day. G. J. Snyder, Nat. Mater., 2012, 11, 422.
21. M. Kirkham, P. Majsztrik, E. Skoug, D. Morelli, H. Wang, W. D. Porter, E. Payzant and E. Lara-Curzio, J. Mater. Res., 2011, 26, 2001.
22. C. Barreteau, D. Bérardan, E. Amzallag, L. Zhao and N. Dragoe, Chem. Mater., 2012, 24, 3168.
23. G. Dennler, R. Chmielowski, S. Jacob, F. Capet, P. Roussel, S. Zastrow, K. Nielsch, I. Opahle and G. K. H. Madsen, Adv. Energy Mater., 2014, 4, 1301581.
24. J. L. Feldman, D. J. Singh, I. I. Mazin, D. Mandrus and B. C. Sales, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R9209.
25. D. Wee, B. Kozinsky, N. Marzari and M. Fornari, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 045204.
26. L. Pan, D. Berardan, L. Zhao, C. Barreteau and N. Dragoe, Appl. Phys. Lett., 2013, 102, 023902.
27. S. C. Abrahams and J. L. Bernstein, J. Chem. Phys., 1974, 61, 1140.
28. A. N. Skomorokhov, D. M. Trots, M. Knapp, N. N. Bickulova and H. Fuess, J. Alloys Compd., 2006, 421, 64.
29. Y. Goto, M. Tanaki, Y. Okusa, T. Shibuya, K. Yasuoka, M. Matoba and Y. Kamihara, Appl. Phys. Lett., 2014, 105, 022104.
30. M. Yasukawa, K. Ueda and H. Hosono, J. Appl. Phys., 2004, 95, 3594.
31. H. Hiramatsu, H. Yanagi, T. Kamiya, K. Ueda, M. Hirano and H. Hosono, Chem. Mater., 2008, 20, 326.
32. S. Sallis, L. F. J. Piper, J. Francis, J. Tate, H. Hiramatsu, T. Kamiya and H. Hosono, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085207.
33. A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422.

---

Footnote

† Electronic supplementary information (ESI) available: Final observed, calculated and difference profiles for neutron refinements, with final refined parameters and selected bond distances and angles; phonon dispersion curves, vibrational density of states, maps of total energy response to atomic displacements, and calculated Born effective charges. See DOI: 10.1039/c5cp06192j

---