Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A zero dimensional model of lithium–sulfur batteries during charge and discharge†
Monica
Marinescu
*,
Teng
Zhang
and
Gregory J.
Offer
Department of Mechanical Engineering, Imperial College London, SW7 2AZ, UK. E-mail: monica.marinescu@imperial.ac.uk
First published on 12th November 2015
Abstract
Lithium–sulfur cells present an attractive alternative to Li-ion batteries due to their large energy density, safety, and possible low cost. Their successful commercialisation is dependent on improving their performance, but also on acquiring sufficient understanding of the underlying mechanisms to allow for the development of predictive models for operational cells. To address the latter, we present a zero dimensional model that predicts many of the features observed in the behaviour of a lithium–sulfur cell during charge and discharge. The model accounts for two electrochemical reactions via the Nernst formulation, power limitations through Butler–Volmer kinetics, and precipitation/dissolution of one species, including nucleation. It is shown that the flat shape of the low voltage plateau typical of the lithium–sulfur cell discharge is caused by precipitation. During charge, it is predicted that the dissolution can act as a bottleneck, because for large enough currents the amount that dissolves becomes limited. This results in reduced charge capacity and an earlier onset of the high plateau reaction, such that the two voltage plateaus merge. By including these effects, the model improves on the existing zero dimensional models, while requiring considerably fewer input parameters and computational resources than one dimensional models. The model also predicts that, due to precipitation, the customary way of experimentally obtaining the open circuit voltage from a low rate discharge might not be suitable for lithium–sulfur. This model can provide the basis for mechanistic studies, identification of dominant effects in a real cell, predictions of operational behaviour under realistic loads, and control algorithms for applications.
1 Introduction
Lithium sulfur batteries (Li–S) are seen as a candidate for the next generation of batteries, as they are potentially low cost and have a theoretical energy density of ∼2500 W h kg−1 and a practical one estimated at ∼600 W h kg−1.1 These figures of merit represent a step change improvement compared to the energy density of current Li-ion technology of 250 W h kg−1 (theoretical maximum 400 W h kg−1)1 and are possible due to the fact that the Li–S mechanism is different from that of Li-ion cells. Energy is stored and released through phase conversion rather than intercalation, and each sulfur atom can, in principle, contribute sixteen electrons to the circuit. The phase conversion mechanism, however, brings about many new challenges that must be addressed before Li–S can be considered competitive for large scale deployment. Currently, relatively high energy densities are achieved at cell level (300–400 W h kg−1), but with the limited cycle life of a few hundred cycles, as commercialised by OXIS Energy and inferred from cathode development data.2 Conversely, thousands of cycles are achieved for significantly lower energy densities, similar to those exhibited by lithium ion chemistries, as commercialised by OXIS Energy. Long cycle life can be achieved either by using excess electrolyte and Li in the cell,3 or by limiting the operating voltage window.4 The use of Li–S in applications is currently limited by low charge efficiency and relatively high self-discharge rates, but their inherent safety is an advantage in some niche applications.5In order to improve the practical energy densities and cycle life of Li–S, most studies are currently aimed at decreasing the polysulfide shuttle and increasing sulfur utilisation, by improving material properties,6,7 and by revealing the underlying mechanisms through characterisation experiments,8 amongst others. The necessary step of linking characterisation with design has not been explored sufficiently in the literature. Mechanistic models based on characterisation studies have been proposed, as discussed below, but none have been used yet to help design better cells or direct materials research. This state is similar to that of the early days of incumbent lithium ion chemistries.9
The first documented Li–S model was developed by Mikhaylik and Akridge10 and focused on studying the interplay between polysulfide shuttle and charging current. Their two-step reaction zero dimensional model includes heat generation as a result of the shuttle phenomenon, based on conclusions from their earlier study.11 An expansion on the Nernst description of a zero dimensional Li–S cathode is explored by Moy et al.,12 by adding intermediate reaction steps in the chain of polysulfide reduction, which they relate to the typical regions of the discharge curve. A one dimensional steady state model of polysulfide diffusion through the separator is added, with the aim of interpreting the results of their proposed method for shuttle rate measurement and of predicting capacity fade caused by shuttle. While providing a good fit to experimental data, their model is only applicable to situations in which the cell is maintained at constant voltage. Capacity fade predictions based on a similarly simple reaction chain were obtained by Risse et al.13 from a Markov chain model. None of these models account for diffusion limitations, precipitation/dissolution of insulating polysulfides and kinetic limitations, ignoring activation overpotentials. These phenomena can contribute to the cell voltage performance and capacity fade. Because of this and despite being useful for understanding some of the cell mechanisms, these models are of limited use for predictions of cell performance under operational conditions.
A more comprehensive one dimensional model proposed by Kumaresan et al.14 includes activation overpotentials in the form of Butler–Volmer kinetics, diffusion limitations of multicomponent transport in a dilute electrolyte, and precipitation of species via a rate constant, including nucleation. Polysulfide shuttle, however, is not included. The model allows for a detailed analysis of the interplay between the mechanisms in the system during cell discharge, providing direct access to the time evolution and spatial distribution of polysulfide species and to the various contributions to the cell potential. While it reproduces some of the main features of the discharge curve, such as the presence of two plateaus with a voltage dip in-between, a detailed sensitivity analysis by Ghaznavi and Chen15–17 shows that their model as published is not suitable to predict behaviour during charge and capacity fade.
The framework of a similar model was developed by Neidhardt et al.,18 and used to reproduce the cell response to constant current charge, discharge and electrochemical impedance spectroscopy experiments.19 The model includes the presence of electrical double layers at the surface of either electrode. Polysulfide shuttle via an added reaction at the anode with resulting irreversible precipitation is included by Hofmann et al.,20 allowing for the exploration of further Li–S features, such as low Coulombic efficiency and capacity fade.
While no existing model is able to reproduce all known features of the Li–S behaviour, one dimensional mechanistic models are the most promising in their ability to direct research towards improved cell performance. However, there are two major drawbacks to the use of such models for prediction in applications. Firstly, they require a large number of physical and chemical parameters whose values are difficult to obtain, such that their quantitative predictions are usually unreliable. More information helpful in determining the values of rate constants, equilibrium concentrations, or reaction pathways should become available as a result of advances in characterisation studies.8 A second drawback is the models' need for significant computational power, making them unsuitable as a basis for identification and control algorithms. Attempts to produce reduced order models derived directly from physical models of Li–S cells are expected to be extremely useful for control and application engineers.
For the purpose of Li–S cell simulation for use in applications, a suitable model needs to include the following functionality:
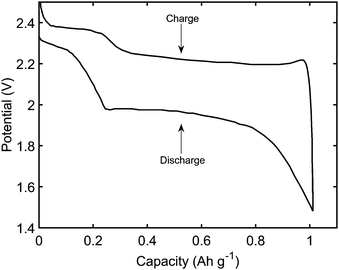
(i) retrieve the main features of a typical constant current performance, shown in Fig. 1; during discharge: the existence of two plateaus, with a dip in-between; during charge: the initial sharp increase in voltage, and a less pronounced difference between the two plateaus,
(ii) predict the cell response to dynamic loads, by allowing charge, discharge, and switching between the two,
(iii) include the effect of current on the voltage response, and thus account for power limitation and shuttle effects, and
(iv) provide information on the the amount of stored energy throughout operation, offering the possibility of including cell degradation and capacity fade.
We present a zero-dimensional model that aims to fulfill these requirements with relatively modest computational expense. The model is based on the simple two-step electrochemical reaction chain proposed by Mikhaylik and Akridge.10 The choice of a short reduction chain is also supported by density functional theory calculations,21 where the S2−4 → S2−2 and S2−2 → S2− reactions were found to have relatively similar standard potentials (2.22 V vs. 2.18 V). Reaction kinetics limitations are introduced via the Butler–Volmer relation. The shuttling of high order polysulfides is modelled via a constant shuttle rate, as in Mikhaylik and Akridge,10 such that it can take place both during charge and discharge and is only indirectly dependent on voltage. While precipitation can be a determining mechanism for the performance of Li–S cells, the debate regarding which species are precipitating alongside Li2S is ongoing. Experimental characterisation studies usually infer the presence of Li2S2,22 while first principles studies predict various levels of stability for the Li2S2 compound.23–25 In the present model, only the precipitation of the most reduced sulfur species is allowed, modelled via a constant precipitation rate including nucleation and the effect of a saturation concentration.
As a zero dimensional model, transport limitations cannot be retrieved. Despite this simplification, charge and discharge predictions are similar to those obtained from the more computationally intensive one dimensional models. This observation is supported by the conclusion of Ghaznavi and Chen17 that species transport becomes limiting in the one-dimensional model of Kumaresan et al.14 only in the limit of much lower diffusion coefficients than the values used.
Finally, it is worth mentioning that the concept of an open circuit voltage (OCV), which lies at the core of operational models for Li-ion intercalation batteries, is not well defined in the case of Li–S. Moreover, obtaining the OCV curve by using the same experimental procedure as for Li-ion intercalation batteries is not necessarily valid. Mikhaylik and Akridge10 used the common interpretation of the OCV as the discharge voltage curve at low enough constant current, in order to parametrise the standard potentials for the two redox reactions. This approach is not strictly valid in the upper plateau, if the phenomenon of shuttle is present during discharge. Precipitation was also shown to have a determining effect on the flatness of the lower voltage plateau.14,26 Shuttle and precipitation/dissolution affect the experimentally obtained OCV for both charge and discharge in ways that need to be understood and quantified further. For Li–S cells, discharge/charge at decreasing current rates does not necessarily lead to an equilibrium state, or a state that is an appropriate input for operational models. As a result, it might not be possible to directly employ the same framework as that used for intercalation Li-ion for Li–S operational models, be they equivalent circuit models or mechanistic models. This situation makes the approach of equivalent circuit modelling, the tool of choice for engineers, especially unreliable when modelling Li–S cells. Indeed, all Li–S equivalent circuit models currently available in the literature are used for interpreting impedance spectroscopy data,27,28 are developed for a quasi-static state and thus would not be appropriate for the simulation of a cell during operation.
2 Model
2.1 Equilibrium
In the present model, the same two-step reaction chain as in Mikhaylik and Akridge10 is used, under the assumption that a single electrochemical reaction dominates each of the two discharge regions:| S08 + 4e− ↔ 2S2−4, | (1a) |
| S2−4 + 4e− ↔ 2S2−↓ + S2−2. | (1b) |
The equilibrium potential for the two reactions is given by the Nernst equations
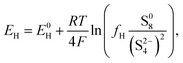 | (2a) |
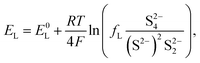 | (2b) |
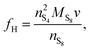 | (3a) |
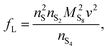 | (3b) |
The voltage of the cell was approximated by Mikhaylik and Akridge10 as EH = EL = V. The first equality is valid for two reactions occurring simultaneously at the same electrode. The second equality is strictly valid only for the case of zero net current, when the forward and backward reactions are in equilibrium. This is not the case for a cell under charge/discharge.
The Nernst expressions in eqn (2) warrant a short discussion, as the inherent assumptions are sometimes overlooked. The Nernst equation as written in eqn (2a) and (2b) is strictly valid for a half cell reduction reaction, at the cathode. A battery, however, contains two half cells, since the electrochemical reactions take place at the two electrodes simultaneously. The expression of the anode potential as a result of Li oxidation is omitted in Mikhaylik and Akridge,10 under the assumption that its value is comparatively small. The Nernst potential of the reaction at the lithium anode is included in Kumaresan et al.,14 where its value is calculated to vary by one order of magnitude less than the variation of reaction potentials at the cathode. The small variation is a result of their model predicting a relatively constant average Li-ion concentration throughout cell operation. The prediction itself has not yet been validated. The charge transfer overpotential at the anode is not included. In the light of their estimations, the anode potential is ignored in the present model. The validity of this assumption, however, remains to be verified experimentally.
A second observation is that the Nernst potential in its original form contains the ratio of reactant to product activities rather than concentrations. For example, for the reaction in eqn (1a) the Nernst potential should read
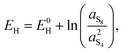 | (4) |
(1) γ = 1, an assumption strictly valid at very low concentrations, and
(2) c0 = 1 mol L−1, corresponding also to the concentration at which E0L and E0H should be measured.
While neither condition above is expected to be met for the Li–S system, these assumptions continue to be made here, as in previous models. Various models to approximate the activity coefficient at moderate and strong concentrations, such as extensions to the Debye–Hückel approximation30 or the Pitzer's equations,31 have been derived mainly for aqueous systems. Their predictions have not been validated for the concentrated multispecies non-aqueous electrolyte solutions typical of the Li–S system, nor are appropriate parameter values available. While obtaining reliable E0 values might possible via computational simulations,21 many other parameter values are unlikely to be within experimental reach in Li–S cells, such that leaving them as fitting parameters may be a necessary lasting compromise.
2.2 Reaction kinetics
The presence of current in the outside circuit corresponds to a non-equilibrium state: electrochemical reactions with a net flow of electrons occur at the electrode. It is assumed that the currents related to the two electrochemical reactions are described by the Butler–Volmer approximation: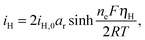 | (5a) |
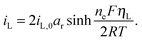 | (5b) |
A non-zero surface overpotential is a measure of the driving force for a reaction to occur and is given by the difference between the apparent (measured) voltage of the cell, here of the cathode, and the reaction Nernst potential:
| ηH = V − EH | (6a) |
| ηL = V − EL. | (6b) |
Charge conservation dictates that the measured cell current I is given by the combined contribution of the two reactions
| I = iH + iL. | (7) |
2.3 Shuttle and precipitation
The shuttling of high order polysulfides and the precipitation of low order polysulfides are characteristics of Li–S cells that have been observed in various electrolytes. In the present model, the two effects are described in a conceptually similar manner. A simple but effective model for the shuttle with qualitatively good estimates of the resulting decrease in charge efficiency was proposed by Mikhaylik and Akridge.10 The effect is modelled by a shuttle rate ks acting to decrease S08, in the same direction as the reduction reaction S08 → S2−4, but without contributing to the reaction current.Similar to shuttle, the precipitation reaction removes from electrolyte an amount of S2− proportional to a precipitation rate kp. There are three direct effects related to precipitation, regarding electrolyte conductivity, nucleation and cathode active surface area. Firstly, the fact that sulfur ions are removed from electrolyte causes a lowering of ionic concentration and results in a variation of the electrolyte conductivity.26 The discharge capacity of the cell is reduced if the species precipitating could otherwise participate in further reduction reactions.14 In this model the sole precipitating species is the last one in the reacting chain, such that precipitation does not lead to reduced capacity during discharge. A second effect related to precipitation is the nucleation phenomenon: the presence of already precipitated material offers a nucleation surface for further precipitation to occur, as long as the concentration in the electrolyte is above a given saturation concentration. Here a simple model for the effect of nucleation is considered, which assumes that the precipitating amount is proportional to the amount of material already precipitated, as described by eqn (8e). Thirdly, the precipitated sulfur is electrically insulating; when it covers an active cathode/electrolyte interface, rather than agglomerate in solution or over already inactive cathode area, the active surface area is decreased. As further reactions are hindered from taking place, the reaction overpotential should increase, affecting, in turn, the exchange current term in the Butler–Volmer relation in eqn (5b). This last effect is ignored here, due to lack of experimental data. Unutilised sulfur due to pore blocking is a capacity fade phenomenon beyond the scope of this study.
2.4 Time evolution of species
The two electrochemical reactions allowed, together with the assumptions on the shuttle and precipitation phenomena described above, lead to the following time-evolution relations for the various sulfur species in the system: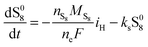 | (8a) |
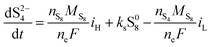 | (8b) |
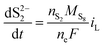 | (8c) |
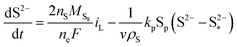 | (8d) |
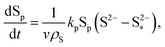 | (8e) |
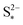 the saturation mass of S2−, assumed to be constant.
the saturation mass of S2−, assumed to be constant.
2.5 Computational implementation and initial conditions
Eqn (2) and (5)–(8) form a differential algebraic system that can be solved for the twelve unknowns: the Nernst potentials EH, EL, the contributions to the total current from the two reactions iH, iL, the cell voltage V, here equal to the cathode voltage, the overpotentials ηH, ηL, and the mass of the five forms of sulfur S08, S2−4, S2−2, S2− and Sp. The Jacobian for the system is calculated analytically and the system is solved in Matlab using a second order solver. For the Matlab code please see the ESI.†The initial conditions for all variables are calculated self consistently from chosen values of V, S08 and Sp for discharge, and V, Sp and S2− for charge. If the initial split between iH and iL in eqn (7) is known, the initial conditions for the other parameters can be calculated as follows. For discharge, ηH is obtained from eqn (5a), EH, from eqn (6a) and S2−4 from eqn (2a). A similar sequence is followed for the low plateau reaction, with the term (S2−)2S2−2 obtained from eqn (2b), and the assumption of S2−2 = S2− + Sp allowing for the calculation of S2− and S2−2. For charge, a similar procedure is used to obtain values for EH and EL; S2−2 is calculated as above, and used in eqn (2b) to obtain S2−4, which in turn is used in eqn (2a) to solve for S08. In this way, the initial conditions are calculated without the need of solving the non-linear system of equations. As a drawback, the total sulfur mass in the system is not specifically constrained such that the three initial values must be chosen to reflect a system with the desired total sulfur mass.
For an initial state far enough from the boundary between plateaus, the split of I can be assumed as I = iH, iL = 0 for discharge and I = iL, iH = 0 for charge. In the following analysis, only discharge from a fully charged state and charge from a fully discharged state are considered, making this assumption valid.
2.6 Model use
A fully operational model can be built on the basis of the model developed here. To this purpose, contributions from all Ohmic losses in the system should be subtracted from the voltage output shown in Fig. 2. These include losses caused by the contact resistance of the studied cell, as well as by the resistivity of the electrolyte as a function of the varying polysulfide concentration, shown in Zhang et al.26 to be required for correct estimates of cell impedance.While the two step mechanism assumed here predicts many known performance features, experimental studies indicate that Li–S charge/discharge occurs through more complex mechanisms.32 Further reactions and species can be included in the following manner, consistent to the current model. Electrochemical reactions are described by an equilibrium potential as given by their Nernst equation, and by a current–overpotential relation given by the Butler–Volmer approximation, where the overpotentials are linked to the potential of the whole cell, and the reaction currents sum up to the total external current. Chemical reactions could be described by forward and backward reaction rates. The time evolution of all species in the system leads to production and consumption as a result of all types of reactions, together with the effect of shuttle on higher order polysulfides and the effect of precipitation/dissolution on lower order polysulfides.
The choice of cell components, its geometry and size, all contribute to its behaviour. The choice of electrolyte, for example, is well documented to affect many properties inside the cell, impacting on many model parameters. The magnitude of the polysulfide shuttle, and thus of ks, is affected by electrolyte choice and additives.33 The choice of electrolyte also impacts on the free solvation energies of ions, and thus implicitly on the electrode potentials, or the Nernst potentials of the various reactions, and ultimately on the cathode and cell voltage.34 The saturation concentration of the various species, determining the initiation of precipitation/dissolution, is also expected to change as a result of electrolyte choice. Moreover, the actual mechanisms leading to charge/discharge can be affected, as different solvents promote different reaction paths.34 Finally, if capacity fade due to reactions occurring at the anode surface is included in the model, the effect of electrolyte additives promoting a solid electrolyte interphase would also need to be considered.35 In fitting the model parameters to a particular cell, many have to be inferred rather than obtained from independent experiments. As a result, many of these effects would be included automatically.
3 Results and discussion
The system parameters and their values are given in Table 1, where the subscript H denotes the high plateau reaction eqn (1a) and L the low plateau reaction eqn (1b).3.1 Discharge and charge
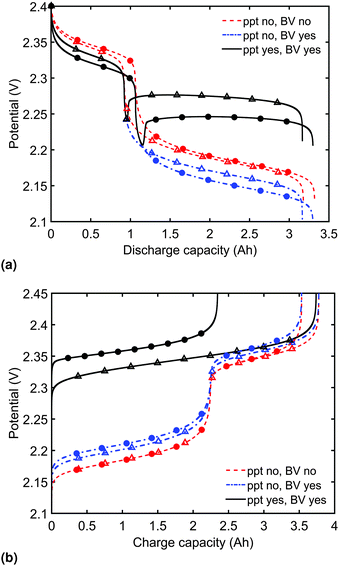
Model predictions for the cell voltage during constant current discharge for two current rates are illustrated in Fig. 2(a). In the absence of precipitation and overpotential effects, the outputs of Mikhaylik and Akridge10 are retrieved (ppt no, BV no). In this case, the magnitude of the discharge current affects the cell behaviour only through its interplay with the shuttle: the higher the current, the higher the discharge efficiency in the high plateau, and correspondingly the higher the total discharge capacity. The value of the current has no effect on the height of the two voltage plateaus.In reality, the magnitude of the discharge current is expected to impact on the discharge curve even in the absence of a shuttle effect; a cell cannot provide infinite instantaneous power due to losses from diffusion and charge transfer reactions. To account for the latter, as the discharge current is increased, greater losses should be caused by an increasing reaction overpotential. Predictions from the model including the voltage–overpotential relation in Fig. 2(a) indeed show that the accessible cell voltage is significantly lower than that predicted by the Mikhaylik model. The total capacity of the cell as defined by the state at which all available sulfur has reacted down the reaction chain to low order polysulfides does not change upon the addition of precipitation of end products and of current–overpotential relations. In practice, however, the capacity of a cell is defined by the charge available within a given voltage range. While the theoretical capacity of the cell remains the same as in the simpler model, in the model including kinetic limitations the voltage of the lower plateau decreases as the discharge current increases. As a result, the cell provides less usable capacity within a set voltage range, even before accounting for Ohmic losses.
The discharge curve predicted by the model with kinetic limitations but without precipitation in Fig. 2(a) (ppt no, BV yes) is still qualitatively different from those seen in typical experimental results, where the lower plateau is significantly flatter. The final set of discharge curves plotted in Fig. 2(a) (ppt yes, BV yes) exhibit the full model capabilities, including the effect of precipitation. The dip between the two voltage plateaus and the elevated flat voltage in the lower plateau are both revealed as effects of precipitation. The effect of precipitation is further analysed in Section 3.2.
Predictions of cell voltage during constant current charge are given in Fig. 2(b). For the simplest model ignoring both kinetic limitations and precipitation effects, the charging rate only affects the voltage at the end of charge, counteracting the effect of shuttle. During charge, the addition of a current-dependent reaction overpotential to the model by Mikhaylik and Akridge10 introduces an increase in cell voltage, effectively decreasing the charge capacity for a set voltage interval. The addition of precipitation further increases the cell voltage by introducing a large resistance associated with the dissolution of Sp. For a larger charging current, less Sp can be dissolved within the shorter time frame, increasing the cell voltage and leading to a charge capacity that is significantly reduced. As in the case of discharge, the charge voltage curve becomes similar to experimental data upon inclusion of precipitation effects. For charge, the presence of gradual dissolution removes the clear boundary between the two plateaus, as detailed in Section 3.2. In all cases presented, the charging current is strong enough to compensate for the shuttle, such that the cell can reach the nominal voltage for fully charged.
It should be noted that the choice of initial conditions for Fig. 2(b) is not unique. In comparing predictions for charge from a fully discharged state between a system where precipitation is allowed and one without precipitation, choosing the initial conditions is not straightforward. When fully discharged, an ideal cell following the present model would contain all sulfur in the form of S2−2, S2− and Sp in ratios influenced by the two precipitation parameters, kp and 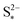 . In the absence of precipitation, the fully discharged cell contains S2− and S2−2 only, in a 1
. In the absence of precipitation, the fully discharged cell contains S2− and S2−2 only, in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio. For a given total sulfur mass, these two conditions do not correspond to the same value of cell voltage. For comparison reasons, the same starting voltage was chosen for the predictions in Fig. 2(b). As a result, the predictions correspond to cells of different sulfur masses, with a variation of 2.898 × 10−4 g, or 0.364 × 10−3 Ah in their theoretical cell capacity, which was considered small enough to be ignored. This particular problem does not arise for discharge from a fully charged cell, where it is assumed that all sulfur is in the form of S08 for all model variants. A similarly small current-dependent variation in the total sulfur mass due to the way in which initial conditions are calculated arises when comparing predictions from the model including kinetic limitations to those from the model ignoring them. Either different values of iH,0, iL,0 but the same iH, iL, or different iH, iL, such as due to different current rates, but fixed iH,0, iL,0 cause a variation in ηH, ηL. For the discharge curves in Fig. 2(a), the maximum variation in mS corresponds to 30.8 × 10−3 Ah.
1 mass ratio. For a given total sulfur mass, these two conditions do not correspond to the same value of cell voltage. For comparison reasons, the same starting voltage was chosen for the predictions in Fig. 2(b). As a result, the predictions correspond to cells of different sulfur masses, with a variation of 2.898 × 10−4 g, or 0.364 × 10−3 Ah in their theoretical cell capacity, which was considered small enough to be ignored. This particular problem does not arise for discharge from a fully charged cell, where it is assumed that all sulfur is in the form of S08 for all model variants. A similarly small current-dependent variation in the total sulfur mass due to the way in which initial conditions are calculated arises when comparing predictions from the model including kinetic limitations to those from the model ignoring them. Either different values of iH,0, iL,0 but the same iH, iL, or different iH, iL, such as due to different current rates, but fixed iH,0, iL,0 cause a variation in ηH, ηL. For the discharge curves in Fig. 2(a), the maximum variation in mS corresponds to 30.8 × 10−3 Ah.
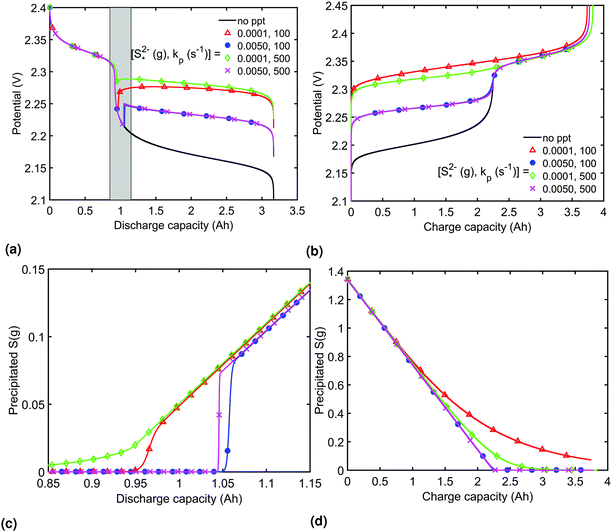
3.2 Effect of precipitation
The presence of precipitation can significantly impact the shape of the discharge and charge voltage curves. In general, the occurrence of precipitation raises the voltage in the low plateau, compared to that given by a Nernst model, as seen for various values of the precipitation parameters in Fig. 3(a) and (b). The cell voltage in the low plateau traces the evolution of EH in eqn (2a), if the assumption ηH ≈ 0 can be made. During discharge, as S2− is gradually extracted from solution by precipitation, the low plateau reaction is driven forward and more S2−4 is consumed. This in turn raises the Nernst voltage of the high plateau reaction, and thus also V, as observed also in Zhang et al.26The value of 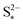 determines the state during discharge at which the precipitate starts forming, and thus affects the width of the voltage dip between the high and the low plateau. Higher values of
determines the state during discharge at which the precipitate starts forming, and thus affects the width of the voltage dip between the high and the low plateau. Higher values of 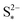 allow for a later start of precipitation, an effectively faster initial rate of precipitation and a larger amount of S2− in the electrolyte at any point during the discharge, as shown in Fig. 3(c). The latter has a significant effect on the value of the voltage in the low plateau: the smaller the amount of Sp, the lower the voltage, corresponding to a smaller departure from the Nernst voltage.
allow for a later start of precipitation, an effectively faster initial rate of precipitation and a larger amount of S2− in the electrolyte at any point during the discharge, as shown in Fig. 3(c). The latter has a significant effect on the value of the voltage in the low plateau: the smaller the amount of Sp, the lower the voltage, corresponding to a smaller departure from the Nernst voltage.
Increasing the precipitation rate kp has qualitatively similar effects on the voltage curve to decreasing 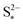 . The effect of kp is modulated by
. The effect of kp is modulated by 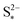 : the larger the latter, the less Sp is formed and the equilibrium is reached faster, lowering the importance of kp. In the limit of infinitely fast precipitation, the cell voltage in the low plateau is determined by
: the larger the latter, the less Sp is formed and the equilibrium is reached faster, lowering the importance of kp. In the limit of infinitely fast precipitation, the cell voltage in the low plateau is determined by 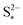 only. This cell voltage corresponds to the equilibrium voltage, similar to the concept of the open circuit voltage for intercalation Li-ion batteries.
only. This cell voltage corresponds to the equilibrium voltage, similar to the concept of the open circuit voltage for intercalation Li-ion batteries.
In the absence of current overpotential and precipitation effects, I/ks was shown to be a scaling factor for the voltage response of the cell in the model of Mikhaylik and Akridge.10 Similarly, in the absence of shuttle and overpotential effects, I/kp can be considered the determining factor, due to the way in which shuttle and precipitation are described in competition with the applied current. As at least two of the three contributions, i.e. reaction overpotential, precipitation and shuttle, are usually present at any time during operation, the I/ks and I/kp factors are only indicative of the performance of a real cell, rather than serving as scaling factors. For relatively low overpotentials, I/ks is indicative of the discharge voltage in the high plateau, while I/kp serves this purpose in the low plateau.
As I/kp is performance-determining for fixed 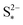 in the low plateau, an experimental OCV curve for a Li–S cell can only be obtained for a constant current discharge at currents much lower than the rate of precipitation. A value of the latter is not readily available from literature, but could indicate a prohibitively low recomended value of I. Rest periods during discharge at rates as low as C/48 were found to lead to significant voltage recovery.36 In the high plateau, moreover, shuttle would affect the discharge. In the model by Mikhaylik and Akridge,10 the voltage response to a C/30 discharge is considered to be the OCV. E0H and E0L are read directly from the data, at the points in the discharge capacity that correspond to those species concentration ratios that cancel the logarithmic terms in the Nernst equations, such that EH = E0H and EL = E0L respectively. The values thus obtained differ from simulation predictions,21 possibly due to automatically encompassing non-vanishing overpotentials from charge transfer and precipitation effects.
in the low plateau, an experimental OCV curve for a Li–S cell can only be obtained for a constant current discharge at currents much lower than the rate of precipitation. A value of the latter is not readily available from literature, but could indicate a prohibitively low recomended value of I. Rest periods during discharge at rates as low as C/48 were found to lead to significant voltage recovery.36 In the high plateau, moreover, shuttle would affect the discharge. In the model by Mikhaylik and Akridge,10 the voltage response to a C/30 discharge is considered to be the OCV. E0H and E0L are read directly from the data, at the points in the discharge capacity that correspond to those species concentration ratios that cancel the logarithmic terms in the Nernst equations, such that EH = E0H and EL = E0L respectively. The values thus obtained differ from simulation predictions,21 possibly due to automatically encompassing non-vanishing overpotentials from charge transfer and precipitation effects.
In order to analyse the effect of dissolution during charge, identical initial conditions are chosen for the four charging systems in Fig. 3(b), for an easier comparison. In reality, it is expected that, if charged from fully discharged, the different cells would start from different initial voltages and amounts of Sp. During charge, higher kp and lower  values result in a slower dissolution. Unlike for discharge, where the theoretical cell capacity is independent of precipitation rate, the charge capacity does depend on the system's ability to dissolve the precipitated species fast enough, as this ability impacts sulfur utilisation. During charge, a slow dissolution of Sp can act as a bottleneck, leading to the early formation of high plateau species, here S08, and to reduced capacity. The effect of this bottleneck on the cell voltage is already visible in Fig. 2(b) (ppt yes, BV yes) for charge at two different currents. The mechanism of the bottleneck becomes apparent when tracking the contribution of the two electrochemical reactions to the total current, shown in Fig. 4(a), and the evolution of species in the system, in Fig. 4(b). Thus, in the presence of slow dissolution, the boundary between the high and low plateaus becomes less sharp, leading to the disappearance of a distinct low plateau during charge. A slower dissolution rate during charge also corresponds to a larger initial jump in voltage, and a higher voltage during charge, as seen in Fig. 3(b).
values result in a slower dissolution. Unlike for discharge, where the theoretical cell capacity is independent of precipitation rate, the charge capacity does depend on the system's ability to dissolve the precipitated species fast enough, as this ability impacts sulfur utilisation. During charge, a slow dissolution of Sp can act as a bottleneck, leading to the early formation of high plateau species, here S08, and to reduced capacity. The effect of this bottleneck on the cell voltage is already visible in Fig. 2(b) (ppt yes, BV yes) for charge at two different currents. The mechanism of the bottleneck becomes apparent when tracking the contribution of the two electrochemical reactions to the total current, shown in Fig. 4(a), and the evolution of species in the system, in Fig. 4(b). Thus, in the presence of slow dissolution, the boundary between the high and low plateaus becomes less sharp, leading to the disappearance of a distinct low plateau during charge. A slower dissolution rate during charge also corresponds to a larger initial jump in voltage, and a higher voltage during charge, as seen in Fig. 3(b).
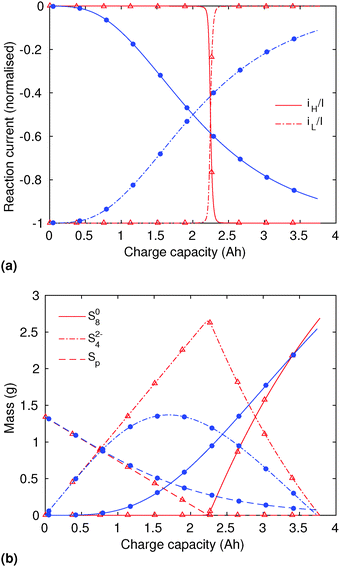 | ||
Fig. 4 (a) Simulated reaction currents and (b) species evolution during a 1.7 A (C/2) constant current charge with high saturation concentration  = 0.005 g, kp = 100 1/s, (red △) and low saturation concentration = 0.005 g, kp = 100 1/s, (red △) and low saturation concentration  = 0.0001 g, kp = 100 1/s (blue ●). The corresponding voltage is illustrated in Fig. 3(b) with the same symbols. The slower dissolution acts as a bottleneck during charge, triggering an earlier onset of the high plateau reaction and eliminating the boundary between the plateaus. Symbols distinguish between data sets rather than denote computed values. = 0.0001 g, kp = 100 1/s (blue ●). The corresponding voltage is illustrated in Fig. 3(b) with the same symbols. The slower dissolution acts as a bottleneck during charge, triggering an earlier onset of the high plateau reaction and eliminating the boundary between the plateaus. Symbols distinguish between data sets rather than denote computed values. | ||
4 Conclusions
We describe a zero dimensional model for predicting the voltage response of a Li–S cell under the assumption of a two-step electrochemical reaction chain. By including kinetic limitations according to the Butler–Volmer approximation and a simple model of precipitation/dissolution, important features of the discharge and charge voltage curves are reproduced, such as the flat low voltage plateau and the dip between voltage plateaus during discharge, and the possible merging of the two plateaus when dissolution is the limiting phenomenon during charge. In the present model, the precipitating species does not participate in further reduction reactions, such that the theoretical discharge capacity of the cell does not change upon including precipitation effects. Dissolution, however, can become the limiting process for high charging currents, reducing the cell capacity.Comparative to the existing one dimensional models,14,19 the model presented here offers a tool for analysing the evolution of species concentration and the interplay between reaction and precipitation parameters with significantly lower computational requirements. Beyond the analysis of mechanisms inside a Li–S cell and their effects, this model is a suitable platform for predictive and diagnostic methods used by control engineers in evaluating the performance of Li–S cells in various applications.
The model also enables the interpretation of an open circuit voltage for Li–S, and indicates that such experimental data can be obtained from constant current discharge only at prohibitively low currents. The approach of using Nernst equations to model the current-free state can eliminate the need to define and obtain the open circuit voltage for a Li–S cell. In exchange, however, parameter values must be obtained from other modelling and experimental data, such as standard reaction potentials from simulations, but also precipitation and shuttle parameters.
The model can be easily expanded to include the voltage contribution from the anode and that from the concentration-dependent electrolyte resistivity, as considered in Zhang et al.,26 for the purpose of comparison to experimental data. Other features that might play a role in the mechanism of Li–S cells, such as a longer chain of electrochemical reactions,12 the existence of chemical reactions, that of parallel electrochemical reaction paths, or the precipitation/dissolution of other species can also be included. Each of these additions increases the number of parameters that must be obtained from experimental data, such that the need of any such improvement should be based on experimental evidence of the feature's importance in the studied cell.
Acknowledgements
The authors would like to thank the Engineering and Physical Sciences Research Council in the UK for funding this work under the Revolutionary Electric Vehicle Battery (REVB) project EP/L505298/1, and acknowledge useful discussions with Mark Wild and Laura O'Neill from OXIS Energy.References
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19–30 CrossRef CAS PubMed.
- J. Brückner, S. Thieme, F. Böttger-Hiller, I. Bauer, H. T. Grossmann, P. Strubel, H. Althues, S. Spange and S. Kaskel, Adv. Funct. Mater., 2014, 24, 1284–1289 CrossRef.
- M. Hagen, D. Hanselmann, K. Ahlbrecht, R. Maça, D. Gerber and J. Tübke, Adv. Energy Mater., 2015, 5, 1401986 Search PubMed.
- Y.-S. Su, Y. Fu, T. Cochell and A. Manthiram, Nat. Commun., 2013, 4, 2985 Search PubMed.
- I. A. Hunt, Y. Patel, M. Szczygielski, L. Kabacik and G. J. Offer, J. Energy Storage, 2015, 2, 25–29 CrossRef.
- A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Chem. Rev., 2014, 114, 11751–11787 CrossRef CAS PubMed.
- D. Bresser, S. Passerini and B. Scrosati, Chem. Commun., 2013, 49, 10545–10562 RSC.
- R. Xu, J. Lu and K. Amine, Adv. Energy Mater., 2015, 1500408 Search PubMed.
- R. M. Spotnitz, Electrochem. Soc. Interface, 2005, 14, 39–42 CAS.
- Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2004, 151, A1969 CrossRef CAS.
- Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2003, 150, A306 CrossRef CAS.
- D. Moy, A. Manivannan and S. R. Narayanan, J. Electrochem. Soc., 2014, 162, A1–A7 CrossRef.
- S. Risse, S. Angioletti-Uberti, J. Dzubiella and M. Ballauff, J. Power Sources, 2014, 267, 648–654 CrossRef CAS.
- K. Kumaresan, Y. Mikhaylik and R. E. White, J. Electrochem. Soc., 2008, 155, A576 CrossRef CAS.
- M. Ghaznavi and P. Chen, J. Power Sources, 2014, 257, 394–401 CrossRef CAS.
- M. Ghaznavi and P. Chen, J. Power Sources, 2014, 257, 402–411 CrossRef CAS.
- M. Ghaznavi and P. Chen, Electrochim. Acta, 2014, 575–585 CrossRef CAS.
- J. P. Neidhardt, D. N. Fronczek, T. Jahnke, T. Danner, B. Horstmann and W. G. Bessler, J. Electrochem. Soc., 2012, 159, A1528–A1542 CrossRef CAS.
- D. N. Fronczek and W. G. Bessler, J. Power Sources, 2013, 6–11 Search PubMed.
- A. F. Hofmann, D. N. Fronczek and W. G. Bessler, J. Power Sources, 2014, 259, 300–310 CrossRef CAS.
- L. Wang, T. Zhang, S. Yang, F. Cheng, J. Liang and J. Chen, J. Energy Chem., 2013, 22, 72–77 CrossRef CAS.
- S. Waluś, C. Barchasz, R. Bouchet, J.-C. Leprêtre, J.-F. Colin, J.-F. Martin, E. Elkam, C. Baehtz and F. Alloin, Adv. Energy Mater., 2015, 5, 1500165 Search PubMed.
- H. Park, H. S. Koh and D. J. Siegel, J. Phys. Chem. C, 2015, 119, 4675–4683 CAS.
- G. Yang, S. Shi, J. Yang and Y. Ma, J. Mater. Chem. A, 2015, 3, 8865–8869 CAS.
- P. Partovi-Azar, T. D. Kühne and P. Kaghazchi, Phys. Chem. Chem. Phys., 2015, 22009–22014 RSC.
- T. Zhang, M. Marinescu, L. O'Neill, M. Wild and G. Offer, Phys. Chem. Chem. Phys., 2015, 17, 22581–22586 RSC.
- Z. Deng, Z. Zhang, Y. Lai, J. Liu, J. Li and Y. Liu, J. Electrochem. Soc., 2013, 160, A553–A558 CrossRef CAS.
- V. Kolosnitsyn, E. Kuzmina and S. Mochalov, J. Power Sources, 2014, 252, 28–34 CrossRef CAS.
- Q. Wang, J. Zheng, E. Walter, H. Pan, D. Lv, P. Zuo, H. Chen, Z. D. Deng, B. Y. Liaw, X. Yu, X. Yang, J.-G. Zhang, J. Liu and J. Xiao, J. Electrochem. Soc., 2015, 162, A474–A478 CrossRef CAS.
- G. Scatchard, Chem. Rev., 1936, 19, 309–327 CrossRef CAS.
- K. S. Pitzer, J. Phys. Chem., 1973, 77, 268–277 CrossRef CAS.
- M. Cuisinier, P.-E. Cabelguen, S. Evers, G. He, M. Kolbeck, A. Garsuch, T. Bolin, M. Balasubramanian and L. F. Nazar, J. Phys. Chem. Lett., 2013, 4, 3227–3232 CrossRef CAS.
- N. Azimi, Z. Xue, L. Hu, C. Takoudis, S. Zhang and Z. Zhang, Electrochim. Acta, 2015, 154, 205–210 CrossRef CAS.
- H. Schneider, C. Gollub, T. Weiss, J. Kulisch, K. Leitner, R. Schmidt, M. M. Safont-Sempere, Y. Mikhaylik, T. Kelley, C. Scordilis-Kelley, M. Laramie and H. Du, J. Electrochem. Soc., 2014, 161, A1399–A1406 CrossRef CAS.
- M. Barghamadi, A. S. Best, A. I. Bhatt, A. F. Hollenkamp, P. J. Mahon, M. Musameh and T. Rüther, J. Power Sources, 2015, 295, 212–220 CrossRef CAS.
- C. E. Parfitt, PhD thesis, University of Warwick, 2012.
Footnote |
| † Electronic supplementary information (ESI) available: Matlab code solving the system of equations and producing the plots. See DOI: 10.1039/c5cp05755h |
| This journal is © the Owner Societies 2016 |