Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Very fast bulk Li ion diffusivity in crystalline Li1.5Al0.5Ti1.5(PO4)3 as seen using NMR relaxometry
Viktor
Epp
*ab,
Qianli
Ma
c,
Eva-Maria
Hammer†
c,
Frank
Tietz
cd and
Martin
Wilkening
*ab
aChristian Doppler Laboratory for Lithium Batteries, and Institute for Chemistry and Technology of Materials, Graz University of Technology (NAWI Graz), Stremayrgasse 9, 8010 Graz, Austria. E-mail: viktor.epp@tugraz.at; wilkening@tugraz.at
bDFG Research Unit 1277, Mobility of Lithium Ions in Solids, Graz University of Technology, Austria
cForschungszentrum Jülich GmbH, Institute of Energy and Climate Research, Materials Synthesis and Processing (IEK-1), 52425 Jülich, Germany
dHelmholtz-Institute Münster, c/o Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
First published on 10th November 2015
Abstract
The realization of large powerful all-solid-state batteries is still hampered by the availability of environmentally friendly and low-cost Li ion conductors that can easily be produced on a large scale and with high reproducibility. Advanced solid electrolytes benefit from fast ion-selective transport and non-flammability, but they may have low electrochemical stability with respect to Li metal. Sol–gel-synthesized lithium titanium aluminum phosphate Li1.5Al0.5Ti1.5(PO4)3 (LATP), which was prepared via a new synthesis route taking advantage of an annealing step at relatively low temperatures, has the potential to become one of the major players in this field although it may suffer from reduction upon direct contact with metallic lithium. Its ion dynamics is, however, as yet poorly understood. In the present study, 7Li nuclear magnetic resonance (NMR) spectroscopy was used to monitor the key Li jump processes on the atomic scale. NMR relaxation clearly reveals heterogeneous dynamics comprising distinct ultra-fast and slower diffusion processes. The high Li ion self-diffusion coefficients deduced originate from a rapid Li exchange with activation energies as low as 0.16 eV which means that sol–gel synthesized LATP is superior to other solid electrolytes. Our NMR results fully support recent theoretical investigations on the underlying diffusion mechanism, indicating that to rapidly jump from site to site, the ions use interstitial sites connected by low-energy barriers in LATP.
1. Introduction
It is hoped that the continuing demand for efficient electrochemical energy storage systems will be met, at least in the medium term, by rechargeable Li-based batteries that include, in particular, Li metal batteries with high energy densities.1–7 Considering the conventional lithium-ion battery technology, great effort has been devoted to enhancing power, capacity, lifetime, and safety. Besides incremental improvements to existing systems, the availability of suitable solid electrolytes8–13 is advantageous because of two considerations: (i) abandoning of highly flammable liquid electrolytes is expected to greatly improve safety and longevity, i.e., to reduce aging processes; and (ii) the suppression of Li dendrite growth by making use of solid electrolytes working as both dense inorganic membranes and separators would allow the use of metallic Li as the anode material, instantly multiplying current energy densities. Moreover, fast solid ion-conductors may take over the same function in Li/sulfur batteries as well as in non-aqueous, and possibly even aqueous, Li/oxygen batteries.Even without the use of Li anodes, all-solid-state batteries may be advantageous in (hybrid) automotive applications because they can easily withstand higher operation temperatures.14 This also includes the use of industrial waste heat in stationary energy storage systems. Compared with the conductivity of liquid electrolytes, ion transport in solid electrolytes is often one order of magnitude slower and is regarded as one of the main drawbacks. Therefore, either thinner membranes or higher operation temperatures, e.g., 80 °C, would be beneficial.
Research on solid electrolytes focuses on a wide range of materials including, in particular, various sulfides15–20 and garnet-type oxides.21–24 Although we have witnessed remarkable progress over the last few years, the optimum compound has not been found yet. Only a few materials have been identified whose ionic conductivities are on par with those of liquid electrolytes.16,18–21,25–29 In our opinion, the renewed interest in Li-containing titanium aluminum phosphates (LATP) might boost research on solid Li ion electrolytes to a new level.25,30–32
To some extent, the present electrolytes suffer from the disadvantages of high-temperature synthesis routes, reproducibility issues concerning stoichiometry and defect chemistry, blocking grain boundaries, metastability, or even electrochemical instability. In contrast to garnet-type electrolytes, LATP-type compounds can be prepared more simply and with higher reproducibility because of the lower sintering temperatures needed (900 °C vs. temperatures higher than 1100 °C).27 This directly prevents Li loss and ensures that the bulk and intra-grain properties are controlled more effectively. Combined with a high ionic conductivity, electrochemical robustness with respect to Li, e.g., through the application of protection layers, and negligible electronic conductivity, LATP-based compounds are expected to perform best among the electrolytes studied so far. Apart from the conduction pathway, little is known, however, about the elementary steps of Li ion hopping, which govern bulk ion transport and which are the key properties of a powerful electrolyte. An elegant way to study slow and very fast bulk ion dynamics is provided by the use of Li nuclear magnetic resonance (NMR) spectroscopy, i.e., by NMR line shape and relaxation measurements.10,33,34 Since NMR is a contactless method, there is no need for special sample preparation; powder samples can be used that have been stored under an inert gas atmosphere, i.e., fire-sealed in small glass ampoules.
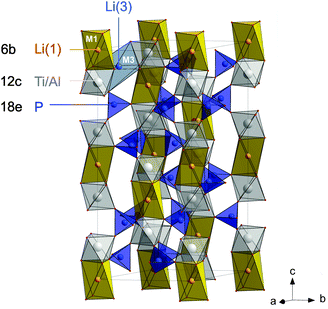
In the present study, we chose Li1+xAlxTi2−x(PO4)3 with x = 0.5 as one of the most promising compounds of the LATP family25 to study bulk ion conductivity in depth. The sample with μm-sized crystallites was prepared by a novel sol–gel method that allowed us to control the composition and morphology of the product obtained (see below). Importantly, the low sintering temperatures prevent, in particular, Li loss during the final annealing step. Rhombohedral Li1.5Al0.5Ti1.5(PO4)3 crystallizes with the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c. It is composed of alternating, corner-sharing [PO4] tetrahedra and [TiO6] octahedra, in which Li is reported to occupy mainly M1 sites (see Fig. 1) and to a lesser extent M3 sites.35 In a recent neutron diffraction study it was found that in LATP, besides M1, Li ions occupy a position close to M2 but displaced towards b, therein denoted as M2′.36 The replacement of Ti4+ by Al3+ ions needs extra Li ions for charge compensation and these ions occupy the interstitial voids.29,37,38 This enhancement of the number of charge carriers directly affects Li ion dynamics.
c. It is composed of alternating, corner-sharing [PO4] tetrahedra and [TiO6] octahedra, in which Li is reported to occupy mainly M1 sites (see Fig. 1) and to a lesser extent M3 sites.35 In a recent neutron diffraction study it was found that in LATP, besides M1, Li ions occupy a position close to M2 but displaced towards b, therein denoted as M2′.36 The replacement of Ti4+ by Al3+ ions needs extra Li ions for charge compensation and these ions occupy the interstitial voids.29,37,38 This enhancement of the number of charge carriers directly affects Li ion dynamics.
In the case of Li1.5Al0.5Ti1.5(PO4)3 we found an exceptionally high Li ion diffusivity. NMR relaxometry (see below) revealed several diffusion-induced rate peaks that definitely point to complex ion dynamics. The very low activation energies deduced (0.16 eV), which we reliably assigned to Li ion translational motion, are in excellent agreement with those recently predicted theoretically.39 The superposition of several diffusion processes gradually activated with increasing temperature results in an overall Li diffusivity that is in between those of Al-stabilized garnet oxides21,23,24 and argyrodite-type sulfides.40,41 The latter, together with the various compounds of the Li10GeP2S12 group,16,18 represent the fastest ion conductors studied over the past few years.18,42 While sulfides are highly hygroscopic, garnet oxides may suffer from reproducibility problems with respect to purity, composition and morphology because of the higher annealing temperatures needed. In contrast, LATP-based electrolytes might be advantageous in terms of preparation and device fabrication.
2. Experimental
For the preparation of Li1.5Al0.5Ti1.5(PO4)3 we developed a new sol–gel synthesis method. Stoichiometric amounts of LiNO3 (99%, Alfa Aesar), Al(NO3)3·9H2O (99%, Alfa Aesar), titanium(IV) isopropoxide (97%, Aldrich) and NH4H2PO4 (99%, Merck) were used. Titanium(IV) isopropoxide (97%, Aldrich) was first added to deionized water immediately forming a precipitate of titanium hydroxide. The fresh precipitate was filtered, washed and dissolved in nitric acid (65%, Aldrich). When a clear TiO2+ nitrate solution was formed, a 2-fold molar amount of citric acid monohydrate (99%, Merck) was added to the solution to stabilize it. LiNO3 and Al(NO3)3·9H2O were then added to the TiO2+ nitrate solution while stirring. After the salts were dissolved, NH4H2PO4 was added to the solution and a sol was immediately formed. Stirring was continued for another 0.5 h. After about 1 h, a stiff gel was spontaneously obtained. The gel was dried, calcined and milled in ethanol with zirconia balls on a milling bench. The ball-milled powder was put into a cylindrical pressing mold and pressed at a uniaxial pressure of 100 MPa. The pressed pellets were then sintered at 900 °C. White samples with a pure rhombohedral phase were obtained after sintering. The density of the pellets was over 95% of the theoretical density. More information can be found elsewhere.43Bulk ion dynamics on the angstrom length scale was studied using various time-domain 7Li NMR techniques including, in particular, variable-temperature spin-locking relaxometry. This allowed an unprecedented investigation of Li ion translational dynamics on different time and length scales. The measurements were conducted using an Avance III 300 solid-state NMR spectrometer connected to a 7 T cryomagnet (Bruker BioSpin); the nominal Larmor frequency ω0/2π was 116 MHz. We used the spin-lock technique and the saturation recovery technique to record longitudinal (R1 ≡ 1/T1) as well as transversal spin–lattice relaxation (SLR) rates (R1ρ ≡ 1/T1ρ) by applying short NMR excitation pulse lengths on the order of 2 μs. 7Li NMR spectra were obtained via Fourier transformation of the free induction decays recorded by a single-pulse 90° experiment. At selected temperatures we recorded NMR echoes with the sequence 90°–te–64° (20 μs < te < 60 μs) to overcome receiver dead-time effects, i.e., to capture sharply decaying components of the transient signals. While SLR NMR measurements in the laboratory frame are sensitive to ion dynamics of the order of the Larmor frequency, i.e., in the 108 Hz range, those performed in the rotating frame at a locking frequency ω1/2π of 30 kHz track diffusion parameters on the scale of 104 Hz. The SLR rates were obtained by fitting stretched exponentials to the corresponding magnetization transients. A more detailed description of the experimental setup can be found in earlier publications.44–46 Additionally, preliminary impedance measurements were performed using the Concept 80 system (Novocontrol), providing a frequency range of 3 μHz to 20 MHz; for further details of the setup we also refer to earlier publications.46–48
3. Results and discussion
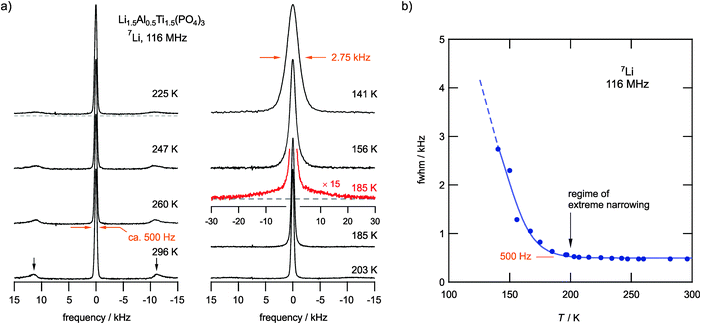
Our NMR line-shape analysis provides first insights into Li ion dynamics that can be made visible by averaging the dipolar magnetic and electric quadrupolar interactions. Recorded 7Li NMR spectra are shown in Fig. 2a. At low temperatures they are composed of a dipolarly broadened NMR central line, which is best described by a Voigt profile, and a broad quadrupole component with a width of ca. 24 kHz at 185 K (see the corresponding echo spectrum in Fig. 2a). The line width of the central line decreases with increasing temperature due to the averaging of dipole–dipole interactions. Furthermore, at T > 200 K the broad quadrupole component has transformed into sharp satellite intensities; at 300 K the corresponding distinctly shaped powder pattern is fully developed. Since 7Li is a spin-3/2 nucleus, the 90° singularities result from the interactions of the nuclear quadrupole moment with a non-vanishing electric field gradient (EFG) at the nuclear site. The appearance of an averaged powder pattern at higher T directly reveals rapid Li diffusivity. From the position of the singularities at 296 K, a quadrupole coupling constant of CQ(7Li) ≈ 45.4 kHz can be deduced if we assume an averaged EFG with axial symmetry. The value of CQ is to some extent dependent on T since various diffusion processes are activated stepwise with increasing temperature (see below). This behaviour is well known in the literature and belongs to the so-called ‘universalities’ in NMR line narrowing.49,50 A complete averaging leading to vanishing satellite signals is only expected for materials with a sufficiently large number of electrically distinct Li sites, as is the case for amorphous materials.Plotting the line width (full width at half maximum, FWHM) of the central NMR line as a function of T, Fig. 2b reveals that the onset of significant motional line narrowing is well below 140 K. In perfect agreement with this observation, the regime of extreme NMR line narrowing, determined by a line width of only 480 Hz, is already reached at temperatures as low as 200 K, i.e., 100 K below room temperature. This value is similar to those observed for other fast ion conductors;41,51 it does not change much even if we increase the temperature up to 500 K.
The onset of line narrowing at temperatures as low as 150 K clearly shows an impressively fast Li ion exchange among the magnetically different Li sites in LATP. Anticipating a rigid lattice line width of several kHz, full averaging is reached if the corresponding jump rate exceeds this value; thus, we have to deal with rates on the order of 104 s−1 at approximately 200 K.
The extraordinarily high Li diffusivity that leads to homonuclear dipole–dipole averaging is perfectly confirmed by the SLR NMR rates R1(ρ) recorded in both the laboratory and the rotating frame of reference.52 We used the recorded SLR data to quantify the diffusion processes in terms of activation energies and diffusion coefficients.
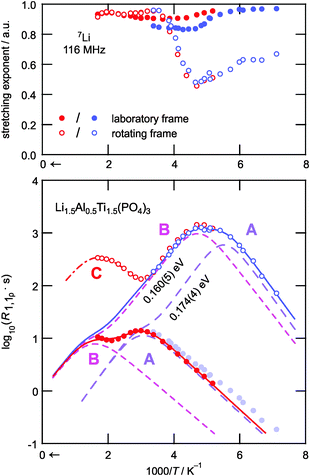
In Fig. 3 the characteristic diffusion-induced rate peaks are displayed using an Arrhenius representation; the corresponding stretching exponents γ are also shown. While almost exponential transients were obtained in the case of R1, γ of the transients in the rotating frame takes values of ca. 0.6 at low T. Most likely this is due to the coupling of the Li spins with paramagnetic centers as pointed out by Tse and Hartmann.53 With increasing T, γ(R1ρ) passes through a minimum that corresponds to the maxima in R1ρ. This feature has also been observed for other Li ion conductors, see, e.g., ref. 40. In the high-T limit the transients attain values of almost 1. This temperature behavior might point to heterogeneous dynamics, i.e., spin reservoirs with distinct ion dynamics; further experiments are, however, needed to clarify the origins of the temperature dependence of the stretching exponents.
Coming back to the relaxation rate peaks shown in the lower part of Fig. 3, the jump rates at the temperatures of their maxima are on the order of 108 s−1 and 104 s−1 depending whether the measurements were performed in the laboratory frame or in the rotating frame. The data seem to suggest three distinct relaxation processes in the accessible temperature range, as evidenced by the number of maxima marked by A, B, and C in the figure. The process reflected by maximum C is only partially observable in the rotating frame at T ≥ 600 K. The peak might reflect Li motion along a separate diffusion pathway that is activated at elevated temperatures only. Alternatively, it could represent rotational dynamics of the [PO4] or [TiO6] polyhedra. Further studies are needed to clarify this slow motion process. In contrast, the relaxation rate peaks A and B in both frames of reference are attributed to translational Li+ hopping; they can be best described as a sum of two individual BPP-type expressions R1 = R1,A + R1,B and R1ρ = R1ρ,A + R1ρ,B, respectively. According to NMR relaxation theory the proportionality of the summands is given by the following expressions:54–56
| R1,α ∝ J(ω0) + 4J(2ω0), | (1a) |
| R1ρ,α ∝ 6J(2ω1) + 10J(ω0) + 4J(2ω0); (α = A, B). | (1b) |
For isotropic, random 3D jump relaxation processes, the underlying spectral density function J(ω) can be expressed by56
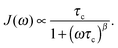 | (2) |
The correlation rate τc−1, being the key parameter in this study, is of the order of the Li+ jump rate; its temperature dependence is, in the simplest case, described using an Arrhenius relation
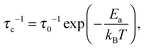 | (3) |
At first glance, the following might be assumed: the peak pair A could be the result of dipolar Li spin relaxation in the immediate vicinity of paramagnetic centers, which would cause a relaxation shoulder of the main rate peak B. Such a behavior has been observed for several glasses by Müller-Warmuth and co-workers.57 Since, however, a pronounced paramagnetic background relaxation is absent for the R1 rates, we exclude this possibility of explaining the two rate peaks observed. Moreover, the corresponding R1 rate peaks are well separated on the inverse temperature scale. Hence, we attribute the two observed peak maxima A and B to two dynamic processes that represent distinct Li+ elementary hopping processes in LATP. These processes could include jumps between M1 and M3 sites or also involve other interstitial sites. As pointed out by Lang et al., incorporation of Al3+ causes the additional Li ions to occupy M3 sites.39 At the same time Li+ ions on M1 are displaced towards Al sites. This might result in a facile jump process as compared to Al-free LTP. As has been shown by Lang et al. the additional Li ions prefer to reside near the Al centers.39 Such trapping effects would result in diffusion processes being activated at elevated T.
In order to extract the underlying diffusion parameters associated with the relaxation peaks, a global fit analysis was performed. Here, the rates R1 and R1ρ are analyzed simultaneously, i.e., by linking Ea and τ0−1 that give rise to each peak. The resulting joint fits are shown as solid lines in Fig. 3 while the individual peak pairs are rendered as dashed lines. To be successful, it is necessary to formally replace the locking frequency ω1 in the expression for R1ρ,α by an effective frequency ωeff,α, which takes into account local (magnetic and electric) fields. Since no information on these fields is available, ωeff,α was left as a free, i.e., variable, parameter in the fit analysis. This results in virtually the same activation energies, i.e. Ea,A = 0.17 eV and Ea,B = 0.16 eV for both relaxation processes, while the pre-exponential factors of the Arrhenius terms turn out to be τ0,A−1 ≈ 3 × 1011 s−1 and τ0,B−1 ≈ 1 × 1010 s−1, respectively. The effective fields as obtained from the fits are ωeff,A ≈ 2.1 × 106 s−1 (≈11 × ω1) and ωeff,B ≈ 8.6 × 105 s−1 (≈4.6 × ω1).
Surprisingly, the determined activation energies are quite low. Similar values have recently been calculated for lithium titanium phosphate by Elsässer and co-workers on the basis of density functional theory: interstitial Li hopping (0.19–0.20 eV) is energetically preferred compared to vacancy-assisted migration.39 Obviously, the interstitial diffusion mechanism suggested theoretically is confirmed experimentally by 7Li NMR relaxometry.
The difference in pre-exponential factors τ0,A−1 and τ0,B−1 might be justified in different configurational entropies affecting the two diffusion processes. Depending on the exact diffusion pathway the ions may have access to a different number of available positions. Trapping effects because of Al centres (see above) may come into play, too. The different ωeff values obtained might be the consequence of the site occupancy of paramagnetic impurities.
The diffusion parameters obtained by NMR can be used to calculate Li self-diffusion coefficients, which are the key parameters for the characterization of solid electrolytes. By employing the Einstein–Smoluchowski relation58 and by assuming an uncorrelated jump diffusion with a mean diffusion length of about 3 Å, a value of D ≈ 3 × 10−9 cm2 s−1 is obtained at room temperature (peak B). For peak A we obtain D ≈ 5 × 10−8 cm2 s−1 at 300 K. Such a value corresponds to ionic conductivities on the order of 10−3 S cm−1. This is observed by impedance spectroscopy: preliminary measurements of the bulk ion transport point to values of approx. 3 × 10−3 S cm−1 at 300 K. The corresponding activation energy of bulk ion transport amounts to 0.26 eV which is significantly lower than the mean values known for garnet-type oxides (0.34 eV), see below.23
Considering the activation energies from both NMR (0.16–0.17 eV, low T range) and impedance spectroscopy (0.26 eV) there are, at first glance, discrepancies, which can easily be understood in terms of a heterogeneous potential landscape to which the ions are exposed. In contrast to SLR NMR, which is sensitive to ion dynamics on the angstrom length scale, thus sensing activation barriers between next neighboring Li sites, impedance (or conductivity) spectroscopy probes long-range motions considering conductivities in the low-frequency range. The latter can be identified with DC values. Long-range ion transport through the crystal lattice is characterized by 0.26 eV, which is a mean value of all the barriers the ions have to overcome. Obviously, this also includes those which appear in SLR NMR at higher temperature, see peak C in Fig. 3.
Finally, we should compare the results of the NMR relaxometry responses with other fast-conducting solid electrolytes. Here, besides Li10GeP2S12 and Li7P3S11,18,20 garnet-type cubic-Li6.6La0.3Zr1.6Ta0.4O12 and argyrodite-type Li6PS5Br41 serve as the boundaries of current research. Note, polycrystalline Li6.6La3Zr1.6Ta0.4O12 was synthesized by a solid-state reaction using stoichiometric amounts of LiOH, La2O3, ZrO2 and Ta2O5. After ball-milling in ethanol, the dried powder was pressed into pellets and calcined at 850 °C for 20 h in Al2O3 crucibles. Subsequent wet milling and sintering in pressed pellets was repeated first at 1000 °C, then at 1100 °C. The Arrhenius plot of Fig. 4 provides a succinct way to compare the diffusivities of the three samples via spin-lock NMR relaxometry. Since the rates shown were compared at similar locking frequencies, the position of the peak maxima directly reflects the extent of Li ion diffusivity. The more the peak is shifted towards lower temperatures the higher is the Li ion mobility. Li6PS5Br can be identified as the compound with the highest Li-ion diffusivity (Tmax = 167 K, 0.20 eV) and the garnet Li6.6La0.3Zr1.6Ta0.4O12 that with the lowest (Tmax = 307 K, 0.34 eV). The diffusivity of our LATP sample lies between the other two with respect to the relaxation process B (or even A). Hence, in terms of Li ion transport, the phosphate clearly shows superior properties as compared to oxide garnets.
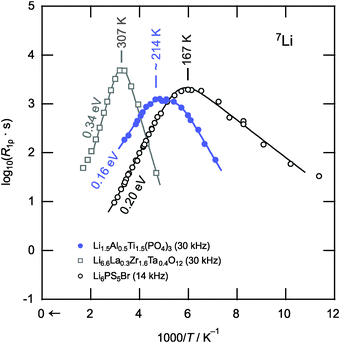 | ||
| Fig. 4 Comparison of the 7Li NMR SLR rates R1ρ shown in Fig. 2 with those obtained for Li6.6La0.3Zr1.6Ta0.4O12 and Li6PS5Br,41 representing members of two other promising candidates for solid electrolytes, viz. garnet-type oxides and structurally complex sulfides, respectively. The Li ion diffusivity as seen via NMR relaxometry clearly increases in the order Li6.6La0.3Zr1.6Ta0.4O12 < Li1.5Al0.5Ti1.5(PO4)3 < Li6PS5Br highlighting the extraordinary diffusion properties of LATP-based compounds. | ||
4. Summary
To conclude, by making use of spin-lock and spin–lattice relaxation 7Li NMR we were able to directly analyze bulk Li ion diffusivities in polycrystalline Li1.5Al0.5Ti1.5(PO4)3 which is expected to be one of the next-generation solid electrolytes for Li-based batteries. The Li ion diffusivity in Li1.5Al0.5Ti1.5(PO4)3 is extremely high and can easily compete with that of sulfide-based electrolytes, which, however, may suffer from hygroscopic properties that complicate both preparation and processing on a commercial level. 7Li NMR relaxometry revealed several distinct diffusion processes pointing to a complex overall diffusion mechanism. The activation energies obtained (0.16–0.17 eV) are in excellent agreement with those recently calculated by Lang et al. (0.19 eV) for migrating interstitials in LATP.39 This is one of the first important steps towards fully understanding the underlying ion transport mechanisms in lithium aluminium titanium phosphates.Acknowledgements
We would like to thank our colleagues at TU Graz for valuable discussions. Financial support from the Austrian Federal Ministry of Science, Research and Economy, and the Austrian National Foundation for Research, Technology and Development is greatly appreciated. In addition, financial support from the Helmholtz Association in the framework of the project programs “Helmholtz Energy Alliance – stationary electrochemical solid-state storage and conversion” and “HGF initiative for mobile/stationary energy storage systems” is gratefully acknowledged. Moreover, we thank the Deutsche Forschungsgemeinschaft (DFG Research Unit 1277, grant no. WI3600/2-2 and 4-1) for financial support.References
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19 CrossRef CAS PubMed.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19 CrossRef CAS PubMed.
- M. R. Palacin, Chem. Soc. Rev., 2009, 38, 2565 RSC.
- P. G. Bruce, B. Scrosati and J.-M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930 CrossRef CAS PubMed.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652 CrossRef CAS PubMed.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271 CrossRef CAS PubMed.
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359 CrossRef CAS PubMed.
- J. Sakamoto, in Handbook Solid State Batteries, ed. N. J. Dudney, W. C. West and J. Nanda, World Scientific, New Jersey, Hong Kong, 2015, p. 391 Search PubMed.
- Y. S. Jung, D. Y. Oh, Y. J. Nam and K. H. Park, Isr. J. Chem., 2015, 55, 472 CrossRef CAS.
- V. Epp and M. Wilkening, in Handbook Solid State Batteries, ed. N. J. Dudney, W. C. West and J. Nanda, World Scientific, New Jersey, Hong Kong, 2015, p. 133 Search PubMed.
- C. Cao, Z. Li, X.-L. Wang, X. Zhao and W.-Q. Han, Front. Energy Res., 2014, 2, 25 Search PubMed.
- K. Takada, Acta Mater., 2013, 61, 759 CrossRef CAS.
- P. Knauth, Solid State Ionics, 2009, 180, 911 CrossRef CAS.
- M. Nagao, H. Kitaura, A. Hayashi and M. Tatsumisago, J. Electrochem. Soc., 2013, 160, A819 CrossRef CAS.
- G. Sahu, Z. Lin, J. Li, Z. Liu, N. Dudney and C. Liang, Energy Environ. Sci., 2014, 7, 1053 Search PubMed.
- P. Bron, S. Johansson, K. Zick, J. Schmedt auf der Günne, S. Dehnen and B. Roling, J. Am. Chem. Soc., 2013, 135, 15694 CrossRef CAS PubMed.
- T. Kaib, S. Haddadpour, M. Kapitein, P. Bron, C. Schröder, H. Eckert, B. Roling and S. Dehnen, Chem. Mater., 2012, 24, 2211 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682 CrossRef CAS PubMed.
- H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Angew. Chem., Int. Ed., 2008, 47, 755 CrossRef CAS PubMed.
- F. Mizuno, A. Hayashi, K. Tadanaga and M. Tatsumisago, Adv. Mater., 2005, 17, 918 CrossRef CAS.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714 RSC.
- J. Wolfenstine, J. Ratchford, E. Rangasamy, J. Sakamoto and J. L. Allen, Mater. Chem. Phys., 2012, 134, 571 CrossRef CAS.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378 RSC.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778 CrossRef CAS PubMed.
- K. Arbi, W. Bucheli, R. Jiménez and J. Sanz, J. Eur. Ceram. Soc., 2015, 35, 1477 CrossRef CAS.
- K. Takahashi, J. Ohmura, D. Im, D. J. Lee, T. Zhang, N. Imanishi, A. Hirano, M. B. Phillipps, Y. Takeda and O. Yamamoto, J. Electrochem. Soc., 2012, 159, A342 CrossRef CAS.
- J. L. Narváez-Semanate and A. C. M. Rodrigues, Solid State Ionics, 2010, 181, 1197 CrossRef.
- J. Fu, Solid State Ionics, 1997, 96, 195 CrossRef CAS.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, J. Electrochem. Soc., 1990, 137, 1023 CrossRef CAS.
- E. C. Bucharsky, K. G. Schell, A. Hintennach and M. J. Hoffmann, Solid State Ionics, 2015, 274, 77 CrossRef CAS.
- H. Morimoto, M. Hirukawa, A. Matsumoto, T. Kurahayashi, N. Ito and S. Tobishima, Electrochemistry, 2014, 82, 870 CrossRef CAS.
- C. R. Mariappan, Appl. Phys. A: Mater. Sci. Process., 2014, 117, 847 CrossRef CAS.
- M. Wilkening and P. Heitjans, ChemPhysChem, 2012, 13, 53 CrossRef CAS PubMed.
- R. Böhmer, K. R. Jeffrey and M. Vogel, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87 CrossRef.
- K. Arbi, S. Mandal, J. M. Rojo and J. Sanz, Chem. Mater., 2002, 14, 1091 CrossRef CAS.
- M. Pérez-Estébanez, J. Isasi-Marín, D. M. Többens, A. Rivera-Calzada and C. León, Solid State Ionics, 2014, 266, 1 CrossRef.
- P. Maldonado-Manso, E. R. Losilla, M. Martínez-Lara, M. A. G. Aranda, S. Bruque, F. E. Mouahid and M. Zahir, Chem. Mater., 2003, 15, 1879 CrossRef CAS.
- J. Fu, J. Mater. Sci., 1998, 33, 1549 CrossRef CAS.
- B. Lang, B. Ziebarth and C. Elsässer, Chem. Mater., 2015, 27, 5040 CrossRef CAS.
- V. Epp, Ö. Gün, H.-J. Deiseroth and M. Wilkening, Phys. Chem. Chem. Phys., 2013, 15, 7123 RSC.
- V. Epp, Ö. Gün, H.-J. Deiseroth and M. Wilkening, J. Phys. Chem. Lett., 2013, 4, 2118 CrossRef CAS.
- A. Kuhn, V. Duppel and B. V Lotsch, Energy Environ. Sci., 2013, 6, 3548 CAS.
- Q. Ma, F. Tietz and O. Guillon, 2015, submitted.
- A. Dunst, V. Epp, I. Hanzu, S. A. Freunberger and M. Wilkening, Energy Environ. Sci., 2014, 7, 2739 CAS.
- J. Langer, V. Epp, M. Sternad and M. Wilkening, Solid State Ionics, 2015, 276, 56 CrossRef CAS.
- D. Wohlmuth, V. Epp and M. Wilkening, ChemPhysChem, 2015, 16, 2582 CrossRef CAS PubMed.
- D. Wohlmuth, V. Epp, P. Bottke, I. Hanzu, B. Bitschnau, I. Letofsky-Papst, M. Kriechbaum, H. Amenitsch, F. Hofer and M. Wilkening, J. Mater. Chem. A, 2014, 2, 20295 CAS.
- F. Preishuber-Pflügl, P. Bottke, V. Pregartner, B. Bitschnau and M. Wilkening, Phys. Chem. Chem. Phys., 2014, 16, 9580 RSC.
- R. Bertermann and W. Müller-Warmuth, Z. Naturforsch., A: Phys. Sci., 1998, 53a, 863 Search PubMed.
- A. Kuhn, P. Sreeraj, R. Pöttgen, H.-D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018 CrossRef CAS PubMed.
- S. Narayanan, V. Epp, M. Wilkening and V. Thangadurai, RSC Adv., 2012, 2, 2553 RSC.
- A. Kuhn, S. Narayanan, L. Spencer, G. R. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 94302 CrossRef.
- D. Tse and S. R. Hartmann, Phys. Rev. Lett., 1968, 21, 511 CrossRef CAS.
- A. Abragam, The Principles of Nuclear Magnetism, Oxford University Press, Oxford, UK, 1961 Search PubMed.
- S. W. Kelly and C. A. Sholl, J. Phys.: Condens. Matter, 1992, 4, 3317 CrossRef.
- N. Bloembergen, E. M. Purcell and R. V Pound, Phys. Rev., 1948, 73, 679 CrossRef CAS.
- M. Grüne and W. Müller-Warmuth, Solid State Nucl. Magn. Reson., 1995, 5, 145 CrossRef.
- H. Mehrer, Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes, Springer, Berlin, New York, 2007 Search PubMed.
Footnote |
| † Present address: Ceres Power Ltd., Viking House, Foundry Lane, Horsham RH13 5PX, UK. |
| This journal is © the Owner Societies 2015 |