Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Misfit stabilized embedded nanoparticles in metallic alloys
Yu. N.
Gornostyrev
abc and
M. I.
Katsnelson
*cd
aInstitute of Quantum Materials Science, CJSC, Ekaterinburg 620075, Russia
bInstitute of Metal Physics, Russian Academy of Sciences—Ural Division, Ekaterinburg 620041, Russia
cUral Federal University, Theoretical Physics and Applied Mathematics Department, Mira str. 19, Ekaterinburg, 620002, Russia
dRadboud University, Institute for Molecules and Materials, Heyendaalseweg 135, Nijmegen, 6525 AJ, Netherlands. E-mail: M.Katsnelson@science.ru.nl
First published on 24th September 2015
Abstract
Nanoscale inhomogeneities are typical for numerous metallic alloys and crucially important for their practical applications. At the same time, stabilization mechanisms of such a state are poorly understood. We present a general overview of the problem, together with a more detailed discussion of the prototype example, namely, Guinier–Preston zones in Al-based alloys. It is shown that coherent strain due to a misfit between inclusion and host crystal lattices plays a decisive role in the emergence of the inhomogeneous state. We suggest a model explaining the formation of ultrathin plates (with the thickness of a few lattice constants) typical for Al–Cu alloys. Discreteness of the array of misfit dislocations and long-ranged elastic interactions between them are the key ingredients of the model. This opens a way for a general understanding of the nature of (meta)stable embedded nanoparticles in practically important systems.
Introduction
One of the basic concepts in physics and chemistry of solids and materials science is the formation of microstructures which depend on chemical compositions and thermal treatment conditions.1 Of particular interest are microstructures with nanoscale elements2 (tens to thousands interatomic distances), whose properties differ essentially from those of single molecules/atoms as well as of bulk materials.3 Their peculiarities are generally explained in terms of high surface-to-volume ratios and/or size effects4 in fundamental properties of materials (such as, e.g., size quantization of an electron energy spectrum in embedded nanoparticles5). We are just in the very beginning of the way, and specific physical mechanisms responsible for formation and stability of nano-scale microstructures are still debatable.6A typical example is a microstructure formed by the quenching of a high temperature state, which presents either structural inhomogeneities or products of phase decomposition. In the former case, a tweed-like microstructure with short-range crystallographic order arises, characteristic of a quenched pre-transition state (for example see ref. 7–9). In the latter case, the kinetics of the first-order phase transition10 is crucially important and the nanoscale microstructure is formed due to freezing/stabilization of an incomplete stage of the phase transformation. It can result in a regular or chaotic pattern structure; typically, long-range interactions play an essential role there.11 One of the examples of the regular pattern is a nanocomposite permanent magnet ALNICO12 and Sm(CoFeCuZr)7.513 where the basket-weave microstructure arises as a result of spinodal decomposition of an alloy.10 The regular pattern structure can correspond to a stable or metastable state of a system as it takes place in the cases of stripe magnetic domains,14–18 “polytwinned” antiphase domain structures in tetragonal ordered alloys,19,20 lath martensite21–23 or perlite in steels;24 the latter is a particular case of the well-known eutectoid decomposition.25 The stabilization mechanisms for the regular nanoscale microstructures are related to the tendency to minimization of the energy of long-range interactions. Morphology of the formed structure depends on external fields26,27 and their gradients,27,28 as well as on the dissipation of the stored energy, by plastic relaxation in the case of elastic interaction.22,23 There are even some rigorous mathematical results on the formation of stripes and checkerboard patterns in the Ising model with the long-range interactions included;29 the computational simulations see, e.g., in ref. 30.
Here we focus on the other class of materials, which attract increasing attention in the last few decades. In this case, the microstructure contains stable or long-living metastable nanosized-scale precipitates embedded in a host.31 Such a heterogeneous state is typical for the so called nanoscale granular materials32 and was observed in many technologically important alloys. Examples include pre-Guinier–Preston zones33 (or K-state21) and Guinier–Preston–Bagaryatsky zones in aluminum alloys34,35 which are supposed to play a decisive role in their strengthening,36 heterophase fluctuations37 resulting in an athermal omega-phase in Ti- and Zr-based alloys38–40 and in Cu–Zn systems,41 precipitates of Co in Cu,42 Cu in Fe,43 Pb in Al.44
The common feature of these structural states is their stability at a moderate temperature, the precipitates are neither grow to a macroscopic size nor disappear. The conventional theory of structural transformations in solids has difficulties in explaining such states, which lies very deeply; actually, it follows just from the separation of free energy of the multiphase system into bulk and surface contributions.10,21 This assumption is by no way self-evident since a coherent precipitate of a new phase creates long-range deformations in the host. At a phenomenological level, possible violation of extensivity of thermodynamic quantities on the nanoscale was discussed in ref. 4. However, as was shown by Eshelby,45 the energy of coherent precipitates, at least, for the inclusion of the ellipsoidal shape, is proportional to the volume and therefore it is just a renormalization of the bulk contribution of the energy.
Coherent conjugation when crystal structures of the inclusion and the host are matched at the interface by a small homogeneous deformation is typical for small inclusions. With the inclusion growth, a character of conjugation is changed and the coherence is lost for large enough inclusions; in this case, a tangential component of the deformation field is no more continuous at the interface. In this work, we demonstrate that for a partially coherent precipitate a special situation takes place. To provide the partially coherent state one has to introduce topological defects, namely, misfit dislocations,21,46 and their interaction energy turns out to be different from both bulk and surface contribution to the total energy. This additional energy results in a stabilization of the nanosize precipitate.
Two examples of nanoscale microstructures
Before considering physical mechanisms of stabilization of the nanoscale microstructures, we discuss in a bit more detail on two particular examples to make the problem clearer. These examples are practically important and show most typical features of the loss of coherence by precipitates.A Athermal omega-phase formation
The athermal omega-phase is observed in numerous titanium and zirconium alloys at the quenching after homogenizing annealing at temperatures corresponding to the stable beta-phase (bcc).40 It is observed only as precipitates (and never as a bulk phase) by a displacive mechanism that transforms the structure from bcc (beta) to hexagonal (omega) via a collapse of the {111} planes of the parent bcc phase (Fig. 1). The athermal omega precipitates are typically considered to inherit the composition of the parent beta matrix. As a rule, the omega-phase in the titanium alloy with beta-stabilizing elements such as V, Cr, Mn, Fe, Co and Ni appears in the form of fine ellipsoidal particles with long axes along 〈111〉 and distributed uniformly over the whole of the grain volume.38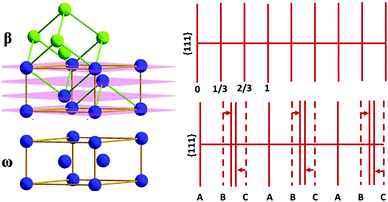 | ||
| Fig. 1 Relationship between bcc and omega phase crystal lattices (left) and β – ω transformation by collapse of certain {111} planes (right). | ||
The athermal omega-phase provides us an example of a precipitate coherently conjugated with the host crystal lattice despite essential differences in the crystal structures. The truly coherent conjugation corresponds to the so-called commensurate athermal omega-phase. This situation is quite exclusive (it happens in elemental Ti, Zr and Hf under pressure), the incommensurate athermal omega phase is much more typical,40 the omega–beta mismatch (that is, amplitude of displacements of the {111} planes) depends on the concentration of the dopant. Such a conjugation is semi-coherent and includes appearance of domain boundaries or topological defects as suggested in ref. 47.
On subsequent isothermal annealing, coarsening of the omega-phase precipitates is accompanied by the diffusional partitioning of the alloying elements. As a result, the isothermal omega-phase is formed with a reduced concentration of the alloying elements and a larger lattice mismatch that finally leads to the loss of coherency. Thus, the formation of the omega-phase precipitates results from concurrent compositional and structural instabilities of titanium- and zirconium-based alloys.48 The detailed theory of formation of the athermal omega-phase is still absent. One can assume that the peculiar structural state of beta + omega titanium based alloys is responsible for their anomalous electronic properties such as negative temperature coefficient of resistivity5 and provides an efficient mechanism of giant ultrasound attenuation49 observed in these alloys.50
B Guinier–Preston zones and their structural features
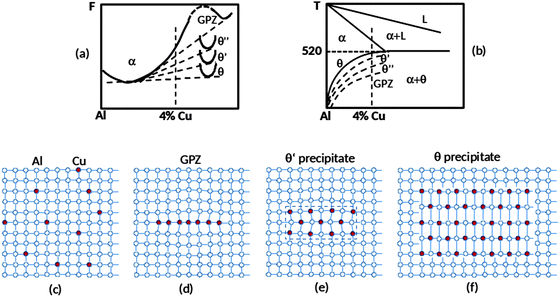
Though AlCu-based alloys have been discovered more than 100 years ago, still nowadays they are of great importance due to their light-weight constructions36,51 such as a fuselage of aircrafts (including new Airbus A380). The prominent properties of AlCu-based alloys (mainly AlCuMg) are their low specific weight combined with hardness and tensile strength, which is comparable to those of steels. This hardening of Al is crucially dependent on coherent meta-stable precipitates formed at the annealing at the temperatures corresponding to the equilibrium solid solution with further quenching and aging at room or moderately high temperature. In binary AlCu alloys these precipitates are thin Cu platelets of a few nanometer thickness on the {100}-planes in fcc-Al; they are called Guinier–Preston zones (GPZs).34Tempering of AlCu alloys above room temperature leads to the growth of GPZs and their transformation which includes several steps (Fig. 2): GPZ I → θ′′ particles (GP II zones) → θ′ phase particles → θ phase particles. The GPZ I zones have only one Cu layer in the {100} plane (Fig. 2d). The θ′′ particles contain two or more {100} Cu layers separated by three aluminum planes. GPZ I and II are precipitates coherently conjugated with the host. The θ′ particles are larger and semicoherent with the Al host, that is, they are conjugated with the host via the formation of misfit dislocations.52 Finally, the θ particles are inclusions of a thermodynamically stable phase Al2Cu incoherent with the host. The highest strength of the alloy is reached just before the precipitates loss coherency, when the compensation of long-range internal stresses takes place. Despite a long history of investigations of GPZs the key questions on the mechanisms providing their stabilization and, thus, unique mechanical properties of Al-based alloys are still open. In particular, it is unclear, what is the exact role of quenched-in vacancies. It was suggested35 that the latter are crucially important on early stage of GPZ formation because they provide relaxation of the strain due to size mismatch between the host and the solvent atoms. However, the relative concentration of quenched-in vacancies and solute atoms is just about 1/1000.36 It seems to be too small to affect the structure of precipitates but can accelerate essentially diffusion processes providing a decomposition of homogeneous alloy at room temperature. This is a common believe that a tiny platelet shape of GPZs provides the gain in the energy on coherent strains.35 However, to our knowledge, possible (meta)stability of this state has never been really demonstrated. Such demonstration is the main aim of this paper.
Coherent inclusion problem
The concept of coherent conjugation is crucially important for the rest of our paper. Incoherent conjugation corresponds to the coexistence of two or more macroscopically large pieces of different phases. Under such conditions, each phase has a structure for minimizing its chemical potential and the role of interface energy in the total energy balance is negligible. For the case of nanoscale inclusions it can be more important to minimize the interface energy than the bulk energy of the inclusion. It requires an optimization of the interface to avoid energetically expensive jumps in atomic positions and to make the displacement field across the interface as smooth as possible. This kind of conjugation is called coherent.Early stage of precipitation results in the appearance of particles coherently conjugated with the host; their structure can be, generally speaking, different from that of the corresponding bulk phase. In particular, the lattice parameters of the athermal omega-phase are essentially different from those in the equilibrium (e.g., at high pressures) thermal omega-phase40 and the structure of GPZs is essentially different from the equilibrium Al2Cu phase.52 The coherent long-range deformation in the host created by the particle modifies the conditions of phase equilibrium in the system, the former are now dependent on the size and the shape of the precipitates.53,54 Such a picture is valid for small enough particles. When their size grows above a typical crossover size determining by the energy balance between bulk differences of chemical potentials and elastic energy of the deformations we reach the true thermodynamic phase equilibrium (as required by Gibbs conditions), which does not depend on the particle sizes if one neglects the surface (interface) energy. The latter case corresponds to spinodal or binodal lines of equilibrium at the phase diagram21 while under the coherent strains a new phase can be reached at larger overcooling. In this section, we consider an isolated particle coherently conjugated to the host. In the next section the system under the near-crossover conditions would be considered when a semicoherent conjugation of the precipitates with the host.
Eshelby's solution45 for an ellipsoidal inclusion in an infinite homogeneous isotropic elastic material played a key role in understanding of the precipitation. As was shown by Eshelby, the energy of elastic strains created by an ellipsoidal coherent inclusion of a new phase in the host has the form
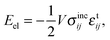 | (1) |
| σincij = Cijkl(Sklmnεtmn − εtkl) | (2) |
This limitation has motivated studies of Eshelby-type inclusion problems using extensions of the classical elasticity theories, which contain material length scale parameters58 or the curvature of interfaces.59,60 These approaches predict size-dependent elastic strains for inclusions of few nanometers and were applied to investigation of the effect of lattice mismatch on properties of nanostructures such as buried quantum dots,59,61 nanowires62 and composites.63
Here we follow the traditional approach of Eshelby and consider another mechanism of the size-dependent behavior suggested at the qualitative level in ref. 54, namely, a crossover from the coherent to the incoherent conjugation of the inclusion with the host. As was shown in ref. 21, the minimum of the elastic energy is reached for the coherent inclusion with the shape of a narrow plate. Therefore we restrict ourselves by the consideration of the penny-like-shape inclusion, a typical case for the inclusions with a large lattice mismatch and small surface tension.21
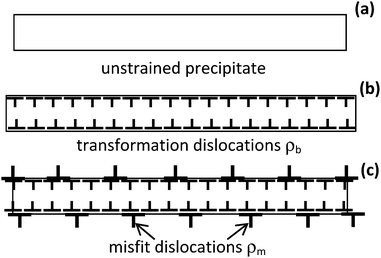
We would use the dislocation model of the conjugation of inclusion with the host; its equivalence to the Eshelby approach was discussed in ref. 64. Namely, we assume that the conjugation is accompanied by the appearance of continuously distributed dislocations and/or dislocation loops at the interface (Fig. 3). If the total tensor of intrinsic deformations created by such defects is equal to the intrinsic deformation tensor of the inclusion this, of course, provides also equality of strains. The network of virtual dislocations is characterized by the tensor dislocation density
| ρbij = ρξξibj | (3) |
| ρbij = −eiklnkεtlj | (4) |
To determine elastic energy of the coherent inclusion we have to take into account interaction energies and each dislocation family and between the families. Taking into account that the Burgers vectors have opposite signs at the lower and upper surfaces of the plate we obtain:
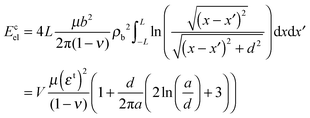 | (5) |
Coherent to incoherent crossover
The simplest model describing a transition from the coherent regime to the incoherent regime is the Frenkel–Kontorova model of an atomic chain lying at an incommensurate substrate.46,66,67 In this model, the incoherent regime corresponds to the case when elastic energy is much larger than the energy of interaction with the substrate so that the atomic chain remains undeformed. In contrast, in the case of very strong interaction energy the atomic chain takes the interatomic distance of the substrate (coherent regime). When both contributions are relevant the semicoherent regime arises. In this case the chain consists of coherent pieces interrupted by topological defects (solitons). One can assume that in the three-dimensional case the transition between the coherent and the incoherent regimes also involves a superlattice of topological defects, a key idea for further consideration.The mechanism of partially coherent strain compensation by an array of misfit dislocations was suggested long ago by Nabarro68 (see also recent review69). In that approach, the effect of misfit dislocations was reduced to a local renormalization of lattice mismatch. Below we develop this idea by a straightforward calculation of different contribution to the total energy. Contrary to ref. 68 and 69 we do not take into account possible locking of the dislocations by the Peierls relief since in close packed metallic systems such as Al–Cu the latter in known to be negligible.70
We assume that the semicoherent conjugation between the inclusion and the host is carried out by the formation of an additional network of misfit dislocations at the interface (Fig. 3c) with the Burgers vectors opposite to those of virtual dislocations (4) which are responsible for the transformation deformation. In terms of ref. 23 these dislocations provide the plastic part of misfit strain relaxation. An additional contribution to the elastic energy arises, due to the interaction within families of misfit dislocations:
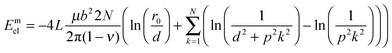 | (6) |
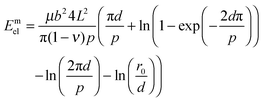 | (7) |
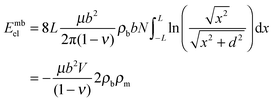 | (8) |
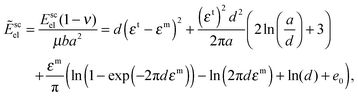 | (9) |
Expression (9) has a transparent physical meaning. The first contribution in the right-hand side coincides with the coherent strain energy (5), with the lattice mismatch decreased by the value εm by introducing misfit dislocations. The second contribution proportional to d/a, as in eqn (5), gives the energy of deformations created by the inclusion edges. It becomes essential if εm ≈ εt which suppresses the bulk contribution. At last, the third term proportional to the density of misfit dislocations describes the renormalization of the surface tension. The density of the misfit dislocations ρm and the corresponding deformation εm minimizing the energy Ẽscel for the case of a thin plate (d ≪ a) depend only on d and e0.
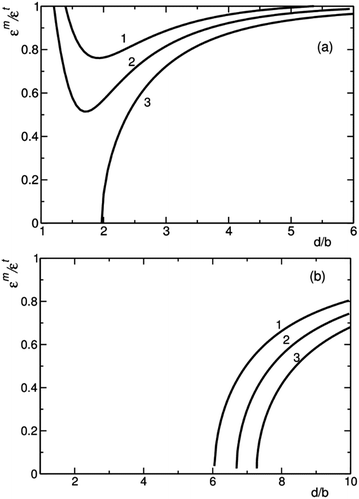
Fig. 4 displays the dependence of the ratio εm/εt on d obtained by numerical minimization of eqn (9) for different e0. For a large misfit εt = 0.1 and small core energy (small e0) formation of the misfit dislocations and, thus, the transition from the coherent to the semicoherent inclusion is energetically favourable for any d. In this case, the ratio εm/εt remains close to 1 (the curves 1, 2 in Fig. 4a) reaching minimum at d ≈ b, and misfit dislocations compensate lattice mismatch between the precipitate and the host phases almost completely. With the increase of the parameter e0 > 0.5 or decrease the value of misfit εt the behaviour εm(d) is changed qualitatively and the formation of the misfit dislocations is possible only for d larger than some critical value dcr (the curve 3 in Fig. 4a and b).
The curves in Fig. 4a correspond to the case of quite large misfit; its decrease results in the growth of dcr (Fig. 4b). The issue on the critical inclusion size corresponding to the loss of coherence has been discussed already72–74 by analysing the energetics of creation of the first dislocation loop. The value of dcr as calculated here is smaller (approximately twice) than predicted by Brooks criterion dcr ≈ b/2εt (ref. 72) and depends on the core energy e0. For the large misfit and small enough values of e0 the model predicts a qualitatively different behaviour in comparison with the previous considerations. In this case, a gradual loss of coherence takes place with the inclusion growth. It is a “soft” scenario in contrast to “hard” coherent – semi-coherent crossover which realizes for a small misfit and/or larger core energy for d > dcr.
Stabilization of nano-inclusion due to misfit strains
Total formation energy of the plate inclusion has the form| Einc = da2Δf + 2σa2 + Escel, | (10) |
Substituting eqn (9) into eqn (10) one can represent the inclusion energy per unit area as
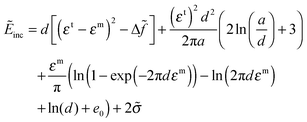 | (11) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) and
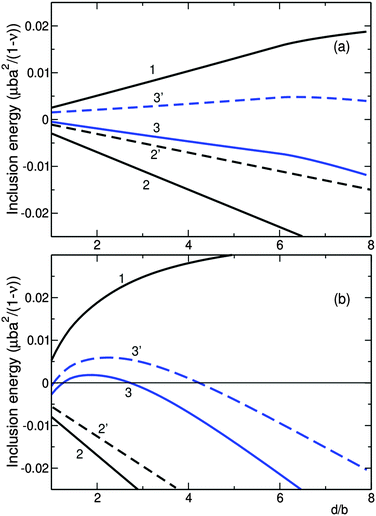
and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) are the energy densities multiplied by (1 − ν)/μba2, (1 − ν)/μ and (1 − ν)/μb, respectively. Fig. 5 shows the inclusion energy as a function of d for the cases of “hard” (a) and “soft” (b) coherent – semi-coherent crossover. The curve 2, 2′ corresponds to the incoherent inclusion when elastic strains are absent. Its slope is determined by the change of the free energy Δf at the formation of the new phase and vanishes at the temperature of the phase equilibrium. The curve 1 presents the elastic energy Ẽscel(d). In the hard case (Fig. 5a) the function Ẽscel(d) changes linearly while d < dcr, with the slope determining by the energy of coherent strains. In the soft case the loss of coherence occurs gradually and the slope of Ẽscel(d) curve (Fig. 5b) decreases. An overcooling is necessary in the both cases to initiate decomposition in the presence of coherent strains.
are the energy densities multiplied by (1 − ν)/μba2, (1 − ν)/μ and (1 − ν)/μb, respectively. Fig. 5 shows the inclusion energy as a function of d for the cases of “hard” (a) and “soft” (b) coherent – semi-coherent crossover. The curve 2, 2′ corresponds to the incoherent inclusion when elastic strains are absent. Its slope is determined by the change of the free energy Δf at the formation of the new phase and vanishes at the temperature of the phase equilibrium. The curve 1 presents the elastic energy Ẽscel(d). In the hard case (Fig. 5a) the function Ẽscel(d) changes linearly while d < dcr, with the slope determining by the energy of coherent strains. In the soft case the loss of coherence occurs gradually and the slope of Ẽscel(d) curve (Fig. 5b) decreases. An overcooling is necessary in the both cases to initiate decomposition in the presence of coherent strains.
The total energy of inclusion results from competition of elastic and chemical contributions (including surface energy). For the hard crossover (Fig. 5a) the function Ẽinc(d) varies linearly at d < dcr and changes the slope after the loss of coherence (curve 3). In the case of small overcooling (small slope of curve 2) the energy Ẽinc(d) increases in dependence on d ≈ dcr (curve 3′) and inclusion is unable to grow in normal direction. On the other hand, for the soft crossover (Fig. 5b) the total energy depends non-monotonously on d, regardless of overcooling. Thus, to transform the thin plate to the thick one it is necessary to overcome the energy barrier for the cases of soft crossover. In these situations as well as for the hard crossover and small overcooling one can expect a formation of metastable plate precipitate.
Let us discuss now a relation of our model to GPZs in Al–Cu alloys. GPZ-I exists at the temperatures T < 200 °C are just monolayers of Cu characterized by large lattice mismatch εt = 0.1; at T > 200 °C GPZ-I are solved and the θ′-phase is formed instead.76 According to the results of ab initio calculations77 the energy gain at the formation of GPZs is about 0.01–0.02 eV/at, which agrees well with the temperature range of their existence and corresponds to Δ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) = 0.004/0.008. A reasonable estimate of the energy of the coherent interface is about 0.1–0.2 J m−2 which corresponds to
= 0.004/0.008. A reasonable estimate of the energy of the coherent interface is about 0.1–0.2 J m−2 which corresponds to ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 0.001. According to our consideration this is within the soft regime when the increase of thickness of GPZ-I is energetically unfavourable due to generation of misfit dislocations. On the other hand, the θ′-phase arising at higher temperatures and corresponding to the chemical composition Al2Cu that has smaller lattice mismatch εt = 0.02 which corresponds to our hard regime. Contrary to the case GPZ-I, in this case thin plates are not stable (curve 3 in Fig. 5a). Indeed, the thickness of θ′-phase plates increases rapidly during a continual heating.76
= 0.001. According to our consideration this is within the soft regime when the increase of thickness of GPZ-I is energetically unfavourable due to generation of misfit dislocations. On the other hand, the θ′-phase arising at higher temperatures and corresponding to the chemical composition Al2Cu that has smaller lattice mismatch εt = 0.02 which corresponds to our hard regime. Contrary to the case GPZ-I, in this case thin plates are not stable (curve 3 in Fig. 5a). Indeed, the thickness of θ′-phase plates increases rapidly during a continual heating.76
Local energy minimum corresponds to d = 0 which means, within our model based on the continual elasticity theory, a few interatomic distances. This means also stability of completely coherent inclusion with zero density of misfit dislocations. Our model always predicts either atomically thin coherent plates or unrestricted incoherent growth of the new phase. Experimentally, in all the cases GPZs do have a thickness of the order of interatomic distances and are completely coherent.
Of course, our model is oversimplified (using continual elasticity, the free energy difference and surface tension are supposed to be independent of the size of precipitate) and neglects some details, which are important for the quantitative description. The main aim is to demonstrate mechanisms of stabilizing an atomically thin plate rather than to provide a complete quantitative theory of metastable precipitates in real Al–Cu alloys. In the latter, the structural evolution is accompanied by changes in chemical composition and crystal lattices of the inclusion phases (see Fig. 2). However, it should be noted that dislocation arrays are not the only way for semicoherent conjugation of the inclusion and the host and other topological defects may be involved. In particular, as was shown in ref. 78, the conjugation of precipitates of topological close packed (Frank–Kasper) phases may be provided by a network of structural disclinations rather than dislocations. The formation of such precipitates in W(Mo)–Re alloys can be an explanation of anomalous solubility of interstitial impurity and improvement of mechanical properties (rhenium effect).79,80
Conclusions
To summarize, energetics of partially coherent precipitate turns out to be quite peculiar. In both limiting cases, namely, incoherent precipitate and completely coherent precipitate,9 the total free energy can be represented as a sum of bulk and surface contributions which are proportional to the volume of the precipitate and to the area of the interface between the precipitate and the host, respectively. This is not surprising since in both limiting cases there is no need to introduce any topological defects which can make the story much more complicated.78 These defects are unavoidable in the partially coherent case. Due to a long-range character of interaction between the topological defects, their interaction energy may have unusual dependence on geometry of the system, which, as we have shown, may result in the stabilization of the precipitate and determine its equilibrium shape. For the future, it would be important to generalize our quite simple model to the case of precipitates of arbitrary shapes. In particular, contrary to the case of Al–Cu, for Al–Zn–Mg alloys spherical shapes of the inclusions are typical.81 As was mentioned above, inclusions of the athermal omega-phase in Ti and Zr based alloys are usually ellipsoidal.38,39 Note also that in this paper we discuss only stabilization of the isolated precipitate; these “topologically generated” interactions can be important also for the interaction between the precipitates and thus to the formation of mesostructure of inhomogeneous alloys.Acknowledgements
MIK acknowledges a financial support by ERC Advanced Grant No. 338957 FEMTO/NANO and by NWO via Spinoza Prize. YNG acknowledges financial support from the Russian Science Foundation (grant 14-12-00673).References
- H. Gleiter, Acta Mater., 2000, 48, 1 CrossRef CAS.
- Nanoparticles: From Theory to Application, ed. G. Schmid, Wiley-VCH, Weinheim, 2010 Search PubMed.
- C. Bustamante, J. Liphardt and F. Ritort, Phys. Today, 2005, 58, 43 CrossRef CAS.
- T. L. Hill, Thermodynamics of Small Systems, Dover, New York, 1994 Search PubMed.
- M. I. Katsnelson and A. V. Trefilov, JETP Lett., 1994, 59, 211 Search PubMed; M. I. Katsnelson and A. V. Trefilov, JETP Lett., 1995, 61, 941 Search PubMed.
- Q. Jiang and C. C. Yang, Curr. Nanosci., 2008, 4, 179 CrossRef CAS.
- J. A. Krumhansl and R. J. Gooding, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 3047 CrossRef CAS; S. Kartha, J. A. Krumhansl, J. P. Sethna and L. K. Wickham, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 803 CrossRef.
- G. van Tendeloo, D. Broddin, C. Leroux, D. Schryvers, L. E. Tanner, J. van Landuit and S. Amelinckx, Phase Transitions, 1990, 27, 61 CrossRef CAS.
- I. K. Razumov, Yu. N. Gornostyrev and M. I. Katsnelson, J. Phys.: Condens. Matter, 2013, 25, 135401 CrossRef CAS PubMed; I. K. Razumov, D. V. Boukhvalov, M. W. Petrik, V. N. Urtsev, A. V. Shmakov, M. I. Katsnelson and Yu. N. Gornostyrev, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094101 CrossRef.
- A. J. Bray, Adv. Phys., 1994, 43, 357 CrossRef.
- M. Seul and D. Andelman, Science, 1995, 267, 476 CrossRef CAS PubMed; E. Dagotto, Science, 2005, 309, 257 CrossRef PubMed; G. Tarjus, S. A. Kivelson, Z. Nussinov and P. Viot, J. Phys.: Condens. Matter, 2005, 17, R1143 CrossRef.
- K. J. de Vos, J. Appl. Phys., 1966, 37, 1100 CrossRef.
- O. Gutfleisch, High-Temperature Samarium Cobalt Permanent Magnets, in Nanoscale Magnetic Materials and Applications, ed. J. P. Liuet al., Springer, Berlin, 2009 Search PubMed.
- C. Kittel, Phys. Rev., 1946, 70, 965 CrossRef CAS.
- A. Hubert and R. Schäfer, Magnetic Domains, Springer, Berlin, 1998 Search PubMed.
- M. Seul and R. Wolfe, Phys. Rev. Lett., 1992, 68, 2460 CrossRef CAS PubMed.
- M. Seul and D. Andelman, Science, 1995, 267, 476 CrossRef CAS PubMed.
- R. Bru
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) as, H. Hafermann, M. I. Katsnelson, I. L. Soroka, O. Eriksson and B. Hjörvarsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 064411 CrossRef.
as, H. Hafermann, M. I. Katsnelson, I. L. Soroka, O. Eriksson and B. Hjörvarsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 064411 CrossRef. - J. Lyubina, B. Rellinghaus, O. Guitfleisch and M. Albreht, Structure and magnetic properties of L10 – ordered Fe–Pt alloys and nanoparticles, in Handbook of Magnetic Materials, ed. K. H. J. Buschow, Elsevier, Amsterdam, 2011, vol. 19 Search PubMed.
- K. D. Belashchenko, I. R. Pankratov, G. D. Samolyuk and V. G. Vaks, J. Phys.: Condens. Matter, 2002, 14, 565 CrossRef CAS.
- A. G. Khachaturyan, Theory of Structural Transformations in Solids, Wiley, New York, 1983 Search PubMed.
- V. I. Levitas and D. L. Preston, Phys. Lett. A, 2005, 343, 32 CrossRef CAS.
- V. I. Levitas and M. Javanbakht, J. Mech. Phys. Solids, 2015, 82, 287 CrossRef CAS.
- W. C. Leslie and E. Hornbogen, Physical metallurgy of steel, in Physical Metallurgy, ed. R. W. Cahn and P. Haasen, Elsevier, Amsterdam, 1994 Search PubMed.
- Y. Brechet and C. Hutchinson, Defect-induced dynamic pattern formation in metals and alloys, Solid State Physics, Elsevier, Amsterdam, 2006, vol. 60, p. 182 Search PubMed.
- M. B. Berkenpas, W. C. Johnson and D. E. Laughlin, J. Mater. Res., 1986, 1, 635 CrossRef CAS.
- S. Fu, D. Yi, H. Liu, Y. Jiang, B. Wang and Z. Hu, Trans. Nonferrous Met. Soc. China, 2014, 24, 2282 CrossRef CAS.
- B. Aichmayer, P. Fratzl, S. Puri and G. Saller, Phys. Rev. Lett., 2003, 91, 015701 CrossRef PubMed.
- A. Giuliani, J. L. Lebowitz and E. H. Lieb, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 064205 CrossRef; A. Giuliani, E. H. Lieb and R. Seiringer, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 064401 CrossRef.
- I. K. Razumov, Yu. N. Gornostyrev and M. I. Katsnelson, Europhys. Lett., 2007, 80, 66001 CrossRef.
- H. Gleiter, Prog. Mater. Sci., 1998, 33, 223 CrossRef.
- K. Chattopadhyay and V. Bhattacharya, J. Indian Inst. Sci., 2009, 89, 48 Search PubMed.
- A. Guinier, Nature, 1938, 142, 569 CrossRef CAS; G. D. Preston, Proc. R. Soc. London, Ser. A, 1938, 167, 526 CrossRef.
- Y. A. Bagaryatsky, Dokl. Akad. Nauk SSSR, 1952, 87, 559 Search PubMed.
- T. E. M. Staab, B. Klobes, I. Kohlbach, B. Korff, M. Haaks, E. Dudzik and K. Maier, J. Phys.: Conf. Ser., 2011, 265, 012018 CrossRef.
- F. W. Gayle and M. Goodway, Science, 1994, 266, 1015 CrossRef CAS PubMed.
- J. Frenkel, J. Chem. Phys., 1939, 7, 538 CrossRef; M. A. Krivoglaz, Sov. Phys. JETP, 1983, 57, 205 Search PubMed.
- E. W. Collings, The Physical Metallurgy of Titanium Alloys, ASM, Metals Park, Ohio, 1984 Search PubMed.
- D. L. Douglass, The Metallurgy of Zirconium, IAEA, Vienna, 1971 Search PubMed.
- S. K. Sikka, Y. K. Vohra and R. Chidambaram, Prog. Mater. Sci., 1982, 27, 245 CrossRef CAS.
- H. Kubo and S. Furjami, Mater. Sci. Eng., A, 2006, 438–440, 181 CrossRef.
- J. W. Martin and F. J. Humphreys, Scr. Metall., 1974, 8, 679 CrossRef CAS.
- M. E. Fine, J. Z. Liu and M. D. Asta, Mater. Sci. Eng., A, 2007, 463, 271 CrossRef.
- H. Rösner, et al. , Acta Mater., 2010, 58, 162 CrossRef.
- J. D. Eshelby, Proc. R. Soc. London, Ser. A, 1957, 241, 376 CrossRef; J. D. Eshelby, Proc. R. Soc. London, Ser. A, 1959, 252, 561 CrossRef.
- F. C. Frank and J. H. van der Merwe, Proc. R. Soc. London, Ser. A, 1949, 198, 205 CrossRef CAS; F. C. Frank and J. H. van der Merwe, Proc. R. Soc. London, Ser. A, 1949, 198, 216 CrossRef.
- B. Horovitz, J. L. Murrey and J. A. Krumhansl, Phys. Rev. B: Solid State, 1978, 18, 3549 CrossRef CAS.
- A. Devaraj, S. Nag, R. Srinivasan, R. E. A. Williams, S. Banerjee, R. Banerjee and H. L. Fraser, Acta Mater., 2012, 60, 596 CrossRef CAS.
- Yu. N. Gornostyrev, M. I. Katsnelson and A. V. Trefilov, JETP Lett., 1994, 60, 221 Search PubMed.
- A. S. Shcherbakov, M. I. Katsnelson, A. V. Trefilov, E. N. Bulatov, N. V. Volkenshtein and E. G. Valiulin, JETP Lett., 1987, 44, 504 Search PubMed.
- C. Wolverton and V. Ozolins, Phys. Rev. Lett., 2001, 86, 5518 CrossRef CAS PubMed.
- J. L. Murray, Int. Met. Rev., 1985, 30, 211 CAS.
- R. O. Williams, Metall. Trans., 1980, 11A, 247 CrossRef CAS.
- J. W. Cahn and F. Larche, Acta Metall., 1984, 32, 1915 CrossRef CAS.
- J. Cho, M. S. Joshi and C. T. Sun, Compos. Sci. Technol., 2006, 66, 1941 CrossRef CAS.
- V. Marcadon, E. Herve and A. Zaoui, Int. J. Solids Struct., 2007, 44, 8213 CrossRef.
- X.-L. Gao, Math. Mech. Solids, 2008, 13, 357 CrossRef.
- X.-L. Gao and H. M. Ma, Proc. R. Soc. London, Ser. A, 2010, 466, 2425 CrossRef.
- P. Sharma and S. Ganti, J. Appl. Mech., 2004, 71, 663 CrossRef.
- H. L. Duan, J. Wang, Z. P. Huang and B. L. Karihaloo, Proc. R. Soc. London, Ser. A, 2005, 461, 3335 CrossRef.
- V. G. Stoleru, D. Pal and E. Towe, Physica E, 2002, 15, 131 CrossRef CAS.
- D. A. Faux, J. R. Downes and E. P. O'Reilly, J. Appl. Phys., 1997, 82, 3754 CrossRef CAS.
- P. Sharma and A. Dasgupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 224110 CrossRef.
- F. Kroupa and L. Lejček, Czech. J. Phys. B, 1970, 20, 1063 CrossRef.
- R. Bullough and B. A. Bilby, Proc. Phys. Soc., 1956, B69, 1276 CrossRef.
- P. Bak, Rep. Prog. Phys., 1982, 45, 587 CrossRef.
- O. M. Braun and Y. S. Kivshar, The Frenkel–Kontorova Model: Concepts, Methods, and Applications, Springer, Berlin, 2004 Search PubMed.
- F. R. N. Nabarro, Proc. R. Soc. London, Ser. A, 1940, 175, 519 CrossRef CAS.
- W. A. Jesser, S. Afr. J. Sci., 2008, 104, 379 Search PubMed.
- J. Hirth and J. Lothe, Theory of Dislocations, Wiley, New York, 1982 Search PubMed.
- N. I. Medvedeva, Yu. N. Gornostyrev and A. J. Freeman, Acta Mater., 2004, 52, 675 CrossRef CAS.
- H. Brooks, Theory of internal boundaries, Metal Interfaces, American Society for Metals, Cleveland, Ohio, 1952, p. 20 Search PubMed.
- D. A. Porter and K. E. Easterling, Phase Transformations in Metals and Alloys, Chapman and Hall, London, 1992 Search PubMed.
- L. M. Brown and G. R. Woolhouse, Philos. Mag., 1970, 21, 329 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon Press, NY, 1980 Search PubMed.
- C. Tsao, E. Huang, M. Wen, T. Kuo, S. Jeng, U. Jeng and Y. Sun, J. Alloys Compd., 2013, 579, 138 CrossRef CAS.
- V. Vaithyanathan, C. Wolverton and L. Q. Chen, Acta Mater., 2004, 52, 2973 CrossRef CAS.
- Yu. N. Gornostyrev, M. I. Katsnelson and A. V. Trefilov, J. Phys.: Condens. Matter, 1997, 9, 7837 CrossRef CAS.
- A. D. Korotaev, A. N. Tyumentsev, V. V. Manako and Yu. P. Pinzhin, in Rhenium and Rhenium alloys, ed. B. D. Bryskin, TMS, Warrendale, 1997, p. 771 Search PubMed.
- Yu. N. Gornostyrev, M. I. Katsnelson and A. V. Trefilov, in Rhenium and Rhenium alloys, ed. B. D. Bryskin, TMS, Warrendale, 1997, p. 681 Search PubMed; Yu. N. Gornostyrev, M. I. Katsnelson, A. V. Trefilov and R. F. Sabirianov, Fiz. Met. Metalloved., 1992, 11, 5 Search PubMed.
- A. Deschamps, F. Livet and Y. Brechet, Acta Mater., 1999, 47, 281 CrossRef CAS.
| This journal is © the Owner Societies 2015 |