 Open Access Article
Open Access ArticleCamera-based single-molecule FRET detection with improved time resolution†
Shazia
Farooq
and
Johannes
Hohlbein
*
Laboratory of Biophysics, Wageningen UR, Dreijenlaan 3, 6703 HA Wageningen, The Netherlands. E-mail: johannes.hohlbein@wur.nl
First published on 28th September 2015
Abstract
The achievable time resolution of camera-based single-molecule detection is often limited by the frame rate of the camera. Especially in experiments utilizing single-molecule Förster resonance energy transfer (smFRET) to probe conformational dynamics of biomolecules, increasing the frame rate by either pixel-binning or cropping the field of view decreases the number of molecules that can be monitored simultaneously. Here, we present a generalised excitation scheme termed stroboscopic alternating-laser excitation (sALEX) that significantly improves the time resolution without sacrificing highly parallelised detection in total internal reflection fluorescence (TIRF) microscopy. In addition, we adapt a technique known from diffusion-based confocal microscopy to analyse the complex shape of FRET efficiency histograms. We apply both sALEX and dynamic probability distribution analysis (dPDA) to resolve conformational dynamics of interconverting DNA hairpins in the millisecond time range.
Introduction
Powerful methods based on the detection of fluorescence emitted from single molecules have significantly expanded our capabilities to study biological and chemical processes at the molecular level.1–4 One prominent technique is single-molecule Förster resonance energy transfer (smFRET), which is used to monitor distances and molecular interactions in the nanometre range.5–7 In addition to providing static structural information,8,9 there is a growing interest in applying smFRET to probe conformational dynamics within single enzymes10,11 and, ideally, even to probe those dynamics during reactions such as monitoring conformational changes of DNA polymerases during DNA synthesis. However, the two standard schemes for smFRET detection,12 diffusion-based confocal microscopy and camera-based total internal reflection fluorescence (TIRF) or widefield microscopy,13,14 are ultimately limited in their ability to combine parallel detection of many molecules with obtaining data at sufficiently high time resolution. Recent attempts of achieving higher time resolution in FRET microscopy involve camera-based detection in combination with micro- and nanofluidic devices,15 tethering of fluorescently labelled species to slowly diffusing liposomes in confocal microscopy16 or utilising correlation and transition-point analysis together with short binning of fluorescence lifetime-resolved confocal data.10,17,18We have previously reported on the conformational landscape of the unliganded DNA polymerase I, which exhibits fast conformational changes between an open and a closed conformation of the fingers-subdomain in the low millisecond time range.5,11,19,20 However, the DNA pol I dynamics are too slow to directly resolve them using diffusion-based confocal microscopy and too fast to monitor them with a camera. As of 2015, the latest generation of emCCD cameras is achieving frame rates of around 60 Hz for full frame detection (512 by 512 pixel) and sCMOS cameras, which have not yet been widely adapted for single-molecule fluorescence detection, run at frame rates of up to 100 Hz.
Here, we report on a generalised outline for camera-based smFRET detection, which combines the concepts of alternating-laser excitation (ALEX)21–25 and stroboscopic illumination26–28 to achieve a significant improvement in time resolution. In order to analyse dynamics faster than the corresponding frame rates of the camera, we adapt dynamic probability distribution analysis (dPDA), a technique widely used in diffusion-based confocal microscopy,11,29–33 for data obtained using TIRF microscopy allowing us to close the currently existing gap in obtainable time resolution between confocal and camera-based single-molecule detection. In contrast to diffusion-based microscopy, our technique allows monitoring the fate of single, surface-immobilised molecule for extended periods of time with up to hundreds of molecules in parallel. We demonstrate by both simulations and experiments using doubly labelled DNA hairpins34–36 that resolving dynamic conformational states with a lifetime in the order of a few milliseconds is possible.
Experiments and theoretical analysis
Stroboscopic alternating-laser excitation (sALEX)
In our implementation of ALEX, we use stroboscopic illumination to excite donor fluorophores in our FRET system (DNA hairpin, Fig. 1a) only for a short time during each frame acquired by the camera (Fig. 1b). As a result, FRET values calculated from the fluorescence intensities of the molecules in the donor and acceptor detection channel represent short snapshots of the underlying FRET dynamics. Let us consider for simplicity a molecular system that switches between a low and a high FRET state. If the dynamics are faster than the corresponding acquisition rate of the camera, FRET time traces and FRET efficiency histograms measured using the conventional excitation scheme show temporal averaging, whereas the stroboscopic excitation allows a distinction of the two states depending on the duration of each excitation interval (Fig. 1c). After donor excitation, the direct excitation of acceptor molecules allows monitoring their presence and photophysical state.21Single-molecule FRET microscopy
The general design of the single-molecule FRET TIRF setup was described previously.13,21 Instead of a conventional microscope body, we used a RAMM system (rapid-automated-modular-microscope) as a stage holder (ASI, USA) together with a motorised x, y scanning stage with a z-piezo for controlling precise sample placement along the optical axis of the microscope. For excitation, we used a fibre-coupled laser engine (Omicron, Germany) equipped with four lasers of different wavelengths (405 nm, 473 nm, 561 nm, and 642 nm). A home-written LabVIEW program independently controlled the laser intensities and triggered the camera. The single mode fibre generated a Gaussian shaped beam profile and a point source output at the other end of the fibre. The divergent light is collimated (f = 100 mm, Thorlabs, Germany) and a second lens focuses (f = 200 mm, Thorlabs, Germany) the light back into the back focal plane of a 100× NA 1.49 TIRF objective (Nikon, Japan). A custom-made multicolour polychroic mirror (zt405/473/561/640rpc, Chroma, USA) and a multibandpass filter (zet405/473/561/640m, Chroma, USA) are used to block any laser light in the emission path. After spatial filtering of the fluorescence with a two-lens system consisting of two tube lenses (f = 200 mm, Thorlabs, Germany) and an adjustable slit (Thorlabs, Germany), the light was spectrally split using two dichroic mirrors (zt561rdc and zt640rdc, Chroma) and a mirror into three beams corresponding to a blue, green, and red fluorescence detection channel. The three beams were then focused (f = 300 mm) on an Ixon Ultra 897 emCCD camera with 512 × 512 pixel (Andor, Northern-Ireland) that was operated in a photon-counting mode giving direct access to photon numbers.The acquisition rate of the camera was set to 20 Hz. We used laser powers of 1.5 mW (561 nm laser) and 0.75 mW (642 nm) for experiments in which the laser was exciting fluorophores for the full duration of each camera frame (50 ms). In case of stroboscopic excitation (3 ms), we increased the laser powers to 30 mW (561 nm laser) and 15 mW (642 nm) in order to obtain a similar count rate of our fluorophores. Movies were recorded for 1000 frames. Sets of experiments comparing 50 ms excitation with short stroboscopic excitation (3 ms) were performed in the same sample well. Further information on labelling, purification, immobilisation and imaging of DNA can be found in the ESI.†
Image analysis
For image analysis we used a modified version of TwoTone, a freely available, MATLAB-based software package, which identifies molecules and measures the photon counts by fitting the molecular point spread functions to two dimensional Gaussians.13 Molecules with an elongated shape indicating two overlapping molecules or molecules with an inter-molecular distance of less than around 500 nm were withdrawn from further analysis. For all remaining molecule containing both donor and acceptor, we obtained three photon streams DD (donor detection channel after direct excitation of the donor), DA (acceptor detection channel after direct excitation of the donor, FRET channel) and AA (acceptor detection channel after direct excitation of the acceptor) allowing us to calculate the apparent FRET efficiency E* = DA/(DD + DA) and the stoichiometry SPR = (DD + DA)/(DD + DA + AA). The data shown in the FRET efficiency histograms was filtered by applying two threshold criteria to each time frame: DD + DA > 60 photons and AA > 30 photons for simulated data. For the experimental data, we increased the intensity thresholds to DD + DA > 200 photons and AA > 50 photons and used an additional stoichiometry-based threshold of 0.4 ≤ SPR ≤ 0.9 to account for the higher sample complexity featuring donor- and acceptor-only molecules. No other frames or molecules were excluded from analysis unless explicitly stated.Signal to noise considerations in smFRET TIRF microscopy
An analytic expression for the standard deviation σ(E) of observed FRET distributions in TIRF microscopy has been previously derived.13 The expression accounts for heterogeneity in static homogeneous samples caused by shot noise, background photons, noise due to the electron-multiplying gain register of emCCD cameras, read-out noise and dark noise and is given by | (1) |
 is the excess noise factor accounting for noise introduced by the emCCD. The additional factor of 1.33 accounts for the excess heterogeneity introduced by the fitting algorithm of the PSF, which does, in our implementation, not account for shot noise in the recorded images.13,15 Using values introduced in the section describing the simulations yields standard deviations in the order of σ(E) ∼ 0.06 which we used as starting values of the excess widths for data fitting using dynamic probability distribution analysis described below. Under experimental conditions, however, we expect additional heterogeneity introduced by, for example, focal drift and intermolecular heterogeneity.13
is the excess noise factor accounting for noise introduced by the emCCD. The additional factor of 1.33 accounts for the excess heterogeneity introduced by the fitting algorithm of the PSF, which does, in our implementation, not account for shot noise in the recorded images.13,15 Using values introduced in the section describing the simulations yields standard deviations in the order of σ(E) ∼ 0.06 which we used as starting values of the excess widths for data fitting using dynamic probability distribution analysis described below. Under experimental conditions, however, we expect additional heterogeneity introduced by, for example, focal drift and intermolecular heterogeneity.13
Dynamic probability distribution analysis (dPDA) in TIRF microscopy
The acquisition of brief snapshots using sALEX imposes limitations to the way the data of smFRET time traces can be analysed as the conformational changes occurring during periods of no excitation are hidden and cannot be monitored. Thereby, the stroboscopic excitation prevents the analysis of single time traces with hidden Markov modelling (HMM) which has been applied to determine FRET dynamics as long as the dynamics are slower than the rate of data acquisition.37,38 In fact, the brief snapshots are comparable to data from diffusion-based confocal microscopy in which fluorescently labelled entities give rise to short (1–3 ms)20 bursts of fluorescence as the molecules diffuse through the confocal spot. Therefore, we decided to adapt a concept known from diffusion-based confocal microscopy, (dynamic) probability distribution analysis (dPDA), which uses the experimentally obtained distribution of photon counts to recapitulate complex FRET distributions.11,29–33 The shape and width of these distributions is influenced by the potential presence of static FRET species as well as by species dynamically interconverting between two or more conformations.The dynamic model of a two-state system, here represented by a low FRET (open) and high-FRET (closed) DNA hairpin (Fig. 1a), is fully described by two peak positions (Eo* and Ec*), two excess widths (σo and σc) and two rate constants koc and kco. The excess width describes to which extend the width of the histogram of a single static species deviates from the width predicted by shot-noise limited fluorescence emission and detection and has been discussed extensively for confocal microscopy35,39 suggesting that acceptor photophysics is the main source of the observed broadening. In TIRF microscopy, however, additional sources of noise such as camera read-out, stage drift and fitting algorithms have to be considered.13
The dPDA algorithm calculates a semi-empirical histogram of FRET efficiencies based on various parameters and has been described in greater detail for confocal microscopy.11 In our implementation, the algorithm consisted of the following steps: (1) we choose an oversampling factor (normally set to 10) to reduce the statistical noise of the random number generators used and a model of six parameters (Eo*, Ec*, σo, σc, koc and kco). Before fitting, initial guesses of all six parameters were provided. (2) For each molecule and each frame, which fulfilled the three thresholds discussed above (DD + DA, AA, SPR) and a E* standard deviation based threshold criteria discussed below, we calculated the probabilities of finding the molecule in one of the two states based on the initial guesses of the interconversion rates. Using these probabilities and the measured number of photons detected after donor excitation in the particular frame given by DD + DA, we draw two new binominal-distributed random numbers describing the expected number of photons from each conformational state fo,i or fc,i. If necessary, this is repeated, as several interconversions can happen within one frame leading to two final photon numbers of fo and fc for each frame. (3) To account for the excess width of FRET distributions in smFRET TIRF microscopy, we decided to take a different approach to the one previously used for confocal microscopy in which the excess width was introduced by adding normal distributed noise to the distances calculated from the initial guesses of Eo* and Ec*.11,19 Here, we added normal distributed random numbers with a standard deviation given by the excess width σi directly to the initial Ei* value for each valid frame. Even though the original approach would account better for distance fluctuations between the fluorophores, it introduces asymmetry in the later back-calculated FRET histograms due to the non-linear relation between E* and the distances which prevented good fits for our simulated and experimental data. Instead of using both approaches of artificially broadening the predicted FRET efficiency distributions, we decided to use only the addition of noising to the initially set Eo* and Ec* to keep the model as simple as possible. In any case, the contribution of distance variations at the time scale of a single frame can be considered negligible compared to various dynamic and static sources of heterogeneity discussed previously.13 In fact, the authors found that focal drift and intermolecular heterogeneity caused by either slowly-interconverting photophysically distinct states of the acceptor or slow fluctuations in donor–acceptor separation account for most of the detectable excess width.13 (4) Using Eo*, Ec*, fo and fc (again for each frame and each molecule) we draw two new binominal-distributed random numbers describing how many photons can be expected in the donor channel for each of the underlying two conformational states during each frame and the duration of excitation therein. These two numbers are then summed up and normalized by the number of photons measured experimentally or taken from the analysed simulated data to yield an expected FRET efficiency. (5) Steps 2–4 are repeated according to the oversampling factor and normalised accordingly. (6) The histograms of the predicted FRET efficiencies are then compared to the experimentally determined FRET efficiencies. The initially set values are varied to achieve a better agreement of the histograms using a least-mean-squares algorithm implemented in MATLAB and C++.40
To evaluate the goodness of the fit between the simulated or experimental data and the predicted dPDA fit, we calculated the reduced chi-squared statistic as similarly suggested previously:31
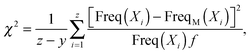 | (2) |
Monte-Carlo simulations of camera-based, single-molecule FRET experiments
The Monte-Carlo simulations were performed using custom written C/C++ software developed to resemble single-molecule experiments as closely as possible. The software was described previously,13,19 but updated to allow the simulation of conformational dynamics faster than the acquisition time of the camera. Discrete time steps of 100 μs were used in which 150 randomly distributed particles would fluoresce and undergo conformational changes resulting in time dependent changes in their FRET efficiencies. We used forward and backward rates set to koc = kco = 200 s−1 leading to a lifetime of 5 ms for each conformational states. Each simulated movie consisted of 1000 frames. The simulated frame time of the camera was set to 50 ms and the excitation time was chosen to be between 1 ms and 50 ms. We simulated an area of 512 by 340 pixel with a virtual pixel size of 130 nm, representing the dimensions of the field of view under experimental conditions. The intensity profile around each molecule position is assumed to be Gaussian in x and y direction and the characteristic width of the point spread function was set to 130 nm for donor and to 150 nm for acceptor fluorophores. We set the brightness to 250 photons per molecule per excitation period for donor and emission after donor excitation and 100 photons per molecule per excitation period for acceptor emission after acceptor emission, values which are achievable under experimental conditions. For the simulated data, we set the Förster radius R0 to 6 nm and the corresponding distances between donor and acceptor fluorophore to 7 nm for the open and to 5 nm for the closed conformation. The leakage describing the probability of detecting photons emitted from the donor in the acceptor detection channel due to the spectral characteristics of the fluorophores and the experimental setup was set to 0.1. The quantum yield of each fluorophore was set to unity. Gaussian distributed background noise was added as follows with a mean value of 4 photons for the donor excitation, donor detection channel (DD channel), 5 photons for the donor excitation, acceptor emission channel (DA channel), 2 photons for the acceptor excitation donor emission channel (AD, which does not contain any further signal and is therefore excluded from further considerations), and 6 photons for the acceptor excitation acceptor emission channel (AA channel). The standard deviation of all background noise was set to 2 photons per pixel. Albeit possible in the simulation, we did not simulate other fluorophore properties such as blinking, bleaching and potential direct excitation of the acceptor by the laser used for donor excitation.Simulation results
sALEX: identification of conformational dynamics in the millisecond time range
We started exploring the potential of sALEX to resolve conformational dynamics by running a set of Monte Carlo simulations using parameters closely resembling experimental conditions and constrains. The main advantage of simulating single-molecule FRET microscopy is that the rates of the conformational changes can be directly set and later be compared to the results obtained from fitting the FRET efficiency histograms by dPDA. For the set of five simulations presented (Fig. 2), we varied the duration of the excitation per frame from 50 ms to 1 ms but kept all remaining parameters constant. Two consecutive frames of the simulated raw data (3 ms excitation time) show the two detection channels after donor excitation (Fig. 2a; DD and DA) and after acceptor excitation (Fig. 2b; AA). Individual particles are visible and those are then analysed to obtain individual time traces and FRET efficiencies. For conformational rates of 200 s−1, an excitation duration of 50 ms during a 50 ms acquisition frame time led to severe averaging of the FRET efficiencies yielding a single, albeit broadened, FRET distribution centred around E* ∼ 0.55 (Fig. 2c, top). Only using an illumination shorter than the lifetime of the respective conformational states (1/200 s−1 = 5 ms) led to the appearance of two global maxima that can be attributed to the open and the closed conformation of the simulated molecules. In fact, exciting the molecules for 1 ms shows two clearly distinguishable species with only limited temporal averaging between them (Fig. 2c, bottom). We plotted single-molecule time trajectories for 50 ms (Fig. 2d) and 3 ms excitation time (Fig. 2e), respectively. As expected, the trajectories of DD, DA and E* in the case of a 3 ms excitation time show fluctuations with larger amplitudes than for 50 ms excitation time.In the simulations we have not included any intermolecular heterogeneity; all molecules undergo conformational changes with dynamics defined by the rate constants. In our experience, this is rarely the case for experimental data in which intermolecular heterogeneity is often present and has to be carefully addressed to avoid “cherry picking” which might lead to biased data interpretation. Here we suggest to use a threshold criterion that is based on calculating the standard deviation of all FRET frames measured for each molecule similar to burst variance analysis in confocal microscopy.19 For the simulated data (Fig. 2b, 3 ms excitation), we plotted the pseudo-colour coded, one dimensional FRET histogram for each molecule showing the expected homogeneity for the simulations (Fig. 3a top panel). For each single time trace, we calculated the standard deviation of all FRET values. Whereas the exact value depends on the FRET peak positions in the FRET histogram and the overall photon count rate per frame, all standard deviation values are here equally centred around 0.2 confirming the homogeneity in the simulated sample. As we will show for the experimental data, non-interconverting molecules can be identified and excluded from further analysis as their standard deviation of FRET values is considerably lower. Taken together, Monte Carlo simulations reveal that the enhanced time resolution of sALEX improves our capabilities of identify heterogeneity in FRET samples.
 | ||
| Fig. 3 Simulations. Analysing conformational dynamics using dynamic probability distribution analysis (dPDA). (a) Top: Colour coded one-dimensional histograms of FRET efficiencies (E*) plotted for each single simulated molecules (for the cumulated histogram of all molecules see Fig. 2b: 3 ms excitation time and koc = kco = 200 s−1) showing the expected homogeneity. Bottom: Standard deviation of the FRET efficiencies for each molecule. (b) The cumulated E* histogram (grey bars; Fig. 2b (3 ms excitation time) and fitted using a dynamic two-species model. After optimization based on a Levenberg–Marquardt algorithm, the final fit (red line) shows small residuals and yielded koc = (205 ± 6) s−1 and kco = (205 ± 6) s−1 (χ2 = 1.4). (c) Plotted χ2 values comparing the PDA model and the simulated data as a function of different forward and backward rates using the fitted peak positions and excess widths obtained in (c) as fixed parameters. (d) Visualization of the predicted histogram (black stairs) based on parameters obtained in (b) for a 3 ms excitation period plotted on top of the histogram of transfer efficiencies obtained from simulated data with a 50 ms excitation period (grey bars) (χ2 = 3.8). No further fitting was performed. | ||
dPDA: quantifying conformational dynamics in the millisecond time range
For the simulations, we set the rates of the interconversions to 200 s−1, which we now aim to recover by analysing the FRET efficiency histograms using dynamic probability distribution analysis (dPDA). We took the simulated data using the 3 ms excitation and chose the following initial guesses iEo* = 0.2, iEc* = 0.8, ikoc = 150 s−1, ikco = 250 s−1 and iσo = iσc = 0.06 for further optimization. The initial peak positions and rates were chosen such that they deviate significantly from the final fit. After fitting, we obtained Eo* = 0.352 ± 0.001, Ec* = 0.773 ± 0.002, koc = (205 ± 6) s−1, kco = (205 ± 6) s−1 and σo = 0.055 ± 0.003 and σc = 0.049 ± 0.003 with χ2 = 1.4 representing an excellent fit with small residuals (Fig. 3b). Whereas the peak position can be visually verified and the excess width can be estimated for the simulations as discussed above, the influence of both rates on the shape of the predicted FRET efficiency histogram is more difficult to assess. Therefore, we fixed the peak positions and the excess widths to the values obtained from the fit and asked, how the χ2 values change for systematically altered rate constants without running the optimization algorithm (Fig. 3c). If we consider a χ2 < 5 as a reasonable approximation of the data using a dPDA prediction, we find that the minimization surface yields rates of koc = kco = (200 ± 30) s−1 in excellent agreement with the simulated rates. Fits of the FRET efficiency histograms for the cases of 10 ms and 1 ms excitation also show excellent agreement with the simulated data and can be found in ESI,† Fig. S1.Finally, we used the six parameters obtained from the original fit of the simulated 3 ms data (Fig. 2b and 3b) to predict the FRET histogram (black stairs) in the case of a 50 ms excitation period (Fig. 3d). As shown before, the simulated data shows a single peak due to the averaging effect of quickly interconverting FRET species. The predicted histogram resembles the data reasonably well (χ2 = 3.8) matching both the mean peak position and the general shape and width of the histogram. The residuals and the PDA prediction show a larger jump at E* = 0.5, which is likely to be an artefact of histogramming E* values calculated from low integer values representing the two detection channels after excitation of the donor. Fitting the single peak with a model of interconverting FRET species is possible albeit not recommended as the six parameters used for building the PDA model would still require constrains derived from fitting the sALEX data to stay within a reasonable value space. Nevertheless, the non-fitted PDA prediction allows to visually confirm the accuracy of values obtained from fitting sALEX data.
dPDA and sALEX for strongly biased equilibria
In order to test the ability of recovering rates in systems which are strongly biased towards one conformation, we set up a simulation using a forward rate of koc = 5 s−1 (lifetime of 200 ms) and a backward rate of kco = 200 s−1 (lifetime of 5 ms). All other parameters were kept as described previously. The resulting FRET histogram assuming an excitation of 3 ms is shown in ESI,† Fig. S2. In our simulated case, the equilibrium ratio is kco/koc = 40 and we therefore expect that the molecules are populating primarily the closed conformation. Even though dPDA is in principle capable of retrieving the rates with kco = (216 ± 15) s−1 and koc = (7 ± 2) s−1 (χ2 = 9.1), any experimental validation of systems featuring equilibrium ratios of larger than around 20, in which, on average, 95% of molecules would be in one conformational state and 5% in another state, is challenging and often simply limited by the uniformity and purity of the sample.Experimental results using DNA hairpins
For the experimental realization of sALEX and application of dPDA, we decided to use simple DNA hairpin molecules labelled with both donor and acceptor fluorophores. By changing the concentration of salt (here NaCl) in the buffer medium, the conformational equilibrium of DNA hairpins can be tuned.34–36,41 We chose a DNA hairpin in which the template DNA showed a self-complementarity of 6 neighboured bases designed to open and close rapidly compared to the frame time of our camera (50 ms). At zero salt concentration, the DNA construct fully populated a low FRET species (E* ∼ 0.16) indicating the open form of the DNA hairpin (Fig. 4a, top panel). The sALEX data showed a very similar distribution characterised by the same peak position (E* ∼ 0.16) and the same shape of the distribution (Fig. 4b, top panel). Upon addition of salt, the peak position of the main distribution in the 50 ms data shifted gradually from the FRET efficiency indicating the open conformation (E* ∼ 0.20) to a FRET efficiency (E* ∼ 0.76) indicating the closed conformation (Fig. 4a). Whilst shifting, the width of the distribution changed reaching its maximum at a salt concentration of around 300 mM NaCl. Only at 400 mM NaCl and above, two underlying species with varying peak positions can be identified.For salt concentrations above 100 mM NaCl, the FRET efficiency histograms of the sALEX data started to differ from the conventional ALEX data as the two main populations representing the open and the closed conformation of the hairpin can now be clearly identified and distinguished in every histogram (Fig. 4b). With increasing salt concentrations the conformational equilibrium shifted towards the closed conformation. Whereas the main peak position of the closed conformation is constant for all concentrations above 100 mM NaCl (Ec* ∼ 0.76), we note a peak shift of the open conformation from Eo* ∼ 0.20) to a FRET efficiency (Eo* ∼ 0.29) consistent with reports describing a compaction of single stranded DNA due to electrostatic screening.42
To prove the high signal to noise ratio obtainable at short excitation times, we plotted individual frames without any additional averaging after green and red excitation, respectively (Fig. 5a and b). Both images allow the identification and subsequent determination of photon counts for single molecules. Before continuing with the determination of rates using dPDA, we note that the histograms in Fig. 4a at NaCl concentrations of 300 mM showed a small shoulder at around E* ∼ 0.20 which cannot be entirely explained by averaging effects due to fast dynamics. Here, we observed the influence of non-converting DNA hairpins which are stuck in the open conformation. For better visualisation and characterisation, we plotted the one dimensional, colour-coded FRET efficiency histograms of every analysed molecule and calculated the corresponding standard deviation from the time traces of the FRET efficiencies (Fig. 5c). Whereas most molecules show low and high FRET values, some (see arrows) show mainly a single conformation leading to lower standard deviations of the analysed individual time traces. Additionally, we plotted individual time traces of a single molecule (Fig. 5d) confirming the experimental realisation of the parameters such as the photon counts chosen for the simulations in Fig. 2 and 3.
 | ||
| Fig. 5 Experimental data using a 3 ms excitation time for a DNA hairpin in presence of 300 mM NaCl. (a and b) Individual frames (343 by 512 pixel with a pixel size of 130 nm) after (a) green and (b) red excitation. (c) Top: Colour coded one-dimensional histograms of FRET efficiencies (E*) from three movies plotted for each analysed molecules (for the cumulated histogram of all molecules see Fig. 4b) showing heterogeneity between the molecules. Bottom: Standard deviations calculated from individual E* time traces. Three representative molecules with a low standard deviation are indicated (arrows). (d) Individual time traces. Upper panel: Donor signal after donor excitation (green trace, DD), acceptor signal after donor excitation (red trace, DA), acceptor signal after acceptor excitation (black trace, AA). Lower panel: Transfer efficiencies (red trace, E*) and stoichiometry (black trace, S). The gaps in the lower time traces are due to photon counts of DD + DA < 200 and AA < 50 photons per frame. (e) The E* histogram after additional filtering for molecules showing a standard deviation of their FRET time trace above 0.1 was fitted using a dynamic two-species model. After optimization, the final fit (red line) shows small residuals and yielded koc = (117 ± 4) s−1, kco = (188 ± 6) s−1 (χ2 = 2.0). (f) Plotted χ2 values comparing the PDA model and the experimental data as a function of different forward and backward rates using the fitted peak positions and excess widths obtained in (e) as fixed parameters. | ||
Due to the low standard deviation calculated from the FRET efficiency time traces of some molecules seen in Fig. 5c we decided to apply an additional threshold of std(Etrace*) > 0.1 to identify traces of non-interconverting DNA hairpins and exclude them from further analysis. The filtered histogram (3 ms, 300 mM NaCl, Fig. 5e) shows only a marginal difference in the relative peak heights of the closed and the open conformation to the corresponding histogram in Fig. 4b. For the PDA fitting, we chose the following starting values iEo* = 0.25, iEc* = 0.75, ikoc = 100 s−1, ikco = 200 s−1 and iσo = iσc = 0.06 and obtained Eo* = 0.217 ± 0.002, Ec* = 0.764 ± 0.003, koc = (117 ± 4) s−1, kco = (188 ± 6) s−1 and σo = 0.087 ± 0.002 and σc = 0.069 ± 0.004 with χ2 = 2.0 representing again an excellent fit with small residuals (Fig. 5e). Similar to the procedure discussed for the simulations, we fixed the positions and the excess widths and calculated the χ2 characterising the goodness of the PDA prediction as a function of various forward and backward rates giving koc = (120 ± 20) s−1 and kco = (195 ± 30) s−1 (Fig. 5f). The results from analysing the conformational rates show for increasing concentrations of NaCl that the rates of the open to close transition increase whereas the rates of the closed to open transition decrease (Fig. 6 and Fig. S1, ESI† for the individual dPDA fits) thereby qualitatively and quantitatively agreeing with observations of a similar DNA hairpin structure.35
 | ||
| Fig. 6 Conformational dynamics of a DNA hairpin under different concentrations of NaCl. Rates were obtained by fitting histograms of FRET efficiencies with dPDA as discussed in the text. For the individual FRET histograms and the corresponding fits see Fig. 5 and ESI,† Fig. S3. The error bars represent 95% confidence intervals of the fit. The greyed area indicate fits with χ2 > 4. | ||
Discussion
We characterised the ability of sALEX and dPDA to identify and quantify conformational dynamics of biomolecules by means of simulations and experimental data. With the simulations we established a comprehensive framework in which a variety of parameters such as conformational rates and distances between the fluorophores can easily be modified allowing to visualise the effect of those parameters on the shape of FRET efficiency histograms. Even without using sALEX for improving the time resolution, the simulations allow realistic predictions of experimentally obtainable data as the simulations explicitly consider sources of noise leading to a significant broadening of FRET distributions in TIRF microscopy.13 We demonstrated that the stroboscopic alternating-laser excitation has a dramatic effect on the shape of the FRET histograms of simulated interconverting species (Fig. 2c). By reducing the duration of the excitation (1 ms or 3 ms) below the simulated lifetime of each conformational state (here 5 ms), we identified the two species whose FRET distributions are otherwise averaged out. As mentioned previously, we should emphasize that by reducing the excitation time below the frame time of the camera required to read and write the data, we lose information about the species between the periods of excitation. This information is largely irrelevant for the case of species in a conformational equilibrium, but has to be considered in cases where reactions such as DNA synthesis are studied.43By recording snapshots of conformational states from individual molecules over extended periods of time, we introduced the analysis of the standard deviation of FRET efficiencies as a convenient way to identify inter molecular heterogeneity (Fig. 3a and 5c). In our case, we simply used a threshold criterion to exclude molecules from further analysis which did not undergo conformational changes. We suggest to use a value in the order of twice the theoretically calculated standard deviation introduced in eqn (1). A more detailed analysis of the FRET standard deviation using, for example, sliding windows of a few frames could be used to analyse other sources of dynamic heterogeneity in single entities such as pausing mechanisms in proteins and enzymes.
For analysing the underlying conformational dynamics in FRET efficiency histograms we implemented dynamic probability distribution analysis in TIRF microscopy. Our simulated data showed, that dPDA can accurately recover simulated conformational rates and that dPDA is therefore a promising tool to extract rates from experimental data. It should be noted that dPDA requires some temporal averaging to determine the rates of interconversions; if two species would be entirely separated in the FRET histogram, we could still provide an upper limit for the underlying rates as we can predict at which rates averaging effects would start to occur.
Along the same lines, the accuracy of the conformational analysis using dPDA benefits from well separated FRET peaks representing the two conformations which can, for dynamic species, be ensured by a sufficiently short excitation and a careful design of the FRET construct leading to relative changes in the donor to acceptor distances above 1 nm. Furthermore, the equilibrium ratio between the two species here defined as kco/koc should be ideally kept around one to avoid cases in which dynamic heterogeneity of a small subset of molecules might severely bias dPDA analysis.
We note that dPDA can be expanded allowing analysis of species interconverting between more than two conformational states as well as combining dynamic and static species in a single sample.
We experimentally demonstrated an effective time resolution of 3 ms for a dynamic system of an interconverting DNA hairpin. The same stem sequence of six complementary bases (5′ TGG ATT) which we used for our experiments has recently been used by Tsukanov et al.35 who obtained opening and closing rates of ∼200 s−1 at a salt concentration of 300 mM NaCl comparable to our results of koc = (117 ± 4) s−1 and kco = (188 ± 6) s−1. Differences in the determined rates can be explained by our choice of a different donor fluorophore (Cy3B instead of ATTO 550) and different labelling positions as it has been shown that both can have a substantial influence on the conformational rates of DNA hairpins.34,44 Similar to the experiments by Tsukanov et al., we observed a decrease of the opening and an increase of the closing rate with increasing concentrations of NaCl. The main advantage of our imaging-based implementation is that it takes only tens of seconds to record the same amount of data that would take tens of minutes (or longer) in confocal microscopy.
Our dPDA fits showed (Fig. S1, ESI† and also Fig. 6) larger χ2 values for conditions in which the DNA hairpin is primarily either in the open or the closed conformation, indicating that dPDA works most reliable if two global peak positions can be seen in the FRET efficiency histogram and both rates are close to each other. In our current experimental implementation, we concentrated on characterizing conformational dynamics that lead to changes in FRET efficiency under equilibrium conditions.
To obtain a broader overview about potential applications of sALEX, two points should be discussed. Firstly, as long as one is mainly interested in detecting FRET efficiencies, (stroboscopic) excitation of the acceptor fluorophore is not required as the stoichiometry parameter is only used to identify molecules bearing both donor and acceptor fluorophore. As recently suggested,21 however, combining protein induced fluorescence enhancement45,46 with single-molecule FRET could generate applications in which the time dependent change in stoichiometry would benefit from increasing the time resolution using stroboscopic excitation. Secondly, our current implementation requires that the molecules of interest are stationary. Whereas the immobilisation of DNA is mostly uses biotin–neutravidin linkage to biotinylated PEG crafted on the glass surface,47 immobilising proteins requires either vesicle encapsulation48,49 or the use of biotinylated, anti-His5/His6-tag antibodies.50
Finally, if we consider the experimentally shown time-resolution of 3 ms as feasible, where is the current technological limit? Our main experimental limitation was the laser power of the green laser (<50 mW before entering the TIRF objective), which prevented us from increasing the time resolution whilst keeping the number of detected photons per excitation period constant. More powerful lasers could help to improve the time resolution further, but ultimately the achievable time resolution is limited by the photostability and the photon count rate of the organic fluorophores. Recent developments in recipes for photo protection such as oxygen scavengers in combination with triplet state quencher reviewed in ref. 51 and 52 or “self-healing” dyes53,54 will help to push the number of photons detectable from single emitters further. Another promising technique in single-molecule detection is the use of nano-antennas which has been shown to increase the achievable count rate of organic fluorophores by up to two orders of magnitude.55
We expect sub-millisecond dynamics to become resolvable in TIRF microscopy especially considering that dPDA allows to analyse distributions of FRET efficiencies in which considerable temporal averaging took place pushing the effective time resolution even below the duration of excitation.
Conclusion
The ability to resolve and characterize conformational dynamics of individual molecules under equilibrium conditions defines single molecule FRET as a powerful technique to study biologically relevant molecules and proteins. Here, we presented two techniques, stroboscopic alternating-laser excitation and dynamic probability distribution analysis for TIRF microscopy, which in combination allow the characterization of conformational dynamics in the 1–20 ms time range. Our sALEX excitation configuration can be easily implemented in existing setups by using, for example, acousto-optical modulators (AOTFs) that allow modulating the intensity of laser sources. Since we used a camera-based implementation that uses the full field of view of the camera instead of relying on cropping or pixel-binning to achieve higher time resolution, hundreds of molecules can be detected in parallel over extended periods. We believe that further developments improving the longevity of fluorophores as well as new technical advances in image acquisition combined with sALEX and dPDA will help to broaden the range of possible applications in single-molecule detection.Acknowledgements
The authors thank Joseph Torella for providing early versions of the PDA software and Jan-Willem Borst, Arjen Bader and Carel Fijen for critically reading the manuscript and providing helpful comments. S. F. is supported by the Netherlands Organization for Scientific Research (NWO) via a FOM (Foundation for Fundamental Research on Matter) grant awarded to Herbert van Amerongen, Wageningen University. J. H. acknowledges support from a Marie Curie Career Integration Grant (#630992).References
- J. Hohlbein, K. Gryte, M. Heilemann and A. N. Kapanidis, Phys. Biol., 2010, 7, 031001 CrossRef PubMed.
- C. Joo, H. Balci, Y. Ishitsuka, C. Buranachai and T. Ha, Annu. Rev. Biochem., 2008, 77, 51–76 CrossRef CAS PubMed.
- W. E. Moerner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 12596–12602 CrossRef CAS PubMed.
- S. Farooq, C. Fijen and J. Hohlbein, Protoplasma, 2013, 251, 317–322 CrossRef PubMed.
- J. Hohlbein, L. Aigrain, T. D. Craggs, O. Bermek, O. Potapova, P. Shoolizadeh, N. D. F. Grindley, C. M. Joyce and A. N. Kapanidis, Nat. Commun., 2013, 4, 2131 Search PubMed.
- S. Preus and L. M. Wilhelmsson, ChemBioChem, 2012, 13, 1990–2001 CrossRef CAS PubMed.
- S. Weiss, Science, 1999, 283, 1676–1683 CrossRef CAS PubMed.
- S. Kalinin, T. Peulen, S. Sindbert, P. J. Rothwell, S. Berger, T. Restle, R. S. Goody, H. Gohlke and C. A. M. Seidel, Nat. Methods, 2012, 9, 1218–1225 CrossRef CAS PubMed.
- A. Muschielok, J. Andrecka, A. Jawhari, F. Brückner, P. Cramer and J. Michaelis, Nat. Methods, 2008, 5, 965–971 CrossRef CAS PubMed.
- K. A. Henzler-Wildman, V. Thai, M. Lei, M. Ott, M. Wolf-Watz, T. Fenn, E. Pozharski, M. A. Wilson, G. A. Petsko, M. Karplus, C. G. Hubner and D. Kern, Nature, 2007, 450, 838–844 CrossRef CAS PubMed.
- Y. Santoso, J. P. Torella and A. N. Kapanidis, ChemPhysChem, 2010, 11, 2209–2219 CrossRef CAS PubMed.
- N. Walter, C. Huang, A. Manzo and M. Sobhy, Nat. Methods, 2008, 5, 475–489 CrossRef CAS PubMed.
- S. J. Holden, S. Uphoff, J. Hohlbein, D. Yadin, L. Le Reste, O. J. Britton and A. N. Kapanidis, Biophys. J., 2010, 99, 3102–3111 CrossRef CAS PubMed.
- D. Axelrod, T. Burghardt and N. Thompson, Annu. Rev. Biophys. Bioeng., 1984, 13, 247–268 CrossRef CAS PubMed.
- S. Tyagi, V. VanDelinder, N. Banterle, G. Fuertes, S. Milles, M. Agez and E. A. Lemke, Nat. Methods, 2014, 11, 297–300 CrossRef CAS PubMed.
- J.-Y. Kim, C. Kim and N. K. Lee, Nat. Commun., 2015, 6, 6992 CrossRef CAS PubMed.
- H. S. Chung, K. McHale, J. M. Louis and W. A. Eaton, Science, 2012, 335, 981–984 CrossRef CAS PubMed.
- L. Olofsson, S. Felekyan, E. Doumazane, P. Scholler, L. Fabre, J. M. Zwier, P. Rondard, C. A. M. Seidel, J.-P. Pin and E. Margeat, Nat. Commun., 2014, 5, 5206 CrossRef CAS PubMed.
- J. P. Torella, S. J. Holden, Y. Santoso, J. Hohlbein and A. N. Kapanidis, Biophys. J., 2011, 100, 1568–1577 CrossRef CAS PubMed.
- Y. Santoso, C. M. Joyce, O. Potapova, L. Le Reste, J. Hohlbein, J. P. Torella, N. D. F. Grindley and A. N. Kapanidis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 715–720 CrossRef CAS PubMed.
- J. Hohlbein, T. D. Craggs and T. Cordes, Chem. Soc. Rev., 2014, 43, 1156–1171 RSC.
- A. N. Kapanidis, N. K. Lee, T. A. Laurence, S. Doose, E. Margeat and S. Weiss, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 8936–8941 CrossRef CAS PubMed.
- N. K. Lee, A. N. Kapanidis, Y. Wang, X. Michalet, J. Mukhopadhyay, R. H. Ebright and S. Weiss, Biophys. J., 2005, 88, 2939–2953 CrossRef CAS PubMed.
- T. Laurence, X. Kong, M. Jager and S. Weiss, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17348–17353 CrossRef CAS PubMed.
- B. K. Müller, E. Zaychikov, C. Bräuchle and D. C. Lamb, Biophys. J., 2005, 89, 3508–3522 CrossRef PubMed.
- J. Elf, G.-W. Li and X. S. Xie, Science, 2007, 316, 1191–1194 CrossRef CAS PubMed.
- C. Flors, J. Hotta, H. Uji-i, P. Dedecker, R. Ando, H. Mizuno, A. Miyawaki and J. Hofkens, J. Am. Chem. Soc., 2007, 129, 13970–13977 CrossRef CAS PubMed.
- S. Blumberg, A. Gajraj, M. W. Pennington and J.-C. Meiners, Biophys. J., 2005, 89, 1272–1281 CrossRef CAS PubMed.
- E. Nir, X. Michalet, K. M. Hamadani, T. A. Laurence, D. Neuhauser, Y. Kovchegov and S. Weiss, J. Phys. Chem. B, 2006, 110, 22103–22124 CrossRef CAS PubMed.
- M. Antonik, S. Felekyan, A. Gaiduk and C. A. M. Seidel, J. Phys. Chem. B, 2006, 110, 6970–6978 CrossRef CAS PubMed.
- S. Kalinin, S. Felekyan, M. Antonik and C. A. M. Seidel, J. Phys. Chem. B, 2007, 111, 10253–10262 CrossRef CAS PubMed.
- S. Kalinin, A. Valeri, M. Antonik, S. Felekyan and C. A. M. Seidel, J. Phys. Chem. B, 2010, 114, 7983–7995 CrossRef CAS PubMed.
- S. Felekyan, H. Sanabria, S. Kalinin, R. Kühnemuth and C. A. M. Seidel, in Methods in Enzymology, ed. S. Y. Tetin, Academic Press, 2013, vol. 519, pp. 39–85 Search PubMed.
- A. Hartmann, G. Krainer and M. Schlierf, Molecules, 2014, 19, 13735–13754 CrossRef PubMed.
- R. Tsukanov, T. E. Tomov, Y. Berger, M. Liber and E. Nir, J. Phys. Chem. B, 2013, 117, 16105–16108 CrossRef CAS PubMed.
- M. I. Wallace, L. Ying, S. Balasubramanian and D. Klenerman, J. Phys. Chem. B, 2000, 104, 11551–11555 CrossRef CAS.
- S. A. McKinney, C. Joo and T. Ha, Biophys. J., 2006, 91, 1941–1951 CrossRef CAS PubMed.
- S. Uphoff, K. Gryte, G. Evans and A. N. Kapanidis, ChemPhysChem, 2011, 12, 571–579 CrossRef CAS PubMed.
- S. Kalinin, E. Sisamakis, S. W. Magennis, S. Felekyan and C. A. M. Seidel, J. Phys. Chem. B, 2010, 114, 6197–6206 CrossRef CAS PubMed.
- M. I. A. Lourakis, levmar: Levenberg–Marquardt nonlinear least squares algorithms in C/C++, 2004 Search PubMed.
- R. Tsukanov, T. E. Tomov, R. Masoud, H. Drory, N. Plavner, M. Liber and E. Nir, J. Phys. Chem. B, 2013, 117, 11932–11942 CrossRef CAS PubMed.
- M. C. Murphy, I. Rasnik, W. Cheng, T. M. Lohman and T. Ha, Biophys. J., 2004, 86, 2530–2537 CrossRef CAS PubMed.
- T. D. Christian, L. J. Romano and D. Rueda, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21109–21114 CrossRef CAS PubMed.
- W. Kügel, A. Muschielok and J. Michaelis, ChemPhysChem, 2012, 13, 1013–1022 CrossRef PubMed.
- H. Hwang, H. Kim and S. Myong, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7414–7418 CrossRef CAS PubMed.
- H. Hwang and S. Myong, Chem. Soc. Rev., 2014, 43, 1221–1229 RSC.
- R. Lamichhane, A. Solem, W. Black and D. Rueda, Methods, 2010, 52, 192–200 CrossRef CAS PubMed.
- E. Boukobza, A. Sonnenfeld and G. Haran, J. Phys. Chem. B, 2001, 105, 12165–12170 CrossRef CAS.
- B. Okumus, T. J. Wilson, D. M. J. Lilley and T. Ha, Biophys. J., 2004, 87, 2798–2806 CrossRef CAS PubMed.
- R. Zhou, S. Kunzelmann, M. R. Webb and T. Ha, Nano Lett., 2011, 11, 5482–5488 CrossRef CAS PubMed.
- T. Ha and P. Tinnefeld, Annu. Rev. Phys. Chem., 2012, 63, 595–617 CrossRef CAS PubMed.
- Q. Zheng, M. F. Juette, S. Jockusch, M. R. Wasserman, Z. Zhou, R. B. Altman and S. C. Blanchard, Chem. Soc. Rev., 2014, 43, 1044–1056 RSC.
- R. B. Altman, Q. Zheng, Z. Zhou, D. S. Terry, J. D. Warren and S. C. Blanchard, Nat. Methods, 2012, 9, 428–429 CrossRef CAS PubMed.
- J. H. M. van der Velde, E. Ploetz, M. Hiermaier, J. Oelerich, J. W. de Vries, G. Roelfes and T. Cordes, ChemPhysChem, 2013, 14, 4084–4093 CrossRef CAS PubMed.
- G. P. Acuna, F. M. Möller, P. Holzmeister, S. Beater, B. Lalkens and P. Tinnefeld, Science, 2012, 338, 506–510 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp04137f |
| This journal is © the Owner Societies 2015 |



