The surface roughness, but not the water molecular orientation varies with temperature at the water–air interface

Abstract

We examine the temperature dependence of the interfacial molecular structure at the water–air interface by combining experimental and simulated sum-frequency generation (SFG) spectroscopy. The experimental SFG spectra of the OH-stretching mode show a decrease in the amplitude at ∼3300 cm⁻¹ with increasing temperature, while the 3700 cm⁻¹ ‘free OH’ SFG feature is insensitive to temperature changes. The simulated spectra are in excellent agreement with experiment. A comparison between interfacial SFG spectra and bulk infrared/Raman spectra reveals that the variation of the SFG signal due to the temperature change is not caused by a temperature-dependent OH bond orientation of the interfacial water molecules, but can be fully accounted for by the temperature dependence of the optical response of water. These results indicate that while the thickness of the interfacial region varies with temperature, the molecular organization of interfacial water at the water–air interface is surprisingly insensitive to temperature changes.

---

Temperature is a critical parameter of water which controls a variety of its macroscopic properties not only in the bulk but also at interfaces. The nature of interfacial water and its temperature dependence have been debated.¹ It is well known, as first postulated by Faraday, that liquid water exists on the ice surface below the bulk freezing point.^2,3 Furthermore, the surface tension of water is affected by temperature and decreases from 76 mN m⁻¹ at 0 °C to 68 mN m⁻¹ at 50 °C.⁴ Although these observations must be related to the hydrogen bond (HB) network at the water interface, questions remain regarding the temperature dependence of the interfacial molecular arrangement of water.

HB interactions in bulk water have been probed using various vibrational spectroscopic techniques such as infrared (IR) and Raman spectroscopy.⁵ Interfacial water molecules can be probed selectively with sum-frequency generation (SFG) spectroscopy. In this technique IR and visible laser pulses are combined at the interface and the sum-frequency is detected. Since this is a second order response, contributions from centrosymmetric media like bulk water are eliminated. With this technique, the interfacial water structure at the water–air interface has been studied and the presence of the dangling, free OH groups has been evidenced, arising from the interruption of the H-bonded network at the interface.^6,7

Although this technique is very suitable to study the variations of the interfacial water structures with temperature change, only a limited number of studies have addressed these at the water–air^6,8–10 and ice–air^11–13 interfaces. At the D₂O–air interface, the OD stretch SFG features in the H-bonded region (∼2300–2500 cm⁻¹) are reduced as well as blue-shifted with increasing temperature, while the peak intensities at the free OD stretch frequency (∼2730 cm⁻¹) are insensitive to the temperature. From the enhancement of the H-bonded OD stretch SFG feature at the water–air interface as well as the water–hydrophobic material interfaces at lower temperatures, it was concluded that the ordering of the interfacial water structure is enhanced at reduced temperatures.⁹ It is, however, not a priori evident that the surface would become increasingly ordered at lower temperatures. Moreover, the optical response of water is known to vary with temperature;¹⁴ this effect has not been considered.

Notably, the second-harmonic generation (SHG) intensity from the water–air interface^15–17 has been reported to be rather insensitive to the temperature (at most by 10% over a 70 K temperature range),¹⁶ which seems at odds with the 40% variation in the hydrogen-bonded OH stretch signal in the SFG spectra over a 40 K temperature range.⁹ However, since the SHG intensity arises from the electronic transition dipole moment of the interfacial water molecules, while the SFG signals arise from the vibrational transition dipole moment, the SHG intensity cannot probe the free OH and hydrogen-bonded OH groups separately. It is thus challenging to make a direct connection between OH bond orientation and temperature-dependent SHG results, whereas SFG, with its molecular specificity, in principle provides such information.

In addition to fundamental interest in the temperature dependence of the interfacial water structure, understanding the temperature dependent SFG spectra is essential to interpret the pump/probe or two-dimensional SFG data.^18–24 In these time-resolved techniques, a specific vibrational mode is excited and the fate of the excitation, e.g. depolarization, spectral diffusion, and vibrational relaxation, is followed in time through transient changes in the SFG spectra. In the course of time – typically a few picoseconds – the excess vibrational energy is transferred to heat. The time-dependent increase in the surface temperature thus also gives rise to non-zero differential SFG spectra. Hence, knowledge on the variation of the SFG spectra with temperature is needed to disentangle the contribution of the interfacial water dynamics to the transient spectra from the appearance of heat.²⁵

In order to explore the effect of temperature on the microscopic structure of the interfacial water and the SFG spectra, we measure the heterodyne-detected SFG (HD-SFG) signals at the water–air interface at ssp polarization and compute the corresponding spectra by using MD simulation with different temperatures. Here, ssp polarization denotes s-polarized SFG, s-polarized visible, and p-polarized IR beams, respectively. Both simulated and experimentally measured OH stretch SFG spectra show a dramatic reduction of the 3250–3350 cm⁻¹ OH stretch band and unchanged amplitude of the free OH (∼3700 cm⁻¹) stretch peak with increasing temperature. We subsequently compare the variation of the interfacial SFG signals with that of the bulk IR/Raman spectra in the simulation, revealing that the temperature dependence of the SFG spectra arises primarily from the variation in the optical response rather than from changes in the interfacial structure. We find that the OH group orientation of the interfacial water molecules is remarkably insensitive to the temperature.

Experimentally, HD-SFG spectra of the H₂O–air interface were measured in a temperature controlled metal trough at 283 ± 1 and 303 ± 1 K. Part of a Ti:Sapphire based regenerative amplifier (Spitfire Ace, Spectra-Physics) was used to pump a TOPAS (Light Conversion) generating broadband IR pulses centered at ∼3300 cm⁻¹ with a full width at half maximum (FWHM) of 400 cm⁻¹. Another part of the laser output was sent through an elaton to obtain narrowband visible pulses around 801 nm with a FWHM of ∼25 cm⁻¹. The IR and visible beams were first overlapped on the surface of a gold mirror to generate the first SFG signal under almost grazing incidence angle (IR and visible incident angle: ∼85 and 75°, respectively). Subsequently the IR and visible pulses and the SFG signal were reflected on a concave mirror with a focal length of 50 mm to the sample, with an angle of incidence of ∼45 and 35° for the IR and visible beams, respectively. After collimation the two SFG signals are sent to the detector where they interfere. The spectra were normalized to the SFG signal from z-cut quartz. The depicted spectra were averaged for two 5 minutes exposures and the height was corrected in between using a height sensor with a resolution of 200 nm (Keyence, LK-G85). The phase changes due to evaporation were less than 10 and 30° at 283 and 303 K, respectively. Following ref. 26 the data were rephased using the SFG data of the D₂O–air interface measured at both temperatures and thus undergoing the same phase drift due to evaporation as the H₂O measurements. Therefore, we estimate that the phase uncertainty in the final spectra is less than 10° for both temperatures. Spectra for additional temperatures can be found in the ESI†, as well as the spectra corrected for the temperature dependent Fresnel factors.

MD simulations with the ab initio based force field model (melting temperature of 265–270 K, see ESI†) at the water–air interface were performed at temperatures of 282, 293, 305, 318, and 331 K. The dipole moment and polarizability can be readily computed with this force field model,^27,28 and the SFG signals were calculated from the simulated dipole moment and polarizability within the truncating response function formalism.^28,29 Note that these ab initio based force field models have been actively developed by several groups.^30–33 In this formalism, the relevant time correlation function is calculated in a manner that allows for delocalization of the vibrational amplitude over several chromophores. The spatial extent over which vibrational delocalization is allowed in the calculations is given by the cutoff radius r_t. The Fourier transform of the time correlation function into the frequency domain provides access to the SFG response. The MD simulation protocols, the SFG signal calculation, and the dependence of the SFG spectra on the value of r_t are provided in the ESI.† Furthermore, the temperature dependences of the self-diffusion constant in the bulk and surface tension at the water–air interface are given in the ESI.†

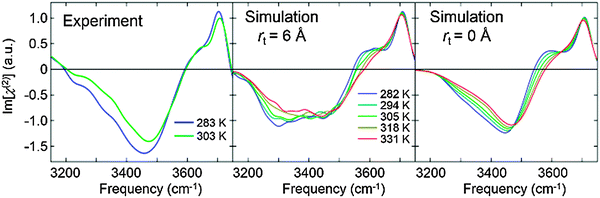
The SFG response of the OH stretch mode was fully converged with r_t = 6 Å (including cross-correlation within the 6 Å cutoff sphere, see the ESI†). The comparison of the simulated and measured SFG spectra is presented in Fig. 1, which reveals good agreement between simulation and experiment: the amplitude at ∼3700 cm⁻¹ is rather insensitive to the temperature, while the amplitude at ∼3300 cm⁻¹ decreases significantly with increasing temperature. We focus here on the 3150 to 3750 cm⁻¹ frequency range as the assignment of the bands in the spectrum is unambiguous in this range.^7,26 In addition, the MD simulation indicates that the positive shoulder at ∼3600 cm⁻¹ becomes more prominent with decreasing temperature. This positive shoulder, also apparent in the experiment, has been assigned to the anti-symmetric stretch mode of the interfacial water molecules donating two HBs.³⁴ The enhanced amplitude for this anti-symmetric mode indicates that the frequencies of the two OH stretch modes in each water molecule overlap more strongly with decreasing temperature, giving rise to larger vibrational energy splitting. The thermal variation of the ∼3600 cm⁻¹ feature is not so prominent in the experimental HD-SFG spectra due to limited signal-to-noise above 3600 cm⁻¹. In any case, our MD simulations capture the temperature dependence of the SFG spectra very well.

Fig. 1 Simulated SFG spectra of the OH stretching frequency with different truncating distances r_t = 0 and 6 Å and experimental ssp SFG spectra. The SFG signals were normalized at the free OH stretch peak of the SFG spectra with r_t = 0 Å at 305 K for the simulation and at 303 K for the experiment.

To investigate the temperature dependence of the vibrational delocalization for χ⁽²⁾ spectra, we also calculated the variation of Im[χ⁽²⁾] with r_t = 0 Å (without cross-correlation), which is also plotted in Fig. 1. Clearly, cross-correlation terms enhance the negative ∼3300 cm⁻¹ feature dramatically. Since the cross-correlation terms allow intermolecular coupling to contribute to the spectra, this peak enhancement arises from the H₂O–H₂O vibrational coupling. The observation of the enhanced amplitude at the red side in the presence of intermolecular coupling is in good agreement with the SFG measurement using the neat H₂O and isotopically diluted H₂O (see Fig. 2 of ref. 26). Surprisingly, also without the intermolecular coupling (r_t = 0 Å), we can see a clear reduction of the SFG response at ∼3300 cm⁻¹ with increasing temperature. This indicates that the intermolecular coupling does not play an essential role in the variation of the SFG amplitude with temperatures. Here, it should be noted that although the intermolecular couplings of the OH stretch chromophores can be controlled with the truncation of the response function, intermolecular coupling effects are inevitably included through the induced molecular dipole moment and polarizability.

We now explore the mechanism of the ∼3300 cm⁻¹ SFG amplitude variation due to the temperature change. The SFG amplitude is determined by (1) the optical properties such as the transition dipole moment, the transition polarizability, and the decay of the dipole and polarizability time correlation functions and (2) the number of the ordered water molecules and the degree of order.^35,36 To conclude that the reduction of the SFG signal arises from the less ordered structure of interfacial water (2), it is required that the temperature dependence of the optical properties (1) is negligible. To examine the temperature dependence of the optical responses by excluding the effects of the ordered water structure, we estimated the variation of the optical responses of the transition dipole moment and polarizability from the IR and Raman responses. Note that the IR and Raman responses arise from the time-correlation functions of transition dipole moment and polarizability, respectively.³⁷ Similar analyses have been made in ref. 38 and 39. We simulated the IR (I_IR) and VV Raman signals (I_Raman) for bulk water with different temperatures and constructed the spectra. Note that since Im[χ_ssp⁽²⁾] is compared with the spectra, we adopted the VV Raman spectra rather than VH Raman spectra.⁴⁰ The simulated spectra are shown in Fig. 2. The temperature dependence of the IR and Raman spectra for the OH stretching mode are consistent with experimental data from literature;^41,42 the IR intensity decreases in the frequency range of 3100 cm⁻¹ < ω < 3550 cm⁻¹ with increasing temperature, while the VV Raman spectra shows a dramatic change in a narrower frequency region (3100 cm⁻¹ < ω < 3350 cm⁻¹).

Fig. 2 Simulated IR, VV Raman, and spectra in the OH stretching frequency range.

Subsequently, we compared the temperature variation of the 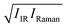amplitudes with that of the simulated Im[χ⁽²⁾] amplitudes. The left panel of Fig. 3 displays the correlation map of their spectral areas integrated in the region of 3250 cm⁻¹ < ω < 3350 cm⁻¹, i.e. the region of the largest change. This figure shows a very clear correlation between the changes in the SFG response and changes in the 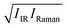spectra, implying that the large reduction of the SFG amplitudes with increasing temperature does not arise from the less ordered OH bonds, but can be fully accounted for by taking into consideration the temperature dependence of the optical properties of water. The origin of the decrease in the temperature-dependent optical response with increasing temperature, is mainly due to a speed-up of the dephasing of the molecular vibrations, and due to weakening of the H-bonded network.

Fig. 3 (left) Correlation map of the spectral area Im[χ⁽²⁾] integrated for 3250 cm⁻¹ < ω < 3350 cm⁻¹vs. the integrated spectra in the same frequency range and the average orientation of the H-bonded OH groups 〈Σcos θ〉. (right) Temperature dependences of 〈Σcos θ〉 and thickness parameter δ. All the data were normalized to the value of the data at 305 K.

To independently confirm that the variation of the SFG spectra with temperature is not caused by changes in the ordering of the OH groups, we compared the integrated Im[χ⁽²⁾] amplitude with the simulated total orientations of the H-bonded OH groups per unit area 〈Σcos θ〉, where θ is the angle formed by the surface normal and the H-bonded OH group. The calculation details are given in the ESI.† The lack of correlation between the temperature dependence of Im[χ⁽²⁾] and average orientation is evident from the left panel of Fig. 3, clearly illustrating that the variation of the H-bonded OH stretch feature in the Im[χ⁽²⁾] spectra is little, if at all, affected by changes in the structure. Indeed, the orientation of the interfacial OH groups with the HB donor is almost unchanged over the temperature range of 280–330 K.

While the average H-bonded OH bond orientation of the interfacial water molecules is insensitive to the temperature, the thermal excitation of capillary waves should affect the interface. To quantify this, we calculated the thickness parameter δ by fitting the function

to the density profile ρ(z) along the surface normal, where z_G is the position of the Gibbs dividing surface and a is the half of the bulk density. The details can be found in the ESI.† The thickness δ, along with the orientational average, vs. temperature is plotted in the right panel of Fig. 3. This clearly shows that, unlike the OH bond orientation, the surface roughness varies substantially with temperature. Here, we would like to note that the interfacial region with the thickness of δ is not the same as the SFG active region. An SFG signal originates from the interfacial region where the net dipole moment along the surface normal does not vanish.

In this paper, we investigated the molecular organization of the interfacial water molecules at the water–air interface and found that the orientation of the water molecules (〈Σcos θ〉) does not change with temperature, whereas the surface roughness (δ) varies. Furthermore, we also reproduced the temperature dependence of the surface tension (see ESI†). It would be important to note that the interfacial region which has the net orientation and less density than the bulk is not the same as the region which affects the surface tension; the surface tension has been determined by the interfacial water organization on larger length scale than the region which the SFG probes. There is thus no inconsistency between no temperature dependence of 〈Σcos θ〉 and the temperature-dependent surface tension.

In conclusion, we investigated the temperature dependence of the SFG spectrum at the water–air interface using a combined experimental and simulated SFG approach. For the OH stretch mode, the SFG amplitude at ∼3700 cm⁻¹ is insensitive to the temperature, while the amplitude at ∼3300 cm⁻¹ decreases with increasing temperature. By comparing the ∼3300 cm⁻¹ peak enhancement in Im[χ⁽²⁾] with the spectra and the average orientations, we conclude that the variation of the SFG amplitude at ∼3300 cm⁻¹ due to the temperature change is the result of the temperature dependence of the optical response. Surprisingly, the OH bond orientation of the interfacial water molecules is largely insensitive to the temperature, despite the substantial change of the SFG response with temperature. Our study illustrates that care must be taken when interpreting temperature-dependent SFG signals in terms of temperature-dependent interfacial structure. This understanding is particularly relevant to the study of temperature-dependent ordered water structures at for example hydrophobic or biological interfaces such as anti-freezing protein–water interface.^9,43 Conclusions based on temperature dependent SFG spectra drawn previously might have to be re-examined by comparing the temperature dependence of the IR and Raman intensity with the SFG spectra.

Conflict of interest

The authors declare no competing financial interests.

Acknowledgements

We thank Dr Johannes Hunger, Dr Grazia Gonella, Prof. Eric Tyrode, Prof. Chuanshan Tian, and Prof. Markus Mezger for fruitful discussions. YN acknowledges the financial support from the German Science Foundation through the TRR146.

References

1. P. Jungwirth and D. J. Tobias, Molecular Structure of Salt Solutions: A New View of the Interface with Implications for Heterogeneous Atmospheric Chemistry, J. Phys. Chem. B, 2001, 105, 10468–10472.
2. A. Döppenschmidt and H.-J. Butt, Measuring the Thickness of the Liquid-like Layer on Ice Surfaces with Atomic Force Microscopy, Langmuir, 2000, 16, 6709–6714.
3. R. Rosenberg, Why Is Ice Slippery?, Phys. Today, 2005, 58, 50–54.
4. N. B. Vargaftik, B. N. Volkov and L. D. Voljak, International Tables of the Surface Tension of Water, J. Phys. Chem. Ref. Data, 1983, 12, 817–820.
5. H. J. Bakker and J. L. Skinner, Vibrational Spectroscopy as a Probe of Structure and Dynamics in Liquid Water, Chem. Rev., 2010, 110, 1498–1517.
6. Q. Du, R. Superfine, E. Freysz and Y. Shen, Vibrational Spectroscopy of Water at the Vapor/water Interface, Phys. Rev. Lett., 1993, 70, 2313–2316.
7. C. Tian and Y. R. Shen, Isotopic Dilution Study of the Water/vapor Interface by Phase-Sensitive Sum-Frequency Vibrational Spectroscopy, J. Am. Chem. Soc., 2009, 131, 2790–2791.
8. C. Schnitzer, S. Baldelli and M. J. Shultz, Sum Frequency Generation by Water on Supercooled H₂SO₄/H₂O Liquid Solutions at Stratospheric Temperature, Chem. Phys. Lett., 1999, 313, 416–420.
9. S. Strazdaite, J. Versluis, E. H. G. Backus and H. J. Bakker, Enhanced Ordering of Water at Hydrophobic Surfaces, J. Chem. Phys., 2014, 140, 054711.
10. M. Bonn, Y. Nagata and E. H. G. Backus, Molecular Structure and Dynamics of Water at the Water–Air Interface Studied with Surface-Specific Vibrational Spectroscopy, Angew. Chem., Int. Ed., 2015, 54, 5560–5576.
11. X. Wei, P. B. Miranda and Y. R. Shen, Surface Vibrational Spectroscopic Study of Surface Melting of Ice, Phys. Rev. Lett., 2001, 86, 1554–1557.
12. H. Groenzin, I. Li, V. Buch and M. J. Shultz, The Single-Crystal, Basal Face of Ice I_h Investigated with Sum Frequency Generation, J. Chem. Phys., 2007, 127, 214502.
13. T. Ishiyama, H. Takahashi and A. Morita, Origin of Vibrational Spectroscopic Response at Ice Surface, J. Phys. Chem. Lett., 2012, 3, 3001–3006.
14. S. A. Corcelli and J. L. Skinner, Infrared and Raman Line Shapes of Dilute HOD in Liquid H₂O and D₂O from 10 to 90 °C, J. Phys. Chem. A, 2005, 109, 6154–6165.
15. M. C. Goh and K. B. Eisenthal, The Energetics of Orientation at the Liquid-Vapor Interface of Water, Chem. Phys. Lett., 1989, 157, 101–104.
16. W. K. Zhang, D. S. Zheng, Y. Y. Xu, H. T. Bian, Y. Guo and H. F. Wang, Reconsideration of Second-Harmonic Generation from Isotropic Liquid Interface: Broken Kleinman Symmetry of Neat Air/water Interface from Dipolar Contribution, J. Chem. Phys., 2005, 123, 224713.
17. W. Zhang, H. Wang and D. Zheng, Quantitative Measurement and Interpretation of Optical Second Harmonic Generation from Molecular Interfaces, Phys. Chem. Chem. Phys., 2006, 8, 4041–4052.
18. J. A. McGuire and Y. R. Shen, Ultrafast Vibrational Dynamics at Water Interfaces, Science, 2006, 313, 1945–1948.
19. A. Ghosh, M. Smits, J. Bredenbeck and M. Bonn, Membrane-Bound Water Is Energetically Decoupled from Nearby Bulk Water: An Ultrafast Surface-Specific Investigation, J. Am. Chem. Soc., 2007, 129, 9608–9609.
20. J. Bredenbeck, A. Ghosh, M. Smits and M. Bonn, Ultrafast Two Dimensional-Infrared Spectroscopy of a Molecular Monolayer, J. Am. Chem. Soc., 2008, 130, 2152–2153.
21. A. Eftekhari-Bafrooei and E. Borguet, Effect of Hydrogen-Bond Strength on the Vibrational Relaxation of Interfacial Water, J. Am. Chem. Soc., 2010, 132, 3756–3761.
22. J. E. Laaser, W. Xiong and M. T. Zanni, Time-Domain SFG Spectroscopy Using Mid-IR Pulse Shaping: Practical and Intrinsic Advantages, J. Phys. Chem. B, 2011, 115, 2536–2546.
23. P. C. Singh, S. Nihonyanagi, S. Yamaguchi and T. Tahara, Communication: Ultrafast Vibrational Dynamics of Hydrogen Bond Network Terminated at the Air/water Interface: A Two-Dimensional Heterodyne-Detected Vibrational Sum Frequency Generation Study, J. Chem. Phys., 2013, 139, 161101.
24. C.-S. Hsieh, M. Okuno, J. Hunger, E. H. G. Backus, Y. Nagata and M. Bonn, Aqueous Heterogeneity at the Air/water Interface Revealed by 2D-HD-SFG Spectroscopy, Angew. Chem., Int. Ed. Engl., 2014, 53, 8146–8149.
25. K. Ramasesha, L. De Marco, A. Mandal and A. Tokmakoff, Water Vibrations Have Strongly Mixed Intra- and Intermolecular Character, Nat. Chem., 2013, 5, 935–940.
26. S. Nihonyanagi, T. Ishiyama, T.-K. Lee, S. Yamaguchi, M. Bonn, A. Morita and T. Tahara, Unified Molecular View of the Air/water Interface Based on Experimental and Theoretical χ⁽²⁾ Spectra of an Isotopically Diluted Water Surface, J. Am. Chem. Soc., 2011, 133, 16875–16880.
27. T. Hasegawa and Y. Tanimura, A Polarizable Water Model for Intramolecular and Intermolecular Vibrational Spectroscopies, J. Phys. Chem. B, 2011, 115, 5545–5553.
28. Y. Nagata, C.-S. Hsieh, T. Hasegawa, J. Voll, E. H. G. Backus and M. Bonn, Water Bending Mode at the Water–Vapor Interface Probed by Sum-Frequency Generation Spectroscopy: A Combined Molecular Dynamics Simulation and Experimental Study, J. Phys. Chem. Lett., 2013, 4, 1872–1877.
29. Y. Nagata and S. Mukamel, Vibrational Sum-Frequency Generation Spectroscopy at the Water/Lipid Interface: Molecular Dynamics Simulation Study, J. Am. Chem. Soc., 2010, 132, 6434–6442.
30. Y. Wang and J. M. Bowman, Ab Initio Potential and Dipole Moment Surfaces for Water. II. Local-Monomer Calculations of the Infrared Spectra of Water Clusters, J. Chem. Phys., 2011, 134, 154510.
31. J. M. Bowman, Y. Wang, H. Liu and J. S. Mancini, Ab Initio Quantum Approaches to the IR Spectroscopy of Water and Hydrates, J. Phys. Chem. Lett., 2015, 6, 366–373.
32. V. Babin, C. Leforestier and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers: Dimer Potential Energy Surface, VRT Spectrum, and Second Virial Coefficient, J. Chem. Theory Comput., 2013, 9, 5395–5403.
33. G. R. Medders and F. Paesani, Infrared and Raman Spectroscopy of Liquid Water through “First Principles” Many-Body Molecular Dynamics, J. Chem. Theory Comput., 2015, 11, 1145–1154.
34. I. V. Stiopkin, C. Weeraman, P. A. Pieniazek, F. Y. Shalhout, J. L. Skinner and A. V. Benderskii, Hydrogen Bonding at the Water Surface Revealed by Isotopic Dilution Spectroscopy, Nature, 2011, 474, 192–195.
35. A. Morita and J. T. Hynes, A Theoretical Analysis of the Sum Frequency Generation Spectrum of the Water Surface, Chem. Phys., 2000, 258, 371–390.
36. B. M. Auer and J. L. Skinner, Vibrational Sum-Frequency Spectroscopy of the Liquid/vapor Interface for Dilute HOD in D₂O, J. Chem. Phys., 2008, 129, 214705.
37. R. W. Boyd, Nonlinear Optics, Academic Press, Waltham, 2003.
38. E. L. Hommel and H. C. Allen, The Air–Liquid Interface of Benzene, Toluene, M-Xylene, and Mesitylene: A Sum Frequency, Raman, and Infrared Spectroscopic Study, Analyst, 2003, 128, 750–755.
39. S. Gopalakrishnan, P. Jungwirth, D. J. Tobias and H. C. Allen, Air–Liquid Interfaces of Aqueous Solutions Containing Ammonium and Sulfate: Spectroscopic and Molecular Dynamics Studies, J. Phys. Chem. B, 2005, 109, 8861–8872.
40. B. M. Auer and J. L. Skinner, IR and Raman Spectra of Liquid Water: Theory and Interpretation, J. Chem. Phys., 2008, 128, 224511.
41. J. R. Scherer, M. K. Go and S. Kint, Raman Spectra and Structure of Water from −10 to 90°, J. Phys. Chem., 1974, 78, 1304–1313.
42. Y. Maréchal, Infrared Spectra of Water. I. Effect of Temperature and of H/D Isotopic Dilution, J. Chem. Phys., 1991, 95, 5565.
43. K. Meister, S. Strazdaite, A. L. Devries, S. Lotze, L. L. C. Olijve, I. K. Voets and H. J. Bakker, Observation of Ice-like Water Layers at an Aqueous Protein Surface, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17732–17736.

---

Footnote

† Electronic supplementary information (ESI) available: MD simulation protocols, calculation of the SFG, IR, and Raman spectra, simulation results, and another experimental data. See DOI: 10.1039/c5cp04022a

---