Coordination structure and charge transfer in microsolvated transition metal hydroxide clusters [MOH]⁺(H₂O)_1–4

Abstract

Infrared vibrational predissociation spectra of transition metal hydroxide clusters, [MOH]⁺(H₂O)_1–4·D₂ with M = Mn, Fe, Co, Ni, Cu, and Zn, are presented and analyzed with the aid of density functional theory calculations. For the [MnOH]⁺, [FeOH]⁺, [CoOH]⁺ and [ZnOH]⁺ species, we find that the first coordination shell contains three water molecules and the four ligands are arranged in a distorted tetrahedral geometry. [CuOH]⁺ can have either two or three water molecules in the first shell arranged in a planar arrangement, while [NiOH]⁺ has an octahedral ligand geometry with the first shell likely closed with five water molecules. Upon closure of the first coordination shell, characteristic stretch frequencies of hydrogen-bonded OH in the 2500–3500 cm⁻¹ region are used to pinpoint the location of the water molecule in the second shell. The relative energetics of different binding sites are found to be metal dependent, dictated by the first-shell coordination geometry and the charge transfer between the hydroxide and the metal center. Finally, the frequency of the hydroxide stretch is found to be sensitive to the vibrational Stark shift induced by the charged metal center, as observed previously for the smaller [MOH]⁺(H₂O) species. Increasing solvation modulates this frequency by reducing the extent of the charge transfer while elongating the M–OH bond.

---

I. Introduction

Interactions between a metal center and its ligands are important for the stability of the complex as well as its functionality. While such interactions can be modified by functional groups on the ligand, it can be further altered by the presence of solvent molecules. For example, the extent of charge transfer between a metal center and a ligand group can be influenced by interactions with nearby polar solvents,^1–4 and the structural arrangement of the ligand groups can also vary depending on local solvation environment. Two recent studies highlight the intricacies present in such solvent-driven changes in metal–ligand interactions for the simple case of [MOH]⁺ complexes. In a vibrational predissociation study by Johnson et al.,⁵ they found that the hydroxide frequency redshifts with increasing solvation in the [MgOH]⁺(H₂O)_1–5 and [CaOH]⁺(H₂O)_1–5 clusters. On the other hand, the same hydroxide stretch blueshifts with increasing solvation in the [CuOH]⁺(H₂O)_1–3 clusters.⁶ Furthermore, these complexes have rather different solvation structures, distinctive from each other when surrounded by three or more water molecules.

In an effort to understand the differences manifested in these prototypical ion pair metal complexes, we recently probed the charge transfer between the metal and hydroxide ligand in the small [MOH]⁺(H₂O) complexes for the Mn–Zn series.⁷ Interestingly, we found that the degree of charge transfer is mainly dictated by the 2nd ionization potential of the transition metal, although such a trend does not hold for the alkali earth metals. Additionally, the vibrational frequency of the hydroxide ligand demonstrates a high sensitivity to the local charge environment, varying by >150 cm⁻¹ depending on the electric field induced by the metal center. This dramatic vibrational Stark shift provides a well behaved correlation between the observed hydroxide frequency and the extent of charge transfer. This trend holds true for [MgOH]⁺ and [CaOH]⁺ as well, allowing the hydroxide frequency to serve as an effective in situ probe of charge transfer. Therefore, the observed opposing trends in the hydroxide stretch for [MgOH]⁺(H₂O)_1–5, [CaOH]⁺(H₂O)_1–5, and [CuOH]⁺(H₂O)_1–3 clusters are likely reflecting different solvent-driven changes in the metal–ligand charge transfer.

Another open question is how the presence of a charged ligand affects the solvation structure of the metal complex. There are only a few studies on the stepwise solvation of ion pairs,^3,5–8 but many reports have focused on the molecular-level interactions controlling solvation of isolated alkali and transition metal ions. Gas-phase studies of these singly and doubly charged clusters have proven an essential tool for understanding fundamental solvation processes. Specifically, coordination numbers and sequential binding energies of water molecules have been previously determined by collision-induced-dissociation mass spectrometry (CID-MS) for the singly charged transition metals Ti–Cu⁹ as well as for Ca²⁺, Mg²⁺, and Fe²⁺, and Zn²⁺.^10–14 Additionally, structures of hydrated singly and doubly charged alkali and transition metal clusters have been very well characterized by photodissociation spectroscopy.^15–26

Building on these results of solvated metal ions, we extend our study of the [MOH]⁺ species to larger clusters to probe the effect of solvation on the M–OH charge transfer as well as to determine how the coordination sphere is influenced by the charged hydroxide ligand. Specifically, we present the infrared predissociation spectroscopy of mass-selected [MOH]⁺(H₂O)_1–4 clusters, with M = Mn, Fe, Co, Ni, Cu, and Zn. The experimental spectra are analyzed with the help of density functional theory calculations. The vibrations in the OH stretch region, between 2600 cm⁻¹ and 3800 cm⁻¹, are used to reveal the coordination number and solvation structure of these clusters. Particularly, several hydration motifs are found for these transition metal clusters, with their relative energies dependent on the metal–hydroxide interaction. We also find a progression of hydroxide frequency behavior as a function of solvation, which is related to the modulation of the vibrational Stark shift. The results point to the water molecules acting as a polarizable medium that affects the charge-transfer interaction even in the molecular solvation regime.

II. Experimental and computational details

The vibrational predissociation spectra of D₂-tagged [MOH]⁺(H₂O)_n (M = Mn–Zn) complexes were acquired using a homebuilt cryogenic ion photofragment spectrometer, described in detail previously.⁶ Ions of interest were generated via electrospray ionization of ∼1 mM aqueous solution of the corresponding metal sulfate, guided by hexapole ion guides through three differentially pumped stages, and collected in a 3D quadrupole ion trap (Jordan TOF) held at 10 K. Buffer gas, consisting of 10% D₂ in a balance of helium, was pulsed into the ion trap for collisional cooling and formation of D₂ adducts, which serve as messengers for vibrational predissociation spectroscopy. After a 90 ms delay allowing for the evacuation of the buffer gas, the cooled ions were extracted from the trap into a time-of-flight mass spectrometer. The species corresponding to the m/z of the [MOH]⁺(H₂O)_n·D₂ ions were isolated using a mass gate and intersected with the output of a Nd:YAG pumped tunable OPO/OPA laser system (Laservision). When the IR photon energy is resonant with a vibrational transition, the absorption of a single photon is sufficient to induce the evaporation of the weakly bound D₂ tag. Photofragment ions corresponding to the bare [MOH]⁺(H₂O)_n species were then separated from the parent ions in a two-stage reflectron. The resulting photofragment intensity as a function of the photon energy yielded linear IR spectra. The final intensities of the experimental spectra were normalized to the laser output power.

To aid the analysis of the experimental spectra, electronic structure calculations were performed using the Gaussian 09 computational package.²⁷ Geometry optimizations, with Gaussian 09 standard tight convergence criteria, and harmonic frequency calculations were carried out at the cam-B3LYP/def2TZVP level of theory. Previous works^7,28 have shown that the cam-B3LYP functional yields reasonable binding energies and more importantly, harmonic vibrational spectra (scaled by a factor of 0.955) that showed good agreement with experiment for [MOH]⁺(H₂O)_n. Charge analysis on the metal and hydroxide were carried out using natural population analysis of NBO 6.²⁹ Lastly, isomer searches were guided by chemical intuition. Various binding sites for each additional water molecule were explored with geometry optimization carried out at normal convergence criteria. Similar structures were eliminated before tight convergence was applied.

III. Results and analysis

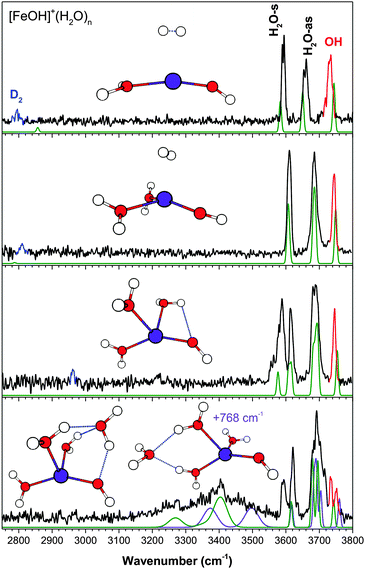
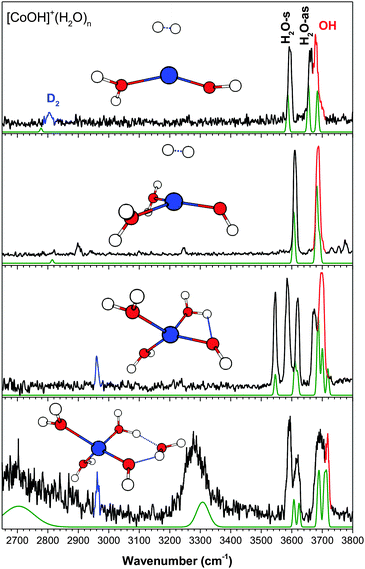
The vibrational spectra of [MOH]⁺(H₂O)_n, with M = Mn, Fe, Co, Ni, Cu, Zn, are shown in Fig. 1–6. For all the metal species studied here, most of the vibrational features are in the 3600–3800 cm⁻¹ free OH region. For the larger n = 4 clusters, all metal species show additional features between 2500–3500 cm⁻¹, characteristic of hydrogen-bonded (H-bonded) OH vibrations. All the experimental peak positions and assignments are summarized in Table 1. The ground states of the [MOH]⁺(H₂O)_n species have the same spin multiplicity as the bare M²⁺ ion. This yields sextet for Mn, quintet for Fe, quartet for Co, triplet for Ni, doublet for Cu, and singlet for Zn.

Fig. 1 The experimental (black) and calculated (purple/green, cam-B3LYP/def2TZVP) vibrational spectra of [MnOH]⁺(H₂O)_n·D₂. Highlighted in red is the hydroxide stretch and in blue is the D₂ stretch.

Fig. 2 The experimental (black) and calculated (purple/green, at cam-B3LYP/def2TZVP) vibrational spectra of [FeOH]⁺(H₂O)_n·D₂. Highlighted in red is the hydroxide stretch and in blue is the D₂ stretch.

Fig. 3 The experimental (black) and calculated (green, at cam-B3LYP/def2TZVP) vibrational spectra of [CoOH]⁺(H₂O)_n·D₂. Highlighted in red is the hydroxide stretch and in blue is the D₂ stretch.

Fig. 4 The experimental (black) and calculated (green, at cam-B3LYP/def2TZVP) vibrational spectra of [NiOH]⁺(H₂O)_n·D₂. Highlighted in red is the hydroxide stretch and in blue is the D₂ stretch.

Fig. 5 The experimental (black) and calculated (green, at cam-B3LYP/def2TZVP) vibrational spectra of [CuOH]⁺(H₂O)_n·D₂. Highlighted in red is the hydroxide stretch and in blue is the D₂ stretch.

Fig. 6 The experimental (black) and calculated (green, at cam-B3LYP/def2TZVP) vibrational spectra of [ZnOH]⁺(H₂O)_n·D₂. Highlighted in red is the hydroxide stretch and in blue is the D₂ stretch.

Table 1 Experimental frequencies and assignments of the [MOH]⁺(H₂O)_2–4 clusters. The subscript denotes the group to which the H-bond is donated

[MOH]^+ (H2O)n	[MnOH]^+	[FeOH]^+	[CoOH]^+	[NiOH]^+	[CuOH]^+	[ZnOH]^+	Assignment
n = 2	2905	2810		2845	2960	∼2950	D2
	3589OH			3525OH	3565D2	3545D2	H2O-s
	3614	3610	3611	3610	3610	3602	H2O-s
	3678			3672	3665	3657	H2O-as
	3697	3685	3686	3688	3685	3678	H2O-as
	3753	3744	3686	3688	3632	3695	Hydroxide
n = 3		2960	2960		2963		D2
	3568OH	3562OH	3545OH	3493OH	3370/3555	3543OH	H2O-s
	3597D2	3586D2	3586D2	3606	3593D2	3580D2	H2O-s
	3624	3615	3619	3626	3625	3614	H2O-s
	3681						H2O-as
	3694	3681	3673	3680	3663–3688	3684	H2O-as
	3705	3691	3700	3691	3706	3698	H2O-as
	3756	3745	3700	3709	3688	3714	Hydroxide
n = 4			2962	2972	2965	2964	D2
	∼2650H2O		∼2650H2O		∼3370	∼2600H2O	H2O-s
	∼3150OH	∼3400H2O	∼3280OH		∼3485H2O	∼3230OH	H2O-s
	3597D2	3593D2	3592D2	3378OH		3590D2	H2O-s
	3623	3620	3617	3612	3615	3612/3625	H2O-s
	3685–3720	3680–3716	3680–3717	3685–3711	3650–3690	3674, 3692, 3720	H2O-as
	3735	3734/3751	3717	3711	3690	3720	Hydroxide

---

The experimental vibrational spectra of the singly hydrated clusters and the [CuOH]⁺(H₂O)_1–3 clusters have been analyzed in detail previously.^6,7 The data are reproduced here for comparison. The assignment process here is similar to that carried out in the previous studies, where the harmonic vibrational spectra calculated at the cam-B3LYP/def2TZVP level serve as the main guidance. The cam-B3LYP functional yielded harmonic vibrational spectra with good agreement with experimental spectra, except for two previously⁶ noted systematic deviations. First, the hydroxide stretch frequency, which is extremely sensitive to the charge transfer between the metal center and the hydroxide, is typically overestimated by ∼10–30 cm⁻¹. Second, the strength of the D₂–H₂O interaction is overestimated, resulting in an overly redshifted symmetric stretch for the D₂ tagged water. This error may arise from anharmonic nature of this weak interaction,³⁰ which is not captured by our harmonic calculations. As discussed in detail in our earlier report on CuOH⁺(H₂O)_n clusters,⁶ higher level ab initio calculations, such as CCSD, can provide a better description of the D₂–H₂O interaction, but the hydroxide frequency is worse. While error in D₂–H₂O interaction only affects that specific water, the error in hydroxide frequency reflects improper treatment of the charge transfer which is likely to affect the whole cluster. For this reason, we rely on the cam-B3LYP calculated harmonic spectra. To simplify the figures and the discussion, only the assigned isomers and their calculated spectra are shown here. Additional isomers and their calculated spectra for the n = 4 clusters are shown in ESI.†

Finally, for the calculated spectra presented here, the D₂ tag is not included once it binds on the water. In our previous study of the [CuOH]⁺ system, it was found that the D₂ tag binds to the metal center for the smaller clusters and moves onto one of the water molecules when the coordination sphere of the metal is filled. This can be deduced from the experimental spectra by looking at the frequency of the weak (nominally forbidden) D₂ stretch. Namely, D₂ interacting directly with the metal center has a frequency lower than 2900 cm⁻¹ while D₂ interacting with a water has a frequency around 2960 cm⁻¹. Additionally, the D₂-perturbed water has a symmetric stretch in the 3580–3600 cm⁻¹ region, ∼30 cm⁻¹ redshifted from the unperturbed symmetric stretch. The exclusion of D₂ in the larger cluster calculations is mainly due to the aforementioned error in the D₂–H₂O interaction. The calculated IR spectra including the D₂ tag typically show greater deviations from experimental spectra than the bare cluster, and therefore do not add any useful information for making assignments. Examples of these calculated results are shown in the ESI† for further considerations. Note that when comparing calculated spectrum of the bare cluster to the experimental spectrum, the most noticeable differences are the lack of D₂ stretch and an additional H₂O stretch in the 3580–3600 cm⁻¹ region.

(a) [MnOH]⁺(H₂O)_n

The experimental IR predissociation spectra of [MnOH]⁺(H₂O)_1–4 with corresponding calculated spectra and geometries are shown in Fig. 1. The experimental spectrum of the singly hydrated species has three bands in the OH stretch region corresponding to the H₂O symmetric (H₂O-s) and antisymmetric (H₂O-as) stretch and the hydroxide (OH) stretch. These three bands remain well-separated up to the n = 3 cluster. Note that the additional features around 3700 cm⁻¹ in the n = 1 spectrum is due to coupling of the H₂O-as stretch with hindered internal rotation.^7,24,26

The n = 2 cluster has the two water molecules and hydroxide arranged in a quasi-planar T geometry with a weak HO–H₂O interaction. This gives rise to a doublet for the H₂O-s and H₂O-as modes. The bare n = 3 cluster has a distorted tetrahedral geometry with two weak HO–H₂O interactions, again giving rise to H₂O-s and H₂O-as doublets. The feature at 3597 cm⁻¹ is assigned to D₂ perturbed H₂O-s while the feature at 3568 cm⁻¹ is assigned to H₂O-s with HO–H₂O interaction. The effect of D₂ tag addition on this spectrum is further analyzed in ESI.† The experimental spectrum of the n = 4 cluster shows two broad and redshifted H-bonding features centered around 2650 cm⁻¹ and 3150 cm⁻¹, indicating that the metal coordination shell is closed at n = 3. The two lowest energy isomers, in which the fourth water is interacting directly with the hydroxide moiety, are found to be present in the experimental spectrum. The first isomer has a four-membered H-bond ring, with the second-shell water accepting an H-bond from a water and donating an H-bond to the hydroxide (AD configuration). This geometry gives rise to the very broad feature at ∼2650 cm⁻¹ corresponding to the H₂O–H₂O H-bond, and a feature at ∼3150 cm⁻¹ corresponding to the HO–H₂O interaction. The other isomer, 251 cm⁻¹ higher in energy, has the second-shell water in a double acceptor–single donor (AAD) configuration. Its presence is responsible for the very broad and asymmetric appearance of the ∼3150 cm⁻¹ feature. Notably, the broad shoulder at ∼3300 cm⁻¹ is likely due to this isomer, corresponding to the two H₂O–H₂O H-bonds. In the ∼3600 cm⁻¹ region, the calculated H₂O-s of the free water molecules for both isomers have the same frequency, and it agrees well with the experimental feature at 3623 cm⁻¹. The 3597 cm⁻¹ feature is therefore assigned to H₂O-s of the D₂ tagged water. The ∼3700 cm⁻¹ region of the experimental spectrum has several partially resolved peaks, which correspond to the H₂O-as stretch of water (or the non H-bonded OH of a water). Lastly, calculations also yielded similar hydroxide stretch frequencies for both isomers, and the bluest experimental feature at 3735 cm⁻¹ is assigned to this vibration.

(b) [FeOH]⁺(H₂O)_n

Fig. 2 shows the experimental IR spectra and calculated results for [FeOH]⁺(H₂O)_1–4. Similar to [MnOH]⁺, the [FeOH]⁺ series has three distinct bands in the OH stretch region corresponding to the H₂O-s, the H₂O-as, and the hydroxide stretch. With increasing solvation, the H₂O-as band and hydroxide stretch move towards each other, but they do not yet overlap in the n = 4 spectrum.

The calculated spectrum of the lowest energy isomer of the n = 2 cluster shows excellent agreement with the experimental spectrum. The water molecules and hydroxide are arranged in a distorted trigonal planar geometry, with the two water molecules essentially equivalent. This results in a simple spectrum with three narrow features slightly blueshifted from those in the n = 1 spectrum. The bare n = 3 cluster is tetrahedral in shape with one weak HO–H₂O interaction. The appearance of the spectrum is very similar to that of [MnOH]⁺(H₂O)₃, and the assignments are similar as well, with the D₂ tag moving onto a water ligand and giving rise to the additional feature at 3586 cm⁻¹.

The experimental spectrum of the n = 4 cluster shows contributions from at least two isomers. This is indicated primarily by the two distinct features in the hydroxide stretch region around 3740 cm⁻¹. The lowest energy isomer has an AAD water interacting directly with the hydroxide. Its calculated spectrum accounts for part of the intensity in the 3200–3500 cm⁻¹ region, as well as the 3734 cm⁻¹ hydroxide peak. The second isomer, 768 cm⁻¹ higher in energy, has the second shell water in an AA configuration accepting two H-bonds from the water ligands opposite the hydroxide. The hydroxide moiety here only has a weak interaction with a nearby water, resulting in the higher frequency 3751 cm⁻¹ feature. No other isomers within ∼1000 cm⁻¹ can account for this peak. This isomer also has two calculated transitions at 3373 and 3497 cm⁻¹ which result in the very broad appearance of the feature at ∼3400 cm⁻¹. The relative intensity of the two hydroxide features indicates an almost equal presence of both isomers, despite the large calculated energy difference. The lack of any intensity around ∼2600 cm⁻¹ indicates that the isomer with an AD second shell water (lowest energy isomer in [MnOH]⁺(H₂O)₄) is not present here, even though it is calculated to only be 257 cm⁻¹ higher in energy than the AAD isomer. It should be noted that the errors in the calculated energetics appear to be larger for the Fe species compared to the other metal species studied here. Lastly, although all the experimentally observed intensities can be accounted for by the two isomers discussed above (the 3593 cm⁻¹ feature correspond to the D₂ perturbed H₂O-s), minor contributions from an additional isomer, with all four water molecules in the first shell, cannot be eliminated. Further discussions are presented in ESI.†

(c) [CoOH]⁺(H₂O)_n

The experimental and calculated IR spectra of [CoOH]⁺(H₂O)_1–4 are shown in Fig. 3. Even for the smallest cluster, the hydroxide stretch is only partially resolved from the H₂O-as band, and they are completely overlapped for the larger clusters. The assigned geometry of the n = 2 cluster, a distorted trigonal planar structure with two nearly equivalent water molecules, is similar to that of [FeOH]⁺. This gives rise to a very simple experimental spectrum, where the 3611 cm⁻¹ feature is assigned to the H₂O-s stretch and the slightly broader 3686 cm⁻¹ feature is assigned to the hydroxide and H₂O-as stretch. This isomer is 100 cm⁻¹ higher in energy than the isomer with a planar T structure, which involves a slight HO–H₂O interaction. Such an interaction would result in a splitting of each water peak, clearly not present in the experimental spectrum. The higher signal-to-noise ratio of the n = 2 spectrum also reveals several small features in the 2900–3300 cm⁻¹ region which are not reproduced in the calculations. Similar features are observed occasionally in the other experimental spectra presented here, and are likely due to combination/overtone bands. Notably, the feature at 3250 cm⁻¹ is likely the overtone of the H₂O bend vibration. Small features are also visible above 3720 cm⁻¹, likely due to combination bands of the water stretch and low frequency libration modes.³¹ The n = 3 cluster has a distorted tetrahedral geometry, similar to that of the [MnOH]⁺ and [FeOH]⁺ species. One of the water molecules interacts with hydroxide, resulting in the 3545 cm⁻¹ feature. The 3586 cm⁻¹ feature is assigned to the D₂-tagged H₂O-s, while the 3619 cm⁻¹ feature is the unperturbed H₂O-s. The partially resolved doublet at 3673 cm⁻¹ and 3700 cm⁻¹ is assigned to the H₂O-as stretches and the overlapping hydroxide stretch.

The coordination shell closes at n = 3 for [CoOH]⁺ as well. The calculated spectrum of the lowest energy isomer of the n = 4 cluster shows an excellent agreement with the experiment, accounting for all the observed spectral features. The geometry of this isomer has the second shell water in an AD configuration, forming an H-bond ring with the hydroxide moiety. The H₂O–H₂O H-bond accounts for the broad 2650 cm⁻¹ feature, and the HO–H₂O H-bond accounts for the 3280 cm⁻¹ feature. The hydroxide stretch is assigned to the higher frequency side of the broad partially resolved H₂O-as band. Isomers with the second shell water in an AAD or AA configuration similar to those of [FeOH]⁺(H₂O)₄ are calculated to be 555 cm⁻¹ and 573 cm⁻¹ higher in energy. They both have calculated intensities in the 3400–3500 cm⁻¹ region, and therefore do not have significant presence in the experimental spectrum.

(d) [NiOH]⁺(H₂O)_n

Fig. 4 shows the experimental and calculated IR spectra for the n = 1–5 clusters of [NiOH]⁺(H₂O)_n. Similar to the [CoOH]⁺ species, the hydroxide stretch of [NiOH]⁺ is overlapped with the H₂O-as band, giving rise to only two bands centered at ∼3600 cm⁻¹ and ∼3700 cm⁻¹ for the n = 1 species. However, there is an additional distinct isolated feature which progressively redshifts with increasing solvation. Furthermore, even in the spectrum of the larger n = 5 cluster, there are no very intense redshifted features, clearly making the solvation of [NiOH]⁺ different than the other metal species presented thus far.

In the n = 2 cluster, the water molecules and hydroxide are in a T-shaped planar geometry. The ∼90° angle between the water and the hydroxide results in a stronger HO–H₂O interaction, giving rise to the redshifted feature at 3525 cm⁻¹. The calculation cannot fully capture this interaction, but the other spectral features have good agreement with the experiment. This isomer is calculated to be 126 cm⁻¹ higher in energy than the lowest energy structure found, which has D₂ on an axial location similar to that of [MnOH]⁺, [FeOH]⁺, and [CoOH]⁺. That geometry, however, does not have an HO–H₂O interaction and cannot account for the 3525 cm⁻¹ experimental feature. In the n = 3 cluster, the water replaces the D₂ in the equatorial position, and the additional repulsion results in a yet stronger HO–H₂O interaction and a redshifted peak at 3493 cm⁻¹. Here, the calculation shows a good overall agreement with the experiment, but the doublet at 3606/3626 cm⁻¹ is calculated to have the same frequency. The increasing HO–H₂O interaction trend continues in the n = 4 cluster, with the fourth water still interacting with the Ni center. We note that the strong HO–H₂O interaction in the n = 4 cluster gives rise to a vibrational feature at 3378 cm⁻¹, which is of similar frequency as that of the H-bonded water stretch due to second shell formation for the other metal species. However, the [NiOH]⁺ feature has comparably narrow width and low intensity in the experimental spectrum, pointing to the difference in its H-bond. The calculated geometry for the n = 5 cluster has an octahedral arrangement, with all six ligands in the first solvation shell. The structure has two water molecules strongly interacting with the hydroxide, with calculated frequencies of 3172 cm⁻¹ and 3251 cm⁻¹. Interestingly, these redshifted features suddenly broaden out in the n = 5 cluster, such that they almost disappear into the baseline. This is similar to the spectra of the n = 4 and 5 clusters of [MgOH]⁺(H₂O)_n and [CaOH]⁺(H₂O)_n.⁵ Note that for the alkali earth species, the extremely broad feature spanning >500 cm⁻¹ arises from a similar HO–H₂O interaction arranged in an octahedral geometry. Isomers with the fifth water in the second shell are all calculated to be ∼1000 cm⁻¹ higher in energy, with significant intensities in the 2500–3400 cm⁻¹ region. Due to insufficient ion signal, the spectrum of [NiOH]⁺(H₂O)₆ cluster could not be collected. This drop in intensity in the mass spectrum from n = 5 to n = 6 suggests the completion of the first coordination shell at n = 5.

(e) [CuOH]⁺(H₂O)_n

The assignment and analysis of the solvated [CuOH]⁺ clusters have been previously published by us for n = 1–3,⁶ and by Sweeney et al.³² for n = 2–9. Recent improvements allowed us to acquire a better signal-to-noise spectrum for the n = 3 cluster and a vibrational spectrum for the n = 4 cluster. Fig. 5 shows the entire n = 1–4 series. In contrast to the metal species discussed so far, the hydroxide stretch in the singly hydrated [CuOH]⁺ lies below the H₂O-s and blueshifts to overlap with the H₂O-as in the n = 3 and 4 clusters. Furthermore, the D₂ tag is already on the water ligand for n = 2 and gives rise to a comparably complex spectrum. Here, the D₂ interaction yields a doublet feature for both H₂O-s and H₂O-as stretch, and is responsible for the differences between the calculated and experimental spectra. The most stable isomer of the n = 3 cluster has a nearly square planar geometry and is the dominant species contributing to the experimental spectrum. The enhanced signal-to-noise spectrum for n = 3 now clearly shows an additional H-bonded feature at 3370 cm⁻¹, indicating the presence of a second isomer as pointed out by Sweeney et al.³² This isomer, calculated to be 432 cm⁻¹ higher in energy here, has the third water in the second shell bonded to two water ligands in an AA configuration, yielding the distinctive H-bond feature.

The calculated spectrum of the lowest energy isomer for the n = 4 cluster agrees well with the experimental spectrum. This is also the lowest energy isomer found by Sweeney et al.³² This isomer, also planar, has three water molecules in the primary metal coordination shell and the fourth water in an AA configuration between two water ligands. It is an extension of both n = 3 isomers. The double H-bond interaction gives rise to the two intense features observed at 3370 cm⁻¹ and 3485 cm⁻¹. Calculations also indicate that the hydroxide stretch is now the highest frequency vibration, overlapped with several H₂O-as vibrations, and they are all assigned to the partially resolved 3690 cm⁻¹ feature. The other low energy isomers reported by Sweeney et al.³² have calculated intensities below 3200 cm⁻¹ and do not appear to contribute to the experimental spectrum observed here.

(f) [ZnOH]⁺(H₂O)_n

Fig. 6 shows the experimental and calculated results for [ZnOH]⁺(H₂O)_1–4. As pointed out for the singly hydrated species,⁷ the calculated results for [ZnOH]⁺ has a slightly larger error (∼20–30 cm⁻¹) for the hydroxide stretch frequency compared to the other metal species. This is true for the larger clusters as well. Furthermore, similar to the [MnOH]⁺ species, the H₂O-as feature in [ZnOH]⁺n = 1 is complicated by coupling of this stretch with hindered internal rotation. The n = 2 cluster has a planar T geometry with the two water molecules nearly equivalent. The calculated spectrum of the bare cluster does not show a good agreement with the experiment. Notably, both the H₂O-s and H₂O-as features are split into a doublet, which is similar to the corresponding [CuOH]⁺ cluster. This points to the D₂ tag residing on a water ligand, and the broad ∼2950 cm⁻¹ D₂ stretch feature further indicate that there may be more than one tag isomer. Specifically, the 3602 cm⁻¹ feature is assigned to the free H₂O-s, which, similar to the n = 1 cluster, is slightly blueshifted from the calculated frequency. The broader and asymmetric feature at 3545 cm⁻¹ is then assigned to the D₂ perturbed H₂O-s. The H₂O-as stretch is also perturbed by the D₂ tag, similar to [CuOH]⁺(H₂O)₂, giving rise to the partially resolved band at 3650–3700 cm⁻¹. The highest frequency side of this band is assigned to the hydroxide stretch.

The experimental spectrum of the n = 3 cluster is similar in appearance to the corresponding [MnOH]⁺, [FeOH]⁺, and [CoOH]⁺ species, in agreement with its calculated geometry being a quasi-tetrahedral structure. The HO–H₂O interaction here gives rise to the feature at 3543 cm⁻¹. The peak at 3580 cm⁻¹ is assigned to the D₂ tagged water stretch and the 3614 cm⁻¹ feature is assigned to the free H₂O-s. The H₂O-as features are again only partially resolved from each other and the 3714 cm⁻¹ hydroxide stretch. Similar to the other tetrahedral species, the Zn coordination shell is complete at n = 3, and the spectrum of the n = 4 cluster has broad and intense features at ∼2600 cm⁻¹ and ∼3230 cm⁻¹. The lowest energy isomer for n = 4 has the second shell water in an AD configuration between a water and the hydroxide. This isomer has two redshifted features in excellent agreement with the experimental features, and it accounts for most of the intensities in the 3600–3800 cm⁻¹ region as well. Minor presence of an additional isomer, with the second shell water in an AAD configuration, cannot be ruled out. See ESI† for additional details.

IV. Discussion

(a) Coordination and solvation structure

The assigned vibrational spectra allow us to take a closer look at the different trends in the coordination geometry and solvation structure. To aid the discussions, we present the experimental spectra and calculated structures of the [MOH]⁺(H₂O)_2–4 clusters grouped by solvation (i.e. n = 2, 3, and 4) in Fig. S8, S9 (ESI†) and Fig. 7.

Fig. 7 The experimental spectra of [MOH]⁺(H₂O)₄·D₂ complexes in the 2400–3800 cm⁻¹ region. Highlighted in blue is the D₂ stretch, in green are the H₂O-s and H₂O-as stretches, in red is the hydroxide stretch, and in magenta are the H-bonded OH stretches involving the second shell water. The grey bars allow for comparison of the H₂O-s and H₂O-as bands for different metals (highlighting the higher frequency edge of the bands).

For the n = 2 clusters (Fig. S8, ESI†), all the metal species have a relatively similar trigonal structure. Specifically, the two water molecules in the [FeOH]⁺ and [CoOH]⁺ clusters are both free and have the same vibrational frequencies. In the [MnOH]⁺ and [NiOH]⁺ clusters, one of the water molecules has a weak interaction with the hydroxide, leading to a splitting in the H₂O-s and H₂O-as modes. In [CuOH]⁺ and [ZnOH]⁺, the water modes are split due to the presence of the D₂ tag on a water, and these features are correspondingly broader and more asymmetrical.

The IR spectra of the n = 3 clusters (Fig. S9, ESI†) highlight the different coordination behaviors of the various metal species. The [MnOH]⁺, [FeOH]⁺, [CoOH]⁺, and [ZnOH]⁺ clusters all have a distorted tetrahedral geometry and the proximity of the ligands leads to one water weakly interacting with the hydroxide. This interaction gives rise to a feature in the 3540–3570 cm⁻¹ region. On the other hand, both the [NiOH]⁺ and the dominant [CuOH]⁺ isomer have a quasi-square-planar geometry. With this structure, the [NiOH]⁺ cluster has the strongest HO–H₂O interaction, with a redshifted frequency of 3493 cm⁻¹. The minor isomer of [CuOH]⁺ yields the first H-bonded OH stretch for this series of [MOH]⁺ clusters. For all the species except Ni, the D₂ tag now resides on a water, and a feature ∼30 cm⁻¹ redshifted from the free H₂O-s is observed in the experimental spectra.

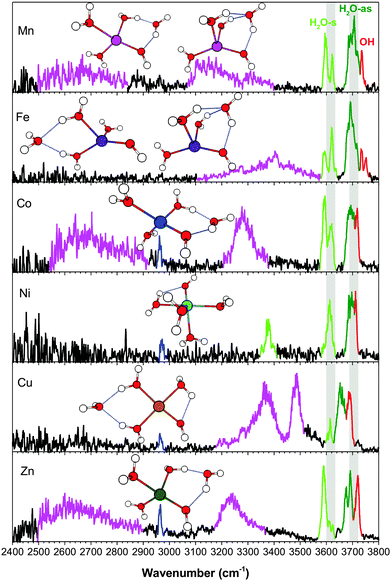
The vibrational spectra of the n = 4 clusters, in the broader 2400–3800 cm⁻¹ region, are shown in Fig. 7. Unlike the smaller clusters, there is now significant activity in the H-bonding region. [NiOH]⁺ is the unique species here, with the fourth water residing in the first solvation shell. The proximity of the ligands in the octahedral coordination leads to a redshifted feature at 3378 cm⁻¹, resulting from the HO–H₂O interaction. This frequency indicates that the interaction is almost as strong as some H₂O–H₂O interactions in the other metal species, though it remains a rather narrow feature with relatively low intensity. For all the other [MOH]⁺(H₂O)₄ clusters, the fourth water resides in the second shell, giving rise to characteristic broad and intense redshifted H-bonded features. The experimental spectra point to two distinct binding sites for the second shell water. First, the [MnOH]⁺, [CoOH]⁺, and [ZnOH]⁺ spectra all have a very broad feature spanning 2500–2900 cm⁻¹, which is absent in the [FeOH]⁺ and [CuOH]⁺ spectra. Calculations show that this feature is due to the second shell water in an AD configuration, forming a ring between a water and the hydroxide. The H₂O–H₂O H-bond in this ring is very strong, giving rise to this low frequency feature. The corresponding HO–H₂O H-bond yields the ∼3200 cm⁻¹ feature. A related motif in which the second shell water is in an AAD configuration between two water molecules and the hydroxide is found for one of the [FeOH]⁺ and [MnOH]⁺ isomers. This configuration has the all the H-bonded features in the 3100–3400 cm⁻¹ region. The weaker H₂O–H₂O interaction here is due to the distribution of the interaction over two equivalent H-bonds. We note that the HO–H₂O interaction here creates a motif in which simple proton transfer to the adjacent oxygen would effectively transfer the location of the hydroxide in the first coordination sphere. The other distinct location for the second shell water is at the opposite side of the cluster, in an AA configuration between two water ligands. This H-bond is of a more typical water–water interaction, and gives rise to features in the 3300–3500 cm⁻¹ region for [CuOH]⁺ and one of the [FeOH]⁺ isomers.

The position and binding motif of the second shell water reveals the relative strength of the H₂O–H₂O and HO–H₂O interactions for the different metal species. As discussed for the singly hydrated species,⁷ electron transfer from the hydroxide to the metal center varies as a function of the 2nd ionization energy of the metal. This makes [CuOH]⁺ the species with the largest charge transfer and therefore the smallest residual charge on the hydroxide (see Table 2). With less charge on the hydroxide, the HO–H₂O interaction becomes less energetically favorable and the second shell water preferably binds in an AA configuration between two water ligands. The [MnOH]⁺, [FeOH]⁺, [CoOH]⁺ and [ZnOH]⁺ species have larger (≥0.7e) NPA charge on the hydroxide ligand, which favors the interaction of the second shell water with the hydroxide. [FeOH]⁺ is different than the other species because it has the AAD motif as a dominant configuration. This can be explained by the geometry of the first coordination shell. The distorted tetrahedral geometry of [FeOH]⁺ has the smallest H₂O–M–H₂O angle in the n = 3 cluster, at about 85°. This favors the AAD interaction, which has a smaller H₂O–M–H₂O angle than the AD motif. Furthermore, the absence of the AD isomer and the strong presence of the AA isomer suggest that the charge on hydroxide is also a factor here, especially considering that [FeOH]⁺ has the second lowest calculated NPA charge on its hydroxide. Similarly, structural considerations may also play a part in the relative stability of the [CuOH]⁺ isomers, where the square planar structure is more strained when accommodating the second shell water in an AD configuration. Altogether, it appears that the solvation structures of [MOH]⁺ are influenced by a combination of charge transfer and coordination geometry.

Table 2 The calculated (cam-B3LYP/def2TZVP) metal (M) NPA charge, hydroxide (OH) NPA charge, and M–OH bond length for the optimized geometries shown in Fig. 1–6. For species where multiple isomers are present in the experimental spectrum, the dominant species is listed. In the case of n = 4 cluster for FeOH, the AAD isomer is listed

[MOH]^+ (H2O)n	n = 1			n = 2			n = 3			n = 4
	M (e)	OH (e)	M–OH (Å)	M (e)	OH (e)	M–OH (Å)	M (e)	OH (e)	M–OH (Å)	M (e)	OH (e)	M–OH (Å)
[MgOH]^+	1.84	−0.90	1.723	1.83	−0.91	1.740	1.82	−0.91	1.789	1.81	−0.89	1.833
[CaOH]^+	1.84	−0.86	1.930	1.83	−0.87	1.958	1.85	−0.90	2.016	1.86	−0.89	2.139
[MnOH]^+	1.54	−0.64	1.758	1.55	−0.70	1.804	1.58	−0.74	1.836	1.61	−0.76	1.878
[FeOH]^+	1.46	−0.58	1.717	1.45	−0.62	1.755	1.50	−0.67	1.778	1.52	−0.70	1.818
[CoOH]^+	1.41	−0.55	1.723	1.42	−0.62	1.761	1.49	−0.68	1.787	1.52	−0.71	1.816
[NiOH]^+	1.31	−0.47	1.695	1.36	−0.57	1.752	1.42	−0.67	1.791	1.47	−0.71	1.808
[CuOH]^+	1.20	−0.32	1.754	1.29	−0.43	1.741	1.40	−0.64	1.811	1.42	−0.67	1.814
[ZnOH]^+	1.61	−0.72	1.740	1.65	−0.76	1.758	1.69	−0.81	1.794	1.71	−0.82	1.823

---

The coordination behavior of the [MOH]⁺ complexes can also be compared to that of the corresponding M⁺(H₂O)_n and M²⁺(H₂O)_n complexes, summarized in Table 3. Previous studies of M²⁺(H₂O)_n clusters by Williams and coworkers^22,23,33 show that the average coordination numbers (CNs) of Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ ions complexed with water are all approximately 6. Cu²⁺ and Zn²⁺ complexes were found to have CN = 4 and CN = 5, respectively. Studies of M⁺(H₂O)_n complexes^18,19,24 showed that Co⁺ and Zn⁺ complexes have CN = 3 while Ni⁺ has CN = 3 or 4.²⁰ Fe⁺ and Cu⁺ clusters both have CN = 2 predominantly, with Fe⁺(H₂O)_n possibly having 4 coordinate geometries as well.^17,21 The [MOH]⁺ species, on the other hand, seem to have CNs somewhere in between the two extremes. Namely, [MnOH]⁺, [FeOH]⁺, [CoOH]⁺, and [ZnOH]⁺ have CN = 4, which is larger than that of the M⁺(H₂O)_n clusters but smaller than that of the known M²⁺(H₂O)_n clusters. Interestingly, [CuOH]⁺ and [NiOH]⁺ have the same coordination numbers as the corresponding M²⁺ ions despite having the lower NPA charge on the metal center. This indicates that neither the formal charge nor NPA charge are sufficient to predict the coordination environment around the metal center, especially when a charged ligand is located in the coordination sphere.

Table 3 Coordination numbers of M⁺, M²⁺, and [MOH]⁺ complexes with water molecules

M	M^+	M^2+	[MOH]^+
Mn	—	6 (ref. 23)	4
Fe	2 or 4 (ref. 17)	6 (ref. 23)	4
Co	3 (ref. 18)	6 (ref. 23)	4
Ni	3 or 4 (ref. 20)	6 (ref. 23)	6
Cu	2 (ref. 21)	4 (ref. 22)	3 or 4
Zn	3 (ref. 19)	5 or 6 (ref. 33)	4

---

(b) Hydroxide frequency

In our previous study on the [MOH]⁺(H₂O) species, we found that the frequency of the hydroxide stretch has a strong dependence on the metal species.⁷ This was attributed to the vibrational Stark shift^34–42 induced by the charged metal center, with charge transfer between the metal ion and the hydroxide ligand being the most important factor in two ways. First, electron transfer from the hydroxide to the metal center reduces the magnitude of the electric field. Second, depletion of the excess electron on the hydroxide reduces the Stark tuning rate, because, unlike the hydroxide anion, the hydroxyl radical frequency is almost insensitive to electric field. Overall the hydroxide frequency was found to be linearly proportional to q_OHq_M/R² where q_OH and q_M are the charge on the hydroxide and the metal, respectively, and R is the distance between the metal and the center of the hydroxide O–H bond.

Here we can look at the effect of solvation on this trend, which is summarized in Fig. 8. The top panel shows that the metal dependence of the hydroxide frequency observed for the n = 1 species continues for the larger clusters. However, the range of the hydroxide frequency narrows significantly with each additional water molecule, and it converges toward ∼3700 cm⁻¹ for all the metal species studied here. Even though the solvation occurs predominately around the metal, the hydroxide frequency shows a high sensitivity to the solvation environment for some species. Notably there is a progression of behavior from [CuOH]⁺ to [MgOH]⁺. The hydroxide frequencies of [CuOH]⁺, [ZnOH]⁺, [NiOH]⁺ and [CoOH]⁺ all blueshift with increasing number of water. On the other hand, the hydroxide frequencies redshift in [MgOH]⁺ and [CaOH]⁺ with increasing solvation.⁵ Finally, hydroxide frequencies of [FeOH]⁺ and [MnOH]⁺ remain fairly constant as a function of solvation.

Fig. 8 Top panel: Experimental hydroxide frequency in MOH⁺(H₂O)_n as a function of n. Bottom panel: Experimental hydroxide frequency as a function of q_OHq_M/R² where q_OH and q_M are the calculated charge on the hydroxide and the metal, respectively, and R is the distance between the metal and the center of the O–H bond. The data for [MgOH]⁺ and [CaOH]⁺ are from ref. 5. The straight line serves as a visual guidance.

We carried out a similar natural population analysis (NPA) for these larger solvation clusters as in our previous study. (Note: for species where multiple isomers are present in the experimental spectrum, the dominant species is considered. In the case of [FeOH]⁺(H₂O)₄, the AAD isomer is considered.) The localized charge on the metal center and the hydroxide moiety are listed in Table 2. The bottom panel of Fig. 8 shows the plot of the hydroxide frequency as a function of q_OHq_M/R², including the [MgOH]⁺ and [CaOH]⁺ species studied by Johnson et al.⁵ With the exception of [ZnOH]⁺, all the other species follow the linear q_OHq_M/R² relationship found for the n = 1 clusters. The offset in the [ZnOH]⁺ series is likely due to errors in the calculation of the Zn–OH interaction and NPA charges as discussed previously for the singly solvated species.⁷ This is partly reflected in the discrepancy between calculated and experimental hydroxide frequencies as discussed in Section III-f. The more scattered appearance of the data points in the center of the plot is likely due to the inherent errors in the charge analysis as well as additional HO–H₂O interactions that affect the hydroxide stretch independent of the electric field. Nonetheless, this graph shows that although the [MgOH]⁺ and [CuOH]⁺ species start at the opposite ends of the plot in the n = 1 cluster, they both move toward the center with increasing number of water molecules. For the n = 4 clusters, all the metal species except for [MgOH]⁺ and [ZnOH]⁺ are congregated around a q_OHq_M/R² of about −0.22 e² Å⁻². This linear relationship indicates that modulation of the Stark shift is the primary reason behind the solvation dependent hydroxide frequency in these [MOH]⁺ complexes, and provides an explanation for the opposing redshift/blueshift trends.

The reason for this behavior is twofold. First, as shown in Table 2, the magnitude of electron transfer between the hydroxide and the metal center is reduced with increasing solvation (i.e., the respective charges on the metal and hydroxide increases). This can be explained by dielectric charge stabilization from the water molecules surrounding the metal center. This effect is more pronounced for the species with larger charge transfer in the small clusters. For example, in [CuOH]⁺ the charge on the metal goes from 1.20 in n = 1 to 1.42 in n = 4. This reduced charge transfer increases both the strength of the electric field and the Stark tuning rate of the hydroxide, leading to a blueshift of the hydroxide frequency. At the same time, a more crowded coordination around the metal center leads to a gradual lengthening of the M–OH bond for all metal species considered here. The longer bond lengths lead to reduced electric field, and a redshift of the hydroxide frequency. This is the dominant effect for the already charge-separated species such as [MgOH]⁺ and [CaOH]⁺. For the [MnOH]⁺ and [FeOH]⁺ species, these two opposing trends effectively cancel out each other, resulting in a relatively constant hydroxide frequency as a function of solvation.

V. Conclusion

The vibrational spectra of [MOH]⁺(H₂O)_n·D₂ (M = Mn, Fe, Co, Ni, Cu and Zn; n = 2–4), acquired using cryogenic ion infrared predissociation spectroscopy are presented. The formation of the second coordination shell is observed for all the metals species except [NiOH]⁺. For [MnOH]⁺, [FeOH]⁺, [CoOH]⁺, and [ZnOH]⁺, the second shell begins with the addition of the fourth water. On the other hand, [CuOH]⁺ can have either a 3-coordinate or a 4-coordinate first shell, with the 4-coordinate shell energetically favored for the n = 4 cluster. [NiOH]⁺ is found to have an octahedral geometry with the first shell likely closed at n = 5. The different coordination numbers also correspond to different geometries, with [CuOH]⁺ adopting a planar structure, [NiOH]⁺ adopting an octahedral structure, and the other species adopting a quasi-tetrahedral structure. For the second shell water, characteristic H-bonded OH vibrations are observed in the 2500–3500 cm⁻¹ region, pointing to different binding sites for different metal species. Specifically, the water molecule in the second shell can adopt either an AD or AAD configuration, interacting directly with the hydroxide moiety, or an AA configuration, interacting only with two water molecules. The relative energetics of different binding sites are found to be dictated by the first shell coordination geometry and the local charge present on the hydroxide. Finally, the hydroxide frequency exhibits very high sensitivity to metal species as well as solvation. Specifically, the [ZnOH]⁺, [CuOH]⁺, [CoOH]⁺ and [NiOH]⁺ clusters showed a blueshifting hydroxide stretch with increasing solvation whereas [FeOH]⁺ and [MnOH]⁺ clusters showed a fairly constant hydroxide stretch for n = 1–4. The modulation of this frequency is dominated by the vibrational Stark shift observed for the n = 1 clusters, despite the increasing and varying H-bonding interactions around the hydroxide moiety.

Acknowledgements

This material is based upon work supported by the National Science Foundation under grant number CHE-1454086. The computational resources used in this work are supported by the National Science Foundation Grant CHE-0840494.

References

1. A. M. Ricks, A. D. Brathwaite and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 11490–11498.
2. E. M. Duffy, B. M. Marsh and E. Garand, J. Phys. Chem. A, 2015, 119, 6326–6332.
3. R. J. Cooper, S. Heiles and E. R. Williams, Phys. Chem. Chem. Phys., 2015, 17, 15963–15975.
4. B. J. Knurr and J. M. Weber, J. Phys. Chem. A, 2015, 119, 843–850.
5. C. J. Johnson, L. C. Dzugan, A. B. Wolk, C. M. Leavitt, J. A. Fournier, A. B. McCoy and M. A. Johnson, J. Phys. Chem. A, 2014, 118, 7590–7597.
6. B. M. Marsh, J. Zhou and E. Garand, J. Phys. Chem. A, 2014, 118, 2063–2071.
7. B. M. Marsh, J. Zhou and E. Garand, Phys. Chem. Chem. Phys., 2015 10.1039/c5cp01522g.
8. L. Jiang, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Am. Chem. Soc., 2010, 132, 7398–7404.
9. N. F. Dalleska, K. Honma, L. S. Sunderlin and P. B. Armentrout, J. Am. Chem. Soc., 1994, 116, 3519–3528.
10. D. R. Carl, R. M. Moision and P. B. Armentrout, Int. J. Mass Spectrom., 2007, 265, 308–325.
11. D. R. Carl and P. B. Armentrout, J. Phys. Chem. A, 2012, 116, 3802–3815.
12. D. R. Carl and P. B. Armentrout, ChemPhysChem, 2013, 14, 681–697.
13. T. E. Cooper, D. R. Carl and P. B. Armentrout, J. Phys. Chem. A, 2009, 113, 13727–13741.
14. T. E. Hofstetter and P. B. Armentrout, J. Phys. Chem. A, 2013, 117, 1110–1123.
15. Y. Inokuchi, K. Ohshimo, F. Misaizu and N. Nishi, J. Phys. Chem. A, 2004, 108, 5034–5040.
16. M. F. Bush, J. T. O'Brien, J. S. Prell, C.-C. Wu, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2009, 131, 13270–13277.
17. K. Ohashi, J. Sasaki, G. Yamamoto, K. Judai, N. Nishi and H. Sekiya, J. Chem. Phys., 2014, 141, 214307.
18. K. Furukawa, K. Ohashi, N. Koga, T. Imamura, K. Judai, N. Nishi and H. Sekiya, Chem. Phys. Lett., 2011, 508, 202–206.
19. B. Bandyopadhyay, K. N. Reishus and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 7794–7803.
20. R. S. Walters, E. D. Pillai and M. A. Duncan, J. Am. Chem. Soc., 2005, 127, 16599–16610.
21. T. Iino, K. Ohashi, Y. Mune, Y. Inokuchi, K. Judai, N. Nishi and H. Sekiya, Chem. Phys. Lett., 2006, 427, 24–28.
22. J. T. O'Brien and E. R. Williams, J. Phys. Chem. A, 2008, 112, 5893–5901.
23. J. T. O'Brien and E. R. Williams, J. Phys. Chem. A, 2011, 115, 14612–14619.
24. P. D. Carnegie, B. Bandyopadhyay and M. A. Duncan, J. Phys. Chem. A, 2011, 115, 7602–7609.
25. A. L. Nicely, D. J. Miller and J. M. Lisy, J. Mol. Spectrosc., 2009, 257, 157–163.
26. T. D. Vaden, B. Forinash and J. M. Lisy, J. Chem. Phys., 2002, 117, 4628–4631.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.
28. A. F. Sweeney and P. B. Armentrout, J. Phys. Chem. A, 2014, 118, 10210–10222.
29. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin-Madison, Madison, WI, USA, 2013.
30. M. Baer, D. Marx and G. Mathias, ChemPhysChem, 2011, 12, 1906–1915.
31. P. D. Carnegie, A. B. McCoy and M. A. Duncan, J. Phys. Chem. A, 2009, 113, 4849–4854.
32. A. F. Sweeney, J. T. O'Brien, E. R. Williams and P. B. Armentrout, Int. J. Mass Spectrom., 2015, 378, 270–280.
33. T. E. Cooper, J. T. O'Brien, E. R. Williams and P. B. Armentrout, J. Phys. Chem. A, 2010, 114, 12646–12655.
34. K. Hermansson, P. A. Bopp, D. Spångberg, L. Pejov, I. Bakó and P. D. Mitev, Chem. Phys. Lett., 2011, 514, 1–15.
35. K. Hermansson, Int. J. Quantum Chem., 1993, 45, 747–758.
36. K. Hermansson, Chem. Phys., 1993, 170, 177–184.
37. S. S. Andrews and S. G. Boxer, J. Phys. Chem. A, 2000, 104, 11853–11863.
38. S. G. Boxer, J. Phys. Chem. B, 2009, 113, 2972–2983.
39. S. H. Brewer and S. Franzen, J. Chem. Phys., 2003, 119, 851–858.
40. T. Mani, D. C. Grills and J. R. Miller, J. Am. Chem. Soc., 2015, 137, 1136–1140.
41. J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 10228–10236.
42. J. S. Prell, J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2011, 133, 4810–4818.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp03914b

---