Photoinduced water splitting via benzoquinone and semiquinone sensitisation

Abstract

The splitting of water into H˙ and OH˙ radicals by sensitisation of a redox-active chromophore with sunlight may eventually become a viable way of producing unlimited, clean and sustainable energy. In this work, we explore the possibility of photo-oxidation of water via sensitisation of benzoquinone with ultraviolet (UV) light in the hydrogen-bonded complex of benzoquinone with a single water molecule. Using state-of-the-art quantum chemical calculations, the mechanisms of electron/proton transfer reactions between photoexcited benzoquinone and water are characterised. In the benzoquinone–H₂O complex, photoexcitation of the chromophore leads to the population of locally excited ππ* and nπ* singlet states, which are coupled to hitherto unknown charge-transfer states. In the latter, an electron is transferred from the oxygen atom of the water molecule to the lowest π* orbital of benzoquinone. These charge-separated states drive the transfer of a proton from the water molecule to the carbonyl acceptor site, yielding the semiquinone–OH˙ biradical. Upon absorption of a second UV photon, the semiquinone radical may undergo O–H bond fission, which generates an H˙ radical and restores the benzoquinone photocatalyst. Our computational results shed light on long-standing questions regarding the nature of the photoreactive electronic states in the aqueous photochemistry of benzoquinone.

---

1. Introduction

The UV mediated photosynthesis of H₂O and CO₂ into glucose and O₂ in plant leaves is crucial for sustaining life on earth.¹ Much of this photochemistry occurs within photosystems I and II and includes the photo-reduction of plastoquinone to plastoquinol. The present work focusses on the excited-state reactivity of the simplest quinone, p-benzoquinone (BQ), with H₂O in the BQ–H₂O hydrogen-bonded complex in the context to the lessons learnt from recent explorations of the photochemistry of the pyridine–H₂O and acridine–H₂O complexes.^2–4 BQ is a photoactive chromophore that exhibits a large redox potential. It is therefore widely used as a hydrogen-accepting reagent in organic syntheses and serves as a dehydration agent.⁵ Such redox activity also makes BQ an efficient precursor in many organic reactions – notably the Diels–Alder reaction.⁶ Experimentally, the redox potential of BQ has been measured to increase upon photoexcitation at selected wavelengths – strongly improving its hydrogen accepting ability.⁷ This property of BQ is of particular interest for the current work in which the excited-state H-atom transfer reaction leading to the oxidation of H₂O via BQ sensitization is explored.

The photoinduced reactivity of quinones with the solvent H₂O has attracted vast attention – with studies spanning about half a century (1950–2000). In these investigations, the lack of knowledge of the precise reaction mechanisms has caused much controversy concerning the finer details of the photoreactivity of quinones with H₂O. Here, we can survey only a subset of the extensive literature in this field to date. Most investigations of the photochemistry of quinones have been conducted in acidic (pH ∼ 3) or neutral (pH ∼ 7) aqueous media and large yields for hydrogenated (quinol) photoproducts with equimolar concentrations have been reported.^7–11 Formation of these products was postulated to proceed via a photoreaction in a triplet excited electronic state that is formed via intersystem crossing (ISC) from an initially excited state of singlet multiplicity. This is a reasonable postulation since such carbonyl group containing systems generally possess high quantum yields for ISC.^12,13 In the case of BQ, the majority photoproducts include semiquinone (BQH˙) and hydroquinone (BQH₂) – formed, respectively, via single or double hydrogenation of BQ, as well as additional minor products resulting from chain reactions of BQ and BQH₂ with OH˙ radicals to form ortho-hydroxy substituted adducts (i.e. benzene-1,2,4-triol and 2-hydroxy-1,4-benzoquinone). It has been suggested that the OH˙ radical formed upon photo-oxidation of H₂O by BQ is not free in solution, but is instead complexed with the resulting BQH˙ radical – forming a biradical.¹⁴ This would explain why the yields of the above described chain reactions involving the OH˙ radical are relatively low.

Variations in the solvent environment influence the photochemistry of quinones and have therefore attracted much attention.^15–17 In alcoholic solvents, photo-excited quinones are also capable of oxidation – yielding hydrogenated products formed via excited-state hydrogen transfer. The rate constant for hydrogen transfer was observed to increase upon increasing the aliphatic chain length – which may reflect a greater stabilization of the resulting RO˙ radical via an increased +I inductive effect. In contrast to quinones in H₂O, the photoreactivity of quinones with tert-butanol is substantially lower and, in addition, the H-atom abstracted by the quinone moiety is exclusively from a C–H bond in the α position to the O–H group. This implies that the resulting tertiary radical intermediate is more stable than the tert-RO˙ radical which is formed by H-atom abstraction from the OH moiety. In general, the observed rate constants associated with photoreactions of quinones with alcohols are significantly lower than those for quinones with water.

Direct measurements of the lifetimes of intermediate species associated with such photo-oxidation reactions have received less attention when compared with ground-state reactivity experiments. Studies of the photoreactivity of quinones in aqueous solution using, for example, ultrafast transient pump–probe spectroscopy are essential for determining the timescales on which the hydrogen-transfer reaction occurs. Ronfard-Haret et al.¹⁸ and Moore et al.¹⁹ performed time-resolved experiments using, respectively, nanosecond flash photolysis and nanosecond resonance Raman spectroscopy – both of which report the appearance of a long-lived semiquinone radical absorption. Such studies cannot give, however, lifetime information for the non-adiabatic excited-state processes involved in the hydrogen-transfer reaction – which are typically ultrafast, that is, proceed on femtosecond timescales. By analogy with other hydrogen-bonded systems that undergo excited-state hydrogen transfer, it is expected that low-energy conical intersections (CIs) govern the ultrafast non-adiabatic processes intrinsic to the observed photoreactions.^20–22 CIs are ubiquitous in many of the ultrafast processes in photochemistry and the pronounced anharmonicity of their potential-energy (PE) surfaces as well as the strong nonadiabatic couplings at CIs are important in driving and controlling photoinduced reactions.^23–27

In view of the lack of time-resolved studies with femtosecond resolution for photoreactions of quinones with hydrogen-donating solvents, first-principles theoretical investigations are essential for the development of a complete mechanistic understanding of these excited-state photoreactions. Here we report the use of ab initio electronic-structure theory to identify the excited electronic states involved in these photoreactions and to establish essential topographic properties of the excited-state PE surfaces involved in the oxidation of H₂O via BQ sensitization. In the present study we have chosen the BQ–H₂O hydrogen bonded complex as a prototypical model system for the exploration of the basic photoinduced reaction mechanisms with accurate first-principles methods. We have explored the excited-state photoreactivity of the BQ–H₂O complex in the singlet and triplet manifolds in an attempt to develop an understanding of the intrinsic hydrogen-transfer mechanisms involved in the photoredox reaction of BQ with H₂O. The theoretical study of spin-forbidden intersystem-crossing (ISC) processes as such is beyond the scope of the present work.

2. Computational methodology

The ground-state equilibrium geometry was optimized in both C₁ and C_s symmetries using Møller-Plesset second-order perturbation theory (MP2),²⁸ coupled with Dunning's correlation consistent double-ζ basis set (cc-pVDZ).²⁹ Vertical excitation energies and oscillator strengths were calculated using the complete-active-space second-order perturbation theory (CASPT2)³⁰ method and the second-order algebraic diagrammatic construction (ADC(2)) method.³¹ The reaction path for H-atom transfer in the electronic ground state was calculated at the MP2 level of theory using the bond length of the hydrogen-bonded OH group of water as the driving coordinate. The S₀ energy was scanned along R_O(2)–H(3) (henceforth simply R_O–H), fixing the O–H bond length at selected values and, at each step, allowing all other internal degrees of freedom to relax to the minimum-energy conformation. The energies of the ¹nπ*, ³nπ*, ¹ππ*, and ³ππ* excited states along the relaxed ground-state path were computed using the ADC(2) method. Relaxed scans along R_O–H were also computed in the ¹ππ* and ³ππ* excited states of charge-transfer character (vide infra) using the ADC(2) method in the excited-state geometry optimizations. In this case, the energies of the electronic ground state and the ¹nπ* and ³nπ* states were computed at the relaxed geometries of the ¹ππ* or ³ππ* states using the MP2 and ADC(2) methods, respectively. To avoid convergence problems, it was necessary to freeze the distance between the donor and acceptor oxygen atoms whilst scanning the relaxed ¹ππ* scan for R_O–H > 1.4 Å. Where the calculation of relaxed scans was not possible due to a failure of excited-state geometry optimization, an approximate reaction path was constructed by linear interpolation in internal coordinates between initial and final geometries.

The CASPT2 calculations for BQ–H₂O were based on a complete-active-space self-consistent-field (CASSCF) reference wave function. Test calculations with varying active spaces were carried out in order to find the active space which describes all significant effects of the ground and excited states in a balanced way whilst minimizing computational expense and convergence problems. The optimal active space for bare BQ was found to comprise of 12 electrons in 10 orbitals (12/10). The active orbital space consisted of four occupied π, four unoccupied π* orbitals and two occupied n orbitals, comprising two a′ and eight a′′ orbitals. In the case of BQ–H₂O, the optimal active space consisted of 14 electrons distributed into 12 orbitals (14/12) – comprising four π and four π* orbitals, two 2p_y lone pairs centered on each of the oxygen atom of BQ, the 2p_x orbital centered on the oxygen atom of water and a σ* orbital localized on the O–H bond of water. In both bare BQ and the BQ–H₂O complex, the CASSCF reference wave function was computed using state-averaged orbitals. The state averaging included three ¹A′ and ³A′ states as well as two ¹A′′ and ³A′′ states.

The ground-state equilibrium geometries of BQH˙ and BQH₂ were calculated using unrestricted and restricted MP2 theory, respectively. Unrelaxed (rigid-body) scans along the O–H stretching coordinates of BQH˙ and BQH₂ were calculated at the CASPT2/aug-cc-pVDZ level of theory, varying the O–H bond distance and keeping all other internal degrees of freedom fixed at the MP2/cc-pVDZ equilibrium geometry of the ground state. It has been shown previously that rigid scans are a good approximation for the photodetachment of H-atoms via repulsive πσ* states.⁴⁶ These calculations were based on a state-averaged CASSCF reference wave function and utilized a (12/11) active space for both BQH˙ and BQH₂. For BQH˙, the active space consisted of four π and three π* orbitals, the O centred 2p_y orbital, the O–H centred σ and σ* orbitals and the 3s Rydberg orbital centered on the hydroxyl O atom. For BQH₂, the active space comprised three π and three π* orbitals, two O centered 2p_x orbitals, the O–H centered σ and σ* orbitals and the 3s Rydberg orbital. Augmentation of the cc-pVDZ basis set is essential for the excited states of πσ* character in BQH˙ and BQH₂ and thus the aug-cc-pVDZ was applied to all atoms.²⁰

All MP2 and ADC(2) calculations were undertaken with Turbomole 6.4³² whereas the CASSCF and CASPT2 calculations were performed using Molpro 2010.1.³³

3. Results and discussion

3.1 Ground-state minimum-energy geometry of the BQ–H₂O complex

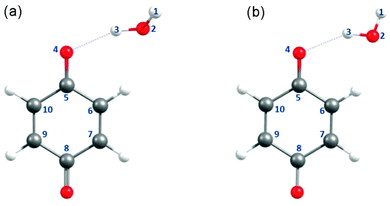
Fig. 1(a) and (b) depict the ground-state minimum-energy geometry of the BQ–H₂O hydrogen-bonded complex optimised with, respectively, C₁ and C_s symmetry constraints. The global minimum-energy configuration in the ground electronic state is depicted in Fig. 1(a) and displays a BQ–H₂O hydrogen-bond length of 2.032 Å and a C5O4⋯H3 hydrogen-bond angle of ∼112°. This bent hydrogen-bond geometry can be understood by recognising that the dominant hydrogen bond acceptor is the in-plane 2p_y non-bonding orbital localised on O(4). The C₁ optimised global minimum is calculated to be only 0.04 eV (∼350 cm⁻¹) more stable than the equivalent configuration optimised with C_s symmetry constraint in which BQ and H₂O are coplanar (Fig. 1(b)). For the purposes of the present study, these subtle differences in the ground-state energy are unimportant. Since the excited-state calculations are greatly simplified in C_s symmetry, the construction of the reaction paths for H-atom transfer and the PE profiles described hereafter were carried out with C_s symmetry constraint – unless stated otherwise.

Fig. 1 Minimum-energy geometries of the BQ–H₂O complex optimised at the MP2/cc-pVDZ level with (a) C₁ and (b) C_s constrained symmetries. The free OH group in (a) is out-of-plane with respect to the aromatic ring plane. (a) Represents the global minimum-energy geometry of BQ–H₂O which is 0.04 eV (350 cm⁻¹) more stable than (b).

3.2 Vertical excitation energies and oscillator strengths

Table 1 lists the calculated vertical excitation energies and oscillator strengths associated with excitations to the low-lying electronic states of BQ and BQ–H₂O. The associated orbitals and orbital promotions for BQ and BQ–H₂O are displayed in Fig. 2.

Table 1 Vertical excitation energies and oscillator strengths (in parentheses) of BQ and BQ–H₂O

State	Vertical excitation energy/eV
	CASSCF/cc-pVDZ	CASPT2/cc-pVDZ	ADC(2)/cc-pVDZ	Experimental value
Benzoquinone
1^1nπ*	3.20 (0.0)	2.47	2.72 (0.0)	2.479^34
2^1nπ*	3.22 (0.0)	2.47	2.80 (0.0)	2.485^34
1^1ππ*	4.90 (0.0)	4.30	4.83 (0.0)	4.070^34
2^1ππ*	6.03 (0.0)	4.56	5.53 (0.0)	—
1^3nπ*	3.05	2.27	2.38	2.314^52
1^3ππ*	3.80	3.34	3.52	—
Benzoquinone–water
1^1nπ*	3.40 (1.1 × 10^−6)	2.71	2.67 (1.7 × 10^−7)	—
2^1nπ*	3.75 (2.3 × 10^−7)	2.90	2.91 (1.93 × 10^−6)	—
1^1ππ*	5.63 (0.0017)	4.34	4.68 (0.0037)	—
2^1ππ*	5.92 (0.0060)	4.49	5.45 (0.5486)	—
1^3nπ*	3.24	2.50	2.33	—
1^3ππ*	3.69	3.23	3.11	—

---

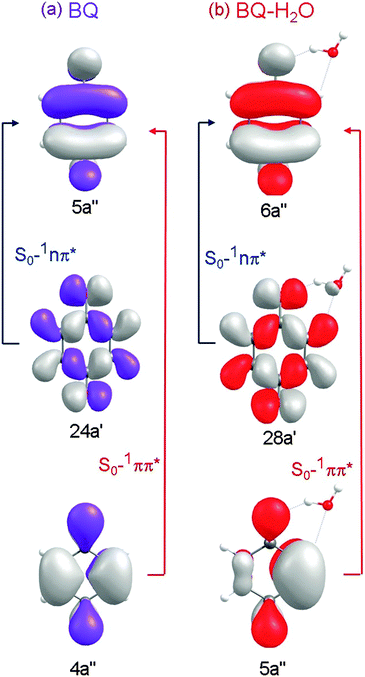Fig. 2 Hartree–Fock orbitals and orbital promotions involved in forming the first three excited singlet states of BQ (left) and the corresponding locally excited singlet states of BQ–H₂O (right).

(A) Bare BQ. The lowest vertically excited singlet states are, respectively, ¹nπ* and ¹ππ* in nature. The transitions to these states are electric-dipole forbidden in the D_2h symmetry group. The ¹ππ* state corresponds to the excitation from the 4a′′(π) orbital to the 5a′′(π*) orbital, see Fig. 2. We note that two quasi-degenerate ¹nπ* states exist in the FC region (see Table 1). These quasi-degenerate states arise via electron promotion from the 2p_y orbitals localised on each oxygen atom to a common π* orbital (5a′′ in Fig. 2). In what follows we will focus solely on the lower of the two quasi-degenerate ¹nπ* states as it is sufficient to do so for the present study. As is evident from Fig. 2, the orbitals involved in the ¹nπ* ← S₀ transition show poor spatial overlap, whereas the ¹ππ* state arises from the 5a′′ ← 4a′′ excitation in which the involved orbitals (as depicted in Fig. 2) show good spatial overlap. Despite the dipole forbidden character, experiments have confirmed that both the ¹nπ* and ¹ππ* states exhibit appreciable absorption cross sections due to vibronic coupling with allowed electronic states.

At the ground-state minimum-energy geometry, CASSCF, CASPT2 and ADC(2) consistently predict the energetic ordering of these states to be ¹nπ* < ¹ππ* – which is in agreement with previous experimental³⁴ and theoretical^35–40 findings, see Table 1. The vertical excitation energies calculated using ADC(2) and CASPT2 are, respectively, 2.72 eV and 2.47 eV for 1¹nπ* and 4.83 and 4.30 eV for ¹ππ* – which are close to the experimentally derived values of 2.7 eV (¹nπ*) and 4.44 eV (¹ππ*).³⁴ As is generally observed, CASPT2 tends to underestimate the energies of ππ* states of aromatic systems, while ADC(2) tends to overestimate the ππ* excitation energies. It is noteworthy that the comparatively inexpensive single-reference ADC(2) method returns vertical excitation energies of comparable accuracy as the multi-reference CASPT2 method.

Excitation energies of the analogous triplet states were also computed using CASSCF, CASPT2 and ADC(2). As expected, these lie lower in energy than the singlet states involving the same orbital promotions (see Fig. 2(a)). The present results are in good agreement with previous theoretical studies of the excitation energies of BQ.^36–40

(B) BQ–H₂O complex. Table 1 also displays the calculated vertical excitation energies of the low-energy electronic states of the BQ–H₂O complex. As with bare BQ, the lowest singlet excited states of BQ–H₂O are ¹nπ* and ¹ππ* in nature. The calculated CASPT2 energies are, respectively, 2.71 eV and 4.34 eV. The ADC(2) vertical excitation energies agree well with those derived from CASPT2. As with bare BQ, two low-lying nπ* states exist below the ¹ππ* state – but unlike BQ, the presence of a chelating H₂O molecule results in a lifting of the quasi-degeneracy such that the two ¹nπ* states are separated by 0.35 eV (cf. 0.02 eV for bare BQ). Analogous to BQ, the dark ¹nπ* states involve orbital promotions from the 2p_y lone pair localised on the O atoms to the ring centred π* orbital. The bright ¹ππ* state also involves the analogous orbital promotion to that of bare BQ – i.e. a ring centred π* ← π excitation. In the Franck–Condon (FC) region, both ¹nπ* and ¹ππ* states are locally excited states of BQ – since both orbitals participating in the electron promotion are localised on BQ.

The triplet states involve the same orbital promotions as those for the analogous singlet excited configurations. The ³ππ* electronic state is located at significantly lower vertical energy than the ¹ππ* electronic state, but still above the lowest ¹nπ* state.

3.3 Excited-state reactivity in the BQ–H₂O complex: electron-driven proton transfer

Where applicable, we refer to the atomic numberings displayed in Fig. 1 in the following description of the excited-state reactivity of the BQ–H₂O complex. Eqn (1) below represents the proposed photoinduced hydrogen-abstraction reaction in the BQ–H₂O complex to form the BQH˙–OH˙ biradical. Eqn (2) describes the photodissociation of the resulting BQH˙ radical that may occur by the absorption of a second photon (vide infra).

BQ–H₂O + hν → BQH˙ + OH˙ (1)

BQH˙ + hν → BQ + H˙ (2)

It should be noted that BQ acts as a photobase in reaction (1), while BQH˙ acts as a photoacid in reaction (2).

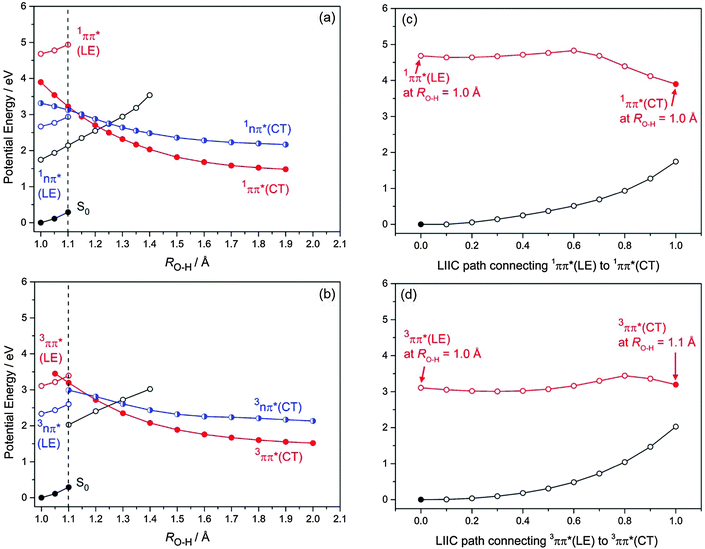
PE profiles for the S₀, ¹nπ* and ¹ππ* states along the O(2)–H(3) bond extension coordinate (corresponding to photoreaction (1)), in the range 1.0 Å ≥ R_O2–H3 ≥ 2.0 Å, are presented in Fig. 3(a). The analogous ³nπ* and ³ππ* PE profiles associated with this photoreaction are displayed in Fig. 3(b). Small values of the O–H bond length (R_O–H ≈ 1.0 Å) correspond to the equilibrium geometry of the BQ–H₂O complex, while large values of the O–H bond length (R_O–H ≈ 2.0 Å) correspond to BQH˙–OH˙ biradicals. The curves in Fig. 3(a) and (b) show the energy profiles of two different minimum-energy reaction paths. The energy of the electronic ground state along the reaction path optimized in the ground state is given by the full black circles on the lower left-hand side. The energies of the locally excited states along this reaction path are represented by the blue (nπ*) and red (ππ*) open circles. For clarity, the energy profiles of the locally excited state are shown only for R_O–H < 1.1 Å (vertical dashed lines in Fig. 3(a) and (b)). The energy of the lowest ππ* state of charge-transfer (CT) character along the reaction path optimized in this excited state is given by the full red circles in Fig. 3(a) and (b). The energies of the S₀ state and the nπ* excited state along this reaction path are given by the open black and half-filled blue circles, respectively. It should be noted that crossings of energy profiles belonging to different reaction paths are apparent crossings, while crossings of energies belonging to the same reaction path are true crossings (that is, either avoided crossings or conical intersections). The crossings of the ππ*(CT) and nπ*(CT) energies with the S₀ energy (open black circles), for example, are true crossings.

Fig. 3 PE profiles of the ground state and the lowest (a) singlet and (b) triplet excited states of the BQ–H₂O complex along minimum-energy reaction paths for hydrogen transfer from the H₂O molecule to BQ. The S₀ energy along the S₀-optimized reaction path is given by the full black circles. The open coloured circles to the left of the vertical dashed line represent the locally excited (LE) excited states of the BQ chromophore. The energy of the ππ* state of charge-transfer character along the reaction path optimized in this state is given by the full red circles. The half-filled blue circles and open black circles represent, respectively, the energies of the nπ*(CT) state and the S₀ state calculated along the ππ*(CT)-optimized reaction path. The energy profiles along the linearly interpolated reaction path leading from the energy minimum of the ¹ππ*(LE) state to the ¹ππ*(CT) state at R_O–H = 1.0 Å is displayed in (c). The energy profiles of the linearly interpolated reaction path connecting the ³ππ*(LE) state at R_O–H = 1.0 Å to the ³ππ*(CT) state at R_O–H = 1.1 Å is shown in (d). These reaction profiles were computed at the ADC(2) level.

As depicted in Fig. 3(a) and (b), the energies of the nπ* and ππ* excited states are parallel to the energy of the ground state along the S₀-optimized reaction path – implying no significant driving force for intermolecular proton transfer in these locally excited states. The locally excited states in the BQ–H₂O complex are therefore nonreactive with respect to water oxidation. In the singlet and triplet ππ* excited states of CT character an electron is promoted from the oxygen 2p_x orbital localised on H₂O to a ring-centred π* orbital (see Fig. 4(a)). In the singlet and triplet nπ* excited states of CT character, an electron is promoted from the 2p_y orbital on H₂O to the same π* orbital. The transfer of a proton from H₂O to BQ in the ¹ππ*(CT) and ¹nπ*(CT) states compensates this charge separation and leads to the pronounced stabilization (by about 2 eV) of the CT states with increasing R_O–H seen in Fig. 3(a) and (b). The neutralization of the electronic charge separation in the CT states provides the driving force for the transfer of the proton from H₂O to BQ (electron-driven proton transfer (EDPT)⁴⁶). The energy of the closed-shell electronic ground state, on the other hand, rises steeply along the reaction paths optimized in the singlet and triplet ππ*(CT) states. As a result, the biradical states arising from proton transfer in the charge-separated states drop below the energy of the ground state for R_O–H > 1.3 Å. They are thus electronically stable species in this region of nuclear coordinate space.

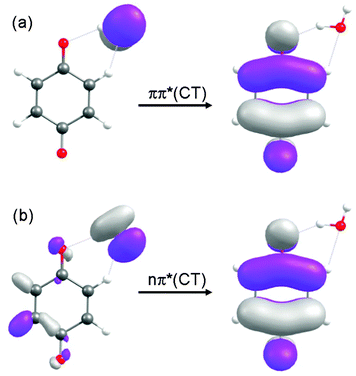Fig. 4 The molecular orbitals involved in the ¹ππ*(CT) and ¹nπ*(CT) states, calculated at R_O–H = 1.0 Å, are displayed in (a) and (b), respectively.

The energy of the ¹nπ*(CT) state at R_O–H = 1.0 Å is ≈0.6 eV below the optimised energy of the locally excited ¹ππ* state, but is ∼0.5 eV above the ¹ππ*(CT) state in the product region (at R_O–H = 1.4 Å) – due to a smaller gradient of the ¹nπ* state along R_O–H. This results in a symmetry-allowed ¹ππ*(CT)/¹nπ*(CT) energy crossing at R_O–H = 1.13 Å which becomes a CI when displacements along out-of-plane coordinates are considered. The energy crossings of the ¹nπ*(CT) and ¹ππ*(CT) states with the S₀ state occur at, respectively, R_O–H = 1.25 Å and = 1.22 Å, see Fig. 3(a). While the ¹nπ*(A′′)/S₀(A′) energy crossing is symmetry-allowed in C_s symmetry, the ¹ππ*/S₀ crossing is an avoided crossing, since both states are of A′ symmetry.

At long range (R_O–H > 1.4 Å), singlet and triplet states of the ππ* and nπ* biradicals are degenerate – reflecting the vanishing exchange integral for the spatially separated unpaired electrons. A ³ππ*(A′)/³nπ*(A′′) symmetry-allowed energy crossing is evident along the proton-transfer path at R_O–H = 1.16 Å. At longer R_O–H, spin-symmetry allowed crossings of the energies of the ³ππ* and ³nπ* states with the energy of the S₀ are located at R_O–H = 1.28 Å and R_O–H = 1.24 Å, respectively.

One key difference in the triplet states compared to the singlet states is the relative energy of the locally excited ³ππ* state in the FC region compared to that of the ³ππ*(CT) state, see Fig. 3(a) and (b). The locally excited ³ππ* state is below the energy of the ³ππ*(CT) state at short R_OH distances – implying the existence of a potential barrier en route to intermolecular hydrogen transfer.

To explore the accessibility of the ¹ππ*(CT) state from the energy minimum of the locally excited ¹ππ* state of BQ, the energy profile of the ¹ππ* state was computed along the linearly interpolated path connecting the minimum of the ¹ππ*(LE) surface with ¹ππ*(CT) energy at R_O–H = 1.0 Å. As depicted in Fig. 3(c), this energy profile exhibits a low barrier of about 0.25 eV. We emphasize that this represents an upper limit to the actual barrier height, since this linearly interpolated reaction path is not a minimum-energy path. The true minimum-energy path connecting the ¹ππ*(LE) and ¹ππ*(CT) states is most likely barrierless. The corresponding profile of the ³ππ* state exhibits a somewhat higher barrier, due to the lower energy of the locally excited ³ππ* state, see Fig. 3(d).

As Fig. 3(a) shows, the vertically excited ¹ππ*(LE) state is located energetically well above the optimized ¹ππ*(CT) state at R_O–H = 1.0 Å. In addition, Fig. 3c indicates a negligible barrier (if any) on the reaction path from the ¹ππ*(LE) state to the ¹ππ*(CT) state. We therefore expect a rapid transition from the locally-excited ¹ππ* state to the charge-transfer state upon vertical excitation of the BQ–H₂O complex, followed by ultrafast proton transfer and formation of the BQH˙–OH˙ biradical product. En route, branching of the population of the ¹ππ*(CT) state to the ¹nπ* and S₀ states may occur at the various energy crossings described above.

ISC may also occur following vertical excitation to the locally excited ¹ππ* state – the energy of which far exceeds the energy of the relaxed ³ππ*(CT) state. In this case, proton transfer in the ³ππ*(CT) state may lead to the formation of the triplet BQH˙–OH˙ biradical. The excess energy becoming available after proton-transfer in the singlet or triplet states (about 2 eV) is substantial and by far sufficient to dissociate the BQH˙–OH˙ biradical, leading to free BQH˙ and OH˙ radicals.

3.4 Photodetachment of H-atoms from semiquinone and hydroquinone

3.4.1 Ground state structures, vertical excitation energies and oscillator strengths. Hydrogenation of BQ at a single O acceptor site leads to the formation of the semiquinone (BQH˙) radical. Disproportionation of two BQH˙ radicals is exoergic and leads to the formation of BQ and the fully hydrogenated species hydroquinone (BQH₂). Hence the H-atom photodetachment reactions of both species have been studied. The ground-state equilibrium structures of BQH˙ and BQH₂ are displayed in Fig. 5.

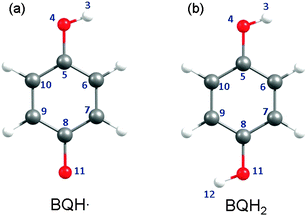Fig. 5 Structures of the BQH˙ radical (left) and the BQH₂ molecule (right). When applicable, the atomic numbering assigned to each structure will be referred to in the main text.

Listed in Table 2 and depicted in Fig. 6 are, respectively, the vertical excitation energies of various low-lying electronic states and the orbital promotions involved in forming the low-lying excited electronic states of BQH˙ and BQH₂.

Table 2 Vertical excitation energies and oscillator strengths (in parentheses) of BQH˙ and BQH₂

State	Vertical excitation energy/eV
	CASSCF/aug-cc-pVDZ	CASPT2/aug-cc-pVDZ
Semiquinone
^2nπ	0.71 (3.3 × 10^−8)	0.90
^2ππ	3.09 (4.1 × 10^−7)	2.75
^2ππ*	4.90 (1.9 × 10^−6)	4.80
^2πσ*	4.94 (0.0001)	4.89
Hydroquinone
^1ππ*	4.63 (0.0306)	4.17
^1πσ*	5.17 (0.0009)	5.00

---

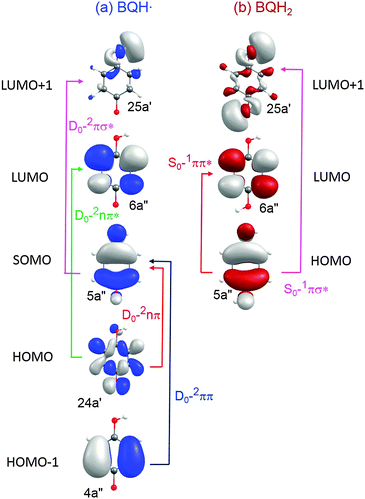Fig. 6 CASSCF orbitals and orbital promotions of the low-energy excited electronic states of BQH˙ and BQH₂.

(A) Semiquinone (BQH˙). The BQH˙ radical is an open-shell species with a single electron in a ring-centred π orbital – i.e. in the 5a′′ singly occupied molecular orbital (SOMO), see Fig. 6(a). The equilibrium geometry of the ground-state BQH˙ radical is planar (Fig. 5(a)). The planar geometry at the C6C5O4H3 dihedral angle can be understood by recognising that the O–H group is a strong π donor and that the O(2p_x) orbital undergoes substantial conjugation with the ring π system.

Upon vertical excitation, the lowest-lying excited states are, in the order of increasing energy, ²nπ, ²ππ, ²ππ* and ²πσ*. The ²nπ and ²ππ electronic states involve the electron promotions SOMO ← HOMO and SOMO ← HOMO−1, respectively (see Fig. 6). In each case, the SOMO and HOMO−1 are ring centred π orbitals and the HOMO is the O(2p_y) non-bonding orbital. The CASPT2 excitation energies of the ²nπ and ²ππ electronic states are, respectively, 0.90 eV and 2.75 eV (see Table 2), placing the absorption maxima of these states in the near infrared and visible regions, respectively. These two states are, however, essentially dark. The ²nπ* and ²πσ* states arise from, respectively, LUMO ← HOMO and LUMO+1 ← SOMO excitations. The LUMO is a ring-centred π* orbital, whereas the LUMO+1 is the σ* orbital localised on the O–H bond (25a′). The CASPT2 vertical excitation energies of the ²ππ* and ²πσ* states are very similar, 4.80 eV and 4.89 eV, respectively, and they carry very little oscillator strength (see Table 2).

(B) Hydroquinone (BQH₂). The ground-state equilibrium geometry of BQH₂ is planar (C_s symmetry). Rotational isomerism of the O–H moieties leads to two distinct, but energetically similar, syn and anti conformations – predicting equal Boltzmann populations of both rotamers at 298 K. For brevity, the following discussion exclusively refers to the anti isomer.

In the FC region, two low-lying electronic states, of ¹ππ* and ¹πσ* nature, exist in the near-UV. The predicted energetic ordering, ¹ππ* < ¹πσ*, is in agreement with analogous systems such as phenol, 4-methoxyphenol and catechol.^41–44 Formation of the ¹ππ* state involves a LUMO ← HOMO electron promotion (Fig. 6(b)). The participating orbitals show good spatial overlap, which is reflected in significant oscillator strength of this transition (Table 2). The vertical excitation energy of the ¹ππ* state is 4.20 eV at the CASPT2 level. ADC(2) predicts 4.60 eV. Both levels of theory predict the S₁–S₀ excitation of BQH₂ to lie in the near UV region. The experimentally derived S₁–S₀ origin line is 4.15 eV (of the anti rotamer), measured via jet-cooled 1 + 1 resonance enhanced multiphoton ionisation (REMPI) spectroscopy.⁴⁵ The REMPI spectrum also reveals a select subset of Franck–Condon active vibrations. All of these lines are much less intense than the electronic origin band, which indicates that the S₀ and S₁ states have similar equilibrium geometries in all nuclear coordinates. At higher vertical excitation energies, CASPT2 predicts the presence of a ¹πσ* state, the energy of which is calculated to be 5.00 eV. This electronic state arises from a σ* ← HOMO electron promotion (Fig. 6(b)) and carries a very low oscillator strength (Table 2).

3.4.2 Hydrogen-detachment reaction path. In photoinduced water splitting with the BQ chromophore (as described above), the water–oxidation reaction (eqn (1)) must be followed by the release of a hydrogen atom from BQH˙ by a second photon (eqn (2)). To explore the feasibility of this reaction, the PE profiles (rigid scans) of BQH˙ and BQH₂ along the hydrogen-detachment (O–H bond fission) coordinate were calculated and are displayed in Fig. 7(a) and (b), respectively. Previous calculations for similar systems showed that the PE profiles of rigid scans are very similar to those of relaxed scans.^42,46

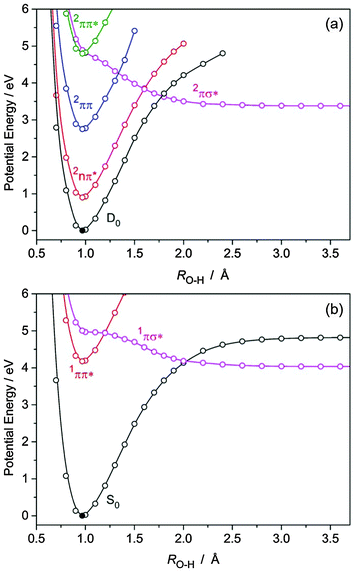Fig. 7 PE profiles of (a) BQH˙ and (b) BQH₂, computed along the R_O–H hydrogen detachment coordinate at the CASPT2/aug-cc-pVDZ level.

(A) Semiquinone (BQH˙). BQH˙ is an exemplar of hypervalent aromatic radicals, the photochemistries of which have thus far received relatively little attention – due to the experimental challenges in preparing such species. Fig. 7(a) presents the PE profiles of the lowest five doublet states of BQH˙ along the R_O–H bond-extension coordinate. Along this coordinate, the D₀, ²nπ, ²ππ and ²ππ* states are all bound, while the ²πσ* state is dissociative with respect to O–H bond elongation. In the FC region, the ²πσ* state exhibits oxygen 3s Rydberg character, which develops progressively O–H centered σ* valence character upon bond extension. The ²πσ* state predissociates the second ²ππ* state near the minimum of the latter. The ²πσ* state correlates asymptotically with BQ in its ground state and an H˙ atom. The calculated bond dissociation energy is D_e[BQH → BQ + H] = 3.38 eV and is lower than the bond dissociation energy of the D₀ state (see Fig. 7(a)). The crossings of the ²πσ*(A′) and ²ππ*(A′′) energies are symmetry-allowed in C_s symmetry, but become conical intersections when out-of-plane vibrational modes are taken into account. Following electronic excitation to the second ²ππ* state, a nonadiabatic transition to the ²πσ* state can occur via nonadiabatic coupling at the ²ππ*/²πσ* CI – which is expected to be ultrafast, given that the ²ππ* and ²πσ* states are essentially degenerate in the FC region.

Following the ²ππ* → ²πσ* nonadiabatic transition, the wave packet in the dissociative ²πσ* state encounters three further CIs with the ²ππ, ²nπ and S₀ states. At these CIs, internal conversion from the ²πσ* state to the ²ππ, ²nπ and D₀ states may occur – the efficiencies of which will depend on the strength of the nonadiabatic couplings and on the local topographies of the PE surfaces at these CIs. Photodetachment of the H-atom requires that the wave packet in the ²πσ* state crosses the ²ππ, ²nπ and D₀ states diabatically. Since there is a dearth of experimental data on the photodissociation dynamics of heterocyclic aromatic radicals and since such data are not likely to become available any time soon, ab initio based nonadiabatic quantum dynamics calculations or quasi-classical trajectory surface-hopping simulations have to be performed in order to estimate the quantum yield of photoinduced H-atom formation from BQH˙. At somewhat higher excitation energies, direct (or vibronically induced) excitation to the nearly dark ²πσ* state could occur and has been previously postulated in related molecules.^44,47–49 In this case, prompt O–H bond fission is expected to occur within tens of femtoseconds (by analogy with phenol),⁴¹ although the role of the ²πσ*/²ππ* and ²πσ*/²nπ* CIs in BQH˙ is unknown.

(B) Hydroquinone (BQH₂). In this sub-section, we discuss the photochemistry of the closed-shell BQH₂ molecule in order to compare and contrast its photochemistry with that of the BQH˙ radical. The discussion of the photochemistry of BQH₂ and the comparisons drawn with BQH˙ benefit greatly from the multitude of available experimental and theoretical data for phenolic molecules (phenol, 4-methoxyphenol, hydroquinone, etc.) – which are lacking for the open-shell analogues such as BQH˙.

Fig. 7(b) presents the PE profiles of the lowest three singlet states of BQH₂ along the R_O–H bond extension coordinate. The situation in BQH₂ is much the same as in phenol or catechol, i.e. the ¹ππ* state is bound and is predissociated by a ¹πσ* state, which is repulsive along the O–H bond extension coordinate and asymptotically correlates with BQH˙ + H˙ products. As such, BQH₂ should undergo O–H bond fission following near-UV excitation to the bright ¹ππ* state – the efficiency of which will depend on the extent to which the ¹ππ* and ¹πσ* states are nonadiabatically coupled. The energy of the ¹πσ*/¹ππ* crossing relative to the ¹ππ* minimum is higher than in the BQH˙ radical, see Fig. 7. Following electronic excitation to the onset of the ¹ππ* state, nonadiabatic tunneling along the O–H coordinate beneath the barrier created by the ¹ππ*/¹πσ* CI is required for population of the dissociative ¹πσ* state – followed by prompt O–H bond fission. In phenol, the equivalent tunneling lifetime has been measured to be ∼2 ns for the lowest vibrational level.⁵¹ It decreases sharply when higher vibrational levels are excited.⁴¹ Analogous with phenol, direct or vibronically induced population of the ¹πσ* state in BQH₂ will drive ultrafast (sub-50 fs) O–H bond fission at elevated photon energies – yielding the asymptotic BQH˙ + H˙ products with a calculated D_e[BQH₂ → BQH˙ + H] of 4.04 eV. The difference in D_e of BQH˙ and BQH₂ can be understood by recognising that the BQH˙ → BQ + H photoreaction forms the closed-shell BQ molecule. In contrast, the BQH₂ → BQH˙ + H˙ photo-reaction forms the chemically less stable open-shell BQH˙ radical.

4. General discussion and conclusions

Ab initio electronic-structure calculations have been used to explore the photoinduced proton-transfer reaction in the BQ–H₂O complex (photoreaction (1)) and the hydrogen photodetachment from the BQH˙ radical that may occur thereafter (photoreaction (2)). Since semiquinone radicals disproportionate spontaneously to yield BQ and BQH₂, the photodetachment of H-atoms could also occur from the latter. We have characterised the minimum-energy pathways connecting the well-known locally excited spectroscopic states of the BQ chromophore to hitherto unknown charge-separated excited states in both the singlet and triplet spin multiplicities of the BQ–H₂O hydrogen-bonded complex. These results clarify controversial key questions concerning the nature of the reactive electronic states involved in the photoreactivity of BQ in aqueous solution. We have provided insights into the mechanisms by which BQ is capable of photo-oxidation of water – which is the initiation step for water splitting with an aromatic photobase (photoreaction (1)).

Photoreaction (1) involves initial excitation to a locally excited singlet electronic state (¹ππ*(LE)) the PE surface of which is adiabatically connected in a barrierless manner to the PE surface of a dark charge-separated singlet electronic state. Following the transition from the ¹ππ*(LE) state to the ¹ππ*(CT) state, the transfer of the proton from the H₂O molecule to BQ neutralizes the electronic charge separation, which results in a substantial energetic stabilisation of the electronic CT states which become neutral biradical states. Since the closed-shell ground state is strongly destabilized by the proton transfer, the ¹ππ* and ¹nπ* biradical product states are lower in energy than the electronic ground state at the equilibrium geometry of the latter (Fig. 3(a)). Importantly, the products of these excited-state electron/proton transfer reactions are radical pairs rather than ion pairs (which are formed in ground-state proton-transfer reactions). The nonadiabatic transitions between the various electronic states are governed by avoided crossings or CIs. At the energy crossings of the biradical states with the S₀ state, the reaction bifurcates into either (i) formation of biradicals or (ii) internal conversion to the electronic ground state, followed by re-formation of the original complex after vibrational energy relaxation.

The LE and CT states in the triplet manifold of the BQ–H₂O complex exhibit essentially identical PE profiles along the hydrogen-transfer coordinate as in the singlet manifold. While photoexcitation of the BQ–H₂O complex leads to the population of singlet excited states, triplet excited states can be populated when ISC competes effectively with the reaction and relaxation processes in the singlet manifold. The ³ππ*(CT)/S₀ and ³nπ*(CT)/S₀ intersections represent allowed crossings to a very good approximation, since the spin–orbit coupling is weak. Therefore, flux evolving on the ³ππ*(CT) state will continue en route to forming the biradical species with little or no perturbation by the electronic ground-state PE surface. The absence of electronic inter-state transitions at the ³ππ*(CT)/S₀ and ³nπ*(CT)/S₀ intersections will likely lead to an enhanced yield of biradical products compared to the singlet manifold.

The BQH˙ radical formed in photoreaction (1) may either serve as a reducing agent or the surplus H-atom may be photodetached via photoreaction (2). A repulsive ²πσ* state is predicted to exist in the near-UV excitation region which may provide a channel for direct and fast H-atom photodetachment. Analogous ¹πσ* states in phenol are known to yield H-atom photoproducts.⁴¹ BQH˙ features, however, low-lying bound ²ππ and ²nπ states, which are intersected by the ²πσ* state en route to O–H bond fission. These additional energy crossings may cause trapping of the population of the ²πσ* state via internal conversion – reducing the quantum yield of BQ + H photoproducts. The probability of IC to the ²ππ and ²nπ states will depend on the strength of the non-adiabatic coupling at the various CIs along the ²πσ* state. These issues require further investigation by electronic-structure and quantum dynamics calculations.

We note that BQH˙ is only partially reduced and contains a free carbonyl oxygen which is available for the oxidation of another H₂O molecule via excited-state hydrogen abstraction. Following photoexcitation by a second photon, the O–H bond fission channel described above may compete with the BQH˙–H₂O + hν → BQH₂ + OH˙ photoreaction involving another water molecule. The relative branching into H-atom abstraction from water or H-atom photodetachment from BQH˙ will depend on the energetics of the second H-atom abstraction process. These questions are beyond the scope of the present study, but deserve future investigation.

An important feature evidenced by the present work is that the excited-state electron/proton-transfer process in BQ–H₂O is exoergic and most likely barrierless, which is not the case in the pyridine–water (Py–H₂O) complex, for example, for which a potential barrier of 0.23 eV for H-atom transfer from the H₂O molecule to pyridine has been predicted at the ADC(2) level.³ We therefore expect that photo-induced proton transfer occurs on a faster timescale and with higher efficiency in the BQ–H₂O complex than in the pyridine–H₂O complex. On the other hand, the H-atom photodetachment from the BQH˙ radical involves curve crossings with three bound electronic states along the O–H bond elongation coordinate, which may reduce the H-atom yield.

BQ, like pyridine, absorbs in the UV and, as such, is not a suitable photocatalyzer for solar water splitting. Moreover, the oscillator strengths of the ¹ππ* transitions in the BQ–H₂O complex are extremely small, since these transitions are dipole-forbidden in the isolated BQ chromophore. The D₀ → ¹ππ* transitions in the BQH˙ radical likewise are in the UV and exhibit very low oscillator strengths. Therefore, the BQ–H₂O complex should be considered as an idealized model system which is suitable for the investigation of the fundamental mechanisms of the coupled electron/proton transfer reactions involved in photoinduced water splitting. The small size of this complex allows the application of relatively accurate first-principles computational methods, including forthcoming quantum mechanical or quasi-classical simulations of the excited-state reaction dynamics. Practically suitable photoactive chromophores should absorb in the visible (or more precisely, within the range of the solar spectrum that reaches the surface of earth) with substantial oscillator strengths. Once the mechanistic details of the electron/proton coupled reactions in the photo-excited BQ–H₂O complex are understood, the next logical step will be the systematic engineering of the quinone chromophore, say A, to optimize its functionality as a photocatalyst for solar water splitting. Relative to BQ, such improvements should involve (i) a shift of the absorption maximum of the chromophore A to longer wavelengths (to within the visible spectrum) by extension of the π-conjugated system, (ii) optimisation of the oscillator strength of A in order to maximise the absorption efficiency, (iii) ensuring low energetic barriers separating the locally excited states and the CT states that drive the proton transfer in the A–H₂O complex and (iv) lowering the absorption maximum of the AH˙ radical whilst maximising its absorption efficiency. Possible candidates which may encompass all or at least some of the above requirements are anthraquinone dyes. These exhibit an extended π-conjugation that leads to a bathochromic shift of the absorption maximum. The singlet ππ* excited electronic states of anthraquinone dyes are electric-dipole allowed and exhibit large absorption cross sections in the visible region, rendering these dyes promising candidates as photocatalyzers for solar water splitting.

A potential drawback of quinones as water-splitting catalysts is the rather high dissociation threshold of the reduced species, as indicated by the calculated dissociation energies of 3.38 eV for BQH˙ and 4.04 eV for BQH₂. This fact is related, of course, to the exceptionally high oxidation potential of photoexcited BQ and implies that near-UV photons are required to drive the photodissociation of BQH˙ or BQH₂. For comparison, the calculated dissociation energies of the pyridinyl and acridinyl radicals are 1.7 eV and 3.0 eV, respectively.^2,4 However, judicious substitution with π-donating groups (such as NH₂ or OMe) has previously been shown to greatly reduce the bond dissociation energy of phenol⁵⁰ – which, to first order, should translate to BQ and anthraquinones, thus lowering the threshold for photoreaction (2).

Acknowledgements

The authors are grateful to Xiaojun Liu and Andrzej Sobolewski for fruitful discussions. T.N.V.K. thanks the Technical University of Munich for a post-doctoral research fellowship. D.T. is grateful for a Ph.D. fellowship granted by the International Max Planck Research School of Advanced Photon Science (IMPRS-APS) and for support by the TUM Graduate School. W.D. thanks the Deutsche Forschungsgemeinschaft for support via the Munich Centre for Advanced Photonics.

References

1. B. Loll, J. Kern, W. Saenger, A. Zouni and J. Biesiadka, Nature, 2005, 438, 1040–1044.
2. X. Liu, A. L. Sobolewski, R. Borelli and W. Domcke, Phys. Chem. Chem. Phys., 2013, 15, 5957–5966.
3. X. Liu, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 7788–7795.
4. X. Liu, A. L. Sobolewski and W. Domcke, J. Phys. Chem. B, 2015, 119, 10664–10672.
5. T.-K. Yang and C.-Y. Shen, Encyclopedia of Reagents for Organic Synthesis, John Wiley & Sons, Ltd, 2001.
6. M. Oda, T. Kawase, T. Okada and T. Enomoto, Org. Synth., 1996, 73, 253.
7. S. M. Beck and L. E. Brus, J. Am. Chem. Soc., 1982, 104, 1103–1104.
8. S. M. Beck and L. E. Brus, J. Am. Chem. Soc., 1982, 104, 4789–4792.
9. A. I. Ononye, A. R. McIntosh and J. R. Bolton, J. Phys. Chem., 1986, 90, 6266–6270.
10. K. C. Kurien and P. A. Robins, J. Chem. Soc. B, 1970, 855–859.
11. A. E. Alegria, A. Ferrer and E. Sepulveda, Photochem. Photobiol., 1997, 66, 436–442.
12. T. Matsumoto, M. Sato and S. Hirayama, Chem. Phys. Lett., 1973, 18, 563–566.
13. R. E. Connors and W. R. Christian, J. Phys. Chem., 1982, 86, 1524–1528.
14. A. Pochon, P. P. Vaughan, D. Gan, P. Vath, N. V. Blough and D. E. Falvey, J. Phys. Chem. A, 2002, 106, 2889–2894.
15. C. F. Wells, Trans. Faraday Soc., 1961, 57, 1703–1718.
16. B. Atkinson and M. Di, Trans. Faraday Soc., 1958, 54, 1331–1339.
17. C. F. Wells, Nature, 1956, 177, 483–484.
18. J.-C. Ronfard-Haret, R. V. Bensasson and E. Amouyal, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 2432–2436.
19. J. N. Moore, D. Phillips and R. E. Hester, J. Phys. Chem., 1988, 92, 5619–5627.
20. S. Perun, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2006, 110, 9031–9038.
21. A. L. Sobolewski, W. Domcke and C. Hättig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906.
22. A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275–9283.
23. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458.
24. S. Clifford, M. J. Bearpark, F. Bernardi, M. Olivucci, M. A. Robb and B. R. Smith, J. Am. Chem. Soc., 1996, 118, 7353–7360.
25. W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections: Electronic Structure, Dynamics and Spectroscopy, World Scientific, Singapore, 2004.
26. W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections: Theory, Computation and Experiment, World Scientific, Singapore, 2011.
27. M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, Wiley-VCH, Weinheim, 1995.
28. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
29. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023.
30. B. O. Roos, P. A. Malmqvist, V. Molina, L. Serrano-Andres and M. Merchan, J. Chem. Phys., 2002, 116, 7526–7536.
31. A. Dreuw and M. Wormit, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82–95.
32. TURBOMOLE V6.4 2012, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
33. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler and R. D. Amos, et al., MOLPRO, University of Cardiff, Cardiff, U.K., 2010.
34. G. Ter Horst and J. Kommandeur, Chem. Phys., 1979, 44, 287–293.
35. R. Pou-Amérigo, M. Merchán and E. Ortí, J. Chem. Phys., 1999, 110, 9536–9546.
36. J. Weber, K. Malsch and G. Hohlneicher, Chem. Phys., 2001, 264, 275–318.
37. Y. Honda, M. Hada, M. Ehara and H. Nakatsuji, J. Phys. Chem. A, 2002, 106, 3838–3849.
38. M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110.
39. M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2010, 133, 174318.
40. P. H. P. Harbach, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 064113.
41. A. Iqbal, L.-J. Pegg and V. G. Stavros, J. Phys. Chem. A, 2008, 112, 9531–9534.
42. T. N. V. Karsili, A. M. Wenge, B. Marchetti and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2014, 16, 588–598.
43. G. A. King, A. L. Devine, M. G. D. Nix, D. E. Kelly and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2008, 10, 6417–6429.
44. O. P. J. Vieuxmaire, Z. Lan, A. L. Sobolewski and W. Domcke, J. Chem. Phys., 2008, 129, 224307.
45. N. Biswas, S. Chakraborty and S. Wategaonkar, J. Phys. Chem. A, 2004, 108, 9074–9081.
46. A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2007, 111, 11725–11735.
47. M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2006, 8, 2610–2618.
48. M. G. D. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 133318.
49. A. L. Devine, M. G. D. Nix, R. N. Dixon and M. N. R. Ashfold, J. Phys. Chem. A, 2008, 112, 9563–9574.
50. T. N. V. Karsili, A. M. Wenge, S. J. Harris, D. Murdock, J. N. Harvey, R. N. Dixon and M. N. R. Ashfold, Chem. Sci., 2013, 4, 2434–2446.
51. G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352.
52. J. Goodman and L. E. Brus, J. Chem. Phys., 1978, 69, 1604.

---

Footnote

† Present address: Max-Planck-Institut für Kohlenforschung, D-45470 Mülheim an der Ruhr, Germany.

---