Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion-specific adsorption and electroosmosis in charged amorphous porous silica†
Remco
Hartkamp
ab,
Bertrand
Siboulet
c,
Jean-François
Dufrêche
c and
Benoit
Coasne
*ab
aInstitut Charles Gerhardt Montpellier, CNRS (UMR 5253), Université Montpellier 2, ENSCM, 8 rue de l'Ecole Normale, 34296 Montpellier Cedex 05, France. E-mail: coasne@mit.edu
bMultiScale Material Science for Energy and Environment, CNRS/MIT (UMI 3466), Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
cInstitute for Separation Chemistry of Marcoule (UMR 5257), CNRS/CEA/Université Montpellier – ENSCM Centre de Marcoule Bât. 426, BP 17171, F-30207 Bagnols-sur-Cèze Cedex, France
First published on 28th August 2015
Abstract
Monovalent and divalent aqueous electrolytes confined in negatively charged porous silica are studied by means of molecular simulations including free energy calculations. Owing to the strong cation adsorption at the surface, surface charge overcompensation (overscreening) occurs which leads to an effective positive surface next to the Stern layer, followed by a negatively charged diffuse layer. A simple Poisson–Boltzmann model in which the single-ion potential of mean force is introduced is shown to capture the most prominent features of ion density profiles near an amorphous silica surface. Nevertheless, due to its mean-field nature, which fails to account for correlations, this simple model does not predict overscreening corresponding to charge inversion at the surface. Such an overscreening drastically affects the transport of confined electrolytes as it leads to flow reversal when subjected to an electric field. A simple continuum theory is shown to capture how the electro-osmotic flow is affected by overscreening and by the apparent enhanced viscosity of the confined electrolytes. Comparison with available experimental data is discussed, as well as the implications of these phenomena for ζ-potential measurements.
1 Introduction
While electrokinetic methods such as electroosmosis and electrophoresis1–3 allow controlling the flow of confined electrolyte solutions, the large surface to volume ratio in nanofluidic devices leads to a variety of new adsorption and transport phenomena.4,5 Understanding the complex structure and flow properties of electrolytes near charged interfaces is therefore of paramount importance to develop and improve nanotechnologies in the field of drug delivery, filtration, energy conversion, etc. Among the possible nanofluidic devices, silica-based materials are important as they can be easily synthesized, tuned and shaped, as well as used to prepare lab-on-a-chip devices.As far as molecular simulation techniques are concerned, in parallel to the abundant literature on pure water confined in crystalline6–9 and amorphous10–14 porous silica, several authors have investigated the adsorption of alkali halide and alkaline earth halide ions at idealized interfaces15,16 or crystalline materials.17,18 More recently, the interfacial properties of aqueous electrolyte solutions with large ion concentrations adsorbed at the surface of amorphous silica have received increasing attention.19–23 A few studies related to electrolyte solutions in amorphous silica have focused on the migration of ions between reservoirs connected by a short neutral20,22,23 or charged24,25 silica pore. The effect of the pore size was investigated in these studies, in addition to structural, dynamical, or dielectric properties. Videla et al.20 compared the densities of NaCl aqueous electrolytes confined in cylindrical pores with radii of 10.0, 15.0, and 17.5 Å in neutral amorphous silica. Axial density profiles of water and ions were found to be correlated with the overall distribution of silanol groups, which indicates that certain silanol groups form more favorable adsorption sites than others. Renou et al.23 found, for amorphous silica with a cylindrical pore of radius 6 Å, that ion polarizability has little effect on the axial ion density profiles of NaCl, while a larger effect was found for NaI in the form of rejection of polarized anions at the pore entrance. Such ion-specific effects can be key to selective removal and separation of ions. Cruz-Chu et al.22 observed for 1 mol L−1 KCl solutions in cylindrical pores of radii of 10 to 30 Å a preferred cation adsorption to dangling oxygen atoms at the silica surface, especially when multiple dangling oxygen atoms appeared next to each other. These sites are easily accessible and provide sufficiently strong interaction energy to disturb the hydration shell of the ion. Consequently, the distribution and flow of electrolyte solutions can be controlled via the distribution of surface groups, as we will further investigate in this study. The flow of ions through pores in contact with bulk-like reservoirs form an important class of fluid–solid interface problems. However, the pore lengths that can be studied using molecular dynamics (MD) simulations are too short to obtain a region at which the influence of the entrance can be neglected and lateral homogeneity can be assumed. Instead, simulations of fully periodic pores allow for the study of confined fluids without any pore entrance effects. Lorenz et al.19 have performed MD simulations of streaming current and electro-osmotic flow of NaCl and CaCl2 solutions in a charged amorphous silica slit pore of 75 Å width. They showed that the electrokinetic flow depends on the ionic strength and that the obtained ion distribution depends on the silica force field and the preparation method. A multiscale approach was proposed, which couples charge distributions from MD simulations with a continuum model. While this approach proved promising, the comparison between simulations and theory was hindered by limited understanding of electroviscous effects. Argyris et al.18 compared the ion distributions of 1 mol L−1 NaCl and CsCl solutions confined in a neutral crystalline silica slit pore of a width of 10.68 Å. Ion-specificity was found to be manifested as a dense layer of sodium ions formed close to the surface while cesium ions do not show such strong layering and are located further from the surface. Chen et al.26 recently studied carbohydrate–calcite interactions for calcite slit pores of widths between 36.5 and 54.8 Å. The carbohydrate was immersed in an aqueous solution with brine concentrations of Na+, Ca2+, Mg2+, and Cl−. The authors found that different terminations of the calcite crystal structure resulted in different ion adsorption behavior, including the occurrence of overscreening. Interestingly, it was found that an increase of the brine concentration resulted in a reduction of the carbohydrate–calcite hydrogen-bond interaction due to more screening from the salt adsorbed onto the calcite surface.
Despite many insights gained from earlier studies, many questions surrounding ion-specificity and liquid–solid interfaces remain unanswered. This includes gaining a full understanding of the underlying mechanisms and consequences of overscreening and local viscosity enhancement. Another open problem is the development of a theoretical description of the unique properties of nano-confined electrolytic fluids. This paper aims at determining the behavior of various aqueous electrolyte solutions confined in charged amorphous silica. In addition to conventional electrolytes (NaCl and KCl), we consider radionuclides, such as CsCl and SrCl2, which are relevant to decontamination of nuclear effluents (such as in the framework of nuclear accidents). The selective removal of 137Cs and 90Sr ions from contaminated effluents is indeed crucial as they tend to be confused by bio-organisms with K+ and Ca2+, respectively, which possess similar solvation properties. Here, we consider the possibility to selectively filter these harmful radionuclides using ionic exchange in nanoporous silica27–29 as a promising alternative to classical liquid–liquid separation techniques. We first determine, by means of molecular simulations, ion adsorption at the charged surface of porous silica. We show that ion adsorption is relatively well accounted for by a modified Poisson–Boltzmann equation in which the potential of mean force is introduced for a single solvated ion near a silica surface. In contrast, owing to its mean-field nature, this simple model does not capture overscreening (i.e. overcompensation of the surface charge by the counterions) which is observed in our simulations as a result of ion–ion correlations and static localized surface charges considered in our model of porous silica. By simulating the electro-osmotic flow induced by an electric field, we study the effect of such overscreening on the transport properties of the confined electrolytes. The remaining part of this paper is organized into five sections. In Section 2 we discuss the preparation and details of our simulations. Equilibrium molecular dynamics results are shown in Section 3. A modified Poisson–Boltzmann model is presented and discussed in Section 4. We perform electro-osmotic flow simulations and apply a continuum model in Section 5. Finally, Section 6 summarizes our findings and conclusions.
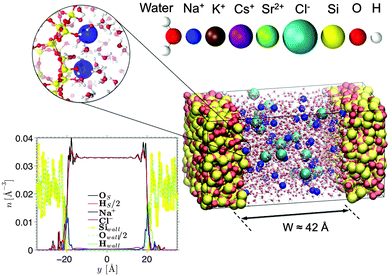
2 Computational methods
2.1 Models
Fig. 1 shows a typical molecular configuration of porous silica considered in this work. y is the axis perpendicular to the surface, defined as y = 0 located at the pore center. The procedure for the preparation of silica walls is described in detail elsewhere.30 In brief, a block of cristobalite is first melted at T = 4000 K. Using a simulated annealing technique, the material is then quenched until 300 K to reach an amorphous state at which the structure factor is validated against experimental measurements. A surface is created by cutting the silica block and removing the un-coordinated Si atoms, as well as the O atoms that are no longer connected to any Si atom. The dangling bonds of the O atoms at the surface are then saturated by adding an H atom to form a silanol group. As explained by Villemot et al.31 the number of OH bonds is adjusted to reach a final silanol density of 5OH nm−2 (based on the frontal surface area), which agrees well with experimental measurements.32 Following previous studies on porous silica,33,34 the surface roughness of the slit pore is determined by simulating small angle neutron scattering (Fig. S1 in the ESI†); a Porod exponent of ∼4 is found, indicating a smooth surface. This is confirmed by a small variation in the height of the oxygen atoms at the surface which has a standard deviation of 1.2 Å (although, as expected for glass, it is a bit larger than for cristobalite ∼0.7 Å). The size of our surface is 35.8 Å × 35.8 Å, which corresponds to 64 surface groups per wall. Some of these (1 out of 8) are deprotonated to create a negative surface charge density of σS = −0.1 C m−2. This surface charge in combination with an ionic strength of 0.6 M corresponds to a pH value of ∼7.0–8.0, depending on the electrolyte species. The walls are approximately 15 Å thick, which are chosen such that there is no notable effect of finite thickness on the interfacial fluid properties. Two silica walls are placed parallel to each other at a distance of approximately 42 Å in order to create a slit pore (the directions parallel to the walls are infinite thanks to the use of periodic boundary conditions). The distance between the walls is chosen to be sufficiently large so that the electric double layers from both walls are separated and the electro-osmotic flow velocity becomes independent of the channel width.Based on the approximate volume of the silica pore, 20 Cl− ions and 36 monovalent cations (or 18 divalent cations) are inserted into the channel to compensate the negative surface charge while reaching an average concentration of 0.6 M (mol L−1) (close to that of seawater). Water molecules, described using the TIP4P/2005 rigid model,35 are then added using Grand Canonical Monte Carlo (GCMC) simulations. This water model is selected as it has been shown to be successful in reproducing the transport properties of water.9,36 The number of water molecules in our systems ranges from 1736 for the CsCl system to 1822 for the SrCl2 system. GCMC simulations (constant chemical potential and temperature simulations in which the number of water molecules varies) are needed to prepare the confined electrolytes, as the number of water molecules does not scale exactly with the accessible volume. An interesting result of our GCMC simulations (not shown here) is that by making the surface more negatively charged and adding cations to compensate (thus reducing the volume accessible to water) the number of water molecules actually increases. This is explained by the ordering of water molecules around ions.
2.2 Molecular dynamics
MD simulations are performed using LAMMPS37 with a simulation time step of 1 fs. The fluid temperature is kept at 300 K via a Nosé–Hoover thermostat with a coupling time constant of 100 fs. Dispersion interactions are described using a Lennard-Jones potential, with a cutoff length of 10 Å and a tail correction to compensate for the truncated part. The particle–particle–particle–mesh (P3M)38 method is used to calculate electrostatic interactions, where we truncate the real part at 10 Å. The SHAKE algorithm is used to preserve the rigid structure of water molecules. The force field parameters optimized for the TIP4P/Ew water model by Joung and Cheatham are used for monovalent ions.39 The parameters for Na+ and Cl− have been confirmed to be transferable to TIP4P/2005 water,40 while transferability of the parameters for K+ and Cs+ is shown in Fig. S2 in the ESI.† The parameters recently presented by Mamatkulov et al. are used for strontium.41 These parameters have been optimized for SPC/E and shown to be transferable to TIP4P/2005.42 The Lorentz–Berthelot combination rules are used to calculate cross-species interactions, where the parameters for silica are taken from Lee and Rossky.43 The force field parameters are listed in Table SI in the ESI.† The polarizability is not included as electrostatic forces near hydrophilic charged surfaces are much larger than the polarization forces.23,44 It should be noted that possible charge transfer between the different cations and the oxygen atoms of the silica surface occurs to some limited yet non-negligible extent. However, considering that the force fields used in the present work rely on effective parameters, which are adjusted against available experimental data, they include in an implicit fashion this contribution. Similarly, these force fields include other contributions such as 3-body and 4-body interactions as well as polarizability, which correspond to the electron cloud response to the local electrical field created by other surrounding atoms. Overall, these other interactions, which contribute to a lesser extent to the total internal energy than the Coulombic and dispersive interactions, are usually omitted in molecular simulations of aqueous electrolyte solutions.2.3 Potential of mean force
A large adsorption energy of ions can make it difficult to sample phase space via equilibrium MD simulations. This applies also to a single ion near an uncharged wall (which will be considered in Section 4). We therefore use the Umbrella Sampling technique to efficiently calculate the free energy profile as a function of the position across the channel.45 This method deters the ion from being far from the position y0 (called a ‘sampling window’) by imposing an energy penalty as a function of the distance from this position. A short simulation is run to collect data on where the ion resides when subject to the imposed energy penalty. The position y0 is then shifted and the process is repeated several times. This eventually results in many histograms, each resulting from a simulation with a known energy bias. Using the weighted histogram analysis method (WHAM) the unbiased density of states (and thus the corresponding free energy profile) can be iteratively reconstructed from the histograms.46 We apply Umbrella Sampling using a harmonic energy bias with a spring constant of 0.12 eV Å−2 (1.95 N m−1). We use 60 sampling windows with a spacing of 0.75 Å. The sampling windows are located in the domain y ∈ [−22.125, 22.125], with y = 0 being at the center of the channel. The spring stiffness in combination with the width of the sampling windows results in partially overlapping histograms, which is needed for the reconstruction of the unbiased profile. The system is equilibrated for 200 ps after the bias potential is imposed. We subsequently collect data over the next 500 ps. We confirm that the equilibration time and the sampling time are sufficiently long. We also validate that the spring stiffness is large enough so that large energy barriers can be sampled accurately. This is done by performing Umbrella Sampling with an increased stiffness of 0.2 eV Å−2 and comparing the reconstructed energy profile. Furthermore, since the walls and the solvent are charge neutral, the single-ion system has a net charge equal to the charge of the ion. A correction is applied to the treatment of the electrostatic interactions to prevent artifacts in the energy and pressure due to non-neutrality of the simulation system.47The harmonic energy bias is applied in the direction normal to the walls, while ion movement in the other directions is suppressed. This is needed since the ion would otherwise drift to local energy minima at the surface. In order to capture the effect of the surface structure we probe the density of states (DoS) profiles ρ(y) at 9 randomly chosen x–z positions in front of the silica surface. Mapping each profile to the left half of the channel (y < 0) gives us p = 18 unique profiles since the structure of both walls is different. The potential of mean force (PMF) is then calculated from the arithmetic average of various DoS profiles as follows:
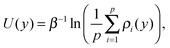 | (1) |
3 Molecular dynamics results
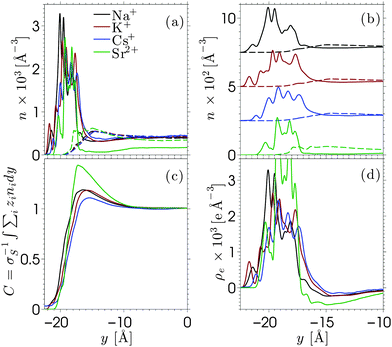
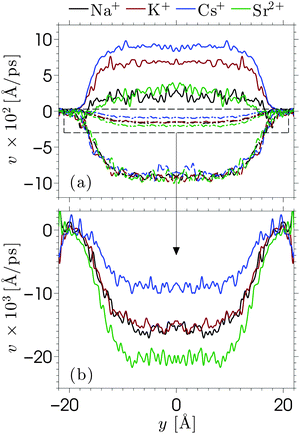
Equilibrium MD simulations are performed for 80 ns, the last 30 ns of which are used to accumulate statistics by storing data every 25 ps. As discussed in detail below, for each simulation, two different initial configurations are considered in which the ions are distributed near the center of the channel. Fig. 2 shows the number density profile of the different electrolyte solutions, where y = 0 corresponds to the center of the channel. Fig. 2a shows the ion number density profiles of the cations (full lines) and the chloride ions (dashed lines). These profiles are shifted vertically in Fig. 2b for the sake of clarity. Fig. 2c shows the charge screening factor, calculated as: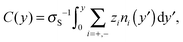 | (2) |
The ion density profiles in Fig. 2 show a dense layer of cations adsorbed at the negatively charged silica walls, while the anions are repelled by the walls. The adsorbed cations form the Stern layer in the classical model of the electric double layer (EDL).48 The thickness of the adsorbed layer is larger than the Debye length of the solution (λD ≈ 3 Å) and larger than the Lennard-Jones diameters of the cations (see Table SI in the ESI†). This is partially due to disorder at the surface, which induces broadening of the Stern layer. While the cation layer is located at a similar position for each electrolyte solution, it is slightly shifted towards the pore center as the cation size increases. The area under the strontium number density profile is smaller than that of the monovalent cations, since only half the number of divalent ions are needed to compensate the negative charges of silica and chloride ions.
For each electrolyte, next to the adsorbed layer, the confined electrolyte is partially depleted of cations while anions are in excess. Such overscreening occurs when the cations overcompensate the negative surface charge (i.e. C(y) > 1 in Fig. 2c), thus causing an effective positive surface near the silica surface. The transition between a positively and a negatively charged layer, which is often referred to as charge inversion (CI), is typically observed for multivalent electrolytes or concentrated monovalent electrolytes. Overscreening, which is mostly pronounced for SrCl2 followed by NaCl, KCl, and CsCl, increases with the charge density of the cations and the size asymmetry of the electrolytes.42 While the microscopic origins of overscreening remain poorly understood,49 Faraudo and Travesset50 explain that overscreening results from the correlation free energy between ions in the Stern layer, as well as from ion–wall correlations. The correlation free energy required to cause overscreening decreases strongly with increasing ionic strength. In other words, overscreening occurs typically above a critical ion concentration which is strongly dependent on the exact structure and hydrophilicity of the surface.20 Overscreening has even been shown to occur at millimolar concentrations of organic monovalent ions near a hydrophobic colloidal particle.51 The solvation free energy was said to be the dominant mechanism in this case, while this was also found to be the mechanism that prevented overscreening near a hydrophilic colloid in the same electrolyte solution. The experimental results suggest that overscreening for monovalent electrolytes (especially KCl and CsCl) near a silica surface occurs at larger concentrations than those considered here, while various computational studies find overscreening under conditions similar to ours.15,16,21,52–56 Several factors and uncertainties can be responsible for quantitative differences between experimental and theoretical studies. In the first place, from an experimental point of view, the critical concentrations at which overscreening occurs for monovalent ions are often very high and measuring electric properties at such large ionic strengths can lead to a significant dependence on the measurement technique.57,58 van der Heyden et al.52 introduced streaming current measurements as a new experimental approach to study overscreening. They measured the effective surface charge and the streaming current near a silica surface for monovalent, divalent, and trivalent electrolytes at concentrations up to 1 M. Their data confirmed that overscreening occurs above a critical concentration. The onset for CaCl2 and MgCl2 solutions in their system was located around 0.4 M. No charge inversion was observed for KCl (the only monovalent electrolyte considered in the study), but the data suggest that the onset of overscreening for KCl is not far above 1 M. These experiments give a good insight into the qualitative dependence on ion concentration and an indication of the concentrations at which overscreening could occur under the conditions of these experiments. However, a quantitative comparison with other studies remains challenging since values can depend for example on how the samples are prepared.
As for molecular simulations, the local properties of the electrolyte solution depend strongly on the ion concentration as well as the influence of confinement and the simulation model. An example of the effect of different force fields is given by Lorenz et al.,19 who compared the density distribution of CaCl2 near charged amorphous silica for different force fields and material preparation methods. Both simulations showed overscreening and almost the same charge inversion point but the distributions of cations in the Stern layer were significantly different. Considering that the force fields used in our work were developed to reproduce both the solvation free energy and activity of the ions,41 it can be assumed that they describe correctly the experimental solubilities in water. Ion precipitation at the surface, which leads to overscreening, can be seen as a surface solubility phenomenon in the spirit of recent studies on enhanced gas solubility in solvents confined in nanoporous media.59,60 To further confirm that overscreening observed in the present work is physical, we checked that the problem of accessible timescales in MD simulations does not affect our results. As briefly mentioned at the beginning of this section, each profile in Fig. 2 has been obtained from the average between two simulations with different initial configurations. The comparisons between the independent simulations are shown in Fig. S3–S5 in the ESI.† The two simulations show very good agreement for the monovalent electrolytes. We also run additional simulations in which Na+ and Cl− ions are initially distributed in a way that corresponds to no overscreening (these configurations are obtained from simulations in which the surface was homogeneously charged). We then relax the systems and determine the ion density profiles shown in Fig. S6 in the ESI.† From these additional simulations we find that each of them converges rapidly to a configuration that shows overscreening, which is consistent with the data shown in Fig. 2. The deprotonated silanol groups form highly preferable adsorption sites for the cations. The number of charge sites equals the number of excess cations in the system and we observe that almost each charge site forms a direct contact pair with at least one cation. Some additional cations might also adsorb (and thus overscreen the surface charge) at open spaces where the repulsion from other cations is small. As for SrCl2 (Fig. S5 in the ESI†), the two independent simulations converge to different yet similar and equivalent ion density profiles. The in-plane structure of the adsorbed cation layer shows that cations adsorb in different sites, due to the fact that there are fewer divalent cations than accessible sites. Once a divalent ion adsorbs to a deprotonated silanol group, it stays there for a long time due to the large binding energy. Averaging between multiple simulations (as was done in the present work) is a way to improve sampling for a system with ergodic hindrances.
4 Electrostatic model
The Poisson–Boltzmann (PB) equation is the combination of the Poisson equation, which relates the Laplacian of the electric potential ϕ to the distribution of charges n, and the Boltzmann distribution, which describes how the distribution of ions is related to the electric potential. The one-dimensional PB equation is given by: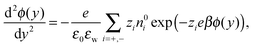 | (3) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) y·∇yϕ(wall) = −σS and ∇yϕ(0) = 0, where
y·∇yϕ(wall) = −σS and ∇yϕ(0) = 0, where ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) y = ±1 indicates the sign of the y-direction normal to the wall.
y = ±1 indicates the sign of the y-direction normal to the wall.
The PB equation successfully predict the charge distribution in systems with small ion concentrations, surface charge densities, and ion valencies, such as in the case of some colloidal systems or dilute electrolytes. On the other hand, systems with large charge concentration or surface charge densities give rise to effects that are generally not accounted for in the PB model. For instance, in situations with a large surface charge density, or large counter-ions: due to steric repulsions it might not be energetically preferable to screen the surface charge via a dense Stern layer. This results in ion crowding in a wider region near the surface.62 The PB equation does not account for this possibility, since information about the shapes and sizes of ions is not included. Similarly, ion-specific information is needed to explain specific (non-Coulombic) adsorption effects. Furthermore, electrostatic ion–ion correlations are typically very important in the case of ionic liquids or concentrated multivalent electrolytes. Finally, the boundary conditions described above require the surface charge to be located at a fixed location at the edge of the domain using which the differential equation is solved. However, in reality the charge is often discretely distributed among the sites on a rough surface and ions might penetrate into the amorphous matrix.
A rich variety of modified Poisson–Boltzmann (MPB) equations have been proposed in the literature, to predict ion distributions more accurately under certain conditions. Examples of modifications that have been studied in the literature are: the addition of ion specificity,63–65 the inclusion of electrostatic and non-electrostatic ion–ion correlations,66–68 and accounting for variations in the dielectric constant of the solvent.69,70 Most of these studies involved a model electrolyte near a flat wall. Here, our objective is to use a simple model that is capable of predicting the ion distribution near an amorphous discretely charged wall. The structure and charge distribution of the solid surface affect the effective ion–solid interaction. This now becomes dependent not only on the y-position of the ion (i.e. the position with respect to the center of the channel), but also on its lateral position relative to the wall. A number of other effects are important to accurately describe the fluid–solid interface. For example, when a solvated ion approaches the interface within a few angstroms, the hydration shell around the ion forms a resistance for the ion to approach the surface closer. Whether an ion and the surface remain separated by a solvent layer or a direct ion–surface contact is formed depends on the balance between the interactions between ions, water, and the surface.71 The balance between these competing interactions governs to what extent ion adsorption and the corresponding EDL are ion-specific or dependent on the surface properties. For example, hydrophilicity is known to have an influence on ion adsorption.20,51 Another interfacial effect that could be accounted for in a continuum model is the image force that an ion feels near the interface between two media with different dielectric constants, such as the silica–water interface. Attempts have been made to predict the effective adsorption energy by including each of these contributions individually in a model.69,72 However, this requires a large number of approximations and empirical quantities and has shown to be only moderately successful. Alternatively, we suggest to extend the PB model by including the Helmholtz free energy associated with a single solvated ion near a charge-neutral surface. The simulated ion distributions at finite ion concentration (see Fig. 2) are the results of the combined effect of ion-specific adsorption, ion–ion correlations, dielectric variations, and the surface charge density. By calculating the free energy profile for a single ion we investigate how important specific adsorption is for the ion distribution normal to the surface. Furthermore, the surface needs to be charge-neutral since the effect of the negative surface charge on the ion distribution is already accounted for via the boundary conditions. To express the free-energy in terms of a potential of mean force (PMF) we modify the Boltzmann distribution as follows:
ni = n0i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−zieβϕ − βUPMFi), exp(−zieβϕ − βUPMFi), | (4) |
The surface charge density can be expressed as an average accessible surface area per unit charge: 159 Å2 e−1, which is much larger than the specific charge area of cesium (8.9 Å2 e−1), the largest ion in our study. Therefore, steric effects between ions are assumed to be minor, while the influence of the ion size on the ion–surface energy is accounted for in the PMF. The low packing density of the ions in combination with low valencies suggests that electrostatic ion correlations will also not be dominant in our case. The presence of a (polar) solvent can affect the properties of the EDL since the dielectric tensor of the solvent varies locally. Dielectric variations are not explicitly taken into account in the MPB equation, but the solvent structure near the interface is indirectly included in the PMFs. However, since the PMFs are calculated near a neutral surface, the dielectric variations that are accounted for in our model do not include the effect that the surface charge has on the orientation of interfacial water molecules. Studies that include dielectric variations in the electrostatic model can be found in the literature.74–77
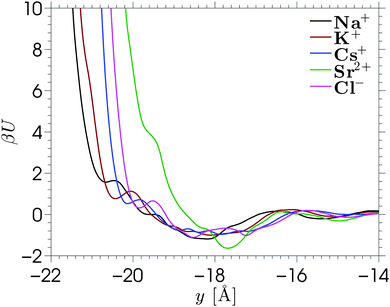
The single-ion PMFs, which are calculated using the Umbrella Sampling technique (see Section 2.3), are shown in Fig. 3 for each of the ion species considered in this work. Each of the PMFs shows a minimum around y = −18 Å. These minima are smooth and shallow compared to the free energy profiles corresponding to single x–z positions (shown in Fig. S7 in the ESI,† with further details shown in Fig. S8 and S9). The free energy converges to zero further from the wall, where the ion–wall interaction and the influence of the wall on the solvent structure are small. The profiles are calculated over the whole pore width, but the figure shows the interesting region near the silica surface. Very close to the wall the free energy asymptotes due to direct contact with wall atoms, leading to steric repulsions. The location of the free energy asymptotes for the monovalent cations shows an ordering based on the sizes of the ions (Na+ < K+ < Cs+), with the smallest ion approaching nearest to the silica surface. These PMFs overlap almost perfectly if they are shifted horizontally to the left by the Lennard-Jones radii of the respective ions, implying that we observe no size-selective penetration of pockets at the surface. The PMF corresponding to Sr2+ asymptotes further from the silica surface, despite the small ionic radius. This counterintuitive result is caused by the strong hydration shell of the divalent ion. Hence, the asymptote of this PMF corresponds to a solvent-separated contact, while direct contact with the silica surface would require a greater energy to sufficiently distort the hydration shell.
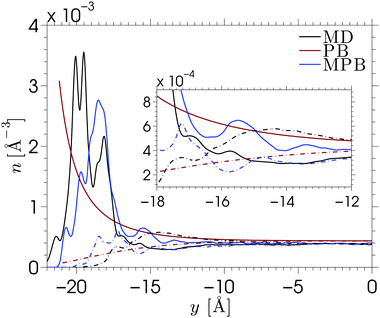
The MPB equation is solved for each of the electrolytes by substituting the PMFs corresponding to the cations and Cl− into eqn (4). We show the result corresponding to NaCl in Fig. 4. The results for other electrolyte solutions, which are qualitatively similar, can be found in Fig. S10 in the ESI.† Solutions of the conventional nonlinear Poisson–Boltzmann (PB) equation and the MPB model are compared against the MD simulation data for a surface charge density of σS = −0.1 C m−2. Fig. 4 shows the number density profiles of Na+ (full lines) and Cl− (dash-dotted lines). The inset of the figure shows a magnification of the diffuse part of the EDL. As expected, the PB density profiles show a diffuse regime in which the cation density decays monotonically towards the bulk density, while the anion density increases monotonically towards this value. The edge of the domain for the PB equation is chosen at ywall = −21.2 Å, which corresponds to the average y-position of the hydrogen atoms at the surface. While the actual location of the amorphous wall is ambiguous, the choice of the location of the edge of the domain (where the boundary condition is applied) has a strong effect on the solution of the standard PB equation.
The ion density profiles predicted by the MPB model show a much better agreement with the MD data for each of the electrolytes, especially for KCl and CsCl. Due to the addition of the PMFs, the cation density at the edge of the domain is now no longer the maximum value, instead a density peak is formed. This also allows us to locate the edge of the domain slightly further into the wall (ywall = −23 Å) to account for the fact that ions can penetrate the surface beyond the location of the surface groups. The figure shows that MPB reproduces the magnitude and location of the cation distribution near an amorphous wall. However, a few differences between the model and the MD simulations can be seen. The difference between the shape of the cation layer obtained from simulations and theoretical prediction is explained by the localized charges at the surface. The cations adsorb to the wall at energetically preferable locations, being at the charge sites. The one-dimensional mean-field theory does not account for the fact that the electrostatic energy near the wall varies across the x–z plane, and that ions are located where it is energetically favorable. Instead, MPB assumes that ions will be homogeneously distributed across the x–z plane. Similarly, in the calculation of the PMF it was assumed that each x–z position is equally probable (hence the arithmetic average of the densities of state). A different approach to solving the MPB problem would be to solve the model separately for each of the energy profiles (corresponding to different x–z positions) and the average between the solutions of the model. This would then allow for applying different boundary conditions to the different calculations, effectively providing a method to include the inhomogeneous distribution of the surface charge in the model. This approach is not attempted in the current work.
The predicted location of the cation density peak is a consequence of the balance between the free energy of a single ion near an uncharged wall and the electrostatic cation–wall attraction that enters the equation via the boundary conditions. Since the boundary condition is not directly applied at the fluid–solid interface, the electrostatic field that is felt in the channel will be slightly smaller when the boundary condition is applied closer to the fluid–solid interface. We find that the solution of the MPB is dominated by the PMF, such that the location of the edge of the domain has little influence on the density profiles. However, since the PMFs were calculated for single-ion systems, the prediction of the anion peak is based on the chloride–wall interaction, while in reality the adsorbed layer of cations would strongly affect the location of the anions in the electric double layer.‡ The fact that it is energetically preferable for the chloride ions to be located near the cation layer rather than near the silica surface shows important consequences for overscreening. Our MPB model is not able to account for this ion–ion effect. More generally, our model fails to predict overscreening since dielectric variations and electrostatic correlations are not taken into account. Nonlocal electrostatic correlations would enable the model to predict the partial depletion of cations and enhancement of anions directly adjacent to the Stern layer.16,78 Such corrections were not considered here since our main objective is to extend the simple mean-field theory to account for the specific adsorption at the rugged silica surface.
5 Electro-osmotic flow
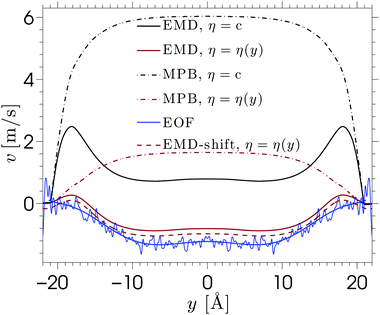
When an electric field E is applied to the confined aqueous electrolyte, a force fi = eziE acts on the ions, where zi is the valence of ion species i. Consequently, cations are accelerated in the direction of the field, and anions in the opposite direction. Ions create a fluid flow by dragging the surrounding water along, where the rate at which energy is transferred onto the water depends on the velocities of the ions as well as the interaction forces with the surrounding water molecules. The resulting electro-osmotic flow (EOF) profile is a product of the competing positive and negative contributions of ions to the flow. The electrolyte solutions in this study have an overall positive charge, which would suggest a net flow in the direction of the electric field. However, the adsorption of cations onto the silica surface causes many cations near the interface to be partially or fully immobilized (which means that these ions transfer less or no energy to the water), such that the effective flow velocity is not linearly proportional to the excess of positive charges present in the fluid. In fact, the ion mobility and density distribution in the EDL determine the EOF velocity (the velocity in the center of the channel), since the fluid beyond the EDL is charge-neutral and thus has no net contribution to the flow. Interestingly, this means that the EOF velocity is independent of the channel width, as long as the double layers of both channel walls are separated from each other (typically for concentrated solutions and/or large channels). The ion distributions in Fig. 2 showed that for our data charge-neutrality is reached approximately at 8 Å from the center of the channel.We apply an electric field Ex = −dϕ/dx = 0.2 V nm−1 in the positive x-direction. We have confirmed that the response to this field strength is still in the linear regime and that the flow velocity induced by this electric field remains very small compared to the velocity corresponding to thermal energy. A Nosé–Hoover thermostat, with a relaxation time of 100 fs, is coupled to the directions perpendicular to the electric field to ensure that the thermostat does not interfere with the streaming motion. We start from an equilibrium configuration and equilibrate the system for 10 ns with the field turned on. We then average over a steady state for another 100 ns by storing the data every 25 ps. Such long simulations are needed because the competing ion contributions result in a small EOF velocity and thus also a small signal-to-noise ratio.79 The cation, anion, and water velocity profiles are shown in Fig. 5. The statistical uncertainty in the data is of similar magnitude as the fluctuations in the profiles and thus omitted for clarity. The anion velocities are approximately the same for each of the electrolytes, while the cation velocities vary strongly between the different electrolytes. The cation velocities increase with their diffusivity in bulk water taken at similar ion concentration.42 This suggests that the ion migration in water is the key-mechanism for ion transport, even under the influence of an electric field. The water velocity profiles are in between the cation and anion profiles, with a total mass flux in the negative directions. The ordering of these profiles indicates that flow reversal is connected to overscreening, but this does not fully explain the EOF profiles. We have seen that the overscreening for NaCl is larger than for KCl, while their EOF velocity profiles are quite comparable. Ion-specific hydration properties and differences in the enhanced apparent viscosity effect for both simulation systems play a role. If we only consider the cations, the velocity profile corresponding to Na+ is larger than that of K+. However, the number of Na+ ions that contribute to the flow is slightly smaller due to stronger adsorption at the surface. Furthermore, fully hydrated Na+ has a smaller coordination number than K+ (6 and 7, respectively), but the binding strength with the surrounding water molecules is larger for Na+. All these factors contribute to some extent to the resulting EOF velocity.
Continuum theory can help to elucidate the effect of overscreening and viscosity enhancement on the electro-osmotic flow. The one-dimensional conservation of momentum equation for a system at the steady-state is given by the Stokes equation:
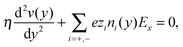 | (5) |
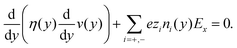 | (6) |
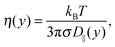 | (7) |
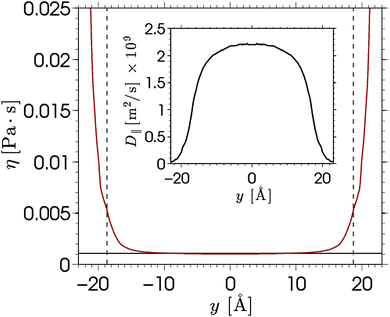
The viscosity near the wall increases with respect to the bulk value and shows an asymptote around y = ±22, which is beyond the point where any flow is observed in the EOF simulations (see Fig. 5). The velocity profile predicted from eqn (6) shows good qualitative agreement with the EOF velocity measured from the MD simulations. The large difference between the two predicted velocity profiles illustrates the effect that the local viscosity enhancement has on the electrokinetic flow velocity. Note that the predicted velocity profile is very sensitive to the viscosity profile, while an accurate calculation of a local viscosity profile is hard and controversial.81 Nevertheless, the effect that the enhanced viscosity has on the velocity profile is confirmed even when the viscosity profile is assumed to be a simple step function.70 So far, the only data used for the predicted velocity profile have been obtained from equilibrium MD simulations. Rather than using equilibrium MD data, we can solve eqn (5) and (6) using the density profiles predicted using the MPB equation. These results are also shown in Fig. 6. Since the MPB equation did not predict overscreening, the contribution of cations exceeds that of the anions everywhere across the channel. Therefore, the velocity is positive everywhere and monotonically increases towards the middle of the channel. Accounting for the enhanced viscosity effect decreases somewhat the positive contribution of the cations, but still it cannot capture the qualitatively different trend seen in the simulation data. These results illustrate the large effect that even a small amount of overscreening or viscosity enhancement has on the EOF velocity profile.
Further predictive improvement can be achieved if the location of the shear plane is known. This is the location at which the fluid velocity is zero, which is an important concept in experimental studies.§ This could serve as a boundary condition for eqn (6). The dashed line in Fig. 6 shows the predicted velocity profile shifted down such that its shear plane coincides with the one observed in the EOF simulations. This leads to very good agreement. Thus, the first layer of solvent and ions appear to be almost immobile.82 The fact that these immobile ions cannot transmit charges or momentum to the fluid strongly reduces, and even inverses, the electro-osmotic flow. This phenomenon can be modelled by a space-dependent viscosity, or by a traditional method which considers a specific location for the plane of shear. It should be noted that no slip occurs at the silica surface and stick boundary conditions can be applied for hydrophilic silica surfaces, as has been demonstrated using Poiseuille flow.14
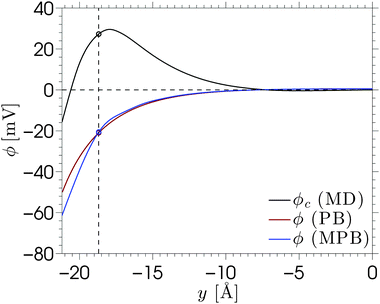
Another important quantity in electrokinetics is the ζ-potential, which represents the electric potential at the location of the shear plane. This quantity is typically derived from electrokinetic experiments by measuring the flow velocity uEOF in the bulk region of the channel and applying the Helmholtz–Smoluchowski (HS) equation:
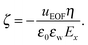 | (8) |
6 Conclusions
We have presented a study of ion adsorption and transport of aqueous solutions confined in an amorphous charged silica slit pore. The structure of the electric double layer was investigated, as well as its relationship with electro-osmotic flow. Theoretical models were presented to predict ion distributions and electro-osmotic velocity profiles. The results presented in this work have important implications for applications ranging from water purification to ion binding to biological membranes. Interesting insights into the dynamics of confined aqueous solutions can be gained from residence times at the pore surface as well as ion pair times. Such typical times, which usually fall in the range between [0.1–1 ns], are attainable using conventional MD simulations and can therefore be used to describe the physical origins at the heart of electrodynamics phenomena such as electroosmosis.Small differences between the adsorption and dynamical properties of confined electrolytes can potentially be used for applications in which ions need to be separated. We have presented a study of the structure and electrokinetic flow of four aqueous electrolyte solutions (NaCl, KCl, CsCl, and SrCl2) confined in charged amorphous porous silica. Our simulation results show a typical picture of overscreening in the electric double layer. The amount of overscreening is the greatest for SrCl2 and much smaller for the monovalent electrolytes NaCl > KCl > CsCl. This ordering is explained on the basis of the sizes and valencies of the cations. A larger ion charge density and localization of charges give rise to stronger correlations, which can lead to overscreening. Particular attention has been devoted to discussing the implications of large interaction energies between ions and surface charge sites. Strong ion binding can cause an ergodic hindrance when the energy barrier associated with unbinding is much larger than the thermal energy of an ion. It has been shown that the monovalent ions in our system do not suffer from such ergodic hindrances, while additional measures are needed to study the adsorption of Sr2+ at the charged silica surface. One of the possible measures is to perform multiple simulations which probe different sections of phase space. Averaging between these simulations gives a more reliable sampling of the true density of states. Another possibility is to use Monte Carlo simulations to equilibrate the system and validate our molecular dynamics results. However, equilibrating with MC suffers from some limitations; for instance, specific MC steps have to be developed in order to allow for collective redistributions which are crucial to equilibrate strongly correlated systems such as electrolyte solutions. Moreover, we note that the use of molecular dynamics in the present work would remain required for the study of transport properties.
A simple modified Poisson–Boltzmann model has been used to predict the adsorption of cations onto the negatively charged disordered silica surface. We have used the potential of mean force to add ion-specific information to the Poisson–Boltzmann model and at the same time account for the disordered structure of the silica surface. This approach has shown to be successful in predicting the location of the ions in the mean-field framework, while the in-plane structure caused by the localized surface charges is not captured by the one-dimensional equation.
Electro-osmotic flow simulations have shown that flow reversal occurs for each of the electrolytes. This is caused by a combination of overscreening and enhancement of the apparent viscosity in the electric double layer. The contributions of both phenomena to the electro-osmotic velocity become clear by comparing the solutions of continuum equations with different profiles for the viscosity and ion density. Small changes in the viscosity or density profiles have large consequences for the predicted electro-osmotic flow profile. Viscosity enhancement reduces the positive contribution to the velocity around the Stern layer, while overscreening contributes negatively to the velocity profile. Viscosity enhancement and overscreening also affect the ζ-potential. We have shown that the classical Helmholtz–Smoluchowski equation leads to a large under-prediction of the ζ-potential for our system, while the true value can be calculated from the ion density profiles.
Acknowledgements
This work has been funded by the French region Languedoc-Roussillon through the program “Chercheurs d'Avenir” (Benoit Coasne, 2011). We thank Lydéric Bocquet and Roland Netz for helpful comments.References
- B. Rotenberg and I. Pagonabarraga, Mol. Phys., 2013, 111, 827–842 CrossRef CAS.
- R. B. Schoch and P. Renaud, Appl. Phys. Lett., 2005, 86, 253111 CrossRef.
- J. Eijkel and A. van den Berg, Microfluid. Nanofluid., 2005, 1, 249–267 CrossRef CAS.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC.
- B. Coasne, A. Galarneau, R. J.-M. Pellenq and F. Di Renzo, Chem. Soc. Rev., 2013, 42, 4141–4171 RSC.
- D. Argyris, D. R. Cole and A. Striolo, J. Phys. Chem. C, 2009, 113, 19591–19600 CAS.
- D. Argyris, N. R. Tummala, A. Striolo and D. R. Cole, J. Phys. Chem. C, 2008, 112, 13587–13599 CAS.
- D. Argyris, D. R. Cole and A. Striolo, Langmuir, 2009, 25, 8025–8035 CrossRef CAS.
- A. P. Markesteijn, R. Hartkamp, S. Luding and J. Westerweel, J. Chem. Phys., 2012, 136, 134104 CrossRef CAS.
- Q. Zhang, K.-Y. Chan and N. Quirke, Mol. Simul., 2009, 35, 1215–1223 CrossRef CAS.
- A. A. Milischuk and B. M. Ladanyi, J. Chem. Phys., 2011, 135, 174709 CrossRef.
- A. A. Hassanali and S. J. Singer, J. Comput. – Aided Mater. Des., 2007, 14, 53–63 CrossRef CAS.
- A. A. Hassanali and S. J. Singer, J. Phys. Chem. B, 2007, 111, 11181–11193 CrossRef CAS.
- B. Siboulet, B. Coasne, J.-F. Dufreche and P. Turq, J. Phys. Chem. B, 2011, 115, 7881–7886 CrossRef CAS.
- H. Yoshida, H. Mizuno, T. Kinjo, H. Washizu and J.-L. Barrat, J. Chem. Phys., 2014, 140, 214701 CrossRef.
- I. Kalcher, J. C. F. Schulz and J. Dzubiella, J. Chem. Phys., 2010, 133, 164511 CrossRef.
- P. A. Bonnaud, B. Coasne and R. J.-M. Pellenq, J. Chem. Phys., 2012, 137, 064706 CrossRef.
- D. Argyris, D. R. Cole and A. Striolo, ACS Nano, 2010, 4, 2035–2042 CrossRef CAS.
- C. D. Lorenz, P. S. Crozier, J. A. Anderson and A. Travesset, J. Phys. Chem. C, 2008, 112, 10222–10232 CAS.
- P. E. Videla, J. Sala, J. Marti, E. Guardia and D. Laria, J. Chem. Phys., 2011, 135, 104503 CrossRef.
- H. Zhang, A. A. Hassanali, Y. K. Shin, C. Knight and S. J. Singer, J. Chem. Phys., 2011, 134, 024705 CrossRef.
- E. R. Cruz-Chu, A. Aksimentiev and K. Schulten, J. Phys. Chem. C, 2009, 113, 1850–1862 CAS.
- R. Renou, A. Ghoufi, A. Szymczyk, H. Zhu, J.-C. Neyt and P. Malfreyt, J. Phys. Chem. C, 2013, 117, 11017–11027 CAS.
- N. R. Haria and C. D. Lorenz, Phys. Chem. Chem. Phys., 2012, 14, 5935–5944 RSC.
- N. R. Haria and C. D. Lorenz, J. Phys. Chem. C, 2015, 119, 12298–12311 CAS.
- H. Chen, A. Z. Panagiotopoulos and E. P. Giannelis, Langmuir, 2015, 31, 2407–2413 CrossRef CAS.
- P. Weisz, CHEMTECH, 1973, 3, 498–505 CAS.
- J. L. Mertz, Z. H. Fard, C. D. Malliakas, M. J. Manos and M. G. Kanatzidis, Chem. Mater., 2013, 25, 2116–2127 CrossRef CAS.
- A. Sachse, A. Merceille, Y. Barré, A. Grandjean, F. Fajula and A. Galarneau, Microporous Mesoporous Mater., 2012, 164, 251–258 CrossRef CAS.
- B. Coasne, L. Viau and A. Vioux, J. Phys. Chem. Lett., 2011, 2, 1150–1154 CrossRef CAS.
- F. Villemot, A. Galarneau and B. Coasne, J. Phys. Chem. C, 2014, 118, 7423–7433 CAS.
- L. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38 CrossRef CAS.
- S. Bhattacharya, B. Coasne, F. R. Hung and K. E. Gubbins, Langmuir, 2009, 25, 5802–5813 CrossRef CAS.
- B. Coasne and P. Ugliengo, Langmuir, 2012, 28, 11131–11141 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS.
- D. Rozmanov and P. G. Kusalik, J. Chem. Phys., 2012, 136, 044507 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer simulation using particles, Taylor & Francis, Inc., Bristol, PA, USA, 1988 Search PubMed.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2009, 113, 13279–13290 CrossRef CAS.
- F. Moucka, M. Lisal and W. R. Smith, J. Phys. Chem. B, 2012, 116, 5468–5478 CrossRef CAS.
- S. Mamatkulov, M. Fyta and R. R. Netz, J. Chem. Phys., 2013, 138, 024505 CrossRef.
- R. Hartkamp and B. Coasne, J. Chem. Phys., 2014, 141, 124508 CrossRef.
- S. H. Lee and P. J. Rossky, J. Chem. Phys., 1994, 100, 3334–3345 CrossRef CAS.
- T. A. Ho and A. Striolo, J. Chem. Phys., 2013, 138, 054117 CrossRef.
- G. Torrie and J. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- S. Bogusz, T. E. Cheatham and B. R. Brooks, J. Chem. Phys., 1998, 108, 7070–7084 CrossRef CAS.
- R. B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839–883 CrossRef CAS.
- J. Lyklema, Colloids Surf., A, 2006, 291, 3–12 CrossRef CAS.
- J. Faraudo and A. Travesset, J. Phys. Chem. C, 2007, 111, 987–994 CAS.
- C. Calero, J. Faraudo and D. Bastos-González, J. Am. Chem. Soc., 2011, 133, 15025–15035 CrossRef CAS.
- F. H. J. van der Heyden, D. Stein, K. Besteman, S. G. Lemay and C. Dekker, Phys. Rev. Lett., 2006, 96, 224502 CrossRef.
- M. Chen, D. Jiang, K. Jiang and Y. Qiu, Proc. – Inst. Mech. Eng., 2014, 1–4 Search PubMed.
- R. Qiao and N. R. Aluru, Phys. Rev. Lett., 2004, 92, 198301 CrossRef CAS.
- Y. Chen, Z. Ni, G. Wang and D. Xu, Li, Nano Lett., 2008, 8, 42–48 CrossRef CAS.
- S. Dewan, V. Carnevale, A. Bankura, A. Eftekhari-Bafrooei, G. Fiorin, M. L. Klein and E. Borguet, Langmuir, 2014, 30, 8056–8065 CrossRef CAS.
- G. Hurwitz, G. R. Guillen and E. M. Hoek, J. Membr. Sci., 2010, 349, 349–357 CrossRef CAS.
- A. Szymczyk, P. Fievet, M. Mullet, J. Reggiani and J. Pagetti, J. Membr. Sci., 1998, 143, 189–195 CrossRef CAS.
- L. N. Ho, S. Clauzier, Y. Schuurman, D. Farrusseng and B. Coasne, J. Phys. Chem. Lett., 2013, 4, 2274–2278 CrossRef CAS.
- S. Clauzier, L. N. Ho, M. Pera-Titus, D. Farrusseng and B. Coasne, J. Phys. Chem. C, 2014, 118, 10720–10727 CAS.
- C. Vega and J. L. F. Abascal, Phys. Chem. Chem. Phys., 2011, 13, 19663–19688 RSC.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef.
- I. Borukhov, D. Andelman and H. Orland, Electrochim. Acta, 2000, 46, 221–229 CrossRef CAS.
- D. M. Huang, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2007, 98, 177801 CrossRef.
- L. Joly, C. Ybert, E. Trizac and L. Bocquet, Phys. Rev. Lett., 2004, 93, 257805 CrossRef.
- M. Jardat, J.-F. Dufreche, V. Marry, B. Rotenberg and P. Turq, Phys. Chem. Chem. Phys., 2009, 11, 2023–2033 RSC.
- I. Kalcher, J. C. F. Schulz and J. Dzubiella, Phys. Rev. Lett., 2010, 104, 097802 CrossRef.
- M. Boström, F. W. Tavares, D. Bratko and B. W. Ninham, J. Phys. Chem. B, 2005, 109, 24489–24494 CrossRef.
- P.-A. Cazade, R. Hartkamp and B. Coasne, J. Phys. Chem. C, 2014, 118, 5061–5072 CAS.
- D. J. Bonthuis and R. R. Netz, Langmuir, 2012, 28, 16049–16059 CrossRef CAS.
- E. Leontidis, M. Christoforou, C. Georgiou and T. Delclos, Curr. Opin. Colloid Interface Sci., 2014, 19, 2–8 CrossRef CAS.
- D. M. Huang, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Langmuir, 2008, 24, 1442–1450 CrossRef CAS.
- D. Frydel and Y. Levin, J. Chem. Phys., 2012, 137, 164703 CrossRef.
- A. Ghoufi, A. Szymczyk, R. Renou and M. Ding, Europhys. Lett., 2012, 99, 37008 CrossRef.
- V. Ballenegger and J.-P. Hansen, J. Chem. Phys., 2005, 122, 114711 CrossRef CAS.
- D. J. Bonthuis, S. Gekle and R. R. Netz, Phys. Rev. Lett., 2011, 107, 166102 CrossRef.
- J. Sala, E. Guardia and J. Marti, J. Chem. Phys., 2010, 132, 214505 CrossRef CAS.
- Y. Rosenfeld, Phys. Rev. Lett., 1989, 63, 980–983 CrossRef CAS.
- R. Qiao, Microfluid. Nanofluid., 2007, 3, 33–38 CrossRef CAS.
- M. Předota, P. T. Cummings and D. J. Wesolowski, J. Phys. Chem. C, 2007, 111, 3071–3079 Search PubMed.
- R. Hartkamp, A. Ghosh, T. Weinhart and S. Luding, J. Chem. Phys., 2012, 137, 044711 CrossRef.
- B. Siboulet, J. Molina, B. Coasne, P. Turq and J.-F. Dufreche, Mol. Phys., 2013, 111, 3410–3417 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Force field parameters and additional graphs to support our findings. See DOI: 10.1039/c5cp03818a |
| ‡ To demonstrate this point we show in Fig. S11 in the ESI† the free energy profiles of the ions calculated from MD simulations. The chloride free energy profiles asymptote further from the wall than in Fig. 3. |
| § Note that there could be additional positions with zero streaming velocity, located between the cation and anion layers moving in opposing directions. This might be expected in the case of concentrated multivalent electrolytes. |
| This journal is © the Owner Societies 2015 |