Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unraveling the complexity of protein backbone dynamics with combined 13C and 15N solid-state NMR relaxation measurements†
Jonathan M.
Lamley
a,
Matthew J.
Lougher
a,
Hans Juergen
Sass
b,
Marco
Rogowski
b,
Stephan
Grzesiek
b and
Józef R.
Lewandowski
 *a
*a
aDepartment of Chemistry, University of Warwick, Coventry CV4 7AL, UK. E-mail: j.r.lewandowski@warwick.ac.uk
bBiozentrum, University Basel, 4056 Basel, Switzerland
First published on 17th July 2015
Abstract
Typically, protein dynamics involve a complex hierarchy of motions occurring on different time scales between conformations separated by a range of different energy barriers. NMR relaxation can in principle provide a site-specific picture of both the time scales and amplitudes of these motions, but independent relaxation rates sensitive to fluctuations in different time scale ranges are required to obtain a faithful representation of the underlying dynamic complexity. This is especially pertinent for relaxation measurements in the solid state, which report on dynamics in a broader window of time scales by more than 3 orders of magnitudes compared to solution NMR relaxation. To aid in unraveling the intricacies of biomolecular dynamics we introduce 13C spin–lattice relaxation in the rotating frame (R1ρ) as a probe of backbone nanosecond-microsecond motions in proteins in the solid state. We present measurements of 13C′ R1ρ rates in fully protonated crystalline protein GB1 at 600 and 850 MHz 1H Larmor frequencies and compare them to 13C′ R1, 15N R1 and R1ρ measured under the same conditions. The addition of carbon relaxation data to the model free analysis of nitrogen relaxation data leads to greatly improved characterization of time scales of protein backbone motions, minimizing the occurrence of fitting artifacts that may be present when 15N data is used alone. We also discuss how internal motions characterized by different time scales contribute to 15N and 13C relaxation rates in the solid state and solution state, leading to fundamental differences between them, as well as phenomena such as underestimation of picosecond-range motions in the solid state and nanosecond-range motions in solution.
Introduction
Slow motions occurring on the nanosecond to millisecond time scale are often fundamental to protein function.1 Solid-state NMR relaxation measurements provide an attractive method for extracting quantitative information about such motions.2–8 Specifically, the time scales and amplitudes of ns-ms internal motions are theoretically accessible through the measurement of site-specific spin–spin (R2) relaxation rates obtained in the solid state, which could thus provide a powerful tool to complement dynamical information available from solution studies, where the time scale of motions accessible with relaxation is limited by the correlation time of overall molecular tumbling. In practice, however, the measurement of R2 rates in solids is difficult, as typically the measured decay rate of the transverse magnetization in a spin echo experiment (R2′ = 1/T2′) is dominated by coherent contributions (e.g. dipolar dephasing from strongly coupled protons9), even in perdeuterated samples where the dense proton networks are diluted with deuterium spins.4 In order to gain insights into dynamic transformations of biomolecules it is the incoherent R2 (in this work referred to simply as the transverse relaxation rate) that is required, which is purely due to the stochastic modulation of local fields by molecular motion.In solution, in the presence of chemical exchange, on-resonance R1ρ (spin–lattice relaxation rate in the rotating frame, R1ρ = 1/T1ρ) is a sum of pure R2 relaxation and a scaled exchange contribution. Variation of the spin-lock field strength in R1ρ experiments can be used to quantify microsecond motions in solution.10 In the solid state, it has been demonstrated for amide 15N that a spin-lock field of greater strength, in combination with a magic angle spinning (MAS) frequency of more 45 kHz, may be used to decouple both the exchange contribution and any contributions from coherent processes, and hence an R1ρ measurement can provide a reliable estimate of incoherent R2.4 It is straightforward to carry this out in a site-specific manner even in fully protonated protein samples without additional heteronuclear decoupling.4 The R1ρ coherent residual is also significantly reduced in perdeuterated samples where the 1H–1H network is diluted.3,11,12 Measurements of 15N R1ρ as a function of the spin lock nutation frequency can be also used to monitor the contribution from exchange processes in solids: at spinning frequencies ≥60 kHz, reliable 15N R1ρ relaxation dispersion can be obtained for nutation frequencies greater than ∼8 kHz in fully protonated proteins4 and also for lower nutation frequencies in perdeuterated proteins with or without additional dilution of the exchangeable proton sites.12,13
Analysis of site-specific values of 15N R1ρ measured in [U-13C,15N]GB1 at a single spin-lock field strength yielded order parameters and correlation times for backbone N–H vector motions, although the overall order parameters found were systematically higher than those measured using relaxation times in the solution state, if a single time scale was assumed for each amide nitrogen.4,1415N R1ρ values obtained in a similar fashion were also recently used to quantify site specific motions in Anabaena Sensory Rhodopsin.15 Recently, a comparison of molecular dynamics (MD) simulations and 15N relaxation measurements in GB1 showed that the order parameters are often dominated by slow motions and that 15N R1 (spin–lattice relaxation rates) and R1ρ may not be sufficient to effectively constrain the complex models required for a realistic description of protein dynamics in the solid state.16 In general, consideration of 15N relaxation alone may lead to an underestimation of the extent of backbone protein dynamics.14 Additional relaxation parameters from 13C nuclei may thus provide further valuable constraints for motional models. In particular, 13C′ rates are sensitive to backbone motions with fluctuations (rotations) occurring about an axis parallel to N–H dipolar vectors, which are not detected by 15N relaxation measurements. 13C relaxation parameters can also provide information on side chain motions,17 which play crucial roles in protein–protein interactions. This information should be highly complementary to 15N side chain measurements that are limited to a few specific residue types such as glutamine and asparagine, which have been used to probe intermolecular interfaces in fibrils.18
Previously, Lewandowski et al. presented an approach for measuring site-specific 13C spin–lattice (R1) relaxation rates in fully protonated [U-13C]-labeled proteins under >60 kHz spinning frequency conditions, which significantly reduce the averaging of the relaxation rates between different sites due to proton-driven spin diffusion.1913C′ R1 rates measured under such conditions may be used to quantify fast and slow protein motions. However, even though the dipolar 13C–13C contribution to 13C R1 rates in [U-13C]-labeled proteins is sensitive to slower (ns–μs) motions (as the expression for 13C R1 involves the J(ωC1 − ωC2) ≈ J(0) spectral density20) other independent 13C relaxation probes are desirable for achieving reliable quantitative analysis of slow dynamics.
In this manuscript we demonstrate the feasibility of measuring site-specific 13C′ R1ρ relaxation rates as a method to probe backbone motions on ps–μs time scales in proteins in the solid state, and show how in combination with 13C′ R1 and 15N R1 and R1ρ measurements they may be used to quantitatively characterize those motions. The methodology presented should aid in constraining models for slow motions in proteins, and also pave the way for considering the directionality of motions.15,21 The results that follow are organized into 5 subsections: in section (i) we investigate the validity of our method by evaluating the extent to which the coherent contributions to the measured 13C R1ρ rates are averaged under typical experimental conditions. In section (ii), we present a comprehensive range of 13C′ and 15N relaxation rate measurements in crystalline [U-13C,15N]GB1 at 600 and 850 MHz 1H Larmor frequencies. We quantify these rates in sections (iii) and (v) using models of increasing complexity. The intriguing results of the simplest model free analysis in section (iii) lead to a discussion in section (iv) on how motions with different time scales contribute to relaxation rates in the solid and solution states, highlighting fundamental differences in how dynamics influence measurements in the two phases. Our exploration provides us with hints to understanding such phenomena as the observation of very high order parameters when analyzing relaxation rates in the solid state and underestimation of nanosecond motions in solution.
Results and discussion
(i) Evaluation of coherent contributions to R1ρ
Measured R1ρ relaxation rates potentially reflect not only the effect of incoherent motions, but also contributions from anisotropic NMR interactions (e.g. dipolar couplings) that might not be completely removed by the magic angle spinning. We first consider the magnitudes of contributions to measured R1ρ rates that originate from such coherent mechanisms, and the degree to which they might hamper extraction of the parameters needed for characterization of molecular motions.Since for the 13C′ nucleus the interactions contributing to the coherent residual are different from those in the previously considered case of 15N,4 it is important to assess the extent to which they are averaged under typical experimental conditions. The coherent contribution depends on the geometry of the molecular system and the extent of the MAS and radio frequency (r.f.) averaging (e.g. faster MAS frequencies lead to better averaging of the coherent residuals). For the same experimental set-up and similar sample geometries, the coherent contribution to 13C R1ρ should be similar and therefore an estimate of an upper limit for this contribution under fast MAS should be obtainable from non-hydrated crystalline amino acids. Crystalline amino acid samples have similar internuclear geometries to proteins but the backbone motions and thus the relaxation rates are minimized.
To obtain such an estimate, on-resonance 13C R1ρ rates in [U-13C]glycine were measured at ωr/2π = 60 kHz and ω0H/2π = 600 MHz. Example decay curves for 13C′ and 13Cα (with a spin-lock pulse nutation frequency of ω1/2π = 17 kHz) are shown in Fig. 1 (inset). Note that in both cases the magnetization decays very little in 0.5 s, the length of the longest employed spin-lock pulse (data points were not sampled at longer spin-lock lengths due to hardware limitations). The main panel of Fig. 1 shows the dependence of the measured R1ρ rates upon the nutation frequency of the spin-lock pulse, again for both 13C′ and 13Cα. Among the different types of carbon sites in proteins, we expect the CH2 group to have the largest coherent contribution to 13C transverse magnetization decay because of the strong proton–proton couplings present and the lack of efficient motional averaging (this is also reflected in methylene carbons being the most difficult type of carbon site geometry to decouple from protons). Even so, R1ρ rates for CαH2 in glycine plateau at a value of just 0.18 ± 0.01 s−1 (T1ρ = 5.68 ± 0.32 s) for 13C nutation frequencies above ∼12 kHz. In the case of 13C′, where there are no directly bonded protons, the measured R1ρ becomes 0.06 ± 0.01 s−1 at nutation frequencies above ∼9 kHz, corresponding to an exceptionally long T1ρ of 16.7 ± 2.8 s. This means that even in the “worst case” of the CH2 group, if the decay of transverse magnetization was purely the result of coherent processes then the coherent residual for protonated 13C would have an upper limit of only ∼0.18 s−1 at 600 MHz 1H Larmor frequency. Similarly, for 13C′, the residual of 0.06 s−1 is virtually negligible (e.g. <1% of the measured 13C′ average R1ρ in [U-13C,15N]GB1, see below). This suggests that much greater decay rates measured in proteins (see below) are primarily determined by contributions induced by stochastic motions. Note that the increasing R1ρ values for nutation frequencies <8 kHz are most likely in large part due to inadequately decoupled coherent contributions. Nevertheless, the rates at a nutation frequency of 2 kHz do not exceed 2.5 s−1, which means that for cases where the exchange contributions to the rates are much larger than that value, relaxation dispersion may provide at least qualitative information about exchange processes.
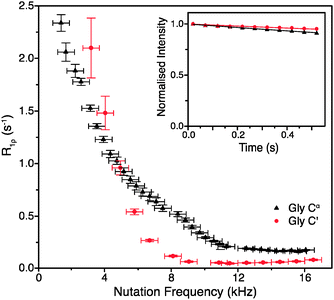 | ||
| Fig. 1 R 1ρ dispersion for 13C′ (red circle) and 13Cα (black triangle) in [U-13C,15N]glycine at ω0H/2π = 600 MHz, ωr/2π = 60 kHz, and (inset) example R1ρ decay curves for with ω1/2π = 17 kHz. | ||
Obviously, the observed R1ρ rates in amino acids such as glycine are not entirely due to coherent processes. In crystalline amino acids the dominant motional contribution to 13C′ relaxation originates from the rotations of CH3 and NH3 groups that modulate 1H–13C′ dipolar couplings.22 As the minimal 1H–13C′ distance for both CH3 and NH3 groups is ∼2.4 Å in glycine and alanine (and indeed the sum of all the dipolar couplings from protons <5 Å from 13C′ is almost the same), the correlation time (τc) of the motions should be the main differentiating factor between the relaxation behaviors of 13C′ in these amino acids.22 The correlation time of NH3 rotation in crystalline glycine at room temperature is shorter (∼0.9 ns) than the correlation times of the rotations of both CH3 and NH3 groups in crystalline alanine: τc for CH3 is ∼1.6 ns, while for NH3τc is orders of magnitude greater.22 The slower motions of the CH3 and NH3 groups in alanine are expected to cause faster 13C′ transverse relaxation than the more rapid rotation of the NH3 group in glycine. Comparison of the R1ρ values measured for 13C′ in these two amino acids therefore allows further assessment of the coherent and relaxation contributions to the decay of transverse 13C′ magnetization under fast MAS conditions.
As expected from the slower correlation times for rotation of CH3 and NH3 groups, the measured R1ρ′s are larger for alanine than for glycine under the same conditions, further confirming that the measured rates are almost exclusively due to relaxation induced by molecular motions. At ω0H/2π = 600 MHz, ωr/2π = 60 kHz and ω1/2π = 16 kHz, the on-resonance 13C′ R1ρ rate for [1-13C]alanine was measured at 0.83 ± 0.07 s−1 (T1ρ = 1.2 ± 0.1 s), which is 14 times larger than the value for glycine 13C′. Note that since the R1ρ rates observed in glycine can be quite well accounted for by the relaxation induced by the incoherent motion of NH3 (for example, for a correlation time of 0.9 ns and an order parameter of 0.65, 13C′ and 13CαR1ρ calculated using a simple model free approach are 0.18 and 0.06 s−1 respectively, i.e. the same as the measured rates), the coherent residuals are in reality even smaller than the values quoted above. An interesting side note is that the measured R1ρ of 0.18 s−1 for CH2 in glycine should correspond to R2′ (minus the exchange contribution) under perfect heteronuclear decoupling conditions. Currently the smallest reported R2′ for CH2 in glycine measured using 400 kHz SPINAL decoupling is ∼4 s−1,23 which is still >20 times larger than the R1ρ measured in this study. This result suggests that, even though it may be difficult to achieve, there is still plenty of room for improvement in heteronuclear decoupling methodology before the relaxation limit for coherence lifetimes is reached.
It should be noted that at rotary resonance and HORROR conditions (ωrf = nωr and ωrf = ωr/2 respectively, n = 1, 2) the coherent residual will be much larger (leading to a faster decay) due to the reintroduction of chemical shift anisotropy (CSA) and/or dipolar couplings. The experimental settings that match these conditions should either be avoided, if one is interested in the pure relaxation contribution,11,21,24,25 or the effect should be taken directly into account.12 As shown for the 15N nucleus, larger R1ρ values are also observed at lower spinning frequencies due to less effective MAS averaging of the coherent residual in protonated samples (Fig. S1, ESI†).
In summary, in order to minimize the coherent contribution and obtain a reliable estimate of the incoherent R2 for 13C (including carbons with directly bonded protons) from R1ρ measurements in fully protonated samples, experiments should be performed at spinning frequencies >45 kHz and employing spin-lock fields of >10 kHz with a reasonable offset from the rotary resonance and HORROR conditions. Additional experimental considerations of “mis-setting” the magic angle (small effect on the measured rate), sample heating (again moderate effect) and polarization transfer during r.f. irradiation (no significant polarization transfer due to either r.f. driven spin diffusion or isotropic mixing are observed) are addressed in the ESI† (see Fig. S2–S4).
(ii) Measurement of 13C′ and 15N R1 and R1ρ relaxation rates
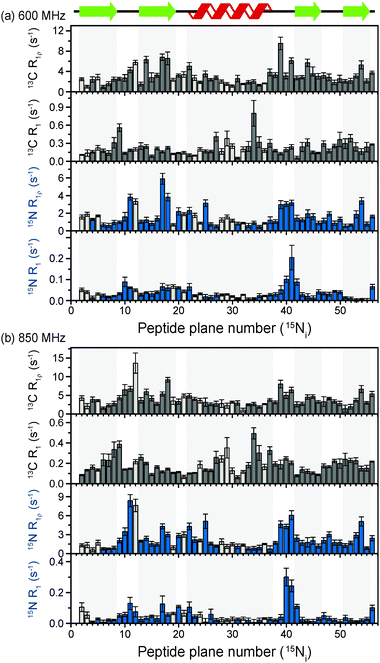
The above discussion suggests that in hydrated proteins in the solid state, R1ρ rates for each individual 13C′ atom in the backbone may be measured in order to build up a dynamic picture of the molecule that should be highly complementary to that emerging from 15N measurements. In this spirit, we measured site-specific 13C′ R1ρ for fully protonated, hydrated microcrystalline [U-13C,15N]GB1 at ω0H/2π = 850 MHz and 600 MHz, with ωr/2π = 60 kHz, ω1/2π = 17 kHz, and a sample temperature of 27 °C. The microcrystalline protein sample was prepared as described previously.26 In order to enhance spectral resolution the effect of one-bond C′–Cα scalar couplings was eliminated in these experiments by including an S3E block in the pulse sequence.27,28 The measured rates are shown in Fig. 2, along with 13C′ R1 and amide 15N R1 and R1ρ measured at both fields under the same experimental conditions. All of the rates are plotted against the number of the peptide plane containing the particular 13C or 15N nucleus (e.g. peptide plane 2 refers to 15N in residue 2 and 13C′ in residue 1). Rates flagged in light gray were extracted from resonances with partial overlap (see spectrum in Fig. S5 for assignments, ESI†) and thus are likely to be less accurate than those derived from fully resolved peaks. Tabulated values for the fit parameters for 13C′ and 15N R1ρ and R1 relaxation curves for all resonances are given in the ESI.† Table S3 (ESI†) (the average rates for 850 and 600 MHz are, respectively, 13C′ R1 0.1 & 0.2 s−1, 13C′ R1ρ 4.2 & 3.2 s−1, 15N R1 0.05 & 0.04 s−1, 15N R1ρ 2.3 & 1.6 s−1).Upon inspection of Fig. 2 it is immediately obvious that, at both fields, the measured 13C′ R1ρ rates and the differences between them across different residues are one to two orders of magnitude greater than the upper limit of the coherent contribution as given by the measurement on glycine at 600 MHz (0.06 ± 0.01 s−1). The rates measured in the protein are evidently almost exclusively due to relaxation induced by molecular motions. It is also clear that there is a strong correlation between rates at different fields, and generally the same features are present in both sets of data. For example, elevated rates are seen in the flexible loop and terminal regions (e.g. T11C′ with R1ρ = 14.6 ± 2.9 s−1 at ω0H/2π = 850 MHz), while generally lower rates are observed in the α-helix and the central residues in β-strands with a minimum of 1.6 ± 0.4 s−1 for L5C′ at ω0H/2π = 850 MHz. Our generous estimate for the upper bound of the coherent residual at ω0H/2π = 600 MHz is in fact more than 11–14 times smaller than the mean experimental error in 13C′ R1ρ (0.68 s−1 at ω0H/2π = 850 MHz and 0.84 s−1 at ω0H/2π = 600 MHz).
While R1ρ and R1 rates for both 15N and 13C vary significantly between residues, many features along the backbone are common between them (in particular for the 15N and 13C located in the same peptide planes, i.e.15Ni and 13Ci−1′, which is expected due to the rigid planar nature of the peptide bond). On the other hand, some features are apparent in the R1 rates that are not present in the R1ρ rates (e.g. a marked increase in 13C R1 at Y33C′). This is likely due to the different dependence of these relaxation rates on the time scales of the motions causing the relaxation. Further analysis of these phenomena is carried out in the following sections via quantitative modeling.
(iii) Quantification of 13C′ and 15N relaxation rates using the simple model free approach
To explore the influence of backbone dynamics on 15N and 13C′ relaxation data in greater depth, in the following we fit our data to simple and extended model free formalism (see below). Nuclear relaxation originates from fluctuations of local magnetic fields, caused by modulation of interactions (e.g. dipolar couplings or CSA) by incoherent molecular motions. Quantitative modeling of 13C′ relaxation is potentially more complex than that of 15N owing to a larger number of interactions that must be included in the modeling. Whereas 15N relaxation is dominated by a dipolar contribution (but with a substantial contribution from the CSA mechanism at higher fields), 13C′ relaxation, even though dominated by the CSA, may require consideration of several other contributions. For example, multiple dipolar contributions including those from Cα, N and nearby protons may need to be included depending on the desired precision of modeling. In particular, slow fluctuations of the dipolar C′–Cα vector may contribute significantly to spin–lattice relaxation, as this depends on the spectral density sampled near zero frequency which increases monotonically with the increasing correlation time of the motions. Under the conditions employed in this study the ratios between the spin-lock field strengths and frequency offsets were such that the tilt angle did not exceed 4° even at 850 MHz. The rates are therefore analyzed here as on-resonance R1ρ (though the effect could be easily included).The main contributions to 15N R1 and R1ρ are the dipolar 15N–1H and 15N CSA contributions:
| R1,N = R1,NH + R1,NCSA | (1) |
| R1ρ,N = R1ρ,NH + R1ρ,NCSA | (2) |
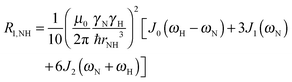 | (3) |
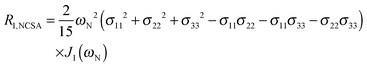 | (4) |
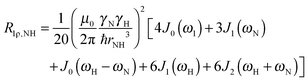 | (5) |
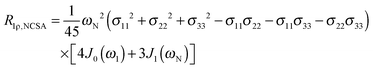 | (6) |
The main contribution to 13C′ R1 and R1ρ is the 13C′ CSA contribution
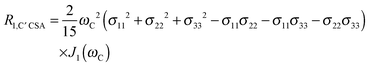 | (7) |
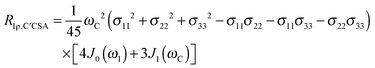 | (8) |
A specific form of the spectral density J(ω) (i.e. the Fourier transform of the correlation function describing the time dependence of local magnetic field fluctuations) needs to be assumed to compute relaxation rates. In the first instance, neglecting any orientational dependence of the relaxation rates, we assume the simplest case of isotropic motion occurring on a single time scale. Accordingly, to model the relaxation rates we use the simple model free (SMF)33,34 formalism with spectral densities expressed as
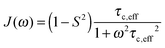 | (9) |
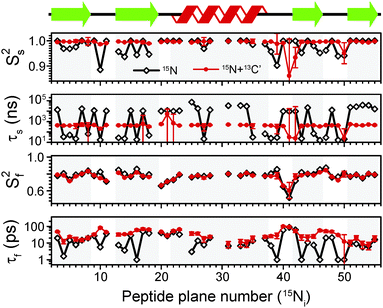
The results of the analysis of our relaxation rates using the SMF form of the spectral density, when 15N and 13C′ R1 and R1ρ relaxation rates are considered separately, are presented in Fig. 3. The S2 values determined from 13C′ and 15N data follow similar trends but the SC′2 values are on average lower than SNH2 by a factor of >0.2 (Fig. 3b). The largest deviations from the overall trend are generally observed for the residues in the loops or edges of the secondary structure elements, e.g. peptide planes 35 to 40.
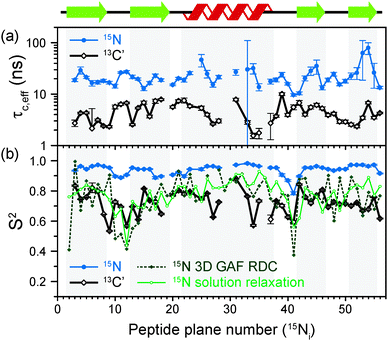 | ||
| Fig. 3 Comparison of results from a simple model free (SMF) analysis of backbone motions in GB1 based on measured 15N and 13C′ R1ρ and R1 rates (see Fig. 2): (a) correlation time (τc,eff) and (b) order parameter for 15N (SNH2, red circle) and 13C′ (SC′2, black square) as a function of peptide plane number (numbering according to the residue number for 15N). The short-dash blue line in (b) depicts SNH2 obtained from GB1 relaxation in solution and the green long-dash line SNH2 obtained as a result of 3D GAF analysis of RDCs in GB3.36,37 The data for which severe peak overlap hindered accurate measurement of relaxation rates were excluded. | ||
In Fig. 3b the SMF order parameters from the solid-state relaxation are also compared to the overall solution-state SNH2 derived from relaxation measurements (and thus reporting generally on <4 ns motions; light green)36 and from residual dipolar couplings (RDC) measurements (and thus reporting on motions up to μs–ms timescale; dark green).37 A number of studies suggest that one should expect a high level of correlation between fast picosecond-nanosecond protein motions in solution and hydrated protein crystals.17,34,39,40 One can imagine that intermolecular interactions, e.g. crystal contacts, may influence slower large-scale motions to a greater extent but even though the details may vary the general motional modes are often similar.12,41,42 Specifically for GB3, which is very similar to GB1 in terms of fold and sequence, it has been demonstrated that the pictures of dynamics in solution and hydrated crystal are very consistent over a wide range of time scales.43 However, in a presence of more extensive specific intermolecular interactions as, e.g. in protein complexes, larger changes in protein dynamics may be observed; this would be true both in hydrated crystals and in solution.13
It is clear that the SNH2 values determined in the solid state are unusually high, if they are to be treated as the overall order parameters (i.e. order parameters for motions in the ps–μs range affecting the solid state relaxation rates).4,14,16 The SC′2 values, however, are similar to the overall SNH2 values determined in solution except for in parts of the helix and the β4 strand, where the SC′2 values are systematically lower. The effective SMF correlation times obtained from 13C′ solid-state data (average ∼5 ns) are also systematically different from the effective correlation times obtained from 15N solid-state data (average ∼23 ns) (see Fig. 3a).
(iv) Differences between results of SMF analyses of 13C′ and 15N relaxation rates
In light of the typically high level of correlation of SNH2 and SC′2 observed in solution NMR studies for the same peptide plane,44 the large offset observed between such values in the solid state may appear initially perplexing. Even in the presence of anisotropic motions,37 one would expect the order parameters and the time scales to be more similar than we observe here. As we will see in the following, the observation of the very high solid state SMF SNH2 order parameters, as well as the overall offsets between SNH2 and SC′2 and between the correlation times, may be understood by considering how motions occurring on different time scales contribute to the spectral densities used to calculate the relaxation rates. Such an inspection provides valuable insights into the fundamental nature of relaxation in the solid state, especially when contrasted against relaxation in the solution state.As mentioned, the exact form of the spectral densities is model-dependent; in section (iii) we used a single time scale SMF analysis, but in general protein motions can occur on multiple time scales. Such a situation can generally be better accounted for by using an extended model free (EMF) analysis, which includes two (or more) different time scales and associated order parameters (where subscript f indicates fast and subscript s slow motion; see ESI† for further details)34,45
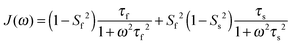 | (10) |
To assess the different contributions of these typical fast and slow motions to relaxation rates calculated by model free analyses, we simulated the spectral density terms for a fast motion (τf = 20 ps, Sf2 = 0.75) and for a smaller amplitude slow motion (10−11 < τs < 10−6 s, Ss2 = 0.95), using solution- and solid-state SMF formalism (see ESI,†eqn (1) and (3)). We also conducted simulations for the same motions occurring simultaneously using solution- and solid-state EMF formalism.
The results of these simulations are shown in Fig. 4, for 15N in both solution and solids and for 13C in solids, as a function of the correlation time of the slow motion. This figure shows the behavior of R1 and R1ρ relaxation rates calculated by an SMF treatment of pure slow motion (dashed blue line) or pure fast motion (dashed red line), as well as by an EMF treatment of both fast and slow motions simultaneously (solid black line).
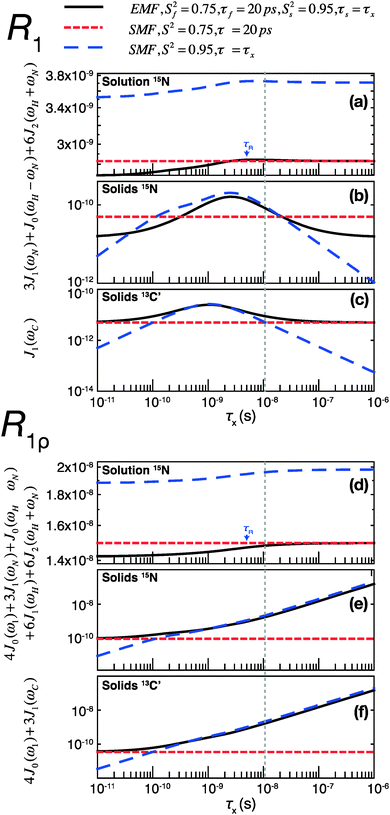 | ||
| Fig. 4 Simulations of contributions of a typical fast picosecond motion and a low-amplitude slow nanosecond motion to the main contributing spectral densities to R1 (a–c) and R1ρ (d–f) rates in solution and solids. (a and d) Spectral densities for 15N dipolar relaxation in solution. (b and e) Spectral densities for 15N dipolar relaxation in solids. (c and f) Spectral densities for 13C′ CSA relaxation in solids. Red short-dashed lines represent spectral densities calculated using the SMF for a fast motion with S2 = 0.75, τf = 20 ps. Blue long-dashed lines represent spectral densities calculated using the SMF for a slow motion with Ss2 = 0.95 and τx as indicated on the horizontal axis. All simulations were performed with ω0H/2π = 600 MHz. The overall rotational diffusion correlation time for the solution simulation was assumed to be 4 ns. The expressions and other parameters used for the simulations are given in the ESI.† | ||
Assuming the motions in GB1 occur on both ps and ns time scales,46 the spectral densities calculated by the EMF will be more “correct”, i.e. the calculated relaxation rates will be closer to those that would be measured experimentally given motion on those two time scales. By analyzing the same two motions separately with the SMF, we can observe how the spectral densities calculated compare to those calculated using the EMF. We can then use these observations to extrapolate to a case where the SMF is used to model a two-component motion.
Fig. 4 illustrates that the same fast and slow motions contribute differently to the spectral densities (and hence calculated relaxation rates) in the solution state and in the solid state. For EMF in the solution state, the presence of overall rotational diffusion modifies the effective correlation times for the fast and slow motions, with the result that the spectral densities (for both R1 and R1ρ) calculated by the EMF are similar to those calculated by the SMF including only the fast motion (see Fig. 4a and d – the black lines closely follow the dashed red lines). Conversely, in the solid state, the absence of overall tumbling means that the fast and slow motion contributions to EMF spectral densities are purely dependent on the order parameters and time scales of those motions. Compared to the solution case, this results in a greater relative contribution of slow motions to the spectral densities. For example, in the case of both 15N and 13C R1ρ, the fast motion contribution to the spectral densities can be smaller than 1% of the slow motion contribution, even if Sf2 is much lower than Ss2. The result of this is that the R1ρ relaxation rates calculated by the EMF are very similar to those calculated for correlation times of >0.1 ns by the SMF using only the slow motion (see Fig. 4e and f – the black lines closely follow the dashed blue lines).
A similar situation arises for R1 in solids: for a wide range of τs the contributions of the small amplitude slow motions to spectral densities are much larger than the contributions of larger amplitude fast motions. Above a certain time scale, however, the fast motion contribution begins to dominate (see Fig. 4b and c – the black line veers off toward the dashed red line above ∼10−8 s). Crucially, the time scale at which this occurs is shorter for 13C than it is for 15N. As a guide, the vertical dashed gray line indicates the slow motion time scale at which the fast motion SMF spectral densities begin to dominate over the slow motion SMF spectral densities for 13C′ R1. At this time scale (and for a range of slower time scales) the slow motion still dominates for 15N. As a result, a situation can occur where the calculated 15N R1 is dominated by the slow motion component while the calculated 13C′ R1 is dominated by the fast motion component.
Consequently, in the solid state, if the SMF approach is used to analyze 15N relaxation rates induced by both a fast motion and a slow motion (of e.g. 15 ns), the data often may be almost entirely accounted for by the slow motion only, even if the amplitude of the slow motion is small compared to that of the fast motion (an observation also made in ref. 14). In such a case, for 15N a good SMF fit will be obtained with an order parameter, SSMF2, closer to the slow motion order parameter, Ss2, rather than the overall order parameter, Soverall2 = Sf2Ss2, and with an effective correlation time faster than the actual correlation time for the slow motion, τs (see also Fig. S6, ESI†). This explains why solid-state SMF analysis of 15N relaxation rates in relatively rigid proteins such as GB1 and ubiquitin yields very high order parameters.4,14 In contrast, the same nanosecond/picosecond motions would result in a much larger contribution from the fast motion for 13C′, with the determined order parameter, SSMF2, being closer to the order parameter for fast motion, Sf2, and the effective correlation time much smaller than the correlation time for the slow motion, τs. This is exactly what we observe when fitting solid-state relaxation in GB1 using SMF formalism (see also Fig. S6, ESI†). Thus the offset between SMF order parameters for 15N and 13C′ confirms that all residues in GB1 undergo motions on at least two distinct time scales – picosecond-range and nanosecond range or even slower.
The dominant contribution of fast picosecond motions to spectral densities in solution leads to the opposite effect to that observed in solids. Based on the analysis of synthetic data, even in the presence of small amplitude nanosecond motions, a good SMF fit can be obtained with motional parameters close to the amplitude and time scale of the fast picosecond motion (i.e. a single-time scale fast motion model can explain the two-time scale motion well when the slow motion has a small amplitude, because the spectral densities calculated by the EMF and SMF are similar). If the amplitude of the slow motion is much smaller than that of the fast motion then the use of EMF may not be statistically justifiable. It is likely that such a phenomenon is partially behind the fact that EMF seems to be required primarily only for modeling residues in loop regions of proteins, where the amplitudes of slow motions are sufficiently large to lead to a statistically valid improvement of an EMF fit over an SMF fit. Another consequence of this behavior is that, in solution, a large number of independent data points (e.g. data at several different magnetic fields) may be necessary to identify motions that are slow (but still faster than the correlation time for the overall rotational diffusion) but of relatively small amplitude. In line with these observations, recent relaxometry experiments show that nanosecond motions are likely to be significantly underestimated by the traditional EMF analysis based on solution relaxation data obtained at one or two magnetic field strengths.47
The above considerations of the spectral densities in the solid state have profound consequences for the interpretation of the solid-state relaxation data. Firstly, even in relatively rigid systems such as GB1, SH3 or ubiquitin, solid-state relaxation data need to be interpreted by models including multiple time scales.2,5,48 This is also consistent with the hierarchy of protein motions established by variable temperature relaxation measurements in the solid state, where at least two motional modes with distinct activation energies were identified for backbone motions.49 Secondly, relaxation rates alone are not sufficient to obtain a good estimate of the overall order parameter. Notably, the addition of 13C′ R1 and R1ρ to the analysis of 15N R1 and R1ρ does not assist in obtaining a good estimate of the overall order parameter (only one parameter out of four, 13C′ R1, is dominated by the fast motion; when weights of the data points in the fitting procedure are related to the experimental errors no special weight is given to 13C′ R1, resulting in slow motion domination overall). Lack of sensitivity to fast motions may in fact be beneficial in certain situations, for example when modeling concerted anisotropic motions of protein fragments.15,21 In such a case, neglecting fast picosecond motions in the fitting routine should not incur large errors for estimating the amplitudes of slow overall motions. Currently, the only way to obtain an estimate of Soverall2 and Sf2 is to constrain the overall amplitudes of motion by an independent measurement of dipolar couplings or CSA.2,5,14 In the absence of an overall constraint on the order parameter, even though the relaxation rates originate from motions on multiple time scales, employing EMF is unlikely to yield realistic values for Sf2.14,16 A caveat of this approach is that a relatively small error in the determination of the dipolar order parameter may lead to quite a significant error in the subsequent estimate of Sf2.16
(v) Extended model free analysis of peptide plane motions
The above discussion indicates that to adequately describe dynamics in crystalline GB1 using relaxation, we need to consider models involving motions occurring on at least two timescales. In case of crystalline SH3, Zinkevich et al. argued that often three time scales are required.48 In another study,13 we found that only a handful of residues exhibit microsecond-scale motions based 15N R1ρ relaxation dispersion (clear dispersion is observed for residues 17, 19, 20, 44, 46, 49–53; note that the microsecond motions for these residues are likely too slow to effectively influence the measured dipolar order parameter), suggesting that for the majority of residues the dynamics can be well-described by motions in the ps-ns range. Note that data informing on millisecond-scale motions are currently not available. For motions in this range of time scales, measurements of dipolar couplings may be used to constrain the overall amplitude of motions (in general, dipolar couplings are averaged by motions faster than their inverse) and the expressions for R1ρ presented above can be used without including the influence of spinning frequency,24 which should generally be included if the motions in the μs–ms regime are present (see ESI†).First, to establish our baseline, we performed a fit using only 15N R1 and R1ρ data measured at 600 MHz and 850 MHz magnetic fields, with dipolar NH order parameters16,29 used to constrain the overall amplitude of motions. This scheme represents roughly the current state of the art in the literature.2,5,14,48,50 To model 15N relaxation we have included dipolar contributions from the directly bonded proton, Cα and C′, site-specific 15N CSA (see ESI†), and dipolar contributions from other protons implemented as an additional effective NH coupling.51 The results of the fits are presented in Fig. 5 (black diamonds and lines). The emerging picture of the dynamics in crystalline GB1 is consistent with similar analyses on other model crystalline systems such as SH3 and ubiquitin: all residues seem to be characterized by larger amplitude picosecond motions and smaller amplitude (order parameters close to 1) slow motions with a correlation time in the ns–μs range. Only a few of residues in loops exhibit larger than average slow motions. Notably, the order parameters for the fast picosecond motions are on average similar to the overall order parameters for GB1/GB3 in solution,36,46,52 providing yet another example that indicates the overall high level of similarity of fast picosecond dynamics for globular proteins in solution and in hydrated crystals.34
In spite of this reassuringly familiar view of GB1 dynamics, there are a few points of concern: for a number of residues the fast correlation times are in the low-picosecond regime (or at the 1 ps bound imposed in the fitting procedure; several such points were also found in a recent EMF analysis of 15N relaxation in ubiquitin14) and for the majority of the residues slow correlation times are in the microsecond regime. Both of these features are likely to be fitting artifacts, with the data not providing sufficient basis for an accurate description of the dynamics. Motions with correlation times of a few picoseconds have a negligible effect on the measured relaxation rates and as such these kinds of motions are unlikely to be accurately determined from relaxation measurements. On the other hand, the omnipresence of microsecond motions is inconsistent with the lack of microsecond exchange as demonstrated by 15N R1ρ relaxation dispersion in crystalline GB113 (similarly, in ubiquitin a few residues, e.g. 10, 44, 63, were found where microsecond motions were detected through an EMF analysis of 15N relaxation rates but not confirmed in 15N relaxation dispersion12,14). An examination of the determined parameters reveals that for many residues, the parameters for the fast motion are such that they have negligible contributions to R1ρ and the parameters for the slow motions have negligible contributions to R1. These results suggest that even though the considered data set is sufficient to obtain fairly reasonable estimates of the amplitudes of motion, it is not sufficient to provide accurate determination of time scales of motions.
This situation may improve as data measured at a larger number of magnetic fields, or at least much more different magnetic fields, is available to provide better sampling of the spectral density at different frequencies. Indeed, if we include 15N R1 and R1ρ previously measured at a magnetic field of 1000 MHz,4 the “artifactual” microsecond slow motions and 1 ps fast motions are eliminated for several residues (see ESI†). For many others, however, microsecond motions are still detected, in direct disagreement with the relaxation dispersion data. The situation is not greatly improved by using the expressions for R1ρ that explicitly include spinning frequency effects (see ESI†).24
A potential solution to this problem could be to supplement the data with measurements that allow, at the same magnetic fields, to sample spectral densities at very different frequencies, for example 13C′ data. Typically, in solution, order parameters for 15N and 13C′ in the same peptide planes are highly correlated, with only a slight offset between them.44 This is expected because due to the planarity of the peptide bond 15N and 13C′ are likely to undergo similar motions. Even though such motions are expected to be anisotropic in nature,37,44 to the first approximation data can be treated reasonably well by assuming isotropic fluctuations of the peptide planes.44
Following the assumption of isotropic peptide plane motions we refitted the data, adding 13C′ R1 and R1ρ data at 600 MHz and 850 MHz magnetic fields to the EMF analysis. To model 13C′ relaxation we included site-specific 13C′ CSA, dipolar contributions from the couplings to Cα, N and HN, and dipolar contributions from other protons implemented as an additional effective 13C′–1H coupling51 (see ESI†). The results of the combined 13C′ and 15N fits (red circles and lines) are depicted in Fig. 5, where they are overlaid with the results of analysis based on 15N data only. For most residues, the changes in order parameters upon inclusion of 13C′ relaxation rates in the analysis are relatively small. However, there is a pronounced effect on the determined time scales. In particular, the slow correlation times are less than 1 μs for most residues (average ∼500 ns), in line with the results of 15N relaxation dispersion. The overall fairly consistent time scale for slow motions in the secondary structure elements (very different time scales only appear in the loops) may be suggestive of an overall small amplitude motion.21 A few resonances for which clear relaxation dispersion is observable may require a model that includes motions occurring on three time scales but it is not entirely obvious how one could constrain their amplitude. In addition, the artifactual low picosecond motions are removed and the overall trend of time scales along the protein backbone varies more “smoothly” from residue to residue. Interestingly, the determined fast correlation times become overall similar to the fast correlation times determined in GB1 under similar conditions in solution, which, together with similar Sf2 (ref. 36) (see ESI†), again further highlighting the similarity of fast dynamics in solution and hydrated crystals.
To further validate the obtained picture of GB1 dynamics, we back-calculated 15N R1 and R1ρ rates for 1000 MHz 1H Larmor frequency based on the EMF analysis of 600 and 850 MHz data and compared them in Fig. 6 to previously-measured experimental values.4 In spite of the fact that the measurements at 1000 MHz were not conducted at the exact same temperature as those at 600/850 MHz, the back-calculated values agree reasonably well with the experimental values (see ESI†).
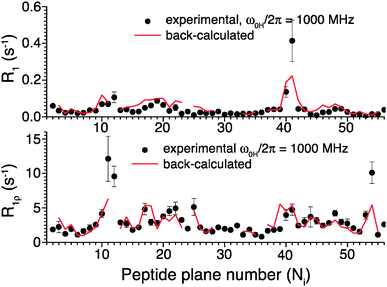 | ||
| Fig. 6 Comparison of 15N R1 and R1ρ relaxation rates measured in crystalline GB1 at 1 GHz 1H Larmor frequency (black points)4 and those back-calculated from an EMF analysis based on 15N and 13C′ relaxation rates measured at 600 and 850 MHz 1H Larmor frequencies in Fig. 5 (red line). | ||
It might be useful to highlight that the results of the performed analyses are not greatly affected by the precise choice of bond length and CSA magnitude. In the solid state, relatively large changes in bond lengths of CSA have minimal effects on the results of model free analysis of relaxation rates. For example, regardless of whether rNH = 1.02 Å or rNH = 1.04 Å is used to model the 15N relaxation, the obtained order parameters and correlation times are virtually the same except for cases of large amplitude motions (see ESI†). This observation relates to the fact that in the solid state in a presence of slow motions small changes in order parameters lead to large changes in R1ρ, in fact, the dependence of rate on order parameter is much steeper than the dependence on bond length or CSA magnitude. In contrast, in solution the effect of such slow motions is effectively “truncated” by the overall rotational diffusion leading to a reverse situation where the dependence of the rates on bond length or CSA magnitude is steeper than the dependence on order parameter. As a result, even though the amplitudes of motions determined from the analysis of relaxation rates in solution may vary significantly depending on the precise choice of magnitude for modulated interactions, the amplitudes of motions determined from the analysis of relaxation rates in solid state will be affected to a lesser degree by similar variations. To model 15N and 13C′ CSA relaxation we used here site-specific values obtained from a model where the CSA tensor was parameterized using isotropic chemical shift and based on measurements performed on crystalline GB1. However, in the performed model free analysis the use of other models of CSA (e.g. similar parameterizations obtained from measurements on ubiquitin in solution, or generic average CSA) has only a small effect on the obtained results (again except when large amplitude motions are concerned). Such a difference in behavior between solution and solid-state relaxation analysis traces back, again, to the forms of spectral densities and the absence of the dominant term from overall rotational diffusion in the solid state.
Experimental
NMR experiments were conducted on a Bruker Avance III spectrometer operating at 20.0 T (ω0H/2π = 850 MHz) and a Bruker Avance II+ spectrometer operating at 14.1 T (ω0H/2π = 600 MHz), using a Bruker 1.3 mm triple-resonance probe at each field. Unless otherwise stated, experiments were performed at 60 kHz MAS frequency, at a sample temperature of 27.0 ± 0.5 °C as measured by the 1H chemical shift of water with respect to DSS.53 The pulse sequence used to collect 13C′ R1ρ rates (Fig. S10a, ESI†) was based on a standard NCO double-CP (DCP54) sequence followed by a spin-lock pulse on the carbon channel whose length was incremented across each series of experiments. An S3E block27 was added to enhance resolution in the direct dimension by removing the effect of one-bond C′–Cα scalar couplings. A similar sequence (but with the spin-lock pulse instead on the 15N channel, before the indirect acquisition (t1) period) was used to measure site-specific backbone amide 15N R1ρ rates (see Fig. S10, ESI†). For all 13C′ and 15N R1ρ experiments (unless otherwise stated), the spin-lock nutation frequency was set to 17 kHz, calibrated using nutation spectra. Nutation spectra also allowed us to determine the average r.f. inhomogeneity, which was on the order of 15%.13C and 15N R1 rates were measured using sequences based on a standard NCO, but with a delay period (directly before t1 acquisition for 15N R1, directly after 15N–13C CP for 13C′ R1) that was incremented between experiments. π/2 pulses were applied either side of this delay (100 kHz on 13C for 13C′ R1, 83.3 kHz on 15N for 15N R1). All sequences are given in Fig. S10 (ESI†). The Bruker pulse sequences are available from the authors' website.
All sequences were initialized with a 100 kHz π/2 1H pulse, followed by adiabatic double quantum cross-polarization55 from 1H to 15N (1.5 ms, ω1H/2π ≈ 50 kHz, ω1N/2π = 10 kHz). After t1 evolution, magnetization was transferred to 13C by a second adiabatic CP (9 ms, ω1N/2π ≈ 50 kHz, ω1C/2π = 10 kHz). During t1 (t1,max = 10 ms) and t2 (40 ms at 850 MHz, 25 ms at 600 MHz) acquisition, slpTPPM decoupling19 was applied at a field strength of ∼15 kHz.
Spectra were processed with TopSpin 2.1, and the relaxation series were subsequently analysed using CcpNmr Analysis 2.2.2. Final relaxation curve fitting was completed in Matlab. Data were fitted to I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Rt), with I0 and R being the fit parameters.
exp(−Rt), with I0 and R being the fit parameters.
Fitting of the relaxation data to SMF and EMF was performed in Matlab. All the expressions for the rates, spectral densities as well as magnitudes of interactions are detailed in the ESI.† The minimization was performed using code based on the fminsearch function with several random starting points to ensure a global minimum was found. The best-fit amplitude and time scale parameters for all the models were determined by minimizing the χ2 target function:
 | (11) |
Conclusions
In summary, we have introduced 13C R1ρ measurements as a robust quantitative probe of slow protein motions in the solid state that is highly complementary to 15N relaxation measurements. We showed that solid-state R1ρ rates are exceedingly sensitive to even very small-amplitude slow conformational changes. A comparison of simple model free analyses of 15N and 13C′ R1 and R1ρ data illustrated that relaxation in GB1 in solid state is in general induced by motions occurring on multiple time scales, but usually dominated by the slower nanosecond-range motions. Analyzing the differences between solution- and solid-state spectral densities, we could explain why very high order parameters are obtained from simple model free analyses of 15N relaxation in the solid state, and why nanosecond motions are likely to be underestimated in a standard relaxation analysis of solution NMR relaxation data. We also showed that by combining 15N and 13C′ relaxation data it is possible to obtain a more physically meaningful dynamical description of proteins that is highly complementary to the picture provided by other techniques. Finally, combining 15N and 13C′ measurements in such a manner paves the way to considering anisotropic peptide plane motions, which will be considered in a future manuscript.Acknowledgements
We thank Dr Dinu Iuga for the assistance with acquiring data at the UK 850 MHz Solid-state NMR Facility. We thank Prof. Steven Brown for providing the crystalline amino acid samples. JML and MJL acknowledge support of the EPSRC. JRL acknowledges support of Research Development Fund from University of Warwick, EPSRC grant EP/L025906/1 and BBSRC grant BB/L022761/1. The UK 850 MHz Solid-state NMR Facility used in this research was funded by EPSRC and BBSRC, as well as the University of Warwick, including part funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands (AWM) and the European Regional Development Fund (ERDF). SG acknowledges funding by the Swiss National Science Foundation grant 310030_149927. Raw NMR data and Matlab scripts used for the analysis can be obtained from the authors upon request.Notes and references
- K. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef CAS PubMed.
- V. Chevelkov, U. Fink and B. Reif, J. Biomol. NMR, 2009, 45, 197–206 CrossRef CAS PubMed.
- A. Krushelnitsky, T. Zinkevich, D. Reichert, V. Chevelkov and B. Reif, J. Am. Chem. Soc., 2010, 132, 11850–11853 CrossRef CAS PubMed.
- J. R. Lewandowski, H. J. Sass, S. Grzesiek, M. Blackledge and L. Emsley, J. Am. Chem. Soc., 2011, 133, 16762–16765 CrossRef CAS PubMed.
- P. Schanda, B. H. Meier and M. Ernst, J. Am. Chem. Soc., 2010, 132, 15957–15967 CrossRef CAS PubMed.
- M. Tollinger, A. C. Sivertsen, B. H. Meier, M. Ernst and P. Schanda, J. Am. Chem. Soc., 2012, 134, 14800–14807 CrossRef CAS PubMed.
- J. J. Helmus, K. Surewicz, W. K. Surewicz and C. P. Jaroniec, J. Am. Chem. Soc., 2010, 132, 2393–2403 CrossRef CAS PubMed.
- J. Yang, M. L. Tasayco and T. Polenova, J. Am. Chem. Soc., 2009, 131, 13690–13702 CrossRef CAS PubMed.
- K. Schmidt-Rohr and H. W. Spiess, Multidimensional solid-state NMR and polymers, Academic Press, London, 1994 Search PubMed.
- A. Mittermaier and L. E. Kay, Science, 2006, 312, 224–228 CrossRef CAS PubMed.
- C. M. Quinn and A. E. McDermott, J. Magn. Reson., 2012, 222, 1–7 CrossRef CAS PubMed.
- P. Ma, J. D. Haller, J. Zajakala, P. Macek, A. C. Sivertsen, D. Willbold, J. Boisbouvier and P. Schanda, Angew. Chem., Int. Ed. Engl., 2014, 53, 4312–4317 CrossRef CAS PubMed.
- J. M. Lamley, C. Oster and J. R. Lewandowski, unpublished.
- J. D. Haller and P. Schanda, J. Biomol. NMR, 2013, 57, 263–280 CrossRef CAS PubMed.
- D. B. Good, S. Wang, M. E. Ward, J. Struppe, L. S. Brown, J. R. Lewandowski and V. Ladizhansky, J. Am. Chem. Soc., 2014, 136, 2833–2842 CrossRef CAS PubMed.
- L. Mollica, M. Baias, J. R. Lewandowski, B. J. Wylie, L. J. Sperling, C. M. Rienstra, L. Emsley and M. Blackledge, J. Phys. Chem. Lett., 2012, 3, 3657–3662 CrossRef CAS.
- V. Agarwal, Y. Xue, B. Reif and N. R. Skrynnikov, J. Am. Chem. Soc., 2008, 130, 16611–16621 CrossRef CAS PubMed.
- J. R. Lewandowski, P. C. A. van der Wel, M. Rigney, N. Grigorieff and R. G. Griffin, J. Am. Chem. Soc., 2011, 133, 14686–14698 CrossRef CAS PubMed.
- J. R. Lewandowski, J. Sein, H. J. Sass, S. Grzesiek, M. Blackledge and L. Emsley, J. Am. Chem. Soc., 2010, 132, 8252–8254 CrossRef CAS PubMed.
- T. Yamazaki, R. Muhandiram and L. E. Kay, J. Am. Chem. Soc., 1994, 116, 8266–8278 CrossRef CAS.
- J. R. Lewandowski, J. Sein, M. Blackledge and L. Emsley, J. Am. Chem. Soc., 2010, 132, 1246–1248 CrossRef CAS PubMed.
- A. Naito, S. Ganapathy, K. Akasaka and C. A. Mcdowell, J. Magn. Reson., 1983, 54, 226–235 CAS.
- S. K. Vasa, H. Janssen, E. R. H. Van Eck and A. P. M. Kentgens, Phys. Chem. Chem. Phys., 2011, 13, 104–106 RSC.
- R. Kurbanov, T. Zinkevich and A. Krushelnitsky, J. Chem. Phys., 2011, 135, 184104 CrossRef PubMed.
- C. M. Quinn and A. E. McDermott, J. Biomol. NMR, 2009, 45, 5–8 CrossRef CAS PubMed.
- W. T. Franks, D. H. Zhou, B. J. Wylie, B. G. Money, D. T. Graesser, H. L. Frericks, G. Sahota and C. M. Rienstra, J. Am. Chem. Soc., 2005, 127, 12291–12305 CrossRef CAS PubMed.
- S. Laage, A. Lesage, L. Emsley, I. Bertini, I. C. Felli, R. Pierattelli and G. Pintacuda, J. Am. Chem. Soc., 2009, 131, 10816–10817 CrossRef CAS PubMed.
- I. Bertini, L. Emsley, I. C. Felli, S. Laage, A. Lesage, J. R. Lewandowski, A. Marchetti, R. Pierattelli and G. Pintacuda, Chem. Sci., 2011, 2, 345–348 RSC.
- B. J. Wylie, L. J. Sperling, A. J. Nieuwkoop, W. T. Franks, E. Oldfield and C. M. Rienstra, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16974–16979 CrossRef CAS PubMed.
- B. J. Wylie, L. J. Sperling, H. L. Frericks, G. J. Shah, W. T. Franks and C. M. Rienstra, J. Am. Chem. Soc., 2007, 129, 5318–5319 CrossRef CAS PubMed.
- K. Loth, P. Pelupessy and G. Bodenhausen, J. Am. Chem. Soc., 2005, 127, 6062–6068 CrossRef CAS PubMed.
- P. R. L. Markwick and M. Sattler, J. Am. Chem. Soc., 2004, 126, 11424–11425 CrossRef CAS PubMed.
- G. Lipari and A. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- V. Chevelkov, A. V. Zhuravleva, Y. Xue, B. Reif and N. R. Skrynnikov, J. Am. Chem. Soc., 2007, 129, 12594–12595 CrossRef CAS PubMed.
- D. A. Torchia and A. Szabo, J. Magn. Reson., 1982, 49, 107–121 CAS.
- J. J. Barchi, B. Grasberger, A. M. Gronenborn and G. M. Clore, Protein Sci., 1994, 3, 15–21 CrossRef CAS PubMed.
- G. Bouvignies, P. Bernado, S. Meier, K. Cho, S. Grzesiek, R. Bruschweiler and M. Blackledge, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13885–13890 CrossRef CAS PubMed.
- M. J. Knight, A. J. Pell, I. Bertini, I. C. Felli, L. Gonnelli, R. Pierattelli, T. Herrmann, L. Emsley and G. Pintacuda, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11095–11100 CrossRef CAS PubMed.
- H. B. Cole and D. A. Torchia, Chem. Phys., 1991, 158, 271–281 CrossRef CAS.
- A. Tamura, M. Matsushita, A. Naito, S. Kojima, K. I. Miura and K. Akasaka, Protein Sci., 1996, 5, 127–139 CrossRef CAS PubMed.
- G. L. Olsen, M. F. Bardaro, D. C. Echodu, G. P. Drobny and G. Varani, J. Biomol. NMR, 2009, 45, 133–142 CrossRef CAS PubMed.
- J. C. Williams and A. E. McDermott, Biochemistry, 1995, 34, 8309–8319 CrossRef CAS.
- G. M. Clore and C. D. Schwieters, J. Mol. Biol., 2006, 355, 879–886 CrossRef CAS PubMed.
- S. L. Chang and N. Tjandra, J. Magn. Reson., 2005, 174, 43–53 CrossRef CAS PubMed.
- G. M. Clore, A. Szabo, A. Bax, L. E. Kay, P. C. Driscoll and A. M. Gronenborn, J. Am. Chem. Soc., 1990, 112, 4989–4991 CrossRef CAS.
- D. Idiyatullin, V. A. Daragan and K. H. Mayo, J. Phys. Chem. B, 2003, 107, 2602–2609 CrossRef CAS.
- C. Charlier, S. N. Khan, T. Marquardsen, P. Pelupessy, V. Reiss, D. Sakellariou, G. Bodenhausen, F. Engelke and F. Ferrage, J. Am. Chem. Soc., 2013, 135, 18665–18672 CrossRef CAS PubMed.
- T. Zinkevich, V. Chevelkov, B. Reif, K. Saalwächter and A. Krushelnitsky, J. Biomol. NMR, 2013, 57, 219–235 CrossRef CAS PubMed.
- J. R. Lewandowski, M. E. Halse, M. Blackledge and L. Emsley, Science, 2015, 348, 578–581 CrossRef CAS PubMed.
- N. Giraud, M. Blackledge, M. Goldman, A. Bockmann, A. Lesage, F. Penin and L. Emsley, J. Am. Chem. Soc., 2005, 127, 18190–18201 CrossRef CAS PubMed.
- S. F. Lienin, T. Bremi, B. Brutscher, R. Bruschweiler and R. R. Ernst, J. Am. Chem. Soc., 1998, 120, 9870–9879 CrossRef CAS.
- Y. E. Shapiro and E. Meirovitch, J. Phys. Chem. B, 2012, 116, 4056–4068 CrossRef CAS PubMed.
- J. Cavanagh, W. J. Fairbrother, A. G. I. Palmer, N. J. Skelton and M. Rance, Protein NMR Spectroscopy, Academic Press, 2nd edn, 2006 Search PubMed.
- J. Schaefer, R. A. Mckay and E. O. Stejskal, J. Magn. Reson., 1979, 34, 443–447 CAS.
- S. Hediger, B. H. Meier and R. R. Ernst, Chem. Phys. Lett., 1995, 240, 449–456 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures and tables. Pulse sequences. Expressions for spectral densities and relaxation rates. Consideration of magic angle mis-adjustment, r.f. induced heating and polarization transfer during the R1ρ measurements. See DOI: 10.1039/c5cp03484a |
| This journal is © the Owner Societies 2015 |