Open Access Article
Open Access ArticleElectronic coherence and the kinetics of inter-complex energy transfer in light-harvesting systems
Pengfei
Huo
and
Thomas F.
Miller III
*
Division of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125, USA. E-mail: tfm@caltech.edu
First published on 1st June 2015
Abstract
We apply real-time path-integral dynamics simulations to characterize the role of electronic coherence in inter-complex excitation energy transfer (EET) processes. The analysis is performed using a system-bath model that exhibits the essential features of light-harvesting networks, including strong intra-complex electronic coupling and weak inter-complex coupling. Strong intra-complex coupling is known to generate both static and dynamic electron coherences, which delocalize the exciton over multiple chromophores and potentially influence the inter-complex EET dynamics. With numerical results from partial linearized density matrix (PLDM) real-time path-integral calculations, it is found that both static and dynamic coherence are correlated with the rate of inter-complex EET. To distinguish the impact of these two types of intra-complex coherence on the rate of inter-complex EET, we use Multi-Chromophore Förster Resonance Energy Transfer (MC-FRET) theory to map the original parameterization of the system-bath model to an alternative parameterization for which the effects of static coherence are preserved while the effects of dynamic coherence are largely eliminated. It is then shown that both parameterizations of the model (i.e., the original that supports dynamic coherence and the alternative that eliminates it), exhibit nearly identical EET kinetics and population dynamics over a wide range of parameters. These observations are found to hold for cases in which either the EET donor or acceptor is a dimeric complex and for cases in which the dimeric complex is either symmetric or asymmetric. The results from this study suggest that dynamic coherence plays only a minor role in the actual kinetics of inter-complex EET, whereas static coherence largely governs the kinetics of incoherent inter-complex EET in light-harvesting networks.
1 Introduction
The extraordinary efficiency of excitation energy transfer (EET) in natural light-harvesting systems is generally attributed to rapid timescales of incoherent exciton-transfer (∼50 ps) in comparison to the nanosecond-timescale excitation lifetime.1 Nonetheless, recent 2D-spectroscopy experiments have observed transient intra-complex electronic coherence in natural2–6 and artificial light harvesting systems,7–9 which raises questions about the role of intra-complex electronic coherence in facilitating EET across multi-meric complexes.10–12 In this work, we combine real-time path-integral dynamics simulations13,14 and analysis from Multi-Chromophore Förster Resonance Energy Transfer (MC-FRET) theory15–17 to examine the role of electronic coherence on the kinetics of EET in light-harvesting systems.Light-harvesting systems are typically comprised of multiple complexes, which are in turn comprised of multiple light-absorbing chromophores. For example, Photosystem II is comprised of the CP43, CP47, and reaction center complexes, each of which includes multiple chromophores.18–20 In most light-harvesting systems, chromophores within a complex exhibit strong electronic coupling due to their close-packed configurations.11,12,18,19 The electronic coupling between chromophores in different complexes, however, is typically much weaker due to the larger distances of separation, leading to incoherent dynamics for EET between complexes. The manifestation of electronic coherences in EET has been the subject of significant experimental2,3 and theoretical11,12,21–32 attention. In the current work, we specifically focus on the way in which intra-complex electronic coherence affects inter-complex EET kinetics, which is crucial to the efficiency of light-harvesting systems. We address this issue by distinguishing between static and dynamic types of electronic coherence and by examining the relative impact of these two types of intra-complex coherence on the kinetics of inter-complex EET.
Fig. 1 introduces the simple model for inter-complex energy transfer that is employed in this study.11,12,22 The model exhibits an EET donor complex that consists of a pair of chromophores and an acceptor complex that consists of a single chromophore (Fig. 1a). Inter-complex electronic coupling is described via the parameter δ and intra-complex electronic coupling is given by Δ, where the latter is a function of the tilt angle, θ, between the two chromophores of the dimer (Fig. 1b). The intra-complex coupling can be varied via the chromophore-dipole tilt angle (Fig. 1c); previous theoretical work has found that the sign of the intra-complex coupling has a significant influence on both the rate of inter-complex EET and non-linear spectroscopic features.22,33,34 Despite its simplicity, this model exhibits many of the essential features of EET in light-harvesting systems for regimes in which the intra-complex coupling is relatively large (βΔ > ∼1, where β = 1/kBT) and the inter-complex coupling is small (βδ ≪ 1).
The current work focuses on characterizing the effect of electronic coherence on the kinetics of EET in light-harvesting systems. In doing so, we will follow earlier work by distinguishing between static coherence and dynamic coherence.10,12,35
Static coherence (also known as “exciton delocalization”) is a time-independent feature associated with shifts in the intra-complex energy eigenspectrum.10,18,36,37 It can be characterized in terms of the off-diagonal elements of the projector for the donor-complex eigenstates, such that
〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) α|D2〉 = 〈D1|α〉〈α|D2〉 = c1αc2α*, α|D2〉 = 〈D1|α〉〈α|D2〉 = c1αc2α*, | (1) |
Dynamic coherence is a time-dependent feature associated with transient superpositions among the local excitations on individual chromophores.12,18,38 It is most commonly characterized in terms of the off-diagonal elements of the projector for the time-dependent wavefunction of the exciton, such that
〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)|D2〉 = 〈D1|ψ(t)〉〈ψ(t)|D2〉 = c1(t)c2*(t), (t)|D2〉 = 〈D1|ψ(t)〉〈ψ(t)|D2〉 = c1(t)c2*(t), | (2) |
To characterize the relative contributions of static and dynamic electronic coherence in facilitating inter-complex EET, we use MC-FRET theory15–17 to construct an alternative parametrization of the model in Fig. 1, such that the effects of static coherence are preserved, while dynamic coherence is eliminated via the removal of the intra-complex electronic coupling. Using the partial linearized density matrix (PLDM) path-integral method,13,14 we investigate the EET for the model system, considering both the original parameterization that supports dynamic coherence and the alternative parameterization that eliminates dynamic coherence. The numerical results show nearly identical inter-complex EET kinetics for both sets of parameters over a broad range of EET regimes. These results suggest that static coherence largely governs the kinetics of inter-complex EET in light-harvesting networks, whereas dynamic coherence plays only a minimal role.
2 Model system
The model system employed in this study (Fig. 1) assumes the form of the Frenkel-exciton tight-binding Hamiltonian,39| Ĥ = Ĥs + Ĥint + Ĥb. | (3) |
| Ĥs = ĤDs + ĤAs + ĤCs. | (4) |
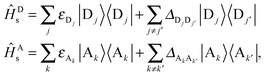 | (5) |
 | (6) |
Within the dipole approximation, the intra-complex electronic coupling can be related to the relative orientation of the transition dipole associated with individual chromophores using
 | (7) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) j is the transition dipole associated with the ground to excited transition on chromophore Dj,
j is the transition dipole associated with the ground to excited transition on chromophore Dj,  and
and  are the vector and unit vector pointed from chromophore Dj to Dj′. As illustrated in Fig. 1c, Δjj′ can be modulated by varying the tilt angle θ of the dipoles. For tilt angles associated with positive value of intra-complex electronic coupling, the donor complex corresponds to an H-type aggregate; for negative values of the coupling, the donor complex is a J-type aggregate.34,40 While the inter-complex electronic couplings can also be modeled in terms of the tilt angle, this dependence is much weaker and is thus assumed here to be independent of the tilt angle.
are the vector and unit vector pointed from chromophore Dj to Dj′. As illustrated in Fig. 1c, Δjj′ can be modulated by varying the tilt angle θ of the dipoles. For tilt angles associated with positive value of intra-complex electronic coupling, the donor complex corresponds to an H-type aggregate; for negative values of the coupling, the donor complex is a J-type aggregate.34,40 While the inter-complex electronic couplings can also be modeled in terms of the tilt angle, this dependence is much weaker and is thus assumed here to be independent of the tilt angle.
The model incorporates the effect of a dissipative environment via linear coupling of each chromophore site to a corresponding harmonic bath, using
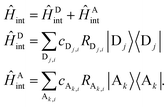 | (8) |
| Ĥb = ĤDb + ĤAb | (9) |
 | (10) |
 .
.
The system-bath coupling constants cDj,i and cAk,i are sampled from the Debye–Drude form of the spectral density,21,41
 | (11) |
 , and the bath relaxation time is τ. We assume that an independent and identical bath is coupled to each chromophore state.
, and the bath relaxation time is τ. We assume that an independent and identical bath is coupled to each chromophore state.
For use in the following sections, we introduce notation for the Hamiltonian operators associated with the donor and acceptor complexes,
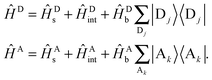 | (12) |
3 Partial linearized density matrix dynamics
EET rate constants and time-dependent reduced density matrix elements are obtained from thermal time correlation functions. In this study, we use the PLDM path-integral dynamics method to compute the necessary correlation functions.13,14 In this section, we review expressions for the EET rate constant and reduced density matrix in terms of time correlation functions, we briefly outline the PLDM method for describing EET dynamics, and we present benchmark results for EET between a single donor and single acceptor model.The general expression for the time-dependent reduced density matrix is13,42
ρij(t) = Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0)eiĤt/ℏ|i〉〈j|e−iĤt/ℏ], (0)eiĤt/ℏ|i〉〈j|e−iĤt/ℏ], | (13) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0) is the initial density operator. Unless otherwise specified, EET rate constants are obtained from the flux-side correlation function42,43 using
(0) is the initial density operator. Unless otherwise specified, EET rate constants are obtained from the flux-side correlation function42,43 using | (14) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif)
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) eiĤt/ℏĥe−iĤt/ℏ], tp is the “plateau time” for flux-side correlation function,42,43
eiĤt/ℏĥe−iĤt/ℏ], tp is the “plateau time” for flux-side correlation function,42,43![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) = e−βĤ, Ĥ is the total Hamiltonian operator, and
= e−βĤ, Ĥ is the total Hamiltonian operator, and  is the reactant partition function. The side operator
is the reactant partition function. The side operator 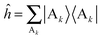 distinguishes between the reactant and product regions, and
distinguishes between the reactant and product regions, and  is the associated flux operator. The rate constant can be equivalently expressed as
is the associated flux operator. The rate constant can be equivalently expressed as  , where Cff(t) = Tr[
, where Cff(t) = Tr[![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif)
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) eiĤt/ℏ
eiĤt/ℏ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) e−iĤt/ℏ], or it can be computed directly from the population dynamics.44–46
e−iĤt/ℏ], or it can be computed directly from the population dynamics.44–46
The time correlation functions in eqn (13) and (14) are computed using the PLDM method.13,14 Expressing the total Hamiltonian in terms of its nuclear kinetic and total potential energy contributions, Ĥ = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) + Vnm(
+ Vnm(![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) )|n〉〈m|, where |n〉, |m〉 ∈ {{|Dj〉}, {|Ak〉}} are the site basis functions, we use the mapping representation of Meyer–Miller–Stock–Thoss47 to transform the discrete electronic states into continuous variables
)|n〉〈m|, where |n〉, |m〉 ∈ {{|Dj〉}, {|Ak〉}} are the site basis functions, we use the mapping representation of Meyer–Miller–Stock–Thoss47 to transform the discrete electronic states into continuous variables  , where
, where  . Applying a linearization approximation42 to the nuclear degrees of freedom and keeping the explicit propagation of the electronic degrees of freedom, we arrive at the general PLDM expression13,14
. Applying a linearization approximation42 to the nuclear degrees of freedom and keeping the explicit propagation of the electronic degrees of freedom, we arrive at the general PLDM expression13,14
 | (15) |
 and
and  are partial Wigner transformations of operators
are partial Wigner transformations of operators ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) Â and
 and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) .
.  provides the initial distributions of electronic degrees of freedom. The terms G0′ and
provides the initial distributions of electronic degrees of freedom. The terms G0′ and  are similarly defined with respect to time propagation in the reversed direction.
are similarly defined with respect to time propagation in the reversed direction.
Classical trajectories are used to evaluate the approximate quantum time correlation function in eqn (15). These trajectories are propagated using the equations of motion13
 | (16) |
 is the classical mapping Hamiltonian,13 and F is the force that acts on the nuclear degrees of freedom.
is the classical mapping Hamiltonian,13 and F is the force that acts on the nuclear degrees of freedom.
In recent work, we have demonstrated the accuracy of the PLDM method for non-adiabatic reaction dynamics associated with electron transfer.14 To further benchmark the accuracy of the method for EET processes, Fig. 2 presents a comparison of PLDM with numerically exact results for the EET rate associated with excitation transfer from a single donor chromophore to a single acceptor chromophore. These results provide a clear picture of how different quantities control the EET rate, as well as the accuracy of the PLDM method in various regimes. Unless otherwise specified, the excitation energy gap between the donor and acceptor is ε = εD − εA = 100 cm−1, the inter-complex electronic coupling is δ = 5 cm−1, the solvent reorganization energy is λ = λD = λA = 100 cm−1, and the solvent response time is τ = 0.1 ps. The solvent bath are discretized following the description in Section 4.
The rate constant in Fig. 2a is calculated from an exponential fit of the population decay of an excitation on the donor. The initial condition for the excitation is ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 0 = |D〉〈D|(
0 = |D〉〈D|(![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b)w. The exciton transfer rate constants in Fig. 2b–d are calculated as the long-time plateau value of the flux-side correlation function, as described in eqn (14). To evaluate the partial-Wigner transformation of the thermal flux operator (e−βĤ
b)w. The exciton transfer rate constants in Fig. 2b–d are calculated as the long-time plateau value of the flux-side correlation function, as described in eqn (14). To evaluate the partial-Wigner transformation of the thermal flux operator (e−βĤ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) )w, we use the approximation14,42,45
)w, we use the approximation14,42,45
 | (17) |
 | (18) |
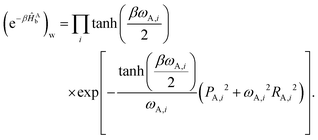 | (19) |
Fig. 2a presents the numerical results of EET rate over a range of solvent reorganization energies, λ, using an inter-complex coupling of δ = 20 cm−1. The EET rate is computed using the PLDM method, as well as with classical Marcus Theory (MT)45 and a Fermi Golden Rule (FGR) expression41,45 that accounts for nuclear quantization (see Appendix A for details). Also included are numerical exact results obtained from the hierarchy equation of motion (HEOM).41 Whereas the FGR and MT descriptions only agree with the exact results for large reorganization energies, PLDM works well over the entire range of λ. Note that a maximal transfer rate is obtained with changing λ; this behavior has been previously discussed in terms of “environment-assisted quantum transport”.12,25,48,49
Fig. 2b presents the numerical results for the EET rate upon varying the inter-complex electronic coupling, δ, and with εD = εA. For small couplings (βδ ≪ 1), the system exhibits non-adiabatic EET dynamics and PLDM agrees with the FGR result. For larger couplings (βδ > 1), PLDM correctly deviates from FGR,14,45 which assumes weak coupling.
Fig. 2c presents PLDM results for the EET rate over a range of values of the energy gap between donor and acceptor states, ε = εD − εA. Here, inter-complex coupling is small (βδ ≪ 1) such that FGR provides an accurate description. The FGR results predict a turnover with maximal rate at ε = λ. Classical MT gives the correct qualitative trend of the EET rate, but it underestimates the rate in the inverted regime (ε > λ). This effect is well understood from the fact that quantized vibrational levels provide additional transfer channels between donor and acceptor states, especially in the inverted regime.50
In Fig. 2d, we explore the effect of the memory time of the bath, τ. By varying τ for the asymmetric model system (ε = 500 cm−1), the EET rate exhibits classical Kramers behavior, as expected.51 For the more interesting symmetric case (ε = 0), the rate increases at the low friction regime (small τ) due to interference effects, as been discussed in previous semi-classical52 and numerically exact51 studies.
4 Calculation details
All remaining results in this paper are performed at T = 300 K. The PLDM method is used to calculate all needed time correlation functions, using 106 trajectories obtained from the equations of motion in eqn (16) to generate tightly converged results.The Debye–Drude form of the spectral density described in eqn (11) is discretized into 500 oscillators,53 with frequencies  and coupling constants
and coupling constants  , where j = 1,…,N and ωm = 20/τ is the cutoff frequency for the oscillators. The solvent reorganization energy for the donor and the acceptor baths is λD = λA = 100 cm−1, and the solvent response time is τ = 0.1 ps. These parameters are chosen to be consistent with natural light harvesting systems.11,41
, where j = 1,…,N and ωm = 20/τ is the cutoff frequency for the oscillators. The solvent reorganization energy for the donor and the acceptor baths is λD = λA = 100 cm−1, and the solvent response time is τ = 0.1 ps. These parameters are chosen to be consistent with natural light harvesting systems.11,41
The time-dependent reduced density matrix ρij(t) is calculated as described in eqn (13), using ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0)w = 1/2[|D1〉〈D1| + |D2〉〈D2|](
(0)w = 1/2[|D1〉〈D1| + |D2〉〈D2|](![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b)w for the Δ = 0 case and
b)w for the Δ = 0 case and ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0)w = |D1〉〈D1|(
(0)w = |D1〉〈D1|(![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b)w for the Δ = ±200 cm−1 cases where (
b)w for the Δ = ±200 cm−1 cases where (![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) b)w are evaluated in the manner of eqn (19).
b)w are evaluated in the manner of eqn (19).
The EET rate constant is calculated using eqn (14). Although the Wigner transformed thermal flux operator (e−βĤ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) )w could be sampled exactly from a path-integral Monte-Carlo based procedure,54,55 we use an approximate expression,14,42 as described in eqn (17)–(19).
)w could be sampled exactly from a path-integral Monte-Carlo based procedure,54,55 we use an approximate expression,14,42 as described in eqn (17)–(19).
For the case of dimeric donor and monomeric acceptor, the site and flux operators are ĥ = |A〉〈A| and
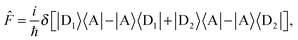 | (20) |
 | (21) |
5 Results
We now present numerical results and analysis for EET between monomeric and dimeric chromophore complexes.5.1 Dynamic coherence in multimeric EET process
We begin by demonstrating the appearance of dynamic coherence in intra-complex EET, for the model system with a dimeric donor complex and a monomeric acceptor complex. For simplicity, we assume that the site energies of the two chromophores in the dimeric complex are degenerate (i.e., εD1 = εD2 = εD for the case of a dimeric donor); the more general case of non-degenerate chromophore dimers will be discussed in Section 5.3. The donor–acceptor energetic gap ε = εD − εA = 500 cm−1 and inter-complex electronic coupling δ = 5 cm−1. The remaining parameters, as well as the initial conditions for these calculations, are described in Section 4.
Fig. 3a and b presents the real and imaginary components of the intra-complex dynamic coherence 〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)|D2〉, as defined in eqn (2). These results demonstrate that the amount of dynamic coherence depends upon the magnitude and sign of the intra-complex electronic coupling, Δ. As the sign of Δ changes from positive to negative values, the dynamic coherence changes correspondingly.
(t)|D2〉, as defined in eqn (2). These results demonstrate that the amount of dynamic coherence depends upon the magnitude and sign of the intra-complex electronic coupling, Δ. As the sign of Δ changes from positive to negative values, the dynamic coherence changes correspondingly.
Fig. 3c presents the time-dependence of the exciton population on the donor complex, 〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)|D1〉 + 〈D2|
(t)|D1〉 + 〈D2|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)|D2〉. This result indicates that the EET kinetics are also strongly influenced by intra-complex coupling. By varying Δ from 200 to −200 cm−1, the EET rate accelerates by nearly a factor of five.
(t)|D2〉. This result indicates that the EET kinetics are also strongly influenced by intra-complex coupling. By varying Δ from 200 to −200 cm−1, the EET rate accelerates by nearly a factor of five.
These results are consistent with recent theoretical results12,21 which illustrate that intra-complex dynamic coherence correlates with the inter-complex EET kinetics. The results might be interpreted to suggest that the EET rate is sensitive to an important role of dynamic coherence; however, in the next sections, we show that if we derive a parameterization of the model that preserves the effects of static coherence in Fig. 3 while largely eliminating the intra-complex dynamic coherence, then the EET kinetics are essentially unchanged.
5.2 Reparametrization of the model
In this section, we derive an alternative parameterization of the system from Section 5.1. In particular, for any original set of parameters for the model, we derive an alternative set of parameters that preserves the effects of static coherence while strictly eliminating the intra-complex electronic coupling, Δ. We end this section by demonstrating that the alternative parameterization largely (and in some cases exactly) eliminates the dynamic coherence for the EET processes studied here.In order to develop an alternative parameterization of the model that eliminates the intra-complex electronic coupling, we follow previous theoretical work40,56 that compares MC-FRET theory,15–17 a rate theory for energy transfer among weakly-coupled multimeric complexes, in both the site and exciton bases. We begin by expressing MC-FRET rate for the system with the original parameterization
 | (22) |
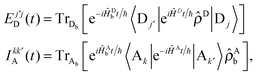 | (23) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) D = e−βĤD/ZD and
D = e−βĤD/ZD and  . The notation TrDb[⋯] indicates the trace taken over the bath degrees of freedom associated with the donor complex.
. The notation TrDb[⋯] indicates the trace taken over the bath degrees of freedom associated with the donor complex.
We now switch from the MC-FRET expression in the chromophore site basis (eqn (22) and (23)) to the corresponding expression in terms of the subsystem exciton representation, for which the basis functions {|α〉} and {|γ〉} satisfy
| ĤDs|α〉 = εα|α〉 and ĤAs|γ〉 = εγ|γ〉. | (24) |
 | (25) |
 | (26) |
 | (27) |
 .
.
Comparison of the MC-FRET rate expressions in the site and exciton bases reveals two ways in which static coherence impacts the EET rate. Firstly, static coherence simply shifts the eigenspectrum εα and εγ associate with donor and acceptor complexes, due to the electronic coupling between the sites. Secondly, comparison of eqn (22) and (26) reveals that static coherence leads to the rescaling of the inter-complex coupling δjk by a factor of cjα*ckγ. Both of these effects have been emphasized in previous work.11,12,40
This analysis shows that for any original parameterization of the model system in the site basis, we can prescribe an alternative parameterization also in the site basis such that the effects of static coherence are preserved and intra-complex electronic coupling is strictly eliminated. Table 1 summarizes the way in which this Static Coherence Preserving (SCP) parameterization of the model can be obtained from the original parameterization; more general expressions for the SCP parameterization are provided in Appendix B.
Note that in the SCP parameterization of the model, the bath modes remain diagonally coupled to the single-chromophore states; the Hamiltonian in the SCP parameterization is thus not an exact similarity transform of the Hamiltonian in the original parameterization. The SCP parameterization should be viewed as a procedure to construct a new system with site energies and inter-complex couplings that preserve the effects of static coherence in an original system, while (as is now shown) largely eliminating dynamic coherence.
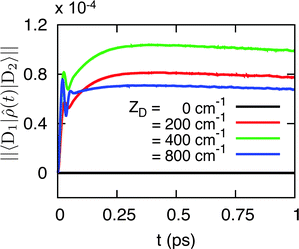
Finally, we numerically demonstrate that the SCP parametrization largely eliminates intra-complex dynamic coherence during the EET process. In Fig. 4 we present the modulus of dynamic coherence ∥〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)|D2〉∥ for the SCP-parametrized model. We consider the SCP parametrization that corresponds to the original parameterization with Δ = −200 cm−1, donor–acceptor energetic gap ε = εD − εA = 500 cm−1, inter-complex electronic coupling δ = 5 cm−1, and a range of values for the intra-complex energy gap ZD = εD1 − εD2. The initial condition for these calculations is 〈D1|
(t)|D2〉∥ for the SCP-parametrized model. We consider the SCP parametrization that corresponds to the original parameterization with Δ = −200 cm−1, donor–acceptor energetic gap ε = εD − εA = 500 cm−1, inter-complex electronic coupling δ = 5 cm−1, and a range of values for the intra-complex energy gap ZD = εD1 − εD2. The initial condition for these calculations is 〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) |D1〉 = 〈D2|
|D1〉 = 〈D2|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) |D2〉 = 1/2.
|D2〉 = 1/2.
It is clear from the figure that in all cases the intra-complex is dramatically reduced from the levels seen in Fig. 3a and b, and for the special case of degenerate donor chromophores (ZD = 0) and symmetric donor–acceptor coupling (δD1A = δD2A), the intra-complex dynamic coherence vanishes completely. Similar results are obtained for Δ = 200 cm−1 with a range of values for ZD (not shown).
For any original parameterization of the model, we have derived an alternative parametrization that preserves the effects of static coherence while largely (and some cases exactly) eliminating dynamic coherence. In the next section, we will directly compare the EET kinetics for the two different parameterizations to examine the isolated effects of dynamic coherence in the EET process.
5.3 The role of dynamic coherence in EET kinetics
Having derived the SCP parameterization to isolate the effects of dynamic coherence from those of static coherence, we return to the model system with a donor complex comprised of a symmetric dimer of chromophores and a monomeric acceptor complex that was studied in Section 5.1.
Fig. 5 compares the EET dynamics obtained for the two parameterizations with a range of values for the electronic coupling. In each case, the results for the SCP parameterization are obtained from the mapping of the original parameterization described in Table 1; furthermore, the initial condition 〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) |D1〉 = 〈D2|
|D1〉 = 〈D2|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) |D2〉 = 1/2 employed for the SCP parameterization was chosen such that the initial exciton population matches that which was considered for the original parameterization (Fig. 3).
|D2〉 = 1/2 employed for the SCP parameterization was chosen such that the initial exciton population matches that which was considered for the original parameterization (Fig. 3).
 | ||
| Fig. 5 EET dynamics for the model with a dimeric donor and monomeric acceptor, comparing the original parameterization (solid curves) and the SCP parameterization (dashed curves). (a) The exciton population on the donor complex. (b) The normalized flux–flux correlation function, Cff(t)/Cff(0). The solid curves in part (a) are identical to those in Fig. 3c. | ||
In Fig. 5a, we present the time-dependence of the exciton population on the donor complex, 〈D1|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)|D1〉 + 〈D2|
(t)|D1〉 + 〈D2|![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t)|D2〉, for the two different parameterizations; the results from the original parameterization are identical to those presented in Fig. 3c. The similarity of the exponential decay in each case makes clear that the kinetics of EET for the two parameterizations is nearly identical. Fig. 5b presents the normalized flux–flux correlation function Cff(t)/Cff(0) for the EET process, which shows that the transient dynamics associated with inter-complex EET is also nearly identical for the two parameterizations. Taken together, these results indicate the static coherence effects play a major role in the kinetics of EET, whereas dynamic coherence makes a much smaller contribution.
(t)|D2〉, for the two different parameterizations; the results from the original parameterization are identical to those presented in Fig. 3c. The similarity of the exponential decay in each case makes clear that the kinetics of EET for the two parameterizations is nearly identical. Fig. 5b presents the normalized flux–flux correlation function Cff(t)/Cff(0) for the EET process, which shows that the transient dynamics associated with inter-complex EET is also nearly identical for the two parameterizations. Taken together, these results indicate the static coherence effects play a major role in the kinetics of EET, whereas dynamic coherence makes a much smaller contribution.
Fig. 6 further illustrates this point by presenting the EET rates for the system discussed in Fig. 5. Indeed, across a wide range of electronic couplings for the original parameterization, the corresponding SCP parameterization exhibits essentially identical rates for inter-complex EET across all regimes.
The turnover behavior seen in Fig. 6 as a function of electronic coupling21 has previously been attributed to a balance between intra-complex dynamic coherence and dissipation to the bath,25,28 which is seemingly inconsistent with the fact that the SCP parameterization (for which dynamic coherence is largely eliminated) still exhibits the turnover behavior. We now investigate the mechanistic origin of this turnover behavior.
The energy-level diagrams at the right of Fig. 6 illustrate how the electronic coupling in the original parameterization leads to a shift of the site energies in the SCP parameterization. For the original parametrization, the donor complex consists of a symmetric dimer (shown at center in red) with a donor–acceptor energy gap of ε = εD − εA, and the two donor chromophores are equally coupled to the acceptor chromophore by δ. In the corresponding SCP parameterization, only one of the two donor chromophores remains coupled to the acceptor chromophore (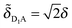 ,
, ![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) D2A = 0) and the energy gap associated with the donor state with non-zero coupling is shifted to a value of
D2A = 0) and the energy gap associated with the donor state with non-zero coupling is shifted to a value of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = εD − εA + Δ. As in the turnover behavior illustrated in Fig. 2c (and also as in the familiar Marcus theory for electron transfer), the relative values of the energy gap
= εD − εA + Δ. As in the turnover behavior illustrated in Fig. 2c (and also as in the familiar Marcus theory for electron transfer), the relative values of the energy gap ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) and the total solvent reorganization energy determine whether the system in Fig. 6 is in the normal, activationless, or inverted regimes. Indeed, the observed turnover in Fig. 6 occurs precisely at the Marcus theory prediction of
and the total solvent reorganization energy determine whether the system in Fig. 6 is in the normal, activationless, or inverted regimes. Indeed, the observed turnover in Fig. 6 occurs precisely at the Marcus theory prediction of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) = λ, for which Δ = −300 cm−1, since εD − εA = 500 cm−1 and λ = 200 cm−1. We thus see that the turnover behavior in Fig. 6 is simply due to a static coherence effect, namely the alignment of the donor and acceptor energy levels that exhibit non-zero coupling, rather than a dynamic coherence effect.
= λ, for which Δ = −300 cm−1, since εD − εA = 500 cm−1 and λ = 200 cm−1. We thus see that the turnover behavior in Fig. 6 is simply due to a static coherence effect, namely the alignment of the donor and acceptor energy levels that exhibit non-zero coupling, rather than a dynamic coherence effect.
Finally, Fig. 7 explores the competing roles of static and dynamic coherence in the EET kinetics for the model system comprised of a monomeric donor complex and an asymmetric dimeric acceptor complex. In the original parameterization, both acceptor chromophores are coupled to the donor chromophore by δ = 5 cm−1, the electronic coupling among the acceptor chromophores assumes values of Δ = ±200 cm−1, and a range of asymmetries between the acceptor site energies ZA = εA1 − εA2 is explored while keeping the donor–acceptor energetic gap εD − (εA1 + εA2)/2 fixed at a value of 500 cm−1. In addition to the EET rates for the system in the original parameterization (red, blue), the figure also presents the corresponding results for the SCP parameterization that largely eliminates dynamic coherence. It is clear that that the rates for the two parameterizations are nearly identical; as for the previously considered case of a dimeric donor complex and a monomeric acceptor complex (Fig. 6), this version of the model indicates that static coherence plays a dominant role in determining the EET kinetics, whereas dynamic coherence plays only a minimal role.
6 Conclusions
In this work, we have used real-time path-integral simulations to characterize the roles of dynamic and static electronic coherence in inter-complex excitation energy transfer (EET) processes that involve multimeric donor and acceptor complexes. Focusing on the regime of weak inter-complex coupling that is of relevance to many light-harvesting networks, we develop a strategy for mapping any original parameterization of the considered system-bath model to an alternative parameterization that preserves the effects of static coherence (including inter-complex energy level alignment) while eliminating dynamic coherence, thus enabling the analysis of the relative impact of these two types of electronic coherence. Across many different regimes for intra-complex coupling and site-energy bias, and considering the cases of EET from a dimeric donor complex to a monomeric acceptor complex and from a monomeric donor complex to a dimeric acceptor complex, we find that both the kinetics of EET and the transient EET population dynamics are almost entirely dominated by static coherence effects; dynamic coherence is found to cause only minor effects. In particular, this conclusion is found to hold for EET systems that exhibit an inversion in the EET rate as a function of intra-complex electronic coupling (Fig. 6), which had in some cases been previously attributed to a dynamic electronic coherence effect. Although the results presented here do not preclude the role of interesting dynamic electronic coherence effects in regimes of larger inter-complex electronic coupling,26,27 nor are they inconsistent with previous findings for the role of vibrational coherence effects,57–64 the conclusions of the present work suggest that static electronic coherence effects are a more important consideration than dynamic electronic coherence effects in the analysis and design of efficient inter-complex EET kinetics for light-harvesting networks. These conclusions are thus consistent with the historical view that emphasizes the importance of energy-level alignment for efficient incoherent energy transfer (i.e., hopping), while suggesting a less important role for more exotic electronic coherence effects that have been recently emphasized.7 Appendix A: Fermi Golden Rule rate
The FGR rate expression is employed in Fig. 2 is | (28) |
 | (29) |
 | (30) |
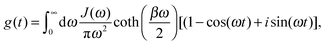 | (31) |
8 Appendix B: general SCP parameterization
Here, we provide expressions for the SCP parametrization for the general case of multimeric donors and acceptor complexes. These relations are summarized in Table 2. For the notation in the table, j and j′ index the chromophores in the donor complex, k and k′ index the chromophores in the acceptor complex. As shown in eqn (24) and (25), the sets {εα} and {εγ} corresponds to the intra-complex energy eigenvalues for the donor and acceptor, respectively, and {cαj} and {cγk} are the associated expansion coefficients for the energy eigenvectors.Acknowledgements
This work was supported by the National Science Foundation (NSF) CAREER Award under Grant No. CHE-1057112. Additionally, T.F.M. acknowledges support from a Camille and Henry Dreyfus Foundation New Faculty Award and an Alfred P. Sloan Foundation Research Fellowship. Computing resources were provided by NERSC (DE-AC02-05CH11231) and XSEDE (TG-CHE130108).References
- R. E. Blankenship, Molecular Mechanism of Photosynthesis, Wiley-Blackwell, 2014 Search PubMed.
- G. Panitchayangkoon, D. V. Voronine, D. Abramavicius, J. R. Carama, N. H. C. Lewis, S. Mukamel and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20908 CrossRef CAS PubMed; G. Panitchayangkoona, D. Hayes, K. A. Fransted, J. R. Caram, E. Harel, J. Wen, R. E. Blankenship and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12766 CrossRef PubMed; G. S. Engel, T. R. Calhoun, E. L. Read, T.-K. Ahn, T. Mancal, Y.-C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782 CrossRef PubMed.
- E. Collini, C. Y. Wong, K. E. Wilk, P. M. G. Curmi, P. Brumer and G. D. Scholes, Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature, Nature, 2010, 463, 644 CrossRef CAS PubMed.
- E. Harel and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 706 CrossRef CAS PubMed; A. F. Fidler, V. P. Singh, P. D. Long, P. D. Dahlberg and G. S. Engel, J. Phys. Chem. Lett., 2013, 4, 1404 CrossRef PubMed; E. Harel and G. S. Engel, Nat. Commun., 2014, 5, 3286 Search PubMed.
- G. S. Schlau-Cohen, A. Ishizaki, T. R. Calhoun, N. S. Ginsberg, M. Ballottari, R. Bassi and G. R. Fleming, Nat. Chem., 2012, 4, 389 CrossRef CAS PubMed; G. S. Schlau-Cohen, T. R. Calhoun, N. S. Ginsberg, M. Ballottari, R. Bassi and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2012, 107, 13276 CrossRef PubMed.
- E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. van Grondelle, Nat. Phys., 2014, 10, 676 Search PubMed.
- E. Cassette, R. D. Pensack, B. Mahler and G. D. Scholes, Nat. Commun., 2015, 6, 6086 Search PubMed.
- D. Hayes, G. B. Griffin and G. S. Engel, Science, 2013, 340, 1431 CrossRef CAS PubMed.
- G. B. Griffin, P. M. Lundin, B. S. Rolczynski, A. Linkin, R. D. McGillicuddy, Z. Bao and G. S. Engel, J. Chem. Phys., 2014, 140, 034903 CrossRef PubMed.
- T. Mancalc, J. Phys. Chem. B, 2013, 117, 11282 CrossRef PubMed.
- J. Strümpfer, M. Sener and K. Schulten, J. Phys. Chem. Lett., 2012, 3, 536 CrossRef PubMed.
- I. Kassal, J. Yuen-Zhou and S. Rahimi-Keshari, J. Phys. Chem. Lett., 2013, 4, 362 CrossRef CAS PubMed.
- P. Huo and D. F. Coker, J. Chem. Phys., 2011, 135, 201101 CrossRef PubMed.
- P. Huo, T. F. Miller III and D. F. Coker, J. Chem. Phys., 2013, 139, 151103 CrossRef PubMed.
- S. Jang, M. D. Newton and R. J. Silbey, Phys. Rev. Lett., 2004, 92, 218301 CrossRef PubMed; S. Jang, M. D. Newton and R. J. Silbey, J. Chem. Phys., 2007, 127, 174710 CrossRef PubMed.
- H. Sumi, J. Phys. Chem. B, 1999, 103, 252 CrossRef CAS.
- J. Ma and J. Cao, J. Chem. Phys., 2015, 142, 094106 CrossRef PubMed; J. Ma, J. Moix and J. Cao, J. Chem. Phys., 2015, 142, 094107 CrossRef PubMed; J. Moix, J. Ma and J. Cao, J. Chem. Phys., 2015, 142, 094108 CrossRef PubMed.
- F. Fassioli, R. Dinshaw, P. C. Arpin and G. D. Scholes, J. R. Soc., Interface, 2013, 11, 20130901 CrossRef PubMed.
- G. Raszewski, W. Saenger and T. Renger, J. Am. Chem. Soc., 2008, 130, 4431 CrossRef CAS PubMed; D. I. G. Bennett, K. Amarnath and G. R. Fleming, J. Am. Chem. Soc., 2013, 135, 9164 CrossRef PubMed.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55 CrossRef CAS PubMed.
- A. Ishizaki and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17255 CrossRef PubMed.
- Q. Ai, T.-C. Yen, B.-Y. Jin and Y.-C. Cheng, J. Phys. Chem. Lett., 2013, 4, 2577 CrossRef CAS.
- S. Hoyer, A. Ishizaki and K. B. Whaley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041911 CrossRef PubMed.
- P. Huo and D. F. Coker, J. Phys. Chem. Lett., 2011, 2, 825 CrossRef CAS.
- F. Caruso, A. W. Chin, A. Datta, S. F. Huelga and M. B. Plenio, J. Chem. Phys., 2009, 131, 105106 CrossRef; A. W. Chin, A. Datta, F. Caruso, S. F. Huelga and M. B. Plenio, New J. Phys., 2010, 12, 065002 CrossRef.
- N. Renaud, D. Powell, A. Zarea, B. Movaghar, M. R. Wasielewski and M. A. Ratner, J. Phys. Chem. A, 2013, 117, 5899 CrossRef CAS PubMed.
- M. Zarea, D. Powell, N. Renaud, M. R. Wasielewski and M. A. Ratner, J. Phys. Chem. B, 2013, 117, 1010 CrossRef CAS PubMed.
- K. M. Pelzer, T. Can, S. K. Gray, D. K. Morr and G. S. Engel, J. Phys. Chem. B, 2014, 118, 2693 CrossRef CAS PubMed.
- T. C. Berkelbach, T. E. Markland and D. R. Reichman, J. Chem. Phys., 2012, 136, 084104 CrossRef PubMed.
- H. W. Kim, A. Kelly, J. W. Park and Y. M. Rhee, J. Am. Chem. Soc., 2012, 134, 11640 CrossRef CAS PubMed.
- M. del Rey, A. W. Chin, S. F. Huelga and M. B. Plenio, J. Phys. Chem. Lett., 2013, 4, 903 CrossRef PubMed.
- P. Bhattacharyya and K. L. Sebastian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062712 CrossRef PubMed.
- C. Creatore, M. A. Parker, S. Emmott and A. W. Chin, Phys. Rev. Lett., 2013, 111, 253601 CrossRef CAS PubMed; Y. Zhang, S. Oh, F. H. Alharbi, G. S. Engel and S. Kais, Phys. Chem. Chem. Phys., 2015, 17, 5743 RSC.
- R. Tempelaar, F. C. Spano, J. Knoester and T. L. C. Jansen, J. Phys. Chem. Lett., 2014, 5, 1505 CrossRef CAS PubMed.
- A. Chenu, P. Maly and T. Mancal, Chem. Phys., 2014, 439, 100 CrossRef CAS.
- J. M. Anna, G. D. Scholes and R. van Grondelle, BioScience, 2013, 64, 14 CrossRef.
- S. Jang and Y.-C. Cheng, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 84 CAS.
- M. Sarovar, A. Ishizaki, G. R. Fleming and K. B. Whaley, Nat. Phys., 2010, 6, 462 Search PubMed.
- A. S. Davydov, Theory of Molecular Excitons, Plenum, New York, 1971 Search PubMed.
- C. Chuang, J. Knoester and J. Cao, J. Phys. Chem. B, 2014, 118, 7827 CrossRef CAS PubMed.
- A. Ishizaki and G. R. Fleming, J. Chem. Phys., 2009, 130, 234111 CrossRef PubMed.
- H. Wang, X. Song, D. Chandler and W. H. Miller, J. Chem. Phys., 1999, 110, 4828 CrossRef CAS.
- W. H. Miller, S. D. Schwartz and J. W. Tromp, J. Chem. Phys., 1983, 79, 4889 CrossRef CAS.
- G. A. Voth, D. Chandler and W. H. Miller, J. Phys. Chem., 1989, 93, 7009 CrossRef CAS.
- W. Xie, S. Bai, L. Zhu and Q. Shi, J. Phys. Chem. A, 2013, 117, 6196 CrossRef CAS PubMed.
- J. O. Richardson and M. Thoss, J. Chem. Phys., 2014, 141, 074106 CrossRef PubMed.
- H. D. Meyer and W. H. Miller, J. Chem. Phys., 1979, 70, 3214 CrossRef CAS; G. Stock and M. Thoss, Phys. Rev. Lett., 1997, 78, 578 CrossRef; G. Stock and M. Thoss, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 64 CrossRef.
- P. Rebentrost, M. Mohseni and A. Aspuru-Guzik, J. Phys. Chem. B, 2009, 113, 9942 CrossRef CAS PubMed.
- J. Cao and R. J. Silbey, J. Phys. Chem. A, 2009, 113, 13825 CrossRef CAS PubMed; J. Moix, J. Wu, P. Huo, D. F. Coker and J. Cao, J. Phys. Chem. Lett., 2011, 2, 3045 CrossRef.
- J. Ulstrup and J. Jortner, J. Chem. Phys., 1975, 63, 4358 CrossRef CAS.
- M. Topaler and N. Makri, J. Phys. Chem., 1996, 100, 4430 CrossRef CAS.
- J. N. Onuchic and P. G. Wolynes, J. Phys. Chem., 1988, 92, 6495 CrossRef CAS.
- P. Huo and D. F. Coker, Mol. Phys., 2012, 110, 1035 CrossRef CAS.
- C.-Y. Hsieh and R. Kapral, Entropy, 2014, 16, 200 CrossRef.
- N. Ananth and T. F. Miller III, J. Chem. Phys., 2010, 133, 234103 CrossRef PubMed.
- L. Cleary, H. Chen, C. Chuang, R. J. Silbey and J. Cao, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8537 CrossRef CAS PubMed.
- D. B. Turner, R. Dinshaw, K.-K. Lee, M. S. Belsley, K. E. Wilk, P. M. G. Curmi and G. D. Scholes, Phys. Chem. Chem. Phys., 2012, 14, 4857 RSC.
- N. Christensson, H. F. Kauffmann, T. Pullerits and T. Mancal, J. Phys. Chem. B, 2012, 116, 7449 CrossRef CAS PubMed.
- V. Tiwari, W. K. Peters and D. M. Jonas, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203 CrossRef CAS PubMed.
- M. B. Plenio, J. Almeida and S. F. Huelga, J. Chem. Phys., 2013, 139, 235102 CrossRef CAS PubMed.
- E. J. O'Reilly and A. Olaya-Castro, Nat. Commun., 2014, 5, 3012 Search PubMed.
- A. W. Chin, J. Prior, R. Rosenbach, F. Caycedo-Soler, S. F. Huelga and M. B. Plenio, Nat. Phys., 2013, 9, 113 Search PubMed.
- E. Collini and G. D. Scholes, Science, 2009, 323, 369 CrossRef CAS PubMed.
- M. J. Bedard-Hearn, F. Sterpone and P. J. Rossky, J. Phys. Chem. A, 2010, 114, 7661 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2015 |




![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif)