Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying solvated electrons' delocalization†
Benjamin G.
Janesko
*a,
Giovanni
Scalmani
b and
Michael J.
Frisch
b
aTexas Christian University, Fort Worth, TX 76129, USA. E-mail: b.janesko@tcu.edu
bGaussian, Inc., 340 Quinnipiac St. Bldg. 40, Wallingford, CT 06492, USA
First published on 21st May 2015
Abstract
Delocalized, solvated electrons are a topic of much recent interest. We apply the electron delocalization range EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u) (J. Chem. Phys., 2014, 141, 144104) to quantify the extent to which a solvated electron at point
;u) (J. Chem. Phys., 2014, 141, 144104) to quantify the extent to which a solvated electron at point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) in a calculated wavefunction delocalizes over distance u. Calculations on electrons in one-dimensional model cavities illustrate fundamental properties of the EDR. Mean-field calculations on hydrated electrons (H2O)n− show that the density-matrix-based EDR reproduces existing molecular-orbital-based measures of delocalization. Correlated calculations on hydrated electrons and electrons in lithium–ammonia clusters illustrates how electron correlation tends to move surface- and cavity-bound electrons onto the cluster or cavity surface. Applications to multiple solvated electrons in lithium–ammonia clusters provide a novel perspective on the interplay of delocalization and strong correlation central to lithium–ammonia solutions' concentration-dependent insulator-to-metal transition. The results motivate continued application of the EDR to simulations of delocalized electrons.
in a calculated wavefunction delocalizes over distance u. Calculations on electrons in one-dimensional model cavities illustrate fundamental properties of the EDR. Mean-field calculations on hydrated electrons (H2O)n− show that the density-matrix-based EDR reproduces existing molecular-orbital-based measures of delocalization. Correlated calculations on hydrated electrons and electrons in lithium–ammonia clusters illustrates how electron correlation tends to move surface- and cavity-bound electrons onto the cluster or cavity surface. Applications to multiple solvated electrons in lithium–ammonia clusters provide a novel perspective on the interplay of delocalization and strong correlation central to lithium–ammonia solutions' concentration-dependent insulator-to-metal transition. The results motivate continued application of the EDR to simulations of delocalized electrons.
I. Introduction
Solvated electrons are a classic chemical system that has attracted much study.1 Mobile2 solvated electrons are responsible for the blue color of dilute lithium–ammonia solutions and the transition to a metallic state seen at high lithium concentrations.3–5 Hydrated electrons are important intermediates in radiation chemistry and in many biological processes.6 Electronic structure calculations have contributed to the understanding of solvated electrons.4,6–10 Calculated vertical detachment energies (VDEs) for electrons solvated in water clusters (H2O)n− suggest11,12 that experimental photoelectron spectra13 may arise from surface-bound electrons. Mixed quantum–classical dynamics simulations suggest models for electrons in bulk water14 and lithium–ammonia solutions.15–17 Several recent studies highlight the importance of the quantum–classical interaction potential.10,18,19 All-electron calculations provide additional insights.4,20–22Ref. 23 provides a recent perspective on the role of delocalization in electron solvation.Solvated electrons' behavior depends on the interplay of electron delocalization and electron–electron correlation. Delocalization denotes the nonclassical “coherence” of electrons between different points in space, e.g., the off-diagonal terms in Fig. 1. This off-diagonal delocalization24 is central to covalent bonding and reactivity. Delocalization is particularly important for highly delocalized solvated electrons.25 Correlation denotes all effects excluded from a mean-field (Hartree–Fock, HF) calculation, including dispersion (van der Waals) interactions. Correlation is important for the stability of solvated electrons,26–35 as well as for lithium–ammonia solutions' transition to the metallic state.4,36
 | ||
| Fig. 1 γ(x;x′) (left) and EDR(x;u) (right) for boxes containing N = 1, 2, 3, 10 noninteracting spinless Fermions. The red line through the N = 3 points γ(L/3,x′) is discussed in the text. | ||
Existing electronic structure methods can accurately treat solvated electrons' VDE.27–29,35 However, quantifying solvated electrons' delocalization remains challenging. Most analyses of delocalization are based on the highest occupied molecular orbital (MO) or spin density from a HF or density functional theory (DFT) wavefunction.4,29 This approach has limitations. MOs are not uniquely defined in many-electron wavefunctions.37 Hartree–Fock MOs and spin densities do not include correlation effects.38 DFT MOs come from a reference system of noninteracting39,40 or partially interacting41 Fermions, which is generally more delocalized than the real system. (The exact Kohn–Sham wavefunction is arguably at least as delocalized as the exact interacting wavefunction, because the Kohn–Sham kinetic energy Ts[ρ] is bound by the exact kinetic energy Ts[ρ] ≤ T[ρ].) Attempts to address these limitations include analyses of DFT electron densities,15–17,42–44 the electron localization function,45,46 and nearly-singly-occupied natural orbitals from correlated wavefunctions.34,35,47–49 New tools to quantify delocalization could complement and extend this work.
We recently proposed the electron delocalization range (EDR) to quantify and visualize electron delocalization.50 The EDR is based on the nonlocal one-particle density matrix γ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,
,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) of a calculated N-electron wavefunction Ψ(
′) of a calculated N-electron wavefunction Ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,
1,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2…
2…![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N),
N),
γ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , ,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) ≡ N∫d3 ′) ≡ N∫d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2…d3 2…d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) NΨ( NΨ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , ,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2… 2…![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N)Ψ*( N)Ψ*(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′, ′,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2… 2…![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N). N). | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,
,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) gives the probability that an electron delocalizes between points
′) gives the probability that an electron delocalizes between points ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′. Diagonal elements lim
′. Diagonal elements lim![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′→
′→![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) γ(
γ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,
,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) = ρ(
′) = ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) give the probability density for finding an electron at
) give the probability density for finding an electron at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) . Bonding interactions between atoms A and B typically correspond to γ(
. Bonding interactions between atoms A and B typically correspond to γ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ∈ A,
∈ A,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′ ∈ B) > 0. The EDR quantifies the degree to which an electron at
′ ∈ B) > 0. The EDR quantifies the degree to which an electron at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) delocalizes over distance |
delocalizes over distance |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′| by contracting γ(
′| by contracting γ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,
,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) with a test function of |
′) with a test function of |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′| that decays over some length scale u:
′| that decays over some length scale u:EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,u) = ∫d3 ,u) = ∫d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′gu( ′gu(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , ,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′)γ( ′)γ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , ,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) ′) | (2) |
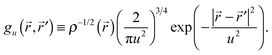 | (3) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u)|2 ≤ 1. Our choice of a Gaussian test function enables analytic integration over
;u)|2 ≤ 1. Our choice of a Gaussian test function enables analytic integration over ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′ in eqn (2), when the molecular orbitals and γ are expanded in standard atom-centered Gaussian basis sets. Global descriptors of delocalization may be obtained from density–weighed averages
′ in eqn (2), when the molecular orbitals and γ are expanded in standard atom-centered Gaussian basis sets. Global descriptors of delocalization may be obtained from density–weighed averages〈EDR(u)〉 = ∫d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′ρ( ′ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )EDR( )EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u), ;u), | (4) |
| ΔEDR(A − B;u) = 〈EDR(u)〉(A) − 〈EDR(u)〉(B). | (5) |
Our previous work showed that the EDR effectively characterizes the delocalization of electrons across multiple length scales.50 EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u) at small distances u ∼ 0.1 Angstrom peaks at points
;u) at small distances u ∼ 0.1 Angstrom peaks at points ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) in the cores of first-row atoms. EDR(
in the cores of first-row atoms. EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u) at larger distances u ∼ 0.5 Angstrom peaks at points
;u) at larger distances u ∼ 0.5 Angstrom peaks at points ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) around the localized lone pairs of, e.g., oxygen atoms. EDR(
around the localized lone pairs of, e.g., oxygen atoms. EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u) at u ∼ 0.6 Angstrom peaks at points
;u) at u ∼ 0.6 Angstrom peaks at points ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) in C–C and C–H bonds. Calculations on a model cavity-bound hydrated electron7,8,51 (H2O)6− showed that EDR(
in C–C and C–H bonds. Calculations on a model cavity-bound hydrated electron7,8,51 (H2O)6− showed that EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u) at points
;u) at points ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) inside the cavity peaked at increasingly large u (from 1.4 Angstrom to 3.3 Angstrom) as the cavity radius increased. Calculations on the strongly correlated electron pair in stretched singlet H2 showed that the EDR quantifies the interplay of delocalization and strong correlation.52–57 These preliminary results motivate further exploration of the EDR for solvated electrons.
inside the cavity peaked at increasingly large u (from 1.4 Angstrom to 3.3 Angstrom) as the cavity radius increased. Calculations on the strongly correlated electron pair in stretched singlet H2 showed that the EDR quantifies the interplay of delocalization and strong correlation.52–57 These preliminary results motivate further exploration of the EDR for solvated electrons.
This work applies the EDR to several problems relevant to solvated electrons. Calculations on simple model systems show how the EDR quantifies “off-diagonal” coherence lengths and electron correlation effects on delocalization. Hartree–Fock calculations on hydrated electrons (H2O)n− show that EDR-based descriptors reproduce existing MO-based measures of hydrated electrons' delocalization.29 Correlated calculations on (H2O)n− and lithium–ammonia clusters4 show that the EDR illustrates localization of surface-bound electrons onto cluster surfaces, and delocalization of cavity-bound electrons onto cavity walls. Calculations on spin-paired diamagnetic species in lithium–ammonia clusters,4 and multireference calculations on multiple solvated electrons,15–17 illustrate the interplay of delocalization and strong correlation relevant to the transition to the metallic state. These results motivate further application of the EDR to delocalized electrons.
II. Computational methods
All molecular calculations use the development version of the Gaussian suite of programs.58 The EDR is evaluated using one-particle density matrices from Hartree–Fock, generalized Kohn–Sham density functional theory (DFT),39,40,59 post-Hartree–Fock, or multireference calculations. Second-order many-body perturbation theory (MP2) and coupled cluster with singles and doubles (CCSD) calculations use the Gaussian default choice of frozen core orbitals. Brückner doubles (BD) calculations60,61 and complete active space self-consistent field (CASSCF) calculations correlate all electrons. Post-Hartree–Fock density matrices are evaluated using the Z-vector method,38,62 with Gaussian keyword “Density = Current”. DFT calculations use various approximate exchange–correlation (XC) functionals. These include the local spin-density approximation with Vosko–Wilk–Nusair correlation functional V (LSDA),63 Becke's three-parameter global hybrid incorporating Lee–Yang–Parr correlation (B3LYP),64–67 the half-and-half global hybrid BHLYP,68 and the long-range-corrected hybrid LC-ωPBE.69 Molecular calculations on open-shell systems are performed spin-unrestricted unless noted otherwise. Molecular calculations evaluate the EDR as described previously.50,70 〈EDR(u)〉 is evaluated by numerical integration of eqn (4) using a standard DFT numerical integration grid.71 The descriptor uav, discussed below, is obtained from a three-point fit to 〈EDR(uj)〉 from an even-tempered set of {uj}.Pictures of calculated molecular geometries use a “ball-and-stick” description of chemical bonds. For example the O–H bonds in the water clusters of Fig. 4 are drawn as lines between the O and H atoms. These bond orders are included solely as a guide to the eye.
Other details of the individual calculations are as follows. The calculations on 1D systems in Section III A, and some test calculations in Section III B 2, use a Mathematica worksheet provided as ESI.† Calculations on H2O and H2O− in Section III A use the aug-cc-pVQZ basis set72,73 and the anion's HF/aug-cc-pVTZ geometry. Calculations on the (H2O)N− clusters in Section III B use the cluster geometries reported in ref. 29, and the 6-31(+,3+)G(d) basis set shown in ref. 27–29 to be suitable for post-Hartree–Fock calculations on hydrated electrons. Calculations on the octahedral (H2O)6− Kevan structure7,8,51 in Sections III B 4–III B 5 use geometries from ref. 51, and rigidly shift each water molecule distance R from the cavity center. Distances are measured from the cavity center to the closest H atom. Calculations combine the 6-31(+,3+)G* basis set on all atoms, and the aug-cc-pVQZ basis functions of hydrogen atom on a “ghost” atom at the cluster center.51
Calculations on the lithium–ammonia clusters in Section III C use the 6-31(+,3+)G(d) basis set. Cluster geometries are obtained from gas-phase B3LYP/6-31+G(d,p) calculations, based on the clusters in ref. 4, 22 and 74. Spatial symmetry is not enforced in these calculations. Geometries are labeled by their approximate symmetries.
Calculations on the lithium–ammonia clusters of Section III D combine an explicit quantum-mechanical (QM) treatment of six solvated electrons with a molecular mechanics (MM) model of the (NH3)20 cavity. QM calculations use a basis set defined by fifteen “ghost” atoms evenly spaced along the cavity center. Two s-type Gaussian functions with exponents 0.5 and 0.1 au are centered at each ghost atom. The cavity walls are made up of five rigid square-planar (NH3)4 units. Each unit has N–N distances 4.55 Angstrom, taken from the Oh-symmetric e−@(NH3)8 cavity of ref. 4. H atom positions are taken from a gas-phase PM675 geometry optimization of square-planar (NH3)4−, constraining the H–N–H groups to lie in a plane and constraining N–N distances to 4.55 Angstrom. This yields reasonable N–H bond lengths 1.02 Angstrom and H–H bond lengths 2.54 Angstrom. The MM calculations replace each H atom in NH3 with a point charge +0.268; and replace each N atom with a point charge −0.804 and a repulsive s-type Gaussian pseudopotential with exponent 0.45 au and prefactor 1.60 Hartree. CASSCF calculations on this system correlate all 6 electrons using 12 orbitals. The Gaussian input file for the CASSCF calculation is included in the ESI.†
It is often useful to assign global descriptors for the delocalization of a solvated electron or electron pair. We define the delocalization length uav of the solvated electron in anion M− as the position of the maximum in ΔEDR(M− – M;u), evaluated at the anion M− optimized ground-state geometry. The corresponding total energy difference E(M−) − E(M) defines the electron's VDE. The left panel of Fig. 3 below illustrates evaluation of uav for H2O−. We define uav of the solvated electron in neutral open-shell Li(NH3)4 (Section III C 1) as the position of the maximum in ΔEDR(Li(NH3)4 − Li(NH3)4+;u), and define uav of the solvated electron pairs in neutral singlet (Li(NH3)4)2 (Section III C 2) as the position of the maximum in ΔEDR([Li(NH3)4]2 − [Li(NH3)4]22+;u). Plots of representative ΔEDR and tables of all species' 〈EDR(u)〉 are included as ESI.† All species' ΔEDR have a single peak giving a unique uav.
III. Results
A. Model systems
This section shows that the EDR quantifies the off-diagonal cohererence of the one-particle density matrix γ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,
,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′), and illustrate how occupancy of highly oscillatory single-particle states (“virtual orbitals”) in correlated wavefunctions tends to reduce the value of the EDR. This effect is important in our subsequent studies of correlation-induced (de)localization of solvated electrons.
′), and illustrate how occupancy of highly oscillatory single-particle states (“virtual orbitals”) in correlated wavefunctions tends to reduce the value of the EDR. This effect is important in our subsequent studies of correlation-induced (de)localization of solvated electrons.
We begin by considering a simple 1D model for the solvated electron,76,77 one or more noninteracting spinless Fermions in a box of length L with infinite walls. One-electron Hamiltonian eigenfunctions are the familiar particle-in-a-box states  , 0 ≤ x ≤ L, ψm(x) = 0 elsewhere; m = 1, 2, 3,…. The EDR is evaluated with 1D test function g1Du(x,x′) = (2/(πu2))1/4ρ−1/2(x)
, 0 ≤ x ≤ L, ψm(x) = 0 elsewhere; m = 1, 2, 3,…. The EDR is evaluated with 1D test function g1Du(x,x′) = (2/(πu2))1/4ρ−1/2(x)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−|x − x′|2/u2). This model system allows us to visualize the entire one-particle density matrix γ(x,x′) in 2D contour plots, which can be directly compared to plots of EDR(x;u).
exp(−|x − x′|2/u2). This model system allows us to visualize the entire one-particle density matrix γ(x,x′) in 2D contour plots, which can be directly compared to plots of EDR(x;u).
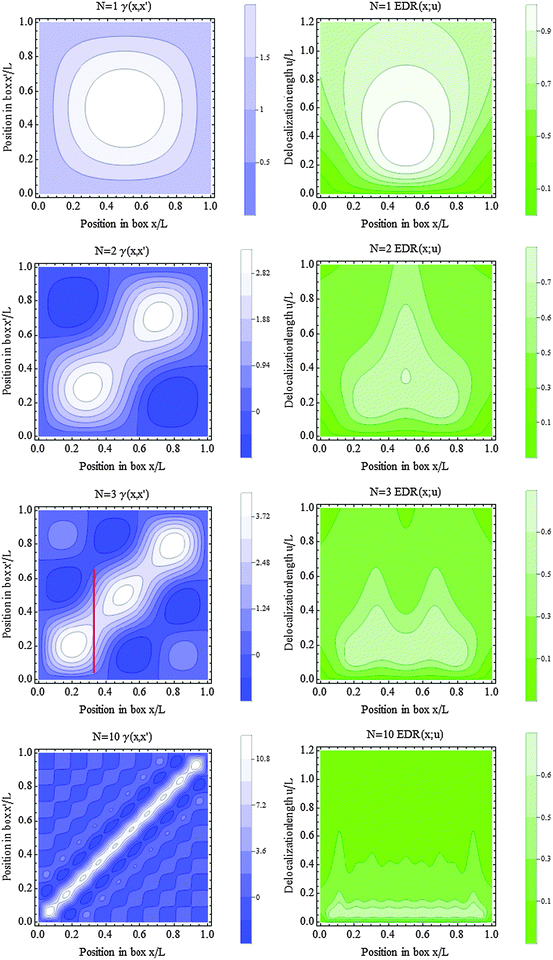
The left panels of Fig. 1 plot γ(x,x′) in the box as a function of the unitless relative positions x/L and x′/L. White regions denote large positive values of γ, blue and black regions denote small and negative γ. The density matrix is largest along the diagonal, and decays with increasing off-diagonal separation |x − x′|. The “width” of the density matrix along the antidiagonal corresponds to the electrons' coherence length,78i.e., the nonclassical “delocalization” of covalent bonds. Increasing the number of noninteracting Fermions in the box increases the electron density and decreases the off-diagonal delocalization length.
The right panels of Fig. 1 plot EDR(x;u) as a function of the unitless relative position x/L on the abscissa, and the unitless relative delocalization length u/L along the ordinate. White regions denote EDR near one, dark green regions denote EDR near or less than zero. Ref. 50 included similar contour plots of the EDR in molecules. Reduced delocalization, i.e., reduced off-diagonal width of the density matrix, shifts the EDR peaks down to smaller delocalization lengths u. In this sense, the EDR at point x captures the nonclassical off-diagonal delocalization of an electron at point x.
One caveat to the above description is that the EDR can predict long delocalization lengths in low-density regions. For example, the N = 3 EDR peaks at relatively large u in the low-density region x ∼ L/3. We suggest that this occurs because the EDR samples a horizontal (or equivalently vertical) rather than antidiagonal slice through the density matrix. To illustrate, the N = 3 system's EDR(x = L/3;u) is obtained by contracting the test function with the “horizontal slice” of points γ(x = L/3,x′). Fig. 3 highlights this horizontal slice of points in the N = 3 density matrix with a red line. The figure shows that these points connect two of the three lobes in the N = 3 density matrix, leading to a relatively large delocalization length. While we speculate that sampling an “antidiagonal” slice γ(x + s/2,x − s/2) could avoid this effect, implementing the resulting integration would be more complicated than our current approach. Moreover, despite this caveat, the overall trend of Fig. 1 is that the EDR provides a reasonable local measure of off-diagonal density matrix delocalization.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−|x − x′|2/u2) for the m = 1 and m = 2 particle in a box states. Results are plotted as functions of the EDR integration variable x′. Position x and length scale u are selected to maximize the resulting EDR(x;u). Fig. 2 shows that the normalized test function overlaps the entire the m = 1 γ(r,r′), but overlaps with at most one lobe of the m = 2 γ(r,r′). This reduced overlap reduces the overall value of the EDR. Fig. S1 (ESI†) confirms that 〈EDR(u)〉 decreases at most u values for the m = 2 and m = 3 states of a single particle in a box.
exp(−|x − x′|2/u2) for the m = 1 and m = 2 particle in a box states. Results are plotted as functions of the EDR integration variable x′. Position x and length scale u are selected to maximize the resulting EDR(x;u). Fig. 2 shows that the normalized test function overlaps the entire the m = 1 γ(r,r′), but overlaps with at most one lobe of the m = 2 γ(r,r′). This reduced overlap reduces the overall value of the EDR. Fig. S1 (ESI†) confirms that 〈EDR(u)〉 decreases at most u values for the m = 2 and m = 3 states of a single particle in a box.
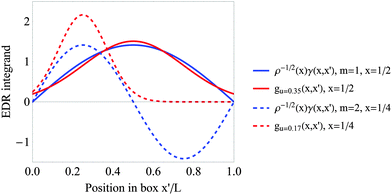 | ||
Fig. 2 The two quantities in the integrand of eqn (2), test function (2/(πu2))1/4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−|x − x′|2/u2) (red) and weighted density matrix ρ−1/2(x)γ(x,x′) (blue), plotted as a function of integration variable x′. Results are plotted for the m = 1 (solid) and m = 2 (dashed) states of a single particle in a box, with x and u selected to maximize EDR(x;u). The normalized test function overlaps with at most one lobe of the normalized m = 2 density matrix, reducing the maximum value of the EDR. exp(−|x − x′|2/u2) (red) and weighted density matrix ρ−1/2(x)γ(x,x′) (blue), plotted as a function of integration variable x′. Results are plotted for the m = 1 (solid) and m = 2 (dashed) states of a single particle in a box, with x and u selected to maximize EDR(x;u). The normalized test function overlaps with at most one lobe of the normalized m = 2 density matrix, reducing the maximum value of the EDR. | ||
The normalization effects in Fig. 2 suggest that any process that increases the occupancy of highly oscillatory single-particle states (“virtual orbitals”) will tend to decrease the EDR. Indeed, we have used this effect to distinguish fractional spin57 in strongly correlated stretched singlet H2.50 In the present work, our efforts to quantify delocalization in post-Hartree–Fock wavefunctions must account for these normalization effects.
Fig. 3 illustrates this by showing different views of correlation in a second model system, H2O−. (This is not intended to represent a realistic hydrated electron, and is included solely to illustrate computed trends.) The left panel of Fig. 3 shows the difference ΔEDR(anion–neutral;u), used to evaluate our descriptor uav of the solvated electron's delocalization length. Horizontal lines denote uav. Correlation binds the solvated electron more tightly and slightly reduces uav. The right panel of Fig. 3 shows the difference ΔEDR(MP2 − HF;u) between correlated and Hartree–Fock calculations on H2O and H2O−. ΔEDR(MP2 − HF;u) has a negative peak in the valence region u ∼ 1 bohr, consistent with the normalization effects in Fig. 2. However, the anion also has a significant positive peak in ΔEDR(MP2 − HF;u) at moderate u ∼ 5 bohr, and a negative peak at u ∼ 30 bohr, both of which are consistent with correlation-induced changes in the structure of the bound electron. Overall, the simple uav descriptor provides a useful measure of correlation effects on localization, though some caution is needed in its interpretation.
 | ||
| Fig. 3 Electron correlation effects on delocalization in H2O−. (left) ΔEDR(anion–neutral;u) for HF and MP2 calculations. Horizontal lines denote the descriptor uav. (right) ΔEDR(MP2 − HF;u) for H2O− and neutral H2O. The normalization effects in Fig. 2 make these curves negative at u = ∼1 bohr. | ||
B. Hydrated electrons
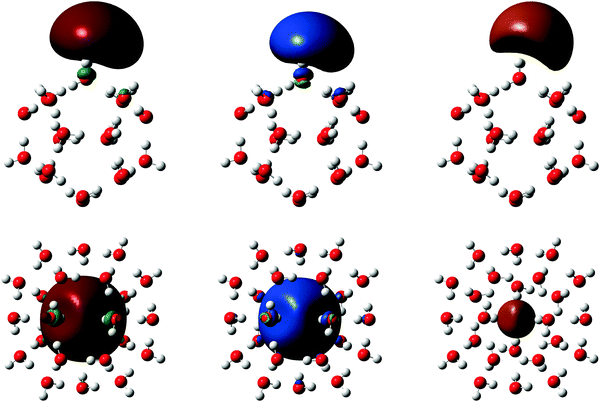
We next consider the EDR's predictions for electrons hydrated in water clusters (H2O)n−. Such clusters have long been studied for their intrinsic interest and as a model for bulk hydrated electrons.6,9–12,27–29 This section shows that the uav descriptor introduced above, evaluated from Hartree–Fock density matrices, recovers existing MO-based measures of hydrated electrons' delocalization.29 The EDR and uav from post-HF calculations suggests that correlation tends to localize surface-bound isomers to cluster surfaces, and delocalize cavity-bound isomers from the cavity center to the cavity wall. DFT calculations can recover these trends, with the BHLYP “half-and-half” functional providing good performance in line with its accurate VDE.27![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) evaluated from MP2 density matrices. EDR(
;uav) evaluated from MP2 density matrices. EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) from Hartree–Fock, LDA, B3LYP, BHLYP and LC-ωPBE79 calculations (Fig. S2 and S3, ESI†) are qualitatively similar. MP2 EDR(
;uav) from Hartree–Fock, LDA, B3LYP, BHLYP and LC-ωPBE79 calculations (Fig. S2 and S3, ESI†) are qualitatively similar. MP2 EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) from the corresponding neutral water clusters have no values >0.2, consistent with the absence of the delocalized solvated electron. Fig. 5 plots ΔEDR(anion–neutral;u) evaluated at different levels of theory. Table 1 presents these structures' computed VDE and uav.
;uav) from the corresponding neutral water clusters have no values >0.2, consistent with the absence of the delocalized solvated electron. Fig. 5 plots ΔEDR(anion–neutral;u) evaluated at different levels of theory. Table 1 presents these structures' computed VDE and uav.
 | ||
| Fig. 5 ΔEDR(anion–neutral;u) for for surface isomer (H2O)20− 512 A and cavity isomer (H2O)24− 51262 B (Fig. 4). Horizontal lines denote the MP2 uav. | ||
| Method | Surface | Cavity | ||
|---|---|---|---|---|
| VDE (eV) | u av (Angstrom) | VDE (eV) | u av (Angstrom) | |
| HF | 0.90 | 5.8 | 0.34 | 2.8 |
| LSDA | 1.82 | 5.2 | 1.67 | 5.0 |
| B3LYP | 1.51 | 5.5 | 1.21 | 5.4 |
| BHLYP | 1.25 | 5.5 | 0.91 | 4.4 |
| LC-ωPBE | 1.18 | 5.0 | 0.92 | 2.6 |
| MP2 | 1.10 | 5.4 | 0.78 | 3.2 |
The most important result in Fig. 4 is that EDR(r;uav) highlights the same region of space as the major lobe of the SOMO and spin density. The SOMO, spin density, and EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) thus capture similar information about the solvated electron.
;uav) thus capture similar information about the solvated electron.
Another important result in Fig. 4 is that the EDR automatically quantifies the solvated electron's delocalization through the uniquely defined average delocalization length uav. The uav in Table 1 are consistent with known trends among DFT methods,27 with LSDA calculations overestimating correlation effects and BHLYP calculations giving results rather close to MP2. The computed uav also show that MP2 correlation localizes the surface-bound electron reducing uav, and delocalizes the cavity-bound electron increasing uav. Fig. S4 (ESI†) confirms this, showing that the difference between MP2 and HF spin densities is positive near the cluster surfaces, and negative far from the (H2O)20− 512 A surface isomer and near the center of the (H2O)24− 51262 B cavity isomer. Perhaps most notably, EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) provides a direct link between the solvated electron's system-averaged delocalization length uav and its real-space location.
;uav) provides a direct link between the solvated electron's system-averaged delocalization length uav and its real-space location.
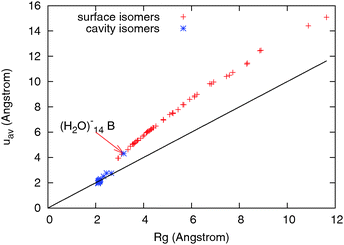 | ||
Fig. 6 Plot of the Hartree–Fock hydrated electron delocalization range uav against the SOMO Rg, for the database of water cluster anions in ref. 29. The black line shows 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence between uav and Rg. 1 correspondence between uav and Rg. | ||
One noteworthy aspect of Fig. 6 is that surface isomers' uav are generally somewhat larger than Rg, while cavity isomers' uav are essentially equal to Rg. We speculate that this is because the EDR test function used to construct uav samples density tails differently from the procedure used to construct Rg. This speculation is consistent with some special cases. A nearly unbound and spherical electron with ψSOMO(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = (2/(πu02))3/4
) = (2/(πu02))3/4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−r2/u02) has uav significantly larger than Rg:
exp(−r2/u02) has uav significantly larger than Rg:  ,
, 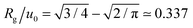 . In contrast, an electron confined in a square 3-D box of dimension L0 gives uav closer to Rg: Rg/L0 ≃ 0.177, uav/L0 ≃ 0.422. (These calculations are included in the Mathematica file provided as ESI.†)
. In contrast, an electron confined in a square 3-D box of dimension L0 gives uav closer to Rg: Rg/L0 ≃ 0.177, uav/L0 ≃ 0.422. (These calculations are included in the Mathematica file provided as ESI.†)
Another noteworthy aspect of Fig. 6 is that the (H2O)14− B “cavity” structure80 lies on the trend for surface isomers. Fig. S7 (ESI†) shows that this isomer's SOMO and HF and MP2 EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) are rather surface-like at the present level of theory. This is consistent with the low VDE found in ref. 29.
;uav) are rather surface-like at the present level of theory. This is consistent with the low VDE found in ref. 29.
 | ||
| Fig. 7 Plot of the change in uav due to electron correlation against VDE, for the (H2O)n−, n ≤ 24 of Fig. 6. | ||
We suggest that the positive Δcuav seen in small cavities arise in part because correlation lets the solvated electron avoid electrons on the surrounding water, enabling it to move from the cavity center onto the cavity surface. This suggestion is consistent with the changes in electron density distribution. Fig. S9 (ESI†) shows that MP2 correlation moves electron density out of the center of the small R = 2.0 Angstrom cavity, and localizes the electron densities in the large R = 6.0 Angstrom cavity. This suggestion is also consistent with ref. 49, which analyzed correlated calculations on the Kevan structure at R = 2.1 Angstrom. That reference found that the solvated electron's mean electron–nuclear nearest-neighbor difference decreased from 3.45 Angstrom in mean-field calculations to 1.39 Angstrom in correlated calculations. Correlation moved the solvated electron from the cavity center and periphery onto the cavity walls. We note that the normalization effects in Fig. 3 may also tend to give Δcuav > 0, thus this result should be interpreted with some care.
 | ||
Fig. 9 Correlation-induced (de)localization of hydrated electrons Δcuav from representative DFT approximations, plotted vs. the MP2 Δcuav of Fig. 7. The thick black line denotes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence with MP2. 1 correspondence with MP2. | ||
C. Ammoniated electrons
We continue by considering isolated and spin-paired electrons solvated in lithium–ammonia solutions. Dilute lithium–ammonia solutions contain separate solvated electrons which form spin-paired species at ∼1 mole percent metal.5,15–17Ref. 4 simulated such species using molecular clusters built from Li(NH3)4+ motifs.81 We use calculations on representative clusters to illustrate the EDR's utility for ammoniated electrons. This section confirms that evaluating the EDR from Hartree–Fock density matrices recovers orbital-based pictures of isolated electrons, confirms that electron correlation tends to localize solvated electrons, and shows how the EDR captures the localizing effects of “strong” correlation in solvated electron pairs.![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) evaluated from MP2 density matrices. EDR(
;uav) evaluated from MP2 density matrices. EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) from Hartree–Fock, LSDA, and B3LYP calculations are qualitatively similar (Fig. S12, ESI†). Fig. S13 (ESI†) plots ΔEDR(anion–neutral;u) and confirms that there is a single peak giving a unique uav. Table 2 reports both structures' VDE and uav computed at different levels of theory.
;uav) from Hartree–Fock, LSDA, and B3LYP calculations are qualitatively similar (Fig. S12, ESI†). Fig. S13 (ESI†) plots ΔEDR(anion–neutral;u) and confirms that there is a single peak giving a unique uav. Table 2 reports both structures' VDE and uav computed at different levels of theory.
 | ||
| Fig. 10 Isosurfaces SOMO = 0.017 bohr−3/2 (left), MP2 spin density = 0.0004 bohr−3 (middle), and MP2 EDR(r;uav) = 0.7 (right) for Li(NH3)4 (top) and e−@(NH3)8 (bottom). | ||
| Method | Li(NH3)4 | e−@(NH3)8 | ||
|---|---|---|---|---|
| VDE (eV) | u av (Angstrom) | VDE (eV) | u av (Angstrom) | |
| HF | 2.44 | 6.8 | 0.19 | 7.1 |
| LSDA | 3.41 | 5.4 | 1.48 | 5.2 |
| B3LYP | 3.22 | 5.7 | 1.09 | 5.7 |
| BHLYP | 2.94 | 6.0 | 0.79 | 5.9 |
| MP2 | 2.74 | 6.2 | 0.53 | 5.9 |
| CCSD | 2.76 | 6.2 | — | — |
We begin by noting that our results match previous work. The Li(NH3)4 CCSD VDE is consistent with the EOM-CCSD values ∼2.9 eV in ref. 22, evaluated with a somewhat different basis set and molecular geometry. Calculations omitting geometry relaxation of Li(NH3)4 upon ionization give an MP2 reaction energy Li(NH3)4 + 8NH3 → Li(NH3)4+ + e−@(NH3)8 of 58.3 kcal mol−1, consistent with the 60.9 kcal mol−1 DFT value in ref. 4. Our B3LYP/6-31+G(d,p) calculations on e−@(NH3)8 give Mulliken spin densities 0.14 on N, −0.5 × 10−2 on H, consistent with the 0.13, −0.6 × 10−2 of ref. 21. The e−@(NH3)8 SOMO is qualitatively consistent with the B3LYP ψSOMO(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = 0.02 electrons per bohr3 contour shown in Fig. 2 of ref. 21, though our SOMO lacks a node at the center of mass. The Li(NH3)4 HF and MP2 uav 6.8 and 6.2 Angstrom are ∼1.5 times the HF SOMO and EOM-CCSD natural orbital
) = 0.02 electrons per bohr3 contour shown in Fig. 2 of ref. 21, though our SOMO lacks a node at the center of mass. The Li(NH3)4 HF and MP2 uav 6.8 and 6.2 Angstrom are ∼1.5 times the HF SOMO and EOM-CCSD natural orbital  4.45 and 4.12 Angstrom reported in ref. 22, consistent with the relation between uav and Rg in Fig. 6.
4.45 and 4.12 Angstrom reported in ref. 22, consistent with the relation between uav and Rg in Fig. 6.
The results in Fig. 10 are consistent with our results for hydrated electrons. EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) highlights approximately the same region of space as the major lobe of the SOMO and the MP2 spin density. This fact, and the correlation-induced localiation of Li(NH3)4 seen in Table 2, suggest that the EDR is consistent with previous orbital- and density-based analyses assigning the the Li(NH3)4 electron to a Rydberg-like state.22 MP2, CCSD, and DFT correlation increase the VDE and reduce uav. While the e−@(NH3)8 SOMO and EDR(
;uav) highlights approximately the same region of space as the major lobe of the SOMO and the MP2 spin density. This fact, and the correlation-induced localiation of Li(NH3)4 seen in Table 2, suggest that the EDR is consistent with previous orbital- and density-based analyses assigning the the Li(NH3)4 electron to a Rydberg-like state.22 MP2, CCSD, and DFT correlation increase the VDE and reduce uav. While the e−@(NH3)8 SOMO and EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) in Fig. 10 appear at first glance to correspond to a cavity-bound electron, the correlation-induced localization Δcuav < 0 in Table 2 matches that of the surface-bound electrons in Fig. 7. This is consistent with previous suggestions4 that the electron occupies surface
;uav) in Fig. 10 appear at first glance to correspond to a cavity-bound electron, the correlation-induced localization Δcuav < 0 in Table 2 matches that of the surface-bound electrons in Fig. 7. This is consistent with previous suggestions4 that the electron occupies surface  bonds.
bonds.
 | ||
Fig. 11 Isosurfaces EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) = 0.7 of the RHF (left), symmetry-broken UHF ↑ and ↓ (middle), and BD (right) EDR of C3v (top) and D3d (bottom) (Li(NH3)4)2. ;uav) = 0.7 of the RHF (left), symmetry-broken UHF ↑ and ↓ (middle), and BD (right) EDR of C3v (top) and D3d (bottom) (Li(NH3)4)2. | ||
Fig. 11 shows EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) from RHF, UHF, and Brückner doubles calculations on solvated electron pairs. Table 3 shows the corresponding VDE and uav. Fig. S15 (ESI†) shows the RHF and UHF frontier orbitals, and Fig. S16 (ESI†) shows the LSDA, B3LYP, and CCSD EDR(
;uav) from RHF, UHF, and Brückner doubles calculations on solvated electron pairs. Table 3 shows the corresponding VDE and uav. Fig. S15 (ESI†) shows the RHF and UHF frontier orbitals, and Fig. S16 (ESI†) shows the LSDA, B3LYP, and CCSD EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav). Just as in Fig. 4 and 10, the RHF and UHF EDR(
;uav). Just as in Fig. 4 and 10, the RHF and UHF EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) highlight the same region of space as the RHF and UHF orbitals in Fig. S15 (ESI†). Both structures have a delocalized threefold symmetric RHF and BD EDR(
;uav) highlight the same region of space as the RHF and UHF orbitals in Fig. S15 (ESI†). Both structures have a delocalized threefold symmetric RHF and BD EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav), while the spin-up and spin-down UHF EDR(
;uav), while the spin-up and spin-down UHF EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) show broken symmetry.
;uav) show broken symmetry.
| Method | C 3v | D 3d | ||
|---|---|---|---|---|
| VDE (eV) | u av (Angstrom) | VDE (eV) | u av (Angstrom) | |
| RHF | 7.13 | 7.2 | 7.09 | 7.0 |
| UHF | 7.38 | 5.5 | 7.28 | 5.6 |
| LSDA | 9.83 | 5.8 | 9.85 | 5.7 |
| B3LYP | 9.27 | 6.2 | 9.25 | 6.1 |
| BHLYP | 8.62 | 6.4 | 8.61 | 6.2 |
| CCSD | 8.30 | 6.3 | 8.26 | 6.2 |
| BD | 8.28 | 6.3 | 8.24 | 6.2 |
The most notable result in Table 3 is the dramatic role of nondynamical correlation. Ref. 4 argued that “the Li(NH3)4 SOMO is like a big hydrogen atom (or alkali metal) SOMO”. We find that (Li(NH3)4)2 is like a stretched (“big”) H2 with significant nondynamical correlation.52 Symmetry-broken UHF calculations stabilize the solvated electron pairs by 0.2–0.25 eV, and reduce their characteristic delocalization length uav by almost 2 Angstrom. Symmetry-restricted CCSD, BD, and DFT calculations increase the VDE consistent with both dynamical and nondymaical correlation, and also significantly localize the electrons. The relatively large CCSD T1 diagnostic84 0.022 suggests that even these calculations may not capture all nondynamical correlation present. However, the results suffice to show how the EDR quantifies the localizing effects of nondynamical correlation.
D. Transition to a metallic state
We conclude by considering how the EDR gives insight into lithium–ammonia solutions' transition to a metallic state. Previous simulations suggest that solvated spin-paired electrons coalesce into tunnel-like extended states at 2–9 mole percent metal.15–17 We simulate the coalescence of three such electron pairs confined in an extended (NH3)20 cavity (Fig. 12). The model system is small enough to permit accurate CASSCF calculations of “strong” nondynamical correlation. We emphasize that this model system does not capture all aspects of coalescence. For example, the six electrons are confined to the cavity by the localized basis set, the electron–NH3 interactions are treated by a simple pseudopotential, and the cavity geometry is fixed at an artificial high-symmetry state. However, we suggest that this model suffices to illustrate the interplay of delocalization and nondynamical correlation. | ||
Fig. 12 EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u = 2.6 Angstrom) = 0.6 isosurfaces for RHF (top), LSDA (middle), and CASSCF (bottom) calculations on six electrons in an ammonia cavity. ;u = 2.6 Angstrom) = 0.6 isosurfaces for RHF (top), LSDA (middle), and CASSCF (bottom) calculations on six electrons in an ammonia cavity. | ||
Fig. 12 plots the EDR at u = 2.6 Angstrom from RHF, UHF, and CASSCF(6,12) calculations. This u value maximizes the RHF 〈EDR(u)〉, and is thus representative of the solvated electrons. Fig. 13 offers a complimentary perspective, showing EDR(x;u) for all delocalization lengths u, evaluated at points x along the cavity center and plotted using the conventions of Fig. 1. Fig. 13 also includes a UHF calculation on the heptet state of six unpaired electrons. Fig. S18 (ESI†) shows the corresponding electron densities.
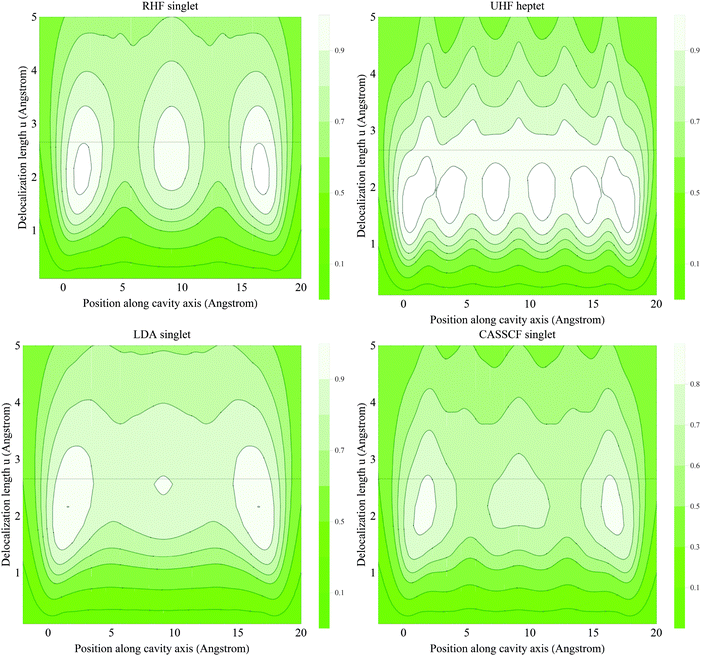 | ||
| Fig. 13 EDR(x;u) for multiple u values, plotted for points x along the center of the cavity in Fig. 12. Horizontal lines denote the u value plotted in Fig. 12. | ||
The EDR in Fig. 12 and 13 illustrates the interplay of electron delocalization and correlation. The singlet RHF electrons form three electron pairs with limited inter-pair delocalization. The UHF heptet in Fig. 13 instead shows six nearly isolated electrons, shifted down to shorter delocalization lengths. CASSCF calculations on the singlet state show a mixture of these two effects. The CASSCF EDR shows a modest amount of inter-pair delocalization, consistent with the inter-pair interactions important to the transition to the metallic state.36 The EDR also shifts down to lower delocalization lengths, consistent with the aforementioned correlation-induced localization. The CASSCF EDR is generally smaller (darker) than that from the RHF calculation, consistent with the normalization effects in Fig. 2. Finally, the LSDA captures the increased inter-pair interactions of CASSCF, but does not capture the detailed structure of the CASSCF state or the “full downward” shift to smaller delocalization lengths u.
IV. Conclusions
The results presented here illustrate that the electron delocalization range EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;u) is a useful theoretical tool for visualizing and quantifying the delocalization of solvated electrons. The density matrix plots in Fig. 1 illustrate how the EDR provides a specific, quantitative probe of the “off-diagonal” delocalization (coherence) critical to chemical bonding and reactivity. Fig. 6 illustrates that system-averaged uav obtained from the EDR can reproduce existing MO-based measures of solvated electrons' average delocalization. Importantly, Fig. 4 shows that EDR(
;u) is a useful theoretical tool for visualizing and quantifying the delocalization of solvated electrons. The density matrix plots in Fig. 1 illustrate how the EDR provides a specific, quantitative probe of the “off-diagonal” delocalization (coherence) critical to chemical bonding and reactivity. Fig. 6 illustrates that system-averaged uav obtained from the EDR can reproduce existing MO-based measures of solvated electrons' average delocalization. Importantly, Fig. 4 shows that EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) directly links this system-averaged quantity back to a real-space picture. EDR(
;uav) directly links this system-averaged quantity back to a real-space picture. EDR(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ;uav) highlights precisely the region of space containing the solvated electron, without requiring special selections or localization of orbitals. Such connections between system-averaged and real-space properties will help interpret the chemistry of more complicated systems. Finally, our studies of spin-paired electrons show that the density-matrix-based EDR is readily applicable to strongly correlated singlets systems where spin-density-based descriptors are unavailable (in the absence of symmetry breaking) and orbital-based descriptors can be qualitatively incorrect. To illustrate, Fig. S19 (ESI†) shows the natural orbital occupancies (MO-basis density matrix eigenvalues) from the CASSCF(6,12) calculations in Fig. 12 and 13. The first five natural orbitals have signficantly noininteger values, indicating a breakdown of the MO approximation. Overall, these results motivate continued application of the EDR to quantify and interpret the calculated electronic structures of delocalized and solvated electrons.
;uav) highlights precisely the region of space containing the solvated electron, without requiring special selections or localization of orbitals. Such connections between system-averaged and real-space properties will help interpret the chemistry of more complicated systems. Finally, our studies of spin-paired electrons show that the density-matrix-based EDR is readily applicable to strongly correlated singlets systems where spin-density-based descriptors are unavailable (in the absence of symmetry breaking) and orbital-based descriptors can be qualitatively incorrect. To illustrate, Fig. S19 (ESI†) shows the natural orbital occupancies (MO-basis density matrix eigenvalues) from the CASSCF(6,12) calculations in Fig. 12 and 13. The first five natural orbitals have signficantly noininteger values, indicating a breakdown of the MO approximation. Overall, these results motivate continued application of the EDR to quantify and interpret the calculated electronic structures of delocalized and solvated electrons.
Acknowledgements
BGJ acknowledges support by the Department of Chemistry at Texas Christian University. The authors thank John M. Herbert for useful comments on the SOMO Rg of ref. 29.References
- B. Abel, U. Buck, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2012, 14, 22 RSC.
- K. Maeda, M. T. J. Lodge, J. Harmer, J. H. Freed and P. P. Edwards, J. Am. Chem. Soc., 2012, 134, 9209 CrossRef CAS PubMed.
- W. Weyl, Ann. Phys., 1864, 121, 606 Search PubMed.
- E. Zurek, P. P. Edwards and R. Hoffmann, Angew. Chem., Int. Ed., 2009, 48, 8191 CrossRef PubMed.
- M. T. J. H. Lodge, P. Cullen, N. H. Rees, N. Spencer, K. Maeda, J. R. Harmer, M. O. Jones and P. P. Edwards, J. Phys. Chem. B, 2013, 117, 13322 CrossRef CAS PubMed.
- L. Turi and P. Rossky, Chem. Rev., 2012, 112, 5641 CrossRef CAS PubMed.
- D.-F. Feng and L. Kevan, Chem. Rev., 1980, 80, 1 CrossRef CAS.
- L. Kevan, Acc. Chem. Res., 1981, 14, 138 CrossRef CAS.
- L. D. Jacobson and J. M. Herbert, Int. Rev. Phys. Chem., 2011, 30, 1 CrossRef.
- J. R. Casey, A. Kahros and B. J. Schwartz, J. Phys. Chem. B, 2013, 117, 14173 CrossRef CAS PubMed.
- R. N. Barnett, U. Landman, C. L. Cleveland and J. Jortner, J. Chem. Phys., 1988, 88, 4421 CrossRef CAS.
- R. N. Barnett, U. Landman, C. L. Cleveland and J. Jortner, J. Chem. Phys., 1988, 88, 4429 CrossRef CAS.
- J. R. R. Verlet, A. E. Bragg, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Science, 2005, 307, 93 CrossRef CAS PubMed.
- B. J. Schwartz and P. J. Rossky, J. Chem. Phys., 1994, 101, 6902 CrossRef.
- Z. Deng, G. J. Martyna and M. L. Klein, Phys. Rev. Lett., 1992, 68, 2496 CrossRef CAS PubMed.
- Z. Deng, G. J. Martyna and M. L. Klein, Phys. Rev. Lett., 1993, 71, 267 CrossRef CAS PubMed.
- Z. Deng, G. J. Martyna and M. L. Klein, J. Phys. Chem., 1994, 100, 7590 CrossRef CAS.
- R. E. Larsen, W. J. Glover and B. J. Schwartz, Science, 2010, 329, 65 CrossRef CAS PubMed.
- J. M. Herbert and L. D. Jacobson, J. Phys. Chem. A, 2011, 115, 14470 CrossRef CAS PubMed.
- F. Uhlig, O. Marsalek and P. Jungwirth, J. Phys. Chem. Lett., 2012, 3, 3071 CrossRef CAS PubMed.
- I. A. Shkrob, J. Phys. Chem. A, 2006, 110, 3967 CrossRef CAS PubMed.
- T. Sommerfeld and K. M. Dreux, J. Chem. Phys., 2012, 137, 244302 CrossRef PubMed.
- D. Ben-Amotz, J. Phys. Chem. Lett., 2011, 2, 1216 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
- Distinctions among, e.g., “core” and “valence” electrons are a colloquialism used here to aid understanding. All calculations treat electrons as indistinguishable Fermions.
- F. Wang and K. D. Jordan, J. Chem. Phys., 2002, 116, 6973 CrossRef CAS.
- J. M. Herbert and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 5217 CrossRef CAS PubMed.
- J. M. Herbert and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 68 RSC.
- C. F. Williams and J. M. Herbert, J. Phys. Chem. A, 2008, 112, 6171 CrossRef CAS PubMed.
- V. P. Vysotskiy, L. S. Cederbaum, T. Sommerfeld, V. K. Voora and K. D. Jordan, J. Chem. Theory Comput., 2012, 8, 893 CrossRef CAS.
- M. Gutowski, P. Skurski, A. I. Boldyrev, J. Simons and K. D. Jordan, Phys. Rev. Appl., 1996, 54, 1906 CAS.
- M. Gutowski and P. Skurski, J. Chem. Phys., 1997, 107, 2968 CrossRef CAS.
- M. Gutowski, K. D. Jordan and P. Skurski, J. Phys. Chem. A, 1998, 102, 2624 CrossRef CAS.
- T. Sommerfeld, B. Bhattarai, V. P. Vysotskiy and L. S. Cederbaum, J. Chem. Phys., 2010, 133, 114301 CrossRef PubMed.
- T. Sommerfeld, K. M. Dreux and R. Joshi, J. Phys. Chem. A, 2014, 118, 7320 CrossRef CAS PubMed.
- N. F. Mott, J. Phys. Chem., 1980, 84, 1199 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS.
- K. B. Wiberg, C. M. Hadad, T. J. LePage, C. J. Breneman and M. J. Frisch, J. Phys. Chem., 1992, 96, 671 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- F. Della Sala and A. Görling, J. Chem. Phys., 2001, 115, 5718 CrossRef CAS.
- F. Uhlig, J. M. Herbert, M. P. Coons and P. Jungwirth, J. Phys. Chem. A, 2014, 118, 7507 CrossRef CAS PubMed.
- R. F. W. Bader and M. E. Stephens, J. Am. Chem. Soc., 1975, 97, 7391 CrossRef CAS.
- R. W. F. Bader and G. L. Heard, J. Chem. Phys., 1999, 111, 8789 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- A. Savin, J. Mol. Struct., 2005, 727, 127 CrossRef CAS.
- T. Sommerfeld, J. Phys. Chem. A, 2008, 112, 11817 CrossRef CAS PubMed.
- T. Sommerfeld, A. DeFusco and K. D. Jordan, J. Phys. Chem. A, 2008, 112, 11021 CrossRef CAS PubMed.
- T. Sommerfeld, J. Chem. Theory Comput., 2013, 9, 4866 CrossRef CAS.
- B. G. Janesko, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2014, 141, 144104 CrossRef PubMed.
- E. R. Johnson, A. Otero-de-la Roza and S. G. Dale, J. Chem. Phys., 2013, 139, 184116 CrossRef PubMed.
- O. Gunnarsson and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 4274 CrossRef CAS.
- D. Cremer, Mol. Phys., 2001, 99, 1899 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 2003, 119, 2972 CrossRef CAS.
- R. Ponec and D. L. Cooper, J. Phys. Chem. A, 2007, 111, 11294 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, L. A. Constantin, J. Sun and G. I. Csonka, J. Chem. Theory Comput., 2009, 5, 902 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, J. Chem. Phys., 2008, 129, 121104 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson and H. Nakatsuji, et al., Gaussian Development Version, Revision H.35, Gaussian, Inc, Wallingford, CT, 2010 Search PubMed.
- A. Seidl, A. Görling, P. Vogl, J. A. Majewski and M. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 3764 CrossRef CAS.
- G. E. Scuseria and H. F. Schaefer III, Chem. Phys. Lett., 1987, 142, 354 CrossRef CAS.
- N. C. Handy, J. A. Pople, M. Head-Gordon, K. Raghavachari and G. W. Trucks, Chem. Phys. Lett., 1989, 164, 185 CrossRef CAS.
- N. C. Handy and H. F. Schaefer III, J. Chem. Phys., 1984, 81, 5031 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- A. D. Becke, Phys. Rev. Appl., 1988, 38, 3098 CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- B. G. Janesko, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2014, 141, 034103 CrossRef PubMed.
- R. E. Stratman, G. E. Scuseria and M. J. Frisch, Chem. Phys. Lett., 1996, 257, 213 CrossRef.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099 CrossRef CAS.
- K. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283 CrossRef CAS.
- K. Hashimoto and K. Daigoku, Phys. Chem. Chem. Phys., 2009, 11, 9391 RSC.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173 CrossRef CAS PubMed.
- R. A. Ogg Jr., Phys. Rev., 1946, 69, 668 CrossRef.
- J. Jortner, J. Chem. Phys., 1959, 30, 839 CrossRef CAS.
- S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171 CrossRef CAS PubMed.
- O. A. Vydrov, J. Heyd, A. V. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106 CrossRef PubMed.
- A. Khan, J. Chem. Phys., 2006, 125, 024307 CrossRef PubMed.
- H. Thompson, J. C. Wasse, N. T. Skipper, S. Hayama, D. T. Bowron and A. K. Soper, J. Am. Chem. Soc., 2003, 125, 2572 CrossRef CAS PubMed.
- J. F. Stanton, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1992, 97, 5554 CrossRef CAS.
- L. A. Barnes and R. Lindh, Chem. Phys. Lett., 1994, 223, 207 CrossRef CAS.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp01967b |
| This journal is © the Owner Societies 2015 |