Contrasting the optical properties of the different isomers of oligophenylene

Abstract

We use a combination of Time-Dependent Density Functional Theory (TD-DFT) and approximate Coupled Cluster Theory (RI-CC2) to compare trends in the optical gap and fluorescence energies of ortho-, meta- and para-oligomers of phenylene. We find that RI-CC2 and TD-DFT calculations using three different commonly employed XC-potentials (B3LYP, BHLYP and CAM-B3LYP) generally give consistent predictions. Most importantly, the fluorescence energy of m-phenylene is predicted to be independent of oligomer length, the fluorescence energy of p-phenylene to decrease with oligomer length and that of o-phenylene to increase. The origins of these differences in behaviour between the different isomers are analysed and found to stem from a subtle combination of steric and electronic factors.

---

Introduction

Polyphenylene is perhaps one of the simplest conjugated polymers imaginable; consisting of a chain of aromatic phenylene units linked together by single carbon–carbon bonds. This simplicity is, however, deceptive as polyphenylene can occur in three different structural isomers; poly(ortho-phenylene) (o-phenylene), poly(meta-phenylene) (m-phenylene) and poly(para-phenylene) (p-phenylene) (see Scheme 1). These three isomers differ in through which carbon atoms the phenylene units are linked and, importantly, all have significantly different optical properties. For example, experimentally the fluorescence spectrum of oligomers of p-phenylene is known to red shift with increasing chain length^1–5 while for oligomers of o-phenylene, surprisingly, it shifts to the blue.^6–9 In contrast, m-phenylene is effectively non-conjugated¹⁰ and its optical properties virutually independent of chain length.

Scheme 1 Structures of the p-terphenyl (A), m-terphenyl (B) and o-terphenyl (C) oligomers.

The differences in the optical properties of the different phenylene isomers are not merely of academic interest. Polyphenylene finds application in light emitting diodes¹¹ and as photocatalyst^12–16 for the reduction of protons to molecular hydrogen and carbon dioxide to formic acid, both in the presence of a suitable electron donor. Most of these applications involve p-phenylene and it stands to reason that the other isomers would give rise to a different performance in such applications. Indeed a study that explicitly compared the ability of o-terphenyl, m-terphenyl and p-terphenyl oligomers to act as photocatalyst for the reduction of carbon dioxide found that p-terphenyl was significant more active than the other two isomers, and interestingly also more active than the p-phenylene polymer.¹⁴

Elucidating the origin of the starkly different optical properties of the isomers of such a conceptually simple polymer is clearly both an academically and practically relevant question. Not surprisingly, there is thus a large number of computational studies on the optical^3,4,6,8 and related structural^9,10 properties of oligomers of phenylene. Such studies generally focus on only one of the three isomers and attempt to correlate its structural and optical properties. Here we go a step further, and study oligomers of all three isomers of phenylene on an equal footing in order to uncover the overarching structural and electronic features that explain the deviation between the optical properties of the different isomers. In order to minimise the chance of computational artefacts complicating the comparison between the different isomers, we not only use time-dependent density functional theory (TD-DFT) to calculate the optical properties of the oligomers but also, where possible, approximate couple cluster theory. Finally, we carefully consider the treatment of intramolecular dispersive interactions, which will prove to be especially crucial in the case of o-phenylene.

Computational methodology

The computational investigation of the optical properties of oligophenylenes was carried-out using a six-step approach. First, for every system, a conformational search was performed in order to find the lowest-energy conformers. Second, the singlet ground state (S0) of selected conformers was optimized using Density Functional Theory^17,18 (DFT). Third, for selected structures (trimer and hexamer), harmonic frequency calculations were performed to verify that the stationary points obtained in the S0 optimization indeed correspond to ground-state minima. Fourth, the vertical excitation energies of the oligomers were calculated using both Time Dependent-DFT¹⁹ (TD-DFT) and the approximate coupled-clusters singles-and-doubles method²⁰ (CC2). Fifth, for each oligomer, the geometry of the first excited state (S1) was relaxed using TD-DFT to obtain the S1 minimum energy structure and predict its photoluminescence (PL) energy. Finally, for selected oligomers (trimer and hexamer), numerical TD-DFT frequency calculations were performed on the S1 relaxed geometries to verify that they indeed correspond to minima.

For the conformational sampling, we employed the OPLS-2005 forcefield²¹ and the low-mode sampling algorithm,²² as implemented in Macromodel 9.9.²³ We used a combination of 10 000 Monte Carlo search steps and minimum and maximum low-mode move distances of 3 and 20 Å respectively. All the structures located within an energy window of 200 kJ mol⁻¹ relative to the lowest energy conformer were saved.

The DFT and TD-DFT calculations employed three different hybrid Exchange–Correlation (XC) potentials; B3LYP,^24–27 BHLYP²⁶ and CAM-B3LYP.²⁸ The B3LYP and BHLYP XC-potentials includes 20 and 50% Hartree-Fock-like exchange (HFLE) respectively, whereas the percentage of HFLE in CAM-B3LYP, a range separated XC-potential, changes from 19 to 65 with increasing interelectronic separation. As a result the asymptotic behaviour of the CAM-B3LYP XC-potential (the derivative of the XC-potential with respect to the interelectronic separation r) will be closer to the formal 1/r dependence of the exact XC-potential. Furthermore, in all TD-DFT calculations, the Tamm–Dancoff approximation to TD-DFT²⁹ was used, which fixes among other things problems with triplet instabilities present in full TD-DFT.^29,30 Finally, we performed in the case of B3LYP also calculations using Grimme's D3 empirical dispersion correction.^31–33

In the B3LYP and BHLYP calculations, the double-ζ DZP³⁴ basis set was used, while the CAM-B3LYP calculations typically employed the 6-31G** split-valence basis set.³⁵ A limited number of calculations with other basis-sets such as the larger triple-ζ def2-TZVP³⁶ were performed for selected systems in order to check the effect of the basis set size on the results.

The CC2 calculations were carried-out using the frozen core approximation and the resolution-of-the-identity (RI-CC2) approximation to the electron repulsion integrals. The majority of RI-CC2 calculations, for reasons of computational tractability, further employed the small def2-SV(P)³⁴ split-valence basis. However for single points on the smallest oligomers, calculations with the larger triple-ζ def2-TZVPP³⁶ basis set were also performed.

Finally, all B3LYP, BHLYP and RI-CC2 calculations were performed with the Turbomole 6.5 code.^37,38 The CAM-B3LYP calculations used NWChem 6.0³⁹ except in the case of the TD-DFT S1 relaxations, which were performed using GAMESS-US⁴⁰ (version 1 October 2010 R1).

Results and discussion

Having introduced our computational approach, we will now report and analyse the results of our calculations on the oligomers of the different isomers of phenylene. We will start with a brief discussion of the classes of conformers considered for each isomer and their characteristic structural features before moving on to an in-depth analysis of the predicted absorption (optical gap) and fluorescence (fluorescence energy) spectra.

Structural models

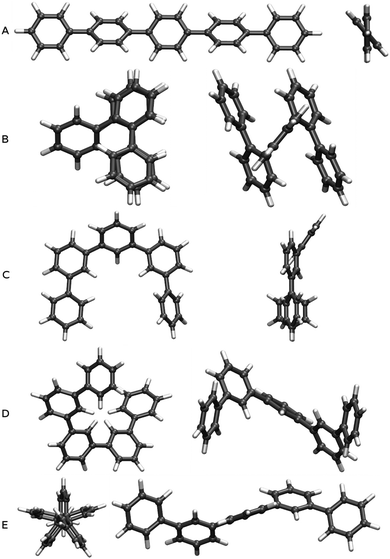
We built oligomers of o-, m- and p-phenylene and performed conformer searches to find the low energy conformers for each oligomer, where we specifically focus on classes of ordered conformers (see Section ESI-1 of the ESI†). For each isomer, we considered oligomers ranging from the trimer (3 phenylene repeat units) to the octamer (8 units). The dimer is not considered since it is the same for o-, m- and p-phenylene. Because of the high symmetry of benzene, the labels o-, m- and p- only become meaningful for oligomers of 3 units of phenylene or more.

The class of p-phenylene conformer we focus on are the lowest-energy structures for each oligomer length. It consists of a linear backbone, and has alternating torsion angles of approximately +37° and −37° (see Fig. 1A). Another slightly higher energy class of p-phenylene conformer also has a linear backbone, but with +37° torsion angles between each phenylene unit, making it essentially helical. The latter structural difference, however, is of limited significance in the context of our study, since the optical properties of both conformers are generally very similar (see Section ESI-1 of the ESI†).

Fig. 1 Top and side views of B3LYP optimised ground state geometries of the lowest energy conformers of p-quinquephenyl (A) and o-quinquephenyl (B), as well as three low energy conformers of m-quinquephenyl (flat structure: C; large helix: D; small helix: E).

The class of o-phenylene conformer we focus on are again the lowest-energy structures for each oligomer length (when taking into account the dispersion correction). This class of conformer has a helical backbone, where phenylenes stack every three units (see Fig. 1B). For m-phenylene, finally, we consider three low-energy conformers: the flat lowest-energy conformer (see Fig. 1C), and two conformers with helical backbones (large helix and small helix, see Fig. 1D and E). All those three m-phenylene conformers yield almost identical optical properties (see Section ESI-1 of the ESI†), and are treated collectively below.

Effect of isomer and oligomer length on the optical gap

The variation of the optical gap, the lowest vertical excitation energy, with the oligomer length for the different phenylene isomers is shown in Fig. 2 (see also Section ESI-2 of the ESI†). As can be seen, TD-DFT using all the three density potentials considered (B3-LYP, BH-LYP and CAM-B3LYP), as well as RI-CC2, generally yield the same qualitative trends. Moreover, quantitatively the predictions of RI-CC2 lie in between those obtained using TD-B3YLP and TD-CAM-B3LYP. The effect of increasing the basis-set quality in the DFT calculations to def2-TZVP finally is very small (see Section ESI-3 of the ESI†).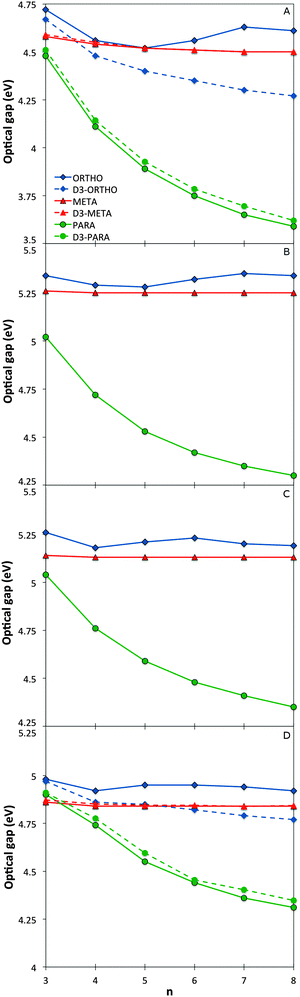

Fig. 2 Optical gap values as a function of oligomer length for the different phenylene isomers calculated with TD-B3LYP (A), BHLYP (B), CAM-B3LYP (C) and RI-CC2 (D).

For p-phenylene, a pronounced red shift in the optical gap with increasing oligomer length is observed, as previously reported in the literature^1,3–5 (see also Section ESI-3 of the ESI†). o-Phenylenes show similar behaviour, again in line with literature.^6,8,9 However in this case, use of Grimme's dispersion correction^31–33 to DFT (DFT-D3) is needed to accurately describe Van der Waals interactions (arene–arene π-stacking) between the phenylene units, due to their spatial proximity. Calculations on o-phenylene without the use of DFT-D3 in contrast predict that the optical gap first decreases then increases and ultimately decreases again with increasing oligomer length. Finally, for m-phenylene, increasing the oligomer length does not result in any significant change in the calculated optical gap values beyond the trimer, again in agreement with literature¹⁰ where they are described as “conjugation breakers”.

Finally, the effective conjugation length of o-, m-, and p-phenylene was calculated in the case of TD-B3LYP using the methodology of Meier and co-workers.⁴¹ Among the three isomers, p-phenylene is predicted to have the longest effective conjugation length (∼20 repeat units, λ_∞ ≈ 370 nm, E_∞ ≈ 3.35 eV), followed by o-phenylene (∼10 units, λ_∞ ≈ 293 nm, E_∞ ≈ 4.23 eV), and ultimately m-phenylene (∼6 units, λ_∞ ≈ 276 nm, E_∞ ≈ 4.49 eV). The here predicted p- and o-phenylene conjugation lengths are larger than the values obtained from experimental spectra; 9 and ∼4 respectively, but the calculations and experiment agree on the relative conjugation lengths of the different isomers.^7,41 The consistent difference in the absolute magnitude of conjugation lengths between the calculations and experiment is probably due to a combination of three factors. Firstly, our calculations ignore thermal effects that might reduce the effective conjugation length, secondly, experimentally the spectra of many longer oligomers do not show well-defined peaks, and thirdly, the general insolubility of the same oligomers in most solvents means that experimental spectroscopy is inherently limited to short oligomers.

Link between structure, topology and optical gap

Naïve considerations based on Hückel or perturbation theory would suggest that the optical gap of phenylene oligomers and polymers is linked to the overlap between the π-systems of adjacent phenylene units and that the predominant structural parameter controlling this overlap is the interphenylene torsion angle. Flat structures with torsion angles of ∼0° are expected to have maximum π-systems overlap and as a result small optical gap values while structures with torsion angles approaching 90° should have large(r) optical gap values not dissimilar to that of the monomer. For the case where torsion angles do not change much with the oligomer length, true for all systems studied here except o-phenylene when optimised with standard DFT instead of dispersion corrected DFT-D, one would thus expect to see this also reflected in the trends of optical gap with oligomer length. More specifically, one would expect for the optical gap to smoothly decrease with oligomer length in an approximate 1/n fashion and the long oligomer limit of the optical gap (E_o∞) of different isomers to be smallest for the isomer with the smallest torsion angles. Indeed p-phenylene oligomers have consistently smaller average torsion angles than o-phenylene oligomers (37° versus 50°, see Fig. 3, when concentrating on the DFT-D optimised geometry in the case of o-phenylene) and steadily lower optical gap values and a longer effective conjugation length. Also, a D_2h version of the p-phenylene trimer, a transition state with two imaginary frequencies but 90° torsion angles, is predicted by TD-B3LYP to have a much larger optical gap than the p-phenylene trimer minimum energy geometry (5.28 vs. 4.49 eV), which lies rather close to that predicted for benzene (5.51 eV). The only minor issue with this naïve theoretical picture is that visualisation of the orbitals relevant for the optical gap (e.g. HOMO → LUMO in the case of p-phenylene, see Fig. S3 in Section ESI-4 of the ESI†), as well as the excited state-ground state density differences, suggests that the naïve picture might be slightly too simple. While the HOMO is typically localised on the constituent phenylene units and has π-like character, the LUMO is predominantly localised along the interphenylene bonds (π-like) with minor π*-like contributions on the phenylene units.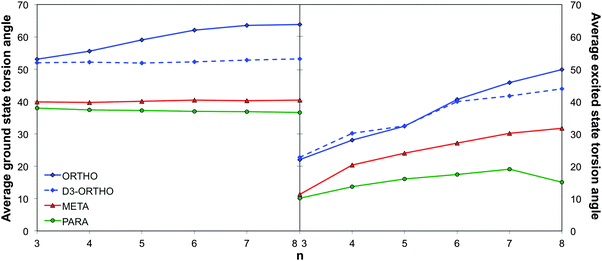

Fig. 3 TD-B3LYP average ground (right) and excited state (left) interphenylene torsion angles as a function of oligomer length for the different phenylene isomers.

The case of using standard DFT when describing o-phenylene, where the optical gap is predicted to decrease, increase and decrease again, is a more complicated. The fact that o-phenylene forms helical structures with close contact between non-directly adjacent phenylene units means a more accurate description of non-covalent dispersion interactions is required than available in standard DFT. As a result, while DFT and dispersion corrected DFT-D predict essentially identical structures and optical gap values for p- and m-phenylene, their predictions differ considerably for o-phenylene. As can be seen in Fig. 3, use of standard DFT results in the prediction that the average interphenylene torsion angle of o-phenylene increases with oligomer length rather than stays constant. As a result the trend in the optical gap for o-phenylene and plain DFT is a convolution of two trends; the decrease in optical gap with increasing oligomer length and the increase in the optical gap with increasing torsion angle. It should be noted here that the effect of the dispersion correction is purely structural and single point TD-DFT vertical excitation energy calculations with DFT and DFT-D give identical results.

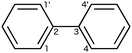
Which brings us to the non-conjugated nature of m-phenylene oligomers. From the average interphenylene torsion angle values for m-phenylene in Fig. 3 it is clear that that this lack of conjugation is not due to the torsion angle being close to 90°. As a matter of fact the average torsion angle values for o-phenylene oligomers are only very slightly larger than those of p-phenylene oligomers. Having ruled out that the lack of direct geometrical overlap is the origin of the lack of conjugation, we can consider alternative explanations. The most promising of such an alternative explanations, is the proposal by Hong and co-workers¹⁰ that the lack of overlap between the π-systems of adjacent phenylene units arises from the fact that the frontier orbitals contributing to this excitation only have small coefficients on the meta C atoms. Indeed, using DFT we find that for the dimer the atoms meta- with respect to the interphenylene bond have a much lower contribution to the frontier orbitals than the atoms that lie para- or ortho-. Similarly, in the valence bond perspective of van Veen and co-workers,⁴²m-phenylene is cross-conjugated,^43,44 meaning that one can not conceive a direct pathway involving alternating double and single bonds between more than two phenylene units (see Scheme 2), while the other two phenylene isomers are omniconjugated, and have such pathways. Both explanations thus suggest that the origin of the lack of conjugation in m-phenylene oligomers in a topological rather than a geometric feature. As a result, while the optical gap of p- and o-phenylene can be controlled by changing the interphenylene torsion angle by tuning of the steric bulk of substituents, this strategy does not work for m-phenylene.

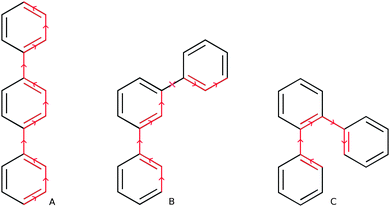Scheme 2 Direct pathways of alternating double and single bonds in p- and o-terphenyl (A & C) and absence of such a pathway in m-terphenyl (B).

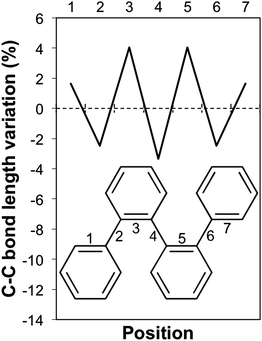
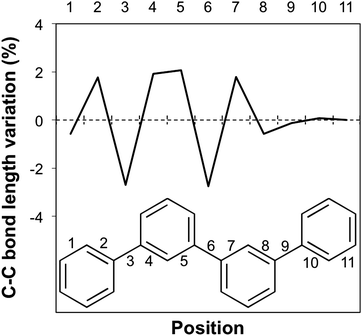
The break in conjugation when introducing m-phenylene units, finally, can conveniently be observed by modelling an oligomer consisting of two p-phenylene regions (3 or 4 units, depending on the perspective) separated by a m-phenylene segment in the centre of the molecule (see Fig. 4). For this oligomers the TD-B3LYP predicted optical gap (4.06 eV) is very similar to the optical gap of an isolated p-phenylene tetramer (4.11 eV) and much larger than the value for the p-octamer (3.58 eV). This effect can also be observed from the electron density difference between the ground and the excited state (negative density difference in blue, positive difference in red), which shows that the lowest energy singlet excitation only involves to the para-chain ends (see Fig. 4).

Fig. 4 TD-B3LYP ground-excited state density difference plot for an oligomer consisting of two p-phenylene regions separated by a m-phenylene segment in the centre of the molecule (negative density difference in blue, positive density difference in red).

Effect of isomer and oligomer length on the fluorescence energy

Just as for the optical gap, all the method combinations used generally agree on the trends of fluorescence energies with respect to oligomer length for the different phenylene isomers (see Fig. 5). However, as expected from the literature^2,3,7,8 these predicted trends are very different from one isomer to the other. The m-phenylene isomers are predicted to have the highest fluorescence energies, of the order of 3.8 eV in the case of TD-B3LYP, and show effectively no variation in fluorescence energy with oligomer length. The fluorescence energies of p-phenylene isomers, in contrast, show a distinct red shift with increasing oligomer length, while we predict a rather unique blue shift in fluorescence energies for the o-phenylene isomers. The only structure where there is contention about the description is o-terphenylene. Here TD-DFT calculations with all XC-potentials considered predict an excited state minimum while RI-CC2 finds what appears to be a conical intersection between the ground and lowest excited state potential energy surface, where all three phenylene rings end up lying in approximately the same plane.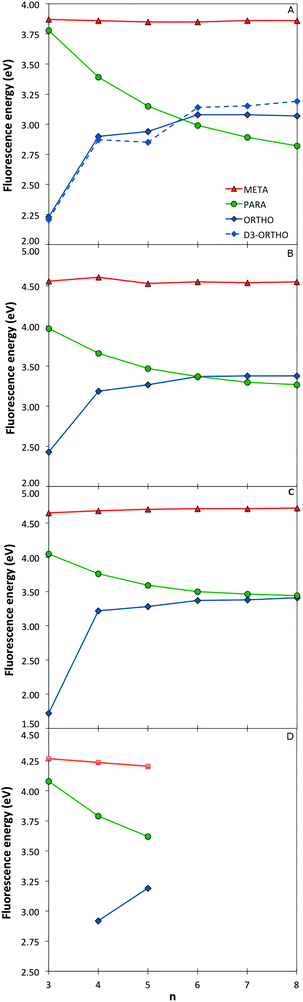

Fig. 5 Fluorescence energy values as a function of oligomer length for the different phenylene isomers calculated with TD-B3LYP (A), BHLYP (B), CAM-B3LYP (C) and RI-CC2 (D).

Degree of excited state relaxation and localisation of the excited state for the different phenylene isomers

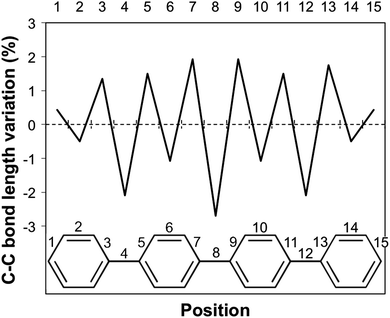
Having discussed the trend in fluorescence with oligomer length, we now move on to an in-depth discussion of the differences in excited state relaxation and fluorescence between the different phenylene isomers. We focus here on the results obtained using (TD-)B3LYP but, where insightful, we also make reference to the predictions of excited state relaxation calculations using the other XC-potential, as well as RI-CC2. Concentrating first on the Stokes shift and its contributions due to the stabilisation of the excited state (Excited State Stabilisation Energy, ESSE) and destabilisation of the ground state (Ground State Destabilisation Energy, GSDE, see Fig. S4 in Section ESI-5 of the ESI†), we see that for p-phenylene the Stokes shift gradually increases with oligomer length and that the contributions of the ESSE are roughly 25% larger than those of the GSDE. For o-phenylene, in contrast, though in line with the blue shift observed in the fluorescence energy, the Stokes shift decreases with increasing oligomer length, however, not as smoothly as it increases for p-phenylene. Use of TD-B3LYP + D, which is not necessarily a panacea in this case because the parameters of the dispersion correction should in principle be different for the ground and excited state but are not in practice, also yields slightly different results than obtained when using standard (TD-)B3LYP. Both methods, however, do agree that for the o-phenylene shorter oligomers the GSDE is considerably larger than the ESSE, while for the longer oligomers they are of similar magnitude. The Stokes shift of the m-phenylene oligomers, finally, is just like their optical gap and fluorescence energy virtually independent of oligomer length and the smallest in magnitude of all three isomers, where just as for p-phenylene the ESSE contribution is approximately 25% larger than that due to GSDE. Overall, it is clear that the Stokes shift not merely finds its origin in the stabilisation of the excited state but also has a large component due to the destabilisation of the ground state at the excited state minimum energy geometry.

A structural comparison of TD-B3LYP geometries shows that in the case of p-phenylene oligomers the main differences between the ground and relaxed excited state minimum energy structures responsible for the fluorescence are (i) a decrease in the interphenylene torsion angles relative to those in the ground state (see Fig. 3, 6, and Fig. S5 in Section ESI-5 of the ESI†) and (ii) a para-quinone like distortion of the bond lengths (see Fig. 7). Both distortions are in all cases symmetrically delocalised over the whole chain with the largest distortion in the centre.

Fig. 6 Variation of the TD-B3LYP calculated excited state interphenylene torsion angles along the oligomer for the different p-phenylene oligomers.

Fig. 7 Para-quinone bond length distortion for the p-phenylene tetramer.

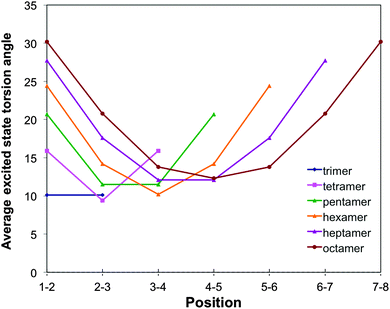
For o-phenylene, a similar reduction in torsion angles relative to the ground state is observed (see Fig. 3, 8 and Fig. S6 and S7 in Section ESI-5 of the ESI†) but now combined with an ortho rather than a para-quinone like distortion of the bond lengths (as previously discussed by Hartley,⁸ see Fig. 9). Interestingly, the reduction of the torsion angle and the ortho-quinone like distortion of the bond lengths go together with two other types of distortions that are essentially unique to the excited state minimum of o-phenylene oligomers. Firstly, (i) there is a significant distortion of the planarity of the phenylene unit and, secondly, (ii) after excited state relaxations the interphenylene bonds typically do not lie (anymore) in the same plane as either of the phenylene units they connect. Both of these latter “planarity” distortions are to a certain extent already present in the ground state structure of o-phenylene oligomers but become magnified enormously after excited state relaxation. A tell tale sign, finally, of (ii) is that the magnitude of the torsion angle between two phenylene units is different depending on which pair of atoms beyond those directly involved in the phenylene–phenylene bond are chosen to represent the interphenylene torsion angle (by up to approximately 20°, see torsion angles 1–2–3–4 and 1′–2–3–4′ in Scheme 3) and the values in Fig. 3 and 8 are thus averages of the two unique angle choices.

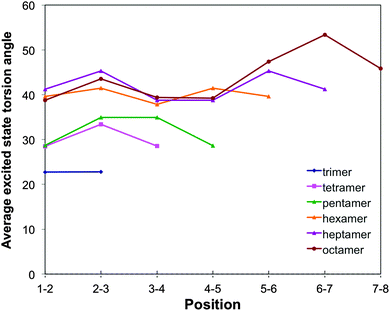Fig. 8 Variation of the TD-B3LYP + D calculated excited state interphenylene torsion angles along the oligomer for the different o-phenylene oligomers.

Fig. 9 Ortho-quinone bond length distortion for the o-phenylene tetramer.

Scheme 3 The two unique torsion angle choices 1–2–3–4 and 1′–2–3–4′.

The number of phenylene units involved in the distortion and the degree to which it is predicted to be symmetric, differ with oligomer length and the use of dispersion correction. TD-B3LYP + D predict that the excited state minima remain symmetrical up to the heptamer, where most likely the excited state is delocalised over the whole oligomer length. The maximum distortion relative to the ground state structure is for all these oligomers in the centre of the chain and the most flattest torsion angles generally occur at either end of the oligomer. For the octamer, in contrast, TD-B3LYP + D predicts an asymmetric excited state minimum, where the excited state appears to localise on one side of the oligomer. Use of plain TD-B3LYP yields for oligomers up to and including the pentamer symmetric excited state minima with a delocalised excited state, and for the longer oligomers asymmetric structures, where the excited state has localised on one site of the chain (similar to that of the TD-B3LYP + D octamer excited state minimum). The increase of selected torsion angles far away from where the excited state localises in asymmetric excited state minima (i.e. torsion angles that are actually larger than in the ground state structure, as previously observed by Hartley⁸) is only observed in our calculations in the absence of dispersion correction. RI-CC2 calculations, finally, only numerically tractable for up to the pentamer, yield symmetric excited state minima, similar to those found with TD-B3LYP + D and plain TD-B3LYP.

For m-phenylene, finally, excited state relaxation results in an extremely well localised excited state (see Fig. 3, 10 and Fig. S8 in Section ESI-5 of the ESI†). In line with the lack of conjugation in this isomer, already discussed above, always only two adjacent torsion angles and the associated two interphenylene bond distances are significantly distorted. The distortion in terms of intraphenylene bond distance changes (see Fig. 11) is limited to the three phenylene units around these torsion angles and does not follow a simple pattern, perhaps because there is no such thing as a meta-quinone like distortion.

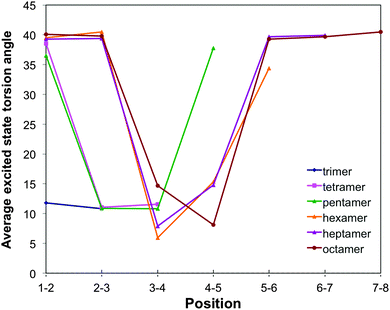Fig. 10 Variation of the TD-B3LYP calculated excited state interphenylene torsion angles along the oligomer for the different m-phenylene oligomers.

Fig. 11 Bond length distortion for the m-phenylene tetramer.

Instability of o-terphenyl

Which brings us to a reflection on the description of excited state relaxation in o-terphenyl by TD-DFT and RI-CC2. As the RI-CC2 method is known to struggle with the description of conical intersections due to their inherent multireference nature, and as the D1 diagnostic⁴⁵ that probes for possible mutireference issue within the context of RI-CC2 indeed explodes at this point to 0.26, we are careful not to over interpret the RI-CC2 result for o-terphenyl. However, we do note that o-terphenyl is the exception amongst the (o-)phenylene oligomers as it is known experimentally to undergo photocyclisation to 4a,4b-dihydrotriphenylene (DHT) via a conical intersection^46,47 rather than display fluorescence,⁸ shedding doubt on the TD-DFT excited state optimisation results for this particular structure. The observed instability is probably related to the fact that the pattern of bond-length elongations and contractions associated with the excited state ortho-quinone like distortion is similar to the bond length pattern in the ground state structure of DHT. The longer o-phenylene oligomers also display the same ortho-quinone like distortion but the steric repulsions with the rest of the oligomer means that in these cases a section of three adjacent phenylene units cannot become approximately co-planar, ruling out cyclisation and explaining why these structures are fluorescent instead.

Difference between o- and p-phenyl

Which leaves us with two pertinent interrelated questions to consider; (i) why for shorter oligomers is the fluorescence energy of p-phenylene larger than that of o-phenylene oligomers, and (ii) why for o-phenylene does the fluorescence energy increase with oligomer length rather than decrease as generally observed for polymers? Both issues we know as a result of the RI-CC2 calculations not to be artefacts of the use of TD-DFT or a particular XC-potential.

Focussing first on the question of the origin of the difference between o- and p-phenylene, it is clear that this cannot be simply related to the magnitude of the excited state interphenylene torsion angle. Comparing oligomers of similar size, the torsion angles in the excited state structure of o-phenylene are consistently significantly larger than that of p-phenylene (see Fig. 3, 6 and 8). As the excited state for these smaller oligomers is always delocalised one would thus, based on the link between torsion angle and π-systems overlap, naively have expected the fluorescence energy of o-phenylene to be larger than that of p-phenylene. Similarly, for short o- and p-phenylene oligomers the change in torsion angle between the ground and excited state is similar in magnitude but the Stokes shift (and its ESSE and GSDE components) is much larger in the case of o-phenylene than for p-phenylene oligomers of the same size. Also, the excited state interphenylene bond distances of o- and p-phenylene oligomers of the same size are very similar (see Fig. S9 in Section ESI-5 of the ESI†), suggesting no link between this structural degree of freedom and the fact the fluorescence energy of p-phenylene is larger than that of o-phenylene either. Finally, partial excited state optimisation of dimeric clusters cut from the o-phenylene trimer and tetramer excited state minima, where all atoms but the newly added one or two terminating hydrogen atoms are held fixed, have larger fluorescence energies than the fully optimised dimer. The planarity distortions thus also cannot explain the low o-phenylene fluorescence energies, at least not for dimer fragments. Having effectively ruled out most structural explanations, it thus stands to reason that the lower fluorescence energies of short o-phenylene oligomers relative to their p-phenylene counterparts must find its origin in the inherent electronic structure of o-phenylene in general, and the presence of an ortho-rather than a para-quinone like distortion in particular, as the optical gap appears well behaved. Support for this hypothesis comes from the observation that, independent of the XC-potential employed and oligomer length, the difference between the Kohn–Sham orbital energy gap for the pair(s) of orbitals responsible for the lowest energy TD-DFT excitation and its TD-DFT energy is always considerably larger for o-phenylene than for p-phenylene. For example, in the case of TD-B3LYP the energy difference between the Kohn–Sham gap and the lowest TD-B3LYP excitation energy is of the order of 0.1–0.2 eV for the p-phenylene oligomer excited state minima and 0.4–0.6 eV for their o-phenylene counterparts. In linear response TD-DFT the Kohn–Sham gap is the zeroth-order approximation to the lowest TD-DFT excitation energy, with all higher-order corrections due to a combination of the contributions of the Hartree and XC kernel (f_XC, the functional derivative of the XC-potential with respect to the density⁴⁸). The larger difference between the Kohn–Sham gap and lowest TD-DFT excitation energy for o-phenylene oligomers thus suggest that the Hartree and f_XC correction is much larger for o-phenylene than for p-phenylene and that the two oligomers indeed fundamentally differ in their many-body electronic structure beyond simply the constituting Kohn–Sham orbitals.

Which brings us, finally, to with the question of the origin of the characteristic blue shift of the fluorescence energies of o-phenylene oligomers with increasing oligomer length. Focussing on the oligomers with symmetric excited state minima and delocalised excited states, it is clear that the torsion angles of the excited state minima steadily increase with oligomer length for o-phenylene (e.g. in terms of the average torsion angle for TD-B3LYP + D an increase from 23° for the trimer to 40° for the hexamer, see Fig. 3). For p-phenylene there is also an increase in the excited state torsion angle with oligomer length but the magnitude of the change is considerably smaller than for o-phenylene (e.g. in terms of the average torsion angle for TD-B3LYP an increase from 10° for the trimer to 17° for the hexamer, see Fig. 3). If we now assume that the change of fluorescence energy with oligomer length is a balance between two competing effects; the decrease in excitation energy with increasing oligomer length and the increase in excitation energy with increasing torsion angle, then it appears that for o-phenylene and p-phenylene different terms dominate. For p-phenylene oligomers, the increase in torsion angle with oligomer size is relatively small and the decrease in excitation energy with increasing oligomer length dominates, resulting in the conventional red shift in fluorescence energy with oligomer length. While for o-phenylene oligomers the increase in excitation energy with increasing torsion angle dominates, giving rise to the rather unique blue shift with oligomer length. The large change in torsion angle with increasing o-phenylene oligomer length, finally, is probably related to an increase in steric repulsion due to a growth of the number of intraoligomer close arene–arene π-stacking contacts with increasing oligomer length (i.e. 0, 1, 2 and 3 for n = 3, 4, 5 and 6 respectively). Such close arene–arene π-stacking contacts are completely absent in p-phenylene oligomers and all other “straight” conjugated polymers, while for helical structures their effect probably decreases with increasing size of the pitch (4 in the case of o-phenylene), explaining why a blue shift in fluorescence energy with increasing oligomer length is such a rare phenomena.

Conclusions

In conclusion, we show through a combination of TD-DFT and approximate correlated wavefunction RI-CC2 calculations that the three isomers of oligophenylene, while chemically similar, display quite different absorption and especially fluorescence properties. More specifically, we show that both TD-DFT and RI-CC2 predict that all m-phenylene oligomers essentially have the same fluorescence signature while the fluorescence energy of p-phenylene oligomers decreases with oligomer length and that of o-phenylene increase. In the case of m-phenylene we discuss that the lack of change in fluorescence energy with oligomer length is a topological feature of the bonding in phenylene, while the difference between o- and p-phenylene arises from a combination of steric and electronic factors. We further show that these electronic factors, fascinatingly, result in the fluorescence of small o-phenylene oligomers to be significantly red shifted relative to their p-phenylene counterparts. Following on from that, we argue that the rarity of a blue shift in fluorescence energy with increasing oligomer length, as observed for o-phenylene oligomers, is probably related to the absence of close intraoligomer arene–arene π-stacking contacts in most other oligomers and polymers. Finally, we hypothesize that the reason that o-terphenyl experimentally photocyclises to 4a,4b-dihydrotriphenylene while the longer o-phenylene oligomers do not and are fluorescent is due to the fact that the steric bulk of the longer oligomers do not allow for the planarization required for cyclisation.

Acknowledgements

We kindly acknowledge Prof. D. Adams, Dr C. Butchosa, Prof. A. Cooper and Dr F. Cora for stimulating discussions. M.A.Z. acknowledges the UK Engineering and Physical Sciences Research Council (EPSRC) for a Career Acceleration Fellowship (Grant EP/I004424/1). Computational time on the IRIDIS regional high-performance computing service provided by the e-Infrastructure South Centre for Innovation (EPSRC Grants EP/K000144/1 and EP/K000136/1), on Archer the UK's national high-performance computing service (via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC grant EP/L000202/1) and also the EPSRC United Kingdom National Service for Computational Chemistry Software (NSCCS) at Imperial College London is gratefully acknowledged.

References

1. C. Seoul, W.-J. Song, G.-W. Kang and C. Lee, Synth. Met., 2002, 130, 9–16.
2. E. Artacho, M. Rohlfing, M. Côté, P. D. Haynes, R. J. Needs and C. Molteni, Phys. Rev. Lett., 2004, 93, 116401.
3. V. Lukeš, A. J. A. Aquino, H. Lischka and H.-F. Kauffmann, J. Phys. Chem. B, 2007, 111, 7954–7962.
4. K. Park, T.-W. Lee, M.-J. Yoon and J.-I. Choe, Bull. Korean Chem. Soc., 2014, 531–538.
5. M. Banerjee, R. Shukla and R. Rathore, J. Am. Chem. Soc., 2009, 131, 1780–1786.
6. J. He, J. L. Crase, S. H. Wadumethrige, K. Thakur, L. Dai, S. Zou, R. Rathore and C. S. Hartley, J. Am. Chem. Soc., 2010, 132, 13848–13857.
7. S. M. Mathew and C. S. Hartley, Macromolecules, 2011, 44, 8425–8432.
8. C. S. Hartley, J. Org. Chem., 2011, 76, 9188–9191.
9. S. M. Mathew, J. T. Engle, C. J. Ziegler and C. S. Hartley, J. Am. Chem. Soc., 2013, 135, 6714–6722.
10. S. Y. Hong, D. Y. Kim, C. Y. Kim and R. Hoffmann, Macromolecules, 2001, 34, 6474–6481.
11. G. Grem, G. Leditzky, B. Ullrich and G. Leising, Adv. Mater., 1992, 4, 36–37.
12. S. Yanagida, A. Kabumoto, K. Mizumoto, C. Pac and K. Yoshino, J. Chem. Soc., Chem. Commun., 1985, 474–475.
13. T. Shibata, A. Kabumoto, T. Shiragami, O. Ishitani, C. Pac and S. Yanagida, J. Phys. Chem., 1990, 94, 2068–2076.
14. S. Matsuoka, T. Kohzuki, C. Pac and S. Yanagida, Chem. Lett., 1990, 2047–2048.
15. S. Matsuoka, H. Fujii, T. Yamada, C. Pac, A. Ishida, S. Takamuku, M. Kusaba, N. Nakashima and S. Yanagida, J. Phys. Chem., 1991, 95, 5802–5808.
16. R. S. Sprick, J.-X. Jiang, B. Bonillo, S. Ren, T. Ratvijitvech, P. Guiglion, M. A. Zwijnenburg, D. J. Adams and A. I. Cooper, J. Am. Chem. Soc., 2015, 137, 3265–3270.
17. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871.
18. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138.
19. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000.
20. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
21. W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666.
22. I. Kolossváry and W. C. Guida, J. Am. Chem. Soc., 1996, 118, 5011–5019.
23. F. Mohamadi, N. G. J. Richards, W. C. Guida, R. Liskamp, M. Lipton, C. Caufield, G. Chang, T. Hendrickson and W. C. Still, J. Comput. Chem., 1990, 11, 440–467.
24. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
25. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
26. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
27. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
28. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
29. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
30. M. J. G. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578–3585.
31. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
32. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
33. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
34. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
35. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
36. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
37. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
38. C. van Wüllen, J. Comput. Chem., 2011, 32, 1195–1201.
39. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
40. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
41. H. Meier, U. Stalmach and H. Kolshorn, Acta Polym., 1997, 48, 379–384.
42. M. H. van der Veen, M. T. Rispens, H. T. Jonkman and J. C. Hummelen, Adv. Funct. Mater., 2004, 14, 215–223.
43. M. Trætteberg and H. Hopf, Acta Chem. Scand., 1994, 48, 989–993.
44. M. Gholami and R. R. Tykwinski, Chem. Rev., 2006, 106, 4997–5027.
45. C. L. Janssen and I. M. B. Nielsen, Chem. Phys. Lett., 1998, 290, 423–430.
46. N. Kharasch, T. G. Alston, H. B. Lewis and W. Wolf, Chem. Commun., 1965, 242–243.
47. M. S. Molloy, J. A. Snyder and A. E. Bragg, J. Phys. Chem. A, 2014, 118, 3913–3925.
48. M. A. Marques, N. T. Maitra, F. M. Nogueira, E. K. Gross and A. Rubio, Fundamentals of time-dependent density functional theory, Springer, 2012.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp01916h

---