Effects of electronic structure on the hydration of PbNO₃⁺ and SrNO₃⁺ ion pairs

Abstract

Hydration of PbNO₃⁺ and SrNO₃⁺ with up to 30 water molecules was investigated with infrared photodissociation (IRPD) spectroscopy and with theory. These ions are the same size, yet the IRPD spectra of these ion pairs for n = 2–8 are significantly different. Bands in the bonded O–H region (∼3000–3550 cm⁻¹) indicate that the onset of a second hydration shell begins at n = 5 for PbNO₃⁺ and n = 6 for SrNO₃⁺. Spectra for [PbNO₃]⁺(H₂O)_2–5 and [SrNO₃]⁺(H₂O)_3–6 indicate that the structures of clusters with Pb(II) are hemidirected with a void in the coordinate sphere. A natural bond orbital analysis of [PbNO₃]⁺(H₂O)₅ indicates that the anisotropic solvation of the ion is due to a region of asymmetric electron density on Pb(II) that can be explained by charge transfer from the nitrate and water ligands into unoccupied p-orbitals on Pb(II). There are differences in the IRPD spectra of PbNO₃⁺ and SrNO₃⁺ with up to 25 water molecules attached. IR intensity in the bonded O–H region is blue-shifted by ∼50 cm⁻¹ in nanodrops containing SrNO₃⁺ compared to those containing PbNO₃⁺, indicative of a greater perturbation of the water H-bond network by strontium. The free O–H stretches of surface water molecules in nanodrops containing 10, 15, 20, and 25 water molecules are red-shifted by ∼3–8 cm⁻¹ for PbNO₃⁺ compared to those for SrNO₃⁺, consistent with more charge transfer between water molecules and Pb(II). These results demonstrate that the different electronic structure of these ions significantly influences how they are solvated.

---

Introduction

Lead is one of the most widely dispersed toxins in the environment, and its deleterious effects on human health have been recognized since the 1960s.^1–3 Once ingested, lead deposits into tissues in the central nervous system^4,5 and various organs throughout the body,⁶ disrupting their function. Divalent lead in particular inhibits the function of regulatory metalloproteins by acting as a heavy-metal substitute for metal ion cofactors. Pb(II) can bind to the Ca(II)-regulated calmodulin messenger protein^7,8 thereby falsely activating cell signaling processes.^9,10 Other calcium-dependent enzymes are affected by Pb(II), including protein kinase C, whose activity can be stimulated by picomolar concentrations of lead.¹¹ Similarly, Pb(II) has been found to inhibit the function of Zn(II) and Fe(II) metalloenzymes involved in heme biosynthesis,^2,12 resulting in anemia. Lead binding depends both on its specific interaction with proteins but also its interactions with water. Knowledge of the coordination chemistry of divalent lead is thus important for understanding its biological activity.

The stability of lead in an oxidation state two less than the group valency is a characteristic shared amongst the heavier p-block elements, the so-called “inert pair effect”.¹³ This property has been explained by a relativistic contraction of the 6s orbital, which stabilizes the electrons against oxidation and confers chemical inertness.^14,15 Although these inert electrons do not participate in chemical bonding, crystal structures of Pb(II)-containing complexes indicate that they can be categorized into two broad families depending on the apparent stereochemical activity of the inert pair.^16,17 In holodirected complexes, electron density is evenly distributed around the metal ion, as are ligands in the coordination sphere. Just the opposite is the case in hemidirected Pb(II)-complexes, where asymmetric electron density on the ion results in voids in the coordination sphere. Shimoni-Livny and co-workers conducted a survey of the binding preferences of lead by analyzing 329 crystal structures of lead-containing compounds.¹⁶ They reported that Pb(II) can adopt coordination numbers (CN) ranging from 2–10, with the exclusive formation of hemidirected structures for CN = 2–5, the exclusive formation of holodirected structures for CN = 9–10, and the presence of both structures for CN = 6–8. It was initially postulated that the asymmetric electron density on Pb(II) arises from a mixing of the occupied atomic 6s orbital with unoccupied 6p orbitals, creating directional s–p hybrid orbitals.¹⁸Ab initio calculations on solid-state Pb(II) complexes indicate that the 6s electrons remain largely unhybridized, and that asymmetric electron density on the ion is due to charge transfer between the ligands and vacant 6p orbitals on Pb(II).¹⁹ These findings better explain the presence of both holo- and hemidirected structures for the intermediate CNs of Pb(II), where there is a dependence on the identity of the ligand.

Although there is much data for solid-state Pb(II) complexes, there is little experimental data on the hydration of lead in aqueous solution.¹⁷ An early proton magnetic resonance measurement indicated that the primary hydration number for Pb(II) is 5.7,²⁰ although this value has been called into question.²¹ Persson et al. measured an extended X-ray absorption fine structure spectrum of a 0.1 M solution of Pb(ClO₄)₂, and from the broad distribution of Pb–O bond distances concluded that Pb(II) is hemidirected in aqueous solution.¹⁷Ab initio calculations on Pb²⁺(H₂O)_n clusters indicate that hemidirected structures are favored for n < 6, with holodirected structures becoming energetically competitive at n = 6.^22,23 In contrast, molecular dynamics simulations of aqueous Pb(II) indicate predominantly holodirected structures.^21,24 Even less is known about solvated lead complexes.

Solvated ions can be readily formed by electrospray ionization and probed using infrared photodissociation spectroscopy in conjunction with quantum computational chemistry to obtain information about the structures of ions solvated by water^25–45 as well as other ligands.^46–48 Stace and co-workers showed that many complexes of Pb(II) with organic ligands are stable in the gas phase,^49,50 but that gaseous clusters of Pb²⁺(H₂O)_n are unstable to hydrolysis for n < 11 and consequently are not present in electrospray ionization (ESI) mass spectra.⁵¹ However, they report that hydrates of the contact ion pair [PbNO₃]⁺(H₂O)_n are stable at small cluster sizes, and Raman measurements indicate that ion pairing between metal ions and nitrate can occur in solution.⁵² IRPD studies of ion pair hydrates have so far been limited to two reports on the first hydration shell of metal hydroxides,^53,54 and a report on [MgNO₃]⁺(H₂O)_1–4.⁵⁵ How the hydration of an ion pair evolves past the completion of an inner shell around the metal ion has hitherto not been studied.

Here, the hydration of [PbNO₃]⁺(H₂O)_n and [SrNO₃]⁺(H₂O)_n is probed with IRPD spectroscopy, with the latter species serving as a reference for an ion pair incorporating a metal ion with a closed shell of electrons. IRPD spectra of [MNO₃]⁺(H₂O)_n with 2 ≤ n ≤ 8 show that the onset of hydrogen bonding (H-bonding) begins at n = 5 for PbNO₃⁺ and n = 6 for SrNO₃⁺ indicating differences in their inner hydration shells. Comparisons between IRPD and calculated spectra of [PbNO₃]⁺(H₂O)_2–5 and [SrNO₃]⁺(H₂O)_3–6 show that hemidirected structures are energetically favorable for PbNO₃⁺. We attribute this structural preference to charge transfer between the nitrate and water ligands and unoccupied 6p orbitals on Pb(II). IRPD spectra of larger hydrates of these ion pairs show that differences in their hydration persist up to n = 25, well past the first hydration shell.

Experimental

IRPD Spectroscopy

IRPD spectra of hydrated PbNO₃⁺ and SrNO₃⁺ were acquired using a 7.0 T Fourier-transform ion cyclotron resonance mass spectrometer coupled to a tunable OPO/OPA tabletop laser system. A detailed description of the apparatus and experiment can be found elsewhere.⁵⁶ Briefly, hydrated ions are generated from nanoelectrospray ionization of 3–5 mM aqueous solutions of Pb(NO₃)₂ (J.T. Baker, Phillipsburg, NJ) and Sr(NO₃)₂ (Mallinckrodt, Paris, KY) using borosilicate glass capillaries that are pulled to an inner tip diameter of ∼1 μm. A platinum wire is inserted into the capillary tube so that it is in contact with the solution, and a ∼ +600 V potential relative to the heated capillary entrance of the mass spectrometer is applied to the wire to initiate electrospray. Ions are directed from atmosphere through five stages of differential pumping into the ion cell using electrostatic lenses. The cell is surrounded by a temperature-regulated copper jacket⁵⁷ that is equilibrated to 133 K for 8 h prior to experiments. A pulse of dry nitrogen gas is introduced into the vacuum chamber at a pressure of ∼10⁻⁶ Torr for ∼5 s to aid with thermalizing and trapping the ions. This is followed by a ∼7 s delay to reduce the pressure in the cell to <10⁻⁸ Torr. Precursor ions are selected using stored waveform inverse Fourier transforms.

Mass-selected clusters are photodissociated at specific frequencies using an OPO/OPA laser system (LaserVision, Bellevue, WA) pumped by the 1064 nm fundamental of a Nd:YAG laser (Continuum Surelight I-10, Santa Clara, CA) at a 10 Hz repetition rate with pulse energies between ∼1–4 mJ between 3000–3800 cm⁻¹. Irradiation times between 1 to 10 s are used to produce substantial, but not complete, fragmentation of the isolated precursor ions which dissociate by the sequential loss of water molecules. First-order photodissociation rate constants are determined from the relative abundances of the precursor and fragment ions, and are corrected for frequency-dependent variations in laser power as well as blackbody infrared radiative dissociation (BIRD), which occurs as a result of the absorption of blackbody photons from the 133 K ion cell and cell jacket.

Computational chemistry

Low-energy structures of PbNO₃⁺ and SrNO₃⁺ with between 2 and 10 water molecules attached were generated in Macromodel 9.1 (Schrödinger, Inc., Portland, OR) by a Monte Carlo conformational search using an OPLS2005 force field with an energy cutoff of 40 kJ mol⁻¹. Anywhere between tens to hundreds of geometries were identified depending on the cluster size. From the resulting pool of low-energy structures, structures representing different isomers and water molecule binding sites were selected for geometry optimization in Q-Chem 4.1⁵⁸ (Q-Chem, Inc., Pittsburgh, PA) at the B3LYP/aug-cc-pVDZ level of theory (using the CRENBL effective core potential for Sr and Pb) prior to vibrational frequency and intensity calculations at the same level of theory. For calculated spectra, vibrational frequencies were scaled by 0.958 and convolved with a 60 and 15 cm⁻¹ fwhm Gaussian for the 3000–3510 cm⁻¹ and 3510–3800 cm⁻¹ regions, respectively. Zero-point energies, enthalpy, and entropy corrections at 133 K were calculated for these structures using unscaled B3LYP/aug-cc-pVDZ harmonic oscillator vibrational frequencies. Additional optimizations on [PbNO₃]⁺(H₂O)_4–5 and [SrNO₃]⁺(H₂O)_4–5 were performed using the B3LYP functional with the 6-31++G** basis set, and the MP2 level of theory with both aug-cc-pVDZ and 6-31++G** basis sets. Zero-point energy, enthalpy, and entropy corrections for these structures were calculated using unscaled harmonic frequencies obtained at the corresponding level of theory after geometry optimization. The wave functions of PbNO₃⁺ and SrNO₃⁺ with 5 water molecules attached were analyzed using the natural bond orbital (NBO) package of Reed and Weinhold, NBO 5.0,⁵⁹ that is incorporated in Q-Chem 4.1.

Results and discussion

IRPD spectra of small PbNO₃⁺ and SrNO₃⁺ hydrates

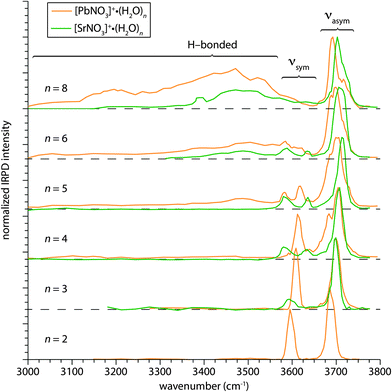
The structures of [PbNO₃]⁺(H₂O)_n and [SrNO₃]⁺(H₂O)_n with n between 2 and 8 were investigated by measuring IRPD spectra in the hydrogen stretch region (∼3000–3800 cm⁻¹) at 133 K (Fig. 1). Vibrational resonances in this region arise from both hydrogen-bonded (H-bonded) and “free” O–H stretches of water molecules. The frequencies of these oscillators are influenced by their local environment within the cluster, the ion charge state,^31–33 proximity to the charge,³² and participation in hydrogen bonding.^34–38 The overlaid spectra of PbNO₃⁺ and SrNO₃⁺ hydrates shown in Fig. 1 can be delineated into two principal spectral regions. Resonances in the higher-frequency free O–H region (∼3550–3800 cm⁻¹) arise from O–H oscillators that are not involved in H-bonding and are relatively sharp bands. The broad bands of dissociation observed in the lower-frequency region (∼3000–3600 cm⁻¹) are a result of bonded O–H stretches, including both water–water and water–nitrate hydrogen bonds.

Fig. 1 IRPD spectra of [PbNO₃]⁺(H₂O)_2–6,8 and [SrNO₃]⁺(H₂O)_3–6,8 measured at 133 K.

The IRPD spectra of the size selected PbNO₃⁺ and SrNO₃⁺ clusters are significantly different, especially in the bonded O–H region, indicating that the solvation of these two ion pairs by water is also significantly different. The onset of dissociation in the bonded O–H region indicates the formation of a second shell of water molecules in the hydration of various cations, including alkali and alkaline metal ions,^25,26,39 transition metal ions,^{28,29,40–42,60} and polyatomic ions.^30,61 In the IRPD spectrum of [PbNO₃]⁺(H₂O)₅, there is a broad region of dissociation with a maximum near 3475 cm⁻¹ that extends down to 3000 cm⁻¹, indicating H-bonding within the cluster. By comparison, evidence of H-bonding in the IRPD spectra of [SrNO₃]⁺(H₂O)_n occurs at n ≥ 6, indicating that Sr(II) can accommodate an additional water molecule in its inner hydration shell. It is intriguing that the formation of a second hydration shell begins at a smaller cluster size for PbNO₃⁺ than SrNO₃⁺ considering that both Pb(II) and Sr(II) have nearly identical crystallographic ionic radii (133 and 132 pm, respectively).⁶² This difference in the onset of second shell formation suggests that the hydration of these ions is significantly affected by the differences in the electronic structures of lead and strontium. For the n = 6 and 8 cluster sizes, the intensity in the bonded O–H region of [SrNO₃]⁺(H₂O)_n is less than that of [PbNO₃]⁺(H₂O)_n, consistent with the [SrNO₃]⁺(H₂O)_n clusters containing fewer H-bonds, although other factors also influence the intensities of these bands.

Features in the free O–H region of the [PbNO₃]⁺(H₂O)_n and [SrNO₃]⁺(H₂O)_n spectra also provide structural information. The free O–H region can be subdivided into two regions arising from the antisymmetric and symmetric stretches of water molecules, which appear between 3650–3750 cm⁻¹ and 3550–3650 cm⁻¹, respectively (Fig. 1). The onset of H-bonding in the bonded O–H region is accompanied by changes in the free O–H band structure. There are two distinct symmetric stretching bands in the spectrum of [PbNO₃]⁺(H₂O)₅, whereas the symmetric stretching bands near 3600 cm⁻¹ are degenerate for the smaller PbNO₃⁺ hydrates. This indicates that water molecules in [PbNO₃]⁺(H₂O)₅ reside in different environments, as would be expected of inner shell versus outer shell water molecules. Changes in the free O–H band structure of [SrNO₃]⁺(H₂O)_n spectra also accompany the onset of H-bonding in the n = 6 cluster. Most apparent is the broadening of the antisymmetric stretching band centered on 3715 cm⁻¹ in IRPD spectrum of [SrNO₃]⁺(H₂O)₅ upon the addition of a water molecule, indicating the greater diversity of water molecule binding sites in [SrNO₃]⁺(H₂O)₆.

Calculated lowest-energy structures for [MNO₃]⁺(H₂O)_n

Calculated lowest-energy isomers of [PbNO₃]⁺(H₂O)_n and [SrNO₃]⁺(H₂O)_n for n = 2–10 at the B3LYP/aug-cc-pVDZ level of theory are shown in Fig. 2. There are differences between the calculated structures of PbNO₃⁺ and SrNO₃⁺ hydrates at the smallest cluster size (n = 2) that persist up to the largest calculated hydrates at n = 10. There is an energetic preference for hemidirected coordination complexes of PbNO₃⁺, where there is a void in the coordination sphere around Pb(II). The directed electron density on Pb(II) apparently repels water molecules from the ion on the side opposite to the nitrate ligand. The structural effects of this repulsive domain are made evident by comparing lowest-energy structures of [PbNO₃]⁺(H₂O)₂ and [SrNO₃]⁺(H₂O)₂. Water molecules reside above and below the plane of the nitrate ion in [PbNO₃]⁺(H₂O)₂, aligning an O–H bond along the Pb–O axis of the ion pair. The structure for [SrNO₃]⁺(H₂O)₂ has the ligands distributed in such a way that repulsion between them is minimized.

Fig. 2 Calculated lowest-energy structures at 133 K of (a) [PbNO₃]⁺(H₂O)_2–6,8,10 and (b) [SrNO₃]⁺(H₂O)_2–6,8,10 at the B3LYP/aug-cc-pVDZ level of theory.

The anisotropic hydration of PbNO₃⁺ relative to the more isotropic hydration of SrNO₃⁺ is a motif that persists in the calculated structures of the larger hydrates of these ions, qualitatively explaining some of the features in the IRPD spectra (Fig. 1). Although the lowest-energy structures of the hydrated ion pairs are similar at n = 3, those of PbNO₃⁺ and SrNO₃⁺ with four water molecules attached are significantly different. For [PbNO₃]⁺(H₂O)₄, lead is hemidirected and the water molecules hydrate the ion pair anisotropically whereas the water molecules are more isotropically arranged around [SrNO₃]⁺(H₂O)₄. As a consequence of their quasi-spherical distribution in [SrNO₃]⁺(H₂O)₄, water molecules reside in substantially different binding sites around the strontium ion, consistent with the presence of multiple symmetric stretching bands in the IRPD spectrum of [SrNO₃]⁺(H₂O)₄ (Fig. 1). Structural differences are even more apparent for the n = 5 clusters. The lowest-energy structure identified for [PbNO₃]⁺(H₂O)₅ is hemidirectional, with water–water H-bonds preferentially forming over direct solvation of Pb(II). The presence of a second shell water molecule in this structure is consistent with the photodissociation observed in the bonded O–H region of the IRPD spectrum of [PbNO₃]⁺(H₂O)₅. In contrast, water molecules in the structure of [SrNO₃]⁺(H₂O)₅ form a complete inner solvation shell around Sr(II), consistent with the absence of H-bonded stretches in the IRPD spectrum of this cluster.

The hemidirected nature of Pb(II) is calculated to be energetically favorable in structures of [PbNO₃]⁺(H₂O)_n for the larger n = 6, 8, and 10 cluster sizes as well. A comparison of the structures of [SrNO₃]⁺(H₂O)_n and [PbNO₃]⁺(H₂O)_n at these cluster sizes shows that the steric repulsion from the directional electron density on Pb(II) plays an important role in the difference in the hydration of these two ions. In general, water molecules coordinate isotropically to Sr(II), filling out the inner shell of the cation. Subsequent water molecules that attach to the SrNO₃⁺ ion pair form a bridge between this inner shell and the nitrate anion, accepting H-bonds from inner shell water molecules and donating H-bonds to nitrate. In contrast, a full inner shell around Pb(II) in PbNO₃⁺ does not form in this range of cluster sizes, leading to structures where the ion pair is not isotropically solvated by water. The directional distribution of electron density on Pb establishes a “hydrophobic” surface that repels water molecules away from part of the ion so they preferentially form water–water H-bonds, eschewing short-range ion–dipole interactions with the cation. It is interesting to note that for both [SrNO₃]⁺(H₂O)_n and [PbNO₃]⁺(H₂O)_n, these calculations predict that the nitrate ligand transitions from being bidentate to monodentate between the n = 8 and 10 cluster sizes, presumably to maximize the number of H-bonds formed between water molecules and nitrate.

Structures of [MNO₃]⁺(H₂O)_2–3

To obtain more detailed information about structures, the IRPD spectra are compared to calculated spectra of low-energy isomers. The IRPD spectra of [PbNO₃]⁺(H₂O)_2–3 and [SrNO₃]⁺(H₂O)₃ shown in Fig. 1 have simple band structures, and a detailed comparison between experiment and theory can be found in the ESI.† An IRPD spectrum of [SrNO₃]⁺(H₂O)₂ was not acquired at 133 K because photodissociation for this stable complex was not observed for up to 60 s of laser irradiation. Calculations indicate that the water molecule binding energy for [SrNO₃]⁺(H₂O)₂ (∼103 kJ mol⁻¹) is significantly higher than that for [PbNO₃]⁺(H₂O)₂ (∼77 kJ mol⁻¹), consistent with the absence of observable photodissociation for the former ion under these conditions (Table S1, ESI†). The two bands appearing at 3595 cm⁻¹ and 3685 cm⁻¹ in the IRPD spectrum of [PbNO₃]⁺(H₂O)₂ correspond to the symmetric and antisymmetric stretches of water molecules, which are substantially red-shifted from their neutral values in water vapor of 3657 cm⁻¹ and 3756 cm⁻¹, respectively.⁶³ The calculated spectrum of the lowest-energy isomer of [PbNO₃]⁺(H₂O)₂ matches closely with the IRPD spectrum (Fig. S1, ESI†). Similarly, the IRPD spectra of [PbNO₃]⁺(H₂O)₃ and [SrNO₃]⁺(H₂O)₃ have resonances associated with the symmetric and antisymmetric stretching motions of water molecules, and match most closely with the calculated spectra of the lowest-energy isomers (Fig. S2 and S3, ESI†). The broadened symmetric stretching band in the IRPD spectrum of [SrNO₃]⁺(H₂O)₃ may arise from the existence of low-lying isomers where water molecules are distributed more evenly around the strontium ion (Fig. S3, ESI†). The maximum infrared photodissociation rate constant for [SrNO₃]⁺(H₂O)₃ is about four times lower than that for [PbNO₃]⁺(H₂O)₃ indicating that water molecules in this complex are more tightly bound and that the absorption of multiple photons may be required to induce observable laser-induced photodissociation on the timescale of the experiment.

Structures of [MNO₃]⁺(H₂O)₄

The IRPD spectrum of [SrNO₃]⁺(H₂O)₄ along with calculated infrared spectra of four low-energy isomers are shown in Fig. 3. The most intense band in the experimental spectrum is the antisymmetric stretch at 3708 cm⁻¹ that is closely reproduced in the calculated spectra of isomers 4a–4c. The positions of water molecules around the strontium ion in these three isomers differ substantially, yet the antisymmetric stretching bands are similar, indicating that the antisymmetric stretching frequencies of these inner shell water molecules are not sensitive to their position around the ion pair. The two well-defined bands in this region near 3585 cm⁻¹ and 3635 cm⁻¹ do not unequivocally correspond to the symmetric stretching bands in the calculated spectrum of any single isomer. The spectrum of isomer 4c (+2.5 kJ mol⁻¹) is arguably the best fit with experiment, reproducing the measured number of resonances, although the lowest-energy symmetric stretch is calculated to be ∼60 cm⁻¹ lower than that in the IRPD spectrum. These calculations indicate that the frequencies of the symmetric stretching bands are sensitive to the positions of water molecules within the cluster, and discrepancies between experiment and theory could arise from uncertainties in harmonic oscillator frequencies and intensities⁶⁴ as well as the presence of energetically competitive isomers. For ions where there are many interconverting isomers or that have vibrations that are significantly anharmonic, calculated harmonic spectra of low-energy isomers can differ from the experimental infrared spectra.^65,66 Uncertainties as a result of the harmonic frequency approximation can also affect calculated Gibbs free energies, which may affect the relative energetic ordering of isomers presented here. Structure 4d (+25.1 kJ mol⁻¹) is the lowest-energy isomer identified that includes a hydrogen bond and is significantly higher in energy than all the isomers without H-bonding (4a–4c). The poor match between its calculated spectrum and the IRPD spectrum, most notably the calculated H-bonded stretch centered on 3182 cm⁻¹ that is absent in the experiment, indicate that it does not constitute a significant fraction of the experimental population.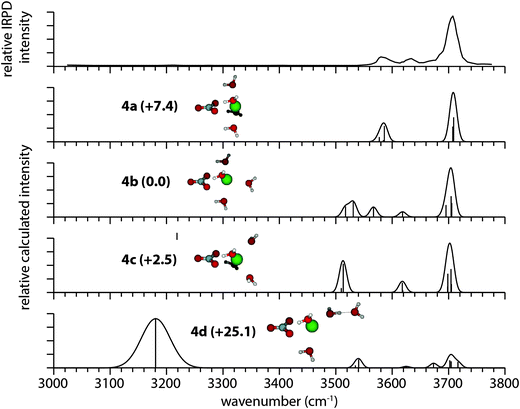

Fig. 3 IRPD spectrum of [SrNO₃]⁺(H₂O)₄ and calculated spectra of low-energy isomers at the B3LYP/aug-cc-pVDZ level of theory, along with their relative Gibbs free energies in kJ mol⁻¹ at 133 K.

The experimental and calculated infrared spectra for [PbNO₃]⁺(H₂O)₄ are shown in Fig. 4. The lowest-energy isomer (4a) reproduces the water antisymmetric and symmetric stretching bands in the IRPD spectrum near 3705 cm⁻¹ and 3612 cm⁻¹, respectively, but there are additional features in the experimental spectrum of [PbNO₃]⁺(H₂O)₄ that cannot be explained by isomer 4a alone. An intense band at 3684 cm⁻¹ is present in the antisymmetric stretching region, as well as two broad regions of low intensity in the bonded O–H region near 3460 cm⁻¹ and 3100 cm⁻¹. Collectively, these resonances may arise from a minor population of structures in which there is hydrogen bonding, such as isomer 4b (+8.1 kJ mol⁻¹). This structure has a resonance at 3686 cm⁻¹ corresponding to the antisymmetric free O–H stretch of a water molecule donating one H-bond. The bonded O–H stretch of this water molecule is calculated to occur at 3052 cm⁻¹, which could account for the small recorded resonance near 3100 cm⁻¹. The experimentally observed dissociation between 3300–3500 cm⁻¹ is not reproduced in any of the calculated spectra, and we postulate that this band may arise from an O–H oscillator forming a weak H-bond with nitrate. Isomers 4c and 4d have calculated spectra in poor agreement with the IRPD spectrum in the free O–H region, and it is unlikely that they contribute significantly to the experimental population.

Fig. 4 IRPD spectrum of [PbNO₃]⁺(H₂O)₄ and calculated spectra of low-energy isomers at the B3LYP/aug-cc-pVDZ level of theory, along with their relative Gibbs free energies in kJ mol⁻¹ at 133 K.

Structures of [MNO₃]⁺(H₂O)₅

The IRPD and calculated spectra of [SrNO₃]⁺(H₂O)₅ are shown in Fig. 5. There is good agreement between the IRPD spectrum and the calculated spectrum for lowest-energy isomer 5a. In this structure, there is no H-bonding and water molecules spherically solvate the strontium ion. There is no spectroscopic evidence for a substantial population of isomers with H-bonded structures, such as isomers 5b–5e, which are >14 kJ mol⁻¹ higher in energy.

Fig. 5 IRPD spectrum of [SrNO₃]⁺(H₂O)₅ and calculated spectra of low-energy isomers at the B3LYP/aug-cc-pVDZ level of theory, along with their relative Gibbs free energies in kJ mol⁻¹ at 133 K.

The IRPD spectrum of [PbNO₃]⁺(H₂O)₅ (Fig. 6) differs significantly from that of [SrNO₃]⁺(H₂O)₅ (Fig. 5). In striking contrast to [SrNO₃]⁺(H₂O)₅, there is substantial dissociation in the bonded O–H region of [PbNO₃]⁺(H₂O)₅ signifying the onset of H-bonding in this cluster. The water molecule binding energies of these ions differ, and this difference affects the relative dissociation efficiencies of these ions which is a complicating factor in comparing spectral intensities in the bonded O–H region. The water molecule binding energies decrease with increasing cluster size (Table S1, ESI†), and at n = 5, the water molecule binding energies of these two ions are within 20 kJ mol⁻¹. The maximum infrared rate constant for SrNO₃⁺ is within a factor of ∼2 of that for PbNO₃⁺ at n = 5. This indicates that the differences in the relative binding energies of water to these ions has a relatively small effect on the ability to observe photodissociation, and that the differences in the spectra of these two ions in the H-bonding region are significant.

Fig. 6 IRPD spectrum of [PbNO₃]⁺(H₂O)₅ and calculated spectra of low-energy isomers at the B3LYP/aug-cc-pVDZ level of theory, along with their relative Gibbs free energies in kJ mol⁻¹ at 133 K.

The best matches between experiment and theory for [PbNO₃]⁺(H₂O)₅ are isomer 5b (+1.7 kJ mol⁻¹) and lowest-energy isomer 5c, indicating the presence of both isomers in the experiment (Fig. 6). The broad antisymmetric stretching band between 3660–3740 cm⁻¹ in the IRPD spectrum is consistent with a combination of the antisymmetric stretches calculated for 5b and 5c. There are two free O–H symmetric stretching bands centered on 3620 cm⁻¹ and 3585 cm⁻¹ in the IRPD spectrum. These resonances are closely matched by the calculated symmetric stretches of isomer 5b at 3611 cm⁻¹ and 3570 cm⁻¹. The greater relative intensity of the higher-energy symmetric stretch in the experimental spectrum is consistent with the presence of isomer 5c, which is calculated to have a symmetric stretching band centered on 3605 cm⁻¹.

Resonances in the bonded O–H region of the [PbNO₃]⁺(H₂O)₅ spectrum can also be attributed to a combination of isomers 5b and 5c. The experimental band that has a maximum near 3475 cm⁻¹ corresponds to the O–H stretch of the second shell water molecule in isomer 5c that weakly H-bonds with nitrate and is predicted to occur at 3504 cm⁻¹. The broad region of dissociation in the lowest-energy region of the experimental spectrum can be attributed to isomer 5b, which has a water-water H-bond calculated to have a resonance near 3134 cm⁻¹. In general, the agreement between experimental and calculated frequencies and intensities is poorer in the bonded O–H region. Such discrepancies have been observed in the calculated spectra of a variety of hydrated gaseous ions investigated by IRPD spectroscopy.^{25,30,34,67–69} and can be attributed to uncertainties associated with using the harmonic approximation, as well as effects of basis set and level of theory used.⁶⁴ IRPD action spectra can also differ from computed spectra owing to fragmentation efficiencies that depend on the photon energy.^70,71

For larger hydrates of SrNO₃⁺ and PbNO₃⁺, a comparison between experiment and theory is more challenging owing to the increasing number of possible isomers and increasing computational difficulty with increasing cluster size. Our results for [SrNO₃]⁺(H₂O)₆, however, indicate that the outer shell water molecule accepts a H-bond from an inner shell water molecule and donates a weak H-bond to nitrate, thus forming a bridge between the hydration shell around Sr(II) and nitrate (Fig. S4, ESI†). The effects of basis set and type of theory on the energetic ordering of isomers was evaluated from single point calculations on optimized structures of the hydrated ions with n = 4 and 5 using two types of theory (MP2 and DFT/B3LYP) in conjunction with two different basis sets (aug-cc-pVDZ and 6-31++G**). There is no significant energetic reordering of the isomers for any of the ions investigated, and in all cases, the same lowest-energy structure was identified (Tables S2 and S3, ESI†).

NBO analysis of [PbNO₃]⁺(H₂O)₅

A NBO analysis⁷² of the lowest-energy isomer of [PbNO₃]⁺(H₂O)₅ was performed to elucidate the relationship between the apparent hemidirected nature of Pb(II) in this complex and its electronic structure. The filled NBOs ϕ_i that represent the natural Lewis structure of a molecule commonly account for >99.9% of the total electron density.⁷³ The remaining electron density is described by non-Lewis NBOs ϕ_j of lower occupancy that describe portions of the molecular valence space not associated with the localized Lewis structure. Occupancy of these non-Lewis NBOs thus accounts for irreducible delocalization effects in the description of the total electron density and leads to a lowering of the electronic energy. The resonance delocalization of electron density from filled (donor) ϕ_i NBOs to unfilled (acceptor) ϕ_j NBOs constitutes charge transfer between the orbitals, and can be calculated from second order perturbation theory.⁷⁴ Analyses of these stabilizing donor–acceptor interactions have led to chemically intuitive descriptions of hyperconjugative effects,⁷⁵ H-bonded systems,^76,77 and ion–molecule complexes.⁷³

Results from an NBO analysis of [PbNO₃]⁺(H₂O)₅ indicates that the electron density is strongly resonance delocalized, with the occupancy of Lewis NBOs accounting for only 99.16% of the total electron density. Shown in Fig. 7a is a set of three unfilled, non-Lewis NBOs that are primarily responsible for this delocalization, accepting charge from filled Lewis NBOs on the water and nitrate ligands (Fig. 7b). These acceptor orbitals are localized 6p atomic orbitals on Pb(II). The orientation of the 6p₁ orbital in particular is consistent with a region of repulsive electron density that could partially explain the hemidirected character of Pb(II).

Fig. 7 (a) Unfilled NBOs centered on Pb(II) that accept charge. (b) Filled NBOs on the nitrate and water ligands that donate charge. (c) NBO of valence 6s electrons on Pb(II) that has almost pure s character. All orbitals are plotted using an isosurface value of 0.05 e Å⁻³.

Calculated stabilization energies due to charge transfer between donor NBOs on the water and nitrate ligands and the acceptor 6p NBOs on Pb are shown in Table 1. The most stabilizing interaction (91.6 kJ mol⁻¹) occurs between a lone pair on an oxygen atom of nitrate (LP₁) and the 6p₁ orbital on Pb. These orbitals are relatively close in energy and have good spatial overlap (Fig. 7) making this the most favorable charge transfer interaction. The next most stabilizing interaction occurs between a lone pair on the second coordinating oxygen atom of the nitrate ligand (LP₂) and the 6p₁ orbital on Pb(II). Significant charge transfer also occurs between the four inner shell water molecules and the 6p₂ and 6p₃ NBOs on Pb(II). The high occupancies of these 6p orbitals (Table 1), especially the 6p₁ orbital that accepts charge from nitrate, indicate that they play an essential role in accurately describing the electronic structure of [PbNO₃]⁺(H₂O)₅. Charge transfer from nitrate to lead slightly shortens the average nitrate–cation distance to 2.56 Å in this complex as compared to 2.63 Å for [SrNO₃]⁺(H₂O)₅. Conversely, average cation–oxygen bond lengths for inner shell water molecules are somewhat greater for lead (2.68 Å) than strontium (2.62 Å) for n = 5 as a result of the reduced positive charge on the lead cation (Table 2). An analysis of the net atomic Mulliken charges on Pb and Sr in the lowest-energy structures for the n = 2–10 hydrates (Table 2) shows that the net atomic charge on lead is ∼ +0.5 less than strontium for these cluster sizes, indicating that the charge transfer efficiency does not depend strongly on the extent of hydration within this range of cluster sizes.

Table 1 Resonance delocalization energies between donor NBO ϕ_i and acceptor NBO ϕ_j calculated by second order perturbation theory. The occupancies of the acceptor orbitals as well as the acceptor (ε_j) to donor (ε_i) orbital energy difference are also shown

Donor (i)	Acceptor (j)	Stabilization energy (kJ mol^−1)	Occupancy of acceptor	ε j − εi (Hartree)
NO3-LP1	6p2	91.6	0.123	0.39
NO3-LP2	6p1	68.2		0.39
H2O (1)	6p2	60.1	0.098	0.63
H2O (2)	6p3	53.6	0.087	0.55
H2O (3)	6p3	47.7		0.64
H2O (4)	6p2	35.0		0.65
Pb-6s	6p2	5.0		0.46

---

Table 2 Net atomic Mulliken charges on Pb and Sr in the calculated lowest-energy isomers of [PbNO₃]⁺(H₂O)_2–6,8,10 and [SrNO₃]⁺(H₂O)_2–6,8,10 at the B3LYP/aug-cc-pVDZ level of theory

Ion	n = 2	n = 3	n = 4	n = 5	n = 6	n = 8	n = 10
[PbNO3]^+(H2O)n	+1.34	+1.40	+1.43	+1.41	+1.46	+1.54	+1.43
[SrNO3]^+(H2O)n	+1.97	+1.88	+1.87	+1.82	+1.76	+1.92	+2.00

---

Interestingly, the steric influence of lead's 6s electrons (i.e., the “inert pair”) appears to be minor. Fig. 7c shows that the valence NBO associated with these electrons is largely unhybridized, having predominately s character – the amount of p character is calculated to be only 1.47%. These results suggest that the hemidirected nature of the [PbNO₃]⁺(H₂O)₅ complex can mostly be attributed to a charge transfer effect from the nitrate ligand into an unoccupied 6p orbital on lead. This is consistent with ab initio calculations performed on structures of lead solvated by water²² as well as other ligands.⁷⁸ Several groups have found that the calculated hybridization of the inert pair is sensitive to the size of the effective core potential used to describe lead,^22,23 potentially explaining an earlier finding where the 6s electrons were calculated to be more significantly hybridized.¹⁶

Structural signatures in IRPD spectra of larger PbNO₃⁺ and SrNO₃⁺ hydrates

The extent to which the structural differences in nascent hydrates of PbNO₃⁺ and SrNO₃⁺ persist at larger cluster sizes was investigated by measuring IRPD spectra of [PbNO₃]⁺(H₂O)_n and [SrNO₃]⁺(H₂O)_n, where n = 10, 15, 20, 25, 30 (Fig. 8). The IRPD spectra of both ion pairs with up to 25 water molecules attached are distinguishable in the free O–H and bonded O–H regions but are indistinguishable at n = 30 (Fig. 8). Low-energy structures of these ion pairs with 25 water molecules attached generated using molecular mechanics indicate that there are several water molecules in the third solvation shell (Fig. S5, ESI†). This indicates that differences in the electronic structures of PbNO₃⁺ and SrNO₃⁺ influence their hydration past the first and even the second solvation shell.

Fig. 8 IRPD spectra of [PbNO₃]⁺(H₂O)_n and [SrNO₃]⁺(H₂O)_n for n = 10, 15, 20, 25, 30 in the free O–H (∼3650–3750 cm⁻¹) and bonded O–H (∼3000–3650 cm⁻¹) regions. The abscissa in the free O–H region is expanded to make the differences between these bands more clear.

The overall intensity of the bonded O–H stretch region is greater for [PbNO₃]⁺(H₂O)₁₀ than [SrNO₃]⁺(H₂O)₁₀, which reflects the more extensive H-bond network in hydrates of PbNO₃⁺ as a result of the onset of H-bonding at smaller cluster size. At this cluster size, the differences in water molecule binding energies between these clusters is calculated to be ∼6 kJ mol⁻¹ (Table S1, ESI†) and this difference should only have a minor effect on relative dissociation efficiencies in this spectral region. The intensity of this band becomes similar for both ions with increasing cluster size, indicating that the relative differences in the number of H-bonded oscillators and binding energies diminish. It is also apparent that the shape of the bonded O–H feature is more symmetrical for [PbNO₃]⁺(H₂O)_n, with the maximum dissociation at ∼3475 cm⁻¹ for the n = 10 and 15 clusters and slightly red-shifting to ∼3450 cm⁻¹ in the spectra of the larger hydrates. The H-bonded features in the spectra of the larger clusters closely resemble both the bulk infrared spectrum of neutral water⁷⁹ and IRPD spectra of hydrated ions that weakly interact with water,⁶¹ indicating optimal water–water H-bonding within the interior of the nanodrops. In contrast, the bonded O–H regions in the IRPD spectra of [SrNO₃]⁺(H₂O)_n with up to 25 water molecules are blue-shifted up to ∼50 cm⁻¹. This suggests that the H-bond networks in these SrNO₃⁺ nanodrops are more strained as a result of the stronger interaction between Sr(II) and water compared to Pb(II) and water where delocalization of electron density from nitrate reduces the net charge on the ion. This interpretation is consistent with condensed phase measurements of hydrated cations measured by vibrational sum frequency generation,^80,81 where the H-bonded stretches of water molecules are shifted towards higher frequencies for ions with greater charge densities.

The most striking difference in the bonded O–H region of these larger PbNO₃⁺ and SrNO₃⁺ clusters is the band centered near ∼3550 cm⁻¹ in the IRPD spectra of the SrNO₃⁺ hydrates for n = 15, 20, and 25. There are resonances at this frequency in IRPD spectra of hydrated ions that form clathrate structures with ∼20 water molecules attached, including the hydrated proton,^43–45 alkali metal ions,⁸² ammonium,^83,84 and alkylammonium ions⁸⁴ corresponding to water molecules that accept one H-bond and donate two H-bonds (“ADD” water molecules) that are integral to forming cage-like, three-dimensional H-bond networks. Results from Fujii and co-workers indicate that an intense ADD band is a general feature of small water clusters (n ∼ 20–50), where the dominant structural motif is calculated to be “centered cage” structures wherein several water molecules are entrained in a three-dimensional water cage.⁸⁵ The larger size of these ion pairs precludes structures where an ion pair is completely encapsulated by a water cage with only 20 water molecules or so, but it is possible that partial cage-like structures with a high percentage of three-coordinate water molecules can form around the ion pair. Indeed, the lowest-energy structures of [SrNO₃]⁺(H₂O)_2–10 in Fig. 2 suggests such a hydration motif, where water molecules first nucleate around Sr(II) and subsequently align along the approximately dipolar electric field of SrNO₃⁺, forming H-bonds with each other and the nitrate anion. This leads to the beginnings of a cage-like hydration network in the calculated lowest-energy structure of [SrNO₃]⁺(H₂O)₁₀.

Two distinct bands appear in the free O–H region of these larger PbNO₃⁺ and SrNO₃⁺ clusters (Fig. 8): an intense band near 3700 cm⁻¹ associated with water molecules accepting two H-bonds and donating one H-bond (AAD water molecule), and a small band near 3720 cm⁻¹ arising from water molecules that accept and donate only one H-bond (AD water molecule). The free O–H stretches of water molecules in [PbNO₃]⁺(H₂O)_n are red-shifted by 5.6–7.6 cm⁻¹ compared to those in [SrNO₃]⁺(H₂O)_n for n = 10, 15 and 20, but they are closer in frequency at n = 25 (3.3 cm⁻¹) and are indistinguishable at n = 30. The centroid frequencies of the AAD free O–H bands were determined by fitting each peak with a Gaussian function, and the frequencies for all cluster sizes are shown in Fig. S6 (ESI†). The frequencies of free O–H oscillators depend on the charge of the ion and, to a lesser extent, the size of the ion.³² Sr(II) and Pb(II) have the same ionic radii⁶² indicating that the red-shift in the frequency of surface water stretches in hydrates of PbNO₃⁺ is due to higher charge transfer between water molecules and lead. This is consistent with findings by Duncan and co-workers, who reported that charge transfer can red-shift the O–H stretch frequencies in IRPD spectra of water molecules bound to singly charged cations.⁸⁶ As our NBO analysis of [PbNO₃]⁺(H₂O)₅ suggests, the unfilled 6p orbitals of Pb(II) can readily accept charge from donating water and nitrate ligands. Charge transfer from water molecules that are located in outer solvation shells will decrease with increasing cluster size because of poorer overlap with the atomic orbitals on the metal ion. The number of water molecules in the second and higher hydration shells increases relative to the number of water molecules in the first hydration shell and the IRPD spectra increasingly reflect absorption of these outer shell water molecules with increasing cluster size. Thus, the IRPD spectra of these clusters are expected to converge at some cluster size where the contributions to the spectra from water molecules that are significantly perturbed by these ions becomes negligible.

Conclusions

The structures of [PbNO₃]⁺(H₂O)_n and [SrNO₃]⁺(H₂O)_n were investigated with IRPD spectroscopy and with theory. Although these ions are the same size, they differ significantly in their hydration. H-bonded stretches in the IRPD spectra indicate the onset of second shell formation at n = 5 for PbNO₃⁺ (and a minor population of second shell structures at n = 4) and n = 6 for SrNO₃⁺. Calculated structures of PbNO₃⁺ and SrNO₃⁺ with 10 and fewer water molecules indicate that hemidirected structures are favored for Pb(II) where there is a noticeable void in its coordination sphere, and these results are consistent with the IRPD spectra. The asymmetric solvation for hydrates of PbNO₃⁺ is due to the asymmetric electron density on Pb(II) that repels water molecules away from the portion of its coordination sphere opposite to the nitrate ligand, constraining the available binding site for water molecules. Results from an NBO analysis of [PbNO₃]⁺(H₂O)₅ indicate that the asymmetric charge density on Pb(II) is a result of charge transfer from the nitrate and water ligands into vacant 6p orbitals on the ion. In contrast, Sr(II) in SrNO₃⁺ is isotropically solvated by water.

The IRPD spectra of PbNO₃⁺ and SrNO₃⁺ with up to 25 water molecules attached differ. The maximum intensity of the H-bonded stretches of SrNO₃⁺ are blue-shifted compared to those of PbNO₃⁺, indicating a greater perturbation of the water H-bond network by strontium than lead. This is consistent with the higher net atomic Mulliken charges of [SrNO₃]⁺(H₂O)_n compared to [PbNO₃]⁺(H₂O)_n. The intense band at 3550 cm⁻¹ in the spectra of SrNO₃⁺ with 15, 20, and 25 waters attached suggests that partial clathrate-like structures may form around this ion pair. The free O–H stretches of AAD water molecules in hydrates of PbNO₃⁺ are red-shifted by up to ∼8 cm⁻¹ compared to those in hydrates of SrNO₃⁺ for n = 10, 15, 20 but are the same by n = 30. The red-shifting of surface water molecules in [PbNO₃]⁺(H₂O)_n is consistent with the transfer of electron density from their O–H bonds to the lead ion. Collectively, the spectral differences between the larger hydrates of PbNO₃⁺ and SrNO₃⁺ demonstrate that the electronic structure of an ion can play an important role in how it is solvated past the first and even second solvent shells.

Acknowledgements

The authors thank the National Science Foundation (grant CHE-1306720) for generous financial support of this research and are grateful to the German National Academy of Sciences Leopoldina (LPDS 2012–15) for a postdoctoral fellowship and financial support (S.H.).

References

1. C. C. Patterson, Arch. Environ. Health, 1965, 11, 344–360.
2. B. L. Vallee and D. D. Ulmer, Annu. Rev. Biochem., 1972, 41, 91–128.
3. K. R. Mahaffey, Environ. Health Perspect., 1977, 19, 285–295.
4. Y. Finkelstein, M. E. Markowitz and J. F. Rosen, Brain Res. Rev., 1998, 27, 168–176.
5. T. I. Lidsky and J. S. Schneider, Brain, 2003, 126, 5–19.
6. R. A. Goyer and B. C. Rhyne, Int. Rev. Exp. Pathol., 1973, 12, 1–77.
7. M. A. Wilson and A. T. Brunger, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59, 1782–1792.
8. P. Kursula and V. Majava, Acta Crystallogr., Sect. F: Struct. Biol. Cryst. Commun., 2007, 63, 653–656.
9. T. J. B. Simons, Neurotoxicology, 1993, 14, 77–86.
10. C. Marchetti, Neurotoxic. Res., 2003, 5, 221–235.
11. J. Markovac and G. W. Goldstein, Nature, 1988, 334, 71–73.
12. W. W. Ku, D. Slowiejko, L. L. Bestervelt, M. R. Buroker and W. N. Piper, Toxicol. In Vitro, 1990, 4, 763–769.
13. N. V. Sidgwick, The Electronic Theory of Valency, Oxford University Press, Clarendon, 1927.
14. K. S. Pitzer, Acc. Chem. Res., 1979, 12, 272–276.
15. P. Pyykkö, Chem. Rev., 1988, 88, 563–594.
16. L. Shimoni-Livny, J. P. Glusker and C. W. Bock, Inorg. Chem., 1998, 37, 1853–1867.
17. I. Persson, K. Lyczko, D. Lundberg, L. Eriksson and A. Placzek, Inorg. Chem., 2011, 50, 1058–1072.
18. L. E. Orgel, J. Chem. Soc., 1959, 3815–3819.
19. A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422–1428.
20. T. J. Swift and W. G. Sayre, J. Chem. Phys., 1966, 44, 3567–3574.
21. T. S. Hofer and B. M. Rode, J. Chem. Phys., 2004, 121, 6406–6411.
22. M. C. F. Wander and A. E. Clark, Inorg. Chem., 2008, 47, 8233–8241.
23. M. Devereux, M. C. van Severen, O. Parisel, J. P. Piquemal and N. Gresh, J. Chem. Theory Comput., 2011, 7, 138–147.
24. C. Gourlaouen, H. Gerard and O. Parisel, Chemistry, 2006, 12, 5024–5032.
25. M. F. Bush, R. J. Saykally and E. R. Williams, ChemPhysChem, 2007, 8, 2245–2253.
26. D. J. Miller and J. M. Lisy, J. Am. Chem. Soc., 2008, 130, 15393–15404.
27. D. J. Goebbert, E. Garand, T. Wende, R. Bergmann, G. Meijer, K. R. Asmis and D. M. Neumark, J. Phys. Chem. A, 2009, 113, 7584–7592.
28. J. T. O'Brien and E. R. Williams, J. Phys. Chem. A, 2011, 115, 14612–14619.
29. Y. Li, G. Wang, C. Wang and M. Zhou, J. Phys. Chem. A, 2012, 116, 10793–10801.
30. R. J. Cooper, S. Heiles, M. J. DiTucci and E. R. Williams, J. Phys. Chem. A, 2014, 118, 5657–5666.
31. P. D. Carnegie, B. Bandyopadhyay and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 6237–6243.
32. J. S. Prell, J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2011, 133, 4810–4818.
33. J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 10228–10236.
34. J. M. Headrick, E. G. Diken, R. S. Walters, N. I. Hammer, R. A. Christie, J. Cui, E. M. Myshakin, M. A. Duncan, M. A. Johnson and K. D. Jordan, Science, 2005, 308, 1765–1769.
35. N. Heine, M. R. Fagiani, M. Rossi, T. Wende, G. Berden, V. Blum and K. R. Asmis, J. Am. Chem. Soc., 2013, 135, 8266–8273.
36. I. Leon, E. J. Cocinero, A. M. Rijs, J. Millan, E. Alonso, A. Lesarri and J. A. Fernandez, Phys. Chem. Chem. Phys., 2013, 15, 568–575.
37. Y. Inokuchi, T. Ebata, T. R. Rizzo and O. V. Boyarkin, J. Am. Chem. Soc., 2014, 136, 1815–1824.
38. N. Heine, T. I. Yacovitch, F. Schubert, C. Brieger, D. M. Neumark and K. R. Asmis, J. Phys. Chem. A, 2014, 118, 7613–7622.
39. Y. Inokuchi, K. Ohshimo, F. Misaizu and N. Nishi, J. Phys. Chem. A, 2004, 108, 5034–5040.
40. R. S. Walters, E. D. Pillai and M. A. Duncan, J. Am. Chem. Soc., 2005, 127, 16599–16610.
41. T. Iino, K. Ohashi, K. Inoue, K. Judai, N. Nishi and H. Sekiya, J. Chem. Phys., 2007, 126, 194302.
42. T. E. Cooper, J. T. O'Brien, E. R. Williams and P. B. Armentrout, J. Phys. Chem. A, 2010, 114, 12646–12655.
43. J. W. Shin, Science, 2004, 304, 1137–1140.
44. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Science, 2004, 304, 1134–1137.
45. J. A. Fournier, C. J. Johnson, C. T. Wolke, G. H. Weddle, A. B. Wolk and M. A. Johnson, Science, 2014, 344, 1009–1012.
46. A. D. Brathwaite and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 11695–11703.
47. R. Shishido, Y. Kawai and A. Fujii, J. Phys. Chem. A, 2014, 118, 7297–7305.
48. K. N. Reishus, A. D. Brathwaite, J. D. Mosley and M. A. Duncan, J. Phys. Chem. A, 2014, 118, 7516–7525.
49. G. Akibo-Betts, P. E. Barran, L. Puskar, B. Duncombe, H. Cox and A. J. Stace, J. Am. Chem. Soc., 2002, 124, 9257–9264.
50. L. Puskar, P. E. Barran, B. J. Duncombe, D. Chapman and A. J. Stace, J. Phys. Chem. A, 2005, 109, 273–282.
51. K. McQuinn, F. Hof, J. S. McIndoe, X. J. Chen, G. H. Wu and A. J. Stace, Chem. Commun., 2009, 4088–4090.
52. M. R. McCoustra, Phys. Chem. Chem. Phys., 2008, 10, 4676–4677.
53. B. M. Marsh, J. Zhou and E. Garand, J. Phys. Chem. A, 2014, 118, 2063–2071.
54. C. J. Johnson, L. C. Dzugan, A. B. Wolk, C. M. Leavitt, J. A. Fournier, A. B. McCoy and M. A. Johnson, J. Phys. Chem. A, 2014, 118, 7590–7597.
55. L. Jiang, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Am. Chem. Soc., 2010, 132, 7398–7404.
56. M. F. Bush, J. T. O'Brien, J. S. Prell, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 1612–1622.
57. R. L. Wong, K. Paech and E. R. Williams, Int. J. Mass Spectrom., 2004, 232, 59–66.
58. Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko and D. P. O'Neill, et al. , Phys. Chem. Chem. Phys., 2006, 8, 3172–3191.
59. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohman, C. M. Morales and F. Weinhold, NBO 5.0, http://www.chem.wisc.edu/~nbo5.
60. J. T. O'Brien and E. R. Williams, J. Phys. Chem. A, 2008, 112, 5893–5901.
61. J. S. Prell and E. R. Williams, J. Am. Chem. Soc., 2009, 131, 4110–4119.
62. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
63. G. Herzberg, Infrared and Raman Spectra of Polyatomic Molecules, Van Nostrand and Co., Inc., Princeton, NJ, 1945.
64. C. J. Cramer, Essentials of Computational Chemistry Theories and Models, John Wiley & Sons, Ltd, West Sussex, England, 2nd edn, 2004.
65. L. Jiang, S. T. Sun, N. Heine, J. W. Liu, T. I. Yacovitch, T. Wende, Z. F. Liu, D. M. Neumark and K. R. Asmis, Phys. Chem. Chem. Phys., 2014, 16, 1314–1318.
66. V. Brites, J. M. Lisy and M. P. Gaigeot, J. Phys. Chem. A, 2015, 119, 2468–2474.
67. K. Mizuse, N. Mikami and A. Fujii, Angew. Chem., Int. Ed., 2010, 49, 10119–10122.
68. J. S. Prell, T. M. Chang, J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 7811–7819.
69. T. M. Chang, J. S. Prell, E. R. Warrick and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 15805–15813.
70. N. C. Polfer, Chem. Soc. Rev., 2011, 40, 2211–2221.
71. J. S. Prell, T. C. Correra, T. M. Chang, J. A. Biles and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 14733–14735.
72. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
73. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
74. F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379.
75. C. J. Cramer, A. M. Kelterer and A. D. French, J. Comput. Chem., 2001, 22, 1194–1204.
76. M. A. Vallejos, E. L. Angelina and N. M. Peruchena, J. Phys. Chem. A, 2010, 114, 2855–2863.
77. K. Wendler, J. Thar, S. Zahn and B. Kirchner, J. Phys. Chem. A, 2010, 114, 9529–9536.
78. C. Gourlaouen, H. Gerard, J. P. Piquemal and O. Parisel, Chem. – Eur. J., 2008, 14, 2730–2743.
79. M. Freda, A. Piluso, A. Santucci and P. Sassi, Appl. Spectrosc., 2005, 59, 1155–1159.
80. S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Am. Chem. Soc., 2014, 136, 6155–6158.
81. P. A. Covert, K. C. Jena and D. K. Hore, J. Phys. Chem. Lett., 2014, 5, 143–148.
82. R. J. Cooper, T. M. Chang and E. R. Williams, J. Phys. Chem. A, 2013, 117, 6571–6579.
83. E. G. Diken, N. I. Hammer, M. A. Johnson, R. A. Christie and K. D. Jordan, J. Chem. Phys., 2005, 123, 164309.
84. T. M. Chang, R. J. Cooper and E. R. Williams, J. Am. Chem. Soc., 2013, 135, 14821–14830.
85. T. Hamashima, K. Mizuse and A. Fujii, J. Phys. Chem. A, 2011, 115, 620–625.
86. B. Bandyopadhyay, K. N. Reishus and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 7794–7803.

---

Footnotes

† Electronic supplementary information (ESI) available: Water molecules binding energies of lowest-energy isomers for 2 ≤ n ≤ 10, Relative Gibbs free energies of low-energy isomers of [MNO₃]⁺(H₂O)_4–5 calculated at different levels of theory, IRPD spectra of [PbNO₃]⁺(H₂O)_2–3 and [SrNO₃]⁺(H₂O)_3,6 along with calculated spectra of low-energy isomers, low-energy structures of these ion pairs with 25 water molecules attached identified from molecular mechanics, centroid frequencies of the AAD bands of [MNO₃]⁺(H₂O)_n determined from Gaussian fits, and xyz-coordinates of all structures at the B3LYP/aug-cc-pVDZ level of theory. See DOI: 10.1039/c5cp01859e

‡ Current Address: Institute of Inorganic and Analytical Chemistry, Justus-Liebig-University Giessen, 35392 Giessen, Germany.

---