The Jahn–Teller effect in the presence of partial isotopic substitution: the ![[B with combining tilde]](https://www.rsc.org/images/entities/h2_char_0042_0303.gif) 1E′′ state of NH2D and NHD2†
1E′′ state of NH2D and NHD2†
Received
5th March 2015
, Accepted 29th April 2015
First published on 30th April 2015
Abstract
Rotationally resolved resonance enhanced multiphoton ionisation spectra of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH2D are presented and analysed. The analysis indicates a small (34.9 cm−1) lifting of the vibronic degeneracy of the zero point level, approximately equal in sign but opposite in magnitude to the splitting observed in NHD2 in previous work. This observation is consistent with previous measurements on systems with partial isotopic substitution subject to a mild Jahn–Teller effect. A model is developed to calculate the splitting induced by asymmetric isotopic substitution of a degenerate electronic state, based on a harmonic force field with linear and quadratic Jahn–Teller terms added. The force field is developed in internal co-ordinates to allow the same parameters to be used to calculate the pattern of vibronic levels for all four isotopologues. The lifting of the degeneracy of the zero point level on asymmetric substitution comes from the quadratic Jahn–Teller effect; the linear term does not lift the degeneracy.
1E′′ state of NH2D are presented and analysed. The analysis indicates a small (34.9 cm−1) lifting of the vibronic degeneracy of the zero point level, approximately equal in sign but opposite in magnitude to the splitting observed in NHD2 in previous work. This observation is consistent with previous measurements on systems with partial isotopic substitution subject to a mild Jahn–Teller effect. A model is developed to calculate the splitting induced by asymmetric isotopic substitution of a degenerate electronic state, based on a harmonic force field with linear and quadratic Jahn–Teller terms added. The force field is developed in internal co-ordinates to allow the same parameters to be used to calculate the pattern of vibronic levels for all four isotopologues. The lifting of the degeneracy of the zero point level on asymmetric substitution comes from the quadratic Jahn–Teller effect; the linear term does not lift the degeneracy.
Introduction
The Jahn–Teller effect is an important consideration in understanding the structure and spectroscopy of degenerate electronic states. If strong (also known as a static Jahn–Teller effect) the geometry of the molecule changes to break the symmetry. We are focussing here on the dynamic Jahn–Teller effect, where the energy shifts are smaller, typically less than the zero point energy, and thus where the symmetry of the molecule is essentially maintained (or at least gives the best starting point for modelling). To interpret spectra additional terms in the effective Hamiltonian are required to account for the Jahn–Teller effect giving shifts and splittings in both the vibrational and rotational energy levels. These terms are reasonably well understood, (see for example a review by Barckholtz and Miller1) though examples of full rotational analysis are relatively rare in the literature. In this paper we look at the additional complications introduced in the presence of partial isotopic substitution. This breaks the symmetry of the vibrational and rotational terms, but must leave the electronic symmetry unbroken. To understand the resulting energy level pattern requires additional terms above the standard vibrational or rotational Hamiltonian and this paper seeks to understand these by a combination of experimental measurements on a reasonably well understood system and theoretical considerations of the simplest linear and quadratic terms in the potential.
The system looked at here is the electronically degenerate ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia for which the
1E′′ state of ammonia for which the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition gives strong resonance enhanced multiphoton ionization (REMPI) spectra and is a prototypical example of a system with a mild Jahn–Teller effect. It is also an important transition in its own right, as it has become a standard system for probing rotational states of ammonia in the laboratory, as for example in a recent study by Tkac et al.2 on collisions and in cold molecule work such as that by Twyman et al.3
1A1′ transition gives strong resonance enhanced multiphoton ionization (REMPI) spectra and is a prototypical example of a system with a mild Jahn–Teller effect. It is also an important transition in its own right, as it has become a standard system for probing rotational states of ammonia in the laboratory, as for example in a recent study by Tkac et al.2 on collisions and in cold molecule work such as that by Twyman et al.3
The ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state is planar and the degeneracy arises from the 3px,y Rydberg orbital in the plane of the molecule, and so the Jahn–Teller effect is relatively weak, giving vibrational energy level shifts4 of the order of 100 cm−1. The rotational structure can be understood in terms of a standard symmetric top with two additional terms in the rotational Hamiltonian (ζ and q)5 arising from a significant residual electronic angular momentum. This electronic angular momentum (almost one unit) also means the state shows a significant Zeeman effect. The rotational and vibrational structure is reasonably well understood for both NH3 and ND3, but partially isotopically substituted species have not been investigated in any detail. In a previous paper6 we looked at resonance enhanced multiphoton ionisation spectra of NHD2. Formally this molecule has C2v symmetry, and is thus an asymmetric top with no degenerate vibronic states possible but, as discussed above, the degeneracy is only lifted at the vibrational and rotational level. Our analysis of observations indicated that the zero point level was best understood in terms of two closely spaced vibronic states with the symmetries A2 and B1 that correlate with E′′ in D3h. The separation is only 35.1 cm−1, so the additional terms (ζ and q) present in the symmetric top Hamiltonian for NH3 and ND3 are required to model the rotational structure, but transformed to perturbation terms mixing the two states. The terms mixing the vibronic states are only of the order of magnitude of rotational terms, but because the states are so close together the spectra cannot be effectively modelled without them.
1E′′ state is planar and the degeneracy arises from the 3px,y Rydberg orbital in the plane of the molecule, and so the Jahn–Teller effect is relatively weak, giving vibrational energy level shifts4 of the order of 100 cm−1. The rotational structure can be understood in terms of a standard symmetric top with two additional terms in the rotational Hamiltonian (ζ and q)5 arising from a significant residual electronic angular momentum. This electronic angular momentum (almost one unit) also means the state shows a significant Zeeman effect. The rotational and vibrational structure is reasonably well understood for both NH3 and ND3, but partially isotopically substituted species have not been investigated in any detail. In a previous paper6 we looked at resonance enhanced multiphoton ionisation spectra of NHD2. Formally this molecule has C2v symmetry, and is thus an asymmetric top with no degenerate vibronic states possible but, as discussed above, the degeneracy is only lifted at the vibrational and rotational level. Our analysis of observations indicated that the zero point level was best understood in terms of two closely spaced vibronic states with the symmetries A2 and B1 that correlate with E′′ in D3h. The separation is only 35.1 cm−1, so the additional terms (ζ and q) present in the symmetric top Hamiltonian for NH3 and ND3 are required to model the rotational structure, but transformed to perturbation terms mixing the two states. The terms mixing the vibronic states are only of the order of magnitude of rotational terms, but because the states are so close together the spectra cannot be effectively modelled without them.
There have been few comparable studies in the literature; perhaps the most closely related is work by Yu et al.7 on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1′′ state of C5H4D and C5D4H. These spectra were modelled as simple asymmetric tops, with the Jahn–Teller terms accounted for using perturbation theory working through to anomalous values of the rotational constants. The splittings of the zero point levels were approximately equal in magnitude (∼9 cm−1) but opposite in sign for the two isotopologues. A similar pattern of splittings was observed by Melnik et al.8,9 in the
2E1′′ state of C5H4D and C5D4H. These spectra were modelled as simple asymmetric tops, with the Jahn–Teller terms accounted for using perturbation theory working through to anomalous values of the rotational constants. The splittings of the zero point levels were approximately equal in magnitude (∼9 cm−1) but opposite in sign for the two isotopologues. A similar pattern of splittings was observed by Melnik et al.8,9 in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state of CH2DO and CD2HO though the rotational analysis was more complicated than that considered here due to the presence of significant spin–orbit coupling. Other related work is discussed below. There has been correspondingly little theoretical work on asymmetrically isotopically substituted Jahn–Teller systems though there is one particularly relevant recent paper by Iwahara et al.10 This paper showed that vibronic levels of a degenerate electronic state remain degenerate upon arbitrary isotopic substitution, even in the presence of a linear Jahn–Teller effect. For the current work, this implies we must consider both linear and quadratic Jahn–Teller terms.
2E state of CH2DO and CD2HO though the rotational analysis was more complicated than that considered here due to the presence of significant spin–orbit coupling. Other related work is discussed below. There has been correspondingly little theoretical work on asymmetrically isotopically substituted Jahn–Teller systems though there is one particularly relevant recent paper by Iwahara et al.10 This paper showed that vibronic levels of a degenerate electronic state remain degenerate upon arbitrary isotopic substitution, even in the presence of a linear Jahn–Teller effect. For the current work, this implies we must consider both linear and quadratic Jahn–Teller terms.
In the current paper we present a set of spectra of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH2D to complement our earlier spectra of NHD2, and then look at relating the Jahn–Teller effects in all four isotopologues by developing a simple model for the force field in internal coordinates that can be applied without adjustment to all four species.
1E′′ state of NH2D to complement our earlier spectra of NHD2, and then look at relating the Jahn–Teller effects in all four isotopologues by developing a simple model for the force field in internal coordinates that can be applied without adjustment to all four species.
Experimental
Spectra of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D were recorded using resonance enhanced multiphoton ionization spectroscopy (REMPI) in a molecular beam, using the method described previously.6 This gave rotationally resolved spectra with an effective rotational temperature of 3–90 K, that could be varied by adjusting the expansion conditions.
1A1′ transition in NH2D were recorded using resonance enhanced multiphoton ionization spectroscopy (REMPI) in a molecular beam, using the method described previously.6 This gave rotationally resolved spectra with an effective rotational temperature of 3–90 K, that could be varied by adjusting the expansion conditions.
Rotational analysis
The spectra taken covered 7 members of the bending progression (v2), starting with the origin band. Typical spectra of the first 6 bands are shown in Fig. 1. All the bands showed clear rotational structure, and the observed linewidths (∼0.9 cm−1) are probably limited by the laser system, and there was no indication of rotationally or vibrationally dependent predissociation at this resolution.
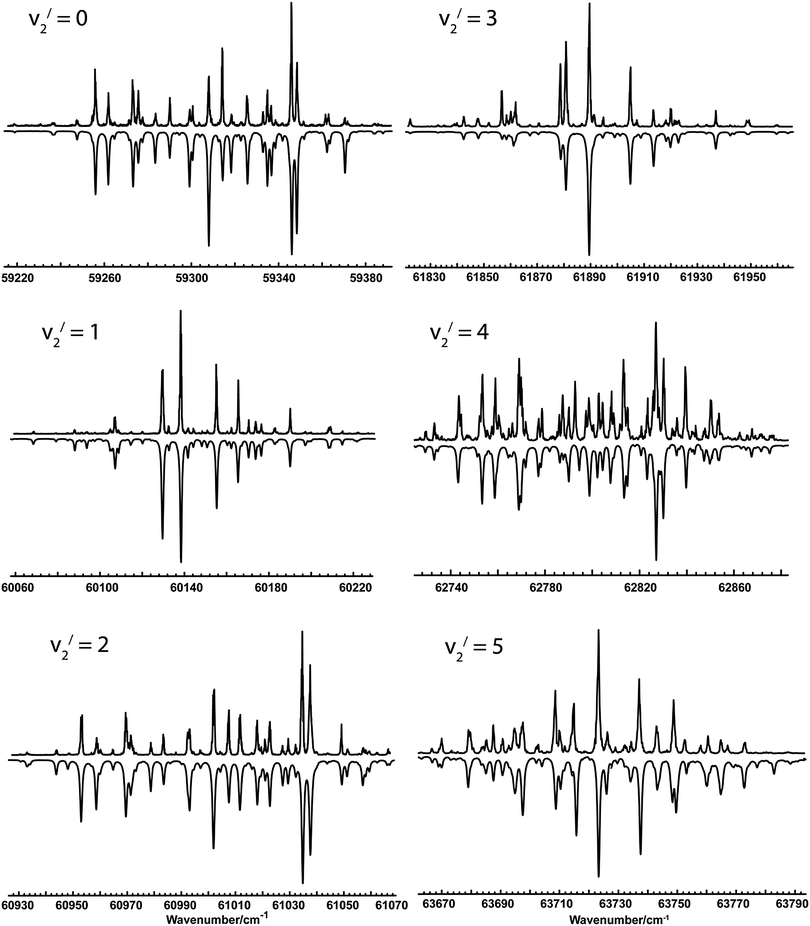 |
| | Fig. 1 MPI spectra of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′– 1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D. In each panel, the upper trace is the experimental spectrum and the lower trace is a simulation using the Hamiltonian and parameters described in the text. 1A1′ transition in NH2D. In each panel, the upper trace is the experimental spectrum and the lower trace is a simulation using the Hamiltonian and parameters described in the text. | |
The theory required for the rotational analysis is developed in our previous paper6 and is only briefly summarised here. The basic model is two distinct vibronic states, for each of which a standard asymmetric top Hamiltonian in a IIIr representation is used as a starting point:
| | | Ĥrot = ½(A + B)(Ĵ2 − Ĵz2) + ¼(A − B)(Ĵ+2 + Ĵ−2) + CĴz2 | (1) |
For the purposes of this paper |+〉 and |−〉 are used to label the two vibronic states, and two additional terms in the Hamiltonian are required to take account of the residual electronic angular momentum, both of which introduce terms acting between the two states. The largest of these is the equivalent of the Coriolis term in symmetric tops:
| | Ĥcor = −2CζĴz![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z z | (2) |
where we have introduced an effective electronic angular momentum operator that has electronic matrix elements:
| | 〈±|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z|±〉 = 0, 〈±| z|±〉 = 0, 〈±|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z|∓〉 = ζ z|∓〉 = ζ | (3) |
The overall matrix elements are therefore −2
Cζ
K. The other term is analogous to
l doubling in symmetric tops, and can be written as:
| | Ĥq = ½iq′(Ĵ+2 − Ĵ−2)(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 − +2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) −2) | (4) |
where
Ĵ+2 −
Ĵ−2 = 2
i(
ĴaĴb +
ĴbĴa) and the electronic operator
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2
+2 −
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2
−2 is discussed below. This has matrix elements:
| | 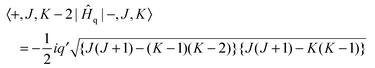 | (5) |
| | 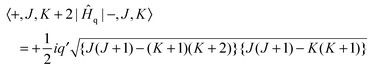 | (6) |
Note that the matrix elements are imaginary, and it is not possible to make a simple adjustment in phase to make all matrix elements real. The equations above are used to calculate the energy levels of the excited state by setting up and diagonalising a (complex) Hamiltonian matrix containing, for a given
J and rovibronic symmetry, all possible values of
K for both vibronic components. To complete the model equal two photon transition moments from the ground state to each of the two excited states is assumed and, as discussed in the previous paper, interference between these two has a significant effect on the pattern of observed transitions. The calculations were carried out using the
PGOPHER program.
11,12 The ground state constants were taken from Fusina
et al.13
The ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition involves a change in geometry from pyramidal to planar, so the transition shows a progression in ν2, the umbrella mode. In the upper state members of this progression alternate between E′′ and E′ symmetry for even and odd v2 respectively, and the selection rules mean that the lower state of the electronic transition alternates between the upper and lower tunnelling component in the ground state. As this results from levels symmetric and antisymmetric with respect to the plane of symmetry of the molecule, which persists for NH2D and NHD2, the same pattern of transitions is observed for all four isopologues. In NH2D the |+〉 levels alternate between A2 (even v2) and B2 (odd v2) and the |−〉 levels alternate between B1 and A1 vibronic symmetry.
1A1′ transition involves a change in geometry from pyramidal to planar, so the transition shows a progression in ν2, the umbrella mode. In the upper state members of this progression alternate between E′′ and E′ symmetry for even and odd v2 respectively, and the selection rules mean that the lower state of the electronic transition alternates between the upper and lower tunnelling component in the ground state. As this results from levels symmetric and antisymmetric with respect to the plane of symmetry of the molecule, which persists for NH2D and NHD2, the same pattern of transitions is observed for all four isopologues. In NH2D the |+〉 levels alternate between A2 (even v2) and B2 (odd v2) and the |−〉 levels alternate between B1 and A1 vibronic symmetry.
Given this model the assignment of the observed spectra was reasonably straightforward, given the guidance of the fits for NHD2. Table 1 shows four alternative fits to the pair of states making up the origin band. These follow the pattern in the previous paper; fit I is the simplest model, assuming two non-interacting asymmetric top states. This gives a reasonable fit, but is clearly worse than the other models which allow for interaction between the states. Fit IV is the most flexible model, adding the two interactions discussed above and allowing A, B and C for both components to float independently. This is clearly a better fit than fit I as the average error drops by a factor of two from 0.53 cm−1 to 0.24 cm−1, but there is significant correlation between the values of C between the two states, as indicated by the large error bars. Fits II and III show two alternative approaches to reducing this correlation; fit II fixes the Coriolis term at a value derived from a simple rigid rotor model (see Table 1 of Yang et al.6) and fit III instead constrains the two C values to be identical. Both these fits are as good as fit IV. The quality of the fits is similar to the corresponding fits in NHD2, and as in that case we choose to recommend fit III, as the parameters are all well determined and none are fixed.
Table 1 Rotational constantsa from alternative fits to the rotational structure of the origin band of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D
1A1′ transition in NH2D
| |
Estimatedb |
Fit I |
Fit II |
Fit III |
Fit IV |
| A2 |
B1 |
A2 |
B1 |
A2 |
B1 |
A2 |
B1 |
|
Units are cm−1; figures in brackets are standard deviations in units of the least significant figure.
Estimated from simple rigid rotor model – see Table 1 of Yang et al.6
Fixed.
|
| Origin |
|
59259.78(20) |
59294.29(24) |
59259.58(10) |
59294.44(10) |
59259.58(10) |
59294.44(10) |
59259.57(11) |
59294.46(12) |
|
A
|
10.42 |
9.564(25) |
10.744(45) |
9.856(26) |
10.780(21) |
9.856(26) |
10.780(21) |
9.872(44) |
10.791(29) |
|
B
|
6.40 |
6.756(37) |
6.663(70) |
6.766(20) |
6.455(34) |
6.766(20) |
6.455(35) |
6.753(31) |
6.443(42) |
|
C
|
3.96 |
2.986(36) |
5.11(15) |
3.949(20) |
3.956(39) |
3.953(18) |
4.102(292) |
3.790(321) |
| 2Cζ |
−6.51 |
0c |
−6.51b |
−6.520(63) |
−6.881(660) |
|
q′ |
|
0c |
0.681(44) |
0.681(44) |
0.676(47) |
|
σ
|
|
0.53 |
0.23 |
0.23 |
0.24 |
|
n
obs
|
|
28 |
18 |
28 |
18 |
28 |
18 |
28 |
18 |
Table 2 shows the results of using fit style III on the other observed bands in NH2D. Experimental spectra and simulations are shown in Fig. 1. More details of each fit, including line listings, are available as supplementary data (ESI†). The overall quality of the fits is good, with the average errors somewhat smaller than the experimental linewidth of ∼0.9 cm−1. The fits for v2 = 4 and 5 were slightly worse than the others, with some lines out of position by of the order of the linewidth. These probably reflect interactions with other vibrational states of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state; such interactions have been seen5 in ND3 and the level of vibrational excitation is such that these are to be expected. The analysis was stopped at v2 = 5; some peaks were seen in the region of v2 = 6, but a complete analysis was not possible because of two complicating factors. Firstly the origin band of the C′ state14 is in this region and secondly the interference between the two transition moments has become sufficiently large that transitions to one of the components becomes very weak. These factors combined meant it was not possible to produce a convincing analysis of the observed spectra for v2 = 6.
state; such interactions have been seen5 in ND3 and the level of vibrational excitation is such that these are to be expected. The analysis was stopped at v2 = 5; some peaks were seen in the region of v2 = 6, but a complete analysis was not possible because of two complicating factors. Firstly the origin band of the C′ state14 is in this region and secondly the interference between the two transition moments has become sufficiently large that transitions to one of the components becomes very weak. These factors combined meant it was not possible to produce a convincing analysis of the observed spectra for v2 = 6.
Table 2 Rotational constantsa for the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D
1A1′ transition in NH2D
| |
v
2 = 0 |
v
2 = 1 |
v
2 = 2 |
v
2 = 3 |
v
2 = 4 |
v
2 = 5 |
|
Figures in brackets are standard deviations in units of the least significant figure.
Error bars are from the fit; a systematic error of up to of 2 cm−1 in the band origins is also possible.
|
| A2 |
Originb/cm−1 |
59259.58(10) |
60092.551(72) |
60957.622(80) |
61848.198(96) |
62759.25(15) |
63685.87(26) |
|
A/cm−1 |
9.856(26) |
9.413(12) |
8.978(20) |
8.449(24) |
7.995(27) |
7.662(64) |
|
B/cm−1 |
6.766(20) |
6.531(15) |
6.346(16) |
6.089(18) |
5.810(28) |
6.214(66) |
|
n
obs
|
28 |
22 |
26 |
24 |
28 |
26 |
|
|
| B1 |
Originb/cm−1 |
59294.44(10) |
60125.044(71) |
60988.109(86) |
61875.263(74) |
62782.87(16) |
63707.14(20) |
|
A/cm−1 |
10.780(21) |
10.135(12) |
9.443(17) |
9.300(22) |
8.884(21) |
7.76(13) |
|
B/cm−1 |
6.455(35) |
6.210(13) |
5.948(26) |
5.768(19) |
5.646(28) |
5.376(49) |
|
n
obs
|
18 |
22 |
16 |
16 |
22 |
18 |
|
|
|
|
C/cm−1 |
3.953(18) |
3.9666(97) |
4.021(14) |
4.077(20) |
4.031(31) |
4.073(23) |
| 2Cζ/cm−1 |
−6.520(63) |
−6.545(34) |
−6.639(46) |
−6.810(76) |
−6.555(83) |
−6.57(10) |
|
q/cm−1 |
0.681(44) |
0.678(14) |
0.657(31) |
0.589(52) |
0.341(76) |
0.96(11) |
|
σ/cm−1 |
0.23 |
0.15 |
0.17 |
0.17 |
0.39 |
0.43 |
Table 3 shows the corresponding constants in NHD2; this is essentially the same as in Yang et al.6 but a better set of ground state constants has been used for these fits. (The changes are minor – mainly a 0.17 cm−1 shift in the band origins.) Comparing these tables indicates very similar trends in for both species – a sensible trend in all of the constants apart from q, which is not always well determined. Both species show a consistent difference between A and B for the two components, with the average for the origin band close to the value predicted from a simple rigid rotor model. The splitting between the two components of the origin band is very close for the two states (34.86 cm−1 for NH2D against 35.11 cm−1 for NHD2) but opposite in sign, with the A2 component at lower energy for NH2D and the B1 component lower for NHD2. The similar pattern of results gives further confirmation of the rotational analysis for these two species.
Table 3 Rotational constantsa for the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NHD2
1A1′ transition in NHD2
| |
v
2 = 0 |
v
2 = 1 |
v
2 = 2 |
v
2 = 3 |
v
2 = 4 |
v
2 = 5 |
v
2 = 6 |
|
Units are cm−1; figures in brackets are standard deviations in units of the least significant figure.
Error bars are from the fit; a systematic error of up to of 2 cm−1 in the band origins is also possible.
|
| A2 |
Originb |
59349.390(77) |
60109.154(46) |
60896.063(56) |
61704.737(37) |
62531.037(47) |
63370.514(53) |
64221.66(24) |
|
A
|
8.377(16) |
7.9686(57) |
7.572(13) |
7.0956(85) |
6.700(13) |
6.3268(66) |
6.001(45) |
|
B
|
5.112(15) |
5.0152(91) |
4.9135(81) |
4.7491(64) |
4.5855(87) |
4.5045(93) |
4.427(62) |
|
n
obs
|
25 |
31 |
29 |
42 |
25 |
28 |
7 |
|
|
| B1 |
Originb |
59314.282(69) |
60077.029(58) |
60866.747(58) |
61678.418(38) |
62507.766(53) |
63350.601(65) |
64205.74(20) |
|
A
|
7.653(11) |
7.3133(79) |
6.999(11) |
6.6633(55) |
6.328(11) |
6.026(11) |
5.651(46) |
|
B
|
5.556(11) |
5.3790(80) |
5.2264(88) |
5.0487(63) |
4.917(13) |
4.7773(96) |
4.678(61) |
|
n
obs
|
30 |
22 |
28 |
37 |
33 |
34 |
10 |
|
|
| Both |
C
|
3.167(12) |
3.1596(68) |
3.2191(48) |
3.2353(47) |
3.2527(63) |
3.2793(56) |
3.190(70) |
| 2Cζ |
−5.264(50) |
−5.283(30) |
−5.273(21) |
−5.333(18) |
−5.405(20) |
−5.388(23) |
−5.39(14) |
|
q
|
0.481(22) |
0.407(16) |
0.353(21) |
0.3116(97) |
0.309(28) |
0.188(38) |
0.30(12) |
|
σ
|
0.18 |
0.12 |
0.12 |
0.12 |
0.12 |
0.13 |
0.24 |
Vibronic analysis
The Jahn–Teller effect in NH3
As indicated in the introduction the observation of equal and opposite splittings in the zero point level has been seen in other systems, so it is instructive to develop a model of the force field including the Jahn–Teller effect that can be used for all four isotopologues to explain this splitting. The ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3 has two Jahn–Teller active modes, the asymmetric stretch, ν3 and the in plane bend, ν4, both with E′ symmetry. (The other two modes are the symmetric (A1′) stretch, ν1 and the umbrella mode, ν2 (A2′′)). The most complete information so far on the Jahn–Teller activity in these modes comes from the study of Allen et al.4 based on a combination of IR-MPI double resonance spectroscopy and other methods. While the pattern of the levels of the Jahn–Teller active modes is not known in full, enough is known to give a good idea as to the likely pattern and magnitude of the effects. The model we are using here is two electronic states that are degenerate at all values of the vibrational co-ordinates, with the Jahn–Teller terms giving matrix elements between the two surfaces. The most significant extra term due to the Jahn–Teller effect is a term linear in the vibrational co-ordinates: Dimensionless normal coordinates, q, are used here. The
1E′′ state of NH3 has two Jahn–Teller active modes, the asymmetric stretch, ν3 and the in plane bend, ν4, both with E′ symmetry. (The other two modes are the symmetric (A1′) stretch, ν1 and the umbrella mode, ν2 (A2′′)). The most complete information so far on the Jahn–Teller activity in these modes comes from the study of Allen et al.4 based on a combination of IR-MPI double resonance spectroscopy and other methods. While the pattern of the levels of the Jahn–Teller active modes is not known in full, enough is known to give a good idea as to the likely pattern and magnitude of the effects. The model we are using here is two electronic states that are degenerate at all values of the vibrational co-ordinates, with the Jahn–Teller terms giving matrix elements between the two surfaces. The most significant extra term due to the Jahn–Teller effect is a term linear in the vibrational co-ordinates: Dimensionless normal coordinates, q, are used here. The ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ±2 operators are taken to connect the components of the degenerate electronic state, which we label with Λ = ±1, approximately the electronic angular momentum of the states:
±2 operators are taken to connect the components of the degenerate electronic state, which we label with Λ = ±1, approximately the electronic angular momentum of the states:| | ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ±2|±1〉 = |∓1〉 ±2|±1〉 = |∓1〉 | (8) |
The initial analysis of Allen et al.4 has ω3 = 3314.1 cm−1, |k3| = 0.165, ω4 = 1625.5 cm−1, |k4| = 0.1905 which suggests that the linear term is significant for both ν3 and ν4. These parameters did not fully account for the observed levels, and an alternative analysis was presented by Allen et al.4 that accounted for more of the observed levels. This added an additional electronic state to the Hamiltonian, and a term linear in q3 mixing this with the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, though a similar fit was also possible using a quadratic Jahn–Teller term of the form:
state, though a similar fit was also possible using a quadratic Jahn–Teller term of the form:| | ĤJT2 = ½gω(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) −2 −2![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 + +2 + ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) +2 +2![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) −2) | (9) |
At the level of second order perturbation theory the two are equivalent, and we will use the latter approach here for simplicity.
Converting to a C2v picture
The Jahn–Teller terms above are expressed in terms of operators appropriate to D3h symmetry, but to apply these to the unsymmetrical isotopologues we must convert everything to states and operators that have the correct symmetry in C2v as well as D3h. For the electronic part the required transformation was discussed in the previous paper:| | 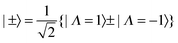 | (10) |
The |±〉 states introduced above in the rotational analysis essentially transform as x and y, as opposed to the Λ = ±1 states which transform as x ± iy. For the Jahn–Teller term we require the matrix elements of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 ±
+2 ± ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2, which can be derived by simple substitution:
−2, which can be derived by simple substitution:| | 〈±|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 + +2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2|±〉 = ±1 and 〈±| −2|±〉 = ±1 and 〈±|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 − +2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2|∓〉 = ∓1 −2|∓〉 = ∓1 | (11) |
The other combinations of operators and signs give zero matrix elements. For the vibrational part we re-express the operator for a single Jahn–Teller mode in terms of Cartesian style components:which makes the linear Jahn–Teller term become:| | ĤJT = kω{![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x( x(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 + +2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) + i −2) + i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y( y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 − +2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)} −2)} | (13) |
This is, of course equivalent to the earlier expression in full symmetry, but in this form the symmetry requirements of the ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x and
x and ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y coordinates become clear. The term multiplying
y coordinates become clear. The term multiplying ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x is diagonal in the |±〉 basis, and must therefore correspond to a totally symmetric co-ordinate in C2v symmetry. It has the effect of adding or subtracting a simple linear term along the x normal co-ordinate. The term multiplying
x is diagonal in the |±〉 basis, and must therefore correspond to a totally symmetric co-ordinate in C2v symmetry. It has the effect of adding or subtracting a simple linear term along the x normal co-ordinate. The term multiplying ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y is purely off-diagonal in the |±〉 basis, and must therefore have the symmetry of the product of the two electronic components. From the previous paper |+〉 has A2 symmetry and |−〉 has B1 symmetry for the electronic origin (which has E′′ symmetry in D3h), requiring
y is purely off-diagonal in the |±〉 basis, and must therefore have the symmetry of the product of the two electronic components. From the previous paper |+〉 has A2 symmetry and |−〉 has B1 symmetry for the electronic origin (which has E′′ symmetry in D3h), requiring ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y to have B2 symmetry so that the overall operator, i
y to have B2 symmetry so that the overall operator, i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y(
y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) is totally symmetric. Note that i
−2) is totally symmetric. Note that i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y(
y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) will give purely imaginary matrix elements, but we can avoid this complication by multiplying one of the electronic basis functions by i.
−2) will give purely imaginary matrix elements, but we can avoid this complication by multiplying one of the electronic basis functions by i.
Applying the same process to the quadratic Jahn–Teller effect yields a more complicated result:
| | ĤJT2 = ½gω{(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 − x2 − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2)( y2)(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 + +2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) − 2i −2) − 2i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y( y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 − +2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)} −2)} | (14) |
Note that again the matrix element off-diagonal in electronic state are purely imaginary, so we can maintain purely real functions by applying the same phase factor as for the linear Jahn–Teller effect.
Modelling the Jahn–Teller effect in a Cartesian basis
Given the above we can exactly reproduce the Jahn–Teller energy level pattern in a Cartesian basis consisting of (harmonic) vibrations along x and y with associated quantum numbers vx and vy, rather than the two dimensional oscillator quantum numbers (v and l) that would more conventionally be used. Similarly the electronic basis can use the |±〉 functions mentioned above. Expressed in this format the Hamiltonian contains three types of terms: firstly the conventional harmonic oscillator terms for each vibration (identical and diagonal in both electronic states):| | Ĥharm = ½ω(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 + x2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) x2 + x2 + ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2 + y2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) y2) y2) | (15) |
a diagonal Jahn–Teller term:| | 〈±|ĤJT|±〉 = ±kω![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x ± ½gω( x ± ½gω(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 − x2 − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2) y2) | (16) |
and a Jahn–Teller term connecting the two electronic states:| | 〈∓|ĤJT|±〉 = kω![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y − gω y − gω![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y y | (17) |
Note that, as suggested above, a phase factor of i has been applied to |−〉 to make the above real. While not immediately obvious, all the eigenvalues of this Hamiltonian are doubly degenerate; see the supplementary notes for an explicit proof of this (ESI†). Including the quadratic terms gives a more complicated picture, which is discussed further below.
This picture can now be converted to the C2v symmetry required for NH2D and ND2H. A major change is that the frequencies associated with ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x and
x and ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y are now different. The requirement that they have different symmetry in C2v introduced above means that they will correspond to different normal modes in the lower symmetry. (The specific forms for NH3 are discussed below, but one of the obvious separations corresponds to the division into N–H and N–D stretches.) The standard harmonic part must now have two distinct vibrational frequencies, which we denote by with ωx and ωy:
y are now different. The requirement that they have different symmetry in C2v introduced above means that they will correspond to different normal modes in the lower symmetry. (The specific forms for NH3 are discussed below, but one of the obvious separations corresponds to the division into N–H and N–D stretches.) The standard harmonic part must now have two distinct vibrational frequencies, which we denote by with ωx and ωy:
| | Ĥharm = ½ωx(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 + x2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) x2) + ½ωy( x2) + ½ωy(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2 + y2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) y2) y2) | (18) |
Similarly, two constants are now required to specify the linear Jahn–Teller effect, as there is no longer any requirement that the linear potential terms along the two normal modes are the same, but the operators involved are otherwise the same:
| | 〈±|ĤJT|±〉 = ±kxωx![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x x | (19) |
| | 〈∓|ĤJT|±〉 = kyωy![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y y | (20) |
The relationships 〈+|
ĤJT|+〉 = −〈−|
ĤJT|−〉 and 〈+|
ĤJT|−〉 = 〈−|
ĤJT|+〉 persist as both components of the electronic state have the same transformation between internal and normal co-ordinates, only differing in the Jahn–Teller terms, so the sign change in
eqn (16) is simply copied across. Interestingly, all levels remain doubly degenerate in the presence of the linear Jahn–Teller effect, even including the term (20) that mixes the two electronic states. This has been formally proved by Iwahara
et al.,
10 and can also be seen on inspecting the detailed form of the Hamiltonian matrices – see the supplementary notes (ESI
†).
The above is in fact an oversimplification; the transformation between internal and normal co-ordinates will introduce Jahn–Teller terms to modes that do not have them for the symmetrical isotopologues. The only requirement is that they have the same symmetry in the sub-group. qx is necessarily totally symmetric (as it produces terms diagonal in electronic state), so any totally symmetric mode can acquire a Jahn–Teller term diagonal in electronic state. Similarly any vibrations with the same symmetry as qy can acquire a Jahn–Teller term off-diagonal in electronic state. For ammonia this mode mixing is worked out in detail below, and indeed occurs for the symmetric stretch, though there is no vibration with the same symmetry as qy so no additional off-diagonal terms are introduced. Importantly, though these result in one or more additional Jahn–Teller terms, the same logic still holds in that two identical matrices are generated and the degeneracy is not lifted by any linear terms. This degeneracy can even persist if the symmetry is lowered so that the qx and qy modes have the same symmetry, which is only possible for ammonia using a third isotope, say tritium to give an isotopologue with three different isotopes, NHDT. This is the result of Iwahara et al.,10 and was confirmed by numerical tests with the model below.
A purely quadratic Jahn–Teller effect gives rather a different picture. The first point to note is that, even in D3h symmetry, some non-degenerate vibronic states are present, and the degeneracies reflects the vibronic symmetry. For example, the overall vibronic symmetry of states with one quantum of a degenerate mode excited is E′′ × E′ = A1′′ + A2′′ + E′′, and three levels are indeed seen. (If only linear terms are included then the A1′′ and A2′′ levels remain degenerate). In addition, the selection rules for the q2 operators of Δv = 0, ±2 means the quadratic terms give rise to effects in first order. This case is worked through in more detail in the supplementary notes (ESI†). Symmetry requires that the vibrationless level in D3h is degenerate.
For the partially substituted species the quadratic Jahn–Teller Hamiltonian includes terms diagonal in the electronic states:
| | 〈±|ĤJT|±〉 = ±½(gxωx![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 − gyωy x2 − gyωy![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2) = ±½(gxx y2) = ±½(gxx![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 − gyy x2 − gyy![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2) y2) | (21) |
and off-diagonal:
| | 〈∓|ĤJT|±〉 = −gxy![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y y | (22) |
We have introduced a slightly different notation here to simplify later equations. The first term is likely to be the most important, as it can give diagonal matrix elements in selected states. Specifically, first order shifts in opposite directions to the vibrationless levels arise, giving an overall splitting of the zero point level of ½(
gxx −
gyy), and these will scale with
v, giving effective harmonic frequencies of approximately
ωx ±
gxx/4 and
ωy− ±
gyy/4. The second term is likely to become important for excited state splittings, as can be seen by considering the matrix for one quantum in the degenerate mode:
| | 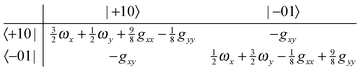 | (23) |
| | 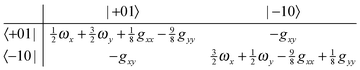 | (24) |
From this it is clear that in addition to the first order splittings (of order
gxx −
gyy) there will be second order shifts of the order of
gxy2/(
gxx −
gyy), which are likely to be significant as all three constants will be the same order of magnitude. As for the linear case, mode mixing will introduce additional potential terms, but all the degeneracies are lifted without them.
Force constant analysis for the ![[B with combining tilde]](https://www.rsc.org/images/entities/h3_char_0042_0303.gif) 1E′′ state of NH3
1E′′ state of NH3
To translate the Jahn–Teller effect to a change in geometry, and to transfer between the various isotopically substituted species requires knowledge of the internal co-ordinates for NH3 so we can derive a potential in terms that are independent of mass. For the purposes of this analysis we choose the simplest possible form for the potential, expressed in internal valence coordinates:| | | V = ½kstretch(δr12 + δr22 + δr32) + ½kbend(δθ12 + δθ22 + δθ32) + ½kumbδϕ2 | (25) |
δri is the change in bond length N–Hi from the equilibrium value. δθi is the change in the HNH bond angle not including bond N–Hi. δϕ describes the out of plane bending motion; formally it is defined as the vector triple product of unit vectors along the N–H bonds as used by Hedberg and Mills.15 We will ignore coupling between internal coordinates, and anharmonicity, as this is a reasonable match to the available information, and should be sufficient to understand the pattern of energy levels. Numerical tests with off-diagonal internal force constant terms (such as kδr1δθ1) set to ground state values confirm that, while there are shifts in levels there is no change in the overall pattern. A conventional harmonic force field analysis was set up in PGOPHER11,12 based on the above; taking ν3 and ν4 as given above for NH3, and ν2 as 898.2 cm−1 (the 1–0 gap) and the rotational constants from the zero point level gives the parameters shown in Table 4.
Table 4 Parameters of a simple harmonic force field for the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3
1E′′ state of NH3
|
r
NH/Å |
1.040 |
|
k
stretch/(aJ Å−2) |
5.8684 |
|
k
bend/aJ |
0.5172 |
|
k
umb/aJ |
0.1850 |
There is limited redundancy here given the lack of a Jahn–Teller analysis on ND3, but a test is available for the symmetric stretch, ν1. This is not known for the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, but the value for the
state, but the value for the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ′ state, which is expected to have similar bonding, is known to be14 3217.0 cm−1. The above constants predict 3143.7 cm−1, reasonable agreement considering anharmonicity and coupling between internal coordinates are being ignored.
′ state, which is expected to have similar bonding, is known to be14 3217.0 cm−1. The above constants predict 3143.7 cm−1, reasonable agreement considering anharmonicity and coupling between internal coordinates are being ignored.
This force field analysis can be used to calculate the magnitude of the Jahn–Teller distortions; this is worked through in detail in the supplementary notes (ESI†), and indicates bond length changes ∼0.014 Å and bond angle changes of the order of 2.2°. This provides some insight into the source of the difference between the A and B constants for the two electronic states; a simple static picture would predict slightly different geometries for the two electronic states, with a corresponding change in rotational geometries. Changing one of the bond angles by 2.2° as suggested above in fact gives a slightly larger change in rotational constants than the observed difference between the A and B values for the two states; the change of 0.014 Å bond length has rather a smaller effect. Given the Jahn–Teller distortion is dynamic, rather than static, we would not expect this to give a quantitative prediction, but it does suggest the shift comes from the Jahn–Teller effect.
Descent in symmetry
To apply the above to the mixed isotopologues we must specify symmetry co-ordinates that are appropriate for both D3h and C2v. From the character tables we can draw up the correlations shown in Tables 5 and 6 between the operators and symmetries for the two. Following the previous paper the C2 axis is taken as x in C2v and the out of plane axis is z. This means that functions with B1 symmetry are anti-symmetric with respect to reflections in the plane of the molecule.
Table 5 Correlation of operators from D3h to C2v
|
D
3h
|
E
|
C
2
|
σ
h
|
σ
v
|
|
C
2v(conventional) |
E
|
C
2(z) |
σ(yz) |
σ(xz) |
|
C
2v(axis choice used here) |
|
C
2(x) |
σ(xy) |
σ(xz) |
Table 6 Correlation of symmetries from D3h to C2v
|
D
3h
|
A1′ |
A2′ |
E′ |
A1′′ |
A2′′ |
E′′ |
|
|
|
C
2v
|
A1 |
B2 |
A1 |
B2 |
A2 |
B1 |
A2 |
B1 |
|
ν
1
|
|
ν
3x
|
ν
3y
|
|
ν
2
|
|+〉 |
|−〉 |
|
ν
4x
|
ν
4y
|
|
|
|
x
|
y
|
|
z
|
|
|
|
|
|
C
s
|
A′ |
A′ |
A′ |
A′ |
A′′ |
A′′ |
A′′ |
A′′ |
Similarly, for the degenerate vibrations we can assign separate symmetries in C2v to the two components, if we make the right choice of components that gives co-ordinates with well-defined symmetries in C2v. A possible choice, not unusual for systems with a C3 axis, for the stretching co-ordinates is:
| | 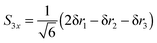 | (26) |
| | 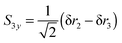 | (27) |
With this choice of co-ordinates, shown in
Fig. 2, and N–H
1 aligned along the
x axis
S3x has A
1 symmetry and
S3y has B
2 symmetry. H
1 is required to be the unique atom in NH
2D and ND
2H to maintain the required symmetry. We make a similar choice for the bending co-ordinates, replacing δ
ri with δ
θi:
| | 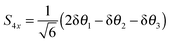 | (28) |
| | 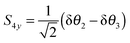 | (29) |
For consistent symmetry properties δ
θi needs to be the change in the angle between the two bonds not involved in δ
ri. For completeness, the non-degenerate symmetry co-ordinates are:
| | 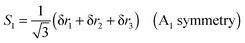 | (30) |
| | | S2 = δϕ (A2′′ symmetry) | (31) |
The transformation between dimensionless normal coordinates and symmetry coordinates is given in the supplementary notes (ESI
†); we simply note here that they are essentially proportional, with a little mixing between the degenerate modes.
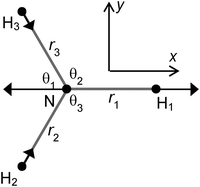 |
| | Fig. 2 Co-ordinate system used. H1 is D in NH2D and H in ND2H. The arrows show the S3x motion. | |
Jahn–Teller terms in internal coordinates
The force field analysis also makes it possible to predict the patter of vibronic energy levels for each of the isotopologues. For this the Jahn–Teller terms need to be converted from (isotope dependent) dimensionless normal coordinates (k3ω3 and k4ω4) as used in (13) above to (isotope independent) internal coordinates. There is no unique way of doing this, particularly as the internal coordinates are redundant, but given that the degenerate stretching and bending modes are reasonably separate, we can take the form for the linear terms as:| | ĤJT3 = kJT3{Ŝ3x(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 + +2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) + iŜ3y( −2) + iŜ3y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 − +2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)} −2)} | (32) |
with a similar term for q4. This is the analogue of eqn (13). In terms of internal valence coordinates this becomes:| | 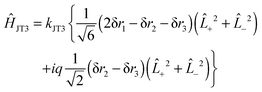 | (33) |
The quadratic terms, eqn (14) become:| | ĤJT2 = ½gJT3{(Ŝ3x2 − Ŝ3y2)(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 + +2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) − 2iŜxŜy( −2) − 2iŜxŜy(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 − +2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)} −2)} | (34) |
This has a rather complicated form when expanded out into internal co-ordinates – see the supplementary notes (ESI†). To use the above forms, the harmonic force field part of the PGOPHER11,12 program was enhanced to take additional linear and quadratic potential terms expressed in internal coordinates, and subject them to the transformation between internal coordinates, Ri, and dimensionless normal co-ordinates, qi, computed as part of the standard force field analysis. Specifically, if we define the matrix relating the two as dint:| | 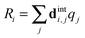 | (35) |
(dint is given for NH3 in the supplementary notes, ESI†) then the potential energy expressed as a sum of terms linear in internal coordinates as:| | 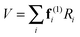 | (36) |
can easily be recast in terms of normal coordinates by a simple matrix multiplication:| | 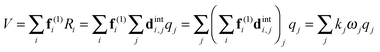 | (37) |
so kjωj can be identified with elements of f(1)dint. Quadratic terms require a double multiplication:| |  | (38) |
and elements of dintTfdint are thus required. The key additional feature in these transformations (not shown in the equations above) is that separate sets of force constants must be tracked, with one set for each of the possible associated electronic matrix elements. For example, for the linear terms, the multipliers of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2 and
−2 and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2 must be kept separate and a separate set of multipliers is required for each state. In PGOPHER these are used to calculate perturbation terms in the vibronic Hamiltonian that are added to the standard harmonic terms.
−2 must be kept separate and a separate set of multipliers is required for each state. In PGOPHER these are used to calculate perturbation terms in the vibronic Hamiltonian that are added to the standard harmonic terms.
To determine the required parameters a fit was performed to selected data from Allen et al.4 The fit was directly to internal coordinate force constants – the conventional kstretch, kbend and kumb and the Jahn–Teller terms kJT3, kJT4 and gJT3. A harmonic force field calculation based on the first three gives the harmonic frequencies for the B state, and the transformation matrix, dint. The latter is used to transform the Jahn–Teller terms to the equivalent normal coordinate terms, k3ω3, k4ω4 and g3ω3 (= g33). These are used to set up a vibronic Hamiltonian matrix for the B state in a harmonic basis, using the operator forms given in eqn (15)–(17) above, summed over all modes. The basis includes two (degenerate) electronic states, each with all vibrational levels with v1 ≤ 1, v2 ≤ 1, v3 ≤ 4 and v4 ≤ 5, sufficient for the energy levels to be converged to rather better than 1 cm−1. The required matrix elements of the normal modes are available in many places – see for example Papoušek and Aliev.16 The Hamiltonian matrix is diagonalised to produce energies to compare with the observed values above. A standard least squares fitting process using numerical derivatives by the PGOPHER program is used to produce the best fit values listed in Table 7 below, with the observed and calculated values given in Table S2 of the supplementary notes (ESI†).
Table 7 Force field in internal coordinates for the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3
1E′′ state of NH3
|
r
NH/Å |
1.040 |
|
k
stretch/(aJ Å−2) |
5.4344 |
|
k
bend/aJ |
0.3820 |
|
k
umb/aJ |
0.1871 |
|
k
JT3/(aJ Å−1) |
0.1659 |
|
k
JT4/(aJ Å−1) |
0.0339 |
|
g
JT3/(aJ Å−2) |
0.3982 |
Note that only the quadratic Jahn–Teller term associated with ν3 was floated (gJT3); floating the equivalent term for ν4 did not improve the fit, probably because no A symmetry levels are known for ν4. The only redundancy present in the fit is in the ν4 levels, so we do not have an independent measure of the reliability of the derived parameters.
The normal coordinate parameters derived from these are given in the top rows of Tables 8 to 11. Note that, because of the small mixing between S3 and S4, a small quadratic Jahn–Teller term is present for ν4, even though we are taking the gJT4 term as zero. This mixing also induces a small quadratic cross term with the equivalent operator forms coming out of the dintTfi,jdint transformation a fairly obvious generalisation of eqn (16) and (17):
| | 〈±|Ĥ(34)JT|±〉 = ±g34(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x 3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x − 4x − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y 3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y) = ±(g3x4x′ 4y) = ±(g3x4x′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x 3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x + g3y4y′ 4x + g3y4y′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y 3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y) 4y) | (39) |
| | 〈∓|Ĥ(34)JT|±〉 = −g34(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x 3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y − 4y − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y 3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x) = g3x4y′ 4x) = g3x4y′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x 3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y + g3y4x′ 4y + g3y4x′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y 3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x 4x | (40) |
We have introduced a separate quantity,
gij′ which is simply the multiplier of the operator
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) i
i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) j
j; in this case
g34 =
g3x4x′ = −
g3y4y′ = −
g3x4y′ = −
g3y4x′ but this notation simplifies the presentation for the less symmetrical species where there are no constrains on the values. Note there is no factor of ½ in these equations as the operator form is strictly (for example) ±½
g34(
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x
3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x
4x +
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x
4x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x
3x −
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y
3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y
4y −
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y
4y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y
3y), which simplifies as above. Neither of the
g4 or
g34 terms are significant, but are included for completeness.
Table 8 Calculated normal mode frequencies (cm−1) the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
| |
ω
1
|
ω
2
|
ω
3x
|
ω
3y
|
ω
4x
|
ω
4y
|
| NH3 |
3025.2 |
892.5 |
3188.0 |
1397.5 |
| NH2D |
3089.2 |
829.2 |
2284.8 |
3187.7 |
1390.1 |
1166.4 |
| ND2H |
2208.5 |
760.5 |
3141.8 |
2369.8 |
1027.8 |
1277.0 |
| ND3 |
2140.0 |
685.1 |
2368.5 |
1021.3 |
Table 9 Calculated linear Jahn–Teller parameters (cm−1) for normal modes of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
| |
k
1
ω
1
|
k
3x
ω
3x
|
k
3y
ω
3y
|
k
4x
ω
4x
|
k
4y
ω
4y
|
| NH3 |
— |
937.5 |
428.0 |
| NH2D |
−615.3 |
624.6 |
935.1 |
397.1 |
393.0 |
| ND2H |
−403.4 |
806.0 |
838.8 |
360.3 |
374.6 |
| ND3 |
— |
831.2 |
342.8 |
Table 10 Calculated quadratic Jahn–Teller parameters (cm−1) diagonal in electronic state for normal modes of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
| |
½g11′ |
½g3x3x′ |
½g3y3y′ |
½g4x4x′ |
½g4y4y′ |
g
13x′ |
g
14x′ |
g
3x4x′ |
g
3y4y′ |
| NH3 |
— |
116.5 |
−116.5 |
0.1 |
−0.1 |
— |
— |
−8.2 |
8.2 |
| NH2D |
49.9 |
46.0 |
−116.5 |
0.5 |
−0.1 |
−95.8 |
10.1 |
−9.7 |
7.0 |
| ND2H |
19.7 |
86.6 |
−85.8 |
0.2 |
−0.5 |
−82.6 |
3.6 |
−7.5 |
14.0 |
| ND3 |
— |
86.0 |
−86.0 |
0.3 |
−0.3 |
— |
— |
−10.9 |
10.9 |
Table 11 Calculated quadratic Jahn–Teller parameters (cm−1) off-diagonal in electronic state for normal modes of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
| |
g
13y′ |
g
3x3y′ |
g
3y4x′ |
g
13y′ |
g
3x4y′ |
g
4x4y′ |
| NH3 |
— |
−233.0 |
8.2 |
— |
8.2 |
−0.3 |
| NH2D |
152.4 |
−146.4 |
15.4 |
−4.6 |
4.4 |
−0.5 |
| ND2H |
82.3 |
−172.3 |
7.4 |
−7.0 |
14.0 |
−0.6 |
| ND3 |
— |
−172.0 |
10.9 |
— |
10.9 |
−0.7 |
Comparing the parameters derived here with those of Allen et al.4 shows some differences, with the linear Jahn–Teller terms rather larger in the current analysis. The differences arise from the different models used; the earlier work included an x44 anharmonicity term, but here this is forced to zero. The previous work included a linear vibrational (in q3) term mixing in a third electronic state but this can be shown to be equivalent to a quadratic Jahn–Teller effect in q3 using second order perturbation theory. We do not have enough experimental information to discriminate between the models, but they do confirm that, within a factor of two, sensible values are being used for the Jahn–Teller parameters.
Predictions for other isotopologues
Given the force field and Jahn–Teller terms expressed in internal coordinates, it is now straightforward to repeat the process above for all the other isotopologues. The normal coordinate parameters for all four species are given in Tables 8 to 11.
Note that, as discussed above, in the less symmetrical species, a linear potential term is introduced into what is formally the symmetric stretch, ν1, but not the umbrella mode, ν2 as it has the wrong symmetry.
For the quadratic terms, several small terms have been included for completeness; the biggest addition in C2v symmetry is likely to come from the g11′ and g13y′ terms adding to g3.
Given the normal mode parameters the vibronic energy levels can be calculated for all 4 isotopologues, and selected levels are listed in Table 12. A matrix diagonalization was required, as described above for NH3, with the basis sets slightly adjusted to ensure convergence, mainly requiring a higher limit in v1 for the C2v species. The notation used to label the vibrational states is such that nm implies m quanta in mode n. For the degenerate modes the quanta along the x and y modes are given separately. The quantum numbers are based on the largest coefficients in the final wavefunctions; this normally gives a clear assignment, though for NH2D a level at 3289.7 cm−1 could also have been assigned to the 3y1 A2 level.
To understand the pattern of levels produced by this model, it is helpful to consider the pattern of levels associated with just the stretching modes, and with terms involving bending omitted. Fig. 3 shows the stretching levels for NH3 with the various possible combinations of Jahn–Teller terms. Note there are two stretching levels, one of which (the asymmetric stretch, v3 = 1) is notionally four fold degenerate, and this is split into two components by the linear Jahn–Teller effect and three by the quadratic Jahn–Teller effect. The other stretching level and the origin remain degenerate. Contrast this with the corresponding energy level diagram for NH2D in Fig. 4, where there are now three stretching levels, each notionally doubly degenerate. The linear Jahn–Teller effect shifts all these levels, but does not lift the degeneracy; this has been discussed above as being a consequence of the form of the Hamiltonian, and is not specific to this case. The largest effect of the linear term is to increase the separation between the two N–H stretching levels, with smaller shifts of the other levels. The quadratic term does lift all the degeneracies, to a small amount for the origin level and rather more for the other levels. Fig. 5 shows the pattern of stretching levels for all four species, calculated including both linear and quadratic terms. The overall trend is of course to lower energies as modes switch from N–H to N–D stretches but the pattern associated with each set of bonds is similar, so the levels associated with the N–H bonds in NH2D is replicated in the N–D bonds in ND2H. The switch from N–H to N–D can also be seen in the detailed form of the normal coordinates – see Table S3 in the supplementary notes (ESI†).
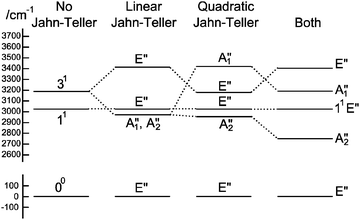 |
| | Fig. 3 Approximate energy level diagram for the stretching vibrational levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis. 1E′′ state of NH3. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis. | |
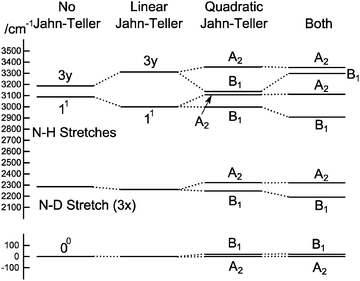 |
| | Fig. 4 Approximate energy level diagram for the stretching vibrational levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH2D. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis. 1E′′ state of NH2D. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis. | |
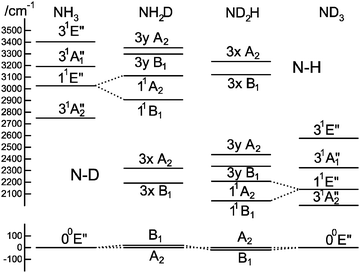 |
| | Fig. 5 Correlation between stretching vibrational levels for different isotopologues of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis. 1E′′ state of ammonia. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis. | |
The only information that we can directly compare with experiment is the origin band, though it would be very informative to have spectra of the excited stretching levels. The key prediction is that the origin level should be split by a relatively small amount, with the sign of the splitting opposite for NH2D and ND2H. Our observations reflect this, with the splittings having the right relative sign (+34.8 and −35.1 cm−1) though about twice the magnitude of the calculated splittings (+18.6 and −18.5 cm−1). Given we have no information on the quadratic Jahn–Teller effect for the bending modes, and that the analysis above shows that the quadratic term is the key contributor to the splitting of the origin band, this is good agreement. Interestingly, the observation of equal and opposite splittings was seen in the two other studies that are directly comparable to this one by Yu et al.7 on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1′′ state of C5H4D (−8.9557 cm−1) and C5D4H (+9.1975 cm−1) and by Melnik et al.8,9 on the
2E1′′ state of C5H4D (−8.9557 cm−1) and C5D4H (+9.1975 cm−1) and by Melnik et al.8,9 on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state of CH2DO (−45.66 cm−1) and CD2HO (+43.44 cm−1).
2E state of CH2DO (−45.66 cm−1) and CD2HO (+43.44 cm−1).
At this stage it is worth comparing the approach taken here with the approaches taken by previous workers in calculating this splitting. Perhaps the earliest consideration of this issue is in the interpretation of ESR data on the negative ions of benzene-d1 and cyclo-octatetraene-d1 by Carrington et al.17 They suggested that kinetic energy considerations would give different zero point energies for different structures. This approach would obviously be appropriate where the different structures had significant barriers between them, but it is less clear that it would be appropriate for cases like the current one where the barriers are much less than the zero point energy.
Later works undertook more detailed measurements and calculations. Scharf et al.18 considered various 1E1u Rydberg states of asymmetrically deuterated benzene. Unfortunately the experimental data available is low resolution, so the zero point splittings cannot be directly measured, but only inferred from different widths of vibronic bands. The experimental results showed a progression in only one of the four possible Jahn–Teller active modes, so only that mode was modelled in a way similar to that done here. The model was restricted to linear terms, and as the mode involved ring distortion ω and k for that mode were assumed unchanged on deuteration. The zero point splitting was accounted for by a single parameter, Ex − Ey, giving the difference in zero point energy in the other modes; in our notation this is equivalent to ½(gxx − gyy) summed over all the other modes. The derivation above shows this is equivalent to assuming the zero point splitting arises from a quadratic Jahn–Teller effect in these other modes. They produced estimates of this quantity based on a simple orbital model. The difference from our model stems partly from choice of definitions, in that they do not consider this difference in second derivatives to be a Jahn–Teller effect.
Eiding and Domcke19 looked at partial isotopic substitution in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1g and
2E1g and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2E2g states of 1,4-C6H4D2+. They modelled the energy levels including several Jahn–Teller active modes using an approach similar to that taken in this paper, but with one essential difference. The reference point taken for all the derivatives with respect to energy was the geometry of the neutral molecule, rather than the ion. (This approach was taken as the aim of that study was to calculate photoelectron spectra.) This meant that the first derivatives with respect to energy for symmetric modes was non zero even in the absence of the Jahn–Teller effect, giving terms comparable in magnitude to the linear Jahn–Teller terms. Values for these first derivatives for both the symmetrical and Jahn–Teller active modes were taken from derivatives of orbital energies from a Hartree–Fock calculation on the neutral molecule. Quadratic Jahn–Teller effects were not included, but the calculations did nevertheless predict non-zero zero-point splittings for the lower symmetry isotopologues. This does not contradict the result of Iwahara et al.10 that linear terms do not give a zero-point splitting due to the use of a non-equilibrium reference geometry as the transformation to the equilibrium geometry will introduce additional terms in the Hamiltonian that are effectively quadratic.
2E2g states of 1,4-C6H4D2+. They modelled the energy levels including several Jahn–Teller active modes using an approach similar to that taken in this paper, but with one essential difference. The reference point taken for all the derivatives with respect to energy was the geometry of the neutral molecule, rather than the ion. (This approach was taken as the aim of that study was to calculate photoelectron spectra.) This meant that the first derivatives with respect to energy for symmetric modes was non zero even in the absence of the Jahn–Teller effect, giving terms comparable in magnitude to the linear Jahn–Teller terms. Values for these first derivatives for both the symmetrical and Jahn–Teller active modes were taken from derivatives of orbital energies from a Hartree–Fock calculation on the neutral molecule. Quadratic Jahn–Teller effects were not included, but the calculations did nevertheless predict non-zero zero-point splittings for the lower symmetry isotopologues. This does not contradict the result of Iwahara et al.10 that linear terms do not give a zero-point splitting due to the use of a non-equilibrium reference geometry as the transformation to the equilibrium geometry will introduce additional terms in the Hamiltonian that are effectively quadratic.
The study by Yu et al.7 on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1′′ state of C5H4D and C5D4H used a similar approach to that used here, but only considered linear Jahn–Teller terms. In addition, in C5H5 the mode with the largest Jahn–Teller activity was thought to involve distortion of the carbon framework, so they assumed deuterium substitution did not alter the Jahn–Teller parameters and so gave no zero point splitting in that mode. They suggested, following Scharf et al.18 that there could be a zero point energy difference in the other modes, but did not attempt to calculate this, and the current work suggests there should not be any if only linear terms are included. They did not discuss quadratic Jahn–Teller effects in detail, though they pointed out that it was shown by Engelking and Lineberger20 using symmetry arguments that the quadratic Jahn–Teller effect must be zero in D5h symmetry. Iwahara et al.10 discuss this specific case, and attribute the splitting of the zero point level to quartic potential terms. Higher terms would give five equivalent minima, and more recent calculations of Bearpark et al.21 suggests that the barrier between them is only 3.6 cm−1. Bearpark et al.21 did calculate zero point energies for different equilibrium structures with differences of the right order of magnitude to the observations, but they do not indicate which value should be compared to the experiment. It is anyway not clear that the approach they used, considering a single electronic surface, will give correct results, especially as they ignored anharmonic effects which must be important with such a surface given the low barrier (3.6 cm−1) in one mode.
2E1′′ state of C5H4D and C5D4H used a similar approach to that used here, but only considered linear Jahn–Teller terms. In addition, in C5H5 the mode with the largest Jahn–Teller activity was thought to involve distortion of the carbon framework, so they assumed deuterium substitution did not alter the Jahn–Teller parameters and so gave no zero point splitting in that mode. They suggested, following Scharf et al.18 that there could be a zero point energy difference in the other modes, but did not attempt to calculate this, and the current work suggests there should not be any if only linear terms are included. They did not discuss quadratic Jahn–Teller effects in detail, though they pointed out that it was shown by Engelking and Lineberger20 using symmetry arguments that the quadratic Jahn–Teller effect must be zero in D5h symmetry. Iwahara et al.10 discuss this specific case, and attribute the splitting of the zero point level to quartic potential terms. Higher terms would give five equivalent minima, and more recent calculations of Bearpark et al.21 suggests that the barrier between them is only 3.6 cm−1. Bearpark et al.21 did calculate zero point energies for different equilibrium structures with differences of the right order of magnitude to the observations, but they do not indicate which value should be compared to the experiment. It is anyway not clear that the approach they used, considering a single electronic surface, will give correct results, especially as they ignored anharmonic effects which must be important with such a surface given the low barrier (3.6 cm−1) in one mode.
Melnik et al.8,9 looked at submillimeter spectra of the lowest vibrational level of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state of CH2DO and CHD2O radicals. Their approach to the rotational energy level pattern was similar to that taken here, though made rather more complicated by the presence of a spin–orbit interaction. They describe a method of calculating the zero point splitting, based on calculating zero point energies at two different minima on the lowest potential energy surface with the unique atom on or off the symmetry plane. This gives promising results, predicting approximately equal and opposite splittings for CH2DO and CHD2O and of the correct order of magnitude, though rather sensitive to the ab initio method used. They do however comment that their method relies on a harmonic frequency model and ignores the upper surface and the coupling between them, and acknowledge that they may be relying on a cancellation of errors, as again the mild Jahn–Teller interaction implies a very anharmonic mode.
2E state of CH2DO and CHD2O radicals. Their approach to the rotational energy level pattern was similar to that taken here, though made rather more complicated by the presence of a spin–orbit interaction. They describe a method of calculating the zero point splitting, based on calculating zero point energies at two different minima on the lowest potential energy surface with the unique atom on or off the symmetry plane. This gives promising results, predicting approximately equal and opposite splittings for CH2DO and CHD2O and of the correct order of magnitude, though rather sensitive to the ab initio method used. They do however comment that their method relies on a harmonic frequency model and ignores the upper surface and the coupling between them, and acknowledge that they may be relying on a cancellation of errors, as again the mild Jahn–Teller interaction implies a very anharmonic mode.
It is also worth mentioning work on the ground state of CH4+, for which significant work on partially deuterated isotopologues has been done22,23 but this is less directly comparable as the starting model is minima with a large barrier between them, though with significant tunnelling between them and thus requiring a different theoretical approach.
Rotational constants
Given a model based on normal co-ordinates, it is also possible to predict the rotational constants for the origin levels by taking into account the variation of the rotational constants with vibrational co-ordinate. The key quantity is the μαβ tensor, essentially the inverse of the moment of inertia tensor, with the diagonal terms the rotational constants. For a summary of the theory and notation see the review by Mills.24 There are many possible terms, of which we discuss the three largest here. We start with the term involving the second derivative of this μαβ tensor:| | 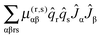 | (41) |
Here α and β label the principal axes, r and s the normal modes and μ(r,s)αβ is the second derivative with respect to normal co-ordinates r and s:| | 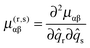 | (42) |
which can in turn be calculated from the first derivative of the moment of inertia tensor with respect to the normal co-ordinates. For r = s this term has matrix elements diagonal in vibrational state proportional to v + ½ and is one of the conventional contributions to the vibrational dependence of the rotational constants.
The vibrational angular momentum also contributes to this vibrational dependence; the relevant term is:
| | 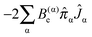 | (43) |
where
![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) α
α is the vibrational angular momentum:
| | 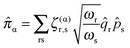 | (44) |
This does not directly contribute to the rotational constants as the Coriolis coupling constant,
ζrs, is zero if
r =
s, but second order perturbation theory does give a term containing
ĴαĴβ, and thus a vibration state dependent contribution to the rotational constants, another conventional contribution to the vibrational constants.
The final conventional contribution involves the first derivative of the μαβ tensor:
| | 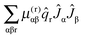 | (45) |
where
| | 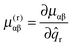 | (46) |
As this contains a single vibrational operator it has selection rules Δ
v = ±1, and thus no diagonal contribution. In conventional theory it becomes significant when combined with cubic anharmonic potential terms, and thus gives a vibrational contribution in second order. In the current analysis we are ignoring anharmonicity, but the Jahn–Teller potential terms also have selection rules Δ
v = ±1, and so provide a similar contribution in second order.
To calculate all the above contributions all that is required are the Coriolis coupling constants and the derivative of the moment of inertia tensor with respect to the normal co-ordinates. Both of these are readily available from the normal co-ordinate analysis. Rather than attempting to derive general expressions for the variation of rotational constants with v using perturbation theory we choose to use a simpler numerical approach as follows:
For each rotational constant, for which the effective operator is μαβĴαĴβ we set up the matrix of 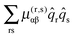 (from (41)) and
(from (41)) and 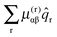 (from (45)) evaluated in the harmonic basis described above used to calculate the vibronic energy levels. Transforming this matrix using the eigenvectors from the energy level calculations then gives the corrections to the rotational constants as the diagonal elements. For the Coriolis terms, eqn (43) a slightly different approach is required. For each principal axis, α, we set up the matrix of −2B(α)e
(from (45)) evaluated in the harmonic basis described above used to calculate the vibronic energy levels. Transforming this matrix using the eigenvectors from the energy level calculations then gives the corrections to the rotational constants as the diagonal elements. For the Coriolis terms, eqn (43) a slightly different approach is required. For each principal axis, α, we set up the matrix of −2B(α)e![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) αĴβ in the same harmonic basis, and again transform this using the eigenvectors from the energy level calculations. The corrections to a rotational constant, Δμαβ, for a given level i are then calculated using second order perturbation theory:
αĴβ in the same harmonic basis, and again transform this using the eigenvectors from the energy level calculations. The corrections to a rotational constant, Δμαβ, for a given level i are then calculated using second order perturbation theory:
| | 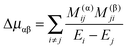 | (47) |
where
M(α) is the transformed matrix and the energies,
Ej, are the exact vibronic energy levels as in
Table 12. This formula can fail for near degenerate levels, so the program excludes states from the sum where |
Ei −
Ej| < 1 cm
−1 and
Mij is non zero, and displays these separately. This test does not exclude any contributions in the current calculations.
Table 12 Predicted vibrational energy levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
| NH3 |
NH2D |
ND2H |
ND3 |
|
Zero point energy given in brackets.
|
| (6160.4)a |
00 E′′ |
(5582.8)a |
00 A2 |
(5023.1)a |
00 A2 |
(4426.2)a |
00 E′′ |
|
|
|
18.8 |
00 B1 |
−18.5 |
00 B1 |
|
|
| 1294.0 |
41 A2′′ |
1129.4 |
4y1 B1 |
977.7 |
4x1 B1 |
934.7 |
41 A1′′ |
| 1294.5 |
41 A1′′ |
1142.7 |
4y1 A2 |
992.7 |
4x1 A2 |
934.7 |
41 A2′′ |
| 1489.0 |
41 E′′ |
1416.9 |
4x1 A2 |
1280.1 |
4y1 A2 |
1094.0 |
41 E′′ |
|
|
|
1433.1 |
4x1 B1 |
1292.5 |
4y1 B1 |
|
|
| 2599.1 |
42 E′′ |
2196.7 |
3x1 B1 |
1976.0 |
4x2 B1 |
1879.1 |
42 E′′ |
|
|
|
2253.7 |
4y2 A2 |
1991.8 |
4x2 A2 |
|
|
| 2764.9 |
31 A2′′ |
2283.8 |
4y2 B1 |
2053.1 |
11 B1 |
2006.3 |
31 A2′′ |
| 2782.3 |
42 E′′ |
2334.2 |
3x1 A2 |
2203.8 |
11 A2 |
2027.9 |
42 E′′ |
|
|
|
2550.4 |
4x14y1 B1 |
2270.0 |
4x14y1 A2 |
|
|
| 2947.8 |
42 A1′′ |
2559.1 |
4x14y1 A2 |
2273.4 |
4x14y1 B1 |
2140.0 |
11 E′′ |
| 2982.1 |
42 A2′′ |
2822.0 |
4x2 A2 |
2361.1 |
3y1 B1 |
|
|
| 3025.2 |
11 E′′ |
2830.4 |
4x2 B1 |
2463.0 |
3y1 A2 |
2155.3 |
42 A1′′ |
|
|
|
2927.6 |
11 B1 |
2572.9 |
4y2 B1 |
2192.3 |
42 A2′′ |
| 3223.5 |
31 A1′′ |
3121.8 |
11 A2 |
2581.7 |
4y2 A2 |
2354.3 |
31 A1′′ |
|
|
|
3276.8 |
3y1 B1 |
3163.3 |
3x1 B1 |
|
|
| 3395.5 |
31 E′′ |
3379.4 |
3y1 A2 |
3212.8 |
3x1 A2 |
2568.4 |
31 E′′ |
The above is expressed in terms of a general tensor element μαβ, though symmetry is sufficiently high for all the off-diagonal terms (α ≠ β) to be zero, though the ab term gives a term between the |+〉 and |−〉 components. In the absence of the Jahn–Teller effect, the sum of the terms described above gives essentially the same result as the harmonic formula for the vibrational dependence of the vibrational constants.24Table 13 gives the calculated and observed values for the rotational constants of the zero point levels.
Table 13 Calculated rotational constants (cm−1) for zero point levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
| |
NH3 |
NH2D |
ND2H |
ND3 |
| A2 |
B1 |
A2 |
B1 |
A2 |
B1 |
A2 |
B1 |
|
Observed values are from this paper and ref. 5.
|
|
A
|
10.695 |
10.378 |
10.690 |
10.378 |
7.821 |
8.395 |
5.316 |
5.163 |
|
B
|
10.378 |
10.695 |
6.459 |
6.426 |
5.315 |
5.160 |
5.163 |
5.316 |
|
C
|
5.180 |
5.180 |
3.969 |
3.910 |
3.124 |
3.156 |
2.588 |
2.588 |
| ½(A + B) |
10.537 |
|
|
|
|
5.239 |
| ½(A–B) |
0.317 |
|
|
|
|
0.153 |
|
|
| Observed valuesa |
|
A
|
|
9.856 |
10.780 |
8.377 |
7.653 |
|
|
B
|
10.4844 |
6.766 |
6.455 |
5.112 |
5.556 |
5.25581 |
|
C
|
5.1565 |
3.953 |
3.167 |
2.59701 |
|
q
|
0.8868 |
0.681 |
0.481 |
0.4729 |
Perhaps the most striking feature of the table is that even for the symmetrical isotopologues the A and B rotational constants are different, in contradiction to what is expected for a symmetric top. In fact the rotational Hamiltonian used already allows for this through the term in q. This can be seen if the standard asymmetric top Hamiltonian is re-expressed in a form close to the symmetric top form:
| | | Ĥrot = AĴa2 + BĴb2 + CĴc2 = ½(A + B)(Ĵa2 + Ĵb2) + ½(A − B)(Ĵa2 − Ĵb2) + CĴc2 = ½(A + B)Ĵ2 + ½(A − B)(Ĵa2 − Ĵb2) + (C − ½(A + B))Ĵc2 | (48) |
Applying the inverse of transformation
(10):
| | 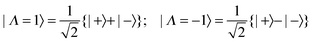 | (49) |
the terms in
Ĥrot giving matrix elements diagonal in vibronic state are simply the standard symmetric top terms, as
A–
B for the |+〉 component is equal to
B–
A for the |−〉 component and the term in
Ĵa2 −
Ĵb2 vanishes. However
Ĥrot does give matrix elements between the two components:
| | | 〈Λ = −1|Ĥrot|Λ = 1〉 = ½{〈+|Ĥrot|+〉 − 〈−|Ĥrot|−〉} = ½(A+ − A−)(Ĵ+2 − Ĵ−2) | (50) |
We have used
A+ for the
A rotational constant for the |+〉 component, and so on and
Ĵ± =
Ĵa ±
iĴb. Comparing this with the corresponding matrix element of the term in the symmetric top Hamiltonian:
| | q(Ĵ+2![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2 + Ĵ−2 −2 + Ĵ−2![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2) +2) | (51) |
allows the identification
q = ½(
A+ −
A−). Note that this term will also give a term mixing the |+〉 and |−〉 components, but we do not work through this here.
Comparing the calculated and observed values for q for NH3 and ND3 reveals a factor of more than 2 between them. There are two factors that make this disagreement unsurprising. One is that our knowledge of the Jahn–Teller terms is incomplete; in this case it is the linear Jahn–Teller term that dominates q. Secondly there can also be a significant electronic contribution to this term, and indeed the previous paper explained the term in q entirely as a rotational-electronic effect. The numbers here suggest both contributions may be significant. This is confirmed by looking at the mixed isotopologues, where changes of the right order of magnitude in the rotational constants are predicted, but not with the right direction. There is no simple way of calculating the electronic effects, though the order of magnitude is expected to be similar to the vibrational terms in this case. The overall conclusion on the rotational structure is that small (∼10%) differences between the rotational constants for the two components of the electronic state are to be expected, with significant contributions from interactions both within the electronic state and with other electronic states.
Conclusions
The model developed to analyse the rotational structure in the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NHD2 has been successfully applied to NH2D, and confirms the validity of the model, and that for cases of a mild Jahn–Teller effect the formal lifting of the degeneracy by partial isotopic substitution leaves significant terms in the Hamiltonian mixing the two components of the state that must be included for a satisfactory simulation of the rotational structure. The observation of approximately equal but opposite splittings in the zero point level for complementary isotopic substitution (here NH2D compared to NHD2) seen before in the literature is further reinforced here. We present a method of calculating this from the Jahn–Teller parameters from any one isotope, though we are limited from quantitative agreement here by a lack of a full knowledge of the required Jahn–Teller parameters. This limitation also applies to our calculation of the rotational constants, which are affected by the Jahn–Teller effect.
1E′′ state of NHD2 has been successfully applied to NH2D, and confirms the validity of the model, and that for cases of a mild Jahn–Teller effect the formal lifting of the degeneracy by partial isotopic substitution leaves significant terms in the Hamiltonian mixing the two components of the state that must be included for a satisfactory simulation of the rotational structure. The observation of approximately equal but opposite splittings in the zero point level for complementary isotopic substitution (here NH2D compared to NHD2) seen before in the literature is further reinforced here. We present a method of calculating this from the Jahn–Teller parameters from any one isotope, though we are limited from quantitative agreement here by a lack of a full knowledge of the required Jahn–Teller parameters. This limitation also applies to our calculation of the rotational constants, which are affected by the Jahn–Teller effect.
Our analysis confirms the result of Iwahara et al.10 that the zero point splitting must come from quadratic or higher Jahn–Teller effects and a linear term is not sufficient to break the symmetry. This is not clear from previous literature analysis of such splittings, which have concentrated on Jahn–Teller active modes that would not be expected to change on isotopic substitution. More recent studies have also concentrated on using properties derived from ab initio calculations on only the lowest of the pair of surfaces to predict this splitting, but it is difficult to have confidence that ignoring the other surface will give correct results, especially given the separation is rather less than the zero point energy. It would be interesting to use ab initio methods to explore both surfaces for this and related cases, though care is likely to be required to avoid artefacts arising from the closely spaced surfaces.
Acknowledgements
Work on this project in Nijmegen was supported by the NWO-CW ECHO project 700.58.029 of the Dutch National Science Foundation. SYTvdM acknowledges financial support from the Netherlands Organization for Scientific Research through a VIDI grant, and the European Research Council through a Starting Grant.
References
- T. A. Barckholtz and T. A. Miller, Int. Rev. Phys. Chem., 1988, 17, 435–524 CrossRef PubMed.
- O. Tkac, A. K. Saha, J. Onvlee, C.-H. Yang, G. Sarma, C. K. Bishwakarma, S. Y. T. van de Meerakker, A. van der Avoird, D. H. Parker and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2014, 16, 477–488 RSC.
- K. S. Twyman, M. T. Bell, B. R. Heazlewood and T. P. Softley, J. Chem. Phys., 2014, 141, 024308 CrossRef PubMed.
- J. M. Allen, M. N. R. Ashfold, R. J. Stickland and C. M. Western, Mol. Phys., 1991, 74, 49–60 CrossRef CAS PubMed.
- M. N. R. Ashfold, R. N. Dixon, N. Little, R. J. Stickland and C. M. Western, J. Chem. Phys., 1988, 89, 1754–1761 CrossRef CAS PubMed.
- C. H. Yang, G. Sarma, A. K. Saha, D. H. Parker and C. M. Western, Phys. Chem. Chem. Phys., 2013, 15, 6390–6399 RSC.
- L. A. Yu, D. W. Cullin, J. M. Williamson and T. A. Miller, J. Chem. Phys., 1993, 98, 2682–2698 CrossRef CAS PubMed.
- D. Melnik, J. Liu, R. F. Curl and T. A. Miller, Mol. Phys., 2007, 105, 529–540 CrossRef CAS PubMed.
- J. L. D. G. Melnik, M.-W. Chen, T. A. Miller and R. F. Curl, J. Chem. Phys., 2011, 135, 094310 CrossRef PubMed.
- N. Iwahara, T. Sato, K. Tanaka and L. F. Chibotaru, EPL, 2012, 100, 43001 CrossRef.
-
C. Western, PGOPHER, a Program for Simulating Rotational, Vibrational and Electronic Structure, http://pgopher.chm.bris.ac.uk Search PubMed.
-
C. Western, PGOPHER version 8.0, University of Bristol Research Data Repository, 2014, DOI: http://10.5523/bris.huflggvpcuc1zvliqed497r2 Search PubMed.
- L. Fusina, G. Dilonardo, J. W. C. Johns and L. Halonen, J. Mol. Spectrosc., 1988, 127, 240–254 CrossRef CAS.
- J. M. Allen, M. N. R. Ashfold, C. L. Bennett and C. M. Western, Chem. Phys. Lett., 1988, 149, 1–9 CrossRef CAS.
- L. Hedberg and I. M. Mills, J. Mol. Spectrosc., 1993, 160, 117–142 CrossRef CAS.
-
D. Papoušek and M. R. Aliev, Molecular Vibrational Rotational Spectra, Elsevier, 1982 Search PubMed.
- A. Carrington, H. C. Longuet-Higgins, R. E. Moss and P. F. Todd, Mol. Phys., 1965, 9, 187–190 CrossRef CAS PubMed.
- B. Scharf, R. Vitenberg, B. Katz and Y. Band, J. Chem. Phys., 1982, 77, 2226–2234 CrossRef CAS PubMed.
- J. Eiding and W. Domcke, Chem. Phys., 1992, 163, 133–147 CrossRef CAS.
- P. C. Engelking and W. C. Lineberger, J. Chem. Phys., 1977, 67, 1412–1417 CrossRef CAS PubMed.
- M. J. Bearpark, M. A. Robb and N. Yamamoto, Spectrochim. Acta, Part A, 1999, 55, 639–646 CrossRef.
- H. J. Wörner and F. Merkt, J. Chem. Phys., 2007, 126, 154304 CrossRef PubMed.
- M. Grütter, H. J. Wörner and F. Merkt, J. Chem. Phys., 2009, 131, 024309 CrossRef PubMed.
-
I. M. Mills, in Molecular Spectroscopy – Modern Research, ed. K. Rao and C. Mathews, Academic Press, 1972, vol. 1, p. 115 Search PubMed.
Footnotes |
† Electronic supplementary information (ESI) available: Details of the fits presented in Table 2 to the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′– 1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D for v2′ = 0–5, including a line listing and correlation matrix and some supplementary notes on the development of the vibronic Hamiltonian. See DOI: 10.1039/c5cp01299f 1A1′ transition in NH2D for v2′ = 0–5, including a line listing and correlation matrix and some supplementary notes on the development of the vibronic Hamiltonian. See DOI: 10.1039/c5cp01299f |
| ‡ Current address: Department of Chemistry, University of Leicester, Leicester, UK. |
| § Current address: Institute of Atomic and Molecular Sciences, Academia Sinica, Taipei, Taiwan. |
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[B with combining tilde]](https://www.rsc.org/images/entities/h2_char_0042_0303.gif) 1E′′ state of NH2D and NHD2†
1E′′ state of NH2D and NHD2†![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH2D are presented and analysed. The analysis indicates a small (34.9 cm−1) lifting of the vibronic degeneracy of the zero point level, approximately equal in sign but opposite in magnitude to the splitting observed in NHD2 in previous work. This observation is consistent with previous measurements on systems with partial isotopic substitution subject to a mild Jahn–Teller effect. A model is developed to calculate the splitting induced by asymmetric isotopic substitution of a degenerate electronic state, based on a harmonic force field with linear and quadratic Jahn–Teller terms added. The force field is developed in internal co-ordinates to allow the same parameters to be used to calculate the pattern of vibronic levels for all four isotopologues. The lifting of the degeneracy of the zero point level on asymmetric substitution comes from the quadratic Jahn–Teller effect; the linear term does not lift the degeneracy.
1E′′ state of NH2D are presented and analysed. The analysis indicates a small (34.9 cm−1) lifting of the vibronic degeneracy of the zero point level, approximately equal in sign but opposite in magnitude to the splitting observed in NHD2 in previous work. This observation is consistent with previous measurements on systems with partial isotopic substitution subject to a mild Jahn–Teller effect. A model is developed to calculate the splitting induced by asymmetric isotopic substitution of a degenerate electronic state, based on a harmonic force field with linear and quadratic Jahn–Teller terms added. The force field is developed in internal co-ordinates to allow the same parameters to be used to calculate the pattern of vibronic levels for all four isotopologues. The lifting of the degeneracy of the zero point level on asymmetric substitution comes from the quadratic Jahn–Teller effect; the linear term does not lift the degeneracy.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia for which the
1E′′ state of ammonia for which the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition gives strong resonance enhanced multiphoton ionization (REMPI) spectra and is a prototypical example of a system with a mild Jahn–Teller effect. It is also an important transition in its own right, as it has become a standard system for probing rotational states of ammonia in the laboratory, as for example in a recent study by Tkac et al.2 on collisions and in cold molecule work such as that by Twyman et al.3
1A1′ transition gives strong resonance enhanced multiphoton ionization (REMPI) spectra and is a prototypical example of a system with a mild Jahn–Teller effect. It is also an important transition in its own right, as it has become a standard system for probing rotational states of ammonia in the laboratory, as for example in a recent study by Tkac et al.2 on collisions and in cold molecule work such as that by Twyman et al.3![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state is planar and the degeneracy arises from the 3px,y Rydberg orbital in the plane of the molecule, and so the Jahn–Teller effect is relatively weak, giving vibrational energy level shifts4 of the order of 100 cm−1. The rotational structure can be understood in terms of a standard symmetric top with two additional terms in the rotational Hamiltonian (ζ and q)5 arising from a significant residual electronic angular momentum. This electronic angular momentum (almost one unit) also means the state shows a significant Zeeman effect. The rotational and vibrational structure is reasonably well understood for both NH3 and ND3, but partially isotopically substituted species have not been investigated in any detail. In a previous paper6 we looked at resonance enhanced multiphoton ionisation spectra of NHD2. Formally this molecule has C2v symmetry, and is thus an asymmetric top with no degenerate vibronic states possible but, as discussed above, the degeneracy is only lifted at the vibrational and rotational level. Our analysis of observations indicated that the zero point level was best understood in terms of two closely spaced vibronic states with the symmetries A2 and B1 that correlate with E′′ in D3h. The separation is only 35.1 cm−1, so the additional terms (ζ and q) present in the symmetric top Hamiltonian for NH3 and ND3 are required to model the rotational structure, but transformed to perturbation terms mixing the two states. The terms mixing the vibronic states are only of the order of magnitude of rotational terms, but because the states are so close together the spectra cannot be effectively modelled without them.
1E′′ state is planar and the degeneracy arises from the 3px,y Rydberg orbital in the plane of the molecule, and so the Jahn–Teller effect is relatively weak, giving vibrational energy level shifts4 of the order of 100 cm−1. The rotational structure can be understood in terms of a standard symmetric top with two additional terms in the rotational Hamiltonian (ζ and q)5 arising from a significant residual electronic angular momentum. This electronic angular momentum (almost one unit) also means the state shows a significant Zeeman effect. The rotational and vibrational structure is reasonably well understood for both NH3 and ND3, but partially isotopically substituted species have not been investigated in any detail. In a previous paper6 we looked at resonance enhanced multiphoton ionisation spectra of NHD2. Formally this molecule has C2v symmetry, and is thus an asymmetric top with no degenerate vibronic states possible but, as discussed above, the degeneracy is only lifted at the vibrational and rotational level. Our analysis of observations indicated that the zero point level was best understood in terms of two closely spaced vibronic states with the symmetries A2 and B1 that correlate with E′′ in D3h. The separation is only 35.1 cm−1, so the additional terms (ζ and q) present in the symmetric top Hamiltonian for NH3 and ND3 are required to model the rotational structure, but transformed to perturbation terms mixing the two states. The terms mixing the vibronic states are only of the order of magnitude of rotational terms, but because the states are so close together the spectra cannot be effectively modelled without them.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1′′ state of C5H4D and C5D4H. These spectra were modelled as simple asymmetric tops, with the Jahn–Teller terms accounted for using perturbation theory working through to anomalous values of the rotational constants. The splittings of the zero point levels were approximately equal in magnitude (∼9 cm−1) but opposite in sign for the two isotopologues. A similar pattern of splittings was observed by Melnik et al.8,9 in the
2E1′′ state of C5H4D and C5D4H. These spectra were modelled as simple asymmetric tops, with the Jahn–Teller terms accounted for using perturbation theory working through to anomalous values of the rotational constants. The splittings of the zero point levels were approximately equal in magnitude (∼9 cm−1) but opposite in sign for the two isotopologues. A similar pattern of splittings was observed by Melnik et al.8,9 in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state of CH2DO and CD2HO though the rotational analysis was more complicated than that considered here due to the presence of significant spin–orbit coupling. Other related work is discussed below. There has been correspondingly little theoretical work on asymmetrically isotopically substituted Jahn–Teller systems though there is one particularly relevant recent paper by Iwahara et al.10 This paper showed that vibronic levels of a degenerate electronic state remain degenerate upon arbitrary isotopic substitution, even in the presence of a linear Jahn–Teller effect. For the current work, this implies we must consider both linear and quadratic Jahn–Teller terms.
2E state of CH2DO and CD2HO though the rotational analysis was more complicated than that considered here due to the presence of significant spin–orbit coupling. Other related work is discussed below. There has been correspondingly little theoretical work on asymmetrically isotopically substituted Jahn–Teller systems though there is one particularly relevant recent paper by Iwahara et al.10 This paper showed that vibronic levels of a degenerate electronic state remain degenerate upon arbitrary isotopic substitution, even in the presence of a linear Jahn–Teller effect. For the current work, this implies we must consider both linear and quadratic Jahn–Teller terms.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH2D to complement our earlier spectra of NHD2, and then look at relating the Jahn–Teller effects in all four isotopologues by developing a simple model for the force field in internal coordinates that can be applied without adjustment to all four species.
1E′′ state of NH2D to complement our earlier spectra of NHD2, and then look at relating the Jahn–Teller effects in all four isotopologues by developing a simple model for the force field in internal coordinates that can be applied without adjustment to all four species.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D were recorded using resonance enhanced multiphoton ionization spectroscopy (REMPI) in a molecular beam, using the method described previously.6 This gave rotationally resolved spectra with an effective rotational temperature of 3–90 K, that could be varied by adjusting the expansion conditions.
1A1′ transition in NH2D were recorded using resonance enhanced multiphoton ionization spectroscopy (REMPI) in a molecular beam, using the method described previously.6 This gave rotationally resolved spectra with an effective rotational temperature of 3–90 K, that could be varied by adjusting the expansion conditions.
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z
z![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z|±〉 = 0, 〈±|
z|±〉 = 0, 〈±|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z|∓〉 = ζ
z|∓〉 = ζ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)
−2)![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2 is discussed below. This has matrix elements:
−2 is discussed below. This has matrix elements: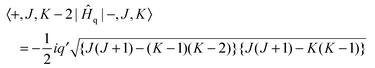
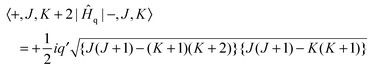
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition involves a change in geometry from pyramidal to planar, so the transition shows a progression in ν2, the umbrella mode. In the upper state members of this progression alternate between E′′ and E′ symmetry for even and odd v2 respectively, and the selection rules mean that the lower state of the electronic transition alternates between the upper and lower tunnelling component in the ground state. As this results from levels symmetric and antisymmetric with respect to the plane of symmetry of the molecule, which persists for NH2D and NHD2, the same pattern of transitions is observed for all four isopologues. In NH2D the |+〉 levels alternate between A2 (even v2) and B2 (odd v2) and the |−〉 levels alternate between B1 and A1 vibronic symmetry.
1A1′ transition involves a change in geometry from pyramidal to planar, so the transition shows a progression in ν2, the umbrella mode. In the upper state members of this progression alternate between E′′ and E′ symmetry for even and odd v2 respectively, and the selection rules mean that the lower state of the electronic transition alternates between the upper and lower tunnelling component in the ground state. As this results from levels symmetric and antisymmetric with respect to the plane of symmetry of the molecule, which persists for NH2D and NHD2, the same pattern of transitions is observed for all four isopologues. In NH2D the |+〉 levels alternate between A2 (even v2) and B2 (odd v2) and the |−〉 levels alternate between B1 and A1 vibronic symmetry.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D
1A1′ transition in NH2D
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state; such interactions have been seen5 in ND3 and the level of vibrational excitation is such that these are to be expected. The analysis was stopped at v2 = 5; some peaks were seen in the region of v2 = 6, but a complete analysis was not possible because of two complicating factors. Firstly the origin band of the C′ state14 is in this region and secondly the interference between the two transition moments has become sufficiently large that transitions to one of the components becomes very weak. These factors combined meant it was not possible to produce a convincing analysis of the observed spectra for v2 = 6.
state; such interactions have been seen5 in ND3 and the level of vibrational excitation is such that these are to be expected. The analysis was stopped at v2 = 5; some peaks were seen in the region of v2 = 6, but a complete analysis was not possible because of two complicating factors. Firstly the origin band of the C′ state14 is in this region and secondly the interference between the two transition moments has become sufficiently large that transitions to one of the components becomes very weak. These factors combined meant it was not possible to produce a convincing analysis of the observed spectra for v2 = 6.![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D
1A1′ transition in NH2D
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NHD2
1A1′ transition in NHD2
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3 has two Jahn–Teller active modes, the asymmetric stretch, ν3 and the in plane bend, ν4, both with E′ symmetry. (The other two modes are the symmetric (A1′) stretch, ν1 and the umbrella mode, ν2 (A2′′)). The most complete information so far on the Jahn–Teller activity in these modes comes from the study of Allen et al.4 based on a combination of IR-MPI double resonance spectroscopy and other methods. While the pattern of the levels of the Jahn–Teller active modes is not known in full, enough is known to give a good idea as to the likely pattern and magnitude of the effects. The model we are using here is two electronic states that are degenerate at all values of the vibrational co-ordinates, with the Jahn–Teller terms giving matrix elements between the two surfaces. The most significant extra term due to the Jahn–Teller effect is a term linear in the vibrational co-ordinates:
1E′′ state of NH3 has two Jahn–Teller active modes, the asymmetric stretch, ν3 and the in plane bend, ν4, both with E′ symmetry. (The other two modes are the symmetric (A1′) stretch, ν1 and the umbrella mode, ν2 (A2′′)). The most complete information so far on the Jahn–Teller activity in these modes comes from the study of Allen et al.4 based on a combination of IR-MPI double resonance spectroscopy and other methods. While the pattern of the levels of the Jahn–Teller active modes is not known in full, enough is known to give a good idea as to the likely pattern and magnitude of the effects. The model we are using here is two electronic states that are degenerate at all values of the vibrational co-ordinates, with the Jahn–Teller terms giving matrix elements between the two surfaces. The most significant extra term due to the Jahn–Teller effect is a term linear in the vibrational co-ordinates:![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) +
+![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) −
−![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)
−2)![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ±2 operators are taken to connect the components of the degenerate electronic state, which we label with Λ = ±1, approximately the electronic angular momentum of the states:
±2 operators are taken to connect the components of the degenerate electronic state, which we label with Λ = ±1, approximately the electronic angular momentum of the states:![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) ±2|±1〉 = |∓1〉
±2|±1〉 = |∓1〉![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, though a similar fit was also possible using a quadratic Jahn–Teller term of the form:
state, though a similar fit was also possible using a quadratic Jahn–Teller term of the form:![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) −2
−2![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) +2
+2![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)
−2)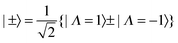
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 ±
+2 ± ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2, which can be derived by simple substitution:
−2, which can be derived by simple substitution:![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2|±〉 = ±1 and 〈±|
−2|±〉 = ±1 and 〈±|![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2|∓〉 = ∓1
−2|∓〉 = ∓1![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ± =
± = ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x ± i
x ± i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y
y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x(
x(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) + i
−2) + i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y(
y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)}
−2)}![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x and
x and ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y coordinates become clear. The term multiplying
y coordinates become clear. The term multiplying ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x is diagonal in the |±〉 basis, and must therefore correspond to a totally symmetric co-ordinate in C2v symmetry. It has the effect of adding or subtracting a simple linear term along the x normal co-ordinate. The term multiplying
x is diagonal in the |±〉 basis, and must therefore correspond to a totally symmetric co-ordinate in C2v symmetry. It has the effect of adding or subtracting a simple linear term along the x normal co-ordinate. The term multiplying ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y is purely off-diagonal in the |±〉 basis, and must therefore have the symmetry of the product of the two electronic components. From the previous paper |+〉 has A2 symmetry and |−〉 has B1 symmetry for the electronic origin (which has E′′ symmetry in D3h), requiring
y is purely off-diagonal in the |±〉 basis, and must therefore have the symmetry of the product of the two electronic components. From the previous paper |+〉 has A2 symmetry and |−〉 has B1 symmetry for the electronic origin (which has E′′ symmetry in D3h), requiring ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y to have B2 symmetry so that the overall operator, i
y to have B2 symmetry so that the overall operator, i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y(
y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) is totally symmetric. Note that i
−2) is totally symmetric. Note that i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y(
y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) will give purely imaginary matrix elements, but we can avoid this complication by multiplying one of the electronic basis functions by i.
−2) will give purely imaginary matrix elements, but we can avoid this complication by multiplying one of the electronic basis functions by i.
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 −
x2 − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2)(
y2)(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) − 2i
−2) − 2i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x
x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y(
y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)}
−2)}![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 +
x2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) x2 +
x2 + ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2 +
y2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) y2)
y2)![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x ± ½gω(
x ± ½gω(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 −
x2 − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2)
y2)![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y − gω
y − gω![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x
x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y
y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x and
x and ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y are now different. The requirement that they have different symmetry in C2v introduced above means that they will correspond to different normal modes in the lower symmetry. (The specific forms for NH3 are discussed below, but one of the obvious separations corresponds to the division into N–H and N–D stretches.) The standard harmonic part must now have two distinct vibrational frequencies, which we denote by with ωx and ωy:
y are now different. The requirement that they have different symmetry in C2v introduced above means that they will correspond to different normal modes in the lower symmetry. (The specific forms for NH3 are discussed below, but one of the obvious separations corresponds to the division into N–H and N–D stretches.) The standard harmonic part must now have two distinct vibrational frequencies, which we denote by with ωx and ωy:![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 +
x2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) x2) + ½ωy(
x2) + ½ωy(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2 +
y2 + ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) y2)
y2)![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x
x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y
y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 − gyωy
x2 − gyωy![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2) = ±½(gxx
y2) = ±½(gxx![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x2 − gyy
x2 − gyy![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y2)
y2)![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) x
x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) y
y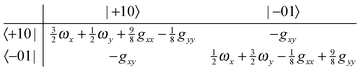
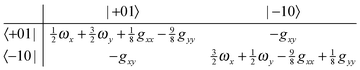
![[B with combining tilde]](https://www.rsc.org/images/entities/h3_char_0042_0303.gif) 1E′′ state of NH3
1E′′ state of NH3![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3
1E′′ state of NH3
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state, but the value for the
state, but the value for the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ′ state, which is expected to have similar bonding, is known to be14 3217.0 cm−1. The above constants predict 3143.7 cm−1, reasonable agreement considering anharmonicity and coupling between internal coordinates are being ignored.
′ state, which is expected to have similar bonding, is known to be14 3217.0 cm−1. The above constants predict 3143.7 cm−1, reasonable agreement considering anharmonicity and coupling between internal coordinates are being ignored.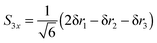
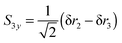
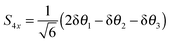
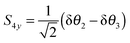
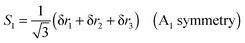
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) + iŜ3y(
−2) + iŜ3y(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)}
−2)}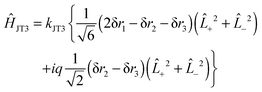
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2) − 2iŜxŜy(
−2) − 2iŜxŜy(![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2)}
−2)}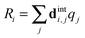
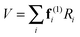
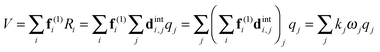
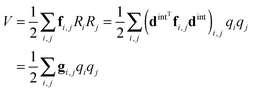
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 +
+2 + ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2 and
−2 and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2 −
+2 − ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2 must be kept separate and a separate set of multipliers is required for each state. In PGOPHER these are used to calculate perturbation terms in the vibronic Hamiltonian that are added to the standard harmonic terms.
−2 must be kept separate and a separate set of multipliers is required for each state. In PGOPHER these are used to calculate perturbation terms in the vibronic Hamiltonian that are added to the standard harmonic terms.
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3
1E′′ state of NH3
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x
3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x −
4x − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y
3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y) = ±(g3x4x′
4y) = ±(g3x4x′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x
3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x + g3y4y′
4x + g3y4y′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y
3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y)
4y)![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x
3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y −
4y − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y
3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x) = g3x4y′
4x) = g3x4y′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x
3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y + g3y4x′
4y + g3y4x′![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y
3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x
4x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) i
i![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) j; in this case g34 = g3x4x′ = −g3y4y′ = −g3x4y′ = −g3y4x′ but this notation simplifies the presentation for the less symmetrical species where there are no constrains on the values. Note there is no factor of ½ in these equations as the operator form is strictly (for example) ±½g34(
j; in this case g34 = g3x4x′ = −g3y4y′ = −g3x4y′ = −g3y4x′ but this notation simplifies the presentation for the less symmetrical species where there are no constrains on the values. Note there is no factor of ½ in these equations as the operator form is strictly (for example) ±½g34(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x
3x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x +
4x + ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4x
4x![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3x −
3x − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y
3y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y −
4y − ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 4y
4y![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 3y), which simplifies as above. Neither of the g4 or g34 terms are significant, but are included for completeness.
3y), which simplifies as above. Neither of the g4 or g34 terms are significant, but are included for completeness.
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia

![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH3. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis.
1E′′ state of NH3. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis.
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NH2D. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis.
1E′′ state of NH2D. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis.
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis.
1E′′ state of ammonia. This was calculated using the parameters in Table 7, but with kJT4 = 0 and only including v4 = 0 levels in the basis.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1′′ state of C5H4D (−8.9557 cm−1) and C5D4H (+9.1975 cm−1) and by Melnik et al.8,9 on the
2E1′′ state of C5H4D (−8.9557 cm−1) and C5D4H (+9.1975 cm−1) and by Melnik et al.8,9 on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state of CH2DO (−45.66 cm−1) and CD2HO (+43.44 cm−1).
2E state of CH2DO (−45.66 cm−1) and CD2HO (+43.44 cm−1).![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1g and
2E1g and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2E2g states of 1,4-C6H4D2+. They modelled the energy levels including several Jahn–Teller active modes using an approach similar to that taken in this paper, but with one essential difference. The reference point taken for all the derivatives with respect to energy was the geometry of the neutral molecule, rather than the ion. (This approach was taken as the aim of that study was to calculate photoelectron spectra.) This meant that the first derivatives with respect to energy for symmetric modes was non zero even in the absence of the Jahn–Teller effect, giving terms comparable in magnitude to the linear Jahn–Teller terms. Values for these first derivatives for both the symmetrical and Jahn–Teller active modes were taken from derivatives of orbital energies from a Hartree–Fock calculation on the neutral molecule. Quadratic Jahn–Teller effects were not included, but the calculations did nevertheless predict non-zero zero-point splittings for the lower symmetry isotopologues. This does not contradict the result of Iwahara et al.10 that linear terms do not give a zero-point splitting due to the use of a non-equilibrium reference geometry as the transformation to the equilibrium geometry will introduce additional terms in the Hamiltonian that are effectively quadratic.
2E2g states of 1,4-C6H4D2+. They modelled the energy levels including several Jahn–Teller active modes using an approach similar to that taken in this paper, but with one essential difference. The reference point taken for all the derivatives with respect to energy was the geometry of the neutral molecule, rather than the ion. (This approach was taken as the aim of that study was to calculate photoelectron spectra.) This meant that the first derivatives with respect to energy for symmetric modes was non zero even in the absence of the Jahn–Teller effect, giving terms comparable in magnitude to the linear Jahn–Teller terms. Values for these first derivatives for both the symmetrical and Jahn–Teller active modes were taken from derivatives of orbital energies from a Hartree–Fock calculation on the neutral molecule. Quadratic Jahn–Teller effects were not included, but the calculations did nevertheless predict non-zero zero-point splittings for the lower symmetry isotopologues. This does not contradict the result of Iwahara et al.10 that linear terms do not give a zero-point splitting due to the use of a non-equilibrium reference geometry as the transformation to the equilibrium geometry will introduce additional terms in the Hamiltonian that are effectively quadratic.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1′′ state of C5H4D and C5D4H used a similar approach to that used here, but only considered linear Jahn–Teller terms. In addition, in C5H5 the mode with the largest Jahn–Teller activity was thought to involve distortion of the carbon framework, so they assumed deuterium substitution did not alter the Jahn–Teller parameters and so gave no zero point splitting in that mode. They suggested, following Scharf et al.18 that there could be a zero point energy difference in the other modes, but did not attempt to calculate this, and the current work suggests there should not be any if only linear terms are included. They did not discuss quadratic Jahn–Teller effects in detail, though they pointed out that it was shown by Engelking and Lineberger20 using symmetry arguments that the quadratic Jahn–Teller effect must be zero in D5h symmetry. Iwahara et al.10 discuss this specific case, and attribute the splitting of the zero point level to quartic potential terms. Higher terms would give five equivalent minima, and more recent calculations of Bearpark et al.21 suggests that the barrier between them is only 3.6 cm−1. Bearpark et al.21 did calculate zero point energies for different equilibrium structures with differences of the right order of magnitude to the observations, but they do not indicate which value should be compared to the experiment. It is anyway not clear that the approach they used, considering a single electronic surface, will give correct results, especially as they ignored anharmonic effects which must be important with such a surface given the low barrier (3.6 cm−1) in one mode.
2E1′′ state of C5H4D and C5D4H used a similar approach to that used here, but only considered linear Jahn–Teller terms. In addition, in C5H5 the mode with the largest Jahn–Teller activity was thought to involve distortion of the carbon framework, so they assumed deuterium substitution did not alter the Jahn–Teller parameters and so gave no zero point splitting in that mode. They suggested, following Scharf et al.18 that there could be a zero point energy difference in the other modes, but did not attempt to calculate this, and the current work suggests there should not be any if only linear terms are included. They did not discuss quadratic Jahn–Teller effects in detail, though they pointed out that it was shown by Engelking and Lineberger20 using symmetry arguments that the quadratic Jahn–Teller effect must be zero in D5h symmetry. Iwahara et al.10 discuss this specific case, and attribute the splitting of the zero point level to quartic potential terms. Higher terms would give five equivalent minima, and more recent calculations of Bearpark et al.21 suggests that the barrier between them is only 3.6 cm−1. Bearpark et al.21 did calculate zero point energies for different equilibrium structures with differences of the right order of magnitude to the observations, but they do not indicate which value should be compared to the experiment. It is anyway not clear that the approach they used, considering a single electronic surface, will give correct results, especially as they ignored anharmonic effects which must be important with such a surface given the low barrier (3.6 cm−1) in one mode.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state of CH2DO and CHD2O radicals. Their approach to the rotational energy level pattern was similar to that taken here, though made rather more complicated by the presence of a spin–orbit interaction. They describe a method of calculating the zero point splitting, based on calculating zero point energies at two different minima on the lowest potential energy surface with the unique atom on or off the symmetry plane. This gives promising results, predicting approximately equal and opposite splittings for CH2DO and CHD2O and of the correct order of magnitude, though rather sensitive to the ab initio method used. They do however comment that their method relies on a harmonic frequency model and ignores the upper surface and the coupling between them, and acknowledge that they may be relying on a cancellation of errors, as again the mild Jahn–Teller interaction implies a very anharmonic mode.
2E state of CH2DO and CHD2O radicals. Their approach to the rotational energy level pattern was similar to that taken here, though made rather more complicated by the presence of a spin–orbit interaction. They describe a method of calculating the zero point splitting, based on calculating zero point energies at two different minima on the lowest potential energy surface with the unique atom on or off the symmetry plane. This gives promising results, predicting approximately equal and opposite splittings for CH2DO and CHD2O and of the correct order of magnitude, though rather sensitive to the ab initio method used. They do however comment that their method relies on a harmonic frequency model and ignores the upper surface and the coupling between them, and acknowledge that they may be relying on a cancellation of errors, as again the mild Jahn–Teller interaction implies a very anharmonic mode.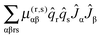
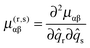
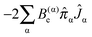
![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) α is the vibrational angular momentum:
α is the vibrational angular momentum: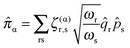
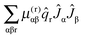
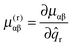
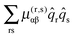 (from (41)) and
(from (41)) and 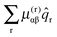 (from (45)) evaluated in the harmonic basis described above used to calculate the vibronic energy levels. Transforming this matrix using the eigenvectors from the energy level calculations then gives the corrections to the rotational constants as the diagonal elements. For the Coriolis terms, eqn (43) a slightly different approach is required. For each principal axis, α, we set up the matrix of −2B(α)e
(from (45)) evaluated in the harmonic basis described above used to calculate the vibronic energy levels. Transforming this matrix using the eigenvectors from the energy level calculations then gives the corrections to the rotational constants as the diagonal elements. For the Coriolis terms, eqn (43) a slightly different approach is required. For each principal axis, α, we set up the matrix of −2B(α)e![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) αĴβ in the same harmonic basis, and again transform this using the eigenvectors from the energy level calculations. The corrections to a rotational constant, Δμαβ, for a given level i are then calculated using second order perturbation theory:
αĴβ in the same harmonic basis, and again transform this using the eigenvectors from the energy level calculations. The corrections to a rotational constant, Δμαβ, for a given level i are then calculated using second order perturbation theory: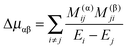
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of ammonia
1E′′ state of ammonia
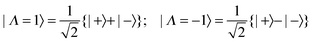
![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) −2 + Ĵ−2
−2 + Ĵ−2![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) +2)
+2)![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′ state of NHD2 has been successfully applied to NH2D, and confirms the validity of the model, and that for cases of a mild Jahn–Teller effect the formal lifting of the degeneracy by partial isotopic substitution leaves significant terms in the Hamiltonian mixing the two components of the state that must be included for a satisfactory simulation of the rotational structure. The observation of approximately equal but opposite splittings in the zero point level for complementary isotopic substitution (here NH2D compared to NHD2) seen before in the literature is further reinforced here. We present a method of calculating this from the Jahn–Teller parameters from any one isotope, though we are limited from quantitative agreement here by a lack of a full knowledge of the required Jahn–Teller parameters. This limitation also applies to our calculation of the rotational constants, which are affected by the Jahn–Teller effect.
1E′′ state of NHD2 has been successfully applied to NH2D, and confirms the validity of the model, and that for cases of a mild Jahn–Teller effect the formal lifting of the degeneracy by partial isotopic substitution leaves significant terms in the Hamiltonian mixing the two components of the state that must be included for a satisfactory simulation of the rotational structure. The observation of approximately equal but opposite splittings in the zero point level for complementary isotopic substitution (here NH2D compared to NHD2) seen before in the literature is further reinforced here. We present a method of calculating this from the Jahn–Teller parameters from any one isotope, though we are limited from quantitative agreement here by a lack of a full knowledge of the required Jahn–Teller parameters. This limitation also applies to our calculation of the rotational constants, which are affected by the Jahn–Teller effect.
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1E′′–
1E′′–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1′ transition in NH2D for v2′ = 0–5, including a line listing and correlation matrix and some supplementary notes on the development of the vibronic Hamiltonian. See DOI: 10.1039/c5cp01299f
1A1′ transition in NH2D for v2′ = 0–5, including a line listing and correlation matrix and some supplementary notes on the development of the vibronic Hamiltonian. See DOI: 10.1039/c5cp01299f

