Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A molecular dynamics study of CaCO3 nanoparticles in a hydrophobic solvent with a stearate co-surfactant†
Michael S.
Bodnarchuk
a,
David M.
Heyes
a,
Angela
Breakspear
b,
Samir
Chahine
b and
Daniele
Dini
*a
aDepartment of Mechanical Engineering, Imperial College London, Exhibition Road, London, SW7, UK. E-mail: m.bodnarchuk@imperial.ac.uk; d.dini@imperial.ac.uk
bBP Technology Centre, Whitchurch Hill, Pangbourne, RG8 7QR, UK
First published on 23rd April 2015
Abstract
Stearates containing overbased detergent nanoparticles (NPs) are used as acid neutralising additives in automotive and marine engine oils. Molecular dynamics (MD) simulations of the self-assembly of calcium carbonate, calcium stearate as a co-surfactant and stabilising surfactants of such NPs in a model explicit molecular hydrophobic solvent have been carried out using a methodology described first by Bodnarchuk et al. [J. Phys. Chem. C, 2014, 118, 21092]. The cores and particles as a whole become more elongated with stearate, and the surfactant molecules are more spaced out in this geometry than in their stearate-free counterparts. The rod dimensions are found to be largely independent of the surfactant type for a given amount of CaCO3. The corresponding particles without stearate were more spherical, the precise shape depending to a greater extent on the chemical architecture of the surfactant molecule. The rod-shaped stearate containing nanoparticles penetrated a model water droplet to a greater depth than the corresponding near-spherical particle, which is possibly facilitated by the dissociation of nanoparticle surfactant molecules onto the surface of the water in this process. These simulations are the first to corroborate the nanoparticle–water penetration mechanism proposed previously by experimental groups investigating the NP acid neutralisation characteristics.
1. Introduction
Calcite, a polymorph of calcium carbonate, is important in Nature (for example in the area of biomineralisation1), medicine (as supports for drug delivery2,3) and various technological applications and in consumer products.4 The particle size can affect its physical and chemical properties.5 Inorganic clusters in solution can adopt a variety of shapes such as flowers,6 rods,7 and tetrahedra,8 which can be controlled using surfactant stabilisers. Calcium carbonate can precipitate in needle shapes,9 for example. The so-called overbased detergent (OD) chemical is an important class of inorganic–organic hybrid nanoparticle which is added to automotive and marine engine oil to act principally as an acid scavanger.10–14 The acid neutralising ability is measured using the total base number (TBN), which is the mass in mg of KOH used to neutralise 1 g of the OD detergent.15 A number of most popular OD surfactants which stabilise the calcium carbonate in oil contain sulphur (e.g. sulphonates and SAP, sulphurised alkyl phenates).Classical theories of micellisation16 indicate that stearate acting as a co-surfactant could be used to expand the core region isotropically by acting as a ‘wedge’, allowing it to accommodate more calcium carbonate. This reduces the amount of (stabilising) surfactant required, which is especially important for sulphur-containing surfactants as there is legislation to reduce the amount of sulphur in the OD.17 The effect of stearate on the state of micellisation and the subsequent acid neutralisation process is still largely unresolved, which is the main focus of this study. Of particular interest is the extent to which the classical picture of micellisation is correct.
There is a history of Molecular Dynamics (MD) computer simulation being applied to model calcium carbonate systems, in more recent times in relation to biomineralisation, for example studies of its growth on ionised organic substrates.19–26 Molecular dynamics simulations carried out by one of the authors and co-workers of calixarate and phenate-stabilised OD nanoparticles with stearate were reported in 2000.15 The nanoparticle construction method in that publication started from a largely preformed surfactant-stabilised CaCO3 core to which stearate ions with counter-ions were added. It was concluded that the incorporation of stearate made the nanoparticle more spherical. Our recent simulations of the OD nanoparticle18 have employed a less biased starting state, in which the chemical components and solvent molecules were initially positioned essentially randomly in the simulation cell. The nanoparticle was then free to self-assemble through thermal motion by cooperative arrangement of the species under the influence of the intermolecular force fields. This is the method used in this study. The other novel feature of the present study is the interaction of the nanoparticles with a model water droplet, which is simulated to explore some aspects of the processes leading up to acid neutralisation. Evidence built up from various studies indicates that the CaCO3 core of the OD particle is predominantly amorphous,12,27–33 making property prediction of calcium carbonate nanoparticles a challenge without adopting computational methods.
2. Simulation details
The OD nanoparticles were stabilised by three different surfactant types, a sulphurised-alkyl phenol (SAP), alkyl-sulphonate and an alkyl-salicylate, as shown in Fig. 1. A co-surfactant, calcium stearate and dispersant molecule were also included in the simulations, whose chemical formulae are also given in Fig. 1.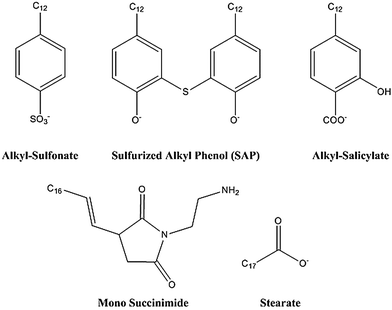 | ||
| Fig. 1 The three surfactant (alkyl sulfonate, sulfurized alkyl phenate, alkyl salicylate), dispersant (mono succinimide) and co-surfactant (stearate) molecule types used in this study. | ||
Two types of self-assembly simulation were performed. In the first (henceforth referred to as the protocol, PI), the calcium and carbonate ions, surfactant and co-surfactant molecules were initially positioned randomly in a model cyclohexane solvent in a periodic cubic MD cell. Cyclohexane is a widely used model hydrophobic solvent in such MD simulations. It has a similar dielectric constant to that of longer alkanes such as decane, and is also typically used to dissolve ODs for their use in engine oils. It is also computationally efficient.
During the simulation these species were observed to self-assemble into an OD nanoparticle. Further equilibration was performed by gradually reducing the ion charges to loosen the structure and then returning the charges to their original values, a procedure described in ref. 18. In ref. 18 it was shown by thermodynamic integration for all the surfactant types used here that the annealing–quenching procedure employed in PI directed the nanoparticle to a lower free energy state.
The second method (henceforth referred to as the protocol, PII) performed the initial OD particle formation without the stearate component. The calcium and stearate ions were then distributed randomly in the simulation cell and allowed to associate with the preformed nanoparticle until a steady state was achieved.
As a further stage in the simulation procedure, the nanoparticles were allowed to interact with a water-droplet consisting of 1000 model water molecules and 23 non-ionic succinimide surfactant molecules,34 at a temperature of 300 K and a pressure of 1 bar. This type of simulation is the first of its kind.
Succinimide molecules are used as dispersants in engine oil, and it was our purpose to make the medium for the OD particles as close as possible to the real system. It was of interest to explore if they interact with this other type of engine oil additive. It was found that their association with the model overbased particles was not noticeable; they stayed dispersed more or less uniformly in the solvent. This ‘negative’ result is nevertheless of interest, but because of this result there is no need to comment further on the role of the succinimide molecules here.
The parameters of all the species were obtained using the online Automated Topology Builder (ATB) server,35,36 and Table 1 gives the number of species included in the different simulations. The quantities of Ca2+ and CO32− were chosen to give a total base number of approximately 250. This table provides information about the number of various species employed in each of the simulations. The top six rows are for the nanoparticle in a hydrophobic solvent and the bottom three rows are for MD simulations with a water droplet.
| System | Code | S | St | Cy | Ca2+ | CO32− | H2O | Su |
|---|---|---|---|---|---|---|---|---|
| SAP | A | 6 | 6 | 2864 | 19 | 10 | 0 | 0 |
| Sulphonate | B | 12 | 6 | 3531 | 19 | 10 | 0 | 0 |
| Salicylate | C | 12 | 6 | 3560 | 19 | 10 | 0 | 0 |
| SAP | D | 6 | 6 | 3082 | 29 | 20 | 0 | 0 |
| Sulphonate | E | 12 | 6 | 3321 | 29 | 20 | 0 | 0 |
| Salicylate | F | 12 | 6 | 3510 | 29 | 20 | 0 | 0 |
| SAP + droplet | G | 6 | 6 | 5846 | 29 | 20 | 1000 | 23 |
| Sulphonate + droplet | H | 12 | 6 | 6355 | 29 | 20 | 1000 | 23 |
| Salicylate + droplet | I | 12 | 6 | 5732 | 29 | 20 | 1000 | 23 |
Simulations were performed using the Molecular Dynamics (MD) simulation code, GROMACS v4.5.5.37,38 The particle mesh Ewald method39 was used to compute the electrostatic terms in the potential, with interactions between atoms within 1.0 nm evaluated every time step and every five steps for atom pairs further apart. Non-bonded van der Waals terms were treated using the Lennard-Jones pair potential with a cut-off of 1.2 nm. Verlet's leapfrog equation of motion integrator was used with a time step of 2 fs. The bond distances and angles of water molecules were constrained using the SETTLE algorithm,40 and all other bonds were constrained using LINCS.41 Temperature was regulated using a velocity rescaling thermostat with a coupling time of 0.1 ps,42–44 and pressure was controlled using the Parrinello–Rahman barostat.45 Each self-assembly simulation was performed for 40 ns in the NPT ensemble, with structural data collected over the last 5 ns. Simulations containing the nanoparticle formed and a water drop were performed for 20 ns in the NPT ensemble. Structural analysis was performed using the inbuilt GROMACS packages g_sas, g_gyrate and g_dist. The accessible surface area, SA, was found using a probe molecule of diameter, 1.4 Å. The radius of gyration, Rg,46 is an objective measure of the radius of the particle, which was calculated both for the CaCO3 core and the entire nanoparticle using the respective centre of masses as follows,
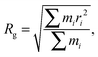 | (1) |
The shape of the nanoparticle was determined using a literature asphericity order parameter, A3,47,48 derived from the moment of inertia tensor which was accumulated during the simulation as follows,
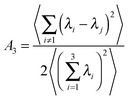 | (2) |
3. Results and discussion
In this section the structural characteristics of the nanoparticles formed in the presence of cyclohexane are discussed. Then the results of MD simulations of the different types of nanoparticles interacting with a water droplet in an explicit hydrophobic solvent are presented and discussed.3.1. Self-assembly simulations
To assess the influence of stearate on the self-assembly process, the same initial chemical compositions, as previously used for the stearate-free case,18 were adopted but with an additional six stearate and three Ca2+ ions included in the simulation (simulations A to C in Table 1). Two or three nanoparticles were formed during the self-assembly stage, presumably because there was too much surfactant to cover the surface area of the CaCO3 core of a single particle (the total surface area of several nanoparticles is greater than a single one, with the same total amount of calcium carbonate in each case). Doubling the amount of CaCO3 in the mixture to 20 Ca2+ ions produced a single nanoparticle (simulations D to F in Table 1).The structural characteristics of the SAP, sulphonate and salicylate-based nanoparticles formed in the presence of stearate are summarised in Table 2.
| Surfactant | Method | Core SA/nm2 | R g-core/nm | R g-total/nm | A 3 |
|---|---|---|---|---|---|
| SAP | PI | 12.73 (0.20) | 0.89 (0.01) | 1.45 (0.02) | 0.14 |
| Sulphonate | PI | 12.54 (0.28) | 0.93 (0.01) | 1.48 (0.01) | 0.15 |
| Salicylate | PI | 12.31 (0.37) | 0.91 (0.05) | 1.52 (0.02) | 0.13 |
| SAP | PII | 12.08 (0.21) | 0.62 (0.01) | 1.10 (0.01) | 0.04 |
| Sulphonate | PII | 11.23 (0.22) | 0.59 (0.02) | 1.16 (0.02) | 0.03 |
| Salicylate | PII | 11.58 (0.23) | 0.68 (0.02) | 1.14 (0.02) | 0.06 |
Table 2 shows that the surface area, radius of gyration and asphericity parameter of the nanoparticles are smaller when the stearate is added after the main core had formed (i.e., using PII) compared with the PI strategy. Also within the set of surfactant types there is a statistically significant variation in these quantities in the PII case. This is similar to what was previously found by simulations performed without stearate,18 which also produced a sulphonate nanoparticle in which the core was more compact (i.e., with a smaller radius of gyration) than that formed from the other two surfactant classes. In ref. 18 it was shown by thermodynamic integration for all the surfactant types used here that the annealing–quenching procedure employed in PI directed the nanoparticle to a lower free energy state compared to previous self-assembly strategies. The same behaviour was observed in this study. The SAP, sulphonate and salicylate nanoparticles formed during PI were found to be stabilised by −2750, −3000 and −2920 kJ mol−1, respectively, upon annealing. In comparison, the addition of stearate post core formation was found to stabilise the particles by only approximately −1000 kJ mol−1. The PI procedure produced nanoparticles with a lower free energy than those formed by PII which did not allow the stearate molecules to fully relax into the nanoparticle during an annealing process. Nanoparticles formed using PI therefore have a lower thermodynamic free energy and more closely resemble those made experimentally.
The nanoparticles are more rod-shaped when produced using PI, as is evident by comparing the A3 values for the PI and PII sets. The PII-type nanoparticles are significantly more spherical, suggesting that the addition of stearate after the initial core had formed does not allow sufficient time for rearrangement to a rod-like shape to occur during a typical simulation time (i.e., the activation free energy being too high compared with kBT).
The PI structural descriptors of Table 2 are statistically indistinguishable for the three surfactant types. The negative charge surrounding the stearate head-group is more localised than for the sulphonate surfactant, and is therefore likely to dominate the structure of that type of nanoparticle.
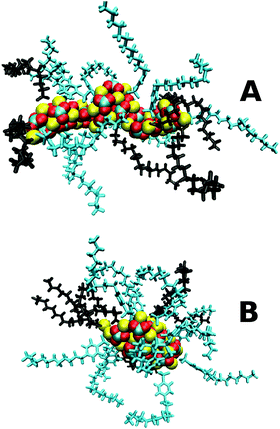
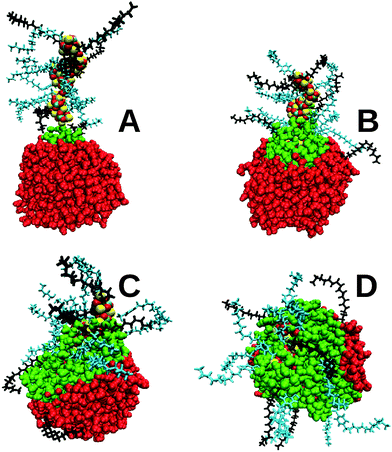
Completed simulation snapshots of the sulphonate-based stearate containing nanoparticle at the end of the 40 ns PI and PII procedures are shown in Fig. 2, which confirm what can be inferred from Table 2 that the PI procedure produces a more elongated core and rod shaped particle.
The results are consistent with experimental evidence,7,49 and theory,50 that rod-shaped surfactants tend to form rod-shaped micelles. The stearate co-surfactant has a significantly smaller head-group than the three main surfactants used to stabilise the nanoparticle, promoting the formation of a rod-shaped particle. The surfactant molecules are more spaced out along the rod (frame (a)) than for the more spherically shaped particle (frame (b)), hence the insensitivity of the core surface area and radii of gyration to the surfactant type in the PI class of nanoparticles. It may be concluded that the nanoparticle produced in this study using PI is closer to the optimal free energy structure compared to the original work performed some 15 years ago when computer resources and software capability were more limited.15 The experimental systems are therefore more likely to resemble those shown in Fig. 2A than Fig. 2B.
3.2. Interaction with water
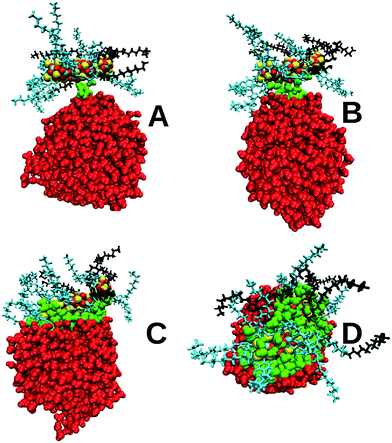
The primary role of overbased detergents is to neutralise acidic byproducts of combustion inside automotive and marine engines. The acids (mainly nitric and sulphuric acid) are formed from combustion gases dissolved in the water droplets present in the lubricant. There is some evidence that the overbased detergents attach onto water droplets via a three stage process.51,52 First, the overbased nanoparticle diffuses by thermal motion close to a water droplet. Then a water bridge is formed between the two particles. Finally, water molecules increasingly coat the OD nanoparticle, forming a strong interface between the two and which allows more ready neutralisation of any acid in the water droplet (the acid is not included in these simulations). This proposed mechanism is predominantly based upon reaction rate experiments and microcapilliary visualisations, and to the knowledge of the authors no simulations have been carried out to confirm or refute this mechanism.Fig. 3 and 4 for the SAP-stearate and sulphonate-stearate particles formed using PI (simulations G and H in Table 1), respectively, demonstrate that this proposed mechanism is supported by the MD simulations (the behaviour of the salicylate nanoparticle, simulation I, is shown in the ESI†). A short-lived bridge is formed within 500 ps, before the water molecules begin to coat the core. In both cases, the OD nanoparticle fully attaches itself to the water droplet. The majority of the core had penetrated into the droplet approximately 2 ns after the initial bridge formation. Note that in Fig. 3 and 4 the water molecules which are within 7 Å of the core are shown in green.
 | ||
| Fig. 4 As for Fig. 3 except the behaviour of the sulphonate/stearate nanoparticle is shown. | ||
All three nanoparticles demonstrate some degree of surfactant dissociation from the CaCO3 core which is possibly driven by the larger number of potentially favourable calcium ion–water interactions, which outweigh the interactions between the surfactant molecules and the core. The surfactant-dissociation facilitates increased core penetratation into the water droplet since the presence of a surfactant acts as a hydrophobic steric barrier between the core and water. In all cases the accessible hydrophobic surface area of the core upon penetration is zero, indicating close to total coverage of the core by the water droplet. Fig. 6A shows that, for the sulphonate case, most of the core is surrounded by water molecules in the final stages, with a number of surfactant molecules distributed around the droplet surface. Fu and co-workers have shown that increased neutralisation rates are found for overbased particles containing surfactants which can dissociate from the CaCO3 core,53,54 and these simulations give support to this view in that increased penetration of the core into an acidic droplet will accompany partial dissociation of the surfactant molecules from the nanoparticle.
Successful core-droplet docking was observed in approximately three out of four simulations, independent of the surfactant type. As a prelude to the absorption the initial angle of approach between the core and the droplet varied. An equal number of side-on (Fig. 3A) and head-on (Fig. 4A) approaches was observed, suggesting that there is no favoured orientation for attachment to occur.55 The two approaches took between 1 and 5 ns to yield fully immersed cores, further suggesting that there is no significant dependence of outcome on the angle of approach.
The same simulations were performed for the spherical stearate-containing particles formed using PII. Fig. 5 shows how the distance between the centre of mass for the PI and PII nanoparticles and the water droplet changes upon initial contact between the two species.
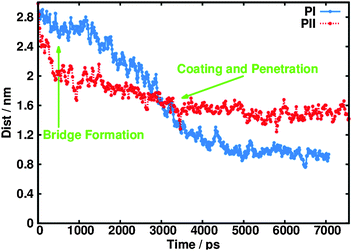 | ||
| Fig. 5 Variation in the distance between the centre of mass of the nanoparticle and the water droplet as a function of time after initial contact is made. | ||
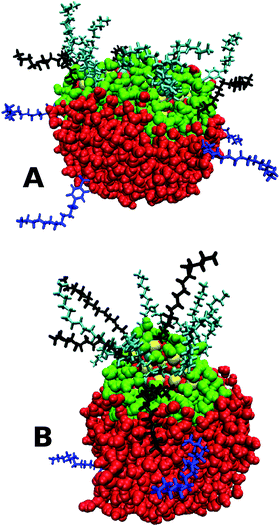 | ||
| Fig. 6 MD snapshots at the end of a 20 ns simulation of a sulphonate/stearate nanoparticle (PI = A, PII = B) and a representative water droplet, showing the dissociated surfactant molecules (in blue) from the core. The same colour scheme as Fig. 3 is used for the molecules. | ||
The spherical nanoparticle formed using PII does not penetrate as much into the water droplet compared to PI. Treating the entire NP as a single entity or an effective ‘molecule’, the total interaction energy between the NP and the water was −9600 kJ mol−1 for the sulphonate PI particle and −6400 kJ mol−1 for the PII particle, highlighting that more favourable interactions are made with the more penetrative rod-shaped particle. The time for immersion into the droplet is broadly similar for the two procedures after initial bridge formation (PI: 4 ns, PII: 3 ns). Adsorption of the PII CaCO3 core into the droplet occurred in only about one in five of the simulations, with approximately half the number of surfactants dissociated from the core compared to PI. Fig. 6B shows the fully immersed core alongside the dissociated sulphonate surfactants, and demonstrates the reduced penetration into the middle of the droplet.
The reduced frequency of successful dockings using the PII particles suggests that shape is both an important factor in the adsorption of overbased detergents and also the degree of penetration into the water droplet.
Such factors could have implications for the rate of reaction for such detergents. It is reasonable to assume that species which penetrate deeper and more frequently into water droplets will have an increased rate of reaction due to a larger reactive interface with the acid.53,54 This work has shown that molecular simulations could have potential in helping us to predict surfactants which form more water-accessible nanoparticles, which will be more reactive.
4. Conclusions
This work builds on previous molecular simulations by some of us which concluded that the shape and size of nanoparticles can be controlled by the choice of stabilising surfactant type.18 The MD simulations carried out here suggest that stearate acting as a co-surfactant in the synthesis of overbased detergents causes a major change in particle shape, and potentially reactivity as an acid neutralisation agent. This co-surfactant induces a normally near-spherical nanoparticle to adopt a rod-like shape, whose dimensions are less dependent on the chemical formula of the surfactant stabiliser than is the case for nanoparticles formed without the stearate additional component. Although these are not typical micellar systems, in having a solid core with specific surfactant binding criteria, the classical literature description and the explanation of the influence of a cosurfactant as causing a uniform ‘swelling’ of a micelle does not appear to be applicable to this class of nanoparticles. The transformation into a more rod shaped structure could affect its diffusional behaviour in the oil of an automotive or marine engine and even perhaps the rate of reaction with acid in water droplets found therein. When exposed to a model water droplet, incorporated in the computer model as a new feature, the stearate co-surfactants were found to dissociate from the core, thereby allowing the nanoparticle to absorb deeper into the droplet where the core ions on the surface can interact energetically favourably with the water molecules. Previous simulations18 only investigated the effects of trace water on the carbonate core, and not with a similarly sized water droplet to the nanoparticle. These simulations are therefore the first of their kind and are a significant step towards the molecular modelling of the overbased detergent function in a realistic chemical environment.The results corroborate the experimentally-derived hypothesis which relates the strength of nanoparticle–water association to surfactant dissociation onto the surface of the water droplet during this process. The reduced water penetration of a more spherical particle (formed here by adding stearate late in the self-assembly process) suggests that the shape of the nanoparticle is an important factor in governing the mechanism and kinetics of the assocation process of the overbased particle with bulk water, as a precursor to the process of acid neutralisation. It is reasonable to assume that nanoparticles which adsorb deeper into a water droplet will exhibit faster reaction times because of the greater exposure of the core to any acid in the water.
Such studies may ultimately help us to identify promising chemical compositions for overbased detergents which have reduced sulphur content and favourable neutralisation kinetics tailored to the demands of specfic types of engine operation.
Acknowledgements
M.S.B. thanks BP for the award of a Research Fellowship.References
- J. H. Harding and D. M. Duffy, J. Mater. Chem., 2005, 16, 1105–1112 RSC.
- Y. Ueno, H. Futagawa, Y. Takagi, A. Ueno and Y. Mizushima, J. Controlled Release, 2005, 103, 93–98 CrossRef CAS PubMed.
- D. Shan, M. Zhu, H. Xue and S. Cosnier, Biosens. Bioelectron., 2007, 22, 1612–1617 CrossRef CAS PubMed.
- U. Aschauer, D. Spagnoli, P. Bowen and S. C. Parker, J. Colloid Interface Sci., 2010, 346, 226–231 CrossRef CAS PubMed.
- C. Y. Tai and C.-K. Chen, Chem. Eng. Sci., 2008, 63, 3632–3642 CrossRef CAS PubMed.
- W. L. Noorduin, A. Grinthal, L. Mahadevan and J. Aizenberg, Science, 2013, 340, 832–837 CrossRef CAS PubMed.
- J. B. F. N. Engberts and J. Kevelam, Curr. Opin. Colloid Interface Sci., 1996, 1, 779–789 CrossRef CAS.
- M.-P. Pileni, Nat. Mater., 2003, 2, 145–150 CrossRef CAS PubMed.
- F. Rauscher, P. Veit and K. Sundmacher, Colloids. Surf., A, 2005, 254, 183–191 CrossRef CAS PubMed.
- C. L. Lee, P. J. Dowding, A. R. Doyle, K. M. Bakker, S. S. Lam, S. E. Rogers and A. F. Routh, Langmuir, 2013, 13, 14763–14771 CrossRef PubMed.
- J. A. Griffiths, R. Bolton, D. M. Heyes, J. H. Clint and S. E. Taylor, J. Chem. Soc., Faraday Trans., 1995, 91, 687–696 RSC.
- J. A. Griffiths and D. M. Heyes, Langmuir, 1996, 12, 2418–2424 CrossRef CAS.
- C. A. Bearchell, D. M. Heyes, D. J. Moreton and S. E. Taylor, Phys. Chem. Chem. Phys., 2001, 3, 4774–4783 RSC.
- C. A. Bearchell, J. A. Edgar, D. M. Heyes and S. E. Taylor, J. Colloid Interface Sci., 1999, 210, 231–240 CrossRef CAS PubMed.
- C. Bearchell, T. Danks, D. M. Heyes, D. J. Moreton and S. E. Taylor, Phys. Chem. Chem. Phys., 2000, 2, 5197–5207 RSC.
- J. N. Israelachvilli, Intermolecular and Surface Forces, Academic Press, London and New York, 2nd edn, 1991 Search PubMed.
- EMSA, The 0.1 sulphur in fuel requirement as from 1 January 2015 in SECAs, Lisbon, 2010 Search PubMed.
- M. S. Bodnarchuk, D. M. Heyes, D. Dini, S. Chahine and S. Edwards, J. Phys. Chem. C, 2014, 118, 21092–21103 CAS.
- D. M. Duffy and J. H. Harding, J. Mater. Chem., 2002, 12, 3419–3425 RSC.
- D. M. Duffy and J. H. Harding, Langmuir, 2004, 20, 7637–7642 CrossRef CAS PubMed.
- D. M. Duffy and J. H. Harding, Surf. Sci., 2005, 595, 151–156 CrossRef CAS PubMed.
- C. L. Freeman, J. H. Harding and D. M. Duffy, Langmuir, 2008, 24, 9607–9615 CrossRef CAS PubMed.
- D. Quigley, P. M. Rodger, C. L. Freeman, J. H. Harding and D. M. Duffy, J. Chem. Phys., 2008, 131, 094703 CrossRef PubMed.
- J. P. Allen, A. Marmier and S. C. Parker, J. Phys. Chem. C, 2012, 116, 13240–13251 CAS.
- J. P. Allen, S. C. Parker and M. S. D. Read, Geochim. Cosmochim. Acta, 2009, 73, A29 Search PubMed.
- J. P. Allen, S. C. Parker and D. W. Price, Geochim. Cosmochim. Acta, 2008, 72, A16 Search PubMed.
- V. Bakunin, A. Suslov, G. Kuzmina, O. Parenago and A. Topchiev, J. Nanopart. Res., 2004, 6, 273–284 CrossRef CAS.
- L. K. Hudson, J. Eastoe and P. J. Dowding, Adv. Colloid Interface Sci., 2006, 123–126, 425–431 CrossRef CAS PubMed.
- B. Niemann, F. Rauscher, D. Adityawarman, K. Voigt and A. Sundmacher, Chem. Eng. Process., 2006, 45, 917–935 CrossRef CAS PubMed.
- D. Quigley and P. M. Rodger, J. Chem. Phys., 2008, 128, 221101 CrossRef CAS PubMed.
- F. Nudelman, E. Sonmezler, P. H. H. Bomans, G. de With and N. A. J. M. Sommerdijk, Nanoscale, 2010, 2, 2436–2439 RSC.
- D. Liu, M. Zhang, G. Zhao and X. Wang, Tribol. Lett., 2011, 45, 265–273 CrossRef.
- F. Gilberti, G. A. Tribello and M. Parrinello, J. Chem. Theory Comput., 2013, 9, 2526–2530 CrossRef.
- A. Tomlinson, T. N. Danks, D. M. Heyes, S. E. Taylor and D. J. Moreton, Langmuir, 1997, 13, 5881–5893 CrossRef CAS.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037 CrossRef CAS.
- S. Canzar, M. El-Kebir, R. Pool, K. Elbassioni, A. E. Mark, D. P. Geerke, L. Stougie and G. W. Klau, J. Comput. Biol., 2013, 20, 188–198 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS PubMed.
- S. Migamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- L. V. Woodcock, Chem. Phys. Lett., 1971, 10, 257–261 CrossRef CAS.
- S. Nosé, Prog. Theor. Phys. Suppl., 1991, 103, 1–46 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS PubMed.
- N. Cooper, A. Tedder, D. M. Heyes and J. R. Melrose, J. Phys.: Condens. Matter, 1989, 1, 6217–6230 CrossRef.
- J. Rudnick and G. Gaspari, J. Phys. A: Math. Gen., 1986, 19, L191–L193 CrossRef.
- J. Rudnick and G. Gaspari, Science, 1987, 237, 384–389 CAS.
- J. J. H. Nusselder and J. B. F. N. Engberts, J. Org. Chem., 1991, 56, 5522–5527 CrossRef CAS.
- J. N. Israelachvili, D. J. Mitchell and B. J. Ninham, J. Chem. Soc., Faraday Trans., 1976, 2, 1525–1568 RSC.
- R. C. Wu, C. B. Campbell and K. D. Papadopoulos, Ind. Eng. Chem. Res., 2000, 39, 3926–3931 CrossRef CAS.
- R. C. Wu, K. D. Papadopoulos and C. B. Campbell, AIChE J., 2000, 46, 1471–1477 CrossRef CAS PubMed.
- J. Fu, Y. Lu, C. B. Campbell and K. D. Papadopoulos, Ind. Eng. Chem. Res., 2006, 45, 5619–5627 CrossRef CAS.
- J. Fu, Y. Lu, C. B. Campbell and K. D. Papadopoulos, Tribol. Lett., 2006, 22, 221–225 CrossRef CAS.
- R. Aveyard, B. D. Beake and J. H. Clint, J. Chem. Soc., Faraday Trans., 1996, 92, 4271–4277 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp00428d |
| This journal is © the Owner Societies 2015 |