Theoretical analysis of [5.5.6]cyclacenes: electronic properties, strain energies and substituent effects

Abstract

A novel class of cyclic conjugated molecules, composed of annelated five- and six-membered rings, is proposed and theoretically investigated using density functional theory and multireference methods with regards to their structures, strain energies, aromaticity (NICS values), electronic ground states, band gaps, and the effect of substituents. These [5.5.6]_ncyclacenes are predicted to be low band gap materials (below 1 eV) with, depending on their size, closed-shell singlet ground states. The strain energies from n = 4 upwards lie in the range of the synthetically known [n]cycloparaphenylenes. An investigation of the effect of rim-substitution by methyl, alkynyl, thiomethyl or phenyl groups on the electronic ground states showed that thiomethyl-substitution leads to [5.5.6]_ncyclacenes with closed-shell singlet ground states for all sizes n investigated.

---

Introduction

Hoop-shaped molecules, consisting of linearly connected or annelated conjugated rings, have attracted chemists since 1954.¹ Of particular interest are their potentially aromatic character, their conjugative and optoelectronic properties, and their use in host–guest chemistry.^2–13 Prominent examples are [6]_ncyclacenes (1_n), which can be regarded as subunits of zig-zag carbon nanotubes (CNTs) as well as cyclo[n]phenacenes (2_n) and [n]cycloparaphenylenes ([n]CPPs) (3_n) as subunits of armchair CNTs (Fig. 1). While a derivative of cyclo[10]phenacene^14,15 and several [n]CPPs^7,16–33 have been synthesized, [6]_ncyclacenes (1_n) have remained elusive to synthesis up to date.^{2,5–7,34–45} The reason for this is likely found in their electronic character: [6]_ncyclacenes, which have been the subject of a number of theoretical investigations,^46–55 are predicted to possess open-shell singlet diradical ground states,⁵² while for cyclo[n]phenacenes (2_n) large singlet–triplet splittings are expected.⁵⁶ This difference in stability can, according to Clar,⁵⁷ be deduced from the number of aromatic sextets that can be drawn: none for 1_n and n for 2_n, resulting in a significantly higher stability for 2_n. Alternative structures to 1_n consisting of not only six- but also five- to eight-membered rings have been proposed and in few cases synthesized. [6.8]₃Cyclacene (4)^58–60 and several derivatives of [4.8]₃cyclacenes (5)^61–63 could be synthesized, and [5.7]_ncyclacenes⁶⁴ as isomers of 1_n were proposed and predicted to possess closed-shell singlet ground states. Cyclacenes consisting of annelated five- and six-membered rings have not been investigated yet, although this combination of ring sizes is prevalent in graphitic materials such as fullerenes and the end-caps of CNTs and in optoelectronic materials.^65–67 Herein, [5.5.6]_ncyclacenes (6_n) are proposed as a new cyclacene family and investigated with regards to their structures, strain energies, aromaticity, electronic ground states, band gaps, and the effect of substituents. In cyclacenes 6_n, an aromatic sextet can be drawn in every six-membered ring, thereby indicating that a high stability can be anticipated.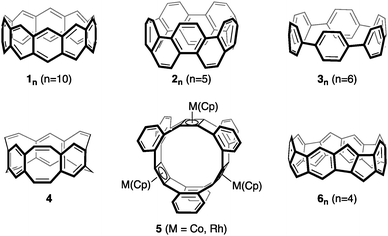

Fig. 1 [6]₁₀Cyclacene (1₁₀), cyclo[10]phenacene (2₅), [6]cycloparaphenylene (3₆), [6.8]₃cyclacene (4), (Cp)M-capped [4.8]₃cyclacene derivatives 5, and [5.5.6]₄cyclacene (6₄).

Results and discussion

Computational details

The geometries and strain energies of 6_n (n = 3–8) were calculated using density functional theory (DFT). The geometries and energies of triplet and open-shell singlet states were assessed using DFT and time-dependent DFT (TDDFT). For single-point energies a combination of complete active space self-consistent field (CASSCF)^68,69 calculations with second-order perturbation theory (CASPT2) was employed.⁷⁰ NMR chemical shifts for NICS (Nucleus Independent Chemical Shift)^71,72 values were calculated using the GIAO (Gauge Including Atomic Orbital)⁷³ method. All DFT calculations were performed with the Turbomole⁷⁴ program package including D3⁷⁵ and using the resolution-of-identity (RI) approximation.^76,77 CASSCF and CASPT2 calculations were done with Molpro.^78,79 All singlet and triplet geometries (6_n and 10_n–13_n) were first optimized using PBE⁸⁰-D3/def2-SVP⁸¹ followed by harmonic vibrational frequency analyses to confirm minima as stationary points. The structures were then re-optimized using TPSS⁸²-D3 or BP86^83–85-D3 in combination with the triple-ζ basis set def2-TZVP.⁸⁶

Geometries and strain energies

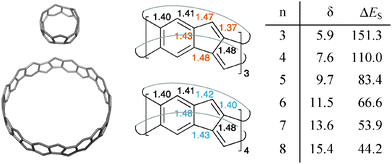
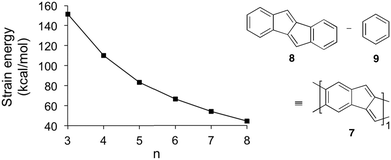
The [5.5.6]_ncyclacenes (6_n) (n = 3–8, optimized using TPSS-D3/def2-TZVP in C₁ symmetries) all possess almost perfect D_n symmetrical structures. Bond lengths of 6₃ and 6₄ as representative examples and diameters of 6_n are listed in Fig. 2. The strain energy of hoop-shaped molecules is an important parameter and can present a challenge to their synthesis. For [5.5.6]_ncyclacenes (6_n), strain energies were estimated by comparison with the hypothetical strain-free subunit 7 at the TPSS-D3/def2-TZVP level of theory (Fig. 3).

Fig. 2 Calculated structures of 6₃ and 6₈, bond lengths (Å) in 6₃ and 6₄, and diameters δ (Å) and strain energies ΔE_S (kcal mol⁻¹) of [5.5.6]_ncyclacenes (6_n) (TPSS-D3/def2-TZVP, optimized in point group C₁).

Fig. 3 Plot of strain energy vs. hoop size n of [5.5.6]_ncyclacenes (6_n) (TPSS-D3/def2-TZVP, optimized in point group C₁; strain energies were calculated by subtracting n-times the energy of 7 from the energy of 6_n) and homodesmotic equation used to calculate the energy of the strain-free subunit 7.

The energy of 7 was calculated using the homodesmotic equation shown in Fig. 3 as the energy difference between dibenzo[a,e]pentalene (DBP, 8) and benzene (9). Homodesmotic equations⁸⁷ have been used before to calculate strain energies of bent sp² hybridized structures.^60,64,88 Subtracting n-times the energy of 7 from the energy of cyclacene 6_n gives a measure of its strain energy.

With increasing hoop size the strain energies of [5.5.6]_ncyclacenes (6_n) decrease from 151 kcal mol⁻¹ for n = 3 to 44 kcal mol⁻¹ for n = 8 (Fig. 2 and 3). In order to set these values in relation to experimentally known compounds, a comparison with the well-investigated [n]CPPs (3_n) is suitable. For [6]CPP, which has been synthesized and is a stable compounds,^21,22 the strain energy was calculated according to Segawa et al.⁸⁸ to be 86 kcal mol⁻¹ (TPSS-D3/def2-TZVP), and recently the even smaller and more strained [5]CPP was synthesized.¹⁸ While for cyclacenes 6_n for n = 3 and 4 higher strain energies were calculated (110 kcal mol⁻¹ for 6₄), from n = 5 upwards (83 kcal mol⁻¹) the strain energies of cyclacenes 6_n lie well below that of [6]CPP.

An evaluation of the calculated bond lengths in [5.5.6]_ncyclacenes (6_n) shows that four of the bonds in the five-membered rings vary between odd and even numbers of n (colored values in Fig. 2). For odd n (6₃, 6₅, and 6₇), all bond lengths are similar to those in DBP (8, see ESI,† Table S1), displaying little bond lengths alternation in the six-membered rings and a short length for the double bond in the five-membered rings. This indicates the presence of an aromatic sextet in each phenyl ring. For even n (6₄, 6₆, and 6₈), both “transannular” bonds, connecting the top and bottom rim of the cyclacenes, are relatively long (1.48 Å), formally resulting in two conjugated annulenes with equalized bond lengths between 1.40 and 1.43 Å connected by transannular (single) bonds.

Aromatic character

NICS values were calculated (B3LYP^89,90/def2-QZVP⁹¹ on TPSS-D3/def2-TZVP optimized geometries) to assess the aromatic character of cyclacenes 6_n (Table 1). Strongly positive values denote antiaromaticity, while significantly negative values point towards aromaticity.^71,72 As location the geometrical centers of the molecules were chosen as well as a point 1 Å above the center of the individual five- and six-membered rings (NICS(1)).^71,72 The NICS values vary between odd and even numbers of n: at the center of 6_n, the NICS values are slightly positive for odd n, while for even n strongly negative NICS values are found. For odd n, the NICS(1) values above the five- and six-membered rings adopt values similar to those of DBP (8, Table 1) and show only small variations with increasing hoop size. The absolute NICS(1) values above the six-membered rings are small for both odd and even n, giving no clear indication of aromaticity. The NICS(1) values above the five-membered rings are slightly larger in absolute value, but adopt a significant value only for n = 8 (11.2), indicating some degree of antiaromaticity. Hence, for odd sizes of n the NICS values indicate properties similar to DBP (8), which is a stable compound in spite of its electron count (16π electrons).

Table 1 NICS values^a of cyclacenes 6_n and dibenzopentalene (8)

a B3LYP/def2-QZVP//TPSS-D3/def2-TZVP. b NICS value in the center of the molecule. c NICS(1) 1 Å above the 5-membered ring. d NICS(1) 1 Å above the 6-membered ring (both outside the hoop).

---

Electronic ground states

Next the electronic ground states of [5.5.6]_ncyclacenes (6_n) were investigated. Since [6]_ncyclacenes (1_n) were predicted to possess open-shell singlet diradical ground states,⁵² which likely inhibited their synthesis up to date,^{2,5–7,34–44} the stability of both the triplet and open-shell singlet relative to the closed-shell singlet states in cyclacenes 6_n is of interest. In order to increase computational speed, and since the optimized structures of cyclacenes 6_n showed almost perfect D_n symmetries, their geometries were re-optimized in the respective D_n point group using TPSS-D3 and BP86-D3 in combination with def2-TZVP. The energy differences between structures optimized in C₁ and in D_n symmetry were minimal.

To assess whether DFT, which is based on a single-reference configuration, is appropriate to describe the electronic states of [5.5.6]_ncyclacenes (6_n), single-point (SP) multireference CASSCF calculations were performed on the TPSS-D3/def2-TZVP-optimized geometries. For cyclacenes 6₃, 6₄, and 6₅, CASSCF(8,8)/def2-SVP calculations resulted in natural occupation numbers of the four highest occupied orbitals (see ESI,† Table S2) between 1.93 and 1.91 (n = 3), 1.94 to 1.83 (n = 4), and between 1.93 and 1.92 for n = 5. For [6]₆cyclacene (1₆) with a predicted open-shell singlet diradical ground state, the natural occupation numbers of the four highest occupied orbitals were calculated to be between 1.98 and 1.46 (CASSCF(8,8)/6-31G*), resulting in 0.76 electrons outside the closed-shell orbital space and indicating significant multi-configurational character of the singlet state.⁵² These values are significantly lower for [5.5.6]_ncyclacenes (6_n): 0.32 for 6₃, 0.44 for 6₄, and 0.29 for 6₅. Hence, for cyclacenes 6_n, the closed-shell orbital space is almost completely occupied, and a single-reference method such as DFT is considered appropriate.

The structures and energies of the triplet states (T) of cyclacenes 6_n were assessed through optimizations at the BP86-D3/def2-TZVP level of theory using unrestricted wavefunctions (UHF), and their energies were compared to the closed-shell singlet (CSS) states (Fig. 4, T-CSS, and Table 2). For all sizes investigated (n = 3–8), the triplet states are higher in energy than the CS singlet states at this level of theory. The energy differences decrease with increasing hoop size and assume rather small values (below 5 kcal mol⁻¹) for n = 6–8. A variation between odd and even numbers of n is observed, where for odd n the closed-shell singlets are more stabilized than for even n. This could be due to the total π electron count in 6_n resulting in (4m + 2) (odd n) or 4m π electrons (even n).

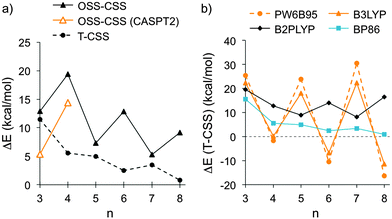Fig. 4 (a) Energy differences between open-shell and closed-shell singlet states (OSS-CSS), calculated using TDDFT (BP86-D3/def2-TZVP) or CASPT2/def2-SVP//TPSS-D3/def2-TZVP, and between triplet (T) and CSS states (BP86-D3/def2-TZVP) of cyclacenes 6_n; (b) energy differences between T and CSS states of 6_n calculated using different density functionals (functional-D3/def2-QZVP//TPSS-D3/def2-TZVP, see also Table 2).

Table 2 Energy differences (kcal mol⁻¹) between triplet (T) or open-shell singlet (OSS) and closed-shell singlet (CSS) states of [5.5.6]_ncyclacenes (6_n) and band gaps (eV)

n		3	4	5	6	7	8
a BP86-D3/def2-TZVP. b From TDDFT calculations. c CASPT2/def2-SVP//TPSS-D3/def2-TZVP. d Functional-D3/def2-QZVP//TPSS-D3/def2-TZVP. e Lowest energy singlet excitation.
ΔE (OSS-CSS)^a^,^b		12.9	19.4	7.3	12.8	5.3	9.1
ΔE (OSS-CSS)^c		5.3	14.4	—	—	—	—
ΔE (T-CSS)^a		11.4	5.5	5.0	2.5	3.5	0.8
ΔE (T-CSS)^d	PW6B95	25.3	−1.6	23.9	−10.5	30.5	−16.3
	B3LYP	22.4	0.1	18.1	−6.8	22.3	−11.4
	B2PLYP	19.5	12.7	8.9	14.0	8.1	16.4
	BP86	15.6	5.6	4.9	2.5	3.4	0.8
Band gap^a^,^b^,^e [eV]		0.72	0.60	0.44	0.35	0.33	0.22

---

The geometries and energies of the open-shell singlet (OSS) states of cyclacenes 6_n were assessed using TDDFT, and energies for n = 3 and 4 were also calculated at the CASPT2 level of theory. In attempted structure optimizations of the OSS states of cyclacenes 6_n using unrestricted wavefunctions (UHF), relaxation to the CSS states occurred. Hence, OSS energies were obtained through structural optimizations of the lowest excited singlet states using TDDFT with BP86-D3/def2-TZVP and compared to the CSS energies (Fig. 4, OSS-CSS, and Table 2). For all sizes investigated (n = 3–8), the open-shell singlet states are higher in energy than the closed-shell singlet as well as the triplet states. A variation between odd and even numbers of n is observed, but the trend is reversed compared to the triplet states. The reason for this is not clear, however, an odd–even variation in relative energies has also been found for [6]_ncyclacenes (1_n).^47,48,52 The SP energies of the CSS and OSS states of 6_n (n = 3 and 4) were also calculated using CASPT2/def2-SVP. In CASPT2, as opposed to CASSCF, dynamic electron correlation is included.⁹² As in the TDDFT calculations, the open-shell singlets have a higher energy then the closed-shell singlets (Fig. 4, OSS-CSS (CASPT2), and Table 2), but the energy differences are smaller. This result is not surprising, since it is known that the CASPT2 approximation overestimates the stabilization of biradical states.^93,94

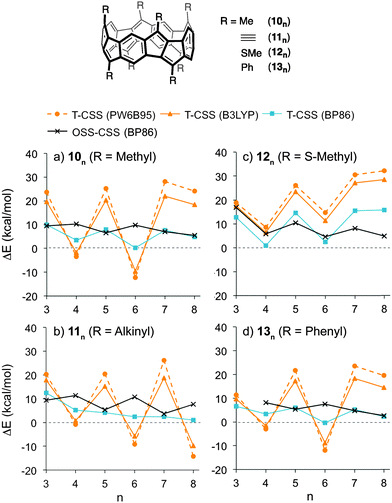
The assessment of the electronic states of [5.5.6]_ncyclacenes (6_n) shows that at the BP86-D3/def2-TZVP level of theory their ground states are closed-shell singlets. However, with increasing n the triplet states become more stabilized, and hence the question arose which ground states other density functionals would predict. For this investigation a variety of exchange–correlation functionals was chosen: the generalized gradient approximation (GGA) functional BP86, the meta-GGA functional TPSS, the hybrid GGA functionals BHLYP,⁹⁵ PW6B95,⁹⁶ PBE0,^97,98 and B3LYP, and the double-hybrid functional B2PLYP,⁹⁹ each in combination with the quadruple-ζ basis set def2-QZVP. SP energies of the singlet and triplet states of cyclacenes 6_n were calculated on the respective TPSS-D3/def2-TZVP-optimized D_n geometries. A comparison of the resulting T-CSS energy differences (Fig. 4, Table 2 and ESI,† Table S8) allows several conclusions: a variation between odd and even numbers of n is found for all types of functionals. Its extent increases with growing amount of exact (HF) exchange in the functional (0% HF exchange in BP86 and TPSS vs. 28% in PW6B95 and 50% in BHLYP). However, with B2PLYP, which in addition to a large amount (53%) of HF exchange employs perturbative second-order correlation (PT2), the preference for odd or even n is reversed compared to all other functionals employed.

As a result, all hybrid (GGA) functionals investigated predict closed-shell singlet ground states for odd 6_n with n = 3, 5, 7 and triplet ground states for n = 6, 8, while the (meta-)GGA functionals investigated predict a preference for the closed-shell singlet states for all n. According to the double-hybrid functional B2PLYP, which has been shown to outperform the other functionals employed,¹⁰⁰ the ground states of cyclacenes 6_n are closed-shell singlets for all n (3–8) with significant energy differences to the triplet states between 8 and 20 kcal mol⁻¹.

Band gaps

The band gaps of cyclacenes 6_n were estimated from TDDFT calculations as the excitation energies of the first singlet excited states (Table 2). This has been shown to give more accurate values than using the differences between the calculated HOMO and LUMO energies.¹⁰¹ The band gaps of [5.5.6]_ncyclacenes (6_n) decrease with growing hoop size from 0.72 eV (n = 3) to 0.22 eV (n = 8), classifying them as organic semiconductors with small band gaps. In comparison, the band gap for DBP (8) is 1.98 eV at the same level of theory. The frontier molecular orbitals of cyclacenes 6_n are predominantly localized on the pentalene units (Fig. 5). In the odd-membered cyclacenes 6_n (n = 3, 5, 7), HOMO and LUMO resemble their counterparts in DBP (8), while for even n (6₄, 6₆, and 6₈), the reverse is true: the HOMO resembles the LUMO in 8 and vice versa.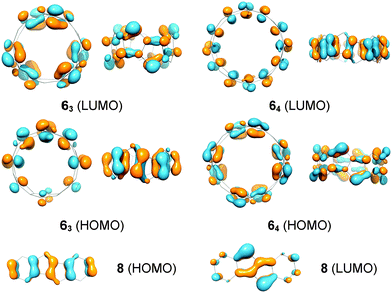

Fig. 5 Frontier molecular orbitals of [5.5.6]_ncyclacenes 6₃ and 6₄ and dibenzopentalene (8) (BP86-D3/def2-TZVP).

Substituent effects

The stability of the closed-shell singlets of [5.5.6]_ncyclacenes (6_n) showed a strong dependence on the density functional employed. Hence it was wondered whether substituents on the cyclacene rim would lead to a stronger preference for the CSS states. This effect has been investigated for linear acenes, where substituents, in particular thioaryl substituents, were shown to stabilize the closed-shell singlet ground state.¹⁰² In cyclacenes 6_n, substituents can be attached either on the five- or on the six-membered rings. Considering the orbital coefficients at the respective carbon atoms in the HOMO and LUMO (Fig. 5), the strongest electronic influence (larger coefficient) can be expected from substitution at the five-membered rings. As substituents, methyl, thiomethyl, alkynyl and phenyl were chosen (10_n–13_n, Fig. 6). The structures of 10_n–13_n were optimized in D_n symmetries (apart from 13₃ and the OSS of 10₃, for which minima were found only in C₁ symmetry) using TPSS-D3/def2-TZVP as well as BP86-D3/def2-TZVP. SP energies of the closed-shell singlets and triplets were calculated using the two hybrid functionals PW6B95 and B3LYP as well as the GGA functional BP86 in combination with def2-QZVP for 10_n–11_n and def2-TZVP for 12_n–13_n. OSS energies were calculated using TDDFT (BP86-D3/def2-TZVP).

Fig. 6 Energy differences between triplet (T) or open-shell singlet (OSS) and closed-shell singlet (CSS) states of substituted cyclacenes 10_n–13_n calculated with different density functionals (functional-D3/def2-QZVP (a, b) or def2-TZVP (c, d) on TPSS-D3/def2-TZVP-optimized geometries).

A comparison of the relative energies (Fig. 6 and ESI†) shows that for methyl (10_n), alkynyl (11_n) or phenyl (13_n) substituents, the T-CSS and OSS-CSS energies are similar to those of the unsubstituted cyclacenes 6_n (Fig. 4) (apart from n = 8 for 10_n and 13_n). Thiomethyl substituents (12_n), on the other hand, have a stabilizing effect on the CSS states. With all functionals investigated, the closed-shell singlet states of 12_n are more stable than the triplet or open-shell singlet states. Hence thiomethyl groups seem to be the best substituent in order to achieve electronically stable ground states.

Conclusions

In summary, [5.5.6]_ncyclacenes (6_n), composed of annelated five- and six-membered rings, have been proposed as a new cyclacene family and theoretically investigated with regards to their structures, strain energies, aromaticity, electronic ground states, band gaps, and the effect of substituents. Generally, a variation between odd and even numbers of n is observed. While in the unsubstituted cyclacenes 6_n for even numbers of n the calculated properties indicate structures with potentially antiaromatic character or low-lying diradical states, for odd n closed-shell singlet ground states are predicted and electronic properties similar to dibenzopentalene (8). For all sizes n, low bandgaps below 1 eV were found. An investigation of substituent effects on the electronic ground states showed that rim-substitution by thiomethyl groups leads to cyclacenes with closed-shell singlet ground states for all sizes n investigated. Hence cyclacenes 6_n or in particular their thiomethyl substituted derivatives 12_n are attractive synthetic targets, and studies towards their synthesis are currently underway in our laboratory.

Acknowledgements

B.E. thanks Prof. Stefan Grimme and Prof. Gebhard Haberhauer for helpful discussions and S. Grimme for usage of computational resources. Generous support by the German Research Foundation (Emmy Noether fellowship for B.E., ES 361/2-1) and the Chemical Industry Trust (Liebig Fellowship, Li 189/11) is gratefully acknowledged.

Notes and references

1. E. Heilbronner, Helv. Chim. Acta, 1954, 37, 921–935.
2. R. Gleiter, B. Esser and S. C. Kornmayer, Acc. Chem. Res., 2009, 42, 1108–1116.
3. L. T. Scott, Angew. Chem., 2003, 115, 4265–4267.
4. L. T. Scott, Angew. Chem., Int. Ed., 2003, 42, 4133–4135.
5. R. Gleiter, B. Hellbach, S. Gath and R. J. Schaller, Pure Appl. Chem., 2006, 78, 699–706.
6. K. Tahara and Y. Tobe, Chem. Rev., 2006, 106, 5274–5290.
7. P. J. Evans and R. Jasti, Top. Curr. Chem., 2014, 349, 249–290.
8. B. D. Steinberg and L. T. Scott, Angew. Chem., 2009, 121, 5504–5507.
9. B. D. Steinberg and L. T. Scott, Angew. Chem., Int. Ed., 2009, 48, 5400–5402.
10. Q. Ye and C. Chi, Chem. Mater., 2014, 26, 4046–4056.
11. K. Itami, Pure Appl. Chem., 2012, 84, 907–916.
12. R. Herges, Modern Cyclophane Chemistry, Wiley-VCH, Weinheim, 2004.
13. A. Schröder, H.-B. Mekelburger and F. Vögtle, Top. Curr. Chem., 1994, 172, 179–201.
14. E. Nakamura, K. Tahara, Y. Matsuo and M. Sawamura, J. Am. Chem. Soc., 2003, 125, 2834–2835.
15. Y. Matsuo, K. Tahara, M. Sawamura and E. Nakamura, J. Am. Chem. Soc., 2004, 126, 8725–8734.
16. R. Friederich, M. Nieger and F. Vögtle, Chem. Ber., 1993, 126, 1723–1732.
17. F. Sibbel, K. Matsui, Y. Segawa, A. Studer and K. Itami, Chem. Commun., 2014, 50, 954–956.
18. P. J. Evans, E. R. Darzi and R. Jasti, Nat. Chem., 2014, 6, 404–408.
19. E. R. Darzi, T. J. Sisto and R. Jasti, J. Org. Chem., 2012, 77, 6624–6628.
20. J. Xia, J. W. Bacon and R. Jasti, Chem. Sci., 2012, 3, 3018–3021.
21. J. Xia and R. Jasti, Angew. Chem., 2012, 124, 2524–2526.
22. J. Xia and R. Jasti, Angew. Chem., Int. Ed., 2012, 51, 2474–2476.
23. T. J. Sisto, M. R. Golder, E. S. Hirst and R. Jasti, J. Am. Chem. Soc., 2011, 133, 15800–15802.
24. T. Iwamoto, Y. Watanabe, Y. Sakamoto, T. Suzuki and S. Yamago, J. Am. Chem. Soc., 2011, 133, 8354–8361.
25. Y. Segawa, P. Šenel, S. Matsuura, H. Omachi and K. Itami, Chem. Lett., 2011, 40, 423–425.
26. Y. Segawa, S. Miyamoto, H. Omachi, S. Matsuura, P. Šenel, T. Sasamori, N. Tokitoh and K. Itami, Angew. Chem., Int. Ed., 2011, 50, 3244–3248.
27. S. Yamago, Y. Watanabe and T. Iwamoto, Angew. Chem., 2010, 122, 769–771.
28. S. Yamago, Y. Watanabe and T. Iwamoto, Angew. Chem., Int. Ed., 2010, 49, 757–759.
29. H. Omachi, S. Matsuura, Y. Segawa and K. Itami, Angew. Chem., 2010, 122, 10400–10403.
30. H. Omachi, S. Matsuura, Y. Segawa and K. Itami, Angew. Chem., Int. Ed., 2010, 49, 10202–10205.
31. H. Takaba, H. Omachi, Y. Yamamoto, J. Bouffard and K. Itami, Angew. Chem., 2009, 121, 6228–6232.
32. H. Takaba, H. Omachi, Y. Yamamoto, J. Bouffard and K. Itami, Angew. Chem., Int. Ed., 2009, 48, 6112–6116.
33. R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647.
34. D. Eisenberg, R. Shenhar and M. Rabinovitz, Chem. Soc. Rev., 2010, 39, 2879–2890.
35. C. Denekamp, A. Etinger, W. Amrein, A. Stanger, M. Stuparu and A. D. Schlüter, Chem. – Eur. J., 2008, 14, 1628–1637.
36. M. Stuparu, D. Lentz, H. Rüegger and A. D. Schlüter, Eur. J. Org. Chem., 2007, 88–100.
37. M. Stuparu, V. Gramlich, A. Stanger and A. D. Schlüter, J. Org. Chem., 2007, 72, 424–430.
38. W. D. Neudorff, D. Lentz, M. Anibarro and A. D. Schlüter, Chem. – Eur. J., 2003, 9, 2745–2757.
39. O. Kintzel, P. Luger, M. Weber and A.-D. Schlüter, Eur. J. Org. Chem., 1998, 99–105.
40. R. M. Cory and C. L. McPhail, Tetrahedron Lett., 1996, 37, 1987–1990.
41. R. M. Cory, C. L. McPhail, A. J. Dikmans and J. J. Vittal, Tetrahedron Lett., 1996, 37, 1983–1986.
42. P. R. Ashton, J. P. Mathias and F. J. Stoddart, Synthesis, 1993, 221–224.
43. P. R. Ashton, G. R. Brown, N. S. Isaacs, D. Giuffrida, F. H. Kohnke, J. P. Mathias, A. M. Z. Slawin, D. R. Smith, J. F. Stoddart and D. J. Williams, J. Am. Chem. Soc., 1992, 114, 6330–6353.
44. A. Godt, V. Enkelmann and A.-D. Schlüter, Angew. Chem., 1989, 101, 1704–1706.
45. A. Godt, V. Enkelmann and A.-D. Schlüter, Angew. Chem., Int. Ed. Engl., 1989, 28, 1680–1682.
46. J. Aihara, J. Chem. Soc., Perkin Trans. 2, 1994, 971–974.
47. H. S. Choi and K. S. Kim, Angew. Chem., 1999, 111, 2400–2402.
48. H. S. Choi and K. S. Kim, Angew. Chem., Int. Ed., 1999, 38, 2256–2258.
49. L. Türker, J. Mol. Struct.: THEOCHEM, 2000, 531, 333–337.
50. L. Türker, J. Mol. Struct.: THEOCHEM, 2001, 536, 235–241.
51. K. N. Houk, P. S. Lee and M. Nendel, J. Org. Chem., 2001, 66, 5517–5521.
52. Z. Chen, D. Jiang, X. Lu, H. F. Bettinger, S. Dai, P. von R. Schleyer and K. N. Houk, Org. Lett., 2007, 9, 5449–5452.
53. M. Z. Kassaee, H. Aref Rad and S. Soleimani Amiri, Monatsh. Chem., 2010, 141, 1313–1319.
54. D. Sadowsky, K. McNeill and C. J. Cramer, Faraday Discuss., 2010, 145, 507–521.
55. H. S. Rzepa, Chem. Rev., 2005, 105, 3697–3715.
56. Y. Matsuo, K. Tahara and E. Nakamura, Org. Lett., 2003, 5, 3181–3184.
57. E. Clar, The aromatic sextet, Wiley, New York, 1972.
58. B. Esser, F. Rominger and R. Gleiter, J. Am. Chem. Soc., 2008, 130, 6716–6717.
59. B. Esser, A. Bandyopadhyay, F. Rominger and R. Gleiter, Chem. – Eur. J., 2009, 15, 3368–3379.
60. B. Esser, J. A. Raskatov and R. Gleiter, Org. Lett., 2007, 9, 4037–4040.
61. B. Hellbach, F. Rominger and R. Gleiter, Angew. Chem., 2004, 116, 5970–5973.
62. B. Hellbach, F. Rominger and R. Gleiter, Angew. Chem., Int. Ed., 2004, 43, 5846–5849.
63. S. C. Kornmayer, B. Hellbach, F. Rominger and R. Gleiter, Chem. – Eur. J., 2009, 15, 3380–3389.
64. E. S. Hirst, F. Wang and R. Jasti, Org. Lett., 2011, 13, 6220–6223.
65. D. T. Chase, A. G. Fix, S. J. Kang, B. D. Rose, C. D. Weber, Y. Zhong, L. N. Zakharov, M. C. Lonergan, C. Nuckolls and M. M. Haley, J. Am. Chem. Soc., 2012, 134, 10349–10352.
66. J. D. Wood, J. L. Jellison, A. D. Finke, L. Wang and K. N. Plunkett, J. Am. Chem. Soc., 2012, 134, 15783–15789.
67. M. Nakano, I. Osaka, K. Takimiya and T. Koganezawa, J. Mater. Chem. C, 2014, 2, 64–70.
68. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063.
69. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267.
70. P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557.
71. P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
72. P. von R. Schleyer, J. Jiao, N. J. R. van E. Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670.
73. M. Häser, R. Ahlrichs, H. P. Baron, P. Weis and H. Horn, Theor. Chim. Acta, 1992, 83, 455–470.
74. R. Ahlrichs, M. Bär, H. Marco, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 (TURBOMOLE, University of Karlsruhe, Germany, 2012, http://www.turbomole.com).
75. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
76. K. Eichkorn, O. Treutler, H. Öhm, H. Marco and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.
77. K. Eichkorn, O. Treutler, H. Öhm, H. Marco and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660.
78. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
79. MOLPRO, Version 2012.1, a package of ab initio programs. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and others, 2012.
80. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
81. A. Schaäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
82. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
83. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
84. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
85. J. P. Perdew, Phys. Rev. B, 1986, 34, 7406.
86. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
87. IUPAC, Compendium of Chemical Terminology (the “Gold Book”), Blackwell Scientific Publications, Oxford, 2nd edn, 1997.
88. Y. Segawa, H. Omachi and K. Itami, Org. Lett., 2010, 12, 2262–2265.
89. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
90. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
91. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
92. W. T. Borden and E. R. Davidson, Acc. Chem. Res., 1996, 29, 67–75.
93. G. Haberhauer and R. Gleiter, J. Am. Chem. Soc., 1999, 121, 4664–4668.
94. G. Haberhauer and R. Gleiter, J. Am. Chem. Soc., 2013, 135, 8022–8030.
95. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
96. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667.
97. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
98. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
99. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
100. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
101. G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561.
102. I. Kaur, W. Jia, R. P. Kopreski, S. Selvarasah, M. R. Dokmeci, C. Pramanik, N. E. McGruer and G. P. Miller, J. Am. Chem. Soc., 2008, 130, 16274–16286.

---

Footnotes

† Electronic supplementary information (ESI) available: Computational details including total energies, Cartesian coordinates, and geometrical parameters. See DOI: 10.1039/c5cp00341e

‡ Current address: Institut für Organische Chemie, Albert-Ludwigs-Universität Freiburg, Albertstr. 21, 79104 Freiburg, Germany. E-mail: E-mail: besser@oc.uni-freiburg.de.

---