Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Surface controlled reduction kinetics of nominally undoped polycrystalline CeO2
Nicole
Knoblauch
a,
Lars
Dörrer
b,
Peter
Fielitz
*b,
Martin
Schmücker
a and
Günter
Borchardt
b
aDeutsches Zentrum für Luft- und Raumfahrt, Institut für Werkstoff-Forschung, Linder Höhe, D-51147 Köln, Germany
bTechnische Universität Clausthal, Institut für Metallurgie, Robert-Koch-Str. 42, D-38678 Clausthal-Zellerfeld, Germany. E-mail: peter.fielitz@tu-clausthal.de
First published on 20th January 2015
Abstract
Ceria is an interesting material for high temperature redox applications like solar-thermal splitting of CO2 and H2O. Technical implementation and reactor design for solar-thermal redox-based fuel generation requires reliable data for the chemical surface exchange coefficient and the chemical diffusivity of oxygen. The results of thermogravimetric relaxation experiments and equilibrium oxygen isotope exchange experiments with subsequent depth profiling analysis suggest that the reduction reaction of even dense samples of pure ceria (1 mm thickness, 93% of theoretical density) with a grain size of about 20 μm is surface reaction controlled. The chemical surface exchange coefficient exhibits a negative apparent activation energy (−64 kJ mol−1). This finding is corroborated by similar data from literature for the tracer surface exchange coefficient. The structure of the derived expression for the apparent activation energy further suggests that the chemical surface exchange coefficient should show only a very weak dependence on temperature for ceria doped with lower valence cations.
1 Introduction
Non-stoichiometric ceria is a promising redox material for water and CO2 splitting not only because of suitable thermodynamics but also because of beneficial reaction kinetics. The H2O/CO2-splitting cycle consists of two thermochemical reactions,1 a high-temperature reduction step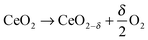 | (1) |
| CeO2−δ + δH2O(g) → CeO2 + δH2(g) | (2a) |
| CeO2−δ + δCO2(g) → CeO2 + δCO(g) | (2b) |
Reduction of CeO2 occurs at elevated temperatures and/or low oxygen partial pressure by the formation of oxygen vacancies as a consequence of gradual oxygen release. Resulting non-stoichiometric ceria is characterized by the suboxide parameter δ determined by applied T/pO2 conditions (1). Subsequent re-oxidation of CeO2−δ in the presence of H2O and/or CO2 according to eqn (2a) and (b) causes H2O/CO2 splitting and hence H2 and/or CO release.
A deeper insight into mechanisms and kinetics of ceria reduction and re-oxidation is required in view of future technical realization. In general, redox kinetics of ceria is either controlled by surface exchange reactions or by bulk transport of oxygen. Previous studies of the reaction kinetics comprise oxygen isotope exchange in chemical equilibrium and relaxation experiments based on oxygen potential changes. Depending on the microstructure of the sample material used in the different studies, the respective authors derived surface exchange coefficients, K, or diffusivities, D, of oxygen, or both of them.2–10 There is also comprehensive literature on the general relation between the tracer parameters, K* and D*, and the corresponding chemical parameters, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) and
and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (see, e.g., Maier11 and references therein) or on the tracer surface exchange coefficient, K* (see, e.g. De Souza,12 Armstrong et al.13), which evoke, however, some controversies as to the meaning of the obtained parameters, especially with respect to the transport regime characterized by a characteristic thickness lc = D/K.14 Especially chemical relaxation experiments are sometimes difficult to categorize with respect to the reaction regime as both
(see, e.g., Maier11 and references therein) or on the tracer surface exchange coefficient, K* (see, e.g. De Souza,12 Armstrong et al.13), which evoke, however, some controversies as to the meaning of the obtained parameters, especially with respect to the transport regime characterized by a characteristic thickness lc = D/K.14 Especially chemical relaxation experiments are sometimes difficult to categorize with respect to the reaction regime as both ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) and
and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) depend on the oxygen activity (which changes with time during the experiment).
depend on the oxygen activity (which changes with time during the experiment).
Further, due to the high (chemical) diffusivity of oxygen in nominally undoped (as well as in appropriately doped) ceria the surface exchange regime should not be excluded a priori even for fairly dense samples (>90% of theoretical density) for the high temperature reduction step. This position will be elaborated in the following section for both the reduction and the (re)oxidation step simultaneously as the phenomenological treatment is the same. The conclusions will then be applied in Sections 3 and 4 to the reduction step of a prototype chemical relaxation experiment (thermogravimetric analysis, TGA) in combination with a prototype equilibrium tracer isotope exchange experiment. The interpretation of the data will partially rely on supporting evidence from the literature.
2 Mathematical modelling
In this section we will mathematically model the kinetics of reduction–oxidation processes of solid oxides in a narrow oxygen potential range. For that, we assume, in a first approximation, that it is sufficient to model the reduction–oxidation process by two constant parameters![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) and
and ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) which depend only on temperature, where
which depend only on temperature, where ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) is an effective chemical oxygen diffusion coefficient and
is an effective chemical oxygen diffusion coefficient and ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) an effective chemical surface exchange coefficient of oxygen at the gas/solid interface. For convenience we simply refer in this chapter to
an effective chemical surface exchange coefficient of oxygen at the gas/solid interface. For convenience we simply refer in this chapter to ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) as oxygen diffusion coefficient and to
as oxygen diffusion coefficient and to ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) as surface exchange coefficient of oxygen and we use in the equations (D,K) instead of (
as surface exchange coefficient of oxygen and we use in the equations (D,K) instead of (![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ,
,![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ). The advantage of such a simple model is that it allows one to derive analytical solutions which yield significant insight into the role the microstructure of a given material has on the overall kinetics of the reduction–oxidation process.
). The advantage of such a simple model is that it allows one to derive analytical solutions which yield significant insight into the role the microstructure of a given material has on the overall kinetics of the reduction–oxidation process.
2.1 Reduction–oxidation kinetics of a sphere
Reduction–oxidation experiments are often performed with powders, which are characterised by an average diameter of the powder particles, so that it is useful to model the reduction–oxidation kinetics of a sphere of radius R. Solving the diffusion equation in the case of radial diffusion and constant diffusion coefficient, D, and considering a constant oxygen surface exchange coefficient, K, at the gas/solid interface the relative mass change of a sphere during the reduction–oxidation process is given by Crank15 (p. 96)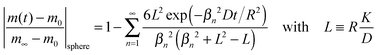 | (3) |
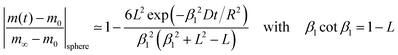 | (4) |
The characteristic time constant of the relative mass change of the sphere is, therefore, given by
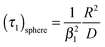 | (5) |
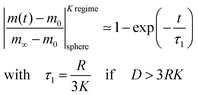 | (6) |
This equation describes the kinetics of the surface exchange regime which is controlled by the surface exchange coefficient, K, of oxygen. This regime is generally reached if the radius of the grains becomes sufficiently small. The factor 3 in the condition D > 3RK was graphically estimated (see L = RK/D < 0.3 in Fig. 1).
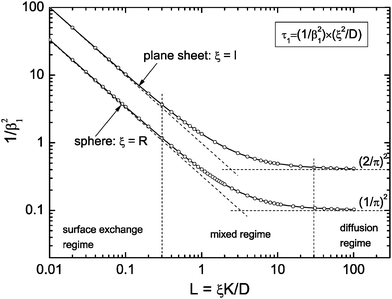 | ||
| Fig. 1 Graphical representation of the term 1/β12 of eqn (5) or (10), respectively. Open points are first roots of βn cot βn = 1 − L and βn tan βn = L, respectively, which are tabulated by Carslaw and Jaeger16 (pp. 491–492). | ||
In the mixed regime (see 0.3 ≤ L ≤ 30 in Fig. 1) the observed kinetics of the reduction–oxidation process is influenced by contributions of both parameters K and D. For sufficiently large spheres the dimensionless parameter L in Fig. 1 becomes sufficiently large (at about L > 30) so that one has β12 ≃ π2. In this case eqn (4) and (5) simplify
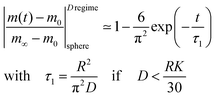 | (7) |
In contrast to eqn (6) this approximation will become inadequate for very short times (one gets 1–6/π2 = 0.39 instead of zero for t = 0). However, as demonstrated in Section 2.3, eqn (7) will be practically applicable if one monitors the time dependence of the reduction–oxidation process up to equilibrium (practically at t > 5·τ1).
2.2 Reduction–oxidation kinetics of a plane sheet
We now consider a plane sheet of thickness h = 2l in which oxygen can leave/penetrate both surfaces in the reduction–oxidation step. This geometry is often a good approximation if powder is pressed and then sintered to dense samples. Solving the diffusion equation in the case of one-dimensional diffusion and constant diffusion coefficient, D, and considering a constant oxygen surface exchange coefficient, K, at the gas/solid interface one obtains for the relative mass change of a plane sheet during the reduction–oxidation process (Crank15 p. 60)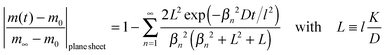 | (8) |
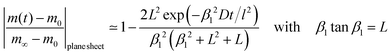 | (9) |
That is, a characteristic time constant of the relative mass change of a plane sheet is given by
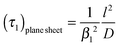 | (10) |
A graphical representation of the term 1/β12 of eqn (10) is presented in Fig. 1. Analogous to the discussion in Section 2.1 one can consider the surface exchange regime which is practically reached for values L < 0.3 so that one has the simple relation β12 ≃ L (see also Appendix A). In this case eqn (9) and (10) simplify
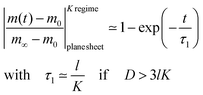 | (11) |
The surface exchange controlled regime is generally reached for sufficiently thin sheets. For sufficiently thick sheets the diffusion controlled regime in Fig. 1 is reached (at about L > 30) so that one has β12 ≃ π2/4. In the diffusion controlled regime eqn (9) simplifies
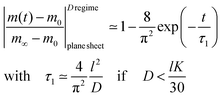 | (12) |
2.3 Application of the approximate solutions as fit equations
To test the accuracy of the approximate equations we calculated the normalized mass change data with the aid of the exact eqn (3) and (8) using Maple software (Waterloo Maple Inc., Canada). For that the first six roots of βn tan βn = L and βn cot βn = 1 − L were used which are tabulated by Carslaw and Jaeger16 (p. 491–492). The calculated data were then fitted by Origin software (OriginLab Inc., USA) using this fit equation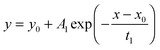 | (13) |
As discussed above (see remarks related to eqn (7)) one can conclude that in the diffusion controlled regime the approximate solutions will not work for very short times (t ≪ τ1). However, in this paper we discuss the kinetics of a reduction–oxidation process which is typically monitored until equilibrium is reached. In Fig. 2 we tested the approximate solution (fit eqn (13)) for this case. If one simply fits eqn (13) to the complete calculated data set one can expect an error of the evaluated time constant of about 17% in the case of the sphere and about 5% in the case of the plane sheet. However, if one excludes short time data one gets significantly more accurate fit values for the time constants. In Fig. 2a (sphere) all data in the range 0 ≤ y ≤ ystart = 0.5 were excluded during a second fitting procedure. One can see that the fit becomes significantly better now and that the error of the evaluated time constant is reduced to about 5% which is practically acceptable. The same strategy (excluding short time data from the fitting procedure) leads in the case of a plane sheet even to an accuracy of 0.2% (see fit #2 in Fig. 2b).
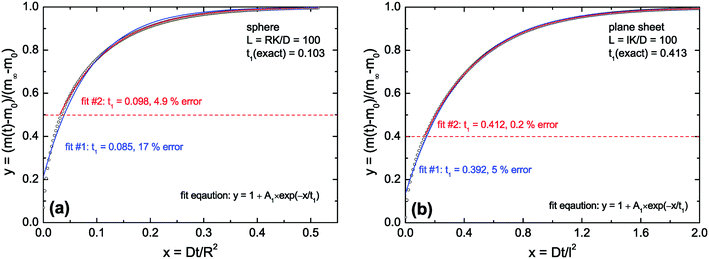 | ||
| Fig. 2 Open points are calculated values for L = 100 (diffusion controlled regime). In (a) eqn (3) was used and in (b) eqn (8) was used (the first six roots in both cases). Fit #1: The complete set of calculated data was fitted by eqn (13). Fit #2: All calculated data in the range 0 ≤ y ≤ ystart were excluded from the fitting procedure, with ystart = 0.5 in the case of a sphere (a) and ystart = 0.4 in the case of a plane sheet (b). | ||
Fig. 3 shows the dependence of the error of the evaluated time constant if the range 0 ≤ y ≤ ystart is excluded during the fitting procedure. One can see that one gets in the case of a plane sheet very accurate time constants if one excludes the data range 0 ≤ y ≤ ystart = 0.3 from fitting. However, in the case of a sphere the same strategy leads to an error of about 10%. To reduce the error to about 5% one must exclude the data range 0 ≤ y ≤ ystart = 0.5 from the fitting procedure. One could argue that this result makes the discussed approximate solutions unusable for spheres. However, one has to keep in mind that we consider typically spheres of microscopic dimensions where one can expect lower values than L = 100 (diffusion controlled regime). Fig. 3 shows that in the mixed regime (L = 5) the accuracy is about 3% if one excludes the data range 0 ≤ y ≤ ystart = 0.3 from fitting. That is, the exclusion of short time data from the fitting procedure with fit eqn (13) is generally a good strategy to evaluate time constants with practically sufficient accuracy.
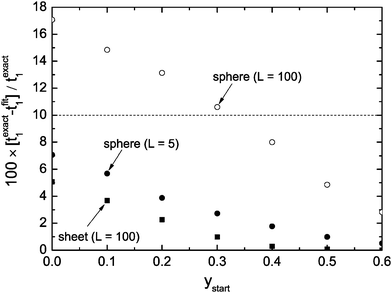 | ||
| Fig. 3 Percentage error of the evaluated time constants, t1, if one excludes the range 0 ≤ y ≤ ystart from the fitting procedure. | ||
2.4 Reduction–oxidation kinetics of polycrystalline solids in the A regime
Powders are pressed into any desired form to produce macroscopic bodies and then sintered at high temperatures to polycrystalline solids. The oxygen transport, and hence, the reduction–oxidation kinetics, of a polycrystalline solid is influenced at least by 4 parameters: In the single crystalline grains of average radius R oxygen is transported with the bulk diffusivity D. In the grain boundaries oxygen is typically transported significantly faster with the grain boundary diffusivity Dgb. The average width of the grain boundaries is taken into account by the parameter ω.The mathematical treatment of grain boundary diffusion is described comprehensively by Kaur et al.19 In the A regime mathematical modelling is significantly simplified because a polycrystalline solid behaves in this regime like a homogeneous medium with some effective diffusivity, Deff, which is given by the Hart–Mortlock equation20,21
| Deff = sgDgb + (1 − sg)D | (14) |
The A regime is reached after the annealing time tA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) regime if the characteristic diffusion depth into the grain is much larger than the mean grain size (2R) of the polycrystalline solid (Kaur et al.19 p. 210) so that one has
regime if the characteristic diffusion depth into the grain is much larger than the mean grain size (2R) of the polycrystalline solid (Kaur et al.19 p. 210) so that one has
 | (15) |
That is, for annealing times t > tA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) regime the reduction–oxidation kinetics of a polycrystalline solid can be modelled like in Sections 2.1 and 2.2 if one replaces D by Deff (defined by eqn (14)) in the corresponding equations.
regime the reduction–oxidation kinetics of a polycrystalline solid can be modelled like in Sections 2.1 and 2.2 if one replaces D by Deff (defined by eqn (14)) in the corresponding equations.
2.5 Concluding remarks
In Sections 2.1 and 2.2 we mathematically modelled the reduction–oxidation process of a homogeneous solid oxide. At least two parameters determine the kinetics of this process, first, the oxygen exchange coefficient, K, at the gas/solid interface, and second, the oxygen diffusion coefficient, D, in the solid. If one assumes that these parameters depend on temperature only one can model the reduction–oxidation process analytically for different geometries of the solid (see eqn (3) and (8)). The analytical solutions allow one to define a dimensionless regime parameter L = ξK/D where ξ corresponds to a characteristic length of the solid (half the thickness of a plane sheet or the radius of a sphere, respectively). Fig. 1 shows that one can distinguish three fundamental kinetic regimes: the surface controlled regime for L < 0.3, the mixed regime in the parameter range 0.3 < L < 30, and the diffusion controlled regime for L > 30. Because the regime parameter L is proportional to the characteristic length of the solid one will generally reach the surface controlled regime if the characteristic length of a given solid at a given temperature (fixed parameters D and K) becomes sufficiently small. That is, the ad hoc hypothesis that the kinetics is surface controlled is principally more reasonable for microscopic geometries than for macroscopic geometries.As discussed in Section 2.3, in the whole range of the dimensionless regime parameter L one can evaluate the characteristic time constant of the reduction–oxidation process by a simple exponential decay function (eqn (13)) with practically sufficient accuracy if the mass loss/gain is monitored up to equilibrium. However, the characteristic time constant is generally, even in this simple model of two constant parameters, a complicated function of the parameters K and D (see eqn (5) and (10)). In the mixed regime one has to know one parameter to evaluate the conjugate parameter by the measured time constant. In the surface controlled regime one can evaluate K and in the diffusion controlled regime one can evaluate D. This, however, requires a correct hypothesis related to the kinetics regime as defined in Fig. 1.
In Section 2.4 we considered a polycrystalline solid. Eqn (15) allows one to estimate the time interval which is required to reach the so called A regime in which a polycrystalline solid can be mathematically modelled like a homogeneous solid. If the A regime is reached the reduction–oxidation process of a polycrystalline solid oxide can be modelled as in Sections 2.1 and 2.2 with an effective oxygen diffusion coefficient (eqn (14)).
3 Experimental
3.1 Sample preparation
CeO2 powders were synthesized using a citric acid assisted combustion method.22 For that the required amount of Ce(NO3)3 × 6H2O (Sigma Aldrich) was dissolved in demineralized water. Afterwards citric acid (VWR chemicals) solution was added in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (cations
2 (cations![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) citric acid) and the obtained mixture was stirred at 100 °C for 1 h. Stepwise increase of the temperature up to 200 °C resulted in a more and more concentrated solution due to water evaporation thus leading to the formation of a very viscous yellow gel. The viscous product was heated to 450 °C for self-ignition. The newly formed yellow powder was calcined in an electrical furnace at 800 °C in air for 2 h to remove any remaining carbonaceous species. The obtained oxide powder was analyzed by X-ray diffractometry (D-5000, Siemens, Germany) using Ni-filtered Cu-Kα radiation. The CaF2-type CeO2 phase (Fig. 4) was identified according to reference data ICDD PDF-00-034-0394.23
citric acid) and the obtained mixture was stirred at 100 °C for 1 h. Stepwise increase of the temperature up to 200 °C resulted in a more and more concentrated solution due to water evaporation thus leading to the formation of a very viscous yellow gel. The viscous product was heated to 450 °C for self-ignition. The newly formed yellow powder was calcined in an electrical furnace at 800 °C in air for 2 h to remove any remaining carbonaceous species. The obtained oxide powder was analyzed by X-ray diffractometry (D-5000, Siemens, Germany) using Ni-filtered Cu-Kα radiation. The CaF2-type CeO2 phase (Fig. 4) was identified according to reference data ICDD PDF-00-034-0394.23
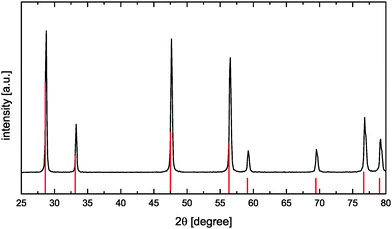 | ||
| Fig. 4 XRD pattern of the synthesized CeO2 sample (reference data according to ICDD PDF-00-034-039423 as red solid vertical lines). | ||
To prepare pellets the powder was milled using a laboratory ball mill [planetary micromill pulverisette 7, Fritzsch, Germany (3 × 10 min, 500 rpm, mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
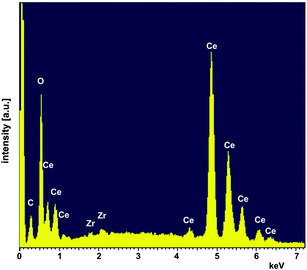
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 powder: isopropyl alcohol: ZrO2 balls)] and uniaxially cold-pressed at a pressure of 283 MPa. After sintering at 1650 °C for 2 h the pellets had a density of 93% (see Table 1). Beside X-ray diffraction the sintered samples were characterized by scanning electron microscopy (SEM, Ultra 55 FEG Carl Zeiss, Germany) equipped with an energy-dispersive X-ray spectroscopy (EDS) system (Fig. 5 and 6). EDS analyses (INCA-Software, Oxford Instruments, Abingdon, UK, Fig. 6) revealed minor impurities of Zr of about 0.58 ± 0.03 at% (at%[Ce] + at%[Zr] + at%[O] = 100 at%) which leads to Ce0.98Zr0.02O2. In a first approximation homovalent Zr does not act as an acceptor in ceria in such a low concentration. Therefore, we refer to our material as nominally undoped.
60 powder: isopropyl alcohol: ZrO2 balls)] and uniaxially cold-pressed at a pressure of 283 MPa. After sintering at 1650 °C for 2 h the pellets had a density of 93% (see Table 1). Beside X-ray diffraction the sintered samples were characterized by scanning electron microscopy (SEM, Ultra 55 FEG Carl Zeiss, Germany) equipped with an energy-dispersive X-ray spectroscopy (EDS) system (Fig. 5 and 6). EDS analyses (INCA-Software, Oxford Instruments, Abingdon, UK, Fig. 6) revealed minor impurities of Zr of about 0.58 ± 0.03 at% (at%[Ce] + at%[Zr] + at%[O] = 100 at%) which leads to Ce0.98Zr0.02O2. In a first approximation homovalent Zr does not act as an acceptor in ceria in such a low concentration. Therefore, we refer to our material as nominally undoped.
| Parameter | Value |
|---|---|
| Thickness | 1.05 mm |
| Diameter | 13.44 mm |
| Weight | 911.4 mg |
| Density | 6.7 g cm−3 |
| Theor. density23 | 7.2 g cm−3 |
 | ||
| Fig. 5 SEM image of the sintered CeO2 pellet with a grain size of about 20 μm and a density of 93% (Angle Selective Backscatter detector). | ||
3.2 Thermogravimetric analysis
Thermogravimetric (TG) analyses were performed using a thermo-balance system STA 449 F3 Jupiter (Netzsch, Germany). A sintered CeO2 pellet (see Table 1) was placed on Pt foil on an Al2O3 plate (diameter: 13 mm). For the reduction steps (at different high temperatures with a heating rate of 20 K min−1, see Fig. 7) argon 5.0 was passed through the sample tube at a flow rate of 85 ml min−1. The partial pressure of the employed gas atmosphere during the reduction step was calculated to be approximately 7 × 10−4 atm by comparing the obtained suboxide compositions with literature data.24 The reduction temperatures were held for several hours for complete reduction. For the subsequent oxidation step the pellet was rapidly cooled (50 K min−1) to 800 °C. After a dwell time of 5 min at 800 °C an argon–oxygen gas mixture was employed for 30 min (35 ml min−1 O2, 50 ml min−1 Ar which corresponds to an oxygen partial pressure of about 0.4 atm). Next, the gas was switched back to pure Ar 5.0 followed by a new reduction step.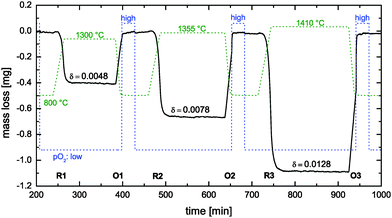 | ||
| Fig. 7 Reduction cycles (R1–R3) und oxidation cycles (O1–O3) during thermogravimetric analysis of a nominally undoped polycrystalline CeO2 pellet (see Table 1). Dashed lines show the time dependence of the temperature and the oxygen partial pressure pO2 (low: 7 × 10−4 atm, high: 0.4 atm). | ||
For data analysis the obtained mass loss curve was corrected by subtraction of a blank run (TG measurement without sample) to minimize device artefacts. Three reduction–oxidation cycles of the CeO2 pellet are shown in Fig. 7. Dashed lines show the monitored time dependence of the temperature and of the oxygen partial pressure. Oxygen nonstoichiometry, δ, of ceria was calculated by
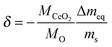 | (16) |
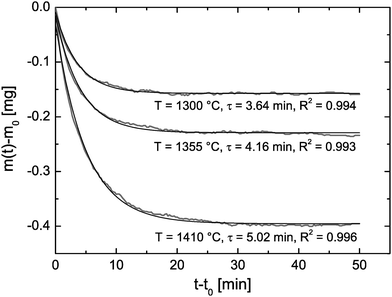 | ||
| Fig. 8 Isothermal time dependence of the mass loss during the reduction cycles R1–R3 in Fig. 7 where m0 is the mass at time t0 when the temperature starts to become constant. Time constants, τ, to reach mass equilibrium are evaluated by fit eqn (13) where the R2 values quantify the fit quality. | ||
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , of oxygen from the time constants shown in Fig. 8 where λ = ξ = 0.5 mm. The corresponding δ values are from Fig. 7. The expected high temperature range of the chemical diffusion coefficient,
, of oxygen from the time constants shown in Fig. 8 where λ = ξ = 0.5 mm. The corresponding δ values are from Fig. 7. The expected high temperature range of the chemical diffusion coefficient, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , was estimated from Fig. 1b of Ackermann et al.8
, was estimated from Fig. 1b of Ackermann et al.8
| T (°C) | p O2 (atm) | δ | τ (min) |
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) = λ/τ (m s−1) = λ/τ (m s−1) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (m2 s−1) (m2 s−1) |
L = ξ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) / /![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) |
|---|---|---|---|---|---|---|
| 1300 | 7 × 10−4 | 0.0048 | 3.64 | 2.29 × 10−6 | 10−7⋯10−8 | 1.1 × (10−2⋯10−1) |
| 1355 | 7 × 10−4 | 0.0078 | 4.16 | 2.00 × 10−6 | 10−7⋯10−8 | 1.0 × (10−2⋯10−1) |
| 1410 | 7 × 10−4 | 0.0128 | 5.02 | 1.66 × 10−6 | 10−7⋯10−8 | 8.3 × (10−3⋯10−2) |
Considering oxidation cycle #1 (see O1 in Fig. 7) one observes that the CeO2 pellet gains mass linearly because the oxidation kinetics is sufficiently fast to follow the linear temperature change (50 K min−1). An increase of the oxygen partial pressure does not change the oxidation state because the pellet is already oxidised up to its maximum oxidation state. However, at oxidation cycles #2 and #3 the pellet does not reach its maximum oxidation state when the oxidation temperature (800 °C) is reached. One can now observe that a rapid increase of the oxygen partial pressure induces a rapid increase of the oxidation kinetics.
3.3 Oxygen isotope exchange
Considering a plane sheet the tracer diffusion coefficient, D*, and the tracer surface exchange coefficient, K*, of oxygen are defined by (compare with eqn (22) which defines the corresponding chemical coefficients for oxygen)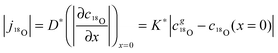 | (17) |
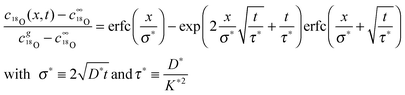 | (18) |
D* and K* data measured by 18O tracer exchange experiments in nominally undoped CeO2 ceramics are already available in the literature.3 Furthermore, tracer coefficients (D*,K*) are not directly applicable to rationalise the features of the reduction–oxidation kinetics during thermogravimetric analysis because the observed kinetics is controlled by chemical coefficients (![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ,
,![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ) which generally differ significantly from tracer coefficients.11 Nevertheless, it was useful to perform also an 18O tracer exchange experiment because in Section 4.1 we will discuss that fast diffusion paths in CeO2 ceramics support the hypothesis that the observed reduction–oxidation kinetics during thermogravimetric analysis is surface controlled. That is, it was in the context of this work interesting to confirm, at least qualitatively, such fast diffusion paths by an 18O exchange experiment.
) which generally differ significantly from tracer coefficients.11 Nevertheless, it was useful to perform also an 18O tracer exchange experiment because in Section 4.1 we will discuss that fast diffusion paths in CeO2 ceramics support the hypothesis that the observed reduction–oxidation kinetics during thermogravimetric analysis is surface controlled. That is, it was in the context of this work interesting to confirm, at least qualitatively, such fast diffusion paths by an 18O exchange experiment.
Fig. 9 shows SIMS depth profiles measured in a nominally undoped polycrystalline CeO2 sample (93% of theoretical density with an average grain size of about 20 μm) which was annealed for 900 s in 200 mbar 18O2 gas (96% atomic fraction) at 700 °C. The sample was pre-annealed for 3 hours in 200 mbar 16O2 at 700 °C. Fig. 9a shows SIMS raw data of the depth distribution of the negative secondary ions 16O−, 18O−, 140Ce− using a Hiden Analytical instrument. Positive 5 keV argon ions were used as primary beam with 400 nA ion current and a spot size of about 60 μm. The raster-scanned area was 450 × 350 μm2 and the area of the analysed zone was 170 × 130 μm2. Negative secondary ions were used for the analysis of the samples. Sample charging was prevented by an electron flood gun. Depth calibration was done by measuring the SIMS crater depth using a surface profiler (Tencor, Alpha Step 500). Differences in sputter yield and ionisation yield can be neglected for isotopes so that the depth distribution of the atomic fraction of 18O isotopes can be quantified by
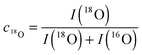 | (19) |
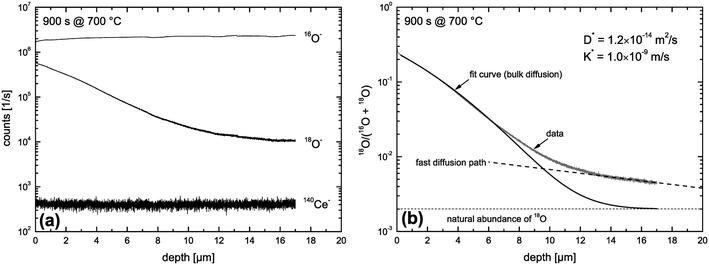 | ||
| Fig. 9 SIMS depth profiles measured in a nominally undoped polycrystalline CeO2 sample which was annealed for 900 s in 200 mbar 18O2 gas at 700 °C. (a) SIMS raw data. (b) Atomic fraction of 18O computed by eqn (19). | ||
The depth distribution of the atomic fraction of 18O isotopes is shown in Fig. 9b. One can see that the atomic fraction of 18O in the sample at x = 0 does not yet reach the atomic fraction of 18O of the gas phase (96%) which clearly indicates a tracer surface exchange coefficient, K*, which is sufficiently low to prevent tracer isotope equilibrium at the gas/solid interface during the annealing time t = 900 s at 700 °C. The most interesting feature of this depth profile, in the context of this work, is the significant tail (above the natural abundance of 18O) which clearly indicates (at least qualitatively) the existence of fast diffusion paths in the CeO2 samples investigated. The 18O tracer coefficients (K*,D*) were evaluated using eqn (18) as fit equation and are plotted in Fig. 10. From these data one can estimate that the characteristic time constant to reach tracer isotope equilibrium at the gas/solid interface is τ* = D*/K*2 = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s at 700 °C.
000 s at 700 °C.
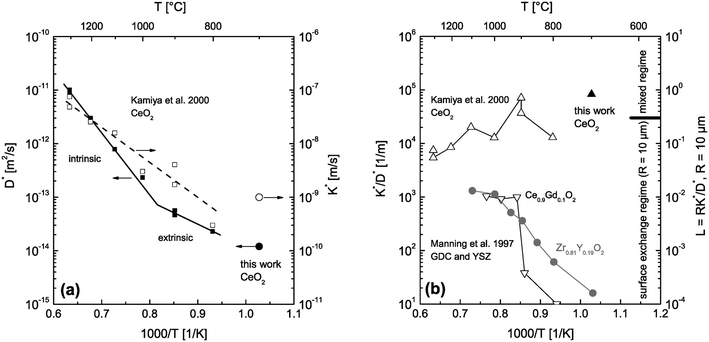 | ||
| Fig. 10 (a) D* and K* data measured by 18O tracer exchange experiments in nominally undoped polycrystalline CeO2 (Kamiya et al.3 and this work). (b) calculated K*/D* values from the data of (a). For comparison K*/D* values are also shown for Gd doped CeO2 (GDC) and Y doped ZrO2 (YSZ).2 The regime parameter L = R·K*/D* was calculated for grains of R = 10 μm and shows which material can be expected to be surface controlled in which temperature range. | ||
4 Discussion
The features of the observed reduction–oxidation kinetics during thermogravimetric analysis of nominally undoped polycrystalline CeO2 (93% density) are summarized in Section 3.2.1. Before one tries to rationalise these observed features one must first make a correct decision concerning the kinetics regime. This will be facilitated by an estimation of the kinetics regime during oxygen tracer exchange.4.1 Estimation of conditions to reach the surface controlled regime during oxygen tracer exchange
As discussed in Section 2.5 one can principally expect that the observed kinetics becomes surface controlled for sufficiently small grains. This principal conclusion is supported by an experimental work of Rutman et al.10 where SIMS analysis and combined residual gas analysis of nano crystals (5 to 50 nm size) of CeO2 + 10%Gd2O3 were used to measure tracer surface exchange and tracer diffusion of oxygen at low temperatures, 337 °C ≤ T ≤ 461 °C. However, isotope surface exchange was found to be the limiting step and solely K* could be determined from the performed tracer exchange experiments.The CeO2 grains in the sintered nominally undoped samples of this work have an average size of about 20 μm. The question arises whether reactions on individual isolated crystals of this size are surface controlled at temperatures used during the reduction step of the thermogravimetric analysis (T ≥ 1300 °C). That is, we first ask what we can expect if we use CeO2 powder (crystals of about 20 μm size) instead of sintered ceramics. To get an estimation we consider D* and K* data measured by 18O tracer exchange experiments in nominally undoped CeO2 (Kamiya et al.3 and this work) which are plotted in Fig. 10a. The left hand axis of Fig. 10b shows the corresponding ratios K*/D*. To evaluate whether small grains are surface controlled during an oxygen tracer exchange one has to consider the regime parameter L = R·K*/D* which indicates a surface controlled regime for values L < 0.3 (see Fig. 1). The regime parameter L is plotted on the right hand axis of Fig. 10b for grains of R = 10 μm. This clearly indicates that the oxygen tracer exchange kinetics of small grains of Gd doped CeO2 (GDC) is surface controlled in the whole temperature range because the ratio K*/D* tends to become temperature independent at higher temperatures.2 (To show that this tendency is not accidental also K*/D* values of Y doped ZrO2 are plotted.2)
After we have seen that the oxygen tracer exchange for small grains (R = 10 μm) of GDC is clearly surface controlled we will answer the question whether a thin dense polycrystalline plane sheet of GDC could also be surface controlled. For that we consider a plane sheet of dense polycrystalline GDC of 1 mm thickness (ξ = 0.5 mm = half the thickness) with an average grain radius R = 10 μm. At T > 600 °C grain boundary blocking effects vanish in GDC27 so that one can describe the oxygen tracer transport in fine-grained polycrystalline GDC by an effective diffusion coefficient Deff* as discussed in Section 2.4. That is, the (surface controlled) regime of polycrystalline GDC will not change if the following equation holds (see Fig. 10b where L ≤ 0.01 for GDC)
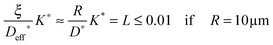 | (20) |
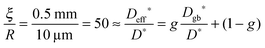 | (21) |
The situation is different for nominally undoped CeO2 (as used in this work) because the oxygen tracer exchange kinetics of small grains (R = 10 μm) tends to be in the mixed regime at lower temperatures and tends to be in the surface controlled regime at higher temperatures (see Fig. 10b). The reason that small grains of GDC are clearly in the surface controlled regime is that the oxygen diffusivity in the grains is increased significantly by Gd doping compared to nominally undoped CeO2.3 The Gd doping increases the concentration of oxygen vacancies, and hence, the diffusivity of oxygen which is assumed to be based on a vacancy mechanism.3
Furthermore, one has to keep in mind that the measured D* and K* data represent CeO2 samples which were pre-annealed in air3 (200 mbar 16O2 gas in this work), and hence, in a highly oxidized state during the 18O exchange experiments. Fig. 10b indicates that even highly oxidized CeO2 grains tend to reach the surface controlled regime at high temperatures, T ≥ 1300 °C, if the radius of the CeO2 grains is about 10 μm. As the reduction of nominally undoped ceria increases the vacancy concentration and thus the oxygen diffusivity one can conclude that a surface controlled regime is also plausible for nominally undoped polycrystalline CeO2 of 1 mm thickness (93% density). This argument and the fact that one can generally expect much higher chemical oxygen diffusion coefficients than tracer oxygen diffusions coefficients11 suggests a surface controlled kinetics regime for the polycrystalline ceria sample used in this work during TG analysis, which will be discussed in the next section.
4.2 Reduction kinetics of CeO2 in the surface controlled regime
We now postulate that the observed reduction kinetics during the performed thermogravimetric analysis (see Fig. 7) is surface controlled. This ad hoc hypothesis is motivated by the above discussion of oxygen tracer diffusion data and will be supported if it allows one to rationalise the observed features of the kinetics summarized in Section 3.2.1.Considering a plane sheet the chemical diffusion coefficient, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , and the chemical surface exchange coefficient,
, and the chemical surface exchange coefficient, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , of oxygen are defined by (compare with eqn (17) which defines the corresponding tracer coefficients for oxygen)
, of oxygen are defined by (compare with eqn (17) which defines the corresponding tracer coefficients for oxygen)
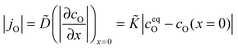 | (22) |
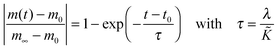 | (23) |
In Table 2 chemical surface exchange coefficients, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , of oxygen are computed with the aid of eqn (23) from the time constants evaluated from the isothermal mass loss in Fig. 8 where λ = 0.5 mm. The expected range of the chemical diffusion coefficient,
, of oxygen are computed with the aid of eqn (23) from the time constants evaluated from the isothermal mass loss in Fig. 8 where λ = 0.5 mm. The expected range of the chemical diffusion coefficient, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , in the considered temperature range was estimated from Fig. 1b of Ackermann et al.8 so that also the expected range of the corresponding regime parameter L is computed in Table 2. The range of L is for all three temperatures less than 0.3 which supports the ad hoc hypothesis of a surface controlled kinetics regime (see Fig. 1).
, in the considered temperature range was estimated from Fig. 1b of Ackermann et al.8 so that also the expected range of the corresponding regime parameter L is computed in Table 2. The range of L is for all three temperatures less than 0.3 which supports the ad hoc hypothesis of a surface controlled kinetics regime (see Fig. 1).
If one compares the chemical surface exchange coefficients, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , in Table 2 with the tracer surface exchange coefficients, K*, in Fig. 10 one finds that
, in Table 2 with the tracer surface exchange coefficients, K*, in Fig. 10 one finds that ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) is about one order of magnitude larger than K* at 1300 °C which is due to the average thermodynamic factor: a straightforward calculation using the data published by Panlener et al.25 shows that it varies between 60⋯500 for 0.2 ≥ δ ≥ 0.03 and that it is virtually independent of temperature. This is in accordance with the general observation
is about one order of magnitude larger than K* at 1300 °C which is due to the average thermodynamic factor: a straightforward calculation using the data published by Panlener et al.25 shows that it varies between 60⋯500 for 0.2 ≥ δ ≥ 0.03 and that it is virtually independent of temperature. This is in accordance with the general observation ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ≫ K*.11 Furthermore, there is a surprising temperature dependence of the evaluated chemical surface exchange coefficient,
≫ K*.11 Furthermore, there is a surprising temperature dependence of the evaluated chemical surface exchange coefficient, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) . It decreases with temperature which is in contrast to the tracer surface exchange coefficients, K*, which increases with temperature (see Fig. 10). From the data of Table 2 one can evaluate the following Arrhenius relation for the chemical surface exchange coefficient of nominally undoped CeO2 (at pO2 = 7 × 10−4 atm)
. It decreases with temperature which is in contrast to the tracer surface exchange coefficients, K*, which increases with temperature (see Fig. 10). From the data of Table 2 one can evaluate the following Arrhenius relation for the chemical surface exchange coefficient of nominally undoped CeO2 (at pO2 = 7 × 10−4 atm)
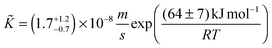 | (24) |
Note the negative apparent activation energy in eqn (24). Its absolute value in common units is (64 ± 7) kJ mol−1 or (0.67 ± 0.07) eV at−1, respectively.
Considering Table 2 one notes that there is an empirical relation, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ∼ δ−0.32, between the chemical surface exchange coefficient and the oxygen nonstoichiometry. Because δ is approximately equal to the concentration of vacancies in nominally undoped CeO2 one can conclude that
∼ δ−0.32, between the chemical surface exchange coefficient and the oxygen nonstoichiometry. Because δ is approximately equal to the concentration of vacancies in nominally undoped CeO2 one can conclude that 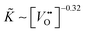 . Please note that our data analysis assumed that
. Please note that our data analysis assumed that ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) is a constant so that eqn (23) is not exact as
is a constant so that eqn (23) is not exact as ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) =
= ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) (δ). However, the assumption
(δ). However, the assumption ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ≈ const. is reasonable if δ is close to the equilibrium value, δ ≈ δeq, which was approximately the case for the isothermal mass loss curves considered in Fig. 8. Furthermore, if one considers the oxidation cycles in Fig. 7 the “jump” of the oxidation rate, which is induced by a “jump” of the oxygen partial pressure, can immediately be rationalised if one sets
≈ const. is reasonable if δ is close to the equilibrium value, δ ≈ δeq, which was approximately the case for the isothermal mass loss curves considered in Fig. 8. Furthermore, if one considers the oxidation cycles in Fig. 7 the “jump” of the oxidation rate, which is induced by a “jump” of the oxygen partial pressure, can immediately be rationalised if one sets ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ∼pO21/n. The relation K* ∼ pO21/4 has been reported for the tracer exchange coefficient in polycrystalline Gd doped CeO2.29
∼pO21/n. The relation K* ∼ pO21/4 has been reported for the tracer exchange coefficient in polycrystalline Gd doped CeO2.29
Summarising, the observed kinetics (see Section 3.2.1) during TG analysis of nominally undoped ceria can be empirically rationalised if the chemical oxygen surface exchange coefficient obeys the following relation
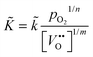 | (25) |
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) =
= ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) (T) is a temperature dependent constant of proportionality.12 A value of m ≈ 3 is estimated from the data for
(T) is a temperature dependent constant of proportionality.12 A value of m ≈ 3 is estimated from the data for ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) in Table 2. For the oxygen tracer surface exchange coefficient of acceptor-doped perovskite and fluorite oxides the empirical relation
in Table 2. For the oxygen tracer surface exchange coefficient of acceptor-doped perovskite and fluorite oxides the empirical relation 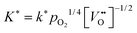 has been reported.12 That is, the assumption that n ≈ 4 in eqn (25) is, at least, a good starting assumption if one tries to confirm eqn (25) quantitatively by future investigations. In this work it was not possible to estimate n in eqn (25) because the oxygen partial pressure was rapidly switched in only one step (from low values to high values or in the opposite direction) and because the response of the mass change was too rapid to be detected reliably (see Fig. 7).
has been reported.12 That is, the assumption that n ≈ 4 in eqn (25) is, at least, a good starting assumption if one tries to confirm eqn (25) quantitatively by future investigations. In this work it was not possible to estimate n in eqn (25) because the oxygen partial pressure was rapidly switched in only one step (from low values to high values or in the opposite direction) and because the response of the mass change was too rapid to be detected reliably (see Fig. 7).
From eqn (25) one concludes that the negative apparent activation energy of the chemical surface exchange coefficient, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , is given by
, is given by
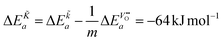 | (26) |
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) a and
a and 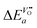 in this equation. The latter parameter can be identified as the formation energy of oxygen vacancies in nominally undoped CeO2. For this quantity, Kamiya et al.3 found 142 kJ mol−1, which is close to the value given by Panhans and Blumenthal,30 152 kJ mol−1. Inserting the average value of 147 kJ mol−1 for
in this equation. The latter parameter can be identified as the formation energy of oxygen vacancies in nominally undoped CeO2. For this quantity, Kamiya et al.3 found 142 kJ mol−1, which is close to the value given by Panhans and Blumenthal,30 152 kJ mol−1. Inserting the average value of 147 kJ mol−1 for 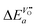 into eqn (26) one gets for m ≈ 3 the negative apparent activation energy ΔE
into eqn (26) one gets for m ≈ 3 the negative apparent activation energy ΔE![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) a ≈ −15 kJ mol−1. Due to the typical errors of experimentally determined energies of activation this value is in fact close to zero and should be observed if the formation energy of oxygen vacancies is negligible. A negligible formation energy of oxygen vacancies can be expected in Gd doped CeO2 (GDC) during oxygen tracer exchange experiments because Gd doping forms temperature independent oxygen vacancies according to the reaction
a ≈ −15 kJ mol−1. Due to the typical errors of experimentally determined energies of activation this value is in fact close to zero and should be observed if the formation energy of oxygen vacancies is negligible. A negligible formation energy of oxygen vacancies can be expected in Gd doped CeO2 (GDC) during oxygen tracer exchange experiments because Gd doping forms temperature independent oxygen vacancies according to the reaction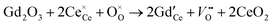 | (27) |
Armstrong et al.6 reported an apparent activation energy 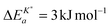 for the oxygen tracer surface exchange coefficient, K*, of GDC. Their experimental method is based on rapid switching of the reactor/furnace feed line between gas streams containing different isotopes of oxygen (18O, 16O) which are monitored by a mass spectrometer.31 Ideally, the only change induced by the switch is a step in oxygen labelling. Temperature, pressure, flow rate, and oxygen partial pressure remain approximately undisturbed. Because powders of the investigated oxides were used (size <1 μm) it was assumed that the oxygen isotope exchange kinetics is surface controlled.
for the oxygen tracer surface exchange coefficient, K*, of GDC. Their experimental method is based on rapid switching of the reactor/furnace feed line between gas streams containing different isotopes of oxygen (18O, 16O) which are monitored by a mass spectrometer.31 Ideally, the only change induced by the switch is a step in oxygen labelling. Temperature, pressure, flow rate, and oxygen partial pressure remain approximately undisturbed. Because powders of the investigated oxides were used (size <1 μm) it was assumed that the oxygen isotope exchange kinetics is surface controlled.
Interestingly enough Armstrong et al.13 recently reported apparent activation energies of K* for different perovskite oxides which have also negative or very small positive values. The reported range of apparent activation energies, 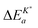 , of the oxygen tracer surface exchange coefficient is
, of the oxygen tracer surface exchange coefficient is 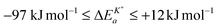 (see Armstrong et al.13 Table 5). Armstrong et al.13 assume that such small, and even negative, apparent activation energies indicate a surface exchange controlled kinetics regime. On the contrary, reported apparent activation energies from SIMS isotope depth profiles or electrical conductivity relaxation are typically measured in the mixed kinetics regime and have much larger positive values (73 kJ mol−1 to 333 kJ mol−1, see Armstrong et al.13 Table 5). The reason is yet unclear why the measured value of the apparent activation energy of the oxygen surface exchange coefficient depends on the kinetics regime.
(see Armstrong et al.13 Table 5). Armstrong et al.13 assume that such small, and even negative, apparent activation energies indicate a surface exchange controlled kinetics regime. On the contrary, reported apparent activation energies from SIMS isotope depth profiles or electrical conductivity relaxation are typically measured in the mixed kinetics regime and have much larger positive values (73 kJ mol−1 to 333 kJ mol−1, see Armstrong et al.13 Table 5). The reason is yet unclear why the measured value of the apparent activation energy of the oxygen surface exchange coefficient depends on the kinetics regime.
5. Conclusions
In Section 3.2.1 the observed features of the reduction–oxidation kinetics during thermogravimetric analysis of nominally undoped CeO2 ceramics are summarized. Before one tries to rationalise these observed features one needs a correct ad hoc hypothesis concerning the kinetics regime (surface controlled kinetics, mixed kinetics, diffusion controlled kinetics, as shown in Fig. 1). The most important parameter to estimate quantitatively the correct kinetics regime is the dimensionless regime parameter, L = ξ·![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) /
/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , where ξ is half the thickness of a plane sheet or the radius of a sphere, respectively. The problem is, however, that both chemical coefficients (
, where ξ is half the thickness of a plane sheet or the radius of a sphere, respectively. The problem is, however, that both chemical coefficients (![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ,
,![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ) are often not available in the literature so that one must consider measured tracer coefficients (K*,D*) together with the thermodynamic factor (if available). As discussed in Section 4.1. measured tracer coefficients of nominally undoped and Gd doped CeO2 suggested the hypothesis that the observed reduction–oxidation kinetics during the performed thermogravimetric analysis is surface controlled for dense polycrystalline samples of 1 mm thickness and 20 μm grain size–especially, if one takes into account that chemical oxygen diffusion coefficients are generally observed to be much larger than oxygen tracer diffusion coefficients.11 Further, the effective oxygen diffusivity can be significantly enhanced due to grain boundary transport.
) are often not available in the literature so that one must consider measured tracer coefficients (K*,D*) together with the thermodynamic factor (if available). As discussed in Section 4.1. measured tracer coefficients of nominally undoped and Gd doped CeO2 suggested the hypothesis that the observed reduction–oxidation kinetics during the performed thermogravimetric analysis is surface controlled for dense polycrystalline samples of 1 mm thickness and 20 μm grain size–especially, if one takes into account that chemical oxygen diffusion coefficients are generally observed to be much larger than oxygen tracer diffusion coefficients.11 Further, the effective oxygen diffusivity can be significantly enhanced due to grain boundary transport.
In Section 4.2 we postulated a surface controlled kinetics regime during the performed thermogravimetric analysis (see Fig. 7) of the sintered nominally undoped CeO2 pellet (see Table 1). This ad hoc hypothesis allowed us to evaluate chemical oxygen surface exchange coefficients, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , as compiled in Table 2, from the observed isothermal reduction kinetics. The chemical oxygen surface exchange coefficients empirically obey a relation expressed by eqn (25). Considering chemical oxygen diffusion coefficients,
, as compiled in Table 2, from the observed isothermal reduction kinetics. The chemical oxygen surface exchange coefficients empirically obey a relation expressed by eqn (25). Considering chemical oxygen diffusion coefficients, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , from the literature (see Table 2) our ad hoc hypothesis is supported because the computed regime parameters, L, indicates a surface exchange regime. This finding is an important design criterion for an efficient microstructure of the ceria inventory of a solar-thermal splitting reactor.
, from the literature (see Table 2) our ad hoc hypothesis is supported because the computed regime parameters, L, indicates a surface exchange regime. This finding is an important design criterion for an efficient microstructure of the ceria inventory of a solar-thermal splitting reactor.
The observed negative apparent activation energy, ΔE![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) a = −64 kJ mol−1, of the chemical oxygen surface exchange coefficient,
a = −64 kJ mol−1, of the chemical oxygen surface exchange coefficient, ![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , is in the range of apparent activation energies of the oxygen tracer surface exchange coefficient, K*, for different perovskite oxides.13 Considering reported formation energies of oxygen vacancies in nominally undoped CeO2,3,30 one can conclude that the apparent activation energy becomes approximately zero if the formation energy of oxygen vacancies becomes negligible as, e.g., in Gd doped CeO2. Armstrong et al.6 reported an in fact negligible value for the apparent activation energy
, is in the range of apparent activation energies of the oxygen tracer surface exchange coefficient, K*, for different perovskite oxides.13 Considering reported formation energies of oxygen vacancies in nominally undoped CeO2,3,30 one can conclude that the apparent activation energy becomes approximately zero if the formation energy of oxygen vacancies becomes negligible as, e.g., in Gd doped CeO2. Armstrong et al.6 reported an in fact negligible value for the apparent activation energy 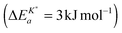 for the oxygen tracer surface exchange coefficient, K*, of GDC.
for the oxygen tracer surface exchange coefficient, K*, of GDC.
Appendix A
If cot β1 is expressed as an infinite series32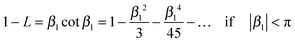 | (A1) |
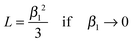 | (A2) |
Combining equations (A2) and (4) one gets eqn (6). Analogously, one can express tanβ1 as an infinite series32
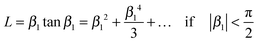 | (A3) |
| L = β12 if β1 → 0 | (A4) |
Combining equations (A4) and (9) one gets eqn (11).
Acknowledgements
We are indebted to Prof. A. Steinfeld and his group for valuable discussions and to Dr M. Schulz and S. Fischer for technical assistance. Financial support by the Initiative and Networking Fund of the Helmholtz Association of German Research Centers within the Virtual Institute SolarSynGas as well as by Deutsche Forschungsgemeinschaft (DFG) for one of the authors (P. F.) is gratefully acknowledged.References
- J. R. Scheffe and A. Steinfeld, Thermodynamic Analysis of Cerium-Based Oxides for Solar Thermochemical Fuel Production, Energy Fuels, 2012, 26, 1928–1936 CrossRef CAS.
- P. S. Manning, J. D. Sirman and J. A. Kilner, Oxygen self-diffusion and surface exchange studies of oxide electrolytes having the fluorite structure, Solid State Ionics, 1997, 93, 125–132 CrossRef.
- M. Kamiya, E. Shimada, Y. Ikuma, M. Komatsu and H. Haneda, Intrinsic and Extrinsic Oxygen Diffusion and Surface Exchange Reaction in Cerium Oxide, J. Electrochem. Soc., 2000, 147, 1222–1227 CrossRef CAS PubMed.
- M. Katsuki, S. Wang, K. Yasumoto and M. Dokiya, The oxygen transport in Gd-doped ceria, Solid State Ionics, 2002, 154–155, 589–595 CrossRef CAS.
- M. Stan, Y. T. Zhu and H. Jiang, Kinetics of oxygen removal from ceria, J. Appl. Phys., 2004, 95, 3358–3361 CrossRef CAS PubMed.
- E. N. Armstrong, K. L. Duncan, D. J. Oh, J. F. Weaver and E. D. Wachsman, Determination of Surface Exchange Coefficients of LSM, LSCF, YSZ, GDC Constituent Materials in Composite SOFC Cathodes, J. Electrochem. Soc., 2011, 158, B492–B499 CrossRef CAS PubMed.
- B. Bulfin, A. J. Lowe, K. A. Keogh, B. E. Murphy, O. Lübben, S. A. Krasnikov and I. V. Shvets, Analytical Model of CeO2 Oxidation and Reduction, J. Phys. Chem. C, 2013, 117, 24129–24137 CAS.
- S. Ackermann, J. R. Scheffe and A. Steinfeld, Diffusion of Oxygen in Ceria at Elevated Temperatures and Its Application to H2O/CO2 Splitting Thermochemical Redox Cycles, J. Phys. Chem. C, 2014, 118, 5216–5225 CAS.
- C. B. Gopal and S. M. Haile, An electrical conductivity relaxation study of oxygen transport in samarium doped ceria, J. Mater. Chem. A, 2014, 2, 2405–2417 CAS.
- J. Rutman, M. Kilo, S. Weber and I. Riess, Tracer surface exchange and diffusion of oxygen in nano crystals of Gd doped CeO2, Solid State Ionics, 2014, 265, 29–37 CrossRef CAS PubMed.
- J. Maier, On the correlation of macroscopic and microscopic rate constants in solid state chemistry, Solid State Ionics, 1998, 112, 197–228 CrossRef CAS.
- R. A. De Souza, A universal empirical expression for the isotope surface exchange coefficients (k*) of acceptor-doped perovskite and fluorite oxides, Phys. Chem. Chem. Phys., 2006, 8, 890–897 RSC.
- E. N. Armstrong, K. L. Duncan and E. D. Wachsman, Effect of A and B-site cations on surface exchange coefficient for ABO3 perovskite materials, Phys. Chem. Chem. Phys., 2013, 15, 2298–2308 RSC.
- P. J. Gellings and H. J. M. Bouwmeester, The CRC handbook of solid state electrochemistry, CRC Press, 1997 Search PubMed.
- J. Crank, The Mathematics of Diffusion, Oxford University Press, 2nd edn, 1975 Search PubMed.
- H. S. Carslaw and J. C. Jaeger, Conduction of Heat in Solids, Clarendon Press, 2nd edn, 1959 Search PubMed.
- H. Dünwald and C. Wagner, Methodik der Messung der Diffusionsgeschwindigkeiten bei Lösungsvorgängen von Gasen in festen Phasen, Z. Phys. Chem., 1934, B24, 53–58 Search PubMed.
- E. Fischer and J. L. Hertz, Measurability of the diffusion and surface exchange coefficients using isotope exchange with thin film and traditional samples, Solid State Ionics, 2012, 218, 18–24 CrossRef CAS PubMed.
- I. Kaur, Y. Mishin and W. Gust, Fundamentals of Grain and Interphase Boundary Diffusion, John Wiley & Sons Ltd, 1995 Search PubMed.
- E. W. Hart, On the role of dislocations in bulk diffusion, Acta Metall., 1957, 5, 597 CrossRef CAS.
- A. J. Mortlock, The effect of segregation on the solute diffusion enhancement due to the presence of dislocations, Acta Metall., 1960, 8, 132–134 CrossRef.
- Q.-L. Meng, C.-i. Lee, T. Ishihara, H. Kaneko and Y. Tamaura, Reactivity of CeO2-based ceramics for solar hydrogen production via a two-step water-splitting cycle with concentrated solar energy, Int. J. Hydrogen Energy, 2011, 36, 13435–13441 CrossRef CAS PubMed.
- Powder Diffraction File, International Center for Diffraction Data (ICDD), Newtown Square, PA 19073-3273, U.S.A.
- I. Ermanoski, N. P. Siegel and E. B. Stechel, A New Reactor Concept for Efficient Solar-Thermochemical Fuel Production, J. Sol. Energy Eng., 2013, 135, 031002 CrossRef.
- R. J. Panlener, R. N. Blumenthal and J. E. Garnier, A Thermodynamic Study of Nonstoichiometric Cerium Dioxide, J. Phys. Chem. Solids, 1975, 36, 1213–1222 CrossRef CAS.
- P. Fielitz and G. Borchardt, On the accurate measurement of oxygen self-diffusivities and surface exchange coefficients in oxides via SIMS depth profiling, Solid State Ionics, 2001, 144, 71–80 CrossRef CAS.
- X.-D. Zhou, W. Huebner, I. Kosacki and H. U. Anderson, Microstructure and Grain-Boundary Effect on Electrical Properties of Gadolinium-Doped Ceria, J. Am. Ceram. Soc., 2002, 85, 1757–1762 CrossRef CAS PubMed.
- P. Fielitz, G. Borchardt, M. Schmücker, H. Schneider and P. Willich, Oxygen Grain-Boundary Diffusion in Polycrystalline Mullite Ceramics, J. Am. Ceram. Soc., 2004, 87, 2232–2236 CAS.
- J. A. Lane and J. A. Kilner, Oxygen surface exchange on gadolinia doped ceria, Solid State Ionics, 2000, 136–137, 927–932 CrossRef CAS.
- M. A. Panhans and R. N. Blumenthal, A thermodynamic and electrical conductivity study of nonstoichiometric cerium dioxide, Solid State Ionics, 1993, 60, 279–298 CrossRef CAS.
- C. C. Kan, H. H. Kan, F. M. Van Assche IV, E. N. Armstrong and E. D. Wachsman, Investigating Oxygen Surface Exchange Kinetics of La0.8Sr.20MnO3−δ and La0.6Sr0.4Co0.2Fe0.8O3−δ Using an Isotopic Tracer, J. Electrochem. Soc., 2008, 155, B985–B993 CrossRef CAS PubMed.
- M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1972 Search PubMed.
| This journal is © the Owner Societies 2015 |