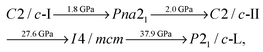Calcium peroxide from ambient to high pressures

Abstract

Structures of calcium peroxide (CaO₂) are investigated in the pressure range 0–200 GPa using the ab initio random structure searching (AIRSS) method and density functional theory (DFT) calculations. At 0 GPa, there are several CaO₂ structures very close in enthalpy, with the ground-state structure dependent on the choice of exchange–correlation functional. Further stable structures for CaO₂ with C2/c, I4/mcm and P2₁/c symmetries emerge at pressures below 40 GPa. These phases are thermodynamically stable against decomposition into CaO and O₂. The stability of CaO₂ with respect to decomposition increases with pressure, with peak stability occurring at the CaO B1–B2 phase transition at 65 GPa. Phonon calculations using the quasiharmonic approximation show that CaO₂ is a stable oxide of calcium at mantle temperatures and pressures, highlighting a possible role for CaO₂ in planetary geochemistry. We sketch the phase diagram for CaO₂, and find at least five new stable phases in the pressure–temperature ranges 0 ≤ P ≤ 60 GPa, 0 ≤ T ≤ 600 K, including two new candidates for the zero-pressure ground state structure.

---

1 Introduction

The typical oxide formed by calcium metal is calcium oxide, CaO, having Ca and O in +2 and −2 oxidation states respectively. Calcium and oxygen can also combine to form calcium peroxide, CaO₂, a compound which enjoys a variety of uses in industry and agriculture. Calcium peroxide is used as a source of chemically bound but easily evolved oxygen in fertilisers, for oxygenation and disinfection of water, and in soil remediation.^1,2

At ambient pressure bulk calcium peroxide decomposes at a temperature of about 620 K.^2,3 Early X-ray diffraction (XRD) experiments assigned a tetragonal ‘calcium carbide’ structure of space group I4/mmm to CaO₂.⁴ This same structure was already known to be formed by heavier alkaline earth metal peroxides.^5,6 Recently, Zhao et al.⁷ used an adaptive genetic algorithm and density functional theory (DFT) calculations to search for structures of CaO₂, finding a new orthorhombic ground state structure of Pna2₁ symmetry, which is calculated to be close to thermodynamic stability at zero pressure and temperature. The simulated XRD pattern from this structure is in good agreement with the available experimental data.⁷ Thermodynamic stability in this case means stability against decomposition via

CaO₂ → CaO + ½O₂. (1)

We are interested in the stabilities of structures of CaO₂ from zero pressure up to 200 GPa, and temperatures up to 1000 K. Calcium and oxygen have high abundances in the Earth's crust and mantle and, because they also have high cosmic abundances, stable compounds formed from these elements at high pressures are key (exo)-planetary building blocks. Understanding the structures of such compounds allows insight into the composition of planetary interiors, including exoplanets. To date, almost no work has been performed investigating CaO₂ as a stable oxide of calcium at high pressures. Some previous work has explored the effect of low pressures (<10 GPa) on the bond lengths and lattice parameters of I4/mmm-CaO₂.⁵ We therefore employ DFT calculations to explore the behaviour of CaO₂ at pressures in the GPa range. DFT calculations provide an excellent avenue for investigating materials properties under pressure, both at pressures accessible to diamond anvil cells⁸ and at terapascal pressures.^9,10 To explore the stability of CaO₂, we search for new crystal structures of this compound at a variety of pressures in the range 0–200 GPa.

2 Methods

Density functional theory calculations are performed using the CASTEP plane-wave pseudopotential code.¹¹ Ultrasoft pseudopotentials¹² generated with the CASTEP code are used for both calcium and oxygen, with core states 1s²2s²2p⁶ and 1s², respectively. We use the Perdew–Burke–Ernzerhof (PBE)¹³ form of the exchange–correlation functional with a plane-wave basis cutoff of 800 eV. A k-point sampling density of 2π × 0.03 Å⁻¹ is used for our CaO and CaO₂ phases. For our oxygen phases, we use a denser k-point sampling of 2π × 0.02 Å⁻¹. Bulk modulii are calculated by fitting static lattice pressure–volume data to the third-order Birch–Murnaghan equation of state.

The electronic density of states is calculated using the OPTADOS code.^14–16 Calculations of phonon frequencies are performed with the CASTEP code and a finite-displacement supercell method, using the quasiharmonic approximation.^17,18

To search for new phases of CaO₂, we use the ab initio random structure searching (AIRSS) technique.¹⁹ AIRSS proceeds by generating random starting structures containing a given number of formula units. Of these, structures which have lattice parameters giving reasonable bond lengths and cell volumes at a particular pressure are then relaxed to an enthalpy minimum, and the lowest enthalpy structures are selected for refinement. AIRSS has proved to be a very powerful tool in predicting new structures, several of which have subsequently been found experimentally. AIRSS searches have for example uncovered high pressure phases of silane,²⁰ and correctly predicted high pressure metallic phases in aluminium hydrides.²¹

In this study, we perform structure searching at pressures of 0, 10, 20, 50, 100, 150 and 200 GPa. The bulk (about 60%) of our searches use cells with 2 or 4 formula units of CaO₂, and we have also performed searches with cells containing 1, 3, 5, 6 and 8 formula units. Not all combinations of pressures and formula unit numbers are searched; further detailed information on the AIRSS searches is given as ESI.† In total, we relax over 25 000 structures in our CaO₂ searches. We supplement our AIRSS searches by calculating the enthalpies of five known alkaline earth metal peroxide structures taken from the Inorganic Crystal Structure Database (ICSD),²² and other authors.^7,23,24 The relevant alkaline earth metal is replaced with calcium where appropriate.

2.1 CaO

CaO undergoes a transition from the rocksalt (Fm3̄m) to the CsCl (Pm3̄m) structure (the B1–B2 transition) around 60–65 GPa. Diamond-anvil-cell experiments indicate a transition pressure of 60 ± 2 GPa at room temperature,²⁵ while DFT calculations give a transition pressure of 65–66 GPa.^26,27 We find a pressure of 65 GPa in the present study, and we therefore use the Fm3̄m rocksalt structure below 65 GPa and the CsCl structure at higher pressures. The bulk modulus of Fm3̄m-CaO has been measured to be 104.9 GPa,²⁸ while our static-lattice DFT calculations give a value of 108.5 GPa. To exclude the possibility that CaO might have a different, more stable structure (other than Fm3̄m or Pm3̄m) over the pressure range 0–200 GPa, we also perform AIRSS on CaO at pressures of 50, 100 and 200 GPa. We do not find any new low-enthalpy structures for CaO at these pressures.

2.2 Solid oxygen

Structure searching over the pressure range 0–200 GPa has already been performed for solid oxygen,^29,30 and we use the lowest enthalpy structures found therein. We also examine the enthalpies of the experimentally-determined α and δ oxygen phases at low pressures.³¹ Choosing the lowest-enthalpy oxygen structure at each pressure, we find that δ-O₂ is stable between 0 and 1.2 GPa, after which an insulating phase with space group Cmcm³¹ is stable up to 41 GPa. A phase of symmetry C2/m³⁰ then becomes stable, remaining so up to 200 GPa. Our spin-polarised calculations show no discernable difference in enthalpy between a δ-O₂ phase with antiferromagnetic spin ordering, and the experimentally-determined ferromagnetic spin-ordering for δ-O₂.³²

These results are not in accord with low-temperature experiments on solid oxygen, which predict α-O₂ to be stable between 0 and about 5 GPa, δ-O₂ to be stable between about 5 and 10 GPa, followed by the ‘ε-O₂’ phase between 10 and 96 GPa, with a further isostructural phase transition around 100 GPa.^33–35 Our DFT calculations do not yield α-O₂; optimising its structure at low pressures simply gives the δ-O₂ structure. The aforementioned C2/m oxygen phase is however very similar in structure to ε-O₂ (which is also of C2/m symmetry), and is within 50 meV per f.u. of that phase in enthalpy over the pressure range 0–200 GPa. Any higher enthalpy structure for oxygen over the pressure range being explored here would only increase the calculated stability of CaO₂, so we proceed with the lowest enthalpy DFT phases for oxygen.

3 Results

3.1 Structure searching and static lattice results

Our structure searching is carried out by minimising the enthalpy at a given pressure within the static-lattice approximation. We discuss these results first before presenting our calculations of the Gibbs free energy.

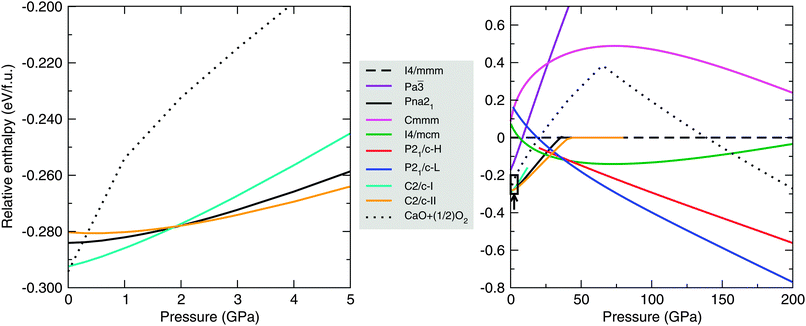
Fig. 1 shows the enthalpy-pressure curves for nine phases of CaO₂. The first five of these, labelled with their space group symmetries I4/mmm, Pa3̄, Pna2₁, Cmmm and I4/mcm in Fig. 1, are known alkaline earth metal peroxide structures as mentioned in Section 2. The other four, with space group symmetries C2/c and P2₁/c, are new CaO₂ structures. These are the lowest-enthalpy phases that turned up during our AIRSS searches. The dotted line in Fig. 1 shows the enthalpy of CaO + ½O₂, calculated using the lowest-enthalpy phases of CaO and O₂ at each pressure. Any CaO₂ phase below this dotted line is stable against decomposition in the manner of eqn (1).

Fig. 1 Static lattice enthalpies, in eV per unit of CaO₂, of calcium peroxide phases in the pressure range 0–5 GPa (left) and 0–200 GPa (right). Enthalpies are given relative to the I4/mmm phase of CaO₂. C2/c-I, C2/c-II, P2₁/c-H and P2₁/c-L are new structures of CaO₂ found using AIRSS. The left-hand plot highlights the enthalpy differences between the Pna2₁ and two C2/c phases at low pressures; C2/c-I is the lowest-enthalpy structure at 0 GPa from our searches. The arrow and box in the right-hand figure indicate the scope of the left-hand figure. Structures of CaO₂ below the dotted line are thermodynamically stable against decomposition into CaO and O₂.

We find the following sequence of phase transitions for CaO₂ by considering the lowest enthalpy structure at each pressure:

with the transition pressures between each structure as indicated by the arrows. The P2₁/c-L phase is then predicted to be stable up to at least 200 GPa.

At 0 GPa, our structure searching reveals a number of CaO₂ phases which are very close (within 10 meV per f.u.) in enthalpy. Within the present approximations (DFT with PBE exchange–correlation), a phase of C2/c symmetry (‘C2/c-I’) is lowest in enthalpy at 0 GPa. This phase is 8.4 meV per f.u. lower in enthalpy than the proposed Pna2₁-symmetry ground state structure of Zhao et al.,⁷ which we note also turned up in our AIRSS searches. Our searches also uncover a second C2/c-symmetry phase (‘C2/c-II’) which is slightly higher in enthalpy than Pna2₁ at 0 GPa. The enthalpies of these three phases at low pressures are shown in more detail in the left-hand panel of Fig. 1.

We find that the calculated XRD patterns for the C2/c-I, C2/c-II and Pna2₁ structures share many similar features with available experimental data,²³ although this XRD data is best fitted by the Pna2₁ structure. The XRD patterns are provided as ESI.† The enthalpy differences between the C2/c-I, -II and Pna2₁ phases at 0 GPa are dependent on the choice of exchange–correlation functional. In Table 1, we show the enthalpies of the Pna2₁ and C2/c-II phases relative to the C2/c-I phase using a variety of different functionals. We find differences in calculated equilibrium volumes as well: for C2/c-I at 0 GPa, the LDA gives a volume of 35.8 ų per f.u., while the PBE functional gives 39.1 ų per f.u. The LDA typically overbinds in DFT calculations, with PBE instead underbinding, so these two volumes likely bracket the true volume of the C2/c-I phase at 0 GPa. Given that dP/dV is about −2.3 GPa Å⁻³ for this phase at 0 GPa, this volume difference (due to functional choice) corresponds to a pressure uncertainty in the neighbourhood of ±3 GPa. In light of this uncertainty, C2/c-I, C2/c-II and Pna2₁ are all reasonable candidates for the structure of CaO₂ at 0 GPa.

Table 1 Enthalpies of the C2/c-II and Pna2₁ phases of CaO₂ at 0 GPa, in meV per unit of CaO₂, relative to the C2/c-I phase using different exchange–correlation functionals

Functional	LDA	PBE	PBESOL	PW91	WC
C2/c-I	0.0	0.0	0.0	0.0	0.0
Pna21	0.1	8.4	2.9	8.7	3.5
C2/c-II	−16.3	12.2	−4.1	12.0	−2.7

---

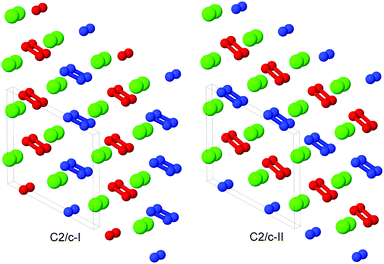
The C2/c-I, -II and Pna2₁ phases exhibit very similar structures. Looking down the b-axis of each phase, calcium atoms form a nearly-hexagonal motif, and we note that the monoclinic angle β is close to 120° for C2/c-I and C2/c-II. For the C2/c-I and -II phases, the peroxide ion axes are almost coplanar, as can be seen in Fig. 2. In C2/c-II, the axes of peroxide ions in the same plane are parallel, while in C2/c-I, they alternate in orientation in the same plane. We use red and blue colouring in Fig. 2 to show peroxide ions with parallel axes. We provide as ESI† further discussion and illustrations of the C2/c-I, -II and Pna2₁ phases, to highlight their similarities and differences.

Fig. 2 2 × 2 × 2 slabs of the C2/c-I (left) and C2/c-II (right) structures, viewed almost down the b-axis. Both structures are very similar, with Ca atoms forming an almost-hexagonal motif when viewed from this angle. Green atoms correspond to Ca atoms, while red and blue correspond to O atoms. All O atoms in peroxide ions with parallel O–O axes are given the same colour.

AIRSS searches also reveal a second phase for CaO₂ with P2₁/c symmetry (‘P2₁/c-H’). As can be seen in the right-hand panel of Fig. 1, our static-lattice calculations show that this is not a stable phase for CaO₂ over the pressure range 0–200 GPa. However around 38 GPa, the enthalpy of this phase lies within 10 meV per f.u. of the I4/mcm and P2₁/c-L phases, opening up the possibility this phase could become stable once we take temperature into account. We consider this further in Section 3.4. The I4/mcm phase reported here is also predicted for MgO₂ above 53 GPa.²⁴

We provide lattice parameters and bulk modulii for the C2/c-I, C2/c-II, I4/mcm, P2₁/c-H and P2₁/c-L phases at 0, 20, 30 and 50 GPa in Table 2.

Table 2 Structures of the C2/c-I, C2/c-II, I4/mcm, P2₁/c-H and P2₁/c-L phases of CaO₂

Pressure (GPa)	Space group	Lattice parameters (Å, deg)			Atom	Atomic coordinates			Wyckoff site	B 0 (GPa)
						x	y	z
a C12/c1 – International Tables, Volume A: unique axis b, cell choice 1. b P121/a1 – International Tables, Volume A: unique axis b, cell choice 3.
0	C2/c (#15)^a (I)	a = 7.041	b = 3.685	c = 6.820	Ca	0.0000	0.6399	0.2500	4e	87
		α = 90.0	β = 117.8	γ = 90.0	O	0.2548	0.1404	0.4119	8f
20	C2/c (#15)^a (II)	a = 6.829	b = 3.403	c = 6.407	Ca	0.0000	0.3413	0.2500	4e	89
		α = 90.0	β = 118.8	γ = 90.0	O	0.1661	0.1553	0.0252	8f
30	I4/mcm (#140)	a = 4.521	b = 4.521	c = 5.745	Ca	0.0000	0.0000	0.2500	4a	114
		α = 90.0	β = 90.0	γ = 90.0	O	0.1143	0.6143	0.0000	8h
30	P21/c-H (#14)^b	a = 6.590	b = 4.842	c = 3.795	Ca	0.0611	0.7628	0.2781	4e	93
		α = 90.0	β = 105.2	γ = 90.0	O	0.1301	0.2714	0.3087	4e
					O	0.2446	0.4378	0.1012	4e
50	P21/c-L (#14)^b	a = 4.223	b = 4.279	c = 5.949	Ca	0.0613	0.5133	0.2539	4e	110
		α = 90.0	β = 98.7	γ = 90.0	O	0.0820	0.0235	0.4019	4e
					O	0.1224	0.1182	0.0089	4e

---

3.2 Bonding and electronic structure

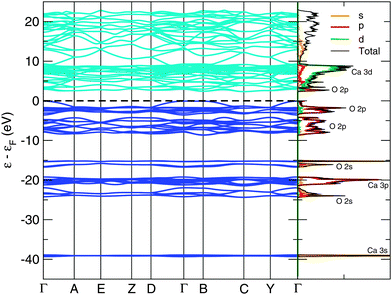
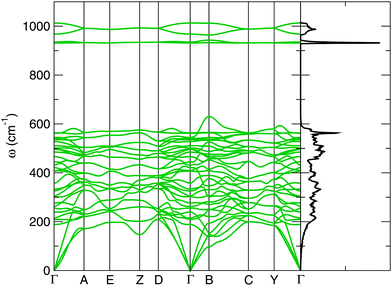
The bandstructure of the P2₁/c-L phase at 50 GPa is shown in Fig. 3. The insulating nature of this phase is evident, with a calculated thermal bandgap of 2.4 eV and optical bandgap of 2.5 eV. These will be underestimates of the true bandgap owing to the use of the PBE functional. The lowest set of 4 bands is comprised almost entirely of Ca 3s orbitals. Above this, we find a central peak flanked by two smaller sidepeaks in the total density of states. The central peak is built from 12 bands and is largely Ca 3p orbitals, while the two sidepeaks contain 4 bands apiece and are dominated by O 2s orbitals. Thus, we have a splitting of the O 2s orbital energy levels, possibly arising from the covalent bonding present in the peroxide [O–O]⁻ ion. Above this, and just below the HOMO (highest occupied molecular orbital), are 20 bands which arise largely from O 2p orbitals. The first orbitals above the Fermi level consist of (unoccupied) O 2p orbitals, followed by a dense band of Ca 3d orbitals. An almost identical pattern of bonding and electronic density of states are found in our other low-enthalpy phases. The bandstructures of the C2/c-I, C2/c-II, I4/mcm and P2₁/c-H phases at 0, 20, 30 and 30 GPa respectively are provided in the ESI.†

Fig. 3 Bandstructure and electronic density of states of the P2₁/c-L phase at 50 GPa. The density of states is shown projected onto the s, p and d angular momentum channels. We calculate a thermal bandgap of 2.4 eV, and an optical bandgap of 2.5 eV. The Fermi level is shown as a black dashed line.

Fig. 4 shows the corresponding phonon band structure and density of states for P2₁/c-L at 50 GPa. The lack of imaginary phonon frequencies indicates the stability of this particular phase. The distinctly separate high frequency bands around 930–1000 cm⁻¹ in Fig. 4 correspond to phonon modes that stretch the O–O covalent bond in the peroxide ions. Two distinct peroxide bond lengths are found in the ions of this structure: 1.44 Å and 1.46 Å, which splits these higher frequency bands. These peroxide O–O bond lengths are somewhat longer those found in molecular oxygen, which has an O–O bond length of 1.207 Ų³ at ambient conditions, and the bond length in C2/m oxygen at 50 GPa, which we calculate as 1.20 Å. These longer O–O bond lengths are however typical of crystalline ionic peroxides.⁵ As with the electronic bandstructures, further phonon bandstructures for the C2/c-I, C2/c-II, I4/mcm and P2₁/c-H phases are given in the ESI.†

Fig. 4 Phonon dispersion relations and density of states for P2₁/c-L CaO₂ at 50 GPa.

3.3 Stability of CaO₂

As can be seen in Fig. 1, our low-enthalpy phases for CaO₂ show remarkable stability against decomposition as pressure increases. We predict CaO₂ to be most stable at the B1–B2 CaO phase transition pressure of 65 GPa. There, the decomposition enthalpy (eqn (1)) of CaO₂ is +0.64 eV per unit of CaO₂ (+62 kJ mol⁻¹).

One implication of the stability of CaO₂ is that it may be preferentially formed over CaO in an oxygen-rich environment under pressure, through the reverse of eqn (1). For example, the pressure in the Earth's lower mantle, at a depth of around 1550 km, is about 65 GPa,²⁵ close to our predicted peak stability pressure for CaO₂. The formation of MgO₂ in this way has also been discussed,²⁴ although much higher pressures (>116 GPa) are needed before MgO₂ is stable against decomposition, whereas CaO₂ is stable from around 0 GPa. The mantle temperature in the Earth at 65 GPa is in the neighbourhood of 2500 K, and our phonon calculations show that under these conditions, ΔG = +0.54 eV per f.u. for the reaction of eqn (1). Hence, CaO₂ is a thermodynamically stable oxide at temperatures and pressures encountered in planetary interiors.

Reactions of the form X + O₂ → Y for species X and Y, such as the reverse of eqn (1), are known as redox buffers. Such reactions are key in determining planetary mantle compositions. In the Earth's mantle, there are a number of such buffers, usually involving the further oxidation of iron and nickel compounds, such as Fe₃O₄ + ¼O₂ → [/]Fe₂O₃ and Ni + ½O₂ → NiO. The natural formation of CaO₂ by further oxidation of CaO in Earth's mantle, while energetically favourable at high pressures and temperatures, would also need to compete against the further oxidation of other such compounds. The average CaO content in the Earth's mantle is about 3%,²⁸ though exoplanet mantles offer a rich variety of alternative compositions.

We highlight the fact that the pressures at which these different CaO₂ phases are predicted to become stable are amenable to experimental study in diamond anvil cells. Very few pressure-induced phase transitions for A[B₂] compounds are experimentally known,³⁶ although at least one example already occurs among the alkaline earth metal peroxides, in BaO₂.³⁶ Equivalently, it would be interesting to test the reactivity of CaO and O₂ under conditions of excess oxygen, as our results suggest that CaO and O₂ are reactive at high pressures. The formation of CaO₂ may require laser heating in a diamond anvil cell to overcome the likely high potential barriers between phases. High pressure phases of CaO₂ could be recoverable at lower pressures, although possibly not at ambient or zero pressure.

3.4 Lattice dynamics

In addition to our static-lattice calculations, we calculate the phonon free energies of our lowest-enthalpy CaO₂ phases, namely those with Pna2₁, C2/c-I/II, I4/mcm, P2₁/c-H and P2₁/c-L symmetries. We encounter no imaginary phonon frequencies over the pressure ranges relevant to these phases, indicating that they are dynamically stable. The relevant thermodynamic potential is now the Gibbs free energy, which includes the phonon pressure. Selecting the lowest Gibbs free energy structure from these six structures gives rise to the T–P phase diagram given in Fig. 5. We note that the upper-left (low-P, high-T) part of the phase diagram is representative only, because at ambient pressures CaO₂ decomposes at temperatures around 620 K.^2,3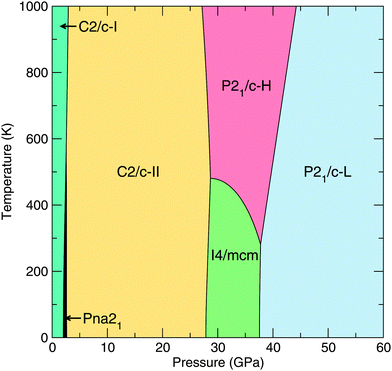

Fig. 5 T–P phase diagram of CaO₂ as calculated using the quasiharmonic approximation and our lowest-enthalpy structures.

We find that the small enthalpy difference between the I4/mcm and P2₁/c-H phases seen in our static-lattice calculations (Fig. 1) closes with increasing temperature, and we see the emergence of P2₁/c-H as a stable phase for CaO₂ at 37.7 GPa and for T > 281 K. The free energy difference between the I4/mcm and P2₁/c-H phases does remain quite small however, around 20 meV per CaO₂ unit at the most over the temperature range 0–1000 K.

At room temperature (300 K), we therefore predict a different sequence of phase transitions than those given in Section 3.1 for our static-lattice calculations. We find that, with PBE exchange–correlation:

with the arrows labelled by the predicted transition pressures. We also provide the equation of state for CaO₂ for our static lattice calculations and at 300 K with our phonon calculations in the ESI.†

The phase diagram of Fig. 5 does not extend all the way to 200 GPa. However, we expect P2₁/c-L to continue to be the most stable phase at high pressures. This is because our structure searching results (which use static-lattice enthalpies) show that the next most stable structure for CaO₂ over the pressure range 100–200 GPa is at least 45 meV per unit of CaO₂ higher in enthalpy. This was not the case at low pressures, where our searches reveal quite a few structures (such as P2₁/c-H) that are close to becoming stable and may therefore do so at high temperatures.

4 Conclusions

Structural changes in CaO₂ under pressure have been explored over the pressure range 0–200 GPa at temperatures up to 1000 K. CaO₂ remains insulating up to pressures of at least 200 GPa. Structure searching and DFT calculations reveal six stable phases for CaO₂ over these pressure and temperature ranges, of which five are reported for the first time in this study. Calculations of the phonon frequencies of these new structures confirms their dynamical stability. The lowest-enthalpy phase of CaO₂ at 0 GPa is dependent on the choice of DFT exchange–correlation functional. At pressures above 40 GPa, a phase of P2₁/c symmetry (‘P2₁/c-L’) emerges for CaO₂ which is predicted to be stable up to 200 GPa, and at mantle pressures and temperatures. CaO₂ is a very stable oxide of calcium at high pressures, and may be a constituent of exoplanet mantles. The pressures at which these CaO₂ phases become stable are readily attainable in diamond anvil cells.

Acknowledgements

Calculations were performed using the Darwin Supercomputer of the University of Cambridge High Performance Computing Service (http://www.hpc.cam.ac.uk/), as well as the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk/). Financial support was provided by the Engineering and Physical Sciences Research Council (UK). JRN acknowledges the support of the Cambridge Commonwealth Trust.

References

1. Y. Qian, X. Zhou, Y. Zhang, W. Zhang and J. Chen, Chemosphere, 2013, 91, 717–723.
2. I. A. Massalimov, A. U. Shayakhmetov and A. G. Mustafin, Russ. J. Appl. Chem., 2010, 83, 1794–1798.
3. This decomposition temperature may be lower for samples of different purities; for example the CRC Handbook³⁷ reports a decomposition temperature of ≈470 K for CaO₂.
4. C. Brosset and N.-G. Vannerberg, Nature, 1956, 177, 238.
5. M. Königstein, A. A. Sokol and C. R. A. Catlow, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 4594–4604.
6. P. D. VerNooy, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, 49, 433–434.
7. X. Zhao, M. C. Nguyen, C.-Z. Wang and K.-M. Ho, RSC Adv., 2013, 3, 22135–22139.
8. S. Ninet, F. Datchi, P. Dumas, M. Mezouar, G. Garbarino, A. Mafety, C. J. Pickard, R. J. Needs and A. M. Saitta, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174103.
9. M. Martinez-Canales, C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2012, 108, 045704.
10. C. J. Pickard, M. Martinez-Canales and R. J. Needs, Phys. Rev. Lett., 2013, 110, 245701.
11. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
12. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
13. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
14. R. J. Nicholls, A. J. Morris, C. J. Pickard and J. R. Yates, J. Phys.: Conf. Ser., 2012, 371, 012062.
15. A. J. Morris, R. J. Nicholls, C. J. Pickard and J. R. Yates, OptaDOS User Guide: Version 1.0.370, 2014, Available online at http://www.cmmp.ucl.ac.uk/ajm/optados/.
16. J. R. Yates, X. Wang, D. Vanderbilt and I. Souza, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195121.
17. B. B. Karki and R. M. Wentzcovitch, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 224304.
18. P. Carrier and R. M. Wentzcovitch, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064116.
19. C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201.
20. C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2006, 97, 045504.
21. C. J. Pickard and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 144114.
22. Crystallographic databases, ed. F. H. Allen, G. Bergerhoff and R. Sievers, International Union of Crystallography, Chester, England, 1987.
23. M. Königstein and C. R. A. Catlow, J. Solid State Chem., 1998, 140, 103–115.
24. Q. Zhu, A. R. Oganov and A. O. Lyakhov, Phys. Chem. Chem. Phys., 2013, 15, 7696–7700.
25. R. Jeanloz, T. J. Ahrens, H. K. Mao and P. M. Bell, Science, 1979, 206, 829–830.
26. M. Catti, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 100101.
27. J. Zhang and J. Kuo, J. Phys.: Condens. Matter, 2009, 21, 015402.
28. N. Soga, J. Geophys. Res., 1968, 73, 5385–5390.
29. J. Sun, M. Martinez-Canales, D. D. Klug, C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2012, 108, 045503.
30. Y. Ma, A. R. Oganov and C. W. Glass, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064101.
31. J. B. Neaton and N. W. Ashcroft, Phys. Rev. Lett., 2002, 88, 205503.
32. I. N. Goncharenko, O. L. Makarova and L. Ulivi, Phys. Rev. Lett., 2004, 93, 055502.
33. L. F. Lundegaard, G. Weck, M. I. McMahon, S. Desgreniers and P. Loubeyre, Nature, 2006, 443, 201–204.
34. H. Fujihisa, Y. Akahama, H. Kawamura, Y. Ohishi, O. Shimomura, H. Yamawaki, M. Sakashita, Y. Gotoh, S. Takeya and K. Honda, Phys. Rev. Lett., 2006, 97, 085503.
35. Y. Akahama, H. Kawamura, D. Häusermann, M. Hanfland and O. Shimomura, Phys. Rev. Lett., 1995, 74, 4690–4693.
36. I. Efthimiopoulos, K. Kunc, S. Karmakar, K. Syassen, M. Hanfland and G. Vajenine, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134125.
37. CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, Taylor and Francis, 2013.

---

Footnote

† Electronic supplementary information (ESI) available: Further details on the AIRSS searches carried out in this study, an equation-of-state diagram for CaO₂, electronic and phonon bandstructures, and supplementary structural diagrams. See DOI: 10.1039/c4cp05644b

---