Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correlating structure with non-linear optical properties in xAs40Se60·(1 − x)As40S60 glasses
Emma R.
Barney
*a,
Nabil S.
Abdel-Moneim
a,
James J.
Towey
a,
Jeremy
Titman
b,
John E.
McCarthy
c,
Henry T.
Bookey
c,
Ajoy
Kar
c,
David
Furniss
a and
Angela B.
Seddon
a
aFaculty of Engineering, University of Nottingham, University Park, Nottingham, NG7 2RD, UK. E-mail: Emma.Barney@nottingham.ac.uk
bSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK
cInstitute of Photonics and Quantum Sciences, School of Engineering and Physical Sciences, Heriot Watt University, Edinburgh EH14 4AS, UK
First published on 23rd January 2015
Abstract
A series of xAs40Se60·(100 − x)As40S60 glasses, where x = 0, 25, 33, 50, 67, 75 and 100 mol% As40Se60, has been studied using neutron and X-ray total scattering, Raman spectroscopy and 77Se MAS-NMR. The results are presented with measurements of non-linear refractive indices, n2, and densities. There is no evidence for the formation of homopolar bonds in these glasses, but neutron correlation functions suggest that there is a non-random distribution of sulfur and selenium atoms in sulfur-rich glasses. The average number of sulfur atoms at a distance of 3–4 Å from a selenium atom, nSeS, deviates from a linear variation with x in glasses containing <50 mol% As40Se60; n2 for these glasses also varies non-linearly with x. Importantly, a direct comparison of n2 and nSeS gives a linear correlation, suggesting that n2 may be related to the distribution of chalcogen atoms in the glasses.
1. Introduction
The low phonon energies, and large non-linear optical responses, exhibited by chalcogenide glasses enable them to transmit, and interact with, a broad spectrum of mid-infrared (mid-IR) light. These properties, coupled with an ability to act as laser hosts via the incorporation of rare earth ions, make chalcogenide glasses ideal candidates for a range of mid-IR applications, including new bright mid-IR fibre laser sources.The As–S–Se glass system is of particular interest because melts require only moderate cooling rates (air cooling) to form a glass and it has a wide glass forming domain. The range of glass formation is bounded by the binary glass forming ranges of x = 5–45 at% As in AsxS100−x, 0–62 at% As in AsxSe100–x, and 0–85 at% Se in SxSe100−x.1,2 As–S–Se glasses show good thermal stability, with resistance to crystallisation during fibre-drawing, and non-linear refractive indices, n2, >100x that of silica.3,4 The effect on glass properties caused by varying the relative amounts of As, Se and S is well documented, but less well understood. For example, reported physical property measurements of xAs40Se60·(100 − x)As40S60 glasses indicate that density3,5 and glass transition temperature, Tg,3,5,6 vary linearly with x yet n2, important for active optical applications, does not.3,4 Understanding the relationship between composition, structure and macroscopic properties will facilitate the development of glass compositions that are designed and tailored for specific optical devices.
Previous structural studies of As–Se–S glasses have predominantly used spectroscopic techniques. However, these methods have limitations in the information they can yield. 77Se Nuclear Magnetic Resonance (NMR) studies give averaged evidence for the local environment of selenium,7,8 but sulfur and arsenic NMR are less informative as bonding information cannot be gained directly. Numerous Raman scattering studies2,3,9–11 have identified the characteristic vibrations of As–S, As–Se, S–S and Se–Se. S–S bond vibrations oscillate at relatively high wave numbers, because both atoms in the bond are light, giving rise to a band in the Raman spectra at 440–500 cm−1.2,3,9–11 When sulfur is bonded to the heavier arsenic or selenium atoms, the bond vibrational frequency was reported to red-shift to ∼270–420 cm−1 and when the heavier oscillators (As and Se) are directly bonded (As–As, As–Se and Se–Se), bands in the wave number range 220–270 cm−1 are observed. Attempts have been made to relate these Raman spectral features to glass structure. However, due to the similar masses of As and Se, deconvolution of contributions from As–S and Se–S at ∼350 cm−1, or As–As, Se–Se and As–Se at ∼250 cm−1, is difficult (see ref. 2 and 10 for examples). One study of As-poor glasses, where homopolar chalcogen–chalcogen (Ch–Ch) bonds are an integral part of the glass network, indicated that there is a preference for Se–Se bonds over those of S–S or S–Se, concluding that selenium chains, and [AsS3] units, are more favourable than [AsSe3] units and sulfur chains.10 However, Raman spectra for pure selenium and pure sulfur showed that Se–Se bonds have a greater oscillator strength than S–S bonds.2 This results in a greater intensity of the Se peaks in the Raman spectrum, and casts doubt on the conclusions drawn in ref. 10. In conclusion, difficulties in quantitatively interpreting spectroscopic measurements, coupled with a lack of structural information beyond the direct bonds in the glass, limit the use of NMR and Raman in aiding the understanding of how chalcogen atoms are distributed in chalcogenide glasses.
In contrast to spectroscopic techniques, neutron and X-ray correlation functions, T(r), yield quantitative measurements of glass structure. The results give information about the local environments of atoms in the glass, and how those structural units link together to form a 3-D glass network. Although there have been several total scattering studies12–14 of the stoichiometric glasses, As40Se60 and As40S60, and of binary glasses with varying cation to anion ratios, As1−xSex and As1−xSx, there are fewer which study the effect of mixing S and Se chalcogen anions on the network structure. Furthermore, there is not much information on how glass structure underpins macroscopic glass properties.
The stoichiometric glass forming system, xAs40Se60·(100 − x)As40S60 (where x = 0, 25, 33, 50, 67, 75, 100 mol%), has been chosen for this study to minimise the number of homopolar (As–As, Ch–Ch) bonds and simplify the structure.13 Along this compositional tie line, an ideal glass would be solely constructed of [AsCh3] units, with each chalcogen bonding to two arsenic atoms to provide the network connectivity. We compare structural insights gained from neutron and X-ray total scattering, supported by Raman and 77Se NMR, with the nonlinear optical performance of chalcogenide glasses, in terms of the nonlinear refractive index, n2.
2. Total scattering theory
2.1. i(Q) and T(r)
A neutron diffraction experiment measures the differential cross-section,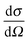 , which is equivalent to the total scattering from the sample, IN(Q), where Q is the magnitude for the scattering vector for elastic scattering.15 The total scattering is the sum of the self-scattering, Is(Q) (the interference between scattered waves from the same nucleus), and the distinct scattering, iN(Q) (the interference between scattered waves from different nuclei);
, which is equivalent to the total scattering from the sample, IN(Q), where Q is the magnitude for the scattering vector for elastic scattering.15 The total scattering is the sum of the self-scattering, Is(Q) (the interference between scattered waves from the same nucleus), and the distinct scattering, iN(Q) (the interference between scattered waves from different nuclei);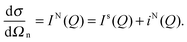 | (1) |
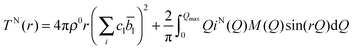 | (2) |
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) l is the coherent neutron scattering length (see Table 1) for element l. The resolution in real-space depends on the modification function and the maximum momentum transfer, Qmax, of the experimental data.
l is the coherent neutron scattering length (see Table 1) for element l. The resolution in real-space depends on the modification function and the maximum momentum transfer, Qmax, of the experimental data.
| Element | Neutron scattering length, b | X-ray form factor, f(0) |
|---|---|---|
| S | 2.847 | 16 |
| As | 6.58 | 33 |
| Se | 7.97 | 34 |
In the case of X-ray diffraction, the scattering data has a form factor dependence. This is removed by normalising the data using the Krogh-Moe and Norman method17,18 to yield the distinct scattering IX(Q). X-rays scatter from the electron cloud of an atom, resulting in a relatively broad ‘electron–electron’ correlation function. To remove this broadening and obtain a correlation function, TX(r), that has good resolution, a sharpened distinct scattering spectra, iX(Q), is required. This is obtained by dividing IX(Q) by 〈f(Q)〉2 (where 〈f(Q)〉 is the mean X-ray form factor for the sample and is related to the atomic number, Z, of the elements involved).19,20 This new function approximates scattering from point sources;
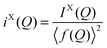 | (3) |
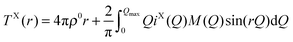 | (4) |
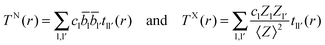 | (5) |
2.2. Extracting coordination numbers from TN(r)
Each peak in the neutron correlation function, TN(r), arising from a particular pair of elements l and l′. The coordination number, nll′, can be calculated from the peak area, All′, and the interatomic distance, rll′, given by the position of the peak and according to: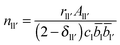 | (6) |
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) l
l![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) l′ is the coefficient for tll′(r). If the coordination number for nll′ and nl′l have been calculated using the area and position of a feature in TN(r) with a defined distance range, then the coordination numbers for ll′ and l′l atom pairs are related by the following identity
l′ is the coefficient for tll′(r). If the coordination number for nll′ and nl′l have been calculated using the area and position of a feature in TN(r) with a defined distance range, then the coordination numbers for ll′ and l′l atom pairs are related by the following identity| nll′cl = nl′lcl′ | (7) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S or Se) units, is comprised of directly bonded As–Ch distances. The second peak arises from the next nearest neighbours in the glass and can comprised of a mix of up to nine X⋯X distances (where ⋯ denotes a non-bonding distance between two atoms). The various contributions can be written as an expansion of eqn (5)
S or Se) units, is comprised of directly bonded As–Ch distances. The second peak arises from the next nearest neighbours in the glass and can comprised of a mix of up to nine X⋯X distances (where ⋯ denotes a non-bonding distance between two atoms). The various contributions can be written as an expansion of eqn (5)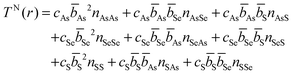 | (8) |
The expected difference between an experimental TN(r) and a TN(r) predicted by a weighted sum of As40Se60 and As40S60 can be calculated by a consideration of the Ch⋯Ch contribution to the second peak in the experimental data. It can be shown, using eqn (6) and (8), that the expected area for a peak comprised of all the possible Ch⋯Ch combinations is related to the total number of chalcogen neighbours, nChCh:
rChChAChCh = cSe![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) Se2nSeSe + cS Se2nSeSe + cS![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) S2nSS + cSe S2nSS + cSe![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) Se Se![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) SnSeS + cS SnSeS + cS![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) S S![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) SenSSe SenSSe | (9) |
| nChCh = nSS + nSSe = nSeSe + nSeS | (10) |
rChChAChCh = nChCh(cSe![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) Se2 + cS Se2 + cS![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) S2) − cSenSeS( S2) − cSenSeS(![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) Se − Se − ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) S)2 S)2 | (11) |
(1) There is a significant difference between the experimental arsenic correlations and those predicted by the weighted sum of the end members.
(2) There was a preference for like anions to cluster together.
(3) The number of S atoms around Se differs from the number of Se atoms around S in the distance range of interest.
3. Experimental setup
3.1. Sample preparation
A series of glasses, xAs40Se60·(100 − x) As40S60, where x = 0, 25, 33, 50, 67, 75 and 100 mol% As40Se60, was made using high purity As (99.99999%, Furukawa Electric Ltd.), Se and S (both 99.999%, Materion). As, and Se, were further purified by heating under vacuum (10−3 Pa) at 310 °C, and 270 °C, prior to batching (15–20 g samples), which was carried out inside a glove-box (≤0.1 ppm O2, ≤0.1 ppm H2O; MBraun). The silica glass ampoules (<1.0 ppm OH, ID/OD = 10 mm/14 mm, MultiLab.) in which the glasses were batched and melted, had been air-baked (1000 °C for 6 hours) and vacuum baked (1000 °C for 6 hours at 10−3 Pa) prior to use. The ampoule was sealed under vacuum (∼10−3 Pa), placed in a rocking furnace held statically, raised at 30 °C h−1 to 250 °C and held isothermally for 2 h to ensure the chalcogens had fully melted. The furnace was then programmed to rock (±30° to horizontal axis) as the ampoule was heated to ∼650 °C (30 °C h−1) before being held isothermally with rocking for 12 h to achieve homogenisation. The furnace was then placed statically vertical and cooled at 60 °C h−1 to ∼570 °C. A final isothermal dwell of ∼2 hours, to fine and refine the glass, was given before quenching the glass. The ampoules were quenched using a jet of nitrogen gas and subsequently annealed at Tg for 30 minutes, before cooling slowly to ambient, producing small glass rod samples.Sample compositions were characterised using a PANalytical MiniPal4 to collect X-ray Fluorescence (XRF) spectra and Scanning Electron Microscopy, in back scattered mode, was used to collect Energy Dispersive X-ray (EDX) spectra. Density measurements were carried out using a Quantachrome Micropycnometer, with helium as the displacement gas. Measurements of the glass transition temperature were carried out using a Perkin Elmer DSC7 Differential Scanning Calorimeter with water circulating chillers and an argon gas flow at the rate of 20 ml min−1. For each measurement an initial “conditioning” temperature run was carried out by heating, and then cooling, the glass through the glass transition temperature, using a ramp rate of 10 °C min−1 to ensure all glasses had the same thermal history. The sample was then heated again at 10 °C min−1 to determine Tg. The value for Tg was calculated using two different methods. The first method was to determine the point of maximum gradient, Tg,max, taken as the maximum point in the derivative of the data. The second method was to calculate an “onset temperature”, Tg,onset, using the intersection of two tangents fitted to the baseline, and the point of maximum gradient in the Tg feature. The first method gives a larger value for Tg than the second.
3.2. Z-scan measurements of n2
A standard Z-scan setup21 was used to measure the nonlinear optical absorption, β, and nonlinear refractive index, n2, of the seven As–S–Se glasses. The laser system was a Spectra Physics optical parametric generator-optical parametric amplifier combination with a Ti:sapphire laser and regenerative amplifier. The laser pulse width was ∼120 fs and the corresponding spectral width was 12 nm. The measurements were performed using a laser of wavelength 1550 nm, pulse repetition rate of 1 kHz and a beam waist of 35 μm. Open and closed (20% transmission) aperture scans were recorded simultaneously to measure the nonlinear coefficients. The samples were prepared by cutting a 10 mm diameter discs from the as-annealed glass rods. Both surfaces of the discs were polished to a 1 μm finish. To ensure the surfaces were parallel, the discs were then hot pressed under vacuum between tungsten carbide plates at a temperature ∼40 °C above Tg. For the measurement, the samples were mounted on a motorised translation stage and the movement and data collection were controlled by computer. Measurements were made at 2 energies (between 50 and 200 nJ, chosen as appropriate for each glass composition) to confirm the reliability of n2 calculated. Further details on the analysis of these samples are given by McCarthy.223.3. Raman scattering
A Horiba LabRAM HR Raman system with a 660 nm LaserQuantum Ignis laser (187 mW set to 25% power) was used to collect Raman scattering data from the sample material. The samples were prepared by cutting a disc from the as-annealed glass rod and polished to a 1 μm finish. The data were collected using a 4 second exposure and accumulated over 10 scans. Repeat measurements at different points on each glass disc were made to ensure that the Raman spectra measured were representative of the whole glass. A background subtraction was performed on each spectrum before fitting was carried out.3.4. 77Se NMR
77Se NMR spectra were recorded at room temperature on an Avance III 600 Bruker spectrometer at a Larmor frequency of 114.497 MHz using a 2.5 mm magic angle spinning (MAS) probe, spinning at 15 kHz. A spin echo pulse sequence was used to acquire the broad line that results from the distribution of isotropic chemical shifts expected for the glassy state. The echo delay was synchronised with the MAS period and set to 66.67 μs. The 77Se π/2 pulse duration was 4 μs and the spectral width was 500 kHz. Acquisition commenced immediately after the π pulse in order to sample the whole echo to increase the signal-to-noise ratio. Given the low natural abundance of 77Se (7.58%), up to 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 scans were required per spectrum, with a relaxation delay of 10 s. Chemical shifts are quoted relative to neat (CH3)2Se.
000 scans were required per spectrum, with a relaxation delay of 10 s. Chemical shifts are quoted relative to neat (CH3)2Se.
3.5. Neutron and X-ray total scattering
For total scattering using neutrons, the as-annealed glass rods were placed inside cylindrical vanadium containers, of inner diameter 10 mm, for the neutron scattering measurements. These vanadium containers were thin-walled, with a thickness of 25 μm, in order to reduce the magnitude of the experimental corrections required. The neutron diffraction patterns were measured using the GeM diffractometer23 at the ISIS pulsed neutron and muon source (Rutherford Appleton Laboratory, Oxfordshire, UK). The data were normalised using a calibration measurement of an 8 mm vanadium rod and were reduced and corrected for attenuation and multiple scattering using standard Gudrun24 and ATLAS25 software to give the distinct scattering spectra, iN(Q). iN(Q) was fitted with a quadratic, of the form A + BQ2, at low Q to extrapolate the data to Q = 0.The X-ray data were collected at the Diamond Light Source (Rutherford Appleton Laboratory, Oxfordshire, UK) using the I15 beamline optimised for the collection of PDF data. The photon energy used for the experiment was 73 keV. The samples were powdered and placed in 1 mm diameter silica capillaries, and the scattering was detected using a Perkin Elmer 2D flat panel 1621 detector. The 2D data were reduced to 1D using Fit2D26,27 and were corrected for detector attenuation as detailed by Skinner et al.28 The 1D data were normalised using the Krogh-Moe and Norman method17,18 and corrected for attenuation and multiple scattering using GudrunX29 to produce the sharpened distinct scattering spectrum, iX(Q).
In both experiments, measurements of the empty instrument and empty container were made for data corrections. Once fully corrected iN(Q) and iX(Q) were Fourier transformed, using the Lorch modification function and a maximum momentum transfer, Qmax, of 35 Å−1 for neutron and 25 Å−1 for X-ray data, to give the total correlation functions, T(r).
Predictions of the interatomic distances between nearest neighbour atoms were made using standard bond valence parameters.30 The calculated bond lengths (presented in Table 2) were used as starting parameters when fitting T(r). Simultaneous fitting to TN(r) and TX(r) was carried out using NXFit.31
| Coordination number | 2.00 | 3.00 | 4.00 |
|---|---|---|---|
| Bond type | Bond lengths | ||
| As–S | 2.11 | 2.26 | 2.37 |
| As–Se | 2.24 | 2.39 | 2.50 |
| As–As | 2.26 | 2.41 | 2.52 |
| S–S | 2.07 | 2.22 | 2.33 |
| Se–S | 2.25 | 2.40 | 2.51 |
| Se–Se | 2.36 | 2.51 | 2.62 |
The neutron diffraction data, in both reciprocal- and real-space, are available from the ISIS Disordered Materials Database.55
4. Results
4.1. Sample characterisation
Densities ranged from 3.19 ± 0.04 g cm−3 for As40S60 to 4.55 ± 0.04 g cm−3 for As40Se60 (Table 3). The linear variation in density with x, shown in Fig. 1a, suggests that there are no non-linear long range changes in the arrangement of the basic structural [AsCh3] units as Se is substituted for S. Tg measurements are shown in Fig. 1b, calculated by two methods. The values of Tg,max and Tg,onset, were found to vary non-linearly with the addition of As40Se60. There was a decrease in Tg,onset of 8 °C on changing the glass composition from As40S60 to As40S45Se15. However, as further selenium is added to the glass network, it was observed that Tg,onset value remain constant, within error, until a composition of As40S15Se45 is reached. On changing the composition of the glass from As40S15Se45 to one with no sulfur at all, As40Se60, a further drop in Tg,onset of 18 °C was observed.| Nominal composition at% | XRF composition at% (±3) | EDX composition at% (±1) | Density g cm−3 (±0.04) | T g | n 2 (×10−18 m2 W−1) (±0.5) | β (×10−12 mW−1) (±0.2) | n SeS (±0.4) | |
|---|---|---|---|---|---|---|---|---|
| Onset (±2) | Maximum gradient (±2) | |||||||
| As40S60 | As43S57 | As40S60 | 3.19 | 198 | 209 | 2.3 | 0.53 | |
| As40S45Se15 | As40S45Se15 | 3.59 | 190 | 200 | 2.3 | 1.0 | 4.4 | |
| As40S40Se20 | As42S39Se19 | As38S40Se22 | 3.69 | 192 | 204 | 3.4 | 2.7 | 4.1 |
| As40S30Se30 | As39S32Se29 | As39S30Se31 | 3.91 | 189 | 199 | 4.5 | 2.0 | 3.6 |
| As40S20Se40 | As41S20Se39 | As38S21Se41 | 4.10 | 188 | 199 | 6.0 | 3.7 | 2.6 |
| As40S15Se45 | As40S14Se46 | 188 | 199 | 6.1 | 2.8 | |||
| As40Se60 | As39Se61 | As39Se61 | 4.55 | 170 | 176 | 10.5 | 2.8 | 0 |
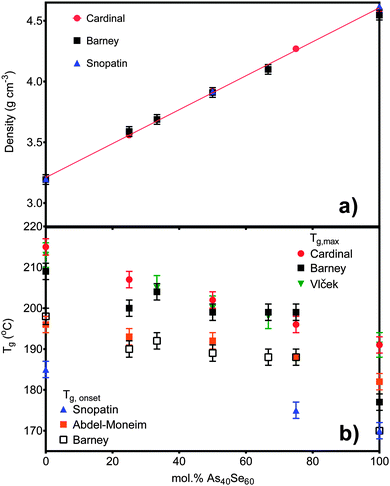 | ||
| Fig. 1 (a) The density measurements for six of the samples in this study compared to literature values published by Cardinal et al.3 and Snopatin et al.5 The density for As40S15Se45 is not shown as the sample size was too small to allow an accurate measurement. (b) The glass transition temperatures for all seven glasses are compared to the literature values published by Cardinal et al.3 and Snopatin et al.5 in addition to those published by Vlček et al.6 and Wang et al.32 The different results are grouped depending on the definition of Tg used. | ||
The XRF and EDX results for glass composition were calculated using standardless calibration programs and are also given in Table 3. EDX measurements for each element were correct, to within 2 at%, at all times. This indicated that, within error, all the glasses had a stoichiometric composition As40Ch60. However, it should be noted that although the compositional analysis carried out by XRF is also consistent with the batched compositions, within error, the binary glass, As40S60, deviated most from the nominal compositions (3 at% excess As). It was expected that XRF would determine the composition of this glass with reasonable accuracy as it is comprise only two components. Therefore, while the batch compositions are assumed to be correct for subsequent analysis, the possibility that As40S60 was arsenic rich is considered in the discussion.
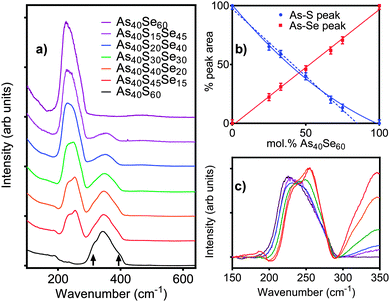
4.2. Raman
The Raman spectral bands, shown in Fig. 2a, are centred at 345 cm−1 for As40S60, characteristic of the vibration of As–S bonds, and 230 cm−1 for As40Se60, characteristic of As–Se bond vibrations.2,3,9–11 The mixed chalcogen samples were composed of As–S and As–Se bonds and so exhibit both peaks. The effect of oscillator strength is shown in Table 4. The area of the As–S peak measured for As40S60 is ∼50% of that measured for the As–Se peak in As40Se60. As a result, the relative intensities of the two peaks cannot be used directly to determine the relative amounts of As–S and As–Se bonds in the mixed chalcogen glasses. Fig. 2b shows the percentage variation in intensity of the As–Se and As–S peaks with x. The intensity of the As–Se peak, as Se was replaced by S, varied linearly, but the As–S peak intensity did not. A linear trend line fitted to the As–S peak intensities measured for x = 0–67 predicted that a Raman spectrum for a glass consisting of 85 mol% As40Se60 would exhibit no As–S peak.| Nominal composition at% | As–Se peak area as % of As40Se60 spectrum | As–S peak area as % of As40S60 spectrum |
|---|---|---|
| As40S60 | 0.0 | 100.0 |
| As40S45Se15 | 22.3 | 65.2 |
| As40S40Se20 | 31.1 | 59.0 |
| As40S30Se30 | 46.0 | 40.0 |
| As40S20Se40 | 61.9 | 20.1 |
| As40S15Se45 | 70.8 | 13.3 |
| As40Se60 | 100.0 | 0.0 |
4.3. 77Se NMR
To check the consistency of the selenium environment with composition, 77Se NMR spectra were collected for As40Se60 and As40S40Se20 (x = 100 and 33) glasses. Gaussian peak fits to the spectra, shown in Fig. 3, were fixed at 380 ppm and the NMR spectra for both glasses could be simulated well with a single peak. A peak with a chemical shift of 380 ppm arises from Se atoms bonded to two arsenic atoms.8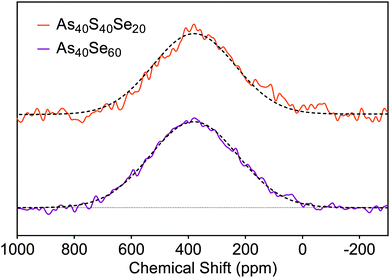 | ||
| Fig. 3 77Se NMR spectra acquired for the As40Se60 and As40S40Se20 samples. The solid lines are the experimental data, and the dashed lines are the peak fits. | ||
4.4. Z-scan measurements of n2
Z-scan measurements of the non-linear refractive index, n2, and non-linear absorption, β, are given in Table 3. There is a slow change in n2 in sulfur rich glasses, varying from 2.3 (±0.5) × 1018 m2 W−1 to 4.5 (±0.5) × 1018 m2 W−1 as the composition is changed from As40S60 to As40Se30S30 (x = 0–50). However, as the selenium content was increased, the rate of change accelerated, reaching a value of 10.5 (±0.5) × 1018 m2 W−1 for As40Se60 (x = 100). Literature measurements for n2 (ref. 3 and 4) are quoted relative to silica making direct comparison of values of n2 difficult. To facilitate a comparison, Fig. 4a shows the values for n2 measured by this study, along with those measured by Cardinal et al.,3 Harbold et al.4 and Wang et al.,32 relative to the values of n2 measured for As40S60. The relative change with x observed by all three studies is similar, with n2 for As40Se60 being 4.0–4.5 times larger than As40S60. Fig. 4b shows that the variation in n2 with x is not linear, but can be fitted with a second order polynomial equation.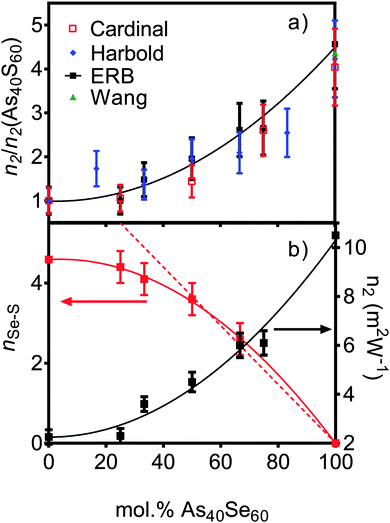 | ||
| Fig. 4 (a) The variation in non-linear optical response of the series of xAs40Se60·(100 − x)As40S60 glasses as measured in this study at 1.55 μm wavelength (black squares). The results are compared to literature results (right y axis) from Cardinal et al.3 at 1.6 μm (red squares), Harbold et al.4 at 1.55 μm and Wang et al.32 at 1.55 μm. To allow direct comparison, the results are normalised to the n2 value for As40S60. (b) The experimental values for n2 (this study – black squares), with nSeS values derived from TN(r) (red squares, x = 0 value is derived from the fit to experimental data) as a function of composition. The solid lines are the polynomial fits to the data. The dashed red line is the line of best fit to nSeS for the x = 50, 67 and 100 mol% As40Se60 samples (when x = 0, y = 7.33). | ||
4.5. Neutron and X-ray scattering
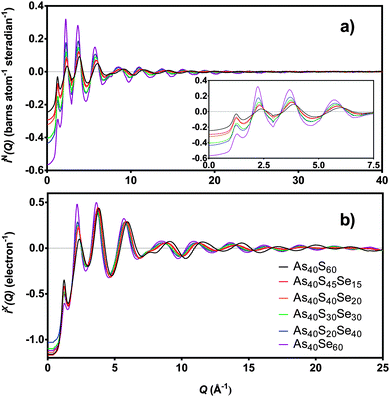
The distinct scattering patterns, measured using neutrons, iN(Q), and X-rays, iX(Q), are shown in Fig. 5 (except As40S15Se45, which was not measured). All diffraction data exhibited a shift in the position of peaks to shorter Q with increasing selenium content. The exception was the position of the pre-peak at 1.26 Å−1, which was unchanged (±0.3 Å−1). The shift in peak position to shorter Q indicated an expansion of the glass network to accommodate the increase in average chalcogen size. The corresponding correlation functions, TN(r) and TX(r), are shown in Fig. 6. There were two well defined peaks at ∼2.35 Å and 3.55 Å in the correlation functions; the former arose from As–Ch bonds and the latter from the shortest, non-bonded, distances for As⋯As/Ch⋯Ch. Some of these short As⋯As and Ch⋯Ch distances arose from the next nearest neighbours within an [AsCh3] unit (Ch–As–Ch) or between two units (As–Ch–As), but an examination of the structure of crystalline As40Se60 (ref. 33) indicated that up to 50% of the contribution to nAsAs may not be caused by As–Ch–As through-bonding, but rather from the close packing of structural units that are not directly connected.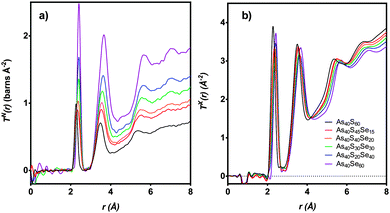 | ||
| Fig. 6 T(r) for six xAs40Se60·(100 − x)As40S60 samples as measured using (a) neutrons and (b) X-rays. As40S15Se45 is not shown as sample was too small for scattering measurements. | ||
Fig. 6 shows that the first peak in the correlation functions, TN(r) and TX(r), for As40S60 was centred at ∼2.27 ± 0.01 Å, while the corresponding peak for As40Se60 was centred at ∼2.41 ± 0.01 Å. The intermediate ternary glasses, which were composed of As–S and As–Se bonds, exhibited a broader first peak in T(r). The average peak position shifts between the distances observed in T(r)s for As40S60 and As40Se60 as Se was substituted for S in the glass network. The positions of the As–Ch and Ch⋯Ch peaks in the correlation functions for As40S60 (2.27 and 3.42 Å) and As40Se60 (2.41 and 3.62 Å) were consistent with Ch–As–Ch bond angles of ∼100°, which is in good agreement with that expected for the trigonal pyramid environment of a three-coordinated lone-pair ion.34
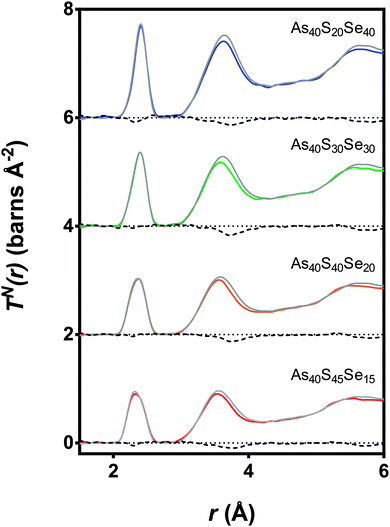
Fig. 7 shows simultaneous fits to the first peak in TX(r) and TN(r) for the xAs40Se60·(100 − x)As40S60 glass system. The fits required two peaks in order to model the As–S and As–Se bonds. The positions, widths and areas of the peaks were allowed to vary freely and the fit parameters are given in Table 5. The As–Se and As–S peak positions were all within 0.01 Å of the bond lengths for As–S and As–Se (2.271 ± 0.001 Å and 2.412 ± 0.001 Å) found by fitting the end member glasses. Furthermore, the coordination numbers for the two bond types, nAsS and nAsSe, were within 0.05 of the predicted average coordination numbers calculated from the glass composition (Table 5), yielding a total coordination number for arsenic in all of the glasses within the range of 3.0 ± 0.1.
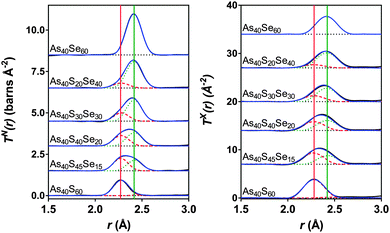 | ||
| Fig. 7 Simultaneous fits to the neutron and X-ray diffraction data. The red dashed lines are the As–S peaks and the green dotted lines are the As–Se peaks. The solid red and green lines show the expected As-S and As-Se bond lengths respectively (see Table 2). The blue line is the sum of the fit and the black line is the experimental data. The black dotted lines show the baseline for each T(r). | ||
| Composition | Correlation | r (Å) | σ (Å) | n AsCh | Calculated nAsCh |
|---|---|---|---|---|---|
| As40S60 | As–S1 | 2.271(1) | 0.0585(2) | 2.86(3) | 3 |
| As–S2 (As–As) | 2.467(3) | 0.029(1) | 0.11(3) (0.09(3)) | ||
| As–S (As–X) total | 2.97(5) (2.95(5)) | ||||
| As40S45Se15 | As–S | 2.273(2) | 0.061(1) | 2.24(3) | 2.25 |
| As–Se | 2.424(2) | 0.074(1) | 0.74(3) | 0.75 | |
| As–Ch total | 2.98(5) | ||||
| As40S40Se20 | As–S | 2.277(2) | 0.066(1) | 1.97(3) | 2 |
| As–Se | 2.419(2) | 0.069(1) | 0.97(3) | 1 | |
| As–Ch total | 2.94(5) | ||||
| As40S30Se30 | As–S | 2.279(2) | 0.061(1) | 1.49(3) | 1.5 |
| As–Se | 2.416(2) | 0.065(1) | 1.48(3) | 1.5 | |
| As–Ch total | 2.97(5) | ||||
| As40S20Se40 | As–S | 2.277(2) | 0.068(1) | 0.95(3) | 1 |
| As–Se | 2.417(2) | 0.069(1) | 1.95(3) | 2 | |
| As–Ch total | 2.90(5) | ||||
| As40Se60 | As–Se | 2.412(1) | 0.0659(2) | 2.93(3) | |
5. Discussion
5.1. Density, glass transition temperature and composition
The measured densities for glasses in the system xAs40Se60·(100 − x)As40S60 shown in Fig. 1a agreed, within error (±0.04 g cm−3), with previously work by Cardinal et al.3 and Snopatin et al.5 and are a first indication that the glass compositions did not deviate from those batched. In contrast, the measurements for the glass transition temperature do not agree with those reported by Cardinal et al. and Snopatin et al. for the same samples.When comparing the glass transition temperatures, Tg, measured in this study with those in the literature (Fig. 1b), it is important to consider how Tg is defined by different researchers. Cardinal et al. clearly state that they define Tg as the point in the region of glass transition with the maximum gradient.3 Data published by Vlček et al.6 yield very similar results to Cardinal et al. and, though it is not explicitly stated, we have assumed that they used a similar definition of Tg. In contrast, Tg values measured by Abdel-Moneim were reported to be calculated using the onset Tg definition.35 The results published by Snopatin et al. for comparable compositions are consistently lower in temperature than all other data sets,5 but the equivalence between the density values given by Cardinal et al. and Snopatin et al. suggests that this difference in reported glass temperatures may arise from a change in definition of Tg rather than because of any major differences in sample composition. The above consideration of results from three different published studies highlights that the definition of Tg used has a significant impact on the values reported, with a difference of ∼10 °C between the Tg,onset and Tg,max for the results in Table 3. Therefore the definition must be clearly stated along with measurements if the results published are to be useful for future researchers. Fig. 1b shows a comparison of Tg,onset and Tg,max measured in this study with the literature. Tg,max values gave generally good agreement with Cardinal et al. and Vlček et al., while the Tg,onset values were closer to those of Abdel-Moneim.35
The glass transition temperatures published by Cardinal et al.,3 Vlček et al.6 and Snopatin et al.5 all decrease linearly as As40Se60 is added to As40S60. Five of the seven Tg,max results agreed, within error, with those of Cardinal et al. and Vlček et al., who observe only a ∼23 °C change in Tg,max across the compositional range. However, the two exceptions, the transition temperatures for As40S45Se15 and As40Se60, have a considerable impact on the interpretation of the data. An analysis of the glass transition temperatures obtained in this study suggest that Tg does not vary linearly in mixed anion glasses, but is instead relatively constant across a wide compositional range. The invariance in the glass transition temperature for glasses in a compositional range from As40S45Se15 to As40S15Se45 suggests that the mixed phase glasses maintain a similar structural motif. Furthermore, the Tg,max values for these glasses were closer to that of As40S60 than As40Se60 indicating that the glass relaxation behaviour is more similar to the sulfide glass than the selenide. Careful analysis of the composition and homogeneity of the glasses is vital to ensure that this interpretation is accurate. The presence of phase separation in the As40Se60 glass, for example, would result in a mix of As–As and Se–Se bonds that could affect Tg. Literature indicates that moving away from the stoichiometric composition, and therefore increasing the number of homopolar bonds, lowers Tg.36,37 However, it should be noted that a review of Tg temperatures for As40Se60, reported in the Sciglass software,38 gave a wide variation in results, ranging from 150 °C to 200 °C, and yielded a mean Tg of 181 °C with a standard deviation of 11 °C. The “anomalous” Tg values reported for As40Se60 in this study were both within this error range.
Compositional analyses of all of the glasses agreed with the batched compositions, within the error of the techniques used (Table 3). The composition for As40S60 determined using XRF (Table 3) was most disparate from the batched composition, suggesting that there may have been a small excess of arsenic in the glass. If this were true, the glass would no longer be comprised of only [AsS3] units, but must have included a number of As–As bonds. The As40Se60 glass, which has an anomalous glass transition temperature, is reported to have a composition of As39Se61 and so is considered to be stoichiometric in all analysis.
5.2. Short range order and homopolar bonds
The glass compositions used in this study have been designed so that, in an ideal glass, each As atom was bonded to three Ch atoms, and each Ch is bonded to two As atoms. Therefore, if homopolar bonds were present, they would have arisen from either an excess of As (as suggested by XRF compositional analysis for As40S60), or from phase separation resulting in As rich and Ch rich regions (see, for example, work by Petri et al.39 and Georgiev et al.40). Phase separation can be intrinsic to the glass, or arise from a lack of inhomogeneity in the glass melt. The structural information gained from Raman spectroscopy, 77Se NMR and neutron and X-ray total scattering were therefore interrogated for evidence of homopolar bonds before stoichiometry (As40Ch60) was accepted.Georgiev et al.40 attributed the weak features, observed in the Raman spectrum of As40S60, at 188 and 233 cm−1 to the vibrations of [As4S4] molecules, which are comprised of As–S and As–As bonds. Using this assignment, and the intensity of the two bands, they estimated that 7% of the As bonds in bulk As40S60 glass were homopolar.40 The correlation functions obtained using neutrons and X-rays, TN(r) and TX(r), were carefully analysed to determine where this concentration of As–As bonding is reasonable.
The simultaneous fits to the correlation functions, TN(r) and TX(r), for As40S60 (Fig. 7) required two peaks to model the distribution of bond lengths fully. The parameters for the fit are given in Table 5. The peak positions, 2.271 ± 0.001 Å and 2.467 ± 0.001 Å, could be interpreted as arising from a distribution of As–S bond lengths, or from As–S and As–As bonds, respectively (see Table 2 and ref. 13). A consideration of the total arsenic coordination number does not aid in determining which interpretation is correct because both yield a total coordination number of 3, within the error of the experiment. The width of the peak fitted at 2.467 Å was 0.029 ± 0.001 Å. This is significantly narrower than the widths of the As–S or As–Se peaks given in Table 5 (∼0.06 Å) and indicates that the peak is not a real measure of a correlation. Furthermore, the second peak is also at a distance that is more than 0.06 Å shorter than the As–As bond length measured using neutrons13 and K edge As EXAFS42 in As rich glasses. Based upon this interpretation, it can be proposed that the slight asymmetry of the As–S peak shape in the neutron correlation function (Fig. 6) arises from a distribution of As–S bond lengths in the glass. Similar asymmetric bond distributions have been observed in correlation functions for oxide glasses containing lone pair cations, such as As, when a Qmax ≥ 30 Å−1 is used for the Fourier transform (i.e. [PbO3]43 and [SbO3]44). For example, a similar two peak fit to the Pb–O distribution in PbO–Al2O3 glasses yielded Pb–O peak positions of ∼2.25 and 2.47 Å.43 In contrast, the presence of small peaks in the Raman spectra at ∼200 cm−1 supports the interpretation that the shoulder arises from a small number of As–As distances in the glass. An As–As coordination number of 0.09 ± 0.03 indicates that between 2 and 4% of arsenic bonds are homopolar, slightly less than the number predicted by Georgiev et al.40 In summary, the measured coordination number of arsenic is close to the expected value of three, and there is some evidence for a small number of As–As bonds. However, the presence of homopolar bonds at these concentrations would have a negligible effect on further analysis and the glass shall be considered as stoichiometric and comprised solely of [AsS3] in the remainder of the discussion. For a more detailed study of As–As bonds in As40S60 careful fitting of TN(r) for a series of AsxS100−x glasses is required to establish robust parameters for S–S, As–S and As–As peaks.
5.3. Changes in network connectivity with composition
Fig. 2c shows the As–Se peak manifold in detail. The Raman spectra have been scaled by the atomic fraction of Se present in the glass to allow a direct comparison the peak intensities and shape. If all Se atoms are bonded to As, the area of the bands in Fig. 2c should be invariant with composition. The linear relationship between x and peak area in Fig. 2b shows this to be true. The average [AsCh3] structural unit in an As40S60 glass changes with the addition of As40Se60 from [AsS3], via the formation of [AsSeS2] and [AsSe2S] units as Se replaces S in the glass network, until all As atoms are in [AsSe3] units. A clear shift in the position of the maximum intensity of the As–Se band to lower wave numbers was observed as Se was added to the glass. Freitas et al.11 and Li et al.10 have previously attributed this red shift to a change in the next nearest neighbours for the selenium atoms. It should be noted that the peak manifolds at ∼250 cm−1 for As40S45Se15 and As40S40Se20 (x = 25 and 33) were similar, indicating that there was little change in the local Se environment at these two compositions.
The experimental neutron correlation functions, TN(r), for four ternary glasses are shown in Fig. 8 with the calculated weighted correlation functions. There was excellent agreement between the experimental data and weighted sum over the distance ranges 0–3.2 Å and 4.25–5.4 Å. For each glass sample, the difference between the experimental correlation function and the calculated weighted sum in the region of the first peak in TN(r) was of the same order as the noise in the low r region. The first significant peak in the residual, attributed to Se⋯S distances, was observed at ∼3.75 Å and is narrow and well defined. The As40S30Se30 glass exhibits the largest residual, because this is the composition where the potential for mixing is maximised. Fig. 9 compares the differences between the experimental Se⋯S correlation and a calculated partial correlation for Se⋯Se distances (calculated from the reported crystal structures using the XTAL program47) in crystalline As40Se60.33 There is close agreement between the first peak maximum for this simulation (3.71 Å) with the residuals (3.75 Å) and a general agreement in the shape of the residuals with the Se⋯Se partial correlation function over the range of 0–10 Å. This supports the hypothesis that the differences shown in Fig. 9 arose from a Ch⋯Ch correlation.
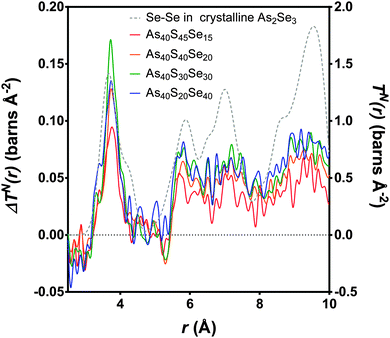 | ||
| Fig. 9 The differences, (ΔTN(r)) as calculated in Fig. 8, between the experimental TN(r) and the weighted sum (coloured lines, left y-axis). The peak with the maximum intensity is the As40S30Se30 glass, where the potential for mixing is at the maximum. The Se–Se partial correlation function is simulated for crystalline As40Se60 (ref. 33) (dashed grey line, right y-axis). | ||
n SeS values for each glass containing selenium were calculated by integrating the area of the peaks at ∼3.75 Å in Fig. 9 and using eqn (11). The results are given in Table 3 and shown in Fig. 4b. If the Se and S anions were evenly distributed throughout the glass, a linear variation would be expected. A linear fit was made to nSeS for glasses containing ≥50 mol% As40Se60, and is shown as a red dashed line in Fig. 4b. An extrapolation of this linear fit to x = 0 indicated that a single Se atom in an arsenic sulphide glass would have 7.3 sulfur neighbours, nSeS = 7.3. This is close to nSeSe = 7.33, calculated from the crystal structure of crystalline As40Se60,33 when using a maximum Se⋯Se distance of 4.0 Å. The good agreement between the extrapolated value for nSeS in the As40S60 and nSeSe in crystalline As40Se60 indicated that the change in nSeS was directly dependent on the total number of sulfur atoms in the glass. Therefore, selenium and sulfur atoms were randomly mixed when >50% of Ch atoms are selenium. However, Fig. 4b shows that values for nSeS deviated from this linear correlation when <50% of the chalcogen atoms in the glass were selenium. To achieve a good fit to all values of nSeS a second order polynomial was required. The intersection of this new fit with x = 0 occurred at 4.6. Such a markedly non-linear variation in nSeS with composition suggested that either there was a preference for like atoms to cluster when there was a high concentration of sulfur in the glass, or that the average number of anions around the Se atom decreased from 7.3 to 4.6 as the amount of sulfur in the glass was increased from 0 to 60 at%. Conclusive evidence in favour of either suggestion is lacking. However, if the total number of Ch atoms around selenium decreased as sulfur was added to the glass, a corresponding expansion of the glass network would be expected. Instead, the shift in peak positions in iN(Q), shown in Fig. 5a, indicated that a network contraction occurs with increased sulfur content.
The interpretation of the Raman spectra in Section 4.3.1 supports the suggestion that nSeS varies non-linearly with x. The shape of the As–Se band in the Raman spectra is strongly influenced by the surrounding environment. However, the shape of the As–Se peaks in Fig. 2c for As40S45Se15 and As40S40Se20 are very similar. This suggests that the local environment of the As–Se bonds was not changing as fast as would be expected if S and Se atoms were mixing randomly in the glass. Furthermore, the non-linear change in the intensity of the As–S peak in the Raman spectra suggested a preference for [AsS3] units to persist in the glass to higher concentrations than random mixing would allow. In summary, the combination of Raman and total scattering data indicates that there may be preferential clustering of selenium and sulfur in xAs40Se60·(100 − x)As40S60 glasses, when there is a high concentration of the sulfur in the glass. As a selenium atom has a radius that is ∼20% larger than sulfur,48 this proposed clustering could be driven by an inability for a network of [AsS3] units to accommodate easily the larger Se atoms.
5.4. A comparison of glass structure with physical properties
The results presented here, coupled with the literature, show that n2 varies non-linearly with composition in this glass system.3,4,49 Several theories have been put forward to explain the structural changes that underpin this non-linear response. Nasu et al.50 related an increase in non-linear optical susceptibility, χ(3) (related to n2) to a denser glass network, highlighting that the low χ(3) measured for GeSe4 corresponds to a high molar volume. However, this is not consistent with the glass system studied here, where the molar volume and n2 both increased as selenium atoms were doped into the network. More recent work by Harbold et al.4 showed that there is a relationship between the band gap energy, Eg, and n2. n2 was shown to increase rapidly when the photon energy of the laser was >0.5Eg. Sanghera et al.49 explicitly related n2 with this normalised photon energy. However, it should be noted that the band gap energy and the onset of the absorption edge, λgap, also showed evidence of non-linear variation with composition.3,49 Therefore, we suggest that the same changes in the glass structure affect both λgap and n2. Petit et al.51 showed an inverse relationship between the density of lone-pairs in the glass and n2. However, this is in direct conflict with the accepted understanding that lone-pairs enhance n2 in heavy metal oxide glasses (see ref. 52 for example). Harbold et al. highlighted this inconsistency and demonstrated that it is possible to maintain constant λgap and n2 values for selected glasses in the Ge–As–Se system that exhibit different lone pair densities.53From the brief discussion above, it is clear that the relationship between n2, λgap, and glass structure is complicated and remains unresolved. The results of this study suggest an alternative structural origin for the non-linear variation in n2 with x in the xAs40Se60·(100 − x)As40S60 glass system. Fig. 10 shows a linear relationship between n2 and nSeS. We therefore propose that the variation in n2 in this series of glasses is related to the arrangement of the chalcogen atoms in the glass. The variation in nSeS only varied linearly, indicating a well-mixed glass, when x > 0.5. For glasses containing low concentrations of Se, there was evidence that the Se and S atoms preferentially cluster, which may result in a sublinear change in the non-linear refractive index of the glass. Work by Maklad et al. supports this interpretation,54 as follows. Careful observation of i absorptions in the xAs40Se60·(100 − x)As40S60 glass system indicated that the expected vibrations from [AsS2Se] and [AsSSe2] units are missing from an x = 40 mol% As40Se60 glass, and are only weakly present in an x = 93 mol% As40Se60 glass. The lack of vibrations from mixed units has been interpreted as a sign of non-random distribution of the chalcogens in these glasses and suggests that [AsS3] and [AsSe3] units form in preference to mixed units such as [AsS2Se], when Se is present in low concentrations. This is in good agreement with the structural results presented here, which suggests that full mixing of the chalcogen atoms does not occur until ∼50 mol% As40Se60 is present. Furthermore, the thermal analysis suggests that the mixed chalcogen glasses retain a more sulfide-like relaxation behaviour across the compositional range.
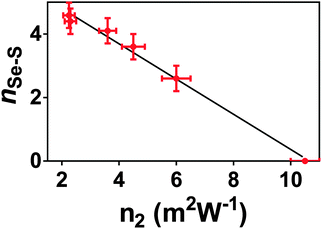 | ||
| Fig. 10 n Se–S plotted against n2. The relationship between these two glass properties varies linearly. nSe–S is, necessarily, zero for As40Se60, and the value for As40S60 is calculated from the second order polynomial fit in Fig. 4b. | ||
6. Conclusions
A series of xAs40Se60·(1 − x)As40S60 glasses, where x = 0, 25, 33.3, 50, 66.7, 75 and 100 mol% As40Se60, was investigated. Values of n2, measured using Z-scan, were found to vary between 2.3(5) × 1018 m2 W−1 for As40S60 to 10.5(5) × 1018 m2 W−1 for As40Se60 and show a nonlinear variation with composition that was modelled using a second order polynomial equation. These results are in reasonable qualitative agreement with the trends in n2 reported elsewhere. Through careful analysis of total correlation functions, obtained using neutrons and X-rays, it has been shown that there is a lower than expected number of sulfur atom nearest neighbours around a selenium atom in glasses containing ≤50 mol% As40Se60. The variation of nSeS with x requires a second order polynomial fit to the data and this non-linear variation is attributed to the clustering of chalcogens in the glass. The observed variation in nSeS was shown to have a linear relationship with n2, and it is suggested that the spatial distribution of chalcogen atoms in the glass is a structural factor contributing to the non-linear changes in n2 with composition. To be able to investigate the medium range structure of this As–S–Se glasses and determine the partial correlation functions for Ch⋯Ch correlations more fully structural modelling methods, such as Molecular Dynamics and Reverse Monte Carlo, will be used.Acknowledgements
Experiments at the ISIS Pulsed Neutron and Muon Source were supported by a beamtime allocation (RB1120102) from the Science and Technology Facilities Council. Special thanks is given to Professor Alex Hannon for support during the experiment. We also thank Diamond Light Source for access to Beamline I15.References
- A. Popescu, Non-Crystalline Chalcogenicides, Kluwer Academic Publishers, Dordrecht, The Netherlands, 2000 Search PubMed.
- F.-Y. Lin, O. Gulbiten, Z. Yang, L. Calvez and P. Lucas, J. Phys. D: Appl. Phys., 2011, 44, 045404 CrossRef.
- T. Cardinal, K. A. Richardson, H. Shim, A. Schulte, R. Beatty, K. Le Foulgoc, C. Meneghini, J. F. Viens and A. Villeneuve, J. Non-Cryst. Solids, 1999, 256–257, 353 CrossRef.
- J. M. Harbold, F. Ö. Ilday, F. W. Wise, J. S. Sanghera, V. Q. Nguyen, L. B. Shaw and I. D. Aggarwal, Opt. Lett., 2002, 27, 119 CrossRef CAS.
- G. E. Snopatin, V. S. Shiryaev, V. G. Plotnichenko, E. M. Dianov and M. F. Churbanov, Inorg. Mater., 2009, 45, 1439 CrossRef CAS.
- M. Vlček, A. V. Stronski, A. Sklenař, T. Wagner and S. O. Kasap, J. Non-Cryst. Solids, 2000, 266–269(Part 2), 964 CrossRef.
- B. Bureau, J. Troles, M. Le Floch, F. Smektala and J. Lucas, J. Non-Cryst. Solids, 2003, 326, 58 CrossRef.
- B. Bureau, J. Troles, M. LeFloch, F. Smektala, G. Silly and J. Lucas, Solid State Sci., 2003, 5, 219 CrossRef CAS.
- R. Golovchak, O. Shpotyuk, J. S. McCloy, B. J. Riley, C. F. Windisch, S. K. Sundaram, A. Kovalskiy and H. Jain, Philos. Mag., 2010, 90, 4489 CrossRef CAS.
- W. Li, S. Seal, C. Rivero, C. Lopez, K. Richardson, A. Pope, A. Schulte, S. Myneni, H. Jain, K. Antoine and A. C. Miller, J. Appl. Phys., 2005, 98, 053503 CrossRef PubMed.
- J. A. Freitas, U. Strom and D. J. Treacy, J. Non-Cryst. Solids, 1983, 59–60, 875 CrossRef CAS.
- A. C. Wright, B. G. Aitken, G. Cuello, R. Haworth, R. N. Sinclair, J. R. Stewart and J. W. Taylor, J. Non-Cryst. Solids, 2011, 357, 2502 CrossRef CAS PubMed.
- E. Bychkov, M. Miloshova, D. L. Price, C. J. Benmore and A. Lorriaux, J. Non-Cryst. Solids, 2006, 352, 63 CrossRef CAS PubMed.
- E. Bychkov, C. J. Benmore and D. L. Price, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 172107 CrossRef.
- A. C. Wright, J. Non-Cryst. Solids, 1989, 112, 33 CrossRef.
- E. Lorch, J. Phys. C: Solid State Phys., 1969, 2, 229 Search PubMed.
- N. Norman, Acta Crystallogr., 1957, 10, 370 CrossRef CAS.
- J. Krogh-Moe, Acta Crystallogr., 1956, 9, 951 CrossRef CAS.
- A. L. Patterson, Z. Kristallogr., 1935, 90, 517 CAS.
- A. K. Soper, J. Phys.: Condens. Matter, 2007, 19, 335206 CrossRef CAS PubMed.
- M. Sheikbahae, A. A. Said, T. H. Wei, Y. Y. Wu, D. J. Hagan, M. J. Soileau and E. W. Vanstryland, Z-Scan – A simple and sensitive technique for non-linear refraction measurements, Spie - Int Soc Optical Engineering, Bellingham, 1990 Search PubMed.
- J. McCarthy, PhD thesis, Institute of Photonics and Quantum Sciences, Heriot-Watt University, 2013.
- A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88 CrossRef CAS PubMed.
- A. K. Soper, Rutherford Appleton Laboratory Technical Report, RAL-TR-2011-013, 2011.
- A. C. Hannon, W. S. Howells and A. K. Soper, IOP Conf. Ser., 1990, 107, 193 Search PubMed.
- A. P. Hammersley, ESRF Internal Report, ESRF98HA01T, 1998.
- A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235 CrossRef.
- L. B. Skinner, C. J. Benmore and J. B. Parise, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 662, 61 CrossRef CAS PubMed.
- A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2011, 44, 714 CrossRef CAS.
- N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192 CrossRef.
- D. M. Pickup, R. Moss and R. J. Newport, J. Appl. Crystallogr., 2014, 47, 1790 CrossRef CAS.
- T. Wang, X. Gai, W. H. Wei, R. P. Wang, Z. Y. Yang, X. Shen, S. Madden and B. Luther-Davies, Opt. Mater. Express, 2014, 4, 1011 CrossRef.
- A. C. Stergiou and P. J. Rentzeperis, Z. Kristallogr., 1985, 173, 185 CrossRef CAS PubMed.
- R. J. Gillespie, Chem. Soc. Rev., 1992, 21, 59 RSC.
- N. S. Abdel-Moneim, PhD thesis, Faculty of Engineering, University of Nottingham, 2012.
- R. Y. Golovchak, A. Kozdras, C. Gorecki and O. I. Shpotyuk, J. Non-Cryst. Solids, 2006, 352, 4960 CrossRef CAS PubMed.
- A. Feltz, H. Aust and A. Blayer, J. Non-Cryst. Solids, 1983, 55, 179 CrossRef CAS.
- MDL SciGlass-6.0. MDL Information Systems, San Leandro, 2003.
- I. Petri, P. S. Salmon and H. E. Fischer, Phys. Rev. Lett., 2000, 84, 2413 CrossRef CAS.
- D. G. Georgiev, P. Boolchand and K. A. Jackson, Philos. Mag., 2003, 83, 2941 CrossRef CAS.
- T. Wagner, S. O. Kasap, M. Vlček, A. Sklenar and A. Stronski, J. Mater. Sci., 1998, 33, 5581 CrossRef CAS.
- C. Y. Yang, M. A. Paesler and D. E. Sayers, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 10342 CrossRef CAS.
- E. R. Barney, A. C. Hannon, D. Holland, D. Winslow, B. Rijal, M. Affatigato and S. A. Feller, J. Non-Cryst. Solids, 2007, 353, 1741 CrossRef CAS PubMed.
- R. G. Orman, D. Holland and A. C. Hannon, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2008, 49, 15 CAS.
- G. Delaizir, M. Dussauze, V. Nazabal, P. Lecante, M. Dollé, P. Rozier, E. I. Kamitsos, P. Jovari and B. Bureau, J. Alloys Compd., 2011, 509, 831 CrossRef CAS PubMed.
- M. Deschamps, C. Roiland, B. Bureau, G. Yang, L. Le Pollès and D. Massiot, Solid State Nucl. Magn. Reson., 2012, 40, 72 CrossRef PubMed.
- A. C. Hannon, Rutherford Appleton Laboratory Report, RAL-93-063, 1993.
- B. Cordero, V. Gómez, A. E. Platero-Prats, R. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832 RSC.
- J. S. Sanghera, C. M. Florea, L. B. Shaw, P. Pureza, V. Q. Nguyen, M. Bashkansky, Z. Dutton and I. D. Aggarwal, J. Non-Cryst. Solids, 2008, 354, 462 CrossRef CAS PubMed.
- H. Nasu, K. Kubodera, M. Kobayashi, M. Nakamura and K. Kamiya, J. Am. Ceram. Soc., 1990, 73, 1794 CrossRef CAS PubMed.
- L. Petit, N. Carlie, A. Humeau, G. Boudebs, H. Jain, A. C. Miller and K. Richardson, Mater. Res. Bull., 2007, 42, 2107 CrossRef CAS PubMed.
- B. Jeansannetas, S. Blanchandin, P. Thomas, P. Marchet, J. C. Champarnaud-Mesjard, T. Merle-Mejean, B. Frit, V. Nazabal, E. Fargin, G. Le Flem, M. O. Martin, B. Bousquet, L. Canioni, S. Le Boiteux, P. Segonds and L. Sarger, J. Solid State Chem., 1999, 146, 329 CrossRef CAS.
- J. M. Harbold, F. O. Ilday, F. W. Wise and B. G. Aitken, IEEE Photonics Technol. Lett., 2002, 14, 822 CrossRef.
- M. S. Maklad, R. K. Mohr, R. E. Howard, P. B. Macedo and C. T. Moynihan, Solid State Commun., 1974, 15, 855 CrossRef CAS.
- A. C. Hannon, Neutron diffraction database, http://www.alexhannon.co.uk/DBindex.htm, last accessed: [29/01/2015] Search PubMed.
| This journal is © the Owner Societies 2015 |