A QCT study of the role of the symmetric and antisymmetric stretch mode excitations of methane in the O(³P) + CH₄ (ν_i = 0, 1; i = 1, 3) reaction

Abstract

Quasi-classical trajectory calculations based on a full-dimensional analytical potential energy surface have been performed at different collision energies to analyze the role of symmetric (ν₁ = 1) and antisymmetric (ν₃ = 1) stretch modes of methane in reactivity and dynamics of the O(³P) + CH₄ (ν_i = 0, 1; i = 1, 3) gas-phase reactions. Both CH stretch modes increase reactivity with respect to the methane vibrational ground-state by factors between 1.5 and 3. Additionally, the ν₁ = 1 mode is slightly more reactive than the ν₃ = 1 mode by factors between 1.4 and 1.1 depending on the collision energy. Both stretch modes give similar pictures of OH product vibrational and angular distributions. The former finding shows inverted OH (0, 1) vibrational population, discarding mode selectivity, and the latter shows a shift of the scattering angle from backward to sideways with the vibrational excitation and therefore a change in the mechanism. For the dynamic properties analyzed, the theoretical results for the ν₃ = 1 mode reproduce the experimental evidence, while those for the ν₁ = 1 mode await confirmation.

---

1. Introduction

The study of the effect of the reactant vibrational excitation on dynamics represents a theoretical and experimental challenge, which is complicated in the case of polyatomic systems due to the increase in the degrees of freedom and possible coupling between vibrational modes. The O(³P) + CH₄ (ν_i = 0, 1) → OH + CH₃ gas-phase reaction is an illustrative example of these difficulties.^1–8 The influence of methane vibrational excitation has been experimentally^1,2,6 and theoretically^3–5,7,8 analyzed in the last decade. Recently, Pan and Liu⁶ studied in a crossed-beam experiment the effects of one-quantum excitation of the methane antisymmetric stretch mode and have planned a future study of the symmetric stretch mode effects. These authors report that vibrational excitation increases reactivity with respect to the vibrational ground-state; that the OH product presents an inverted vibrational distribution, OH (ν′ = 1) : OH (ν′ = 0) ∼ 0.85 : 0.15; and that the backward product vibrational distribution in the vibrational ground-state shifts toward sideways with the vibrational excitation. Motivated by this experiment, two theoretical studies were performed simultaneously^7,8 using quasi-classical trajectory (QCT) calculations on different potential energy surfaces (PES), the Czakó and Bowman surface (CB)⁹ and the PES-2014¹⁰ surface developed by our group, where for a direct comparison with the experiment only CH₃ (ν = 0) was tested. We found that the antisymmetric CH stretch excitation by one quantum increases reactivity with respect to the vibrational ground-state; that the vibrational branching ratio of OH (ν′ = 1) : OH (ν′ = 0) is 0.8 : 0.2; and that the scattering angle shifts from backward to sideways with the vibrational excitation. These results reproduce at least qualitatively the experimental evidence⁶ and improve previous theoretical results using the CB surface.^4,5,7

When vibrational excited molecules are involved an interesting issue is mode selectivity, and for the title reaction previous theoretical results^4,5,7 give contradictory results. Liu et al.⁴ and Czakó et al.⁵ found that excitation of both stretch modes increases reactivity, the symmetric mode having a higher efficacy, although this behaviour is only evident when 8D quantum molecular (QM) studies are performed, while the QCT calculations give similar reactivity, and therefore with no mode selectivity. More recently⁷ Czakó, on analysing only the CH₃ (ν = 0) product, found a similar behaviour in QCT calculations, i.e., the absence of mode selectivity.

Analysis of the coupling terms between the normal modes and the reaction coordinate on the PES-2014 surface shows that while the symmetric stretch mode is strongly coupled to the reaction coordinate, the antisymmetric stretch mode is not coupled. Therefore, with this naïve picture one could expect a great difference in reactivity between both modes, and even a change in dynamics. To understand the effects of the symmetric (ν₁) and antisymmetric (ν₃) stretch modes of methane, which differ by only 172 cm⁻¹, on dynamics in the O(³P) + CH₄ (ν_i = 0, 1; i = 1, 3) reactions, in the present paper we report an exhaustive QCT study using the full-dimensional analytical PES-2014 surface.

2. Computational details

Using the VENUS96 code¹¹ QCT calculations were performed based on the PES-2014 surface. This surface presents an advantage with respect to other surfaces, namely, the energy and first energy derivatives (gradients) are analytical. Thus, at a similar computational time, while the PES-2014 surface is able to calculate millions of trajectories, other surfaces can calculate only thousands of trajectories.

(a) Initial conditions

For a direct comparison with the experiment⁶ and previous theoretical calculations,^7,8 at collision energies of 8.7, 9.7, 12.4 and 18.0 kcal mol⁻¹, independent sets of trajectories were run, each with 1 000 000 trajectories, for the CH₄ in its vibrational ground-state (ν = 0) and symmetric and antisymmetric stretch modes independently excited by one quantum, CH₄ (ν₁ = 1, ν₃ = 1). In addition, trajectories at lower collision energies (5.0 and 6.0 kcal mol⁻¹) were run to determine their threshold behaviour. In total 16 000 000 trajectories were run. For each energy and vibrational state we determined the maximum impact parameter, b_max, while from a Boltzmann distribution rotational energy was obtained by thermal sampling at 298 K. This large number of trajectories minimizes statistical errors and contrasts with the 55 000 trajectories per collision energy run in previous QCT calculations.⁷ The computational advantage is due to the availability of analytical gradients on the PES-2014 surface.

Table 1 lists the CH₄ harmonic vibrational frequencies obtained using the PES-2014 surface together with the experimental values for comparison. In general, this surface reproduces the experimental information, thus permitting a reasonable comparison between the symmetric and antisymmetric stretch modes. These modes differ by only 172 cm⁻¹, and add 2931 and 3103 cm⁻¹ ∼ 8.4 and 8.9 kcal mol⁻¹, respectively, to the total energy.

Table 1 Methane vibrational frequencies (cm⁻¹)

Name	Character	D^a	PES-2014^b	Exp.^c
a Degeneracy. b Harmonic values from ref. 10. c Experimental anharmonic values from ref. 12.
ν 3	Antisymmetric stretch	t	3103	3019
ν 1	Symmetric stretch	a	2931	2917
ν 4	Umbrella bend	t	1335	1306
ν 2	Torsional bend	e	1500	1534

---

(b) Final conditions

A related problem with QCT calculations is the zero-point energy (ZPE) violation. The integral cross section is then calculated using two opposite approaches: standard binning (SB), where all trajectories contribute equally to the dynamics; and Gaussian binning (GB), where Gaussian statistical weights are assigned to each trajectory. In previous studies on this system^8,10 we find that the SB approach gives an adequate dynamics description of the problem, while the GB approach discards a great number of reactive trajectories, and for the same statistical error the cost of the calculation is prohibitive.

In the products of reaction, only the CH₃ (v = 0) state was considered, having taken into account the following approach, which has been successfully tested in previous studies:^8,10 since its ZPE is 18.4 kcal mol⁻¹, and the lowest vibrational mode adds 580 cm⁻¹ ∼ 1.7 kcal mol⁻¹, which gives a total vibrational energy of 20.1 kcal mol⁻¹, we considered only reactive trajectories with vibrational energy below 20.0 kcal mol⁻¹.

The following product notation will be used in the present paper: (n,0)_g,symm,asymm, where n represents the vibrational action of the OH product, 0 the CH₃ co-product vibrational ground-state, and the subscripts g, symm and asymm represent, respectively, the vibrational ground-state and the symmetric and antisymmetric stretch modes independently excited by one quantum in the methane reactant.

Finally, the differential cross section, DCS, was fitted using the Legendre moment method.¹³

3. Results and discussion

(a) Excitation function

For the O(³P) + CH₄ (ν = 0, ν₁ = 1, ν₃ = 1) reactions, the QCT excitation functions (reaction cross section, σ, versus collision energy) are plotted in Fig. 1, together with experimental data⁶ (when available) for comparison.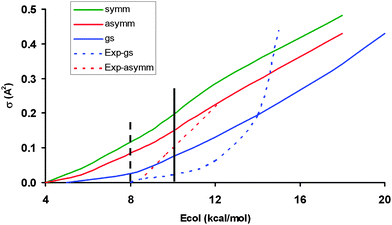

Fig. 1 Reaction cross sections as a function of the collision energy (kcal mol⁻¹) for the CH₄ vibrational ground-state (blue line), CH antisymmetric mode excitation (red line) and CH symmetric stretch mode excitation (green line). The theoretical results include the 2/3 spin–orbit degeneracy factor. Dashed lines correspond to the experimental data,⁶ which are normalized with QCT values at 14.7 kcal mol⁻¹ for the vibrational ground-state and at 12.4 kcal mol⁻¹ for the CH antisymmetric stretch mode. The solid and dashed vertical lines are the theoretical and experimental adiabatic energetic thresholds, respectively. Given the very large number of trajectories, the error bars are negligible, ±0.01, and have not been represented.

The present study analyzes the role of the CH symmetric stretch mode (ν₁ = 1) excitation by one quantum. First, the ν₁ = 1 excitation increases reactivity with respect to the vibrational ground-state by factors between 1.5 and 3 depending on the collision energy. Second, the excitation function presents quasi-linear energy dependence, associated with a softening of the transition state bending potential. These two findings are similar to the behaviour observed for the CH antisymmetric stretch mode excitation (ν₃ = 1) previously studied.⁸ Finally, the CH symmetric stretch mode is 1.8–1.1 times more reactive than the CH antisymmetric mode, in the range of 5.0–18.0 kcal mol⁻¹, and 1.4–1.2 in the experimental range. Unfortunately, no experimental information is available for comparison. Theoretically, previous QCT calculations^4,5,7 on the CB surface have reported similar reactivity for both modes, and only when QM calculations⁴ were performed on this surface it was found that the CH symmetric mode is more reactive than the antisymmetric one. It is expected that this discrepancy using different PESs will inspire future (and planned)⁶ experimental studies.

Next we analyzed these behaviours in more detail. First, the change in the excitation function shape from concave-up (the methane vibrational ground-state) to linear dependency suggests a possible crossing for both functions. This crossing was reported by Czako⁷ using the QCT/CB method and was suggested by the experiment⁶ if the experimental data are extrapolated. Our QCT/PES-2014 results suggest the existence of this crossing, though at higher collision energy, and the fact that it is not as evident as the experiment is a direct consequence of the excitation function shape for the vibrational ground-state theoretically obtained, which presents a lesser curvature than the experiment. In fact, if this function presents better agreement with the experiment, one would expect a crossing of about 15 kcal mol⁻¹. Second, the increase in reactivity with respect to the vibrational ground-state is explained by the energy flow from the CH stretch modes (ν₁,ν₃) to the reaction coordinate. This flow is measured by the coupling between the normal mode i and the motion over the course of the reaction coordinate, F, B_i,F(s) coupling term,

where cⁱ_lγ(s) is the lγ component of the eigenvector for mode i and ν_lγ(s) is the lγ component of the normalized gradient vector. However, using the PES-2014 surface, the analysis of B_i,F(s) terms shows that only the CH symmetric stretch mode is coupled to the reaction coordinate (Fig. 2), and with this naïve picture, one could expect a very different reactivity between the CH symmetric and antisymmetric stretch modes. In order to explain this behaviour, we analyzed the coupling terms between vibrational modes, B_i,i′(s), which give information about the energy flow between the normal vibrational modes i and i′ in the reaction process,

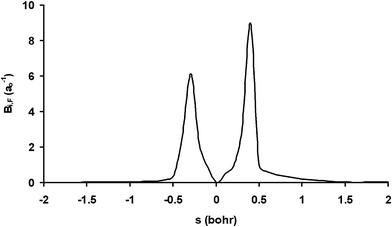Fig. 2 Coupling term, B_i,F(s), for the CH symmetric stretching mode, as a function of the reaction coordinate, s.

In the entrance channel we found that both stretch modes are coupled, indicating energy flow between them. Therefore, part of the energy originally deposited on the CH symmetric stretch mode flows to the antisymmetric one and loses effectiveness, indicating that the reaction is not adiabatic.

Finally, the different threshold behaviour between theory and experiment is analyzed for the CH₄ (ν = 0) vibrational state, where comparison is possible. While experimentally¹⁴ analyzed a reactive threshold at E_o ∼ 8 kcal mol⁻¹ was reported, the adiabatic barrier obtained with the PES-2014 surface is 10.2 kcal mol⁻¹. This discrepancy in energy must arise from tunnelling effects, which are not possible in QCT calculations due to their classical nature. Therefore, all QCT reactivity below this value (10.2 kcal mol⁻¹) is artificial and no reactivity is allowed below this barrier. We propose that these conclusions can be extended to the excited vibrational states, CH₄ (ν₁,ν₃).

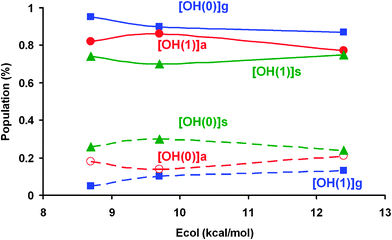
(b) OH vibrational distribution

Fig. 3 shows the OH (ν′ = 0, 1) product vibrational distributions correlated with the CH₃ (ν′ = 0) co-product at different collision energies for methane in the ν₁ = 1 initial vibrational state. The results for CH₄ (ν = 0, ν₃ = 1)^8,10 are also included for comparison.

Fig. 3 QCT OH vibrational distributions of the O(³P) + CH₄ (ν = 0, ν₁ = 1, ν₃ = 1) → OH (ν′ = 0, 1) + CH₃ (0) reactions as a function of collision energy using the standard binning, SB, approach. The subscripts “g”, “s” and “a” stand for the reactant ground-state, and symmetric and antisymmetric stretch modes excited by one quantum.

When the CH symmetric stretching mode is excited by one quantum, an inverted OH (ν′ = 0, 1) vibrational population is obtained, with a ratio of 0.24 : 0.75 at E_col = 12 kcal mol⁻¹, and is scarcely dependent on collision energy. At this collision energy, Czakó⁷ using the QCT/CB method obtained ratios of 0.30 : 0.60 and 0.45 : 0.55 with the SB and GB approaches, respectively, where in the SB approach the difference of 1 is due to the artificial population OH (ν′ = 2).

In both theoretical studies the OH vibrational distributions are similar for the CH symmetric and antisymmetric stretching excitations, although the two studies present different results. To analyze this discrepancy, we use the only experimental data reported, CH₄ (ν₃ = 1).⁶ At E_col = 12.4 kcal mol⁻¹ Pan and Liu⁶ obtained a ratio of OH (ν′ = 0, 1) ∼ 0.15 : 0.85, as compared to 0.21 : 0.77 and 0.45 : 0.55 obtained in our previous work⁸ and by Czakó,⁷ respectively. The best agreement obtained using our PES-2014 surface and the similar behaviour of the CH₄ (ν₃ = 1) and CH₄ (ν₁ = 1) excitations lend confidence to the behaviour found in the present work for the ν₁ mode.

Therefore, the theoretical results rule out mode selectivity in this reaction, which is associated with coupling of both stretching modes in the entrance channel.

(c) Product angular distribution

For an analysis of the dynamics of the symmetric CH stretch mode (ν₁) excitation, Fig. 4 shows the scattering angles at three collision energies, together with the previous results, CH₄ (ν = 0, ν₃ = 1),⁸ for comparison. Compared with the CH₄ (ν = 0) state, the ν₁ = 1 excitation shifts the product angular distribution to sideways from backward distribution, this shift being more evident when the collision energy increases. Therefore, the excitation of this CH stretching mode enlarges the reactive cone of acceptance, associated with high impact parameters. For instance, at E_col = 12.4 kcal mol⁻¹ the b_max impact parameter increases from 2.1 Å for the CH₄ (ν = 0) state to 2.6 Å. This behaviour is similar to that previously found⁸ for the CH antisymmetric stretching excitation. Note that theoretical QCT/CB calculations reported by Czakó⁷ give similar results, i.e., the angular distributions of the symmetric and antisymmetric stretch mode excitations are similar.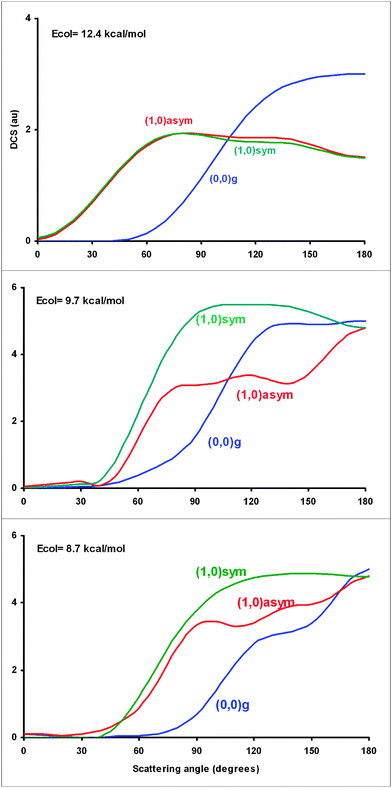

Fig. 4 Differential cross section (arbitrary units) versus scattering angle (degrees) at three collision energies, 12.4, 9.7 and 8.7 kcal mol⁻¹, using the PES-2014 surface. The blue, red and green lines are for CH₄ (ν = 0), CH₄ (ν₃ = 1) and CH₄ (ν₁ = 1) reactions, respectively, and the subscripts “g”, “symm” and “asymm” for the reactant ground-state, and symmetric and antisymmetric stretch modes excited by one quantum. For a correct comparison with the experiment⁶ when available, the results are scaled to the maximum value for each reaction and collision energy. Given the very large number of trajectories, the error bars are negligible and have not been represented.

4. Mechanistic origin of the vibrational excitation effect on reactivity: a comparison between reactions

Two decades ago, Levine¹⁵ studying atom–diatom reactions and Zare et al.¹⁶ studying polyatomic reactions proposed that the mechanism of vibrational enhancement is due to the opening up of the cone of acceptance, extending the range of impact parameters, known as the induced steric mechanism. Although this is a necessary condition to explain qualitatively this effect, it is not a sufficient condition to explain it quantitatively.

We analyzed this behaviour by studying three reactions, Cl(²P) + CH₄ (ν_i = 0, 1), O(³P) + CH₄ (ν_i = 0, 1) and OH + NH₃ (ν_i = 0, 1), as paradigms of “late” (product-like), “central” (neither reactant-like nor product-like) and “early” (reactant-like) barriers. When the stretching mode of the polyatomic reactant is vibrationally excited by one quantum, an increase in reactivity with respect to the vibrational ground-state is produced depending on the system. Thus, for the Cl(²P) + CH₄ reaction, Zare et al.¹⁶ experimentally reported an increase of 30 ± 15, and our group¹⁷ theoretically reported ≈15. In the O(³P) + CH₄ reaction, Pan and Liu⁶ experimentally found an increase of 1.5–3 depending on the collision energy, in agreement with recent theoretical calculations.^4,5,7,8 Finally, for the “early” OH + NH₃ reaction, our group¹⁸ reported QCT calculations with an increase of 1.1–3 depending on the collision energy. Therefore, regardless of the type of reaction, “late”, “central” or “early”, vibrational excitation enhances reactivity with respect to the vibrational ground-state, in agreement with the induced steric mechanism, but with different intensity.

To explain this behaviour we propose that, in addition to the induced steric mechanism, other factors should be taken into account.

(a) Energy-dependent barrier

In the naïve line-of-centre model,¹⁹ the relation between the reaction cross section, σ, and the energy barrier, E_o, is given bywhere p is the steric factor, which excludes collisions in the incorrect configuration for reaction; d is the separation of reactants, which is related to the scattering angle, θ, and the impact parameter, b, by the expressionand E_T is the total energy.

Taking the values from the original papers^8,17,18 and following Zare's suggestion¹⁶ that vibrational excitation removes the barrier energy for reaction (E_o ∼ 0) without changing the p factor, the cross section changes with the vibrational excitation from 0.27pπd² to pπd² for the Cl(²P) + CH₄ reaction, and from 0.60pπd² to pπd² for the O(³P) + CH₄ and OH + NH₃ reactions. Thus, the reaction cross section is enhanced by factors σ*/σ of 3.7, 1.7 and 1.7 for the three reactions, respectively. These line-of-centre predictions are correct for the “central” and “early” reactions, but significantly lower for the Cl(²P) + CH₄ reaction. Therefore, this naïve model (which depends on the energy) is not sufficient to explain the differences.

(b) Angle-dependent barrier

To explain the mechanistic origin of the vibrational enhancement, Levine¹⁵ and Zare et al.¹⁶ proposed the vibrationally induced steric mechanism by opening the reactive cone of acceptance, which is related to weaker requirements for the linearity of the transition-state structure. Therefore, in addition to the energetic requirements, the orientation effect and the angle-dependent barrier must be taken into account.

Using the information from the original papers^8,17,18 and based on the product angular distributions, for the O(³P) + CH₄ (ν_i = 0, 1) and Cl(²P) + CH₄ (ν_i = 0, 1) reactions, it was found theoretically that while the vibrational ground-state shows backward scattering, the methane reactant stretching mode excitation provokes sideways and forward scattering for both reactions, respectively. For the OH + NH₃ reaction the situation is more complicated due to the presence of deep wells in the entry and exit channels, which cloud the final conclusions. In a previous paper¹⁸ we found different mechanisms, and therefore, different dynamics behaviours, depending on the collision energy. Thus, while at high energies all trajectories are direct, with backward scattering, at lower energies a percentage of trajectories are indirect, between 3% and 25%, depending on the collision energy, with backward–forward scattering. The NH stretching mode vibrational excitation by one quantum leads in both cases (direct and indirect) to more forward scattering. Clearly, the effect of the wells in the entry and exit channels also influences the vibrational excitation effect, and this will doubtlessly be studied in the future in more detail, both theoretically and experimentally, especially in the case of polyatomic systems.

Therefore, the stretching mode excitation enlarges the cone of acceptance in all cases, which is associated with large impact parameters, but more effectively in the Cl(²P) + CH₄ reaction, which explains the larger σ*/σ ratio.

(c) Location of the barrier

Finally, the venerable Polanyi's rules (although originally proposed for atom + diatom reactions) show that the location of the barrier (late, central or early) influences the effectiveness of the vibrational energy to surmount the reaction barrier. Thus, vibrational energy is more effective than an equivalent amount of translation energy in the case of “late” barriers, i.e., product-like, because vibrational excitation enlarges the stretching bond, which approaches the product geometry. In this case, the translational energy creates a bottleneck of the reaction. The opposite is true in the case of “early” barrier reactions, while the case of “central” barrier reactions is still an open question.⁴

Based on the data in previous studies^8,17,18 and following Polanyi's rules, the reactant stretching vibrational excitation will increase reactivity more favourably in the case of the Cl(²P) + CH₄ (ν_i = 0, 1) reaction, which is in agreement with experimental/theoretical results. The case of the OH + NH₃ (ν_i = 0, 1) reaction, which presents a σ*/σ ratio of 1.1–3, merits an additional discussion, because the two effects are contrary. In this “early” barrier reaction the vibrational motion, orthogonal to the reaction coordinate, creates a bottleneck in the reactant region, inhibiting the reaction, while the induced steric mechanism by opening up the cone of acceptance favours the reaction. In this case, the latter effect is dominant with respect to the former.

Based on these arguments and in the very limited examples analyzed, we propose a guide for future studies (Table 2), which is merely suggestive, on the effects of vibrational excitation on reactivity. As an application of this guide we analyze two problematic cases.

Table 2 Effects of the vibrational excitation on the reactivity for several reactions, from “late” to “early” barriers^a

Type	Energetic effect	Steric effect	Barrier location	Total
a The symbols “+”, “−” and “= “represent a positive, negative or neutral effect on the reactivity. The larger number of symbols “+” represents a larger effect. “Balanced” indicates that the final result depends on the balance of the “+” and “−” effects.
Late	++	++	++	++
Central	+	+	+	+
Early	+ or =	+	−	Balanced

---

(A) The effect of the CH stretching vibrational excitation on the reactivity of the F + CHD₃ → FH + CD₃ reaction. A priori, in this “early” barrier reaction, vibrational excitation opens the cone of acceptance, leading one to expect an enhancement of reactivity. However, experimentally²⁰ and theoretically²¹ the opposite behaviour was found, so the CH stretching mode excitation by one quantum inhibits the break of this bond.

Let us analyze independently the factors previously identified. This very exothermic reaction is a practically barrierless reaction, and so the influence of the first factor, energy-dependent barrier, is practically negligible, σ*/σ ≈ 1. With respect to the second factor, while the CHD₃ vibrational ground-state shows backward scattering, the CHD₃ (ν = 1) excitation yields forward scattering. Thus, the CH vibrational excitation opens the cone of acceptance, allowing larger impact parameters and favouring the enhancement of reactivity, σ*/σ > 1, which is contrary to the experimental evidence. Finally, considering the third factor, this reaction presents an “early” barrier, and following Polanyi's rules, vibrational energy is scarcely effective to surmount the barrier. This vibrational motion is orthogonal to the reaction coordinate producing a bottleneck in the reactant region, σ*/σ < 1. In agreement with the experiment, the bottleneck effect dominates in the induced steric mechanism, and the final (balanced) result is inhibition of reactivity.

(B) The effect of the bending mode excitation on reactivity in the O(³P) + CH₄ (ν) reaction. In this case we assume similar effects to the stretching mode, although they are not as sharp, due to the difference of energies in play. Zhang and Liu¹ posed the following question, how active is the bend excitation of methane in the reaction with O(³P)? They experimentally reported that excitation of this mode does not promote reactivity, contrary to previous theoretical studies,^22–26 although more recent theoretical studies^5,27 have found that this bending excitation slightly enhances reactivity, which is in better agreement with the experiment.

Let us analyze this effect in function of the three factors previously identified. In the study of the first factor, the energy-dependence barrier, we assumed that the stretching mode excitation removes the barrier reaction (E_o ∼ 0). Now, the bend mode excitation will have a minor effect, by diminishing the barrier but not removing it. The cross section (eqn (3)) changes from 0.60pπd² to 0.80pπd², which represents a σ*/σ factor of 1.3 against 1.7 for the stretching excitation. With regard to the second effect, Czakó et al.⁵ and our group²⁷ reported that bending excitation also opens the cone of acceptance with respect to the vibrational ground-state, but it is less effective than the stretching excitation. In consequence, the enhancement of reactivity will be lower than in the stretching case. Finally, we analyze the third factor, the barrier location. A priori, this factor is independent of the vibrational mode excitation, and therefore its contribution is neutral. In conclusion, the bending mode excitation slightly enhances reactivity, in agreement with the experiment and recent theoretical predictions, and in any case, less than the stretching mode. This enhancement is related to the coupling of the bending mode with the reaction coordinate, suggesting that this mode promotes the reaction.²⁷

Finally, it is important to note that this guide is merely suggestive, because it is based on a limited number of cases; it is focussed on stretching vibrations and there are other factors which can alter or maximize these effects. Below we discuss some factors, but the list is not exhaustive: (i) the presence of stabilized complexes in the entrance/exit channels. In the vibrational ground-state the presence of wells causes many trajectories to be “indirect”, “to visit” the wells, and some to return to reactants, these being non-reactive trajectories. Vibrational excitation gives energy to the system, diminishes the number of “indirect” trajectories, increasing reactivity, independent of whether they are “late”, “central” or “early” barriers. (ii) Another effect affecting this guide is intramolecular vibrational redistribution (IVR), which is important in polyatomic systems. In an adiabatic reaction, one vibrational mode conserves its energy along the reaction path. However, due to IVR energy transfer between modes is possible, losing its initial energy. We found this behaviour in several reactions,^17,18,27 and so conclusions on the vibrational effects remain clouded.

5. Conclusions

From the QCT/PES-2014 results on the role of symmetric (ν₁ = 1) and antisymmetric (ν₃ = 1) stretch mode excitations in the O(³P) + CH₄ (ν_i = 0, 1) reaction at different collision energies, the following conclusions can be highlighted:

(1) In the experimental energy range, the independent excitation by one quantum of symmetric and antisymmetric stretch modes increases reactivity with respect to the vibrational ground-state by factors of 1.5 and 3 depending on the collision energy, where the symmetric mode is slightly more reactive than the antisymmetric one by factors of only 1.4 and 1.1 on the collision energy. A priori, this behaviour could seem strange because only the symmetric mode is coupled to the reaction coordinate and one would expect greater differences. However, the coupling of both modes in the entrance channel yields loss of adiabaticity and consequently levelling of their effects.

(2) Vibrational excitation of both stretch modes yields similar OH product inverted vibrational distributions, OH (0 : 1) ∼ 0.2 : 0.8, discarding mode selectivity in this reaction.

(3) Product angular distribution is also similar for both stretch modes. They yield a shift from the backward hemisphere for the methane vibrational ground-state to the sideways hemisphere, which is more evident when collision energy increases. Thus, the excitation of both modes yields a change in mechanism, from rebound to stripping, associated with large impact parameters.

(4) The theoretical results for the CH₄ (ν = 0) and CH₄ (ν₃ = 1) reactions agree with the available experimental data, and those for the CH₄ (ν₁ = 1) reaction have not yet been experimentally reported.

(5) Finally, we analyze different factors to explain the mechanistic origin of the vibrational excitation effect on reactivity, and we propose a suggestive guide to evaluate its effects.

References

1. B. Zhang and K. Liu, J. Phys. Chem. A, 2005, 109, 6791.
2. F. Wang and K. Liu, Chem. Sci., 2010, 1, 126.
3. W. Yang, F. Meng and D. Wang, J. Phys. Chem. A, 2013, 117, 12236.
4. R. Liu, M. Yang, G. Czakó, J. M. Bowman, J. Li and H. Guo, J. Phys. Chem. Lett., 2012, 3, 3776.
5. G. Czakó, R. Liu, M. Yang, J. M. Bowman and H. Guo, J. Phys. Chem. A, 2013, 117, 6409.
6. H. Pan and K. Liu, J. Chem. Phys., 2014, 140, 191101.
7. G. Czakó, J. Chem. Phys., 2014, 140, 213102.
8. M. Monge-Palacios, E. Gonzalez-Lavado and J. Espinosa Garcia, J. Chem. Phys., 2014, 141, 094307.
9. G. Czakó and J. M. Bowman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7997.
10. E. González-Lavado, J. C. Corchado and J. Espinosa-Garcia, J. Chem. Phys., 2014, 140, 064310.
11. W. L. Hase, R. J. Duchovic, X. Hu, A. Komornicki, K. F. Lim, D.-H. Lu, G. H. Peslherbe, K. N. Swamy, S. R. Van de Linde, A. J. C. Varandas, H. Wang and R. J. Wolf, VENUS96: A General Chemical Dynamics Computer Program, QCPE Bull., 1996, 16, 43.
12. M. W. Chase, C. A. Davis, J. R. Downey, D. J. Frurip, R. A. McDonald and A. N. Syverud, JANAF Thermochemical tables, J. Phys. Chem. Ref. Data, 1985, 14(suppl. 1).
13. D. G. Truhlar and N. C. Blais, J. Chem. Phys., 1977, 67, 1532.
14. J. Zhang and K. Liu, Chem. – Asian J., 2011, 6, 3132.
15. R. D. Levine, J. Chem. Phys., 1990, 94, 8872.
16. W. R. Simpson, T. P. Rakitzis, S. A. Kandel, T. Lev-on and R. Zare, J. Phys. Chem., 1996, 100, 7938.
17. J. Sanson, J. C. Corchado, C. Rangel and J. Espinosa-Garcia, J. Chem. Phys., 2006, 124, 074312.
18. M. Monge-Palacios and J. Espinosa-Garcia, J. Phys. Chem. A, 2013, 117, 5042.
19. R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics and Chemical Reactivity, Oxford University Press, New York, 1987.
20. W. Zhang, H. Kawamata and K. Liu, Science, 2009, 325, 303.
21. G. Czakó and J. M. Bowman, J. Chem. Phys., 2009, 131, 244302.
22. D. C. Clary, Phys. Chem. Chem. Phys., 1999, 1, 1173.
23. J. Palma and D. C. Clary, Phys. Chem. Chem. Phys., 1999, 2, 4106; J. Palma and D. C. Clary, J. Chem. Phys., 2000, 112, 1859; J. Palma and D. C. Clary, J. Chem. Phys., 2001, 115, 2188.
24. J. Palma, J. Echave and D. C. Clary, Chem. Phys. Lett., 2000, 363, 529.
25. B. Kerkeni and D. C. Clary, J. Phys. Chem. A, 2003, 107, 10871.
26. H.-G. Yu and G. Nyman, J. Chem. Phys., 2000, 112, 238.
27. J. Espinosa-Garcia, J. Phys. Chem. A, 2014, 118, 3572.

---