Pool-BCGA: a parallelised generation-free genetic algorithm for the ab initio global optimisation of nanoalloy clusters

Abstract

The Birmingham cluster genetic algorithm is a package that performs global optimisations for homo- and bimetallic clusters based on either first principles methods or empirical potentials. Here, we present a new parallel implementation of the code which employs a pool strategy in order to eliminate sequential steps and significantly improve performance. The new approach meets all requirements of an evolutionary algorithm and contains the main features of the previous implementation. The performance of the pool genetic algorithm is tested using the Gupta potential for the global optimisation of the Au₁₀Pd₁₀ cluster, which demonstrates the high efficiency of the method. The new implementation is also used for the global optimisation of the Au₁₀ and Au₂₀ clusters directly at the density functional theory level.

---

1 Introduction

Modern nanoscience involves the study of promising nanoscale materials, which exhibit a wide variety of interesting physical and chemical properties. Nanoparticles composed of atoms and molecules lie between the atomic and bulk regimes with strongly size and composition dependent properties.¹ It remains desirable to close the gap between well-understood bulk properties and our knowledge of atomic behaviour in nanoscale research.

A detailed structural characterisation of this transition regime is therefore of high interest in order to rationalise the exceptional characteristics of nanoscale materials. Generating geometric structure candidates for a comparison with experimental observations is laborious for large systems and eventually becomes infeasible. From a theoretical view it is useful to carry out a global optimisation of the potential energy surface (PES) as a function of all coordinates, while the level of theory needed has to adequately represent the system being studied.

Since the electronic structure of large nanoparticles is expected to resemble the bulk phase, tailored model or empirical potentials (EPs) such as Gupta,² Sutton–Chen,³ and Murrell–Mottram,⁴ fitted to properties of the solid phase, enable a reasonable description of the PES. For smaller nanoparticles, i.e. nanoclusters, a quantum chemical treatment becomes necessary for which the computational costs are greater than in the case of using EPs. But unbiased global optimisation at this higher level of theory therefore requires the development of an efficient algorithm.

Nanoalloys (nanoparticles composed of more than one metal) are of considerable interest for their catalytic, optical and magnetic properties.⁵ Their global optimisation is further complicated by the presence of a large number of homotops – inequivalent permutational isomers.^6,8 For this reason, the strategy was developed of optimising selected structures with DFT after searching by means of atomistic models using the second-moment approximation to the tight-binding model (SMATB).⁷ Evolutionary algorithms such as the Lamarckian Birmingham cluster genetic algorithm (BCGA),⁹ which combines local minimisation with a genetic algorithm (GA), are useful tools for searching the conformational space for the global minimum (GM) structure and lowest-energy local minima, especially when combined with first principles methods in the density functional theory (DFT) based BCGA approach.¹⁰ This procedure notably enables the theoretical investigation of elaborate mono- and bimetallic clusters using a GA with results consistent with experiments.^11–16 For details on global optimisation algorithms, especially focused on genetic algorithms and basin hopping techniques, the reader is referred to the literature.^17,18

The first use of GAs for global geometry optimisation of molecular clusters was reported by Hartke,¹⁹ and Xiao and Williams,²⁰ using binary encoded geometries and bitwise acting genetic operators on binary strings.^21–23 Later a GA approach that operated on cartesian coordinates of the atoms was introduced by Zeiri,²⁴ which removed the requirement for encoding and decoding binary genes.⁹ This was followed by the development of GAs for cluster optimisation by Deaven and Ho,²⁵ who performed gradient driven local minimisations for newly generated cluster structures. Further, Doye and Wales established how local minimisations effectively transform a multidimensional PES into a staircase-like surface, where the steps represent basins of attraction.²⁶ This coarse-grained representation of the PES reduces the conformational space and therefore simplifies the PES that the GA has to search. The local minimisations generally correspond to a Lamarckian evolution, since individuals pass on a proportion of their characteristics to their offspring. This procedure has been found to improve the efficiency of global optimisations and is implemented within the BCGA program, following the approach of Zeiri using real-valued cartesian coordinates.^9,24 Recent GA implementations are the OGOLEM code for arbitrary mixtures of flexible molecules of Dieterich and Hartke,²⁷ the hybrid ab initio genetic algorithm (HAGA), for surface and gas-phase structures,^28,29 and the gradient embedded genetic algorithm program (GEGA) for the global optimisation of mixed clusters formed by molecules and atoms.^30,31 Very recently the surface BCGA (S-BCGA)³² and the first principles based GA of Vilhelmsen and Hammer³³ for the global optimisation of supported clusters have been reported. Also very recently the perturbation theory re-assignment extended GA for mixed-metallic clusters has proven to be very useful.³⁴

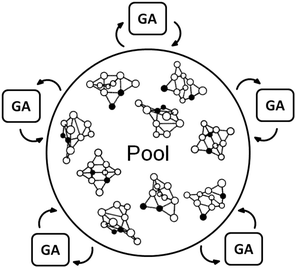
The traditional generation based BCGA program is a sequential code where local optimisations of individuals are not independent from one-another. In fact, a limitation on treatable cluster sizes or rather the level of computational sophistication arises due to the sequentially performed geometry optimisations acting as a bottleneck.³⁵ Newly created individuals of a given population are geometrically relaxed with respect to their total energy. The best population members, with respect to their fitness (determined by a fitness function which depends on the total energy), are then selected for mating and mutation in order to create novel structures and to form the next generation. This cycle is then repeated until the energy of the lowest-lying isomers changes by less than a specified threshold within a certain number of generations. Thus, if more than the optimum number of processors is used in a first principles based global optimisation, the overall CPU time plateaus and the cores are used inefficiently due to the imperfect parallelisation of the local optimisations. In order to improve the efficiency of this approach, the goal must be to enable the independent relaxation of several geometries at the same time as schematically shown in Fig. 1, where several GA processes simultaneously optimise geometries managed by a global database (pool). This, however, cannot be implemented efficiently within the generation-based BCGA program.

Fig. 1 Scheme of a global database (containing structural information) organizing slaves which independently apply genetic operators to the n individuals of the database. The population is held by a master acting as a pool of constant size.

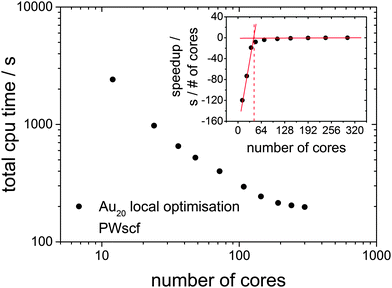
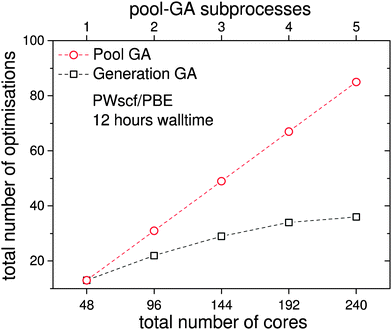
Since the DFT-BCGA code employed here makes use of a plane-wave self-consistent field (PWscf) pseudopotential approach, a benchmark calculation of a geometry optimisation for the predicted GM structure of Au₂₀ (T_d symmetry)^36–38 has been performed in order to demonstrate the importance of an improved GA parallelisation to counter the imperfect DFT parallelisation. The total CPU time in these minimisations, starting from a random atom displaced version of the already optimised structure is shown in Fig. 2. The Au₂₀ cluster was chosen for the benchmark calculations since, especially for such a large system, local optimisations lead to a slowdown in the global optimisation. The corresponding benchmark calculations indicate that the optimum number of processors should be below 100 cores (the best price-performance ratio should be for 36–64, as shown in the inset of Fig. 2) since a larger number of cores would not speed up the calculations efficiently. The total CPU time can be reduced by one order of magnitude going from 10 cores to 100 but does not improve significantly when using up to 300 cores. Benchmark calculations for a local optimisation of the Au₁₀ cluster show the same tendency, with lower absolute CPU time, and are therefore not shown here. This indicates the importance of developing a parallelised GA code which uses several GA subprocesses performing local minimisations on an efficient and ideal number of processors (48 cores in this case) at the same time, managed by a global database (see Fig. 1).

Fig. 2 Logarithmic benchmark plot of a local relaxation for the T_d isomer of Au₂₀ starting from a random atom displaced version of the already optimised structure at the PBE/PWscf level of theory. It is shown, that the optimum number of processors is below 100 cores in this case as using a larger number of cores would not scale efficiently. The inset shows the derivative of the total CPU time versus the number of processors. The optimal number of processors for the global optimisation is in the range 36–64.

In this work, we present a significantly improved GA implementation which incorporates the BCGA and eliminates serial bottlenecks by replacing the generation based GA approach by a flexible pool model,³⁵ here denoted as pool-BCGA. Within this pool strategy individual subprocesses share the entire work leading to a parallelisation of the algorithm. This procedure allows several geometry optimisations to be run at the same time. The gain in speed is obvious as local optimisations are the bottlenecks in a global optimisation, especially when using ab initio methods in local relaxations. In principle, one could also think about running parallel geometry optimisation tasks in the generation based BCGA. But, several ongoing optimisations would have different time demands and therefore each generation would have to wait for the slowest population members leading to processor idle times.

The development of parallel GA implementations has previously been reported for both atomic and molecular clusters,^{27,33,35,40,41} Global geometry optimisation at the DFT⁴² or ab initio⁴³ level is generally found to be very expensive and not suitable for larger clusters, for which global optimisation at a lower level of theory would be appropriate. This leads to the commonly found two-stage procedure of performing the global search at e.g. the force-field or semi-empirical level, followed by a DFT or ab initio refinement of the best candidates.⁴⁴ In the DFT-BCGA code used in this work, the global optimisation is performed at the relatively cheap pseudopotential PWscf level, which enables larger systems to be treated at the DFT level, while the best candidates can still be refined using a higher level of theory. However, the direct GA method is easily implemented with higher level approaches such as MP2 and CC calculations. The flexible concept replaces the generation based algorithm by using a global database consisting of geometric and energetic information about a specified number of individuals. Several independent subprocesses make use of this database by applying mating and mutation operators to the pool members and form new individuals. These new individuals compete with current members of the pool and are immediately added to the pool if they are lower in energy.

We first test the method for the global optimisation of the Au₁₀Pd₁₀ cluster, using the Gupta potential, for an extensive statistical analysis of the new implementation. The 20-atom cluster is also interesting from a catalytic point of view,⁴⁵ and offers an ideal test system, especially due to the large number of homotops N = (N_Au + N_Pd)!/N_Au!N_Pd! ≈ 185 000 for a given geometry.⁸ The resulting knowledge from these investigations, in terms of mating and mutation, is further used for the DFT based global optimisation of the Au₁₀ cluster. It represents a suitable test system for the DFT case in order to compare the efficiency of both implementations, as it has been well studied in the past.^38,46,47 Finally, the parallelisation of the code is tested by carrying out the global optimisation of Au₂₀ at the DFT level, a system previously well studied experimentally^36,37 while geometries have been found by genetic algorithms^38,48 and the basin-hopping approach³⁹ based on DFT.

2 Methodology

2.1 Computational details

In the benchmark calculations, employing the Gupta empirical potential in geometry optimisation steps, many-body scaling parameters are chosen according to values for Au–Pd nanoclusters with 34-/38-atoms⁴⁹ and 98-atoms¹³ from the literature.

In the DFT calculations, the Perdew–Berke–Ernzerhof (PBE) xc functional,⁵⁰ and ultrasoft pseudopotentials of the Rabe–Rappe–Kaxiras–Joannopoulos type,⁵¹ with nonlinear core corrections are employed. For the calculation of electronic energies, a kinetic energy cutoff of 40 Ry and an electronic self consistency criterion of 10⁻⁵ eV are used. The efficiency of electronic convergence for metallic states is improved using the Methfessel–Paxton smearing scheme.⁵² Local relaxations are performed with total energy and force convergence threshold values of 10⁻³ eV and 10⁻² eV Å⁻¹, respectively. All DFT calculations are performed within the Quantum Espresso (QE) package.⁵³

2.2 Pool-BCGA

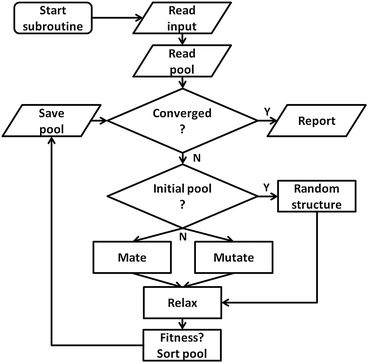
To make use of the flexible parallelisation possibilities associated with a pool configuration, the application of mating and mutation operators to given geometries and their local optimisation and fitness assignment is managed by independently working pool-BCGA subprocesses synchronizing with a global database. As well as handling the atom coordinates and total energy of all structures currently in the pool, the global database is also needed to coordinate the individual subprocesses during runtime. The general workflow of the pool strategy is depicted in Fig. 3. The first step (“initial-mode”) consists of constructing an initial pool of individuals by generating random structures within a spherical or cubic simulation cell, which is set to be larger than the dimensions of the random cluster. This continues until the desired pool size is reached followed by the second step (“pool-mode”). In the pool-mode, mating and mutation operators are employed on clusters chosen according to either a roulette selection condition, where a random selection is weighted by the assigned fitness, or a tournament selection, and adopt the Deaven–Ho crossover method using a cut and splice crossover operator.²⁵ Random rotations are performed on parent clusters which are then cut horizontally about one (1-point) or two (2-point) positions parallel to the xy plane. Complementary fragments are then spliced together. For 1-point crossover, the cutting plane can be chosen at random or weighted according to the relative fitnesses of the two parents, while in the 2-point case the cutting planes are chosen at random.

Fig. 3 The genetic operators are applied by the subprocesses on the members of this pool. The flowchart shows how a single pool subprocess works independently from other instances, while all subprocesses communicate with the global database.

In contrast to the default settings of the generation based GA, where the number of offspring grows with an increasing mutation rate, in a pool-GA calculation mutation and mating are performed with a certain probability as the pool size is kept fixed. This must be taken into account when setting the parameters in a typical pool-GA run. The offspring structures compete with the structures present in the pool according to their total energy after their local optimisation. Offspring with a better fitness (lower total energy) replace higher lying pool members. After checking for repeated optimised structures using a moments of inertia selection routine, the pool is sorted by ascending total energy. Finally, convergence is achieved when the minimum energy in the pool changes by less than a pre-defined energy difference (typically 10⁻³ eV) within a specified total number of optimised geometries. This ensures an elitist behaviour of the GA in combination with good diversity in the pool. If convergence is not reached, the subprocesses start a new cycle, repeating the steps described above.

When executing the pool-GA, general runtime configuration settings are read from input files before the GA initially synchronises with the global database. The GA then enters the pool convergence loop. If the convergence criterion is not reached, the GA continues with a check for the current mode (“initial-” or “pool-mode”). As mentioned above, initial-mode means that new structures are created by randomly choosing atom coordinates inside the simulation cell while the pool-mode uses either mating or mutation operators in order to form new individuals. The new structures are then locally optimised by either passing the atom coordinates to an external ab initio quantum chemistry program (e.g. QE⁵³ or NWChem⁵⁴) or one of the empirical potentials (e.g. Gupta) embedded in the code. This pool-based approach allows the code to be easily restarted if it runs out of CPU time. The user is left free to restart as many subprocesses as preferred, depending on the available computational resources. However, aborted local optimisations are not restarted. Instead, new subprocesses are initiated, starting with new geometries which are generated from the current pool configuration by the evolutionary principles mentioned above.

3 Results and discussion

3.1 Assessment with the Gupta potential: Au₁₀Pd₁₀

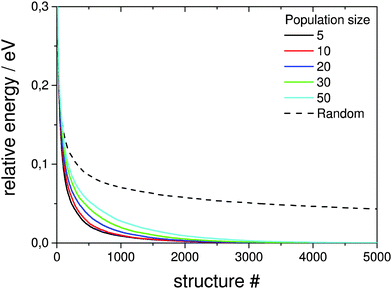
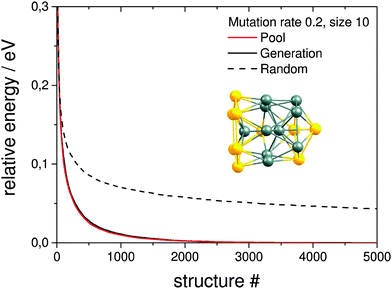
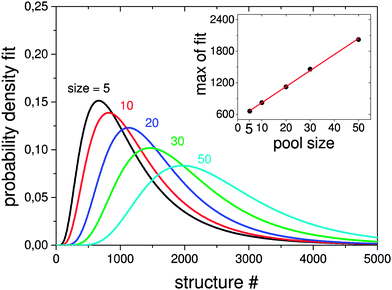
Here the a single pool-GA subprocess and the previous generation based GA are applied to the global optimisation of the Au₁₀Pd₁₀ cluster using the Gupta potential. This procedure serves as a test of the implementation before the GA is extended to the DFT-based version. Using a less expensive calculation also allows the parameter space for using the pool-GA to be classified and to show the equivalence of both implementations. However, only the parameters in which the two implementations differ substantially are tested here. For a detailed description of the BCGA code in general its functionality and settings, the reader is directed to the literature.⁹

Fig. 4 compares the pool-GA, for different pool sizes, to a random structure search. The same mutation rate is used in all calculations, with an atom exchange mutation rate of 0.5 because of homotops, beside the cluster replacement mutation adding new random structures. By applying the atom exchange mutation operator to the replacement mutation, the GA becomes considerably more efficient.^17,55 The solid lines represent averaged evolutionary progress plots from 1000 GA runs for each case. Evolutionary progress plots describe the evolution of the globally lowest-lying structure with the number of generations or optimised structures, respectively. The runs are averaged in order to test reproducibility and permit a meaningful statistical statement. Increasing the population size tends to reduce the efficiency of finding the GM. This is due to the increasing number of individuals in the pool and taking into consideration the same roulette selection scheme and parameters used in all calculations, a higher probability for selecting bad parents is to be expected when the pool size is increased. The optimum population size should be large enough to accommodate a high structural diversity, but small enough to remain largely elitist. A comparison to the generation-based GA, in the same way as mentioned above, shows the same behaviour and is therefore not depicted here. The random structure search, which in both cases acts as an internal standard, illustrates the high efficiency of both GA implementations in general and shows that a single pool-GA subprocess has a comparable efficiency to the generation-based GA. The pool-GA and the generation based approach compare well, as shown in Fig. 5, where both implementations are compared to a random structure search. Typically, the random search is not able to find the GM. Fig. 6 shows lognormal fits to probability densities of finding the GM after a certain number of optimised structures within the 1000 GA runs for several pool sizes. An additional plot, embedded in this figure, describes the linear scale up of the maximum number of optimisations needed versus the pool size. The good comparability of both GA approaches makes the pool-BCGA implementation a powerful tool for the prediction of cluster structures since many subprocesses can be run at the same time, while the convergence of the pool, using a single subprocess, compares well to the generation based code. This allows a much higher efficiency through communication of several subprocesses via the global database.

Fig. 4 Comparison of averaged evolutionary progress plots for different population sizes for a single pool-GA subprocess. A constant mutation rate of 0.2 with an atom exchange rate of 0.5 is employed. Each solid line represents the evolution of the global energetically lowest-lying structure versus the number of optimised structures averaged over 1000 GA runs to demonstrate reproducibility. The implementation is also compared to a random structure search as internal standard for probing the general efficiency and comparability.

Fig. 5 Comparison of averaged evolutionary progress plots for the generation based GA and the single pool-GA for a population size of 10 using a mutation rate of 0.2 and an exchange rate of 0.5. Also included is the result of a random structure search. The GM structure of the Au₁₀Pd₁₀ cluster at the Gupta potential level is embedded.

Fig. 6 Lognormal fits to probability densities of finding the GM in 1000 GA runs depending on the population size. The number of optimisations needed to find the GM scales linearly with the size as can be seen in the inset.

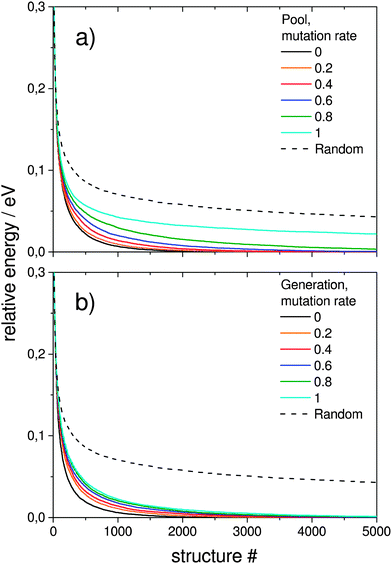
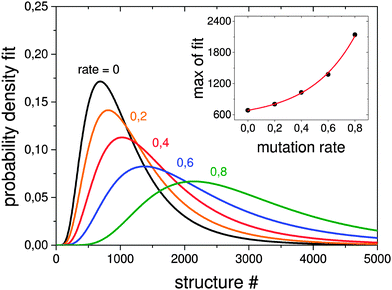
In order to test how the mutation rate influences both a single pool-GA subprocess and the generation based code, Fig. 7 shows averaged evolutionary progress plots where both GAs are compared for different mutation rates while using a population size of 10. The general trend is that mutation reduces the efficiency of finding the GM structure which means that mutation on average produces higher lying structures. While the pool-GA, shown in Fig. 7(a) rapidly loses efficiency with increasing mutation rate, the generational GA (Fig. 7(b)) is less influenced, which initially might appear as an unexpected result. It becomes clearer, however, if one considers, that in the pool implementation the population size is kept fixed. In the traditional BCGA the number of offspring is, by default, 0.8 times the generation size. The mutation rate is then multiplied by the sum of the generation size and the number of offspring. For a population size of 10 and a mutation rate of 0.2, this means 8 offspring are generated from mating and 3.6 mutants on average since (10 + 8) × 0.2 = 3.6. For the pool-GA, therefore, the efficiency seems to be lowered with increasing mutation rate due to the reduced mating rate which makes the implementation less elitist. However, the structural diversity in a given population can be increased by using a low mutation rate and, therefore, it should not be completely neglected. Again lognormal fits to probability densities of finding the GM after a certain number of optimised structures within 1000 GA runs, depending on the mutation rate, are shown in Fig. 8. The plot embedded in this figure shows an exponential scale up of the maximum number of optimisations needed versus the mutation rate. The probability densities for mutation rates larger than 0.8 could not be well fitted due to the very small efficiency of finding the GM.

Fig. 7 Influence of the mutation rate on the averaged evolutionary progress plots averaged over 1000 GA runs for of (a) a single pool-GA subprocess and (b) the generation based GA for a constant size of 10 compared to a random structure search as an internal standard. Mutation reduces the efficiency of finding the GM.

Fig. 8 Lognormal fits to probability densities of finding the GM in 1000 GA runs depending on the mutation rate. The number of optimisations needed to find the GM scales exponentially with the mutation rate as can be seen in the inset. The probability density for higher mutation rates or a random structure search cannot be well fitted due to the very small efficiency of finding the GM.

3.2 Assessment with plane wave DFT

3.2.1 Au₁₀. Since the systematic global optimisation of neutral Au_n (n = 2–20) cluster structures has been reported previously using GAs coupled with DFT,^38,48 we employ this system in order to test the efficiency of the DFT based pool-GA. First, global optimisation is performed for the Au₁₀ cluster using the sequential generation based DFT-BCGA program with a mutation rate of 0.1 and a population size of 10. The pool-GA is further used to perform a global optimisation of the same cluster with a pool size of 10 and a mutation rate of 0.1 in order to test whether both implementations find the GM and the same local minima. Additionally, the total number of optimised structures is compared for both cases in order to explicitly prove the parallelisation efficiency for a given example. The benchmark calculations illustrated in Fig. 9 show the total number of optimised structures for a limit of 12 hours walltime for up to 5 pool subprocesses each ideally running on 48 processors, showing the best price-performance ratio in local relaxations (see Fig. 2). The generation based GA is also compared running on up to 240 cores, which is the same amount as in the calculations using 5 pool subprocesses. It is clear that the sequential GA plateaus when using a large number of cores due to the imperfect DFT parallelisation, while a linear scale-up in the pool-GA case is evident, when using an optimum number of cores.

Fig. 9 Comparison of the total number of geometry optimisations from the pool-GA, with up to five subprocesses each running on 48 cores, to the generation based approach as obtained in 12 hours. A linear scale-up of the total number of optimisations is observed when several parallel working subprocesses are used on an optimum number of cores. The top horizontal axis, showing the number of subprocesses, only corresponds to the pool calculations.

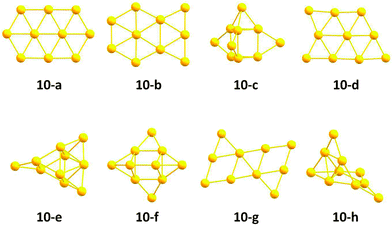
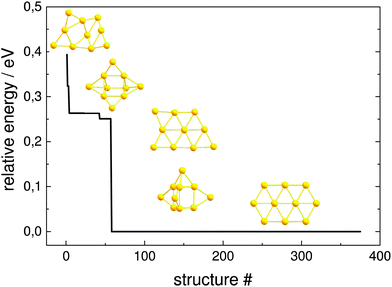
The resulting structures below 0.4 eV from the predicted GM, as obtained at the pwSCF/PBE level of theory, are shown in Fig. 10. Both implementations are able to find identical local minima when optimising a comparable number of structures. The evolutionary progress plot (Fig. 11) shows an example for the pool-GA case, where the GM is found after the optimisation of about 50 structures. This number, however, varies from run to run due to the stochastic nature of the GA, which originates from constructing the initial population by producing random structures. In any case, it shows how the current best (lowest energy) solution evolves towards the planar GM isomer 10-a with D_2h symmetry.

Fig. 10 Structures of Au₁₀ below 0.4 eV from the predicted GM (10-a) as obtained from the DFT-based pool-GA global optimisation approach. The nomenclature of the individual isomers is sorted by increasing energy at the pwSCF/PBE level of theory.

Fig. 11 Evolution of the globally lowest-lying isomer for Au₁₀ with the number of optimised structures within a pool-GA run, relative to the energy E₀ of the GM isomer 10-a. Each step represents a new global minimum depicted here within the pool-GA run.

The potential lowest energy isomers below 0.4 eV, as obtained at this level of theory, including the planar GM isomer 10-a are in agreement with the previous findings of Götz et al.⁴⁷ However, the trigonal prism with both triangular faces and two rectangular faces capped, suggested by Choi et al.,⁵⁶ has been found to lie high in energy at this level of theory, as well as all other isomers found in these previous studies. A new planar isomer 10-g, which has been described for the Au₁₀⁻ cluster,⁵⁷ and a 3D structure 10-e were also found to lie below 0.4 eV. Nevertheless, it should be mentioned that the relative energies obtained at this level of theory, using loose convergence criteria, should always be treated with care. A reminimisation of the structures at a higher level of theory or the use of tighter convergence conditions can unpredictably change the energetic ordering, although 10-a is expected to remain the GM.

The PES can be described by a sequence of local minima inter-connected by transition states where monotonic sequences form funnels.⁵⁸ A given topology, once in a funnel, must eventually overcome several energy barriers in order to reach the GM or another specific local minimum as the PES is explored. This means that a given local optimisation within a GA optimisation task could potentially relax into a so-called metabasin with small geometrical deviation from the minimum. Therefore energetic discrepancies should not only be discussed as depending on the xc functional and pseudopotentials used, but should also be attributed to the cases where local optimisations end in metabasins near a local minimum, leading to an apparently wrong energy ordering.

However, this should not be interpreted as a problem. Genetic algorithms used in this manner can be thought of as a coarse grain filter. The idea is to reduce a large configuration space to a manageable size. The reduced configurational space then opens up the possibility of a more detailed description of only a few isomers at a higher level of theoretical complexity, often required for the description of binary clusters in combination with experiments.

3.2.2 Au₂₀. The ability of the pool-GA to scale linearly with the number of processors is shown in Fig. 9. This allows the global optimisation of cluster structures, directly at the pwSCF/PBE level, for clusters larger than previously possible with the sequential GA in a reasonable time. The pool-GA is used to perform a global optimisation on the Au₂₀ cluster. Calculations were performed with a pool size of 10 and a mutation rate of 0.1. The tetrahedral structure (T_d) of Au₂₀ is well known and has been shown previously by both theory,^38,39,48 and experiment.^36,37

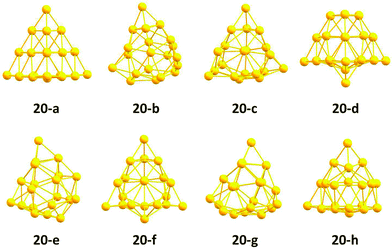
The structures of the putative pool-GA GM and minima lying below 0.5 eV are shown in Fig. 12. The pool-GA successfully finds the tetrahedral structure, 20-a, as the GM. The tetrahedron is first found after the optimisation of only 56 structures. There is a large gap between the GM and the next lowest-lying structure, a distorted geometry with C₁ symmetry. Structures similar to 20-b are seen in minima 20-e and 20-g, while structures 20-c, 20-f and 20-h are C₁ geometries based on more subtle distortions of the tetrahedron.

Fig. 12 Structures of Au₂₀ below 0.5 eV from the predicted GM 20-a as obtained from the generation based DFT-BCGA global optimisation approach. The nomenclature of the individual isomers is guided by the energy order at the pwSCF/PBE level of theory.

4 Conclusions

We have demonstrated the efficiency of the new pool-based parallel implementation of the BCGA. The new implementation leads to a greater efficiency for the global optimisation of monoatomic or binary clusters. The change in implementation makes the approach efficient for an arbitrary numbers of parallel processes, as shown by the benchmark calculations. In addition, the pool-BCGA can also adapt to the given utilisation of a given high-performance computer, as it supports different numbers of processors in order to achieve maximum efficiency. Since processor speed is generally starting to plateau, it will be more and more appropriate to develop better parallel algorithms suitable for future computer architectures. The pool-BCGA is a good example of how this can be done efficiently. Additionally, the use of distributed computing architectures (e.g. BOINC) would be now enabled where server could potentially manage the pool while optimisations can be run on an arbitrary number of clients. Since the amount of data transferred between server and clients is small, bandwidth requirements would be minimal.

By replacing the sequential working generation concept, serial bottlenecks are eliminated. A typical pool calculation can be started as a job array of several pool-GA subprocesses enabling the treatment of larger cluster sizes than previously studied or even opens up the possibility of using a higher level of theory. Alternatively, one can think about using wavefunction based methods in geometry relaxations for the global optimisation of small cluster systems as implemented in program packages such as CFOUR,⁵⁹ or NWChem v6.3,⁵⁴ which enable geometry optimisations based on coupled cluster methods. Such a pool implementation would emerge as the method of choice, especially in this sophisticated task of performing global optimisation using multi-electron wavefunctions to account for electron correlation with higher accuracy.

Also the very recently developed S-BCGA could be improved by using the flexible pool concept, which would allow the study of more complicated supported clusters, such as larger clusters and nanoalloys, and permit calculations at a higher level of theory.

A comparison of the results obtained by the generation- and pool-based BCGA show that the pool-GA is finally able to find all isomers predicted by the generation based implementation while both GAs give results in good agreement with existing global optimisation calculations reported in the literature.

Acknowledgements

The calculations reported here have been performed on the following HPC facilities: The University of Birmingham BlueBEAR facility (ref. 60); the MidPlus Regional Centre of Excellence for Computational Science, Engineering and Mathematics, funded under EPSRC grant EP/K000128/1 (R. L. J.); and via our membership of the UK's HPC Materials Chemistry Consortium funded under EPSRC grant EP/F067496 (R. L. J.). A. S. and R. S. acknowledge financial support by the DFG (grant SCHA 885/10-2) and the Merck'sche Gesellschaft für Kunst und Wissenschaft e.V. We are thankful to group members and collaborators, past and present, for their contributions to this research, particularly in the area of global optimisation. In terms of the development and testing of the DFT based BCGA code, special thanks are extended to Christopher Heard (Chalmers University, Gothenburg) and Sven Heiles (Justus-Liebig-Universität, Gießen).

References

1. W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611–676.
2. F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 48, 22–33.
3. A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139–146.
4. J. N. Murrell and R. E. Mottram, Mol. Phys., 1990, 69, 571–585.
5. R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910.
6. J. Jellinek and E. B. Krissinel, Chem. Phys. Lett., 1996, 4, 283–292.
7. R. Ferrando, A. Fortunelli and R. L. Johnston, Phys. Chem. Chem. Phys., 2008, 10, 640–649.
8. J. Jellinek and E. B. Krissinel, Theory of Atomic and Molecular Clusters, Springer, Berlin, 1999, p. 277.
9. R. L. Johnston, Dalton Trans., 2003, 4193–4207.
10. S. Heiles, A. J. Logsdail, R. Schäfer and R. L. Johnston, Nanoscale, 2012, 4, 1109–1115.
11. S. Heiles, R. L. Johnston and R. Schäfer, J. Phys. Chem. A, 2012, 116, 7756–7764.
12. D. A. Götz, S. Heiles, R. L. Johnston and R. Schäfer, J. Chem. Phys., 2012, 136, 186101.
13. A. Bruma, R. Ismail, L. O. Paz-Borbón, H. Arslan, G. Barcaro, A. Fortunelli, Z. Y. Li and R. L. Johnston, Nanoscale, 2013, 5, 646–652.
14. G. Kwon, G. A. Ferguson, C. J. Heard, E. C. Tyo, C. Yin, J. DeBartolo, S. Seifert, R. E. Winans, A. J. Kropf, J. Greeley, R. L. Johnston, L. A. Curtiss, M. J. Pellin and S. Vajda, ACS Nano, 2013, 7, 5808–5817.
15. A. Shayeghi, C. J. Heard, R. L. Johnston and R. Schäfer, J. Chem. Phys., 2014, 140, 054312.
16. D. A. Götz, A. Shayeghi, R. L. Johnston, P. Schwerdtfeger and R. Schäfer, J. Chem. Phys., 2014, 140, 164313.
17. S. Heiles and R. L. Johnston, Int. J. Quantum Chem., 2013, 113, 2091–2109.
18. G. Rossi and R. Ferrando, J. Phys.: Condens. Matter, 2009, 21, 084208.
19. B. Hartke, J. Phys. Chem., 1993, 97, 9973–9976.
20. Y. Xiao and D. E. Williams, Chem. Phys. Lett., 1993, 215, 17–24.
21. B. Hartke, Chem. Phys. Lett., 1996, 258, 144–148.
22. B. Hartke, H.-J. Flad and D. Michael, Phys. Chem. Chem. Phys., 2001, 3, 5121–5129.
23. B. Hartke, Phys. Chem. Chem. Phys., 2003, 5, 275–284.
24. Y. Zeiri, Phys. Rev. E, 1995, 51, 2769.
25. D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291.
26. D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116.
27. J. M. Dieterich and B. Hartke, Mol. Phys., 2010, 108, 279–291.
28. M. Sierka, Prog. Surf. Sci., 2010, 85, 398–434.
29. K. Kwapien, M. Sierka, J. Döbler, J. Sauer, M. Haertelt, A. Fielicke and G. Meijer, Angew. Chem., 2011, 50, 1716–1719.
30. A. N. Alexandrova, A. I. Boldyrev, Y.-J. Fu, X. Yang, X.-B. Wang and L.-S. Wang, J. Chem. Phys., 2004, 121, 5709–5718.
31. A. N. Alexandrova and A. I. Boldyrev, J. Chem. Theory Comput., 2005, 1, 566–580.
32. C. J. Heard, S. Heiles, S. Vajda and R. L. Johnston, Nanoscale, 2014, 54–57.
33. L. B. Vilhelmsen and B. Hammer, J. Chem. Phys., 2014, 141, 044711.
34. F. Weigend, J. Chem. Phys., 2014, 141, 134103.
35. B. Bandow and B. Hartke, J. Phys. Chem. A, 2006, 110, 5809–5822.
36. J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864–867.
37. P. Gruene, D. M. Rayner, B. Redlich, A. F. G. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674–676.
38. B. Assadollahzadeh and P. Schwerdtfeger, J. Chem. Phys., 2009, 131, 064306.
39. E. Aprá, R. Ferrando and A. Fortunelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205414.
40. Y. Ge and J. D. Head, Chem. Phys. Lett., 2004, 398, 107–112.
41. E. Cantu-Paz, Efficient and Accurate Parallel Genetic Algorithms, Kluwer Academic Publishers, Boston, 2001.
42. A. N. Alexandrova, J. Phys. Chem. A, 2010, 114, 12591–12599.
43. K. Doll, J. C. Schön and M. Jansen, J. Chem. Phys., 2010, 133, 024107.
44. B. Hartke, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 879–887.
45. M. Chen, D. Kumar, C.-W. Yi and D. W. Goodman, Science, 2005, 310, 291–293.
46. A. V. Walker, J. Chem. Phys., 2005, 122, 094310.
47. D. A. Götz, R. Schäfer and P. Schwerdtfeger, J. Comput. Chem., 2013, 34, 1–7.
48. J. Wang, G. Wang and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035418.
49. R. Ismail and R. L. Johnston, Phys. Chem. Chem. Phys., 2010, 12, 8607–8619.
50. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
51. A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230.
52. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
53. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
54. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
55. S. Darby, T. V. Mortimer-Jones, R. L. Johnston and C. Roberts, J. Chem. Phys., 2002, 116, 1536–1550.
56. Y. C. Choi, W. Y. Kim, H. M. Lee and K. S. Kim, J. Chem. Theory Comput., 2009, 5, 1216–1223.
57. F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, J. Chem. Phys., 2002, 117, 6982–6990.
58. R. E. Kunz and R. S. Berry, J. Chem. Phys., 1995, 103, 1904–1912.
59. M. E. Harding, T. Metzroth and J. Gauss, J. Chem. Theory Comput., 2008, 4, 64–74.
60. See http://www.bear.bham.ac.uk/bluebear for a description of the BlueBEAR HPC facility.

---