A DFT approach to the charge transport related properties in columnar stacked π-conjugated N-heterocycle cores including electron donor and acceptor units

Abstract

We present a density functional theory (DFT) study on charge-transport related properties in a series of discotic systems based on 1,3,5-triazine and tris[1,2,4]triazolo[1,3,5]triazine central cores as electron acceptor units, and phenyl-thiophene and N-carbazolyl-thiophene segments as electron donor units. The presence of both electron donor and acceptor moieties in the π-conjugated core could lead to new discotic liquid crystal (DLC) materials which are predicted to display ambipolar charge transport behavior in such a way that electrons could move through the central part of the next cores while holes mainly do through the peripheral groups. A significant increase in hole mobility when N-carbazolyl is present as an electron donor unit in the peripheral region is predicted. In addition, a detailed topological analysis of the electron charge density within the framework provided by Quantum Theory of Atoms in Molecules (QTAIM) has been performed in order to characterize intra- and intermolecular interactions in terms of hydrogen bonds and/or π⋯π stacking which contribute to the stabilization of the columnar stack and the helical self-assembly at the molecular scale.

---

Introduction

Since the first work published in 1977 by Chandrasekhar et al. about benzene-hexa-n-alkanoates,¹ discotic liquid crystals (DLCs) have attracted a lot of attention due to their properties to form nanostructures with a one-dimensional pathway for charge transport and, thus with interesting applications in organic electronics.^2,3 DLC materials are being recognized as a new class of quality organic semiconductors with mobilities in the range 10⁻⁴–1 cm² V⁻¹ s⁻¹. The applicability of these materials in optoelectronics as well as the design of new mesogens with improved electronic properties depend on several molecular properties such as HOMO/LUMO levels, reorganization energy, integral transfer and π-stacking, among others.^4–30

They consist of a central π-conjugated core in which the insertion of lateral chains may lead to ordered, columnar mesophases. Specific substitutions on both, the core and side chains may induce changes in the interdisc and azimuthal angle reducing the steric hindrance and favoring a helical π-stacking along the column as opposite to a face-to-face one. In addition, non-covalent interactions, such as H-bonds and dipole interactions, play an important role in the formation of supramolecular assemblies. As a matter of fact, the role played by specific functional groups in both, the appearance of new inter-disc, non-covalent interactions and charge transport related properties is of high current interest.^21,31–33

Nowadays there is a huge field of research about organic, narrow band gap polymers with ambipolar charge transport behavior. One way to achieve intrinsic ambipolar charge transport in conjugated linear polymers is through the existence of linked electron-donor and acceptor units in the molecular structure, which has shown to be an efficient strategy to reduce the band gap due to the mixing of molecular segments with higher HOMO and lower LUMO.^34–37 However, the design of processable, ambipolar structures formed by ordered liquid crystals (LC) for optoelectronic applications is still a field to explore and represent a new challenge in the development of novel materials with promising applications as field-effect transistors, light-emitting diodes and photovoltaic cells.^38–51

Recently, a new series of DLC conducting materials based on octupolar 1,3,5 triazine central cores, as electron acceptor units, and peripheral, electron donor phenyl-thiophene and N-carbazolyl-thiophene units has been synthesized opening a promising guideline for the design of ambipolar LC materials.⁵² Both thiophene and N-carbazolyl have been widely used in electronic devices, and exhibit p-type semiconductor properties.^53–57 However, not many studies have been devoted to thiophene²⁹ or N-carbazolyl⁵⁵ based discotic systems. To our knowledge, the first hexagonal columnar DLC carbazole derivative with a triphenylene core was synthesized in 2001 by Manickam et al.⁵⁵ while their photoconductivity properties were studied in 2007 concluding that these systems behave as p-type semiconductors.⁵⁶

In this work, we present a detailed quantum chemical investigation on the charge transport-related properties of a series of columnar π-stacked acceptor cores based on 1,3,5-triazine linked to peripheral donor segments whose properties as charge transport carriers have shown an ambipolar behavior from time-of-flight measurements (see Chart 1).⁵² Moreover, aimed at the design of new ambipolar DLC materials we have studied the effect of modifying the nature of both, the acceptor central core and peripheral donor moieties, on charge transport related properties of a series of compounds based on the tris[1,2,4]triazolo[1,3,5] triazine core (see Chart 1) recently synthesized.^58,59 As said before, interdisc distances and orientations of the stacked cores have a great influence on the charge transport related properties. Hence, characterization at the molecular scale of DLCs is an utmost important issue in the study of charge transport properties of the self-assembled structure and to establish structure–property relationships.

Chart 1 Molecular geometry for the selected compounds.

In order to theoretically discern the suitability of the selected systems, some of them not synthesized yet, as the active part of n-, p- or ambipolar materials, different properties such as intramolecular reorganization energy, frontier molecular levels, charge carrier mobility and charge transfer integral have been calculated on the basis of density functional theory (DFT). In addition, the intra- and intermolecular interactions, responsible for the stability of DLC columnar mesophases and, then, of their charge transport related properties, have been characterized on the basis of a topological analysis of electron charge density in terms of critical points as Atoms in Molecules Theory deals with.

Theoretical methodology

Gaussian09 (revision B.01)⁶⁰ suite of programs has been mostly employed for the theoretical calculations. In order to assess charge transport related properties for each system under study, we have used different approximations. First, geometries of the neutral and charged, anionic and cationic, molecules of the selected compounds (Chart 1) were fully optimized at the hybrid B3LYP level^61–63 along with the 6-31G* basis set.⁶⁴ Using these geometries, intramolecular reorganization energies were determined by using B3LYP^61–63 and M06-2X⁶⁵ functionals with 6-31G* and 6-311G** basis sets⁶⁴ by performing single point calculations. Both functionals have shown to give reasonable values for transfer integrals and non-covalent interactions in previous studies.^8,17,21,66 We are aware the best description for anions is expected to be obtained by using diffuse basis sets. However, using the previously mentioned basis sets is expected to render similar results to those obtained when introducing diffuse functions in the basis set.^17,67,68

Second, the columnar stacked π-conjugated cores were modeled by a cluster made up of five molecules. The lateral chains linked to the phenyl or N-carbazolyl rings play an important role in the columnar mesophase stabilization and the relative positions of the disc in the one-dimensional nanostructure. However, as it can be found in the literature, the increase of the chain length does not have a great impact on the magnitude of the charge transport related properties such as transfer integrals and reorganization energies and may overshadow the understanding of the intermolecular interactions inside the columnar stacks.^17,29,69 Thus, the calculations have been performed at the molecular level with methyl/methoxy moieties as shown in Chart 1 which also reduces the computational cost compared with more extended alkyl/alkoxy chains.

Due to the large number of atoms in the clusters, ca. 500–600, their geometries were fully optimized in the context of the two-layer ONIOM model.⁷⁰ This method allows for an effective partition of the system in different (“small” and “large”) subunits, each of them modeled with an increasing accuracy, usually labeled as “high” and “low” levels (see Fig. 1).

Fig. 1 Schematic representation of the cluster.

In our systems, for each 5-membered cluster, three inner molecules were studied at PBE/6-31G*^71,72 (high level) while two outer molecules were studied at PBE/STO-3G⁶⁴ (low level). This partition model allows us to optimize a large system, focusing on the central units which are described in a more realistic environment and avoiding the edge effects. Last, although frequently termed “weak,” dispersion forces can account for a large percentage of the interaction energy of molecular complexes of modest size. The standard approximations to the exchange–correlation functional of DFT cannot describe the dispersion interaction correctly and thus we have also considered dispersion corrections for the PBE functional. We have selected the general chemistry GGA type PBE functional including the so-called Grimme's D2 dispersion correction term, as implemented in Gaussian 09 B.01,⁶⁰ as it has been proven to perform well for large systems at predicting geometry parameters, ionization potential, electron and proton affinities, as well as for describing van der Waals and hydrogen bond interactions at a reasonable computational cost.^73–77

The design of the cluster model implies a careful study of three important parameters such as azimuthal angle, inter-core distance and side displacement which, as known, play an important role in the charge transport process. Thus, several papers have appeared dealing with the impact of both the interdisc separation and the azimuthal angle in the charge carrier mobility inside DLC.^8,17,21 The inter-core distance values for semiconducting columnar mesogens are usually in the range 3.5–4.0 Å. For azimuthal angles, a large range of values can be found depending on the core and the lateral chains yielding either face-to-face or helical architectures on the columnar stack.²¹

According to XRD data, the triazine core derivatives selected in this work stack in a helical pattern along the column axis minimizing in this way the steric hindrance of the side chains.⁵² A similar result was obtained for the tristriazolotriazine core derivative by circular dichroism.⁵⁹

In order to get theoretical information about the most favorable arrangement of the discs inside the cluster, the evolution of the total energy for a couple was calculated as the azimuthal angle varies. The interdisc distance was kept at 3.6 Å since the transfer integral does not show a noticeable sensitivity in this parameter within the range of interest, i.e. 3.5–3.6 Å.¹⁷Fig. 2 shows the barrier to rotation for a couple made up of two units of 2,4,6-tris(thiophene-2-yl)-[1,3,5]triazine and tris[1,2,4]triazolo[1,3,5] triazine. The most stable arrangement was found for cores that rotated each other ca. 60° in both cases, in agreement with the experimental findings for the corresponding DLC compounds. When methoxyphenyl moieties were symmetrically linked to the central cores, we obtained a broader well where the steric hindrance among the peripheral segments would be minimized (see Fig. 1S, ESI†).

Fig. 2 Total energy vs. azimuthal angle for a couple of triazine (up) and tristriazolotriazine (down) cores. Intermolecular distance is fixed at 3.6 Å.

According to these results, a five-membered model cluster with an inter-core distance equal to 3.6 Å and a rotational angle of 60° was built up using as starting point the molecular geometry optimized for each molecule at the B3LYP/6-31G* level. Then, the geometry of the cluster was fully optimized through the ONIOM approach (see above). The charge transfer integral (t) between two molecules in an inner couple within the optimized cluster was estimated following the so-called projective method, using the code J-from-g03.^78,79 Hole and electron mobilities were evaluated through the charge transfer rate k_ET calculated according to Marcus–Levitch–Jortner theory.^80–83

Finally, in order to analyze intra- (from one isolated molecule) and intermolecular interactions (from a couple of two consecutive or alternate molecules), the topological analysis of the electronic charge density was performed within the Quantum Theory of Atoms in Molecules (QTAIM) with the AIM2000 program package.^84,85

Results and discussion

Molecular geometry

Table 1 gathers the α and β dihedral angles (see Chart 1) for the selected compounds at the B3LYP/6-31G* level. X-ray data for 1a and 2a establish α dihedral angle in the range 1–11° ⁵² and 19–62°,⁵⁸ respectively. The discrepancy with the B3LYP/6-31G* value for 2a, i.e. ∼28°, could be due, as will be discussed later, to the stacking of the molecules. As seen from β values, the N-carbazolyl derivative deviates more from planarity in order to decrease the steric hindrance which could limit strongly any mixing between the molecular orbitals of thiophene and N-carbazolyl units. Also, the β dihedral angle appears to be strongly influenced by the charge located on the system. This will show up in the corresponding reorganization energies.

Table 1 Mean torsional angles α and β (in degrees) at the B3LYP/6-31G* level

		1a	1b	1c	2a	2b	2c
α(N–C–C–S/C)	Neutral	1.0	1.1	0.3	28.0	1.2	0.9
	Cation	0.2	0.6	0.3	19.1	0.7	0.5
	Anion	0.7	0.1	0.1	11.4	0.3	0.6
β(S–C—C/N–C)	Neutral	27.6	50.5	51.7		26.1	52.2
	Cation	19.3	46.7	48.0		15.0	45.4
	Anion	17.1	74.7	78.7		12.4	70.4

---

The large deviation from planarity could prevent π-stacking along the column and, at the same time, give rise to non-covalent interactions among neighbor discs leading to an enhanced columnar organization. Thus, in order to understand the spreading of co-planarity between the central core and the peripheral units we characterized first the interatomic interactions within each single disc on the basis of Bader's topological analysis of the charge electron density, ρ_b⁸⁵ (see ESI† for details and Fig. 2S). Accordingly, Table 1S (ESI†) lists the values for the topological parameters of the Bond Critical Points (BCP) for each single disc at the B3LYP/6-31G* level. All the interactions fall into the closed-shell type and they are associated to intramolecular H-bonds as they fulfill the topological criteria proposed by Koch and Popelier.^86,87 C_thiophene⋯H_carbazol, S_thiophene⋯H_carbazol, N_triazol⋯H_phenyl and N_triazol⋯H_thiophene intramolecular contacts were found which enhances the planarity of the core and hinders the rotation of the lateral segments. Fig. 3 shows the intramolecular contacts found in the case of the 2c compound.

Fig. 3 Molecular graph for 2c. Keys for atoms: black = C, red = O, blue = N, gray = H. Small dots represent CPs: red = BCP, yellow = RCP.

According to |V_b|/G_b and bond-degree (BD) H_b/ρ_b indices (see ESI† for details and Fig. 3S and 4S), the S⋯H and N⋯H contacts, mainly accounting for the spreading of the planarity from the central cores to the peripheral groups, turn out to be the weaker and the stronger, respectively. Therefore, it could be expected that at least the N⋯H contacts would remain when they enter into the cluster.

Cluster geometry

The clusters exhibit a π-stacking arrangement typical for a hexagonal, helical coil, minimizing the steric hindrance among the side chains. This result matches the experimental findings for triazine and tristriazolotriazine derivatives.^52,59 In Fig. 4 an upper view of the optimized structure for each cluster is shown.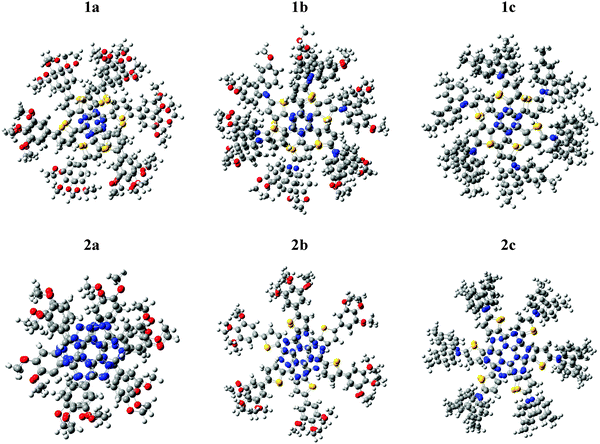

Fig. 4 Upper view of the optimized structures for the five-membered clusters (white: H; grey: C; red: O; yellow: S; blue: N).

Table 2 shows that the α dihedral angle for 1a–c and 2b–c is close to the values in the single molecules. However, the β dihedral angle is smaller in the cluster than in the single molecules, except for 2c. This effect could be due to the flattening packing effect of the molecules in the columnar stack. The largest deviation from planarity is found for 1b, 1c and 2c which may favor a non face-to-face packing in order to reduce the peripheral steric hindrance. As a result, a number of intermolecular contacts among neighboring, nearly parallel N-carbazolyl rings may appear.

Table 2 Mean torsional angles, α and β (in degrees), for the central molecule in the cluster and interdisc distance (in Å) at PBE/6-31G* level^a

	1a	1b	1c	2a	2b	2c
a X-ray experimental data in parenthesis. b Ref. 52. c Ref. 59.
α(N–C–C–S/C)	1.4	1.4	2.9	20.4	0.7	0.9
				28.8
				38.1
β(S–C–C/N–C)	24.6	43.3	39.0	—	25.2	54.6
d(Ccore–Ccore)	3.1(3.3)^b	3.1	3.2	3.3(3.5)^c	3.2	3.1

---

For clustered 2a, the three α-type torsional angles become clearly different each other at odds with those shown by the isolated molecule in agreement with a previous X-ray study.⁵⁸ The inter-core distances predicted for a clustered, central couple as well as those from an X-ray analysis are collected in Table 2.^52,59 Both sets of data are similar but far from the typical value for such a parameter in semiconducting DLCs (∼3.5–4.0 Å). The shortening of the inter-core distance from 2a to 2c may be due to the intermolecular contacts the thiophene ring can give rise as a consequence of the higher facility to accommodate the peripheral segments in the helical columnar stacking.

Inter- and intramolecular, non-covalent interactions may contribute to enhance the intracolumnar order.³³ As those contacts can be of different nature and/or magnitude, here we have performed a QTAIM analysis on couples of discs either consecutive (2,3) and alternate (2,4) in order to characterize the different contacts not only in terms of covalent interactions but also in terms of H-bonds and π⋯π stacking ones as it has been already described in the literature.^88,89 The results appear in Table 3 and Table 1S (ESI†). The contacts can be classified as closed-shell interactions as they all exhibit positive values for ∇²ρ_b and H_b. Fig. 5S (ESI†) shows a schematic representation of the BCPs for the different couples. Some more detailed comments about the AIM results for intramolecular H-bond interactions can be seen in the ESI.†

Table 3 Bond distances, electron density and Laplacian for bond critical points for intermolecular interactions in the selected cluster at the B3LYP/6-31G* level

Cluster	Couple	Bond (A⋯B)^a	Distance (Å)	ρ b (au)	∇^2ρb (au)
a Subscripts “thio”, “carb” “triazol” and “triaz” stand for thiophene, carbazolyl, triazolyl and triazine, respectively.
1a	2,4	Hmeth⋯Hmeth	2.222	0.007	0.0255
	2,3	Ometh⋯Hmeth	2.429	0.011	0.039
		Cmeth⋯Hmeth	2.736	0.007	0.028
		Ctriaz⋯Ctriaz	3.061–3.088	0.008	0.029–0.030
1b	2,4	Ometh⋯Hmeth	2.439–2.757	0.006–0.010	0.025–0.035
		Ccarb⋯Hmeth	2.558–2.763	0.008–0.010	0.031–0.035
		Ccarb⋯Ometh	3.120–3.128	0.008	0.027–0.028
		Ccarb⋯Ccarb	3.217	0.008	0.025
	2,3	Sthio⋯Hthio	2.963	0.008	0.027
		Hthio⋯Hcarb	2.116–2.840	0.006–0.009	0.027–0.034
		Cthio⋯Hcarb	2.562–2.621	0.009–0.010	0.035–0.037
		Sthio⋯Cthio	3.167–3.245	0.010–0.012	0.032–0.039
		Ctriaz⋯Ntriaz	3.106–3.116	0.008	0.026–0.027
1c	2,4	Hmethyl⋯Hmethyl	2.228	0.008	0.027
		Cmethyl⋯Hmethyl	2.613–2.828	0.007–0.010	0.024–0.032
		Ccarb⋯Hmethyl	2.613–2.828	0.007–0.010	0.024–0.032
		Ccarb⋯Ccarb	3.182–3.369	0.007–0.008	0.024–0.026
	2,3	Hthio⋯Hcarb	2.148–2.294	0.007–0.010	0.029–0.040
		Ccarb⋯Hcarb	2.723	0.009	0.029
		Sthio⋯Cthio	3.055–3.331	0.009–0.014	0.027–0.045
		Ctriaz⋯Ntriaz	3.151	0.008	0.025
2a	2,4	Ometh⋯Hmeth	2.577	0.007	0.027
		Hmeth⋯Hmeth	2.263	0.008	0.030
	2,3	Ntriazol⋯Hphenyl	2.519–2.551	0.010–0.011	0.039–0.042
		Hphenyl⋯Hphenyl	2.102–2.266	0.007–0.010	0.028–0.039
		Hphenyl⋯Hmeth	2.102–2.266	0.007–0.010	0.028–0.039
		Hmeth⋯Hmeth	2.102–2.266	0.007–0.010	0.028–0.039
		Ctriaz⋯Ntriaz	3.179–3.194	0.007	0.024
		Ctriaz⋯Ntriazol	3.179–3.194	0.007	0.024
2b	2,4	Hmeth⋯Hmeth	2.295	0.006	0.022
	2,3	Ctriaz⋯Ntriaz	3.130–3.193	0.007–0.008	0.025–0.028
		Ctriazol⋯Ntriazol	3.128–3.146	0.007–0.008	0.025–0.026
		Cthio⋯Ntriazol	3.096	0.009	0.026
2c	2,4	Ccarb⋯Hmethyl	2.736–2.788	0.007–0.008	0.025–0.027
		Ccarb⋯ Ccarb	3.088–3.299	0.008–0.010	0.023–0.030
	2,3	Ctriaz⋯Ntriaz	3.090–3.097	0.009	0.029
		Ctriazol⋯Ntriazol	3.124–3.180	0.007–0.008	0.024–0.026

---

In general, intramolecular H-bonds in the couples are slightly shorter than in their corresponding single units with higher values for ρ_b and ∇²ρ pointing to an increase of the bond strength. As expected, the AIM analysis of the intermolecular interactions becomes more complex because intermolecular contacts are found not only between the conjugated central cores of neighboring discs but also between the peripheral segments in all the selected compounds.

Several intermolecular H-bonds in (2,4) and (2,3) couples are found between neighboring cores which could stabilize the helical disposition of the discs along the column. In addition, π⋯π stacking interactions between both the central part of the cores and the N-carbazolyl groups could play an important role in that stabilization. The core enlargement renders an increase in the number of π⋯π stacking contacts. In addition, a significantly higher number of intermolecular interactions are found in clusters with peripheral N-carbazolyl moieties as compared to those with methoxyphenyl (see Table 3).

A molecular graph of intra- and intermolecular contacts for the (2,4) and (2,3) couples in 2c is shown in Fig. 5 and 6, respectively. The AIM results for the rest of the clusters concerning BCPs associated to the closed-shell interactions can be seen in the ESI† (Table 1S). For couple (2,4), six BCPs associated to C_carb⋯C_carb interactions, a large number of RCPs and, finally, six CCPs between the N-carbazolyl units can be seen in Fig. 5. This result suggests the dominant interaction is the π⋯π stacking along with peripheral C_carb⋯H_methyl H-bonds (see Table 1S, ESI†). These are also observed in the couple (2,4) for 1c.

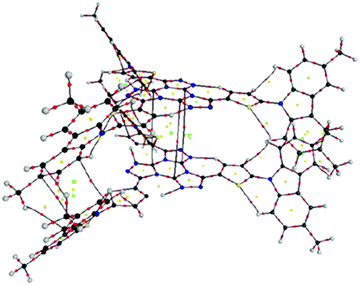Fig. 5 Molecular graph of couple (2,4) for 2c. (black = C, red = O, blue = N, grey = H). Small dots mean critical points (CPs): red = BCP, yellow = RCP, green = cage critical point (CCP).

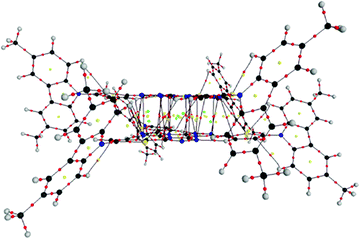Fig. 6 Molecular graph of couple (2,3) for 2c. (black = C, red = O, blue = N, grey = H). Small dots represent CPs: red = BCP, yellow = RCP, green = CCP.

For couple (2,3), eleven BCPs associated to C_triaz⋯N_triaz interactions in 2c (see Table 1S, ESI†), three RCPs and seven CCPs between the tristriazolotriazine central cores (see Fig. 6) are found whereas no intermolecular interactions between the N-carbazolyl segments appear. Therefore π⋯π stacking become the only dominant interactions in the (2,3) couple and, in general, play an important role in the stabilization of the 2c cluster.

The intermolecular contacts between either consecutive (2,3) and alternate (2,4) units through H-bonds and/or π⋯π stacking interactions favor the helical disposition of the discs along the column. However, the core–peripheral intramolecular interactions could force the structure of the discs to flatten favoring their stacking and they could prevent the formation of intermolecular contacts between two adjacent discs. Therefore, the balance between intra and intermolecular interactions is an important issue to be considered when designing new core molecular structures for DLC purposes.

Charge injection

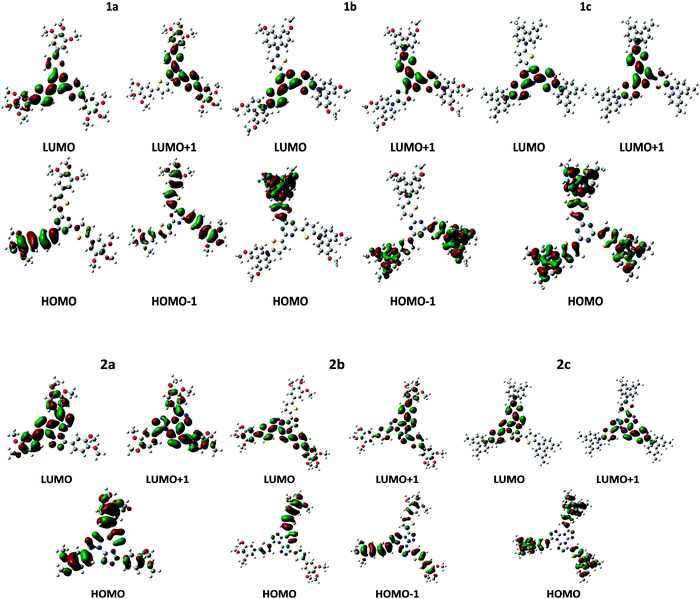
HOMO/LUMO levels, electron affinity and ionization potential are the main parameters controlling the efficiency of charge injection. Although different models for charge injection from the metal electrode into the semiconductor organic material have been proposed theoretically and investigated from an experimental point of view, it is generally accepted that the energy gap between the work function of the electrode, Φ_m, and the LUMO/HOMO of the semiconductor rules the efficiency for electron/hole injection into the active material.^90–92 Koopmans' theorem states that in closed-shell Hartree–Fock theory the first (gas phase) ionization potential, IP, equals to minus the HOMO energy. Although it could be argued that Koopmans' theorem is not applicable to Kohn–Sham orbital energies, Janak's theorem provides a link between frontier orbital energies and ionization potential (IP) and electron affinities (EA), as well.⁹³

For an efficient hole/electron injection, suitable HOMO/LUMO levels and low/high IPs/EAs are desirable. However, low IPs would lead to unintentional doping, and therefore to low ON/OFF ratios,⁹⁴ and EA higher than 4.0 eV could result in a too electrophilic molecule which could be unstable under ambient conditions.⁹³ LUMO and HOMO frontier orbitals of the studied compounds are shown in Fig. 7. As it can be seen, the HOMO is mainly located on the peripheral, electron donor region, while the LUMO is expanded over the central, electron acceptor region of the cores. As described above, the electron donor groups become closer to each other in couple (2,4) increasing the HOMO overlap and then the hole transport. Thus, the electron mobility is facilitated by the overlap between the LUMO orbitals of the electron acceptor units (triazine and tristriazolotriazine cores) while the hole transport would mainly occur through the donor, peripheral groups (phenyl-thiophene and N-carbazolyl-thiophene). Taking into account the helical disposition of the molecules within the columnar stack and the shape of HOMO and LUMO orbitals shown in Fig. 7, this could result in two main channels for charge transport: holes could mainly move through the peripheral groups and electrons through the central part of the neighboring cores.

Fig. 7 HOMOs and LUMOs contours for the selected compounds at the B3LYP/6-31G* level.

Table 4 gathers the theoretical HOMO/LUMO energies along with the experimental band gaps. As it can be seen, B3LYP and M06-2X functionals predict HOMO–LUMO energy gaps wider than the experimental ones, although B3LYP behaves better than M06-2X, regardless of the basis set. Notwithstanding, these values are one order of magnitude larger than those previously reported for ambipolar conjugated polymers.^37,51

Table 4 Theoretical and experimental energy values (eV) for the HOMO and LUMO levels and band gap

		1a	1b	1c	2a	2b	2c
a Ref. 52. Experimental data from ref. 33 in a CH2Cl2 solution. b Ref. 59. Optical value for the energy gaps from film absorption spectra.
B3LYP/6-31G*	LUMO	−1.9216	−1.9687	−2.0607	−1.5118	−2.0150	−2.0767
	HOMO	−5.4794	−5.0019	−5.3178	−5.8223	−5.5581	−5.3553
	E g	3.56	3.03	3.26	4.31	3.54	3.28
B3LYP/6-311G**	LUMO	−2.1684	−2.2062	−2.2623	−1.7401	−2.2416	−2.2914
	HOMO	−5.7074	−5.2372	−5.5327	−6.0489	−5.7823	−5.5869
	E g	3.54	3.03	3.27	4.31	3.54	3.30
M06-2X/6-311G**	LUMO	−1.4522	−1.4786	−1.5086	−0.8514	−1.4550	−1.4656
	HOMO	−6.9883	−6.4653	−6.7259	−7.1076	−7.0345	−6.7787
	E g	5.54	4.99	5.22	6.26	5.58	5.31
Exp.	E g	2.56^a		2.37^a	3.56^b

---

Narrow bandgaps are needed in order to design ambipolar materials. One strategy to get this in semiconducting polymers is to alternate electron donor and accepting units. In this work, a decrease of ca. 1.0 eV is observed when we compare the calculated E_g value for 2a with those for 2b and 2c. In addition, the bandgap also decreases around 0.3 eV when the phenyl-thiophene is changed by N-carbazolyl-thiophene. As a matter of fact, the narrowest band gaps are predicted for 1b, 1c and 2c.

Finally, as seen in Table 4, the E_g predicted for 1a and 2b as well as for 1c and 2c suggests that the substitution of triazine by tristriazolotriazine in the core does not affect significantly the bandgap energies. A word of caution must be said here. Comparison between experimental values of E_g for (1a, 1c) and 2a may be strongly influenced by the very different dielectric constant of CH₂Cl₂ solutions for the former and that of the thin film for the latter.

Fig. 8 renders the theoretical HOMO/LUMO energy levels of the studied compounds along with the work function Φ_m of common electrodes.^90–92 An ohmic contact is achieved when the energy differences are less than 0.3 eV.⁹⁰ According to Cristiano et al.,⁵⁹2a should behave as an electron-transporting system while as seen in Fig. 8, the highest LUMO energy is predicted for it. B3LYP predicts 2c to show the lowest LUMO energy, even though it is still far from the cathode work functions herein shown. As a general trend, a decrease in LUMO energies is predicted when going from 1a to 1b–1c, and also from 2a to 2b–2c. This points out that sticking phenyl- and N-carbazolyl-thiophene groups to the tristriazolotriazine core produces a significant decrease of the LUMO energy level (∼0.5 eV). This decrease is also observed when the phenyl groups are substituted by N-carbazolyl units in both series of studied compounds, although the effect is less pronounced (0.1 eV). For 1b, the HOMO energy is closer to Φ_m,ITO/Φ_m,Au than 1a and 1c and then an easier hole injection should be expected.

Fig. 8 HOMO and LUMO energy levels (eV). (green: M06-2X/6-311G**; red: B3LYP/6-311G**; black: B3LYP/6-31G*).

Also, Φ_m − |E_HOMO| < 0.3 eV and then an ohmic contact could be possible. In addition, the HOMO energy for 2c is higher than those of 2b and 2a, and close to that for 1c. As a general trend the N-carbazolyl unit in the peripheral region produces an increase of the HOMO energy, in agreement with the p character of this substituent.

Other important issues when studying charge injection are the adiabatic, electron affinity (AEA) and ionization potential (AIP) as they must be high/low enough to allow an efficient electron/hole injection into the LUMO/HOMO level (see Table 5).

Table 5 Intramolecular hole (λ₊) and electron (λ₋) reorganization energies, adiabatic ionization potential (AIP) and electron affinities (AEA) (units in eV) at different levels of theory

	Method	λ +	AIP	λ −	AEA
1a	B3LYP/6-31G*	0.588	5.95	0.301	1.03
	B3LYP/6-311G**	0.593	6.19	0.300	1.26
	M06-2X/6-311G**	0.707	7.02	0.341	1.16
1b	B3LYP/6-31G*	0.096	5.96	0.443	1.39
	B3LYP/6-311G**	0.096	5.74	0.449	1.11
	M06-2X/6-311G**	0.114	5.54	0.463	1.49
1c	B3LYP/6-31G*	0.059	6.77	0.421	1.31
	B3LYP/6-311G**	0.059	5.49	0.413	1.45
	M06-2X/6-311G**	0.072	6.06	0.472	1.17
2a	B3LYP/6-31G*	0.553	6.28	0.510	1.46
	B3LYP/6-311G**	0.553	5.92	0.505	1.58
	M06-2X/6-311G**	0.620	7.04	0.576	1.38
2b	B3LYP/6-31G*	0.365	6.26	0.219	1.16
	B3LYP/6-311G**	0.362	6.48	0.164	1.32
	M06-2X/6-311G**	0.573	7.23	0.266	1.07
2c	B3LYP/6-31G*	0.076	6.05	0.305	1.21
	B3LYP/6-311G**	0.074	6.28	0.297	1.45
	M06-2X/6-311G**	0.082	7.09	0.370	1.19

---

Fig. 9 shows that the predicted AEA values are less sensitive to the theoretical method than AIP ones. When phenyl-thiophene is changed to N-carbazolyl-thiophene in both series 1 and 2, a decrease of AIP is predicted at B3LYP/6-311G** and M06-2X/6-311G** levels yielding the lowest values for 1c (B3LYP/6-311G**) and 1b (M06-2X/6-311G**). However, B3LYP/6-31G* predicts an increase when going from 1a to 1c. Fig. 9 also shows that the highest AEA is found for 2a at B3LYP. This result agrees with Cristiano et al.⁵⁹ who suggest the potential electron-transporting character of tristriazolotriazine which could be facilitated by a high AEA. However, when thiophene is added to the tristriazolotriazine central core, the AEA decreases and takes values close to those for the triazine case.

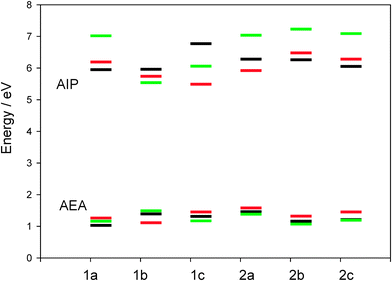Fig. 9 Calculated AIPs and AEAs for the selected systems at different levels of theory (green: M06-2X/6-311G**; red: B3LYP/6-311G**; black: B3LYP/6-31G*).

Therefore, as a general trend, N-carbazolyl-thiophene segments induce both higher/lower AEA/AIP and HOMO/LUMO energy level compared with methoxyphenyl, and then it could be considered as a suitable electron donor unit in searching for new, ambipolar materials when nitrogen rich central cores, as triazine and tristriazolotriazine, act as electron acceptor units.

Charge carrier mobility

Charge transport within the discotic phase mainly occurs by a hopping regime. The charge hopping process could be defined as a self-exchange, charge-transfer reaction between two molecules. The non-adiabatic intermolecular charge transfer rate with vibronic corrections upon mode averaging is given by the Marcus–Levich–Jortner model^80,81 In this expression t is the charge transfer integral (electronic coupling), ΔG⁰ is the energy difference between the electronic states involved in the charge transfer process (equal to zero in the self-exchange process), S_eff = λ_int/ħω_eff is the effective Huang–Rhys factor, related to both λ_int, the internal reorganization energy mainly determined by fast changes in molecular geometry, and ω_eff, the frequency of the effective vibrational mode assisting the process (fixed at ∼1600 cm⁻¹, the breathing mode of aromatic rings, i.e. ħω_eff ∼ 0.2 eV) and λ₀ is the classical (mostly the external) contribution to the reorganization energy.^95–99

Unlike migration of ions in mesophase materials, the electronic charges, i.e. electron and holes, are transported via a rigid solid-like region consisting of a closely packed π-conjugate core moiety of liquid crystalline molecules. As we are interested in electronic transport along the column, we disregard the contribution of the solvation term to the reorganization energy⁴⁷ and we consider the outer contribution to the reorganization energy as due to the nuclear relaxation of the environment caused by electronic polarization.¹⁰⁰

The microscopic evaluation of the external reorganization energy is a difficult task⁹⁴ and that is the reason why not many papers devoted to deal with have been published so far.^100,101 Thus, it is often considered as a tunable parameter.^68,97,102 A typical value in the range 0.1–0.2 eV is generally adopted.^96,99 In this work, we have adopted the value 0.15 eV as a reasonable one for materials with a certain degree of short-range order^68,97,98 and it is also within the range 0.1×–2× the internal reorganization energy whatever the compound selected.¹⁰³

It must be taken into account that λ_ext might depend on the molecular environment. Hence, assuming a unique, fixed value for it could influence the reliability of the final results. The expected non-very different polarizability of the studied compounds, however, may reinforce such a choice¹⁰¹ bearing in mind that the final interest of the paper is not to obtain absolute values of mobilities but rather to outline trends along the series of the selected compounds.

According to the hopping mechanism, the drift mobility (μ_hop) and the diffusion coefficient (D) are related by the Einstein relation¹⁰⁴

where T is the temperature, k_B is the Boltzmann constant and for a one-dimensional system, where only one neighbor is considered, D is given by D = 1/2l²k_ET where l is the hopping distance.¹⁰⁵ It must be said that this model gives values for transfer rates and carrier mobilities which must only be considered as superior and ideal limits.^106,107 The internal reorganization energy is related to the delocalized nature of the HOMO/LUMO and for an isolated molecule consists of the sum of two terms: λ = λ₁ + λ₂, where λ₁ and λ₂ can be calculated directly from the adiabatic potential energy surface as:

λ^±_total = λ^±₁ + λ^±₂

λ^±₁ = E_±(G_N) − E_±(G_±)

λ^±₂ = E_N(G_±) − E_N(G_N)

where (N, +/−) denote neutral and charged states, respectively; E_N(G_N) and E_±(G_±) are the ground-state energies of the neutral and charged states, respectively while E_N(G_±) and E_±(G_N) are the energies of the neutral molecule at the optimal charged geometry and the energy of the charged state at the optimal geometry of the neutral molecule, respectively. The calculated reorganization energies λ_i for the selected compounds are shown in Table 5.

As can be seen, M06-2X yields higher λ_i values for both the negative and positive polarons while the effect of the basis set is almost negligible for B3LYP, with the exception of λ₋ for 2b.

The comparison of the theoretical values for the selected compounds with those previously calculated for other typical DLCs shows that both electron and hole reorganization energies are of the same order of magnitude.^18,26,108 For comparison purposes, from now on we will restrict our discussion to the results obtained at the B3LYP level.

As a general trend, λ₊(λ₋) decreases(increases) when phenyl-thiophene is changed to N-carbazolyl-thiophene ∼0.4(0.1) eV. This effect is observed when the central core is triazine (1b and 1c) and also tristriazolotriazine (2b and 2c). Also, λ₊ values predicted for 1b, 1c and 2c are in the range 0.06–0.1 eV, and they are similar to those calculated for triphenylene (0.18 eV), HATNA (0.14 eV) and HBC (0.10 eV) at the B3LYP/6-31G** level by Lemaur et al.¹⁷

Compound 2a shows λ_+/− which are 0.18/0.29 eV higher than those for 2b. In addition, when methoxyphenyl is changed in 2b to N-carbazolyl to give 2c, λ₋ remains almost constant although λ₊ decreases dramatically up to 0.47 eV from 2a. As a result, the increase in the size of the central core and the number of nitrogen atoms when going from 1a to 2b, keeping the same peripheral group, produces a significant decrease of λ₊ (λ₋) around 0.22 eV (0.1 eV). In addition λ₊ and λ₋ become smaller when the substituent in the N-carbazolyl is methyl (1c) instead of methoxyphenyl (1b).

The smallest λ₋'s are obtained for 2b, 2c and 1a. They are in the range 0.22–0.30 eV and close to those calculated for triphenylene (0.26 eV) and HAT (0.27 eV)¹⁷ and slightly higher than those obtained for electron rich oligoacenes (∼0.10 eV),¹⁰⁹ HATNA (0.10 eV) and HBC (0.14 eV).¹⁷

Despite that λ_i and t can be calculated separately, it is necessary to calculate charge mobility as a function of both parameters to conclude about the p-, n- or ambipolar character of these compounds.

In Table 6t_+/− and μ_+/− values are listed for the compounds studied in this work. As the ratio μ₊/μ₋ points out, a p-type semiconductor behavior in varying degrees should be expected in most cases regardless of the couple, (2,3) or (2,4), dealt with. Electron transport, however, mainly occurs between successive discs as it is the case for 1a and 1c. Due to the less effective overlap of the peripheral groups between successive discs, hole transport occurs not only through the (2,3) couple, but also between two alternate discs, the latter becoming dominant in 1a–c and 2c. This is a consequence of the location of the HOMO/LUMO orbitals and the helical position of the cores as described above.

Table 6 Calculated transfer integral t (eV) and mobility μ (cm² V⁻¹ s⁻¹) for holes and electrons

	Method	Couple	t +	t −	μ +	μ −
1a	B3LYP/6-31G*	2,3	6.58 × 10^−5	8.68 × 10^−2	4.33 × 10^−8	3.16 × 10^−1
	B3LYP/6-311G**		1.86 × 10^−3	7.41 × 10^−2	3.38 × 10^−5	2.03 × 10^−1
	M06-2X/6-311G**		6.66 × 10^−3	9.16 × 10^−2	2.44 × 10^−4	2.87 × 10^−1
	B3LYP/6-31G*	2,4	4.50 × 10^−3	2.74 × 10^−3	8.11 × 10^−4	1.25 × 10^−3
	B3LYP/6-311G**		6.37 × 10^−3	4.20 × 10^−3	1.58 × 10^−3	2.97 × 10^−3
	M06-2X/6-311G**		5.44 × 10^−3	5.32 × 10^−3	6.52 × 10^−4	3.97 × 10^−3
1b	B3LYP/6-31G*	2,3	1.35 × 10^−2	1.04 × 10^−2	2.15 × 10^−2	2.23 × 10^−3
	B3LYP/6-311G**		1.31 × 10^−2	5.58 × 10^−3	2.03 × 10^−2	6.28 × 10^−4
	M06-2X/6-311G**		1.57 × 10^−2	8.73 × 10^−3	2.66 × 10^−2	1.44 × 10^−3
	B3LYP/6-31G*	2,4	1.95 × 10^−2	2.71 × 10^−3	1.79 × 10^−1	6.12 × 10^−4
	B3LYP/6-311G**		2.05 × 10^−2	3.36 × 10^−3	1.98 × 10^−1	9.14 × 10^−4
	M06-2X/6-311G**		2.35 × 10^−2	4.61 × 10^−3	2.38 × 10^−1	1.60 × 10^−3
1c	B3LYP/6-31G*	2,3	1.63 × 10^−2	1.00 × 10^−1	3.85 × 10^−2	2.37 × 10^−1
	B3LYP/6-311G**		1.36 × 10^−2	1.18 × 10^−1	2.66 × 10^−2	3.44 × 10^−1
	M06-2X/6-311G**		8.60 × 10^−3	1.50 × 10^−1	1.00 × 10^−2	4.14 × 10^−1
	B3LYP/6-31G*	2,4	1.09 × 10^−2	4.84 × 10^−3	6.90 × 10^−2	2.22 × 10^−3
	B3LYP/6-311G**		1.34 × 10^−2	4.35 × 10^−3	1.04 × 10^−1	1.86 × 10^−3
	M06-2X/6-311G**		1.54 × 10^−2	4.51 × 10^−3	1.28 × 10^−1	1.50 × 10^−3
2a	B3LYP/6-31G*	2,3	6.99 × 10^−2	3.87 × 10^−2	6.36 × 10^−2	2.42 × 10^−2
	B3LYP/6-311G**		6.85 × 10^−2	3.85 × 10^−2	6.11 × 10^−2	2.45 × 10^−2
	M06-2X/6-311G**		7.22 × 10^−2	5.17 × 10^−2	4.86 × 10^−2	3.11 × 10^−2
	B3LYP/6-31G*	2,4	9.07 × 10^−3	3.93 × 10^−4	4.29 × 10^−3	9.97 × 10^−6
	B3LYP/6-311G**		8.20 × 10^−3	8.19 × 10^−4	3.50 × 10^−3	4.44 × 10^−5
	M06-2X/6-311G**		5.07 × 10^−3	1.01 × 10^−3	9.60 × 10^−4	4.74 × 10^−5
2b	B3LYP/6-31G*	2,3	4.75 × 10^−2	2.33 × 10^−2	7.30 × 10^−2	3.64 × 10^−2
	B3LYP/6-311G**		5.08 × 10^−2	2.01 × 10^−2	8.49 × 10^−2	3.58 × 10^−2
	M06-2X/6-311G**		5.77 × 10^−2	2.41 × 10^−2	3.80 × 10^−2	3.07 × 10^−2
	B3LYP/6-31G*	2,4	4.88 × 10^−3	1.12 × 10^−4	2.89 × 10^−3	3.15 × 10^−6
	B3LYP/6-311G**		5.79 × 10^−3	3.79 × 10^−4	4.14 × 10^−3	4.77 × 10^−5
	M06-2X/6-311G**		5.77 × 10^−3	1.94 × 10^−5	1.43 × 10^−3	7.52 × 10^−8
2c	B3LYP/6-31G*	2,3	2.51 × 10^−2	4.21 × 10^−2	8.09 × 10^−2	7.28 × 10^−2
	B3LYP/6-311G**		2.84 × 10^−2	5.42 × 10^−2	1.05 × 10^−1	1.25 × 10^−1
	M06-2X/6-311G**		3.05 × 10^−2	5.35 × 10^−2	1.16 × 10^−1	8.46 × 10^−2
	B3LYP/6-31G*	2,4	1.13 × 10^−1	2.84 × 10^−3	6.53	1.33 × 10^−3
	B3LYP/6-311G**		1.23 × 10^−1	3.41 × 10^−3	7.81	1.98 × 10^−3
	M06-2X/6-311G**		1.33 × 10^−1	4.76 × 10^−3	8.83	2.68 × 10^−3

---

Hole mobility in the (2,3) couple for 1a (μ₊ ∼ 10⁻⁶ cm² V⁻¹ s⁻¹) is much lower than the electron one (μ₋ ∼ 10⁻¹ cm² V⁻¹ s⁻¹) due to the less effective overlap of the phenyl-thiophene segments, which is increased between two alternate units (μ₊ ∼ 10⁻³ cm² V⁻¹ s⁻¹), in reasonable agreement with values from TOF data.⁵² Thus, experimental μ_−/+ values for a compound similar to 1a but with side –OC₁₂H₂₅ chains were ca. 4 × 10⁻³/3 × 10⁻⁵ cm² V⁻¹ s⁻¹ in Col_h phases.⁵² As expected, there is no quantitative agreement between the theoretical and experimental values due to neglecting the stack dynamics while calculating the mobility, but the theoretical results keep a similar trend.

For 1c no distinct electron mobility could be determined from the experimental measurements,⁵² although the authors predicted a μ₊ value larger than that for 1a, ∼1 × 10⁻³ cm² V⁻¹ s⁻¹ in Col_h phases with –OC₁₂H₂₅ as the side chain. As seen in Table 6, values for μ₊ for 1a and 1c in the (2,4) couples follow the same trend while 1b keeps values larger than those for 1a and 1c, i.e. μ₊ (1a) ≪ μ₊ (1b) > μ₊ (1c). As for μ₋ it drops abruptly when going either from 1a and 1c to 1b both for (2,3) and (2,4) couples.

The higher μ₊ in 1c as compared to 1a could be due to the enhanced HOMO overlap when the N-carbazolyl is in the peripheral region, which is less effective in 1a.⁵² On the other hand, mobilities in 1a and 1c are comparable to those observed for several DLCs as Cu–phthalocyanine derivatives (μ₋ = 2.4 × 10⁻³ cm² V⁻¹ s⁻¹; μ₊ = 2.17 × 10⁻³ cm² V⁻¹ s⁻¹),⁴⁵ HDBP-3 (μ₋ ≈ μ₊ ∼ 10⁻³ cm² V⁻¹ s⁻¹),⁴³ HT5 (μ₋ ≈ μ₊ ∼ 10⁻³ cm² V⁻¹ s⁻¹), HT6 (μ₋ ≈ μ₊ ∼ 10⁻⁴ cm² V⁻¹ s⁻¹) and HHTT (μ₋ ≈ μ₊ ∼ 10⁻³ cm² V⁻¹ s⁻¹),⁵⁰ among others.

For tristriazolotriazine core derivatives, the experimental data point out that 2a could potentially exhibit electron transport properties, although data for mobility have not been reported.⁵⁹ For 2a in the (2,3) couple, theoretical values for μ₊ and μ₋ turn out to be similar to each other, but smaller than μ₋ for 1a. Therefore, the two dimensional expansion of the conjugated core does not seem to play any significant role in improving the electron mobility.

For 2a and 2b, calculations predict similar values for μ₋ and slightly lower than that for 2c in the (2,3) couple. In addition, μ₋ for 2c is lower than that for 1a and 1c, while μ₊ becomes clearly larger than that for 1b and 1c. As for the (2,4) couple, μ₊ for 2c turns out to be nearly two orders of magnitude larger than that for 1c. This fact could be due to the higher overlap of the N-carbazolyl units in 2c which renders larger values for t₊, λ₊ being nearly the same in both systems. Furthermore, despite the distance between central cores in the (2,4) couple is about double that for the (2,3) one, the distance between the N-carbazolyl planes of two (2,4) discs is about 3.8 Å, and then, a higher μ₊ could be obtained if it is considered for l in eqn (2).

The relative mobility μ₋/μ₊ for the (2,3) couple clearly points out that 1a exhibits larger electron mobility than the hole one, in agreement with the experimental data,⁵² as well as 1c, while the opposite behavior is found for 1b regardless of the couple, i.e. (2,3) or (2,4), μ₊ refers to. For 2a and 2b, the hole mobility is larger than the electron one, especially for the (2,4) couple while for 2c the ratio μ₋/μ₊ keeps nearly unity for the (2,3) couple. Finally, the relative mobilities, μ/μ_(1a) keep greater than unity for hole mobility regardless of the couple considered while for electron mobility the ratio keeps lower than unity except for 1c for which a more balanced situation is shown.

Therefore, the new, not yet synthesized molecules, 2b and 2c, are predicted to yield values for charge transport related properties in the same range of those for 1a and 1c, for which ambipolar character has been proven, and thus they could be considered reasonable candidates for ambipolar DLC materials.

Conclusions

Our theoretical study has allowed us to reproduce the relative values for the electron and hole mobilities of the ambipolar compounds 1a and 1c, in agreement with the experimental data. Atoms-in-Molecules (AIM) analysis concludes that core enlargement renders an increase in the number of π⋯π stacking contacts and the intermolecular contacts between either consecutive (2,3) and alternate (2,4) units through H-bonds and/or π⋯π stacking interactions favor the helical disposition of the discs along the column. Core–peripheral intramolecular interactions could force the structure of the discs to flatten favoring their stacking. However, they could prevent the formation of intermolecular contacts between two adjacent discs. Therefore, in order to get stable columnar mesophases when designing new DLCs the competition between inter- and intramolecular interactions should be carefully considered.

In order to interpret the ambipolar charge transport behavior of those compounds, the existence of two main charge transport channels has been proposed, one for the hole transport through the HOMO orbitals located in the peripheral region where the phenyl-thiophene or N-carbazolyl-thiophene segments are present, and another one for electron transport through the LUMO orbitals, located in the central region of the core where the triazine or tristriazolotriazine are present. Furthermore, we have predicted the hole and electron mobilities for two new compounds, named 2b and 2c, which have not been synthesized yet. The last one has shown a significant increase of the hole mobility due to the presence of the N-carbazolyl unit. From a theoretical point of view, the intrinsic nature of these compounds has proven that they are good candidates for ambipolar charge transport, and this feature could play an important role in their applications as organic semiconductors in the future.

Acknowledgements

Support from Consejería de Innovación, Ciencia y Empresa, Junta de Andalucía, Spain (PAI-FQM-337 grant) and Centro Informático Científico de Andalucía is gratefully acknowledged.

References

1. S. Chandrasekhar, B. K. Sadashiva and K. A. Suresh, Pramana, 1977, 9, 471–480.
2. M. O'Neill and S. M. Kelly, Adv. Mater., 2011, 23, 566–584.
3. E. Moulin, J. J. Cid and N. Giuseppone, Adv. Mater., 2013, 25, 477–487.
4. V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J. L. Brédas, Chem. Rev., 2007, 107, 926–952.
5. S. Sergeyev, W. Pisula and Y. H. Geerts, Chem. Soc. Rev., 2007, 36, 1902–1929.
6. X. Feng, V. Marcon, W. Pisula, M. Ryan-Hansen, J. Kirkpatrick, F. Grozema, D. Andrienko, K. Kremer and K. Müllen, Nat. Mater., 2009, 8, 421–426.
7. K. Pieterse, P. A. van Hal, R. Kleppinger, J. A. J. M. Vekemans, R. A. J. Janssen and E. W. Meijer, Chem. Mater., 2001, 13, 2675–2679.
8. K. Senthilkumar, F. C. Grozema, F. M. Bickelhaut and L. D. A. Siebbeles, J. Chem. Phys., 2003, 119, 9809–9817.
9. J. Cornil, V. Lemaur, J. P. Calbert and J. L. Brédas, Adv. Mater., 2002, 14, 726–729.
10. R. I. Gearba, M. Lehmann, J. Levin, D. A. Ivanov, M. H. J. Koch, J. Barberá, M. G. Debije, J. Piris and Y. H. Geerts, Adv. Mater., 2003, 15, 1614–1618.
11. O. D. Jurchescu, J. Bass and T. T. M. Palstra, Appl. Phys. Lett., 2004, 84, 3061–3063.
12. D. A. da Silva Filho, E.-G. Kim and J. L. Brédas, Adv. Mater., 2005, 17, 1072–1076.
13. R. Juarez, M. Moreno-Oliva, M. Ramos, J. Segura, C. Aleman, F. Rodríguez-Ropero, D. Curco, F. Montilla, V. Coropceanu and J. L. Brédas, Chem. – Eur. J., 2011, 17, 10312–10322.
14. M. Lehmann, G. Kestemont, R. Gómez Aspe, C. Buess-Herman, M. H. J. Koch, M. G. Debije, J. Piris, M. P. de Haas, J. M. Warman, M. D. Watson, V. Lemaur, J. Cornil, Y. H. Geerts, R. Gearba and D. A. Ivanov, Chem. – Eur. J., 2005, 11, 3349–3362.
15. B. R. Kaafarani, T. Kondo, J. S. Yu, Q. Zhang, D. Dattilo, C. Risko, S. C. Jones, S. Barlow, B. Domercq, F. Amy, A. Kahn, J. L. Brédas, B. Kippelen and S. Marder, J. Am. Chem. Soc., 2005, 127, 16358–16359.
16. X. Crispin, J. Cornil, R. Friedlein, K. K. Okudaira, V. Lemaur, A. Crispin, G. Kestemont, M. Lehmann, M. Fahlman, R. Lazzaroni, Y. Geerts, G. Wendin, N. Ueno, J. L. Brédas and W. R. Salaneck, J. Am. Chem. Soc., 2004, 126, 11889–11899.
17. V. Lemaur, D. A. da Silva Filho, V. Coropceanu, M. Lehmann, Y. Geerts, J. Piris, M. G. Debije, A. M. van de Craats, K. Senthilkumar, L. D. A. Siebbeles, J. M. Warman, J. L. Brédas and J. Cornil, J. Am. Chem. Soc., 2004, 126, 3271–3279.
18. M. G. Debije, J. Piris, M. P. de Hass, J. M. Warman, Z. Tomovic, C. D. Simpson, M. D. Watson and K. Müllen, J. Am. Chem. Soc., 2004, 126, 4641–4645.
19. Y. Olivier, V. Lemaur, J. L. Brédas and J. Cornil, J. Phys. Chem. A, 2006, 110, 6356–6364.
20. G. Cinacchi and G. Prampolini, J. Phys. Chem. C, 2008, 112, 9501–9509.
21. W. Pisula, X. Feng and K. Müllen, Adv. Mater., 2010, 22, 3634–3649.
22. A. Demenev, S. H. Eichhorn, T. Taerum, D. F. Perepichka, S. Patwardhan, F. C. Grozema and L. D. A. Siebbeles, Chem. Mater., 2010, 22, 1420–1428.
23. L. Wang, G. Nan, X. Yang, Q. Peng, Q. Li and S. Zhigang, Chem. Soc. Rev., 2010, 39, 423–434.
24. J. E. Anthony, A. Facchetti, M. Heeney, S. R. Marder and X. Zhan, Adv. Mater., 2010, 22, 3876–3892.
25. L. A. Haverkate, M. Zbiri, M. R. Johnson, B. Deme, M. Fokko, F. M. Mulder and G. J. Kearley, J. Phys. Chem. B, 2011, 115, 13809–13816.
26. B. R. Kaafarani, Chem. Mater., 2011, 23, 378–396.
27. W. Pisula, X. Feng and K. Müllen, Chem. Mater., 2011, 23, 554–567.
28. L. Lin, H. Geng, Z. Shuai and Y. Luo, Org. Electron., 2012, 13, 2763–2772.
29. G. García, M. Moral, J. M. Granadino-Roldan, A. Garzón, A. Navarro and M. Fernández-Gómez, J. Phys. Chem. C, 2013, 117, 15–22.
30. S. Sanyal, A. K. Manna and S. K. Pati, J. Phys. Chem. C, 2013, 117, 825–836.
31. F. C. Grozema and L. D. A. Siebbeles, Int. Rev. Phys. Chem., 2008, 27, 87–138.
32. C. Lavigueur, E. J. Foster and V. E. Williams, J. Am. Chem. Soc., 2008, 130, 11791–11800.
33. A. Rochefort, E. Bayard and S. Hadj-Messaoud, Adv. Mater., 2007, 19, 1992–1995.
34. G. García, M. Moral, A. Garzón, J. M. Granadino-Roldán, A. Navarro and M. Fernández-Gómez, Org. Electron., 2012, 13, 3244–3253.
35. U. Purushotham and G. N. Sastry, Phys. Chem. Chem. Phys., 2013, 15, 5039–5048.
36. S. Akoudad and J. Roncali, Chem. Commun., 1998, 2081–2082.
37. T. T. Steckler, X. Zhang, J. Hwang, R. Honeyager, S. Ohira, X.-H. Zhang, A. Grant, S. Ellinger, S. A. Odom, D. Sweat, D. B. Tanner, A. G. Rinzler, S. Barlow, J. L. Brédas, B. Kippelen, S. R. Marder and J. R. Reynolds, J. Am. Chem. Soc., 2009, 131, 2824–2826.
38. W. Pisula, A. Menon, M. Stepputat, I. Lieberwirth, U. Kolb, A. Tracz, H. Sirringhaus, T. Pakula and K. Müllen, Adv. Mater., 2005, 17, 684–689.
39. H. Hayashi, W. Nihashi, T. Umeyama, Y. Matano, S. Seki, Y. Shimizu and H. Imahori, J. Am. Chem. Soc., 2011, 133, 10736–10739.
40. M. Funahashi and J.-I. Hanna, Appl. Phys. Lett., 2000, 76, 2574–2576.
41. M. Funahashi and J.-I. Hanna, Appl. Phys. Lett., 1998, 73, 3733–3735.
42. M. Funahashi and J.-I. Hanna, Appl. Phys. Lett., 1997, 71, 602–604.
43. L.-Y. Chen, F.-H. Chien, Y.-W. Liu, W. Zheng, C.-Y. Chiang, C.-Y. Hwang, C.-W. Ong, Y.-K. Lan and H. C. Yang, Org. Electron., 2013, 14, 2065–2070.
44. H. Iino, J.-I. Hanna and D. Haarer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 193–203.
45. H. Fujikake, T. Murashige, M. Sugibayashi and K. Ohta, Appl. Phys. Lett., 2004, 85, 3474–3476.
46. S. Méry, D. Haristoy, J. F. Nicoud, D. Guillon, S. Diele, H. Monobec and Y. Shimizuc, J. Mater. Chem., 2002, 12, 37–41.
47. H. Iino and J.-I. Hanna, Opto-Electron. Rev., 2005, 13, 295–302.
48. G. Saranya, N. Santhanamoorthi, P. Kolandaivel and K. Senthilkumar, Int. J. Quantum Chem., 2012, 112, 713–723.
49. J. Hanna, A. Ohno and H. Iino, Thin Solid Films, 2014, 554, 58–63.
50. H. Iino, Y. Takayashiki, J.-I. Hanna, R. J. Bushby and D. Haarer, Appl. Phys. Lett., 2005, 87, 192105.
51. Z. Chen, M. J. Lee, R. S. Ashraf, Y. Gu, A.-S. Sebastian, M. M. Nielsen, B. Schroeder, T. D. Anthopoulos, M. Heeney, I. McCulloch and H. Sirringhaus, Adv. Mater., 2012, 24, 647–652.
52. T. Yasuda, T. Shimizu, F. Liu, G. Ungar and T. Kato, J. Am. Chem. Soc., 2011, 133, 13437–13444.
53. G. García, J. M. Granadino-Roldán, A. Garzón, M. Moral, T. Peña-Ruiz, A. Navarro, M. P. Fernández-Liencres and M. Fernández-Gómez, J. Phys. Chem. C, 2010, 114, 12325–12334.
54. G. García, A. Garzón, J. M. Granadino-Roldán, M. Moral, M. P. Fernández-Liencres, A. Navarro and M. Fernández-Gómez, Aust. J. Chem., 2010, 63, 1297–1306.
55. M. Manickam, M. Belloni, S. Kumar, S. K. Varshney, D. S. S. Rao, P. R. Ashton, J. A. Preece and N. Spencer, J. Mater. Chem., 2001, 11, 2790–2800.
56. M. J. Sienkowska, H. Monobe, P. Kaszynski and Y. Shimizu, J. Mater. Chem., 2007, 17, 1392–1398.
57. B. R. Kaafarani, A. O. El-Ballouli, R. Trattnig, A. Fonari, S. Sax, B. Wex, C. Risko, R. S. Khnayzer, S. Barlow, D. Patra, T. V. Timofeeva, E. J. W. List, J. L. Brédas and S. R. Marder, J. Mater. Chem. C, 2013, 1, 1638–1650.
58. R. Cristiano, H. Gallardo, A. J. Bortoluzzi, I. H. Bechtold, C. E. M. Campos and R. L. Longo, Chem. Commun., 2008, 5134–5136.
59. R. Cristiano, J. Eccher, I. H. Bechtold, C. N. Tironi, A. A. Vieira, F. Molin and H. Gallardo, Langmuir, 2012, 28, 11590–11598.
60. M. J. Frisch, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2009.
61. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
62. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
63. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
64. W. J. Hehre, L. Radom, P. v. R. Scheleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986.
65. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
66. E. G. Hohenstein, S. T. Chill and C. D. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996–2000.
67. K. A. McGarry, W. Xie, C. Sutton, C. Risko, Y. Wu, V. G. Young Jr., J. L. Brédas, C. D. Frisbie and C. J. Douglas, Chem. Mater., 2013, 25, 2254–2263.
68. J. Idé, R. Mereau, L. Ducasse, F. Castet, Y. Olivier, M. Martinelli, J. Cornil and D. Beljonne, J. Phys. Chem. B, 2011, 115, 5593–5603.
69. A. Demenev, S. H. Eichhron, T. Taerum, D. F. Perepichka, S. Patwardhan, F. C. Grozema, L. D. A. Siebbeles and R. Klenkler, Chem. Mater., 2010, 22, 1420–1428.
70. F. Maseras and K. Morokuma, J. Comput. Chem., 1995, 16, 1170–1179.
71. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
72. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
73. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
74. X. Xua and W. A. Goddard III, J. Chem. Phys., 2004, 121, 4068–4082.
75. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
76. M. Swart, M. Solá and F. M. Bickelhaupt, J. Comput. Methods Sci. Eng., 2009, 9, 69–77.
77. T. Le Bahers, M. Rerat and P. Sautet, J. Phys. Chem. C, 2014, 118, 5997–6008.
78. B. Baumeier, J. Kirkpatrick and D. Andrienko, Phys. Chem. Chem. Phys., 2010, 12, 11103–11113.
79. J. Kirkpatrick, Int. J. Quantum Chem., 2008, 108, 51–56.
80. R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610.
81. P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168.
82. V. Balzani, A. Juris, S. Campagna and S. Serroni, Chem. Rev., 1996, 96, 759–834.
83. J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809.
84. F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545–559.
85. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990.
86. U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754.
87. P. L. A. Popelier, J. Phys. Chem. A, 1998, 102, 1873–1878.
88. M. P. Waller, A. Robertazzi, J. A. Platts, D. E. Hibbs and P. A. William, J. Comput. Chem., 2006, 27, 491–504.
89. R. G. A. Bone and R. F. W. Bader, J. Phys. Chem., 1996, 100, 10892–10911.
90. C. R. Newman, C. D. Frisbie, D. A. da Silva Filho, J. L. Brédas, P. C. Ewback and K. R. Mann, Chem. Mater., 2004, 16, 4436–4451.
91. L. Lindell, A. Burquel, F. L. E. Jakobsson, V. Lemaur, M. Gerggren, R. Lazzaroni, J. Cornil, W. R. Salaneck and X. Crispin, Chem. Mater., 2006, 18, 4246–4252.
92. C. K. Chen, L. Y. Zou, S. Huang, C. G. Min, A. M. Ren, J. K. Feng and C. C. Sun, Org. Electron., 2011, 12, 1198–1210.
93. E. Jansson, P. C. Jha and H. Ågren, Chem. Phys., 2006, 330, 166–171.
94. L. Reséndiz, M. Estrada, A. Cerdeira, B. Iñiguez and M. J. Deen, Org. Electron., 2010, 11, 1920–1927.
95. J. Kirkpatrick, V. Marcon, J. Nelson, K. Kremer and D. Andrienko, Phys. Rev. Lett., 2007, 98, 227402.
96. Y. Geng, J. Wang, S. Wu, H. Li, F. Yu, G. Yang, H. Gao and Z. Su, J. Mater. Chem., 2011, 21, 134–143.
97. J. Idé, R. Méreau, L. Ducasse, F. Castet, H. Bock, Y. Olivier, J. Cornil, D. Beljonne, G. D'Avino, O. M. Roscioni, L. Muccioli and C. Zannoni, J. Am. Chem. Soc., 2014, 136, 2911–2920.
98. E. Di Donato, R. P. Fornari, S. Di Motta, Y. Li, Z. Wang and F. Negri, J. Phys. Chem. B, 2010, 114, 5327–5334.
99. Y. Olivier, L. Muccioli, V. Lemaur, Y. H. Geerts, C. Zannoni and J. Cornil, J. Phys. Chem. B, 2009, 113, 14102–14111.
100. J. E. Norton and J. L. Brédas, J. Am. Chem. Soc., 2008, 130, 12377–12384.
101. P. McMahon and A. Troisi, J. Phys. Chem. Lett., 2010, 1, 941–946.
102. Y.-F. Chang, Z.-Y. Lu, L.-J. An and J.-P. Zhang, J. Phys. Chem. C, 2012, 116, 1195–1199.
103. S. E. Koh, C. Risko, D. A. da Silva Filho, O. Kwon, A. Facchetti, J. L. Brédas, T. J. Marks and M. A. Ratner, Adv. Funct. Mater., 2008, 18, 332–340.
104. P. Pope and C. E. Swenberg, Electronic Process in Organic Crystals and Polymers, Oxford, New York, 2nd edn, 1999.
105. S. Wen, A. Li, J. Song, W. Deng, K. Han and W. A. Goddard III, J. Phys. Chem. B, 2009, 113, 8813–8819.
106. V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345.
107. A. Troisi, Chem. Soc. Rev., 2011, 40, 2347–2358.
108. S. Barlow, Q. Zhang, B. R. Kaafarani, C. Risko, F. Amy, C. K. Chan, B. Domercq, Z. A. Starikova, M. Y. Antipin, T. V. Timofeeva, B. Kippelen, J. L. Brédas, A. Kahn and S. R. Marder, Chem. – Eur. J., 2007, 13, 3537–3547.
109. M. Winkler and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 1805–1815.

---

Footnote

† Electronic supplementary information (ESI) available: Comments on the QTAIM analysis, rotational barrier for the couple of 1a and 2a at the B3LYP/6-31G* level, representation of the intramolecular bond paths in single molecules of the selected compounds, dependence of |V_b|/G_b and H_b/ρ_b indices on the interatomic distance, representation of the inter and intra molecular bond paths for the (2,4) couples and topological properties for single disc and (2,3) and (2,4) couples at the B3LYP/6-31G* level. See DOI: 10.1039/c4cp04220d

---