The vibrational relaxation of NO in Ar: tunneling in a curve-crossing mechanism
Received
12th September 2014
, Accepted 10th October 2014
First published on 14th October 2014
Abstract
Experimental data for the vibrational relaxation NO(X2Π, v = 1) + Ar → NO(X2Π, v = 0) + Ar between 300 and 2000 K are analyzed. The measured rate coefficients k10 greatly exceed Landau–Teller values LTk10. This observation can be attributed to a mechanism involving curve-crossing of the (A′′, v = 1) and (A′, v = 0) vibronic states of the collision system. At high temperatures, the rate coefficients k10 are well represented by the thermally averaged Landau–Zener rate constant LZk10 with an apparent Arrhenius activation energy Ea/kB near 4500 K. At intermediate temperatures, around T = 900 K, the measured k10 values are a factor of two higher than the extrapolated LZk10 values. This deviation is attributed to tunneling in nonadiabatic curve-crossing transitions, which are analyzed within the Airy approximation (linear model for crossing diabatic curves) and an effective mass approach. This suggests a substantial contribution of hindered rotation of NO to the nonadiabatic perturbation. The extrapolation of the Airy probabilities to even lower temperatures (by the Landau–Lifshitz WKB tunneling expression for simple nonlinear model potentials) indicates a further marked increase of the tunneling contribution beyond the extrapolated LZk10. Near 300 K, the k10 can be two to three orders of magnitude higher than the extrapolated LZk10. This agrees with the limited available experimental data for NO–Ar relaxation near room temperature.
1. Introduction
The vibrational relaxation of diatomic molecules AB in a degenerate electronic state upon collisions with chemically inert atoms C proceeds mainly through a curve-crossing mechanism, provided the Landau–Teller path makes a smaller contribution to the inelastic event.1,2 In particular, in the case of the deactivation of the first vibrational state (rate coefficient k10(T)) the relevant crossing diabatic potentials correspond to the least repulsive vibronic state of the system AB(v = 1) + C and the strongest repulsive vibronic state of the system AB(v = 0) + C. An example of this mechanism is the relaxation of NO(X2Π, v = 1) in collisions with noble gas atoms where two crossing vibronic potential energy surfaces (PESs) correspond to the (A′′, v = 1) and (A′, v = 0) vibronic states of the collision system. Being of different symmetry with respect to a reflection of the electron coordinates in the three-atom plane, the two vibronic states are coupled by Coriolis interaction, induced by the rotation of the plane, and by spin–orbit interaction mixing the electronic states of different symmetry. If the nonadiabatic coupling in the crossing region is described by the Landau–Zener (LZ) formalism, the LZ vibrational relaxation rate coefficient LZk10(T) assumes a well-defined temperature dependence3,4 governed mainly by an Arrhenius factor with the activation energy Ea. Within this approach, tunneling nonadiabatic transitions are ignored. Earlier estimates of tunneling corrections to the LZ rate indeed showed that they are negligible at T > 1000 K such that the LZ approach3,4 appeared to be adequate for interpretation of the available experimental data.5,6 In the present work we revisit the question of tunneling nonadiabatic transitions for two reasons. First, earlier estimates were performed on the basis of rather low values of Ea (Ea/kB ≈ 750 K), whereas later experiments suggested a much higher barrier7,8 for which tunneling may be more pronounced. Second, these experiments also indicated a tendency of a slower decrease of k10(T) with decreasing temperature than predicted by the LZ treatment.9,10 It is the aim of the present work to correct the LZ expression for the relaxation rate coefficient and to elucidate implications for NO–Ar collisions that follow from this correction. In our article, Section 2 discusses the evidence for tunneling, and Section 3 presents a description of the tunneling contributions in a linear model of diabatic potential curves. In Section 4 this description is generalized to nonlinear diabatic potential curves. Section 5 applies the results to NO–Ar collisions in the effective mass approximation for two-dimensional (translational/rotational) non-adiabatic dynamics and Section 6 concludes the paper.
2. Evidence for nonadiabatic tunneling in NO(X2Π, v = 1) + Ar → NO(X2Π, v = 0) + Ar collisions
Experimental data for the rate coefficient of the vibrational relaxation NO(X2Π, v = 1) + Ar from ref. 7 (denoted by GTk10(T)) are presented in Fig. 1 as red circles. The figure compares these data with a number of representations.
 |
| | Fig. 1 Landau–Zener (LZ) rate coefficients (dashed red line, LZk10) of the vibrational relaxation NO in Ar fitted to high-temperature experimental data (red points, GTk10(T)) and Landau–Teller rate coefficients (green dotted line, LTk10, rescaled from O2–Ar relaxation data11). Also shown is an experimental result near 300 K from ref. 9 and 10 (blue triangle, S,Kk10). | |
The blue line is drawn through the data points over the temperature range 900–1500 K where the rate coefficients for the competing LT relaxation mechanism LTk10 (green dotted line) lie much lower than the experimental values of k10(T). The LT rate coefficients for NO(X2Π, v = 1) + Ar collisions were estimated by renormalization of experimental data for O2–Ar collisions from ref. 11 taking into account the difference in the vibrational energy release, ΔE10(NO) and ΔE10(O2). The observation LTk10(T) ≪ GTk10(T) allows one to unambiguously attribute the relaxation NO(X2Π, v = 1) + Ar to a curve-crossing mechanism. The figure includes experimental results for substantially lower temperatures (near 300 K, blue triangle) obtained by LIF and IR-UV double resonance techniques.9,10 It is our aim to provide an analysis of the combined set of experimental data.
Once the relaxation mechanism is described within the LZ formalism following ref. 1, 3 and 4, the temperature dependence of LZk10(T), calculated within the transition state method, can be represented as
| | | LZk10(T) = LZAT1/2(T + TSO)exp(−Ea/kBT) | (2.1) |
Here the temperature independent factor
LZA includes contributions of the nonadiabatic coupling. The temperature dependent factors of
eqn (2.1) consist of an Arrhenius factor arising from the probability of arriving at the crossing of the two vibronic PESs on the initial (
A′′,
v = 1) PES, the middle factor related to the coupling (with the linear term,
T, from averaged Coriolis interaction and the temperature independent term,
TSO, from spin–orbit interaction) and the first factor,
T1/2, originating from the width of the channel that passes through the activation energy point
Ea. Within the LZ treatment the nonadiabatic transition for the linear model neglects classically forbidden transitions (
i.e. for collision energies
E below the crossing value
Ea) and includes classically allowed transitions (for
E >
Ea) without accounting for interference effects. The LZ rate coefficient
LZk10 within this approach in
Fig. 1 is fitted by
eqn (2.1) to the high-temperature part of
GTk10, leading to values of
A = 5.0 × 10
−19 cm
3 s
−1,
Ea/
kB = 4500 K, and a parameter
TSO = 3225 K which is proportional to the known spin–orbit splitting of the
X2Π state of NO. We note here that the fitted value
Ea/
kB = 4500 K somewhat differs from the estimated value of
Ea/
kB derived from the
ab initio calculations of potentials in
ref. 12–14 that yield
Ea/
k ≈ 5400 K.
Because of the dominance of the Arrhenius factor, the temperature dependence of the preexponential factor in eqn (2.1) is hardly discernable. The deviations of the experimental points from a straight line, i.e. the difference between the full and dashed curves in Fig. 1, can then be interpreted as a manifestation of tunneling and interference that are ignored by the LZ modeling. We represent these deviations by an expression of the form
| | | k10(T) = C(T)LZk10(T) | (2.2) |
For the lowest temperatures attained in the shock tube experiments (about 900 K),
C(
T) takes a value of about 2.
The following comment on the adiabatic states of the NO(X2Π) + Ar system will be in order. In the asymptotic region, R → ∞, the rotronic (i.e. rotational + electronic) states of NO belong to states that fall into F1 and F2 manifolds of the a–b intermediate Hund coupling case.15 In the region of the strong electrostatic and exchange interaction, where the energy difference DBO between the two Born–Oppenheimer (BO) PESs is much larger than the spin–orbital coupling, the BO states, within the accuracy to A2/DBO, can be specified by the projections of the electron spin onto a space-fixed axis and the symmetry character (symmetric or antisymmetric) of the coordinate wave function (2A′ or 2A′′) with respect to reflection in the system plane (i.e. in the NOAr plane). The BO energies of these states within the accuracy to A2/DBO are then calculated completely neglecting the spin–orbital interaction, and the latter, together with the Coriolis coupling, then considered as a weak perturbation. This scheme of transformation of asymptotic states into the states with strong interfragment interaction is discussed in detail in ref. 16. Within the transition state approach, the initial canonical distribution over the states of collision partners becomes a canonical distribution over the states of the activated complex. A lot of processes can happen on the way from the asymptotic region to the critical surface but they do not show up in the canonical-to-canonical transformation of the distribution function, including the Λ-doublet propensities in the rotationally inelastic Ar–NO(X2Π) scattering.
Within the linear model of weak nonadiabatic coupling, which is the basis of the LZ approximation to k10, the tunneling and the interference effects can be taken into account by expressing the nonadiabatic transition probability through the Airy (Ai) function. We discuss this approach in Section 3 and employ it to the experimental data in Section 5. When eqn (2.2) is applied to experimental conditions near room temperature the factor C(T) exceeds a factor of one hundred such that an analysis by the Airy approximation is not possible. This issue will be discussed in Section 4.
3. Airy approximation for nonadiabatic tunneling
In the weak-coupling limit of the linear model, the non-adiabatic transition probability P(E) for transition between the PESs of two contributing vibronic states is expressed1 through the Airy function (with P(E) = AiP(E)) as| | | AiP(E) ∝ Ai2 (−(E − Ea)/Eq) | (3.1) |
Here E is the energy of the representative point moving on the linear diabatic potential curves that cross at the energy Ea. The characteristic energy parameter Eq depends on the slopes of the diabatic potentials F′ and F′′, their difference ΔF = |F′ − F′′|, and the effective mass μq of the motion along the reaction coordinate q,| | 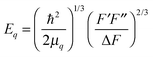 | (3.2) |
The factor in front of Ai2 in eqn (3.1) does not depend on the energy. It is proportional to the square of the coupling interaction, which is responsible to the change of the crossing diabatic potential curves into the nearly-crossing adiabatic curves with small avoided crossing gap. Since in the following we discuss the ratios of probabilities this factor can be disregarded.
The LZ approximation of AiP(E) is obtained from eqn (3.1) when the square of the Airy function, for (E − Ea)/Eq ≫ 1, is replaced by its WKB asymptote which then is averaged over the Stueckelberg (St) oscillations and extended over the classically allowed energy range by extrapolation down to (E − Ea)/Eq ≪ 1,
| |  | (3.3) |
where
Θ is the step function. Within the Airy approximation, the correction factor
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) AiC
AiC(
T) then is expressed through the ratio of the canonically averaged probabilities with the formal energy limits −∞ <
E < ∞;
| |  | (3.4) |
The convergence of the integrals in
eqn (3.4) at the upper limit is guaranteed by the exponential drop in the Boltzmann factor while convergence of the integral in the numerator at the lower limit is a result of the stronger drop of the Airy asymptote compared to the increasing Boltzmann factor. Finally,
AiC(
T) can be expressed analytically as
| |  | (3.5) |
Considering the quality of the Airy approximation in
AiC(
T) one should take into account that
AiC(
T) can overestimate the tunneling effect for two reasons: (i) the triangular barrier formed by the two straight lines of the diabatic curves is too narrow compared to a more realistic crossing and (ii) the extension of collision energies to values much lower than
Ea can lead to incorrect contributions from negative collision energies. It is thus instructive to split
AiC(
T) into two terms,
AiC+ and
AiC− that come from classically allowed and classically forbidden energy ranges (
E >
Ea and
E <
Ea, respectively),
i.e.AiC =
AiC+ +
AiC−. Graphs of
AiC,
AiC+,
AiC−vs. Eq/
kBT are shown in
Fig. 2.
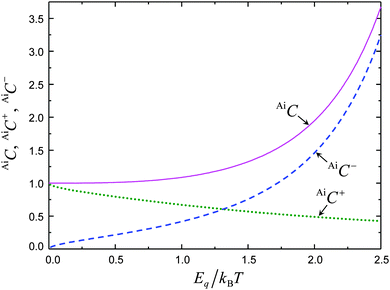 |
| | Fig. 2 Plots of the function AiC from eqn (3.4) and its classically allowed and classically forbidden components AiC+ and AiC− as a function of Eq/kBT (Eq is defined by eqn (3.2)). | |
One should note that the decrease of AiC+ with increasing Eq/kBT is due to the decreasing quality of the WKB approximation in the shrinking effective energy range above the activation barrier, while the fast increase of AiC+ arises from the tunneling transitions.
We now turn to a discussion of the applicability of the linear model. The applicability of the linear model is limited by the condition that it still applies to energies E below the activation threshold (i.e. E < Ea), which substantially contribute to the tunneling probability. The main contribution here comes from energies close to the steepest descent energy E*. The value of E* can be found from the interplay of the Boltzmann factor exp((Ea − E)/kBT) that increases with decreasing E and the asymptotic Airy tunneling probability being proportional to exp(−4(Ea − E)3/2/3Eq3). A steepest descent argument yields
| | | Ea − E* = (1/2 kBT)2Eq3 | (3.6) |
wherefrom one finds
| |  | (3.7) |
If, as an example, one takes the condition of the applicability of the Airy approximation as
Ea −
E* ≤
Ea, this leads to
| | | (Eq/kT)3 ≤ 2(Ea/kBT) | (3.8) |
With the limit
Eq =
Ẽq, that makes
E* equal to
Ea/2 (
i.e. which replaces ≤ in
eqn (3.7) by =), the tunneling correction amounts to
| |  | (3.9) |
For higher values of
Eq,
Eq >
Ẽq, the factor
AiC will be larger, but the corresponding values of
E* will decrease, such that the difference
Ea −
E* is also larger, and the approximation of the linear model becomes more questionable. Assuming that the choice
E* =
Ea/2 corresponds to the minimal value of
E* that meets the criterion for applicability of the linear model,
eqn (3.9) defines the maximum value of
Eq for which
eqn (3.7) is still approximately valid. As an example,
T = 900 K in
Fig. 1 corresponds to
Ea/
kBT ≅ 5. At this temperature, as shown in the figure, the factor
C is about 2. On the other hand,
eqn (3.9) yields exp(
Ea/6
kBT) = 2.3 which appears to be the maximum reliable value of the factor
C expressed through
AiC The given discussion illustrates the limitations of the linear model in accounting for tunneling corrections and its failure for the extrapolation of experimental data to lower temperatures (here below about 900 K).
4. Beyond the Airy approximation: generalized semiclassical treatment
The Airy approximation to the tunneling correction can be considered as a special case of Miller's quantum transition state theory.17 One of the versions of this theory is the optimal trajectory (OT) approach18 which is based on the calculation of the classical action integrals along the tunneling trajectories and the choice of a single optimum trajectory out of the initial Boltzmann ensemble of possible trajectories. The OT begins on one PES, reaches the crossing manifold, and exits on the other PES. The OT leads a part of the Boltzmann ensemble on the initial PES to a distribution on the final PES. The general OT method is outlined in ref. 18. In the following we use a more simplified version, retaining the notion of the reaction coordinate and the effective mass, but going beyond the linear approximation for the diabatic potential curves. This eliminates difficulties related to the multidimensional character of the tunneling process, but improves the incorrect asymptotic behavior of the linear diabatic curves. It allows one to pass to cases where the tunneling contribution is large.
In extending the Airy approximation for curve-crossing situations to lower energies, we apply the same approach as used in our earlier work for an extension of the classical LT treatment for non-crossing curves to a quantum energy regime.19 Here we will follow the Landau idea20 explained in detail in ref. 21. Explicitly, in the semiclassical approximation (SC), the expression for the probability of transitions between crossing diabatic curves, V′ and V′′, takes the form (see eqn (51.8) of ref. 21):
| |  | (4.1) |
where
qc is the crossing point (
i.e. V′(
qc) =
V′′(
qc)) and
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
is any point in the classically allowed region of motion for both
V′ and
V′′ potentials. Note that asymptotically (for
q → ∞)
V′′(
q) converges to zero, while
V′(
q) assumes a quantity −Δ
E10. The collision energy
E varies in the range 0 <
E <
Ea, where the condition
E > 0 secures the applicability of the WKB approximation at the lower limit of the important energy range and the condition
E <
Ea corresponds to an exponentially small probability at the upper limit of the energy range.
The expression of eqn (4.1) is obtained by analytical continuation of the WKB functions from the classically allowed region of the under-barrier energy range into the classically forbidden region. It differs from the expression for the probability to reach the crossing point qc by WKB tunneling, TunnP, from the classically allowed region. The expression for TunnP is similar to that of SCP except that the minus sign in the square brackets in the exponent is replaced by plus, such that the exponential becomes proportional to the product of the tunneling asymptotics of the squared initial and final WKB wave functions.22 Since each of the action integrals in the exponent in eqn (4.1) is supposed to be large under the applicability of the WKB approximation, the change in the sign results in the relation TunnP ≪ SCP. This indicates that the term “tunneling nonadiabatic transition” should not be interpreted too literally: actually, a nonadiabatic transition here occurs as a result of the motion in a classically allowed region which is separated from the crossing point by a region in which the quantum motion is classically forbidden and therefore bears the tunneling character. Again, we note that the potentials in the classically forbidden region must represent analytical continuations of potentials from the classically allowed region. This point is discussed in detail in ref. 23.
Eqn (4.1) allows one to consider the limit when the energy E is only slightly below Ea but the WKB exponent (WKBE) is still large. Then, near the crossing point, where V′(R) = V′(R) = Ea, both potentials are represented by linear functions of R − Rc, and eqn (4.1) is expected to yield the tunneling Airy probability (expressed through the asymptotic representation of the Airy function) for not too large values of Ea − E. Moreover, the complete expression for SCP (with the preexponential factor included) should be identical to the Airy tunneling probability AiP:
| | | SCP|(Ea−E)/Ea≪1,WKBE≫1 → AiP|(Ea−E)/Eq ≫1 | (4.2) |
where
Eq is defined by
eqn (3.2). In this way, the expression of
eqn (4.2) permits a rough estimate of the unknown preexponential factor of
eqn (4.1) provided it can be extrapolated beyond the limits of the linear model.
We will illustrate the above for a model of two exponentially (Exp) decaying potentials
| V′′(q) = Ea exp(−α(q − qc)) |
| | | V′(q) = (Ea + ΔE10) exp(−α(q − qc)) − ΔE10 | (4.3) |
which have adjustable slopes at the crossing point and the asymptotic position of the vibronic energy levels. Besides, the action integrals in
eqn (4.1) can be expressed analytically. For this model,
eqn (4.2) assumes the form
| | | SCExpP ∝ exp(−2WaExpF(ε, δ)) | (4.4) |
with
| |  | (4.5) |
In
eqn (4.4) and (4.5),
ε =
E/
Ea is the scaled energy,
δ = Δ
E10/
Ea is the reduced asymptotic spacing, and

is the WKB parameter (the product of the wave vector for the collision energy
E =
Ea and the range of the potential). The latter is related to the characteristic Massey parameter
ξa for nonadiabatic transitions between the asymptotic states at the collision energy
E =
Ea,
ξa =
Waδ. Note that the applicability of the WKB approximation and the adiabatic behavior at infinity require the fulfillment of the condition
Wa ≫ 1 and
ξa ≫ 1.
For ε close to unity, i.e. 1 − ε ≪ 1, the exponential functions in eqn (4.5) can be replaced by linear ones, so that the expression for ExpF(ε, δ) simplifies to
| |  | (4.6) |
This expression, when substituted into
eqn (4.4) yields the asymptotic Airy probability from
eqn (3.1) with
Eq given by
| |  | (4.7) |
The SCExp tunneling correction
SCExpC is calculated by averaging
SCExpP(
E) over a Boltzmann distribution (counted from the reference energy
E =
Ea) of tunneling energies:
| |  | (4.8) |
The interplay between the Boltzmann factor (increasing with decreasing
E) and the tunneling probability (decreasing with decreasing
E) leads to a pronounced maximum in the integrand such that
WKBC can again be estimated by the steepest descent approximation. This leads to
| |  | (4.9) |
where
| | | ExpΦ(ε; Aa, Wa, δ) = Aa (1 − ε) − 2WaExpF(ε, δ) | (4.10) |
with
Aa =
Ea/
kBT and
ExpM denoting the maximum of
ExpΦ at an optimal energy
ε =
ε*:
| | | ExpM(Aa, Wa, δ) = ExpΦ(ε; Aa, Wa, δ)|ε=ε* | (4.11) |
Note that
ε =
ε* determines the energy of the OT for the above model. If
ε* is close to unity (
i.e. 1 −
ε* ≪ 1), the exponentials in
eqn (4.5) can be approximated by linear functions which yields
| |  | (4.12) |
This result coincides with the Airy correction
AiC in
eqn (3.3) when one uses the relation
Eq3 =
Ea3(1 +
δ)
2/
Wa2δ2. The comparison of
SCExpC with
AiC through
SCLinC allows one to estimate the preexponential factor in the general expression of
eqn (4.8) which is assumed to be of the order of unity as follows from the expression of
eqn (3.3) for
AiC.
Results for ExpM(Aa, Wa, δ) (full curves) and LinM(Aa, Wa, δ) (points) as a function of Aa in Fig. 3 are compared for Ea/kB = 4500 K and ΔE10/kB = 2700 K, which correspond to δ = 0.6. The plots demonstrate the convergence of ExpM(Aa, Wa, δ) to LinM(Aa, Wa, δ) when Aa decreases. E.g., we see a good agreement between the Exp and Lin models for Aa = 3, a qualitative agreement for Aa = 5 and a large difference for Aa = 7. This difference increases dramatically for higher values of Aa when the linear model for low temperatures becomes inadequate. Note that, for Aa = 15 (corresponding to T = 300 K in the present case), SCExpC is quite large reaching up to values of 100–400.
 |
| | Fig. 3 Comparison of ExpM(Aa, Wa, δ) (lines) and LinM(Aa, Wa, δ) (points) as a function of Aa. The convergence of dotted lines to full lines indicates the performance of the Airy approximation (see the text). | |
Two features of Fig. 3 deserve particular attention:
(i) Tunneling contributions for exponential potentials, for not too small values of the Arrhenius parameter Aa, are substantially lower than obtained using the Airy approach. We ascribe this to an overestimation of tunneling by the Airy approach that relies on the linear model with a narrow triangular crossing pattern of diabatic potential curves
(ii) On the other hand, the tunneling contribution for exponential potentials may be particularly large for large Arrhenius factors. For instance, for Aa = 15 (i.e. here for T = 300 K) the values of SCExpC, as judged from their exponents with Wa = 8–10, amount to 150–400. At these values of Aa = 15 and Wa, the optimal energy is E* ≈ Ea/2, and the WKB and Massey parameters are  and
and 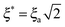 .
.
We believe that conclusion (ii) is quite general and will hold for other nonlinear one-dimensional potentials and for more realistic multidimensional potentials as well. This observation suggests that the NO–Ar system is an interesting example for multidimensional quantum treatments of nonadiabatic tunneling once the adiabatic vibronic PES is reasonably well known. The simplifying features (at room temperature and above) here are the WKB conditions for rotation of NO and NO–Ar translation, and the extensive quenching of interference effects for the initial thermal ensemble which eliminates the need to resort of multidimensional uniform approximations.24–26 The simplest semiclassical counterpart of the multidimensional quantum treatment of the nonadiabatic tunneling might be the optimal trajectory methods18 and more general approaches as described in ref. 27 and 28.
5. Nonadiabatic tunneling in NO(X2Π, v = 1) + Ar → NO(X2Π, v = 1) + Ar collisions
In this section, we analyze the Airy approximation in order to learn more about some features of nonadiabatic tunneling near 900 K (see Fig. 4). We adhere to this approximation not only because of its simplicity, but also since it takes into account contributions from overbarrier transitions. For instance, with C ≅ 2, the latter contribute about 25% to the total value of C (see Fig. 2). We therefore assume that the value of C is given by eqn (3.5) and we regard Eq as a fitting parameter. The performance of this approximation, for Eq/kB = 1800 K, is illustrated in Fig. 4.
 |
| | Fig. 4 The ratio of the experimental (GTk10) and Landau–Zener (LZk10) relaxation rate coefficients (red dashed line) in comparison to the Airy approximation according to eqn (3.5) with Eq/kB = 1430 K (blue dotted line) and Eq/kB = 1800 K (green dotted line). | |
We consider the value Eq/kB = 1800 K as an optimally fitted quantity since the plot of AiC(T) vs. 1/T passes through all error bars of the ratio GTk10/LZk10. In order to demonstrate the high sensitivity of AiC(T) on Eq, we also show a plot of AiC(T) with Eq/kB = 1430 K which is about 20% lower than the optimal value Eq/kB = 1800 K. If the latter value is used within the SC exponential model of Section 4, with Ea/kB = 4500 K, ΔE10/kB = 2700 K, we obtain Wa ≅ 10 and ξa ≅ 6.
On the other hand, a rough estimation of Eq in eqn (3.2) can be made by assuming an exponential dependence of the diabatic curves on the reaction coordinate of eqn (4.3) which expresses Eq by eqn (4.7). The parameter α with the asymptotic behavior of the exchange interaction from ref. 29, is estimated to be close to 2 a.u. Substituting this value in eqn (4.7) and identifying μq with the reduced mass of the collision partners μ = 17.14 a.m.u., we obtain Eq/kB = 1430 K. Fig. 4 shows that this value of Eq/kB apparently is too small for a correct description of the tunneling effect in k10.
Within the same scheme as above, a higher value of Eq might be obtained if the μq could be identified with the effective mass of the coordinate which is normal to the dividing surface in the region close to the lowest crossing energy point Ea. In the present case, the dividing surface becomes a crossing line R = Rc(θ), which is defined as a solution of the equation
In turn, the minimum energy on the
V′′ PES along the crossing line is attained at a certain angle
θ =
θa, and two coordinates
θa and
Ra ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Rc
Rc(
θa) determine the apparent activation energy
Ea =
V′′(
Ra,
θa).
The effective mass μeffa simulates the combined effect of the relative radial motion NO–Ar and the hindered rotational motion of NO along a two-dimensional trajectory that passes through the point Ra, θa normally to the crossing line. The expression for μeffa then reads (see eqn (6) from ref. 29)
| | | μeffa = μ/(1 − μ(dRc/dθ)θ=θa2/I) | (5.2) |
where
I is the moment of inertia of NO,
I =
Mre2 with
M and
re being the reduced mass of NO at the equilibrium internuclear separation
re (
M = 7.27 a.m.u and
re = 2.175 a.u.). Once the quantity (d
Rc/d
θ)
θ=θa2 is known from the form of the crossing line close to
θ =
θa,
eqn (5.2) can serve for the determination of
μeffa and the calculation of
Eq. Otherwise, if
μeffa in
Eq is considered as a fitting parameter for the correct description of nonadiabatic tunneling,
eqn (5.2) defines the quantity (d
Rc/d
θ)
θ=θa2 which sheds some light on the collision dynamics. We use the latter approach to elucidate the activated complex configuration.
The quantity (dRc/dθ)θ=θa as found from eqn (5.2) is given by
| |  | (5.3) |
On the other hand, (d
Rc/d
θ)
θ=θa can be calculated from
eqn (5.1) if one assumes an explicit expression for Δ
V(
R,
θ). This can be derived from the argument that the difference Δ
V(
R,
θ) is determined by the exchange interaction of the electrons of the Ar atom with the electron of NO that occupies the outer 2π′′ molecular orbital.
3,4 Taking this interaction in its asymptotic form when the 2π′′ MO of NO is approximated by a dπ atomic orbital counted from the center of mass of NO,
3,4 we write:
| | | ΔV(R,θ) = ΔE10 exp(−α(R − R0)sin2 2θ | (5.4) |
where
R0 is a reference radius which enters into scaling of Δ
V(
R,
θ). With this definition of Δ
V(
R,
θ), the crossing curve of a two-lobe rosette shape lies inside the circle of radius
R0 and touches it at
θ = π/4 and 3π/4. The calculation of (d
Rc/d
θ)
θ=θa from
eqn (5.2) with the restriction by
eqn (5.4) yields
| | 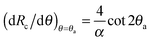 | (5.5) |
This expression determines the value of
θa which is consistent with the fitted value of
μeffa through the intermediate quantity (d
Rc/d
θ)
θ=θa that enters into
eqn (5.3) and (5.5). With
θ counted from the linear Ar–N–O arrangement, one should choose the negative sign for (d
Rc/d
θ)
θ=θa as belonging to the internal side of the first lobe of the rosette. The final result reads
| |  | (5.6) |
With
Eq/
kB = 1800 K we find
μeffa ≈
μ/2 and the above values of
α,
re,
M, and
μ make the r.h.s. of
eqn (3.8) equal to −0.72. This yields
θa = 1.1 which is close to π/3.These results are summarized in
Fig. 5 which shows a part of the lobe (full red line bounded in the lower-right corner to indicate the non-asymptotic region of the exchange interaction). The lobe touches the reference circle at
θ = π/4 (dashed red line), and the equipotential line
V′′(
R,
θ) =
Ea at
θa = π/3 (blue dash-dotted line). The transition state (encircled green region) is located near the latter touching point, and the reaction coordinate is normal to the lobe line at this point (an arrow).
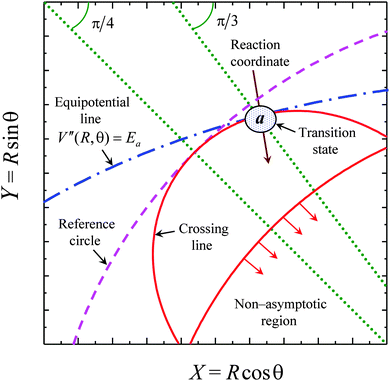 |
| | Fig. 5 Polar representation (coordinates R, θ) in the Cartesian frame (coordinates X = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, Y = R θ, Y = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) of quantities relevant for nonadiabatic tunneling at the internal side of the first lobe (0 < θ < π/2) (see the text for details). θ) of quantities relevant for nonadiabatic tunneling at the internal side of the first lobe (0 < θ < π/2) (see the text for details). | |
Fig. 5, therefore, will provide a qualitatively correct picture of the non-adiabatic transitions near the configuration of the activated complex in a position which is defined through its angular coordinate. What is missing here is the value of the radial coordinate Ra of the activated complex. Instead of this, we have the transition state energy Ea which was recovered from the Arrhenius plot of the LZ rate relaxation coefficient in the temperature range where the tunneling is negligible. The relation between Ea and Ra could be established from the information on the V′′ PES.
6. Conclusion
The present work analyzes deviations from an Arrhenius temperature dependence of the rate constant of the vibrational relaxation of NO(X2Π, v = 1) in Ar. These are attributed to tunneling nonadiabatic transitions between initial (A′′, v = 1) and final (A′, v = 0) vibronic PESs. The tunneling probability is approximately described by a linear model of the nonadiabatic interaction in its weak-coupling limit, when the transition probability can be expressed through the Airy function. The fitting of the parameters in the tunneling correction factor indicates a substantial contribution from the rotation of NO to the nonadiabatic tunneling. Limitations of the linear model, which arise from a too thin barrier and an unrestricted lower bound of the collision energies within a model of linear crossing diabatic curves, are also noted.
The reported experimental value of k10 at T ≈ 300 K being about 10−17 cm3 s−1 (ref. 9 and 10) is about three orders of magnitude higher than the value for LZk10 from the LZ treatment, eqn (2.1) and its extrapolation to room temperature (see Fig. 1). The large difference between k10 and LZk10 apparently can be attributed to tunneling. We note, however, that the Airy approximation certainly breaks down for experiments at temperatures as low as room temperature. (In addition, one should also be aware of reservations about the experimental values of k10 near 300 K which were expressed in ref. 30). Obviously, more experimental measurements of the relaxation rate coefficients at lower temperatures are desirable. Furthermore, more general two-dimensional models of nonadiabatic coupling including tunneling are required which should be based on ab initio calculations of adiabatic PESs for interaction energies above those already available.12–14 Of course, the use of the full multichannel treatment in calculating the rate coefficient would be ideal, but this is not possible unless the dependence of the potentials on the N–O distance is known. Moreover, here it is not clear how one can determine the tunneling correction coefficient without the full quantum calculation of the rate coefficient. In our paper, which addresses a more modest aim to only estimate the tunneling correction without full calculation of the rate coefficient, we have identified the “reaction coordinate” of the transition state approach by considering the shape of the crossing line found from the asymptotic form of the exchange interaction between the 2π′′ electron of MO and electrons of the Ar atom, the approach which has already been introduced quite some time ago3,4 and used recently again.16 In this way, it became possible to derive a simplified expression for the tunneling correction coefficient that depends on two dimensionless parameters, δ and W, which in turn are expressed through the conventional physical parameters, the energy Ea at the crossing point, the steepness of the potentials α at the crossing point and the effective mass μeff for the motion along the “reaction coordinate”. Once the latter is identified, Ea, α, and μeff can be determined for any crossing PES, including those calculated ab initio in different approximations.
We conclude this work by emphasizing the interesting intermediate position of the present relaxation system with a two-state vibronic curve-crossing mechanism between the Landau–Teller mechanism without curve-crossing and even more efficient vibrational relaxation in chemically interacting situations with the participation of several vibronic states. The latter was observed, e.g. for NO relaxation in collisions with NO, NO2, O, Cl and I (see ref. 7, 8 and 31) where it was shown that relaxation and recombination (here forming (NO)2. N2O3, NO2, NOCl, and NOI) are directly related (see ref. 32).
Acknowledgements
We are grateful to I. Litvin for technical help.
References
- E. E. Nikitin, Mol. Phys., 1964, 7, 389 CrossRef CAS.
-
E. E. Nikitin, Theory of Elementary Atomic and Molecular Processes in Gases, Oxford, Clarendon Press, 1974 Search PubMed.
- E. E. Nikitin and S. Ya. Umansky, Faraday Discuss. Chem. Soc., 1972, 53, 7 RSC.
- E. A. Andreev, S. Ya. Umansky and A. A. Zembekov, Chem. Phys. Lett., 1973, 18, 567 CrossRef CAS.
- K. L. Wray, J. Chem. Phys., 1962, 36, 2597 CrossRef CAS PubMed.
- G. Kamimoto and H. Matsui, J. Chem. Phys., 1970, 53, 3987 CrossRef CAS PubMed.
- K. Glaenzer and J. Troe, J. Chem. Phys., 1975, 63, 4352 CrossRef CAS PubMed.
- K. Glaenzer, Chem. Phys., 1977, 22, 367 CrossRef CAS.
- J. C. Stephenson, J. Chem. Phys., 1973, 59, 1523 CrossRef CAS PubMed.
- J. Kosanetzky, U. List, W. Urban, H. Vormann and E. H. Fink, Chem. Phys., 1980, 50, 361 CrossRef CAS.
-
E. E. Nikitin, A. I. Osipov and S. Ya. Umanskii, Khimiya Plazmy, Energoatomizdat, Moscow, 1989, vol. 15, p. 3 Search PubMed.
- M. H. Alexander, J. Chem. Phys., 1999, 111, 426 Search PubMed.
- M. H. Alexander and S. Stolte, J. Chem. Phys., 2000, 112, 8017 CrossRef CAS PubMed.
- M. H. Alexander, P. Soldan, T. G. Wright, Y. Kim, H. Meyer, P. J. Dagdigian and E. P. F. Lee, J. Chem. Phys., 2001, 114, 5588 CrossRef CAS PubMed.
-
R. N. Zare, Angular momentum: Understanding spatial aspects in chemistry and physics, Baker Lecture Series, John Willey & Sons, N.Y., 1988 Search PubMed.
- A. I. Maergoiz, E. E. Nikitin and J. Troe, J. Chem. Phys., 2014, 141, 044302 CrossRef CAS PubMed.
- W. H. Miller, J. Chem. Phys., 1975, 62, 1899 CrossRef CAS PubMed.
- E. E. Nikitin and M. Ya. Ovchinnikova, Chem. Phys., 1989, 138, 45 CrossRef CAS.
- E. E. Nikitin. and J. Troe, Phys. Chem. Chem. Phys., 2008, 10, 1483 RSC.
- L. Landau, Phys. Z. Sowjetunion, 1932, 1, 88 CAS.
-
L. D. Landau and E. M. Lifshitz, Quantum Mechanics, Pergamon Press, Oxford, 1977 Search PubMed.
- E. I. Dashevskaya and E. E. Nikitin, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 63, 271 CrossRef.
- E. E. Nikitin, C. Noda and R. N. Zare, J. Chem. Phys., 1993, 98, 46 CrossRef CAS PubMed.
- M. S. Child and M. Shapiro, Mol. Phys., 1983, 48, 111 CrossRef CAS.
- S. K. Gray and M. S. Child, Mol. Phys., 1984, 51, 189 CrossRef CAS.
- W. H. Miller, Adv. Chem. Phys., 1975, 30, 77 CrossRef CAS.
-
Multidimensional Quantum Mechanics with Trajectories, Collaborative Computational Project on Molecular Quantum Dynamics, ed. D. V. Shalashilin and M. P. de Miranda, Daresbury, UK, 2009 Search PubMed.
-
Quantum trajectories, Collaborative Computational Project on Molecular Quantum Dynamics, ed. K. H. Hughes and G. Parlant, Daresbury, UK, 2011 Search PubMed.
- E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2006, 125, 154315 CrossRef CAS PubMed.
- G. Hancock, M. Morrison and M. Saunders, Phys. Chem. Chem. Phys., 2009, 11, 8507 RSC.
- K. Glaenzer and J. Troe, J. Chem. Phys., 1976, 65, 4324 CrossRef CAS PubMed.
- M. Quack and J. Troe, Ber. Bunsenges. Phys. Chem., 1975, 79, 170 CrossRef CAS.
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 
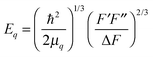

![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) AiC(T) then is expressed through the ratio of the canonically averaged probabilities with the formal energy limits −∞ < E < ∞;
AiC(T) then is expressed through the ratio of the canonically averaged probabilities with the formal energy limits −∞ < E < ∞;





![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) is any point in the classically allowed region of motion for both V′ and V′′ potentials. Note that asymptotically (for q → ∞) V′′(q) converges to zero, while V′(q) assumes a quantity −ΔE10. The collision energy E varies in the range 0 < E < Ea, where the condition E > 0 secures the applicability of the WKB approximation at the lower limit of the important energy range and the condition E < Ea corresponds to an exponentially small probability at the upper limit of the energy range.
is any point in the classically allowed region of motion for both V′ and V′′ potentials. Note that asymptotically (for q → ∞) V′′(q) converges to zero, while V′(q) assumes a quantity −ΔE10. The collision energy E varies in the range 0 < E < Ea, where the condition E > 0 secures the applicability of the WKB approximation at the lower limit of the important energy range and the condition E < Ea corresponds to an exponentially small probability at the upper limit of the energy range.

 is the WKB parameter (the product of the wave vector for the collision energy E = Ea and the range of the potential). The latter is related to the characteristic Massey parameter ξa for nonadiabatic transitions between the asymptotic states at the collision energy E = Ea, ξa = Waδ. Note that the applicability of the WKB approximation and the adiabatic behavior at infinity require the fulfillment of the condition Wa ≫ 1 and ξa ≫ 1.
is the WKB parameter (the product of the wave vector for the collision energy E = Ea and the range of the potential). The latter is related to the characteristic Massey parameter ξa for nonadiabatic transitions between the asymptotic states at the collision energy E = Ea, ξa = Waδ. Note that the applicability of the WKB approximation and the adiabatic behavior at infinity require the fulfillment of the condition Wa ≫ 1 and ξa ≫ 1.





 and
and  .
.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Rc(θa) determine the apparent activation energy Ea = V′′(Ra,θa).
Rc(θa) determine the apparent activation energy Ea = V′′(Ra,θa).

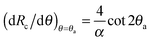




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos