Lithium conductivity in glasses of the Li₂O–Al₂O₃–SiO₂ system

Abstract

To improve the understanding of Li-dynamics in oxide glasses, i.e. the effect of [AlO₄]⁻ tetrahedra and non-bridging oxygens on the potential landscape, electrical conductivity of seven fully polymerized and partly depolymerized lithium aluminosilicate glasses was investigated using impedance spectroscopy (IS). Lithium is the only mobile particle in these materials. Data derived from IS, i.e. activation energies, pre-exponential factors and diffusivities for lithium, are interpreted in light of Raman spectroscopic analyses of local structures in order to identify building units, which are crucial for lithium dynamics and migration. In polymerized glasses (compositional join LiAlSiO₄–LiAlSi₄O₁₀) the direct current (DC) electrical conductivity continuously increases with increasing lithium content while lithium diffusivity is not affected by the Al/Si ratio in the glasses. Hence, the increase in electrical conductivity can be solely assigned to lithium concentration in the glasses. An excess of Li with respect to Al, i.e. the introduction of non-bridging oxygen into the network, causes a decrease in lithium mobility in the glasses. Activation energies in polymerized glasses (66 to 70 kJ mol⁻¹) are significantly lower than those in depolymerized networks (76 to 78 kJ mol⁻¹) while pre-exponential factors are nearly constant across all compositions. Comparison of the data with results for lithium silicates from the literature indicates a minimum in lithium diffusivity for glasses containing both aluminium tetrahedra and non-bridging oxygens. The findings allow a prediction of DC conductivity for a large variety of lithium aluminosilicate glass compositions.

---

1. Introduction

Lithium aluminosilicate glasses and glass–ceramics are of considerable importance in a variety of industrial applications. Li–Al–Si containing minerals like spodumene (LiAlSi₂O₆) and petalite (LiAlSi₄O₁₀) are well known for their negative thermal expansion coefficients and as such are broadly used in high precision thermo- and electro-optics. Li-containing aluminosilicate glasses and nanocrystalline materials are fast ion conductors^1,2 and thus are possible materials for solid lithium ion batteries. However, the mechanisms governing the transport of lithium ions in silicate-based networks are still insufficiently understood. There are indications that Al plays an important role in Li-dynamics in lithium aluminosilicate glasses and that the mechanisms of lithium transport are different from those of aluminium-free lithium silicate glasses.^3,4 The exact nature of the interaction of [AlO₄]⁻ tetrahedra with the mobile Li-cations in comparison to non-bridging oxygen (NBO) atoms in the aluminosilicate matrix is yet to be determined.

This work focuses on the relationship between the local interactions of [AlO₄]⁻ tetrahedra and NBOs with lithium ions, which are the only mobile species in the studied materials. For this purpose we analyzed two series of glasses. Four fully polymerized glasses with a constant Li/Al ratio equal to 1 and a variable Al/Si ratio are compared with a series of three partly depolymerized glasses (Li/Al > 1) with nearly constant lithium content. In these glasses three types of lithium coordinating oxygen atoms are present: (i) Si–O–Si with a formal charge of 0, (ii) Si–O–Al with a formal charge of (−1/4) and (iii) non-bridging oxygen atoms, Si–O⁻, with a formal charge of (−1). These oxygen atoms determine the coordination of lithium in the material both on regularly occupied sites and on interstitial sites, which are passed by lithium during transition between different regular, low potential sites. Impedance spectroscopy is used to investigate the electrical conductivity of the glasses, and Raman spectroscopy provides insights into the network topology. The particular role of aluminium in the network structure will be elaborated by comparison to data for lithium silicate glasses.^3,5

2. Li₂O–Al₂O₃–SiO₂ glasses

In a lithium aluminosilicate (LAS) glass, the glass structure comprises the network-forming SiO₄ and [AlO₄]⁻ tetrahedra units connected via bridging oxygen atoms while Li⁺ represents the network modifying cation and the only mobile species present. The glasses with a Li to Al ratio of 1 : 1 are fully polymerized, meaning that the network contains only bridging oxygen atoms. The incorporation of network-modifiers, such as Li₂O, in excess of the quantity needed for charge compensation of Al³⁺ cations leads to the formation of non-bridging oxygen atoms and a reduction in the degree of glass network polymerization. As a consequence, melting temperatures and melt viscosities decrease.⁶ The degree of polymerization in a silicate glass can be characterized by the ratio of non-bridging oxygen per tetrahedral unit, NBO/T:⁷where M_i represents network modifying cations with charge n. The sum is obtained after all metal cations are subtracted, which are needed for charge compensation. T represents the sum of all tetrahedral coordinated cations.

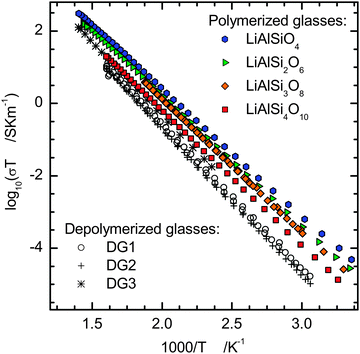
To investigate the transport properties of lithium in different Al–Si–O glass networks, we have analyzed a group of fully polymerized (group 1) and a group of depolymerized glasses (group 2). The fully polymerized glass samples were provided by Alan Whittington, University of Missouri.⁸ Depolymerized glasses were synthesized in the Institute of Mineralogy, Leibniz University of Hanover. The compositions are represented in Fig. 1 and are listed in Table 1. For three of the polymerized glasses compositional analogues exist in nature as minerals: eucryptite, LiAlSiO₄ (EUC); spodumene, LiAlSi₂O₆ (SPO); and petalite, LiAlSi₄O₁₀ (PET). The join is completed with a LiAlSi₃O₈ (FSP) composition, which can be considered as the lithium analogue of albite. The labels in parentheses are used further on in reference to the compositions.

Fig. 1 Ternary diagram of sample composition as mole fraction.

Table 1 Composition of the glasses derived by ICP-OES for lithium and EMPA and ICP-OES measurements for silicon and aluminium in combination

Composition		Li2O (wt%)	1σ	Al2O3^a (wt%)	1σ	SiO2^a (wt%)	1σ	NBO/T^d	Li/Al at. ratio
a Contents of Al2O3 and SiO2 were determined by ca. 5 EMPAs and Li2O content by 2–3 OES analyses. Na2O, K2O and CaO content were below the detection limit of the EMPA, i.e. present in less than 0.01 wt% for Na2O, K2O and 0.015 wt% for CaO. b Samples LiAlSi2O6-1 and LiAlSi3O8-1 from Hofmeister et al.^8 (2009) are identical to our samples LiAlSi2O6 and LiAlSi3O8, respectively. c EMPA data for petalite are from Welsch et al.^15 (2012), but Li2O content was newly determined by OES in this work. d NBO/T is calculated by eqn (1), negative values have no physical meaning but indicate deficiency of Li with respect to Al, consistent with atomic Li/Al ratios.
LiAlSiO4	[EUC]	11.05		40.66	0.36	47.47	0.25	−0.04	0.93
LiAlSi2O6	[SPO]	7.07
LiAlSi2O6-1^b		7.15		27.41		63.79
LiAlSi3O8	[FSP]	5.62		20.68	0.09	73.27	0.04	−0.04	0.89
LiAlSi3O8-1^b		5.60		21.24		72.90		−0.02	0.93
LiAlSi4O10^c	[PET]	4.80		16.37		79.09		−0.03	0.90
DG1		9.40	0.14	17.33	0.25	73.36	0.41	0.19	1.85
DG2		8.83	0.64	11.13	0.08	80.94	0.47	0.24	2.71
DG3		9.49	0.23	9.73	0.27	81.66	0.73	0.29	3.33

---

Theoretically, glasses of group 1 contain only bridging oxygen, which are bonded to two silicon atoms [≡Si–O–Si≡] or between a silicon and aluminium tetrahedra [≡Si–O–Al⁽⁻⁾≡]. According to the Löwenstein rule⁹ neighbouring alumina tetrahedra [≡⁽⁻⁾Al–O–Al⁽⁻⁾≡] are unlikely in aluminosilicates, but NMR spectroscopy gives evidence that such connections may occur in small quantities.¹⁰ Glasses of group 2 contain non-bridging oxygen atoms [≡Si–O⁻] in addition to both types of bridging oxygens observed in group 1.

Regular and interstitial sites of lithium in the glass structures are formed by combinations of these types of oxygen. ⁶Li MAS NMR spectroscopy indicates that silicate glasses have wide distribution of Li coordination numbers between four and six.¹¹ Hence, large differences in lithium mobility can be expected depending on the relative abundance of oxygen species.

3. Experimental procedures

3.1 Glass synthesis and analytics

The depolymerized glasses were prepared by melting powder mixtures of high purity Li₂CO₃, Al₂O₃ and SiO₂ in a platinum crucible at a temperature of 1873 K and subsequent quenching by placing the crucible in water. For improving the quality of the synthesized glass, the melting procedure was repeated twice, with fine milling of the glass product in between. The glasses synthesized in this way were often strained making them prone to breaking and difficult to handle. In order to improve the mechanical stability, the glasses were slowly heated to 723 K, and after 15 to 20 minutes of dwelling time slowly cooled to ambient temperature at a rate of 5 K min⁻¹.

The composition of the synthesized glass samples was analyzed by inductively coupled plasma optical emission spectroscopy (ICP-OES) and electron-microprobe analyses (EMPA). For ICP-OES measurements a defined mass (50 to 150 mg) of glass was dissolved in a mixture of 1 mL hydrofluoric acid (40%), 2 mL phosphorous acid (85%) and 4 mL nitric acid (70%) in a PTFE vessel heated using a microwave MLS START 1500. These measurements were done using a Varian ICP-OES 715 at λ_Al = 308.215 nm, λ_Li = 670.783 nm and λ_Si = 250.690 nm. The content of silicon, aluminium and lithium in the glass sample was recalculated from concentration data of the measured solution and the initial weight.

To control the composition determined by ICP-OES and to check the homogeneity of the glasses, EMPA measurements were carried out. Lithium as a light element is not measurable by EMPA, but Li₂O contents may be estimated as a difference to 100 wt% if all other oxides are quantified. The analyses were performed using a CAMECA SX-100 microprobe. Typically, three to five points were analyzed on each sample. A beam current of 15 nA was used with an acceleration voltage of 15 kV and a beam size of 5 μm, while the counting times were 10 to 20 s depending on the sample. The programmed matrix correction “PAP” by Pouchou and Pichoir¹² was used to correct the measured values of Al and Si. Compositions reported in Table 1 are based on ICP-OES data for Li₂O and EMPA data for Al₂O₃ and SiO₂.

The density of each glass was determined using the buoyancy method, i.e. by measuring the weight in ethanol and in air (Table 2). The accuracy of the measurements was in the order of per mill for standards of a quartz crystal (ρ = 2.684 g cm⁻³) and a silica glass (ρ = 2.203 g cm⁻³).

3.2 Determination of T_g

The glass transition temperature (T_g) of the samples was determined to ensure that high temperature impedance spectroscopy measurements are not affected by structural relaxation of the network and to get information about the thermal stability of the glasses. T_g was derived by differential thermal analyses using the TG/DTA Setsys Evolution 1750 setup. The material was heated up in an alumina crucible (heating rate: 5 K min⁻¹), kept for 10 min at the target temperature and cooled down afterwards (cooling rate: 20 K min⁻¹). A flow of 20 mL min⁻¹ of synthetic air (80% N₂, 20% O₂) was used to purge possibly occurring gaseous products. An empty alumina crucible was taken as a reference, which was periodically measured under the same conditions in order to accurately correct the sample data. T_g values were derived from the DTA curves recorded during heating to avoid falsification by possible crystallization or phase separation at high temperatures. To define T_g the tangent intersection method was applied at the DTA curves (an intersection of two tangents at the curve before minimum). The experimental technique was verified to be correct within ±1.5 K by measurements on the DGG1 standard glass of the German Glass Technical Society.¹³T_g values for the aluminosilicate glasses are listed in Table 2. Derived values for glasses of group 1 agree with literature data within ±5 K for EUC,^8,14 SPO, FSP and PET.⁸

Table 2 Material and lithium conductivity characteristics of analyzed glass compositions

Composition	T g (K)	ρ (g cm^−3)	T-range (K)	log10 A0 (A0 in S K m^−1)	E a (kJ mol^−1)	log10 Dσ at 500 K (Dσ in m^2 s^−1)
LiAlSiO4	922	2.437(1)	298–717	7.4(9)	67.5(0.9)	−12.89(01)
LiAlSi2O6	960	2.381(2)	333–800	7.2(7)	68.9(0.4)	−12.98(01)
LiAlSi3O8	1010	2.322(2)	304–532	7.4(8)	70.5(0.5)	−12.90(01)
LiAlSi4O10	1015	2.309(1)	350–500	7.0(2)	72.5(1.1)	−13.16(01)
DG1	769	2.362(3)	327–625	7.4(1)	76.5(13)	−13.89(01)
DG2	773	2.357(6)	327–626	7.4(8)	77.2(11)	−13.86(01)
DG3	760	2.323(8)	425–714	7.7(7)	78.0(08)	−13.82(01)

---

3.3 Impedance spectroscopy

For the conductivity experiments circular Ag electrodes of 1 mm in diameter were applied. To produce the electrodes, Ag lacquer (Co. Dr Ropertz-GmbH) was deposited and sintered on the sample surfaces at 573 K for 30 minutes. After slowly cooling to room temperature the samples with properly attached sintered electrodes were placed into the impedance sample holder between two Pt-cones. A spring-tension mechanism was applied to one of the Pt-cones via a ceramic rod to ensure good electrical contact. Afterwards the sample holder was inserted into an earth-grounded gold tube, serving as an insulating shield. Impedance measurements were performed in a tube furnace, Nabertherm R50/500/13. During the experiment the temperature was continuously recorded at a distance of 2 and 5 mm from the sample using two electrically shielded type-K thermocouples. The heating rate was varied between 0.8 and 0.9 K min⁻¹. Cooling rates, after switching the furnace off, decrease from 2.4 K min⁻¹ in the high temperature region to 0.7 K min⁻¹ at around 400 K.

The electrical conductivity was measured periodically during heating and cooling using a Novocontrol Alpha AN impedance analyzer equipped with a Novocontrol ZG4 module to allow a four terminal configuration. Before the measurements, the spectrometer was calibrated using a short circuit arrangement and a certified 100 Ω resistance. Additionally, internal high capacity references were used to calibrate the system. Impedance spectra were collected from 0.5 Hz to 2 MHz at each selected temperature. The heating/cooling program was not interrupted for recording impedance data, and the spectra correspond to a temperature interval of ∼8 K at low temperature and 1–3 K at the highest temperature. However, the temperature corresponding to the centre of the conductivity plateau was always determined with a precision better than ±1 K. The accuracy of conductivity measurements was verified to be better than ±0.10 log units by comparison of conductivity data of LiAlSi₂O₆ glasses with literature data.¹⁵

3.4 Raman spectroscopy

The local structural characteristics of each glass were analyzed by Raman spectroscopy before and after experimental runs. The measurements were made on a confocal Bruker Senterra micro-Raman spectrometer equipped with an Olympus BX 51 microscope and an Andor DU420-OE CCD camera. Unpolarized spectra were collected under ambient conditions, using the 532 nm laser excitation line with 20 mW power, under the 50× magnification of an Olympus objective for 10 s with 2 times acquisition repetitions. Instrumental precision was within ±3 cm⁻¹. The spectra were baseline and temperature corrected.^16,17 The reproducibility of a Raman structural signal was confirmed by repeated measurements as well as measurements at different areas of each sample.

4. Results

4.1 Characterization of the glasses

All synthesized glasses are clear, colourless and free of bubbles, inclusions or cracks. The chemical composition of the samples, analyzed by ICP-OES and EMPA, is shown in Table 1. All samples contain lithium, aluminium, silicon and oxygen while other alkalis are below the detection limit of the EMPA. This is important as other alkalis may act as additional charge carriers and mask the effect of lithium mobility. Furthermore, a second alkali may produce a mixed-alkali effect leading to a decrease in conductivity.^18–20 The NBO/T value of the depolymerized glass samples ranges from 0.19 to 0.29. The fraction of NBO compared to total oxygen is in the order of 10–15% in the studied compositions of group 2. The depolymerized glasses show a significantly lower glass transition temperature T_g (760–773 K) than the polymerized glasses (922–1015 K, cf.Table 2).

4.2 Specific conductivity

The results of impedance spectroscopy experiments were used to calculate the specific electrical conductivity, σ, by dividing the measured conductivity with the cell constant (electrode area/sample thickness), usually of ca. 0.015 m. The specific conductivity as a function of frequency for EUC and PET glasses, the end members of our polymerized Li-aluminosilicate glass series, is plotted in Fig. 2 in comparison to the depolymerized glasses DG1 and DG2. Conductivities recorded during the heating and the cooling cycles agree within the 0.10 log units. The specific direct current (DC) conductivity, σ_DC, has been read out from the centre of the low frequency DC-conductivity plateau in the plot of the logarithm of the real part of σ vs. the logarithm of frequency for each temperature. For each composition the data show a linear dependence of log(σ_DCT) on reciprocal temperature in the whole temperature range, i.e. following an Arrhenius relationwhere A₀ is the pre-exponential factor and E_a is the activation energy for ionic conduction. Within the series of polymerized glasses the individual σ_DCT values varied by less than 1 log unit at ∼300 K (cf.Fig. 3). A systematic decrease in conductivity from the silica-poor EUC (LiAlSiO₄) glass towards the silica-rich PET (LiAlSi₄O₁₀) glass is evident. For the depolymerized glasses the differences between the specific conductivities were smaller (within ≈0.25 log units at 440 K), due to a smaller variation in lithium concentration in these glasses. The activation energies of the polymerized glass series vary between 66.4 and 70.4 kJ mol⁻¹ (see Table 2). The value of 67.5 kJ mol⁻¹ determined for the EUC glass is in excellent agreement with E_a derived from data of Johnson et al.²¹ for the eucryptite glass (67.1 kJ mol⁻¹) when plotting their data as log σT vs. 1/T. The activation E_a for the depolymerized glasses is distinctly higher, with values from 76.5 to 78.1 kJ mol⁻¹.

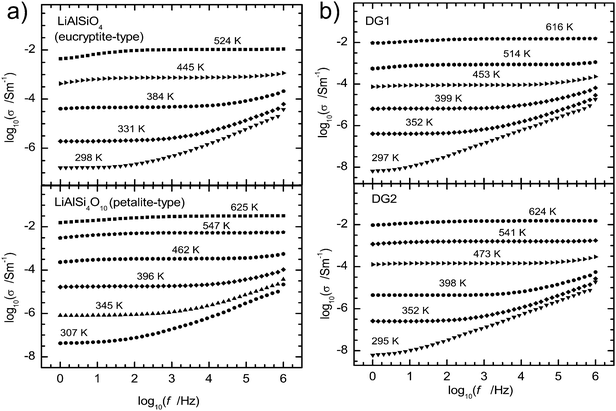Fig. 2 Examples of conductivity plots of polymerized (a) and depolymerized (b) lithium aluminosilicate glasses. The center of the plateau defines the DC electrical conductivity.

Fig. 3 Arrhenius plot for DC electrical conductivity of fully polymerized and depolymerized glasses. For clarity only the heating cycle for all samples is shown. Data trends are coinciding for cooling cycle measurements.

4.3 Raman spectroscopy

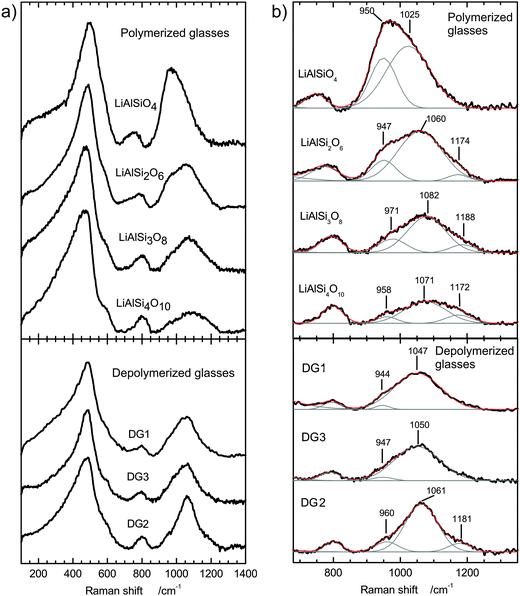
The Raman spectra of the polymerized glasses are of good quality and reproducibility. Raw spectra after temperature and baseline corrections are shown in Fig. 4a. All spectra exhibit three complex bands in the low- and high-frequency regions, centred at around 490, 800 and between 950 and 1200 cm⁻¹. With increasing silica content for polymerized glasses (EUC to PET) the low-frequency band is slightly shifted to lower wavenumbers, while high-frequency bands are shifted to higher wavenumbers. Raman spectra of depolymerized glasses show the same behaviour although less pronounced due to less distinct compositional disparities.

Fig. 4 (a) Raman spectra of a polymerized (above) and depolymerized glass (below) series after baseline and temperature correction. Spectra of both series have been arranged with respect to the increasing silica content and are scaled to the same height of the most intense peak at 496 cm⁻¹. (b) Deconvolution of the high energy region of the spectra, originating from T–O stretching vibrations, by Gaussians in order to identify characteristics of the glasses. The peak at highest wavenumber represents SiO₄-tetrahedra connected to four SiO₄-tetrahedra (Q⁴ species). A shift of the peak position towards lower wavenumbers is due to connections of tetrahedral to AlO₄-tetrahedra and/or non-bridging oxygen.

The spectra were fitted using Gaussian functions in a non-linear curve fit. Following the structural models of Mysen and McMillan,^6,7,22,23 the minimal number of Gaussians was applied to fit the spectral shape in the range from 200 to 1400 cm⁻¹. Generally, the fit reproduced the experimental data with the coefficient of determination R² better than 99.8% and the reduced chi square in the order of 10⁻⁴. Fitted and deconvoluted high-energy regions (from 700 to 1400 cm⁻¹) are shown in Fig. 4b, and the Gaussian profile functions reflect the type and abundance of network-building structural units present. All the conclusions about the structures are made with the assumption of equal Raman scattering cross-section for all postulated structural units. The low-frequency band was assigned to transverse motions of bridging oxygen atoms in T–O–T (T = Si, Al) configurations.²³ This broad band can be described as a combination of transverse vibrations of the fully polymerized Si–O–Si and Al–O–Si network and, in the case of the depolymerized glasses, interactions with structural units containing non-bridging oxygen atoms.²⁴ In lithium aluminosilicate glasses Al has an effect comparable to NBOs on band positions. The centre of the intensive band is close to ∼430 cm⁻¹ for polymerized glasses with high Si-content (FSP and PET) and shifts towards 500 cm⁻¹ for glasses with higher Al-content (EUC, SPO). A similar shift is observed when NBOs are introduced into the aluminosilicate structure.

The band at ∼800 cm⁻¹ can be assigned to vibration movements of silicon and aluminium in the network with a high cation and low oxygen displacement.²⁴ This band is centred at ∼800 cm⁻¹ for all glasses with exception of EUC (760 cm⁻¹) and SPO (782 cm⁻¹). The trend indicates that at a higher alumina-to-silica ratio, a lower bonding strength of Al–O in comparison to Si–O bonds leads to the vibration mode appearing at lower wavenumbers.

The high-frequency region between 900 and 1200 cm⁻¹ was deconvoluted using two Gaussians in the case of the EUC glass, DG1 and DG3 or three Gaussians in the case of other considered compositions (Fig. 4b). The list of the Gaussians used in modelling is given in Table 3. The high-frequency Raman band predominantly arises from stretching vibrations of Si–O, modified by Al in neighbouring tetrahedra. Based on studies of alkaline and earth-alkaline aluminosilicate glasses,^7,22 in glasses without non-bridging oxygens the high-frequency region consists a combination of up to four main types of symmetric vibrations, defined by the number of neighbouring [AlO₄]⁻ tetrahedra connected to one SiO₄ tetrahedron.⁷ Following the well established terminology for structural types in pure silicate glasses, the corresponding species can be denoted Qⁿ(xAl) where n characterizes the number of bridging oxygen and x the number of Al in the neighbouring tetrahedra.²³ In Li-containing Al–Si–O glasses the peak at ∼950 cm⁻¹ represents the structural unit where one Si–O tetrahedron is connected with three neighbouring Al³⁺via oxygen bridges, (SiO)–Si(OAl)₃, or (Q⁴(3Al)). (SiO)₂=Si(OAl)₂ or (Q⁴(2Al)) gives rise to the peak between 1000 and 1060 cm⁻¹ and the peak centred at ∼1170 cm⁻¹ relates to the vibrations of (SiO)₃≡Si(OAl) and (Q⁴(1Al)). This is consistent with the expectation that a higher number of [AlO₄]⁻ tetrahedra connected to a SiO₄ tetrahedron leads to a decrease in frequency, as Al–O bonding is weaker in comparison to a Si–O bond. This effect is even more pronounced in depolymerized glasses, which in addition contain NBOs, as the neighbouring non-bridging oxygen atoms weaken the network bonds in a higher degree than Al.^23,24 In the series of polymerized glasses the results of structural analyses are consistent with the Al-avoiding principle of Löwenstein⁹ and they have a strong tendency for alternating Si–O–Al structure. The structure of EUC is expected to compose of alternating Si- and Al-tetrahedra, which would correspond to a Q⁴(4Al) structural unit. In the high frequency region of the EUC spectrum the strong peak centred at ∼960 cm⁻¹ would correspond to this unit, while the additional weaker component at ∼1075 cm⁻¹ arises from Q⁴(3Al) as a result of deviation from Si–O–Al alternation due to the existence of a small number of Al–O–Al bonds. In the spectra of SPO, FSP and PET, the Gaussians centred at ∼950, ∼1070 and ∼1170 cm⁻¹ can be generally assigned to Q⁴(4Al), Q⁴(3Al) and Q⁴(2Al) units, respectively (see Table 3). The broadness of individual Gaussians, however, indicates that various combinations of the main structural units are present and give rise to the discrete peaks, which cannot individually be defined in the spectra.

Table 3 List of Gaussian replicas used in deconvolution of the unpolarized Raman spectra of each considered composition. Each peak position has been fitted with the less than 10% uncertainty

	LiAlSiO4	LiAlSi2O6	LiAlSi3O8	LiAlSi4O10	DG1	DG2	DG3
Low-energy region (cm^−1)	333	338	385	310	—	—	—
	—	432	—	432	400	403	438
	496	490	472	480	472	490	490
	—	584	589	595	595	601	600
High-energy region (cm^−1)	760	782	800	800	800	806	794
	960	947	971	958	944	960	947
	1075	1060	1082	1071	1047	1061	1050
	—	1174	1188	1172	—	1181	—

---

In the depolymerized glasses DG1–3 the number of Gaussian peaks and peak positions differs slightly in comparison to the polymerized series. In depolymerized glasses the silica network is modified by both [AlO₄]⁻ tetrahedra and the NBOs. This means that the high-energy band is far more complex in comparison, with a combination of modes arising from depolymerized silica tetrahedra with one to two NBOs as well as the Al–O–Si species. It is not possible to resolve the overlapping distinct modes of individual species and their combinations with the non-linear curve fit. Keeping this in mind, the high-frequency parts of the depolymerized glass spectra can be compared with the polymerized series. The spectra fitted with Gaussians reveal broader bands, which would generally comprise the combinations of Q³ with Q⁴(3Al) and Q⁴(2Al) with the possibility of very weak contribution of Q² species. The third Gaussian was needed for fitting the broad additional peak at ∼1180 cm⁻¹ in DG2 spectra, which might correspond to the combination of Q⁴ and Q⁴(1Al).

5. Discussion

5.1 Diffusion in oxide glasses – an overview

Several models were proposed in the past to describe ion motion in oxide glasses, e.g. the Anderson and Stuart²⁵ model, the weak electrolyte model of Ravaine and Souquet²⁶ and Ingram et al.,²⁷ the modified random-network (MRN) transport model of Greaves et al.,²⁸ the jump relaxation model of Funke^29,30 and the site mismatch model of Bunde et al.^31,32 and Ingram.³³ An overview of these models can be found, for instance, in Chakraborty,³⁴ Mehrer³⁵ or Lu and Dieckmann.³⁶ Ideas of the latter two models are combined in the concept of mismatch and relaxation (CMR) of Funke,³⁷ and are further elaborated in the universality concept of Funke et al.³⁸ Ion-conducting materials with quite different kinds of disordered structures have been found to show a striking similarity in their conductivity spectra. The first universality is that, at high temperatures, plots of log conductivity vs. log frequency yield features as shown in Fig. 2, which can be considered as a fingerprint of activated ionic hopping along interconnected sites.^39–41 At low temperatures, e.g. in the cryogenic range, the dielectric loss function, ε′′, is virtually independent of both frequency and temperature. This so-called “second universality” is suggested to reflect non-activated, strictly localized movements of the ions.^42–44

In structurally disordered materials mobile ions no longer experience a static energy landscape as in crystals, but rather single-particle potentials that are time-dependent and non-periodic. As a consequence, movement of ions is not random, but highly correlated.³⁸ A key issue is to relate the observed dynamics of ions with the structure of the potential landscape. The mobility of lithium ions in oxide glasses is determined by short and long range order effects. The short range movement is affected by the direct structural environment of the lithium cation. The activation energy needed for a movement to another place in the structure depends on the coordination of lithium. With a lower energy level of the current location in comparison to neighbouring sites, the higher is the activation energy needed to leave this place. When the ion leaves this negative potential site, it can either remain at the new position with the surrounding matrix adapting to the new situation (the relaxation process) or the ion jumps back to the origin place. A series of successful jumps leads to long range transport phenomena and ions can be transported through the material. This can be supported by forming percolation paths. A jumping lithium ion releases a site with a negative potential, which can be filled by another Li⁺. A hopping mechanism can thus be established leading to a correlated jump phenomenon. Following the jump relaxation model the movement through these percolation paths is the main transport mechanism for fast ion conductors. The introduction of high field strength cations like Ca²⁺ or Mg²⁺ leads to blocking of these pathways and, consequently, to a dramatic decrease in diffusivity and conductivity. The importance of these percolation pathways makes this kind of diffusion mechanism generally prone to blocking effects.^35,45 Data published in the literature show that in the nominally fully polymerized systems NaAlSi₃O₈–CaAl₂Si₂O₈ (ref. 46) and (CaO·Al₂O₃)_x–(2SiO₂)_1−x, x from 0.17 to 0.90³⁶ sodium tracer diffusivity decreases by 4–6 orders of magnitude upon calcium incorporation at temperatures around 1073 K. In the lithium bearing glasses of our study no impact of blocking divalent cations is expected due to low impurity contents (Li/Ca > 500, see Table 1).

5.2 Diffusion of lithium in the Li₂O–Al₂O₃–SiO₂ system

The ionic conductivity is affected by both the mobility and the concentration of the charge carriers. To gain insights into the dynamics of lithium, diffusion coefficients were calculated using the Nernst–Einstein-equation:^19,47,48D_DC corresponds to the self-diffusion coefficient of lithium ions. It is calculated from the specific DC conductivity of the sample (σ_DC,spec.), absolute temperature T, the Boltzmann constant k, charge carrier concentration N and the charge of the diffusing ion q. Charge carrier concentrations are calculated from glass density and glass composition, assuming a statistical distribution of lithium ions. The calculated diffusivities are shown in Fig. 5.

Fig. 5 Temperature depending diffusivities for polymerized and depolymerized glasses calculated from σ_DCT values using the Nernst–Einstein equation.

Diffusivities for the different polymerized glasses are practically indistinguishable. For LiAlSi₂O₆ the data are in good agreement with the results of lithium isotope exchange experiments⁴⁹ and NMR measurements.⁵⁰ There appears to be a trend of slightly increasing activation energy for lithium diffusion with increasing silica content of the glass, but the effect is rather small compared to the error of E_a (Table 2). Lithium diffusivity strongly decreases when introducing NBOs into the aluminosilicate glass matrix, e.g. by 0.6 log units from FSP to DG2 and DG3 at 400 K (Fig. 6a). Comparison with data for lithium trisilicate from Bauer et al.,³ with a similar silica content of 75 mol%, indicates a minimum of lithium mobility for systems containing both NBO and Al–O–Si. The activation energy for diffusion follows the same trend exhibiting a maximum for the depolymerized aluminosilicate glasses (Fig. 6b). Hence, the differences in lithium mobility increase with decreasing temperature.

Fig. 6 Diffusion coefficient (a) and activation energy (b) depending on Li₂O content for the polymerized glass FSP, depolymerized glasses DG2 and DG3 and the lithium trisilicate glass with nearly constant SiO₂ content.

The minimum in alkali diffusivity at half way between the silicate and the fully polymerized aluminosilicate composition is consistent with findings of Terai⁵¹ for sodium tracer diffusion in the Na₂O–Al₂O₃–SiO₂ system. However, Terai reported a continuous increase in activation energy towards the pure silicate composition while our data indicate for lithium a maximum in activation energy at intermediate composition. Molecular dynamics simulations⁵² in the xLi₂O–(0.5 − x)Al₂O₃–0.5SiO₂ system also point to a maximum in activation energy between Al/Li = 0 and Al/Li = 1.

We want to emphasize that all impedance measurements were done at temperatures at least 50 K below the glass transition temperature. Under these conditions the other constituents of the glass structure (Si, Al, O) can be considered as immobile. Additionally it needs to be stressed that concentrations of other alkalis are below 1% of the lithium concentration and, hence, the conductivity data and the derived diffusivity coefficients for lithium represent solely structural differences in the materials.

5.3 Implications for lithium migration paths and glass structures

The Raman spectra are consistent with a statistical distribution of [AlO₄]⁻ tetrahedra in the network of polymerized lithium aluminosilicate glasses. The aluminium avoiding principle theoretically leads, for EUC (chemical composition LiAlSiO₄), to an alternating sequence of [SiO₄]- and [AlO₄]⁻-units, meaning that each Si-tetrahedron is connected to four Al-tetrahedra and vice versa. Lee and Stebbins proved the existence of Al–O–Al (and subsequent Si–O–Si) structural units in alkaline aluminosilicate glasses with an Al/Si ratio of 1 by ¹⁷O 3QMAS NMR analyses,¹⁰ but this can only be attributed as a minor influence and does not alter the global picture. Thus, in the first approximation all oxygen atoms are equal in EUC with a formal charge of (−1/4) and potential sites for lithium in the structure are determined by the flexibility of T–O–T bond angles. Incorporation of SiO₂ into the glass leads to an increase in fraction of Si–O–Si, meaning that the oxygen has a formal charge of 0. In PET (LiAlSi₄O₁₀) glass the fraction of Si–O–Si over total oxygen formally reaches a value of 0.6. Assuming a statistical distribution of types of oxygen, there is still a very high probability for interstitial sites for lithium with 2–3 oxygen bonded to Al. This would further result in low activation energies for lithium diffusion, while the decrease in relative abundance of Si–O–Al may explain the slight increase of E_a with silica content. Compared to crystals of the same composition (LiAlSi₂O₆: α- and β-spodumene; LiAlSi₄O₁₀: petalite) the mobility of lithium in the glasses is decreased by several orders of magnitude.¹⁵ Denser packing in the crystalline phases reduces, on one hand, the number of possible sites, which can host lithium ions and may affect, on the other hand, the energy barrier for transition from one site to the other. A vacancy-controlled transport mechanism was proposed for the densely packed α-spodumene structure, while in the open framework the structure of petalite formation and movement of Li interstitials were assumed to be the dominant mechanism for charge transfer.¹⁵

However, for alkali silicate glasses there is strong evidence for an unmixing of structural units on the nanometre scale (see Discussion in Bauer et al.).³ A separation of Li-rich regions within a Si-rich matrix was observed using different experimental methods^{1,5,54–57,59,60} as well as in theoretical modelling.^5,53,61–63 Analyses of Li–NBO and Li–BO bond lengths and spatial arrangements by NMR,^1,5,59 neutron diffraction,^54,57,58 MDS^5,53,61–63 and the low coordination number of Li^53,58 strongly point toward elongated channel-like arrangements of the Li-rich regions. Quasielastic neutron scattering results corroborate the formation of cation channels for fast ion diffusion in the static Si matrix as a feature of all alkali binary silicates.⁵⁵ Preferential Li cation migration paths can thus be formed between individual interconnected Li-rich regions by cation hopping over the percolation barriers, that is, between the depolymerized Q species. As a consequence, activation energy for lithium diffusion is low (comparable to the polymerized aluminosilicate glasses). As shown by molecular dynamics simulations, the channels are closed when aluminium is inserted into the structure.⁵² As a consequence, the activation energy for lithium migration increases, which is consistent with the electrical conductivity data of our study.

Molecular dynamics simulations indicate the absence of phase separation and/or channel formation in alkali aluminosilicate glasses containing significant amounts of NBOs,^52,64,65 consistent with the Raman spectra of the glasses. The driving force for clustering in the alkali silicate glasses is the optimization of oxygen polyhedra around lithium ions. Oxygen atoms connected to two silicon atoms (Si–O–Si) have relatively small electron density and, therefore, they are not well suited to coordinate lithium ions. In contrast, an oxygen bond to aluminium (Si–O–Al) is much better suited to participate in such lithium polyhedra, as evidenced by the findings on polymerized aluminosilicate glasses. Thus, the high activation energy for lithium diffusion in partially depolymerized aluminosilicate glasses results from the formation of deep local potentials by surrounding lithium ions with NBOs and bridging oxygen bonds in Si–O–Al units. Even in the glass with lowest aluminium content, DG3, the fraction of Si–O–Al to total oxygen is 0.23 and the total fraction of formally charged oxygen is 0.36. The transition of lithium ions from such regular sites to interstitial sites requires high activation energy.

We did not study glasses with an excess of aluminium (Al/Li > 1), but MDS clearly shows that activation energy for lithium diffusion has increased compared to the polymerized system (Al/Li = 1).^52,64,65 So we would expect a decrease in lithium diffusivity as well as in ionic conductivity towards peraluminous composition (Al/Li > 1).

6. Conclusion

The impedance spectroscopic and Raman spectroscopic analyses of a series of 4 polymerized and 3 depolymerized lithium aluminosilicate glasses reveal information about the diffusion characteristics of lithium and their structural and compositional dependence. While polymerized aluminosilicates are fast lithium ion conductors with a wide distribution of lithium percolation paths, the introduction of an excess of network modifiers leads to depolymerization and a drop in conductivity and lithium diffusivity. This is explained with the strong interaction of lithium with the NBOs creating deep local potentials for lithium and, hence, high barriers for the transition of lithium ions into interstitial sites. When decreasing the concentration of aluminum, the glasses tend to unmixing on the nano-scale, driven by clustering of lithium ions and NBOs. As a consequence, high lithium mobility can be achieved by percolation along channel-like nanostructures. Thus, although lithium diffusivities and activation energies for lithium diffusion are similar in polymerized lithium aluminosilicate and in lithium silicate glasses, the network topology and the migration paths differ strongly. The similarity of the transport properties indicates that the barriers for lithium jumps between regularly occupied sites and interstitial sites are comparable for both types of glasses.

Acknowledgements

The authors are grateful for the financial support by DFG via FOR 1277. We thank Eric Wolff for conducting the EMPA measurements and Marc Krey for ICP-OES analysis. Dawid Murawski helped to conduct impedance spectroscopy measurements, Mareille Wittnebel and Sören Wilke supported in glass syntheses and T_g determination.

References

1. A. Kuhn, M. Wilkening and P. Heitjans, Solid State Ionics, 2007, 180, 302–307.
2. H. Staesche, S. Murugavel and B. Roling, Z. Phys. Chem., 2009, 223, 1229–1238.
3. U. Bauer, A.-M. Welsch, H. Behrens, J. Rahn, H. Schmidt and I. Horn, J. Phys. Chem. B, 2013, 117, 15184–15195.
4. D. Raistrick, C. Ho and R. A. Huggins, J. Electrochem. Soc., 1976, 123, 1469–1476.
5. U. Voigt, H. Lammert, H. Eckert and A. Heuer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 064207.
6. B. Mysen, Eur. J. Mineral., 2003, 15, 781–802.
7. B. Mysen, D. Virgo and F. Seifert, Am. Mineral., 1985, 70, 88–105.
8. M. Hofmeister and A. G. Whittington, Contrib. Mineral. Petrol., 2009, 158, 381–400.
9. W. Löwenstein, Am. Mineral., 1954, 39, 92–96.
10. S. K. Lee and J. F. Stebbins, J. Non-Cryst. Solids, 2000, 270, 260–264.
11. Z. Xu and F. Stebbins, Solid State Nucl. Magn. Reson., 1995, 5, 103–112.
12. J. L. Pouchou and F. Pichoir, Electron Probe Quantitation, Plenum Press Div Plenum Publishing Corp, New York, 1991, p. 31.
13. HVG-DGG:http://www.hvg-dgg.de/download/freie-inhalte/standardglas.html (2013).
14. R. T. Johnson, R. M. Biefeld, M. L. Knotek and B. Morosin, J. Electrochem. Soc., 1976, 123, 680–687.
15. A.-M. Welsch, H. Behrens, S. Ross and D. Murawski, Z. Phys. Chem., 2012, 226, 491–511.
16. M. Hass, Solid State Commun., 1969, 7, 1069–1071.
17. R. Shuker and R. Gammon, Phys. Rev. Lett., 1970, 25, 222–225.
18. P. Maass, A. Bunde and M. D. Ingram, Phys. Rev. Lett., 1992, 68(20), 3064–3067.
19. B. Roling, A. Happe, M. D. Ingram and K. Funke, J. Phys. Chem. B, 1999, 103, 4122–4127.
20. M. Tomozawa, J. Non-Cryst. Solids, 1993, 152, 59–69.
21. R. T. Johnson jr., R. M. Biefeld, M. L. Knotek and B. Morosin, J. Electrochem. Soc., 1976, 123, 680–687.
22. B. Mysen, D. Virgo and I. Kushiro, Am. Mineral., 1981, 66, 678–701.
23. P. McMillan and B. Piriou, J. Non-Cryst. Solids, 1982, 53, 279–298.
24. P. McMillan, Am. Mineral., 1984, 69, 622–644.
25. O. L. Anderson and D. A. Stuart, J. Am. Ceram. Soc., 1954, 37, 573–580.
26. D. Ravaine and J. L. Souquet, Phys. Chem. Glasses, 1977, 18, 27–31.
27. M. D. Ingram, J. Non-Cryst. Solids, 1980, 38–39, 371–376.
28. G. N. Greaves, S. J. Gurman, C. R. A. Catlow, A. V. Chadwick, S. Houde-Walter, C. M. B. Henderson and B. R. Dobson, Philos. Mag. A, 1991, 64–65, 1059–1072.
29. K. Funke, Prog. Solid State Chem., 1993, 22, 111–195.
30. K. Funke, Solid State Ionics, 1997, 94, 27–331.
31. A. Bunde, K. Funke and M. D. Ingram, Solid State Ionics, 1996, 86–88, 1311–1317.
32. A. Bunde and P. Maas, J. Non-Cryst. Solids, 1991, 131–133, 1022–1027.
33. M. D. Ingram, P. Maass and A. Bunde, Ber. Bunsen-Ges. Phys. Chem., 1991, 95, 1002–1006.
34. S. Chakraborty, Rev. Mineral. Geochem., 1995, 32, 411–503.
35. H. Mehrer, Diffusion in Solids – Fundamentals, Methods, Materials, Diffusion-controlled processes, Springer, Verlag, Berlin, Heidelberg, Series in Solid-State Sci., 2007, p. 155.
36. H. Lu and R. Dieckmann, J. Non-Cryst. Solids, 2007, 353, 2528–2544.
37. K. Funke, B. Roling and M. Lange, Solid State Ionics, 1998, 105, 195–208.
38. K. Funke, R. D. Banhatti, D. M. Laughman, L. G. Badr, M. Mutke, A. Santic, W. Wrobel, E. M. Fellberg and C. Biermann, Z. Phys. Chem., 2010, 224, 1891–1950.
39. K. Funke, T. Lauxtermann, D. Wilmer and S. M. Bennington, Z. Naturforsch., A: Phys. Sci., 1995, 50, 509–520.
40. K. Jonscher, Nature, 1977, 267, 673–679.
41. B. Roling, Solid State Ionics, 1998, 105, 185–193.
42. J. C. Dyre, J. Appl. Phys., 1988, 64, 2456–2468.
43. H. Jain, Met., Mater. Processes, 1999, 11, 317–320.
44. H. Kahnt, Ber. Bunsen-Ges. Phys. Chem., 1991, 95, 1021–1025.
45. H. Kahnt, J. Non-Cryst. Solids, 1996, 203, 225–231.
46. H. Behrens, Chem. Geol., 1992, 96, 267–275.
47. A. Angell, J. Phys. Chem., 1965, 69–2, 399–403.
48. J. L. Souquet, Annu. Rev. Mater. Sci., 1981, 11, 211–231.
49. A.-M. Welsch, H. Behrens, I. Horn, S. Roß and P. Heitjans, J. Chem. Phys., 2012, 116, 309–318.
50. M. Wilkening, A. Kuhn and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054303.
51. R. Terai, Phys. Chem. Glasses, 1969, 10, 146–152.
52. W. Li and S. H. Garofalini, Solid State Ionics, 2004, 166, 365–373.
53. J. Du and L. R. Corrales, J. Chem. Phys., 2006, 125, 114702.
54. J. Zhao, P. H. Gaskell, M. M. Cluckie and A. K. Soper, J. Non-Cryst. Solids, 1998, 232–234, 721–727.
55. F. Kargl, A. Meyer, M. M. Koza and H. Schober, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 014304.
56. S. K. Lee and J. F. Stebbins, Geochim. Cosmochim. Acta, 2009, 73, 1109–1119.
57. H. Uhlig, M. J. Hoffmann, H.-P. Lamparter, F. Aldringer, R. Bellissent and S. S. Steeb, J. Am. Ceram. Soc., 1996, 79, 2833–2838.
58. C. Hannon, B. Vessal and J. M. Park, J. Non-Cryst. Solids, 1992, 150, 97–102.
59. E. Göbel, W. Müller-Warmuth, H. Olyschläger and H. Dutz, J. Magn. Reson., 1979, 36, 371–387.
60. S. Sen and T. A. Mukerji, J. Non-Cryst. Solids, 2001, 293–295, 268–278.
61. H. Lammert and A. Heuer, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 024204.
62. J. Habasaki and Y. Hiwatari, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144207.
63. R. Prasada Rao, T. D. Tho and S. Adams, Solid State Ionics, 2010, 181, 1–6.
64. D. M. Zirl and S. H. Garofalini, J. Am. Ceram. Soc., 1990, 73, 2848–2856.
65. A. N. Cormack, J. Non-Cryst. Solids, 1998, 234, 188–197.

---