Towards high-level theoretical studies of large biodiesel molecules: an ONIOM [QCISD(T)/CBS:DFT] study of hydrogen abstraction reactions of CnH2n+1COOCmH2m+1 + H†
Lidong
Zhang
and
Peng
Zhang
*
Department of Mechanical Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong. E-mail: pengzhang.zhang@polyu.edu.hk; Fax: +852 23654703; Tel: +852 27666664
First published on 24th October 2014
Abstract
Recent interest in biodiesel combustion urges the need for the theoretical chemical kinetics of large alkyl ester molecules. This is, however, computationally challenging for prevalent high-level electronic structure theory based methods. The hydrogen abstraction reactions of alky esters CnH2n+1COOCmH2m+1 (n = 1–5, 9, 15; m = 1, 2) by a hydrogen radical were investigated by a computational technique based on a two-layer ONIOM method, employing a QCISD(T)/CBS method for the high layer and a DFT method for the low layer. The calculated energy barriers and heats of reaction, using the ONIOM method with a minimum of the required chemically active portion, are in very good agreement with those obtained using the widely accepted high-level QCISD(T)/CBS theory because the computational errors were less than 0.1 kcal mol−1 for all the tested cases. The ONIOM[QCISD(T)/CBS:DFT] method provides a computationally accurate and affordable approach to the high-level theoretical chemical kinetics of large biodiesel molecules.
Introduction
Biofuels have been proposed as a viable solution to contemporary challenges such as energy sustainability, energy security, and climate change. Biodiesel is one of the most widely used biofuels because of its many desirable advantages. In particular, biodiesel can be produced from renewable, locally accessible feedstock. It is environmentally friendly with the potential to reduce harmful emissions such as particulate matter and carbon monoxide.1–3 Furthermore, biodiesel is economically feasible because it can replace or blend with petroleum-based diesel for direct utilization in diesel engines with or without only minor modifications to the engine and fueling system.4,5 Motivated by the practical significance of utilizing biodiesel, numerous studies have been conducted in recent years on the chemical kinetics of its combustion,6–8 with a particular interest in establishing accurate, detailed reaction mechanisms,9–12 required by the CFD (computational fluid dynamics)-based computer-aided design of combustion energy conversion devices fueled with biodiesel.The development of mechanism for biodiesel faces significant challenges. First, biodiesel is a mixture of long-carbon-chain fatty acid alkyl esters with 12–20 carbon atoms and diverse molecular structures, and thus it has distinct physicochemical properties. Consequently, most of the previous studies were focused on prototypical fuels, whose molecules contained shorter carbon chains. These fuels are used as surrogates to mimic the combustion characteristics of real biodiesel. The representative surrogates are methyl butanoate (MB, C3H7COOCH3)13–17 and methyl decanoate (MD, C9H19COOCH3).18,19 Second, a detailed reaction mechanism for a surrogate fuel may consist of a few hundred or even thousand species and a few times more elementary reactions. Specifying accurate temperature (and pressure)-dependent reaction rate constants for such a large number of reactions is a formidable task, especially for the reactions and conditions that are difficult to explore experimentally, although important for combustion chemistry.
Recent advances in theoretical chemical kinetics and electronic structure theory have enabled the prediction of reaction rate constants for relatively small molecules with accuracy comparable to those of well-conducted experiments. For example, the high-pressure rate constant for a hydrogen abstraction reaction, RH + H → R + H2, with a distinct energy barrier along the reaction coordinate, can be well-defined using the conventional transition state theory (TST)20,21
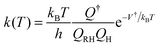 | (1) |
The uncertainty of the theoretical rate constant significantly relies on that of the predicted barrier height. For example, an underestimation of V† by 2 kcal mol−1 can cause a significant increase of k(T) by about a factor of 2 at a typical combustion temperature of 1500 K, whereas an increase by a factor of 7.5 at a typical ignition temperature of 500 K. It is recognized that the uncertainty also relies on other factors, such as the tunneling effect,20,22 at sufficiently low temperatures and torsional anharmonicity23–25 of large molecules. These large uncertainties in the rate constants, if used in a reaction mechanism, can cause the model prediction for combustion parameters, such as laminar flame speed and ignition delay time, to substantially deviate from experimental measurements. A few theoretical methods have been demonstrated to be effective and accurate for organic molecules that are of interest to combustion chemistry.22 The coupled cluster theory, with single and double excitations, and a quasi-perturbative treatment of connected triple excitations [CCSD(T)], with an extrapolation to complete basis set (CBS), yields the predictions of barrier height and reaction energy with uncertainties up to 1.1 kcal mol−1.26 The quadratic configuration interaction with singles, doubles and perturbative inclusion of triples [QCISD(T)/CBS] is usually accurate to around 1.0 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 in the prediction of barrier height, and can be as accurate as 0.6 kcal mol−1 for thermochemistry with the inclusion of a bond additivity correction.28 Unfortunately, none of these methods can be applied to a system with more than 10 non-hydrogen atoms.22 As a result, most reaction rate constants for MB were evaluated at lower levels of CBS-QB329 or B3LYP/6-31G(d,p).30 Only a few important reactions such as MB + H (OH,HO2) were studied at the level of QCISD(T)/CBS.31 To date, no high-level thermochemical and kinetic data are available for MD and larger esters, except a few studies at the level of B3LYP/6-31G(d,p).32,33 Clearly, there is an urgent need to develop methodologies for high-level chemical kinetics of larger biodiesel molecules.
27 in the prediction of barrier height, and can be as accurate as 0.6 kcal mol−1 for thermochemistry with the inclusion of a bond additivity correction.28 Unfortunately, none of these methods can be applied to a system with more than 10 non-hydrogen atoms.22 As a result, most reaction rate constants for MB were evaluated at lower levels of CBS-QB329 or B3LYP/6-31G(d,p).30 Only a few important reactions such as MB + H (OH,HO2) were studied at the level of QCISD(T)/CBS.31 To date, no high-level thermochemical and kinetic data are available for MD and larger esters, except a few studies at the level of B3LYP/6-31G(d,p).32,33 Clearly, there is an urgent need to develop methodologies for high-level chemical kinetics of larger biodiesel molecules.
In the present study, we aim to develop a two-layer ONIOM34 (our own N-layered integrated molecular orbital and molecular mechanics) method for high-level single point energy calculation by employing the high-level ab inito method, QCISD(T)/CBS, for the high layer and the B3LYP-favor density functional theory (DFT) method for the low layer. To the best of our knowledge, the ONIOM-based methods have not been applied to study combustion chemical kinetics, which was mainly focused on relatively small molecules. We systematically tested the method by calculating the energy barriers and the heats of reaction of the hydrogen abstraction reactions of alkyl esters, CnH2n+1COOCmH2m+1 (n = 1–5, m = 1 or 2), by a hydrogen radical, which are the crucial reactions in the combustion of alkyl esters. The calculated ONIOM [QCISD(T)/CBS:DFT] energies were compared with the QCISD(T)/CBS energies. In addition, the method was tested for nonane (C9H20) to extend its applications to the study of hydrocarbon molecules. The ONIOM method was subsequently applied to larger systems, such as methyl decanoate (MD, n = 9, m = 1) and methyl heptadecanoate (n = 15, m = 1), whose molecular sizes are comparable to those of the dominant components of real biodiesel.
Computational methods
The geometric structures and vibrational frequencies for stationary points on the PESs of CnH2n+1COOCmH2m+1 + H (n = 1–5, 9, 15; m = 1, 2) were obtained via DFT, employing the Becke three-parameter functional and the Lee–Yang–Parr correlation functional (B3LYP) with the 6-311++G(d,p) basis set.35,36 This method compromises the computational accuracy and cost, and has been widely used in combustion chemical kinetics. The connections of each saddle point to its local minima were examined using the intrinsic reaction path calculations. Zero-point energy (ZPE) corrections were obtained from the B3LYP/6-311++G(d,p) vibrational frequencies.For relatively small molecules, two high-level QCISD(T)/CBS methods are computationally affordable and used to produce benchmark data to validate the present ONIOM method. The first method, denoted as [QCISD(T)/CBS]1 or [QCISD(T)/CBS]TZ→QZ, is based on the direct extrapolation of the QCISD(T) energies with correlation-consistent, polarized-valence, triple-ζ (cc-pVTZ, denoted as TZ) and quadruple-ζ (cc-pVQZ, denoted QZ) basis sets of Dunning37,38 to the complete basis set (CBS) limit.39
| E[QCISD(T)/CBS]1 = E[QCISD(T)/CBS]TZ→QZ = E[QCISD(T)/QZ] + {E[QCISD(T)/QZ] − E[QCISD(T)/TZ]} × 0.6938 | (2) |
However, this method is very computationally intensive for the studied reactions with n ≥ 3. Therefore, we used the alternative [QCISD(T)/CBS]2 method:40
| E[QCISD(T)/CBS]2 = E[QCISD(T)/CBS]DZ→TZ + {E[MP2/CBS]TZ→QZ − E[MP2/CBS]DZ→TZ} | (3) |
| E[QCISD(T)/CBS]DZ→TZ = E[QCISD(T)/TZ] + {E[QCISD(T)/TZ] − E[QCISD(T)/DZ]} × 0.4629 | (4) |
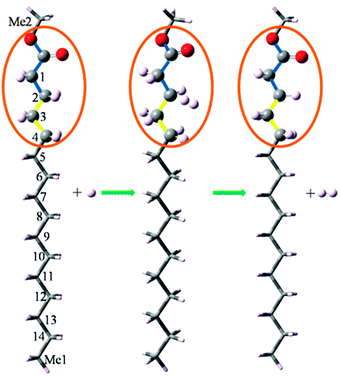
The present ONIOM method models a reaction system (denoted R) by defining two layers within the structure, which are treated at different theoretical levels, as shown in Fig. 1. The chemically active portion34 (denoted CAP) of the molecule is treated at the QCISD(T)/CBS level, while the remaining portion of the molecule is treated at the B3LYP/6-311++G(d,p) level. Because functional groups are always included in the same layer in the present study, using hydrogen atoms as link atoms to saturate the dangling bonds is a satisfactory choice, as substantiated by our calculation results presented in the subsequent section. The CAP consists of the attacking H atom, the CH2 (or CH3) under attack, and the neighboring CH2 (or CH3, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–O) groups. To quantify the influence of the size of the CAP on the calculation accuracy, we denote a CAP by two integers (N1 and N2), where N1 or N2 is the number of the main-chain non-hydrogen atoms on each side of the C atom whose H undergoes attack. Consequently, the total number of non-hydrogen atoms included in the CAP is N1 + N2 + 1. For example, if CAP(2,2) is specified for the reaction C15H31COOCH3 + H → CH3CH2C·H(CH2)12COOCH3 + H2, corresponding to the hydrogen abstraction from the C atom of Index 13, shown in Fig. 1, the five non-hydrogen atoms included in the CAP consists of the C atom of Index 13, the C atoms of Index 11 and 12 on the one side, and the C atoms of Index 14 and Me1 on the other side. Exceptions exist when functional groups are involved in a reaction and will be explained in the subsequent section.
O, C–O) groups. To quantify the influence of the size of the CAP on the calculation accuracy, we denote a CAP by two integers (N1 and N2), where N1 or N2 is the number of the main-chain non-hydrogen atoms on each side of the C atom whose H undergoes attack. Consequently, the total number of non-hydrogen atoms included in the CAP is N1 + N2 + 1. For example, if CAP(2,2) is specified for the reaction C15H31COOCH3 + H → CH3CH2C·H(CH2)12COOCH3 + H2, corresponding to the hydrogen abstraction from the C atom of Index 13, shown in Fig. 1, the five non-hydrogen atoms included in the CAP consists of the C atom of Index 13, the C atoms of Index 11 and 12 on the one side, and the C atoms of Index 14 and Me1 on the other side. Exceptions exist when functional groups are involved in a reaction and will be explained in the subsequent section.
For the reaction C15H31COOCH3 + H → C13H27C·HCH2COOCH3 + H2, shown in Fig. 1, the H atom belonging to the C atom of Index 2 undergoes attack. If a CAP(2,3) is specified for the ONIOM method, the CAP consists of the C atom of Index 2, two non-hydrogen atoms (i.e. the C atoms of Index 3 and 4) on one side, and three non-hydrogen atoms (i.e. the C atom of Index 1, the carbonyl C atom and the alkoxy O atom) on the other side. To maintain the integrity of the functional group, the carbonyl O atom is also included in the CAP, rendering a total number of seven non-hydrogen atoms in the CAP. It should be noted that we always kept a functional group in the same layer in the present study. For example, if CAP(2,2) is specified for the reaction shown in Fig. 1, the two O atoms must also be included in the CAP to keep the whole ester group undivided.
The ONIOM method approximates the energy of the system by the energy of the system at the low level with a correction for the difference between the high level and the low level for the CAP,34
| EONIOM[High:Low] = ELow(R) + EHigh(CAP) − ELow(CAP) | (5) |
| EONIOM[QCISD(T)/CBS:DFT] = EONIOM[QCISD(T)/CBS:DFT]DZ→TZ + {EONIOM[MP2/CBS:DFT]TZ→QZ − EONIOM[MP2/CBS:DFT]DZ→TZ} | (6) |
| EONIOM[QCISD(T)/CBS:DFT]DZ→TZ = EONIOM[QCISD(T)/TZ:DFT] + {EONIOM[QCISD(T)/TZ:DFT] − EONIOM[QCISD(T)/DZ:DFT]} × 0.4629 | (7) |
| EONIOM[MP2/CBS:DFT]TZ→QZ = EONIOM[MP2/QZ:DFT] + {EONIOM[MP2/QZ:DFT] − EONIOM[MP2/TZ:DFT]} × 0.6938 | (8) |
| EONIOM[MP2/CBS:DFT]DZ→TZ = EONIOM[MP2/TZ:DFT] + {EONIOM[MP2/TZ:DFT] − EONIOM[MP2/DZ:DFT]} × 0.4629 | (9) |
The ZPE corrected energy barrier (EB) is calculated by the difference between EONIOM[QCISD(T)/CBS:DFT] + ZPE of the transition state and that of the reactants. The ZPE corrected heat of reaction (HR) is calculated by the difference between EONIOM[QCISD(T)/CBS:DFT] + ZPE of the products and that of the reactants. All the ZPE corrections are obtained at the B3LYP/6-311++G(d,p) level, as discussed above. In the present study, all the calculations were performed with the Gaussian 09 program package.34
Results and discussion
Validation and comparison of [QCISD(T)/CBS]1 and [QCISD(T)/CBS]2
In the present study, [QCISD(T)/CBS]1 was used to study the title reactions up to n = 0–2 and m = 1 and 2, and [QCISD(T)/CBS]2 up to n = 0–5 and m = 1 and 2. To establish the benchmark data for the validation of the present ONIOM method, we first compared the [QCISD(T)/CBS]1 and [QCISD(T)/CBS]2 energies for n = 0–2 and m = 1 and 2 and found they are in an excellent agreement. The discrepancies are less than 0.1 kcal mol−1 and independent of n and m, as shown in Table 1. Consequently, we can use the [QCISD(T)/CBS]2 method to produce benchmark data for n = 0–5 and m = 1 and 2 by assuming that the small, size-independent discrepancies still hold for larger molecules with n = 3–5. In the subsequent discussion, all the ONIOM[QCISD(T)/CBS:DFT] energies will be compared with the [QCISD(T)/CBS]2 energies.| Reactions | EB (kcal mol−1) | HR (kcal mol−1) | ||
|---|---|---|---|---|
| [QCISD(T)/CBS]1 | [QCISD(T)/CBS]2 | [QCISD(T)/CBS]1 | [QCISD(T)/CBS]2 | |
| H + HCOOCH3 → H2 + HCOOCH2 | 11.02 | 10.94 | −4.83 | −4.93 |
| H + HCOOCH2CH3 → H2 + HCOOCHCH3 | 8.72 | 8.65 | −6.70 | −6.73 |
| H + HCOOCH2CH3 → H2 + HCOOCH2CH2 | 11.68 | 11.61 | −2.08 | −2.14 |
| H + CH3COOCH3 → H2 + CH2COOCH3 | 10.18 | 10.10 | −5.69 | −5.71 |
| H + CH3COOCH3 → H2 + CH3COOCH2 | 10.60 | 10.52 | −5.27 | −5.37 |
| H + CH3COOCH2CH3 → H2 + CH2COOCH2CH3 | 10.10 | 10.03 | −5.75 | −5.77 |
| H + CH3COOCH2CH3 → H2 + CH3COOCHCH3 | 8.35 | 8.27 | −6.93 | −6.96 |
| H + CH3COOCH2CH3 → H2 + CH3COOCH2CH2 | 11.50 | 11.43 | −2.21 | −2.28 |
| H + CH3CH2COOCH3 → H2 + CH3CHCOOCH3 | 7.27 | 7.19 | −10.88 | −10.84 |
| H + CH3CH2COOCH3 → H2 + CH2CH2COOCH3 | 11.00 | 10.93 | −3.02 | −3.07 |
| H + CH3CH2COOCH3 → H2 + CH3CH2COOCH2 | 10.51 | 10.43 | −5.35 | −5.45 |
For smaller ester molecules, such as methyl formate (MF, i.e. n = 0 and m = 1), methyl acetate (MA, i.e. n = 1 and m = 1) and methyl butanoate (MB, i.e. n = 3 and m = 1), some high-level theoretical data for the energy barriers of their hydrogen abstraction reactions by H radical are available in the literature. The present calculation results show very good agreement with these data, and the discrepancies are generally less than 0.4 kcal mol−1, as shown in Table S1 of the ESI.†
It should be noted that Zhang et al.41 recently studied the ab initio chemical kinetics of the hydrogen abstraction reactions of MB by hydrogen and hydroxyl radicals. The potential energy surfaces were obtained at the level of [QCISD(T)/CBS]2//B3LYP/6-311++G(d,p). The calculated energy barriers excellently agree with the results of Liu et al.31 at the CCSD(T)/CBS//B3LYP/6-311++G(d,p) level. The calculated rate constants agree well with available high quality theoretical and experimental data. These results substantiate the applicability of the present approach to the chemical kinetics of biodiesel molecules.
Minimally required CAP(N1,N2) for C5H11COOCH3 + H and C9H20 + H
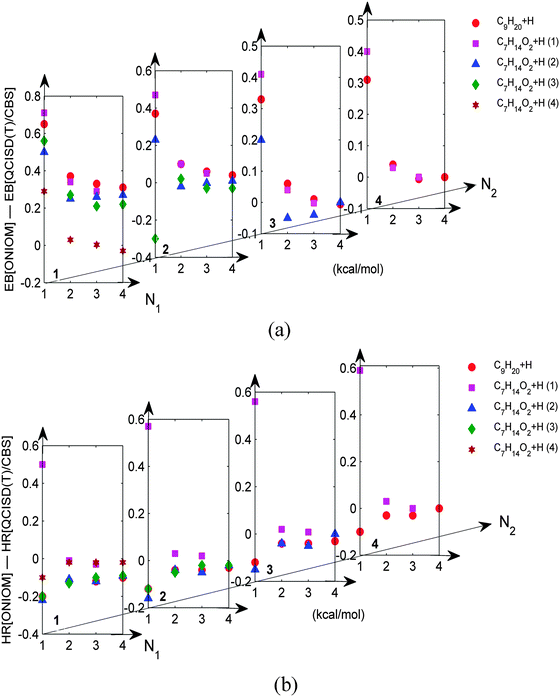
The optimal CAP was systematically explored by thoroughly testing all the possible combinations of (N1 and N2) in the reactions of C5H11COOCH3 + H and C9H20 + H, which are the largest systems studied using the [QCISD(T)/CBS]2 method in the present work. All the six possible sites on C5H11COOCH3 for hydrogen abstraction were considered, and the hydrogen abstraction of C9H20 from the central CH2 was considered. Fig. 2a shows the difference between the energy barrier at the ONIOM[QCISD(T)/CBS:DFT] level, denoted by EB[ONIOM] for simplicity, and that at the [QCISD(T)/CBS]2 level, denoted by EB[QCISD(T)/CBS], as a function of N1 and N2. For clarity, only N1 (and N2) = 1–4 are shown in the figure and more results for N1 (and N2) = 0, 5–7 can be found in Fig. S1 of ESI.†It is seen that, for all the tested CAP, EB[ONIOM] differs from EB[QCISD(T)/CBS] by less than 0.8 kcal mol−1. Furthermore, all the relatively large differences occur for N1 ≤ 1 and N2 ≤ 1. If the CAP is larger than (2,2), the energy difference can be as small as 0.1 kcal mol−1 or even less. Similarly, the difference of the heat of reaction at the two theoretical levels was calculated and shown in Fig. 2b. It was found that HR[ONIOM] again agrees well with HR[QCISD(T)/CBS] for CAP(2,2) and larger CAPs, with the discrepancies being less than 0.1 kcal mol−1. Relatively large discrepancies again occur for N1 ≤ 1 and N2 ≤ 1. These results suggest that CAP(2,2) is minimally required for the studied reactions, and we believe that CAP(2,2) is sufficiently large for other similar systems. Furthermore, the results also substantiate the applicability of the present ONIOM method to hydrocarbon molecules.
CnH2n+1COOCmH2m+1 + H (n = 1–5, m = 1, 2) with the ONIOM/CAP(2,2) or CAP(2,3)
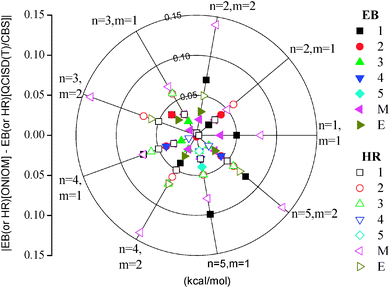
To further validate the preset ONIOM method, we calculated and compared the energy barriers and the heats of reaction for the reactions of CnH2n+1COOCmH2m+1 + H (n = 1–5, m = 1, 2) using CAP(2,2) or CAP(2,3). The inclusion of CAP(2,3) is for situations in which the alkoxy O atom should be included in the CAP to keep the ester group undivided. CAP(2,3) corresponds to the situation illustrated in Fig. 1. It is seen that almost all the differences (absolute values) between EB[ONIOM] (or HR[ONIOM]) and EB[QCISD(T)/CBS] (or HR[QCISD(T)/CBS]) are less than 0.1 kcal mol−1, as shown in Fig. 3, substantiating again the accuracy of the present ONIOM method. All the calculated energies can be found in Table 2. A few exceptional cases were found for the heats of reaction of the hydrogen abstraction reactions at the CH2 (denoted by M in Fig. 3) of the ethyl groups, yielding differences of less than 0.15 kcal mol−1. Increasing the size of the CAP to include the whole ethyl group may reduce the difference to be within 0.1 kcal mol−1.| Reactions | EB (kcal mol−1) | HR (kcal mol−1) | ||
|---|---|---|---|---|
| [QCISD(T)/CBS]2 | ONIOM | [QCISD(T)/CBS]2 | ONIOM | |
| H + CH3(CH2)7CH3 → H2 + CH3(CH2)3CH(CH2)3CH3 | 7.26 | 7.36 | −5.87 | −5.91 |
| H + CH3COOCH3 → H2 + CH2COOCH3 | 10.10 | 10.15 | −5.71 | −5.71 |
| H + CH3COOCH3 → H2 + CH3COOCH2 | 10.52 | 10.54 | −5.37 | −5.29 |
| H + CH3CH2COOCH3 → H2 + CH3CHCOOCH3 | 7.19 | 7.21 | −10.84 | −10.80 |
| H + CH3CH2COOCH3 → H2 + CH2CH2COOCH3 | 10.93 | 10.89 | −3.07 | −3.13 |
| H + CH3CH2COOCH3 → H2 + CH3CH2COOCH2 | 10.43 | 10.40 | −5.45 | −5.51 |
| H + CH3COOCH2CH3 → H2 + CH2COOCH2CH3 | 10.03 | 10.10 | −5.77 | −5.77 |
| H + CH3COOCH2CH3 → H2 + CH3COOCHCH3 | 8.27 | 8.29 | −6.96 | −6.82 |
| H + CH3COOCH2CH3 → H2 + CH3COOCH2CH2 | 11.43 | 11.40 | −2.28 | −2.33 |
| H + CH3CH2CH2COOCH3 → H2 + CH3CH2CHCOOCH3 | 7.10 | 7.14 | −10.19 | −10.16 |
| H + CH3CH2CH2COOCH3 → H2 + CH3CHCH2COOCH3 | 8.29 | 8.26 | −6.00 | −6.05 |
| H + CH3CH2CH2COOCH3 → H2 + CH2CH2CH2COOCH3 | 10.20 | 10.22 | −3.49 | −3.55 |
| H + CH3CH2CH2COOCH3 → H2 + CH3CH2CH2COOCH2 | 10.37 | 10.40 | −5.52 | −5.45 |
| H + CH3CH2COOCH2CH3 → H2 + CH3CHCOOCH2CH3 | 7.14 | 7.19 | −10.83 | −10.79 |
| H + CH3CH2COOCH2CH3 → H2 + CH2CH2COOCH2CH3 | 10.94 | 10.90 | −3.09 | −3.16 |
| H + CH3CH2COOCH2CH3 → H2 + CH3CH2COOCHCH3 | 8.20 | 8.21 | −6.97 | −6.83 |
| H + CH3CH2COOCH2CH3 → H2 + CH3CH2COOCH2CH2 | 11.40 | 11.36 | −2.29 | −2.35 |
| H + CH3CH2CH2CH2COOCH3 → H2 + CH3CH2CH2CHCOOCH3 | 7.05 | 7.12 | −10.39 | −10.36 |
| H + CH3CH2CH2CH2COOCH3 → H2 + CH3CH2CHCH2COOCH3 | 8.20 | 8.16 | −5.66 | −5.71 |
| H + CH3CH2CH2CH2COOCH3 → H2 + CH3CHCH2CH2COOCH3 | 7.54 | 7.56 | −6.34 | −6.40 |
| H + CH3CH2CH2CH2COOCH3 → H2 + CH2CH2CH2CH2COOCH3 | 10.26 | 10.30 | −3.51 | −3.52 |
| H + CH3CH2CH2CH2COOCH3 → H2 + CH3CH2CH2CH2COOCH2 | 10.35 | 10.38 | −5.52 | −5.45 |
| H + CH3CH2CH2COOCH2CH3 → H2 + CH3CH2CHCOOCH2CH3 | 7.12 | 7.16 | −10.24 | −10.20 |
| H + CH3CH2CH2COOCH2CH3 → H2 + CH3CHCH2COOCH2CH3 | 8.32 | 8.27 | −5.99 | −6.05 |
| H + CH3CH2CH2COOCH2CH3 → H2 + CH2CH2CH2COOCH2CH3 | 10.21 | 10.23 | −3.51 | −3.58 |
| H + CH3CH2CH2COOCH2CH3 → H2 + CH3CH2CH2COOCHCH3 | 8.25 | 8.27 | −6.91 | −6.78 |
| H + CH3CH2CH2COOCH2CH3 → H2 + CH3CH2CH2COOCH2CH2 | 11.41 | 11.38 | −2.27 | −2.34 |
| H + CH3CH2CH2CH2CH2COOCH3 → H2 + CH3CH2CH2CH2CHCOOCH3 | 7.05 | 7.15 | −10.29 | −10.26 |
| H + CH3CH2CH2CH2CH2COOCH3 → H2 + CH3CH2CH2CHCH2COOCH3 | 8.20 | 8.20 | −5.65 | −5.70 |
| H + CH3CH2CH2CH2CH2COOCH3 → H2 + CH3CH2CHCH2CH2COOCH3 | 7.47 | 7.49 | −5.92 | −5.97 |
| H + CH3CH2CH2CH2CH2COOCH3 → H2 + CH3CHCH2CH2CH2COOCH3 | 7.69 | 7.72 | −6.28 | −6.30 |
| H + CH3CH2CH2CH2CH2COOCH3 → H2 + CH2CH2CH2CH2CH2COOCH3 | 10.13 | 10.17 | −3.56 | −3.59 |
| H + CH3CH2CH2CH2CH2COOCH3 → H2 + CH3CH2CH2CH2CH2COOCH2 | 10.38 | 10.41 | −5.32 | −5.25 |
| H + CH3CH2CH2CH2COOCH2CH3 → H2 + CH3CH2CH2CHCOOCH2CH3 | 7.05 | 7.12 | −10.39 | −10.34 |
| H + CH3CH2CH2CH2COOCH2CH3 → H2 + CH3CH2CHCH2COOCH2CH3 | 8.20 | 8.16 | −5.62 | −5.69 |
| H + CH3CH2CH2CH2COOCH2CH3 → H2 + CH3CHCH2CH2COOCH2CH3 | 7.50 | 7.52 | −6.34 | −6.40 |
| H + CH3CH2CH2CH2COOCH2CH3 → H2 + CH2CH2CH2CH2COOCH2CH3 | 10.25 | 10.29 | −3.51 | −3.53 |
| H + CH3CH2CH2CH2COOCH2CH3 → H2 + CH3CH2CH2CH2COOCHCH3 | 8.23 | 8.26 | −6.93 | −6.79 |
| H + CH3CH2CH2CH2COOCH2CH3 → H2 + CH3CH2CH2CH2COOCH2CH2 | 11.36 | 11.32 | −2.34 | −2.41 |
| Reactions | EB (kcal mol−1) | HR (kcal mol−1) |
|---|---|---|
| H + CH3(CH2)8COOCH3 → H2 + CH3(CH2)7CHCOOCH3 | 7.22 | −10.33 |
| H + CH3(CH2)8COOCH3 → H2 + CH3(CH2)6CHCH2COOCH3 | 8.29 | −5.66 |
| H + CH3(CH2)8COOCH3 → H2 + CH3(CH2)5CH(CH2)2COOCH3 | 7.46 | −5.86 |
| H + CH3(CH2)8COOCH3 → H2 + CH3(CH2)4CH(CH2)3COOCH3 | 7.54 | −5.82 |
| H + CH3(CH2)8COOCH3 → H2 + CH3(CH2)3CH(CH2)4COOCH3 | 7.37 | −5.87 |
| H + CH3(CH2)8COOCH3 → H2 + CH3(CH2)2CH(CH2)5COOCH3 | 7.42 | −5.89 |
| H + CH3(CH2)8COOCH3 → H2 + CH3CH2CH(CH2)6COOCH3 | 7.38 | −5.96 |
| H + CH3(CH2)8COOCH3 → H2 + CH3CH(CH2)7COOCH3 | 7.49 | −6.35 |
| H + CH3(CH2)8COOCH3 → H2 + CH2(CH2)8COOCH3 | 10.14 | −3.63 |
| H + CH3(CH2)8COOCH3 → H2 + CH3(CH2)8COOCH2 | 10.64 | −5.21 |
ONIOM energies of CnH2n+1COOCmH2m+1 + H (n = 9, 15, m = 1)
Finally, we applied the present method to the larger systems of CnH2n+1COOCmH2m+1 + H (n = 9, 15, m = 1), which have not been studied using high-level theories. All the calculated energies can be found in Tables 3 and 4. The calculated energy barriers are shown in Fig. 4a, and those for n = 5 and m = 1 are also shown in the figure for comparison. It is seen that hydrogen abstraction from the two methyl groups, namely the one connected to the carbon chain (denoted by Me1) and the other connected to the ester group (denoted by Me2), have the highest energy barriers of about 10 kcal mol−1. The energy barriers for hydrogen abstraction from the other sites (refer to Fig. 1) are around 7 kcal mol−1. The results for the heat of reaction are shown in Fig. 4b. The heat of reaction is about −4 kcal mol−1 for Me1, −10 kcal mol−1 for Site 1 (namely the CH2 closest to the ester group), and −6 kcal mol−1 for other sites.| Reactions | EB (kcal mol−1) | HR (kcal mol−1) |
|---|---|---|
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)13CHCOOCH3 | 6.84 | −10.31 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)12CHCH2COOCH3 | 8.13 | −5.83 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)11CH(CH2)2COOCH3 | 7.40 | −5.83 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)10CH(CH2)3COOCH3 | 7.59 | −5.93 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)9CH(CH2)4COOCH3 | 7.25 | −6.06 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)8CH(CH2)5COOCH3 | 7.30 | −6.09 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)7CH(CH2)6COOCH3 | 7.04 | −6.18 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)6CH(CH2)7COOCH3 | 7.27 | −6.23 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)5CH(CH2)8COOCH3 | 7.01 | −6.05 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)4CH(CH2)9COOCH3 | 7.01 | −6.11 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)3CH(CH2)10COOCH3 | 6.95 | −6.55 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)2CH(CH2)11COOCH3 | 6.95 | −6.36 |
| H + CH3(CH2)14COOCH3 → H2 + CH3CH2CH(CH2)12COOCH3 | 6.97 | −6.43 |
| H + CH3(CH2)14COOCH3 → H2 + CH3CH(CH2)13COOCH3 | 7.05 | −6.78 |
| H + CH3(CH2)14COOCH3 → H2 + CH2(CH2)14COOCH3 | 9.70 | −4.11 |
| H + CH3(CH2)14COOCH3 → H2 + CH3(CH2)14COOCH2 | 10.36 | −5.61 |
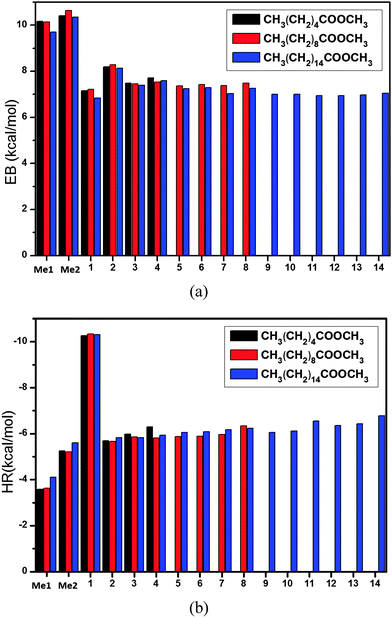 | ||
| Fig. 4 (a) The predicted energy barrier, EB[ONIOM/CAP(2,2)] and (b) the predicted heat of reaction, HR[ONIOM/CAP(2,2)], for the reactions CnH2n+1COOCmH2m+1 + H (n = 9, 15, m = 1) with various hydrogen abstraction sites (refer to Fig. 1). The reactions with (n = 5, m = 1) are shown for comparison. | ||
To the knowledge of the authors, no thermochemical or kinetics data for these large ester molecules are obtained using higher level theoretical methods, such as QCISD(T)/CBS or CCSD(T)/CBS. As a result, a direct validation of the calculated energy barriers and heats of reaction is not available in the literature. The consistent energies reported in Fig. 4 are believed to be reasonable and accurate because the ONIOM method has been extensively validated in the previous sections for smaller molecules.
It should be noted that the group additivity method combined with the Evans–Polanyi relations has been used in many studies to make reasonable estimations for the heats of reaction and energy barriers. However, the uncertainty of the estimations can be up to ±2.0 kcal mol−1,42 which is not satisfactory for high-level chemical kinetics, as discussed in the introduction. A linear correlation for the energy barriers (EB, kcal mol−1) and heats of reaction (HR, kcal mol−1), where EB = 0.844 × HR + 15.013, was found for the reactions CnH2n+1COOCH3 + H → CnH2n+1COOC·H2 + H2 (n = 0–5, 9, 15), and the Evans–Polanyi plot is shown in Fig. S2 in ESI.† Detailed investigation on the existence of linear Evans–Polanyi relations for other similar reactions of alkyl esters might benefit the future study. We believe that the present method is important as it provides accurate theoretical data for developing and validating group contribution based approaches for large molecules.
Another important issue for the present ONIOM method is the computational load. For the ONIOM[QCISD(T)/CBS:DFT] and QCISD(T)/CBS methods used in the present study, most of the computation time is spent on the QCISD(T)/cc-pVTZ calculation, as seen in Table S2 in ESI.† In the present ONIOM calculations with CAP(2,2) or CAP(2,3), the number of non-hydrogen atoms included in the high layer is 5–7, which does not necessarily increase with the size of molecules. Therefore, the computational load of the present ONIOM method remains to be equivalent to that of QCISD(T)/cc-pVTZ for a system containing 5–7 non-hydrogen atoms. Because the QCISD(T)/cc-pVTZ calculation for reactions containing more than 9 non-hydrogen atoms is generally not feasible, such reactions can be studied using the present ONIOM method.
Conclusion
An ONIOM[QCISD(T)/CBS:DFT] method was proposed and systematically validated in the present computational work for the hydrogen abstraction reactions of alkyl esters CnH2n+1COOCmH2m+1 (n = 1–5, 9, 15; m = 1, 2) by a hydrogen radical. Several important conclusions can be obtained from the work. First, the [QCISD(T)/CBS]2 method via an extrapolation from cc-pVDZ, cc-pVTZ to CBS with a MP2-based correction has been proved to be as accurate as the [QCISD(T)/CBS]1 method, whose computational uncertainty is usually about 1.0 kcal mol−1. Second, the use of the chemically active portion (CAP) in the ONIOM method, consisting of at least two main-chain C (or O) atoms (on each side) adjacent to the C atom whose H atom is under hydrogen abstraction, is minimally required to yield small computational errors of less than 0.1 kcal mol−1, compared with the [QCISD(T)/CBS]2 method. Third, the ONIOM method with a minimally required CAP is able to predict the energy barriers and heats of reaction for the studied reactions up to n = 5 with less than 0.1 kcal mol−1 uncertainty for almost all the tested cases. Finally, the predictions for n = 9 and 15 indicate that the energy barriers for hydrogen abstraction from the methyl groups are about 10 kcal mol−1, while they are 7 kcal mol−1 for the abstraction from the other sites. The predicted heats of reaction are about −4 kcal mol−1 for the hydrogen abstraction from the methyl group in the alkyl chain, −10 kcal mol−1 for that from the CH2 closest to the ester group, and −6 kcal mol−1 for the abstraction from other sites. The present method provides a computationally accurate and affordable approach to study the large hydrocarbons and alkyl esters that are of interest to combustion chemistry.Acknowledgements
This work was supported by the Hong Kong Research Grants Council/Early Career Scheme (operating under contract number PolyU 5380/13E) and the Shenzhen Science and Technology Innovation Council (SZSTI) (operating under contract number JCYJ20130401152508650). Lidong Zhang was partly supported by National Key Scientific Instruments and Equipment Development Program of China (2012YQ22011305) and Natural Science Foundation of China (21373193).References
- E. G. Giakoumis, C. D. Rakopoulos, A. M. Dimaratos and D. C. Rakopoulos, Prog. Energy Combust. Sci., 2012, 38, 691–715 CrossRef CAS PubMed.
- M. Lapuerta, O. Armas and J. Rodriguez-Fernandez, Prog. Energy Combust. Sci., 2008, 34, 198–223 CrossRef CAS PubMed.
- J. F. Sun, J. A. Caton and T. J. Jacobs, Prog. Energy Combust. Sci., 2010, 36, 677–695 CrossRef CAS PubMed.
- A. K. Agarwal, Prog. Energy Combust. Sci., 2007, 33, 233–271 CrossRef CAS PubMed.
- G. Knothe, Prog. Energy Combust. Sci., 2010, 36, 364–373 CrossRef CAS PubMed.
- K. Kohse-Hoinghaus, P. Osswald, T. A. Cool, T. Kasper, N. Hansen, F. Qi, C. K. Westbrook and P. R. Westmoreland, Angew. Chem., Int. Ed., 2010, 49, 3572–3597 CrossRef PubMed.
- A. C. Davis and J. S. Francisco, J. Am. Chem. Soc., 2011, 133, 19110–19124 CrossRef CAS PubMed.
- L. Coniglio, H. Bennadji, P. A. Glaude, O. Herbinet and F. Billaud, Prog. Energy Combust. Sci., 2013, 39, 340–382 CrossRef PubMed.
- E. Fisher, W. Pitz, H. Curran and C. Westbrook, Proc. Combust. Inst., 2000, 28, 1579–1586 CrossRef CAS.
- J. Y. W. Lai, K. C. Lin and A. Violi, Prog. Energy Combust. Sci., 2011, 37, 1–14 CrossRef CAS PubMed.
- C. V. Naik, C. K. Westbrook, O. Herbinet, W. J. Pitz and M. Mehl, Proc. Combust. Inst., 2011, 33, 383–389 CrossRef CAS PubMed.
- C. K. Westbrook, C. V. Naik, O. Herbinet, W. J. Pitz, M. Mehl, S. M. Sarathy and H. J. Curran, Combust. Flame, 2011, 158, 742–755 CrossRef CAS PubMed.
- S. Dooley, H. J. Curran and J. M. Simmie, Combust. Flame, 2008, 153, 2–32 CrossRef CAS PubMed.
- S. Gail, M. J. Thomson, S. M. Sarathy, S. A. Syed, P. Dagaut, P. Dievart, A. J. Marchese and F. L. Dryer, Proc. Combust. Inst., 2007, 31, 305–311 CrossRef PubMed.
- C. J. Hayes and D. R. Burgess, Proc. Combust. Inst., 2009, 32, 263–270 CrossRef CAS PubMed.
- W. K. Metcalfe, S. Dooley, H. J. Curran, J. M. Simmie, A. M. El-Nahas and M. V. Navarro, J. Phys. Chem. A, 2007, 111, 4001–4014 CrossRef CAS PubMed.
- B. Yang, C. K. Westbrook, T. A. Cool, N. Hansen and K. Kohse-Hoinghaus, Phys. Chem. Chem. Phys., 2011, 13, 6901–6913 RSC.
- P. Dievart, S. H. Won, S. Dooley, F. L. Dryer and Y. G. Ju, Combust. Flame, 2012, 159, 1793–1805 CrossRef CAS PubMed.
- O. Herbinet, W. J. Pitz and C. K. Westbrook, Combust. Flame, 2008, 154, 507–528 CrossRef CAS PubMed.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- A. Fernandez-Ramos, J. A. Miller, S. J. Klippenstein and D. G. Truhlar, Chem. Rev., 2006, 106, 4518–4584 CrossRef CAS PubMed.
- S. J. Klippenstein, V. S. Pande and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 528–546 CrossRef CAS PubMed.
- J. J. Zheng, P. Seal and D. G. Truhlar, Chem. Sci., 2013, 4, 200–212 RSC.
- J. J. Zheng, T. Yu, E. Papajak, I. M. Alecu, S. L. Mielke and D. G. Truhlar, Phys. Chem. Chem. Phys., 2011, 13, 10885–10907 RSC.
- T. Yu, J. J. Zheng and D. G. Truhlar, Chem. Sci., 2011, 2, 2199–2213 RSC.
- E. Papajak and D. G. Truhlar, J. Chem. Phys., 2012, 137, 064110 CrossRef PubMed.
- J. Zador, C. A. Taatjes and R. X. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421 CrossRef CAS PubMed.
- C. F. Goldsmith, G. R. Magoon and W. H. Green, J. Phys. Chem. A, 2012, 116, 9033–9057 CrossRef CAS PubMed.
- A. M. El-Nahas, M. V. Navarro, J. M. Simmie, J. W. Bozzelli, H. J. Curran, S. Dooley and W. Metcalfe, J. Phys. Chem. A, 2007, 111, 3727–3739 CrossRef CAS PubMed.
- A. Osmont, L. Catoire and I. Gokalp, Int. J. Chem. Kinet., 2007, 39, 481–491 CrossRef CAS.
- W. Liu, R. Sivaramakrishnan, M. J. Davis, S. Som, D. E. Longman and T. F. Lu, Proc. Combust. Inst., 2013, 34, 401–409 CrossRef CAS PubMed.
- A. Osmont, L. Catoire and P. Dagaut, J. Phys. Chem. A, 2010, 114, 3788–3795 CrossRef CAS PubMed.
- A. Osmont, M. Yahyaoui, L. Catoire, I. Gokalp and M. T. Swihart, Combust. Flame, 2008, 155, 334–342 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS PubMed.
- J. M. L. Martin and O. Uzan, Chem. Phys. Lett., 1998, 282, 16–24 CrossRef CAS.
- P. Zhang, S. J. Klippenstein and C. K. Law, J. Phys. Chem. A, 2013, 117, 1890–1906 CrossRef CAS PubMed.
- L. Zhang, Q. Chen and P. Zhang, Proc. Combust. Inst., 2014 DOI:10.1016/j.proci.2014.05.117.
- B. Akih-Kumgeh and J. M. Bergthorson, Combust. Flame, 2011, 158, 1037–1048 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized geometries at the B3LYP/6-311++G(d,p) level for all the stationary points on the potential energy surfaces. See DOI: 10.1039/c4cp03004d |
| This journal is © the Owner Societies 2015 |