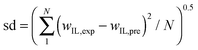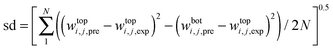Influence of process variables on extraction of Cefalexin in a novel biocompatible ionic liquid based-aqueous two phase system†
Received
3rd July 2014
, Accepted 6th November 2014
First published on 7th November 2014
Abstract
Despite the fact that ionic liquid-based aqueous two phase systems (ATPSs) have been widely studied for extraction purposes, the adequacy of biodegradable organic salts as salting out agents has been left unexploited. In this study, we investigated the ability of sodium-based organic salts in the formation of ATPS in the presence of a common ionic liquid, [C4mim]BF4. In the pioneering aspect of this work, Response Surface Methodology (RSM) based on three-variable central composite design (CCD) was employed for determination of the effect of pH and the initial concentration of phase components on the partition coefficient of Cefalexin. Consequently, regression model equations and contour plots were applied to evaluate the effect of system's parameters on biomolecule's extraction. The tie-line (TL) data were determined for each experimental run and their reliability was confirmed by Othmer–Tobias and Bancroft correlations. In order to investigate the salting-out ability the effective excluded volume (EEV) was determined from the binodal data. Furthermore, FTIR spectra confirmed no chemical interactions between Cefalexin and [C4mim]BF4 in the extraction process. The microscopic structure of the top phase was analyzed by DLS, conductivity and TEM in order to investigate the mechanism of extraction. Hydrophobic interaction, the salting-out effect and the aggregation phenomena played the dominant role in the study of the extraction process.
1. Introduction
The growing demand for pure biotechnologically manufactured chemicals has made that their separation and purification are of great industrial importance. Furthermore, production costs are entirely related to the underlying separation process. Liquid–liquid extraction techniques propose some unique features suitable for bioseparation. Among those high yields, improved selectivity, high effectiveness, and a high purity degree are worth noting.1 Regarding the fact that most biomolecules of interest are manufactured in aqueous media, organic solvents have been widely used for purification purposes. Consequently, their high volatility and toxicity impose some hazardous effects on the environment. As a result, the improvements of new and “greener” separation techniques have been an interesting research platform in the past few decades.1 In the mid-1950's, Albertsson introduced “Aqueous Two Phase System” (ATPS) as a novel method replacing the conventional liquid–liquid extraction technique.2 The ATPS is mostly composed of two immiscible aqueous-rich phases which are mainly formed by the addition of structurally different polymers, a polymer and a salt, or two salts.1,3 Since the bulk of both phases is mainly composed of water, ATPSs provide gentle and compatible media for biomolecules.2–4 Moreover, as the two immiscible phases possess some unique physical and chemical properties, the biomolecules are favourably partitioned between phases. Accordingly, since the pioneering work of Albertsson,5 polymer-based ATPSs have been broadly applied to the recovery and purification of biomolecules.6–11
The innovative research work of Rogers and co-workers in 2003 proposed a novel system of Ionic Liquid (IL) – inorganic salt for the formation of ATPSs.12 The distinct physical and chemical properties of ILs such as non-flammability, tunability, negligible vapor pressure, high selectivity, and a large liquid range make them a reliable choice for industrial application.1,2 Consequently, their negligible volatility and non-flammability characterize them under the common “green solvents” group. Recently, a large set of literature has been aimed for applications of ILs as viable alternatives to polymer based ATPSs.13–18 The major favourable aspect of IL-based over polymer-based ATPSs is the possibility of tailoring their polarities by a suitable manipulation of cation–anion combinations.3
Nonetheless, a large number of studies have applied inorganic salts based on phosphate, sulphates, and carbonate anions19–22 as the salting-out agents in ATPS formation. However, high concentration discharges of these salts in the effluent streams propose some hazardous environmental concerns. As a result, recent research studies have focused on the application of biodegradable organic salts such as tartrate-, citrate-, or acetate-based organic salts as salting out agents.17,23–28
Conventional methods of studying a process, besides being time consuming and requiring a large number of experiments, involve maintaining other factors at an unspecified constant level; therefore, the interaction among the variables is not studied.29,30 Thus, in order to eliminate the limitations of conventional methods a statistical experimental design such as RSM is developed. RSM is a useful tool for developing, improving and optimizing processes while evaluating the significance of several affecting parameters. Also, it enables us to study the interaction among the variables even in the presence of complex interactions.
Considering the fact that organic salts are biodegradable and they are scarcely studied, we investigated salting-out ability of some sodium-based organic salts as a novel alternative in the presence of a common ionic liquid. In addition, Cefalexin was the selected biomolecule to prove the applicability of these systems for extraction purposes. Feed initial ionic liquid and organic salt's concentrations along with its pH are important parameters affecting biomolecule's partitioning in IL-based ATPSs. Many research studies have combined the conductivity, DLS and TEM to investigate the microstructure of ATPSs and the possible mechanism for the extraction.31–36 Recently, TEM was used to characterize the appearance of aggregates in aqueous solution of various ILs.35,36 Also, the possible mechanisms for biomolecule's extraction have been related to microstructure of the IL-rich phase. Thus, in the present study, capacity of IL–organic salt ATPS in partitioning of Cefalexin was investigated by varying these factors using face centred CCD method. Interactions among these factors were investigated and regression equations were evaluated. In addition, FTIR, DLS, conductivity and TEM were employed to study the mechanism of the extraction process.
2. Materials and methods
2.1. Materials
The detailed properties of all the materials used in this work are presented in Table 1. The chemicals were used without further purification and doubled distilled deionized water was used to prepare the samples.
Table 1 Detailed properties of studied materials
| Material |
Chemical formula |
Molar mass (g mol−1) |
Source |
Chemical structure |
Abbreviations |
| 1-Butyl-3-methylimidazolium tetrafluoroborate |
C8H15BF4N2 |
226.02 |
Synthesized |

|
[C4mim]BF4 |
| Tri-sodium citrate-5,5-hydrate |
C6H5Na3O7·5,5H2O |
357.16 |
Merck millipore |

|
Na3Citrate |
| Di-sodium tartrate dihydrate |
C4H4Na2O6·2H2O |
230.08 |
Merck millipore |

|
Na2Tartrate |
| Di-sodium fumarate |
C4H2Na2O4 |
160.04 |
Merck millipore |

|
Na2Fumarate |
| Di-sodium succinate hexahydrate |
C4H4Na2O4·6H2O |
270.15 |
Merck millipore |

|
Na2Succinate |
| Cefalexin |
C16H17N3O4S |
347.39 |
Jaber Ebne Hayyan company |

|
|
2.2. Experimental procedure
2.2.1. Phase diagrams.
Visual determination of cloud points has been employed in most research studies for determination of the binodal curve.7–27 Hence, the phase diagrams were determined by employing the cloud point titration method at 25 ± 1 °C and atmospheric pressure. Aqueous solution of tri-sodium citrate 5,5-hydrate at 40 wt%, di-sodium tartrate dihydrate, disodium succinate hexahydrate, and disodium fumarate at 25 wt%; and [C4mim]BF4 at 80 wt% were prepared and used for determination of the binodal curves.
The experimental procedure consists of two steps: (i) drop-wise addition of each aqueous organic salt solution to ionic liquid's aqueous solution until the detection of a cloudy (biphasic) solution; (ii) drop-wise addition of ultra-pure water until the formation of a monophasic region (limpid solution). The systems' compositions at each point were determined by weight quantification within ±10−4 g. In order to complete the phase diagrams, ionic liquid's aqueous solution was also added to the salt solutions.
The experimental binodal curves were fitted to the following four-parameter equation:3
| | | [IL] = exp(A + B[salt]0.5 + C[salt] + D[salt]2) | (1) |
where [IL] and [salt] are mass fraction percentage of the ionic liquid and organic salts, respectively, and
A,
B,
C, and
D are fitting parameters obtained by data regression.
2.2.2. Determination of TLs.
Merchuk et al.37 initially introduced a gravimetric method for determination of TLs of polymer-based ATPSs. Later, Rogers and co-workers12 successfully employed this method for IL-based ATPSs. In this method, binodal data by eqn (1) are coupled with mass balance relationships, thus compositions of the top and bottom phases are determined by the lever-arm rule. Therefore, for each TL, the following system of four equations and four unknown values (which correspond to [IL]top, [IL]bot, [salt]top, [salt]bot) was solved:| | | [IL]top = exp(A + B[salt]top0.5 + C[salt]top + D[salt]top2) | (2) |
| | | [IL]bot = exp(A + B[salt]bot0.5 + C[salt]bot + D[salt]bot2) | (3) |
| |  | (4) |
| |  | (5) |
where subscripts “top”, “bot”, and “M” refer to the top-phase, the bottom-phase and the mixture, respectively; [IL] and [salt] designate mass fraction percentage of ionic liquid and salt in the solution. Furthermore, α is known to be the ratio between the mass of the top phase and the total mass of the mixture.
The tie-line lengths (TLL) and the slope of TLs (STL) were calculated by the following equations:
| |  | (6) |
| |  | (7) |
2.2.3. DOE.
The classical and conventional methods of studying a process are carried out by varying a single factor while maintaining all the other factors at an unspecified constant level. These methods, besides being time consuming and requiring a large number of experiments, do not give a combined effect of process variables.29 Moreover, they require a large number of experiments to evaluate optimum levels while they are incapable of effective optimization. Considering the limitations of conventional methods, a statistical experimental design such as RSM, which optimizes all the affecting parameters, can be promising.29,38
RSM is a collection of statistical and mathematical techniques which evaluates the regression models and determines the effect of variables even in the presence of complex interactions.39,40 The main objective of RSM is evaluation of the optimum operational conditions for the system or determination of a region that satisfies the desired specifications.29,39 CCD is a well known standard RSM design; which we applied in this work to study the variables that affect the partitioning of the Cefalexin. Generally, the CCD consists of 2n axial runs with 2n full factorial runs and also nc replicates at the center points. The center point replicates are a reliable indication of precision properties and experimental error; moreover, they prove reproducibility of the data.
A central composite face centered design was employed in order to investigate the effect of different parameters of the system on the partitioning of Cefalexin in IL–organic salt ATPSs. The independent variables selected in this study were (i) X1: initial pH of the feed; (ii) X2: organic salt's mass fraction percentage in the feed; (iii) X3: IL's mass fraction percentage in the feed and the partitioning coefficient of Cefalexin (eqn (8)) were dependent on the output response variable.
| |  | (8) |
where [Cef.]
IL is the concentration of Cefalexin in the IL-rich phase and [Cef.]
salt is its respective concentration in the organic salt-rich phase. Moreover, the extraction efficiency for Cefalexin enrichment is determined in accordance with
eqn (9):
| | 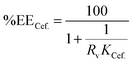 | (9) |
where
Rv is the phase volume ratio which is determined by dividing the volume of the top phase to that of the bottom phase.
Thus 23 full factorial CCD for 3 variables, 2 × 3 axial points and 2 replicates at the center points were employed resulting 16 as the total number of experiments.
The independent variables, Xi, are coded as xi, according to the following relationship:
| |  | (10) |
where
xi is the coded value of
ith independent variable,
Xi the natural value of
ith independent variable,
X0 the natural value of the
ith independent variable at the center point, and ∂
X is the value of step.
Table 2 shows independent variables and their coded and uncoded levels for all investigated organic salt–IL ATPSs. Moreover, this table manifests the fact that for each organic salt the feed's mass fraction percentage varies as the binodal changes.
Table 2 Experimental range and levels of independent process variables for Cefalexin extraction in IL-based ATPSs
| Independent variables |
Ranges and levels |
| Na3Citrate |
Na2Tartrate |
Na2Fumarate |
| (−1) |
(0) |
(+1) |
(−1) |
(0) |
(+1) |
(−1) |
(0) |
(+1) |
| pH (X1) |
4.5 |
5.5 |
6.5 |
4.8 |
5.5 |
6.2 |
4.5 |
5.5 |
6.5 |
| Organic salt (wt%) (X2) |
12 |
13.5 |
15 |
6.8 |
7.4 |
8 |
5 |
5.5 |
6 |
| [C4mim]BF4 (wt%) (X3) |
15 |
17.5 |
20 |
22 |
24 |
26 |
27 |
29.5 |
32 |
An empirical model, which is a mathematical relationship between the response and the independent variables, is of great importance in the study of a process. Each set of responses is used to develop an empirical model using a second degree polynomial equation; as given by the following equation:
| |  | (11) |
where
Y is the predicted response,
b0 the constant coefficient,
bi the linear coefficients,
bii the quadratic coefficients,
bij the interaction coefficients and
xi,
xj are the coded values of independent process variables.
Table 3 demonstrates the complete design matrix of the performed experiments. The IL-based ATPS was prepared by mixing an appropriate amount of [C4mim]BF4 and organic salts to get the required composition in the DOE table. Moreover, a suitable amount of Cefalexin was added to get the concentration of 0.01 g mL−1. All mixtures were gravimetrically prepared within ±10−4 g. Sulfuric acid and Sodium hydroxide were used to adjust the pH of aqueous solutions to the desired values. Consequently, the prepared mixtures were vigorously stirred and kept in small decanters for 48 h for complete phase separation. In order to eliminate the effect of temperature, all samples were incubated at 25 ± 1 °C. Additionally, the same mass fraction percentages were used for TL determination.
Table 3 CCD design matrix along with experimental and predicted response values
| Std order |
x
1
|
x
2
|
x
3
|
Partitioning coefficient |
| Na3Citrate |
Na2Tartrate |
Na2Fumarate |
| Experimental |
Predicted |
Experimental |
Predicted |
Experimental |
Predicted |
| 1 |
−1 |
−1 |
−1 |
1.2579 |
1.3210 |
1.6363 |
1.5810 |
2.7073 |
2.5230 |
| 2 |
1 |
−1 |
−1 |
1.1444 |
1.1490 |
2.0948 |
2.1410 |
2.6236 |
2.4350 |
| 3 |
−1 |
1 |
−1 |
2.0082 |
1.9410 |
3.4852 |
3.5390 |
3.3157 |
3.3210 |
| 4 |
1 |
1 |
−1 |
1.4943 |
1.5490 |
3.2746 |
3.2990 |
3.0301 |
3.0410 |
| 5 |
−1 |
−1 |
1 |
2.5911 |
2.5090 |
2.6632 |
2.6990 |
3.4714 |
3.4610 |
| 6 |
1 |
−1 |
1 |
2.1005 |
2.1410 |
2.2545 |
2.2590 |
3.1052 |
3.1010 |
| 7 |
−1 |
1 |
1 |
2.8585 |
2.8290 |
4.3 |
4.3010 |
3.8688 |
4.0550 |
| 8 |
1 |
1 |
1 |
2.3316 |
2.2410 |
2.9375 |
3.0610 |
3.3181 |
3.5030 |
| 9 |
−1 |
0 |
0 |
1.5850 |
1.7100 |
3.0061 |
2.9900 |
3.2191 |
3.2100 |
| 10 |
1 |
0 |
0 |
1.3774 |
1.3300 |
2.7882 |
2.6500 |
2.8817 |
2.8900 |
| 11 |
0 |
−1 |
0 |
1.7224 |
1.6800 |
2.2696 |
2.2900 |
3.1722 |
3.5300 |
| 12 |
0 |
1 |
0 |
1.9187 |
2.0400 |
3.8412 |
3.6700 |
4.5 |
4.1300 |
| 13 |
0 |
0 |
−1 |
1.6015 |
1.5100 |
2.2031 |
2.2000 |
4.0882 |
4.4500 |
| 14 |
0 |
0 |
1 |
2.2878 |
2.4500 |
2.7857 |
2.6400 |
5.5232 |
5.1500 |
| 15 |
0 |
0 |
0 |
1.7922 |
1.7000 |
2.5229 |
2.6800 |
4.2131 |
4.2500 |
| 16 |
0 |
0 |
0 |
1.7835 |
1.7000 |
2.5114 |
2.6800 |
4.275 |
4.2500 |
The regression and graphical analysis were performed by MINITAB 16 statistical software.
2.3. Analytical techniques
2.3.1. UV spectroscopy.
UV spectroscopy was employed in order to determine the concentration of Cefalexin in each phase after establishment of equilibrium. In order to obtain the wavelength corresponding to the maximum absorbance (λmax), a standard solution of the Cefalexin was taken and the absorbance was determined at different wavelengths using a UV-Vis spectrophotometer (Jasco V-550). The plotted graph of absorbance versus wavelengths indicated λmax to be equal to 261 nm. Slight interferences of the organic salts and the ionic liquid in the quantification of Cefalexin were verified. Furthermore, in order to avoid such interferences, all samples were analyzed against blanks which have the same composition but lack antibiotic.
2.3.2. FTIR analysis.
The surface functional group of the samples was confirmed using a Fourier Transform Infrared (FTIR) spectroscope (Nexus 670-FTIR ESP). Accordingly, FT-IR spectra of pure Cefalexin, pure IL, and Cefalexin in the IL-rich top phase were recorded in the absorption range of 4000 to 400 cm−1.
2.3.3. Conductivity, DLS and TEM.
Electrical conductivity was measured using a WTW Cond 3110 (Germany) at 25 ± 1 °C. Conductivity of different concentrations of IL solution was recorded when its stability was better than 1% within 2 min intervals.
The Dynamic Light Scattering (DLS) method is a technique for measuring particle size typically in the sub micron region. Thus, DLS of pure aqueous solution of the Cefalexin, IL rich top phase without Cefalexin and Cefalexin in the IL rich top phase have been recorded. We analyzed the samples by ZEN 3600 DLS (Malvern, UK). The measurements were performed at 25 ± 1 °C.
Moreover, the microscopic structures of the samples were analyzed using Zeiss (Germany, 100 kV). Consequently, a small drop of each sample solutions was dripped on a copper grid. After application of a filter paper to remove the excess liquid, the samples were dried and imaged under vacuum conditions.
3. Results and discussion
3.1. Phase diagrams
As all the novel ATPSs share the same ionic liquid and the pressure and temperatures are also common, the comparison of the data leads to the evaluation of the effect of the organic salts on ATPS creation. All the studied organic salts were able to create ATPSs with [C4mim]BF4. The experimental phase diagrams of the ternary phase systems composed of [C4mim]BF4 + organic salt + water are depicted in Fig. 1. The complete experimental weight fraction data of the ternary systems are lengthy and they are presented in the ESI.† In order to compare the salting-out behaviour of organic and inorganic salts some experimental studies were conducted and the results are plotted in Fig. 2. In order to avoid the influence of the divergences that could be a mere result of different molecular weight of salts, Fig. 2 is presented in molality units (Fig. 2). In all phase diagrams, the biphasic region is above the saturation curve. As a result, as the curve gets closer to the axes the biphasic area is expanded and consequently liquid–liquid demixing is facilitated i.e., ionic liquid is more easily salted out by sodium-based organic salts. As can be observed, the salting-out ability of organic and inorganic salts is comparable and in some cases organic salts are more effective for liquid–liquid demixing. We found the salting out ability of organic salts in the order: C6H5O7−3 > C4H4O4−2 > C4H4O6−2 > C4H2O4−2. This observation is justified by the fact that ion charge plays a significant role as the trivalent anion has stronger salting out ability than the divalent ones.
 |
| | Fig. 1 Evaluation of the organic salts' effects in the ternary phase diagrams composed of [C4mim]BF4 + sodium based organic salt + H2O:  , Na3Citrate; , Na3Citrate;  , Na2Succinate; , Na2Succinate;  , Na2Tartrate; and , Na2Tartrate; and  , Na2Fumarate. , Na2Fumarate. | |
 |
| | Fig. 2 Ternary phase diagrams of [C4mim]BF4 + sodium based organic salt + H2O at 298 K and atmospheric pressure in molality units:  , Na3Citrate; , Na3Citrate;  , Na3Phosphate; , Na3Phosphate;  , Na2Succinate; , Na2Succinate;  , Na2Tartrate; +, Na2Carbonate and , Na2Tartrate; +, Na2Carbonate and  , Na2Fumarate. , Na2Fumarate. | |
The salting-out inducing ions are also called “Kosmotropes” due to their ability to create water bulk structure.41–43 However, recent studies question the fact that the change in the bulk water structure is the main influencing effect. Evidence through recent studies suggests the presence of interactions between IL and salt ions. Salting-out inducing ions act primarily through an entropic effect due to the creation of hydration complexes which subsequently cause the dehydration of the solute and the increase in the cavity's surface tension.44–46
Nonlinear regression of the experimental phase diagrams derived the parameters of eqn (1), as well as the corresponding correlation coefficients and standard deviations (Table 4). As it can be observed by the R2-value, it is reasonable to confirm the adequacy of eqn (1) in describing the experimental data.
Table 4 Values of parameters (A, B, C and D) of eqn (1) for the IL-based ATPSs at T = 298.15 K
| Biphasic system |
A
|
B
|
C
|
D
|
R
2
|
100sd |
 , ,  ; wIL,exp = experimental IL wt% and wIL,pre = predicted IL wt%. ; wIL,exp = experimental IL wt% and wIL,pre = predicted IL wt%. |
| [C4mim]BF4 + Na3Citrate |
4.6639 |
−0.6436 |
0.0038 |
0.0005 |
0.9989 |
0.874 |
| [C4mim]BF4 + Na2Tartrate |
5.2551 |
−1.3296 |
0.1800 |
−0.0013 |
0.9998 |
0.408 |
| [C4mim]BF4 + Na2Fumarate |
5.3437 |
−1.3094 |
0.1613 |
−0.00095 |
0.9995 |
0.754 |
| [C4mim]BF4 + Na2Succinate |
4.1639 |
−0.2097 |
−0.1707 |
0.0094 |
0.9998 |
0.597 |
3.2. Effective excluded volume and salting-out ability
In 1993, Guan et al.47 proposed a binodal model based on the statistical geometry methods for aqueous solution of polymers. Their theory is based on the concept that any molecular species in a solution is distributed randomly, and thus every system composition along the binodal curve is geometrically saturated solution of each solute in the presence of other.48 In this work, the binodal curves of [C4mim]BF4-organic salts were correlated based on EEV theory for evaluation of the salting-out ability of the organic salts. For the ternary system of IL (1) + organic salt (2) + water (3), the excluded volume theory can be stated by two equations:48| |  | (12) |
| |  | (13) |
where V213*, f213, M1, and M2 are the scaled EEV of organic salt, the volume fraction of unfilled effective available volume after tight packing of salt molecules into the network of [C4mim]BF4, and molecular weight of IL and organic salt, respectively.
The EEV value indicates the compatibility of the components in the system as it represents the smallest space at which each IL molecule will accept an individual salt. The correlation of the experimental binodal data gives the value of EEV and f213 (Table 5). We observed a negligible value for f213 which is due to the size differences between the components. In many experimental studies49,50 the salting-out strength of the salts has been related to EEV. Thus, it is reasonable to conclude that the organic salts with larger values of EEV are stronger salting-out agents. Consequently, the rank order of C6H5O7−3 > C4H4O4−2 > C4H4O6−2 > C4H2O4−2 manifests the ability of anions to create a biphasic region.
Table 5 Values of parameters of EEV of salts using eqn (12) or (13) for the [C4mim]BF4 (1) + salt (2) + water (3) ATPS at T = 298.15 K
| Salt |
V
213* |
f
213
|
R
2
|
100sd |
 ; ; 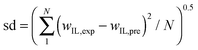 , wIL,exp = experimental IL wt% and wIL,pre = predicted IL wt%. , wIL,exp = experimental IL wt% and wIL,pre = predicted IL wt%. |
| Na3Citrate |
14.054 |
|
0.997 |
0.248 |
| Na2Succinate |
13.800 |
0.012 |
0.993 |
0.130 |
| Na2Tartrate |
12.459 |
|
0.997 |
0.223 |
| Na2Fumarate |
10.445 |
|
0.998 |
0.131 |
| Na3Phosphate |
12.912 |
|
0.954 |
0.352 |
3.3. TL data and correlations
The TL data were obtained for each experimental run in the DOE table. Consequently, upper phase and lower phase compositions along with TLL and STL were determined with variation of independent variables at fixed temperature. For most systems, the concentration of [C4mim]BF4 in the lower phase was fairly small. However, the same behaviour was not observed in the top phase.
The TL compositions were evaluated by employing a gravimetric method along with solution of a system of four equations and four unknowns. We present the resulting TL compositions in Tables 6–8. Moreover, Othmer–Tobias51 and Bancroft52 correlations have been applied for assessment of TLs for [C4mim]BF4-organic salt ATPSs:
| |  | (14) |
| |  | (15) |
Where
a,
b,
c and
d are adjustable parameters which can be calculated from the intercept and the slope of the plotted linear relationships. The values of the adjustable parameters as a function of pH with corresponding correlation coefficients and standard deviations are presented in
Table 9. On the basis of reported
R2-values in
Table 9, it can be concluded that these correlations can be satisfactorily used to correlate the TLs data.
Table 6 Weight fraction percentage (wt%) obtained by DOE for the coexisting phases of [C4mim]BF4 (1) + Na3Citrate (2) + H2O along with their respective values of STL and TLL
| pH |
Std order |
Feed |
Top phase |
Bottom phase |
α
|
STL |
TLL |
|
w
1
|
w
2
|
w
1
|
w
2
|
w
1
|
w
2
|
| Standard uncertainties u are u(w) = 0.0001 and u(T) = 1 K and u(pH) = 0.01. |
| 4.5 |
1 |
15 |
12 |
16.0549 |
9.4245 |
5.506 |
35.1795 |
0.8975 |
−0.405 |
27.831 |
| 3 |
15 |
15 |
17.7161 |
8.3735 |
5.398 |
38.4258 |
0.7795 |
−0.409 |
32.478 |
| 5 |
20 |
12 |
23.1375 |
5.9165 |
5.3845 |
40.3388 |
0.8232 |
−0.515 |
38.730 |
| 7 |
20 |
15 |
25.1031 |
5.2683 |
5.4196 |
42.8053 |
0.7407 |
−0.524 |
42.384 |
| 9 |
17.5 |
13.5 |
20.5086 |
6.9601 |
5.3846 |
39.836 |
0.8010 |
−0.460 |
36.187 |
|
|
| 5.5 |
11 |
17.5 |
12 |
19.3427 |
7.5051 |
5.3942 |
41.5305 |
0.8678 |
−0.409 |
36.773 |
| 12 |
17.5 |
15 |
21.1086 |
6.701 |
5.419 |
42.7835 |
0.7864 |
−0.434 |
39.346 |
| 13 |
15 |
13.5 |
16.6324 |
9.0374 |
5.3847 |
39.7851 |
0.8548 |
−0.365 |
32.740 |
| 14 |
20 |
13.5 |
23.7319 |
5.7101 |
5.4527 |
43.866 |
0.7958 |
−0.479 |
42.308 |
| 15 |
17.5 |
13.5 |
20.137 |
7.1275 |
5.4169 |
42.6993 |
0.8208 |
−0.413 |
38.497 |
| 16 |
17.5 |
13.5 |
20.1197 |
7.1354 |
5.4207 |
42.8463 |
0.8217 |
−0.411 |
38.617 |
|
|
| 6.5 |
2 |
15 |
12 |
16.1602 |
9.352 |
5.6126 |
33.4247 |
0.8754 |
−0.438 |
26.282 |
| 4 |
15 |
15 |
18.1077 |
8.1515 |
5.4679 |
36.0063 |
0.7541 |
−0.453 |
30.588 |
| 6 |
20 |
12 |
23.3109 |
5.8553 |
5.389 |
39.1163 |
0.8152 |
−0.538 |
37.782 |
| 8 |
20 |
15 |
25.3865 |
5.1825 |
5.3954 |
41.6186 |
0.7305 |
−0.548 |
41.56 |
| 10 |
17.5 |
13.5 |
20.7084 |
6.8723 |
5.3968 |
38.5021 |
0.7904 |
−0.484 |
35.140 |
Table 7 Weight fraction percentage (wt%) obtained by DOE for the coexisting phases of [C4mim]BF4 (1) + Na2Tartrate (2) + H2O along with their respective values of STL and TLL
| pH |
Std order |
Feed |
Top phase |
Bottom phase |
α
|
STL |
TLL |
|
w
1
|
w
2
|
w
1
|
w
2
|
w
1
|
w
2
|
| Standard uncertainties u are u(w) = 0.0001 and u(T) = 1 K and u(pH) = 0.01. |
| 4.8 |
1 |
22 |
6.8 |
23.0451 |
5.0942 |
9.4431 |
27.2947 |
0.9231 |
−0.612 |
26.036 |
| 3 |
22 |
8 |
24.0593 |
4.7687 |
9.342 |
27.8621 |
0.8600 |
−0.637 |
27.384 |
| 5 |
26 |
6.8 |
28.3082 |
3.7158 |
9.0614 |
29.4337 |
0.8800 |
−0.748 |
32.122 |
| 7 |
26 |
8 |
29.3371 |
3.5164 |
8.7448 |
31.1835 |
0.8379 |
−0.744 |
34.489 |
| 9 |
24 |
7.4 |
26.2102 |
4.1825 |
9.1308 |
29.0458 |
0.8705 |
−0.686 |
30.164 |
|
|
| 5.5 |
11 |
24 |
6.8 |
25.4185 |
4.3838 |
8.3084 |
33.5292 |
0.9170 |
−0.587 |
33.796 |
| 12 |
24 |
8 |
26.2262 |
4.1786 |
7.9018 |
35.6336 |
0.8785 |
−0.582 |
36.403 |
| 13 |
22 |
7.4 |
23.3192 |
5.0026 |
8.6608 |
31.6415 |
0.9100 |
−0.550 |
30.405 |
| 14 |
26 |
7.4 |
28.2476 |
3.7281 |
7.5046 |
37.6164 |
0.8916 |
−0.612 |
39.732 |
| 15 |
24 |
7.4 |
25.8141 |
4.2813 |
8.0661 |
34.7928 |
0.8977 |
−0.581 |
35.297 |
| 16 |
24 |
7.4 |
25.8822 |
4.2637 |
8.308 |
33.5312 |
0.8928 |
−0.600 |
34.139 |
|
|
| 6.2 |
2 |
22 |
6.8 |
23.2153 |
5.037 |
10.0035 |
24.2024 |
0.9080 |
−0.689 |
23.277 |
| 4 |
22 |
8 |
24.2421 |
4.7137 |
9.6589 |
26.0885 |
0.8462 |
−0.682 |
25.875 |
| 6 |
26 |
6.8 |
28.5012 |
3.677 |
9.2612 |
28.3153 |
0.8690 |
−0.780 |
31.260 |
| 8 |
26 |
8 |
29.4186 |
3.5013 |
8.8589 |
30.5567 |
0.8337 |
−0.759 |
33.980 |
| 10 |
24 |
7.4 |
26.373 |
4.143 |
9.423 |
27.402 |
0.8607 |
−0.728 |
28.784 |
Table 8 Weight fraction percentage (wt%) obtained by DOE for the coexisting phases of [C4mim]BF4 (1) + Na2Fumarate (2) + H2O along with their respective values of STL and TLL
| pH |
Std order |
Feed |
Top phase |
Bottom phase |
α
|
STL |
TLL |
|
w
1
|
w
2
|
w
1
|
w
2
|
w
1
|
w
2
|
| Standard uncertainties u are u(w) = 0.0001 and u(T) = 1 K and u(pH) = 0.01. |
| 4.5 |
1 |
27 |
5 |
28.3306 |
4.0648 |
11.5784 |
15.8385 |
0.9205 |
−1.422 |
20.475 |
| 3 |
27 |
6 |
30.4305 |
3.6657 |
11.2603 |
16.7101 |
0.8210 |
−1.469 |
23.187 |
| 5 |
32 |
5 |
35.4845 |
2.9208 |
10.9888 |
17.5371 |
0.8577 |
−1.675 |
28.525 |
| 7 |
32 |
6 |
37.7968 |
2.6536 |
10.7743 |
18.2533 |
0.7854 |
−1.732 |
31.202 |
| 9 |
29.5 |
5.5 |
33.0055 |
3.2542 |
11.0593 |
17.3144 |
0.8402 |
−1.560 |
26.063 |
|
|
| 5.5 |
11 |
29.5 |
5 |
31.5048 |
3.4848 |
10.4687 |
19.3842 |
0.9046 |
−1.323 |
26.368 |
| 12 |
29.5 |
6 |
33.3085 |
3.2104 |
10.3022 |
20.0617 |
0.8344 |
−1.362 |
28.517 |
| 13 |
27 |
5.5 |
28.9235 |
3.9454 |
10.6438 |
18.7194 |
0.8947 |
−1.237 |
23.503 |
| 14 |
32 |
5.5 |
35.7616 |
2.8868 |
10.1616 |
20.6713 |
0.8530 |
−1.439 |
31.171 |
| 15 |
29.5 |
5.5 |
32.3704 |
3.3488 |
10.3531 |
19.8495 |
0.8696 |
−1.334 |
27.514 |
| 16 |
29.5 |
5.5 |
32.3699 |
3.3489 |
10.3526 |
19.8518 |
0.8696 |
−1.334 |
27.515 |
|
|
| 6.5 |
2 |
27 |
5 |
28.1891 |
4.0942 |
11.1334 |
17.0862 |
0.9302 |
−1.312 |
21.440 |
| 4 |
27 |
6 |
30.0848 |
3.727 |
10.8559 |
17.8733 |
0.8393 |
−1.357 |
23.847 |
| 6 |
32 |
5 |
35.1759 |
2.9595 |
10.6431 |
18.7221 |
0.8705 |
−1.556 |
29.160 |
| 8 |
32 |
6 |
37.4017 |
2.6967 |
10.5351 |
19.1265 |
0.7989 |
−1.635 |
31.492 |
| 10 |
29.5 |
5.5 |
32.7427 |
3.2928 |
10.777 |
18.244 |
0.8523 |
−1.469 |
26.571 |
Table 9 Parameters of Othmer–Tobias and Bancroft equations along with their correlation coefficients R2 and standard deviations (sd)
| Biphasic system |
pH |
Othmer–Tobias |
Bancroft |
100sd1 |
100sd2 |
|
a
|
b
|
R
2
|
c
|
d
|
R
2
|
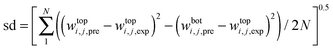 , where N is the number of TLs and j = 1 and j = 2, sd1 and sd2 the mass fraction standard deviation for IL and salt, respectively. , where N is the number of TLs and j = 1 and j = 2, sd1 and sd2 the mass fraction standard deviation for IL and salt, respectively. |
| [C4mim]BF4 + Na3Citrate |
4.5 |
0.557 |
1.862 |
0.906 |
−0.355 |
0.547 |
0.906 |
1.325 |
3.209 |
| 5.5 |
0.636 |
2.379 |
0.916 |
−0.352 |
0.444 |
0.915 |
0.776 |
1.938 |
| 6.5 |
0.504 |
1.689 |
0.964 |
−0.391 |
0.636 |
0.964 |
1.037 |
1.747 |
|
|
| [C4mim]BF4 + Na2Tartrate |
4.8 |
−0.600 |
1.826 |
0.921 |
0.246 |
0.523 |
0.921 |
0.919 |
1.551 |
| 5.5 |
0.497 |
0.868 |
0.909 |
−0.562 |
1.077 |
0.910 |
1.023 |
1.190 |
| 6.2 |
−0.052 |
1.104 |
0.931 |
−0.009 |
0.876 |
0.931 |
1.314 |
1.467 |
|
|
| [C4mim]BF4 + Na2Fumarate |
4.5 |
−3.417 |
2.617 |
0.959 |
1.192 |
0.364 |
0.959 |
0.742 |
1.294 |
| 5.5 |
−2.683 |
2.440 |
0.982 |
0.984 |
0.406 |
0.982 |
0.310 |
0.557 |
| 6.5 |
−3.994 |
3.14 |
0.967 |
1.153 |
0.308 |
0.967 |
0.585 |
1.160 |
3.3.1. Effect of pH on TLs.
Fig. 3 illustrates the effect of pH on the TLLs and STLs at the center points of initial concentration of [C4mim]BF4 and organic salts.
 |
| | Fig. 3 Effect of pH on TLLs and STLs in the center point of IL and organic salt initial concentration in the DOE table. TTL:  , Na3Citrate; , Na3Citrate;  , Na2Tartrate; and , Na2Tartrate; and  , Na2Fumarate. SLL: , Na2Fumarate. SLL:  , Na3Citrate; , Na3Citrate;  , Na2Tartrate; and , Na2Tartrate; and  , Na2Fumarate. , Na2Fumarate. | |
It is obvious that the ternary system of [C4mim]BF4 + Na3Citrate + water and [C4mim]BF4 + Na2Tartrate + water possesses the same behaviour. In these systems, the absolute values of STLs increase in the following order (in coded values): pH = 0 < pH = −1 < pH = +1. Consequently, by changing the pH in this manner the water is driven from the IL-rich phase to the salt-rich phase. However, in the ternary system of [C4mim]BF4 + Na2Fumarate + water absolute values of STLs increase due to the change of pH according to the following trend: pH = 0 < pH = +1 < pH = −1. In this article, we choose [C4mim]BF4–Na2Fumarate ATPS as the basis to represent the graphs as illustrated in Fig. 4.
 |
| | Fig. 4 Demonstration of tie-lines for [C4mim]BF4 + Na2Fumarate + H2O ATPS at pH = 4.5. | |
3.4. Effect of process variables
3.4.1. Effect of feed's initial concentration.
In this work, we studied different initial concentrations of [C4mim]BF4 and organic salts to estimate their subsequent effect on biomolecule's partitioning. The complete design matrix along with response values are presented in Table 3. As visualized in response contour plots in Fig. 5a–c, there is a noticeable increase in Cefalexin's partition coefficient with increase in initial concentration of [C4mim]BF4. This is noticed because the aggregates begin to be more occurring as the IL's initial concentration is increased. Subsequently, the Cefalexin's enrichment is facilitated. Moreover, the same concentration effect is observed for Na3Citrate and Na2Tartrate organic salts. This effect is reasonable. As the salt concentration is increased the space of the bottom phase is more packed, thus Cefalexin is driven to the top phase.
 |
| | Fig. 5 Contour plots of effects of initial concentrations of organic salts and IL on the partitioning coefficient of Cefalexin (a) Na3Citrate, (b) Na2Tartrate and (c) Na2Fumarate. | |
On the other hand, Kcef. increases as Na2Fumarate's initial concentration is changed from 5 wt% to 5.5 wt% but it decreases again as concentration varies from 5.5 wt% to 6 wt%. The water content of the aqueous solution of Cefalexin affects its structure as a hydration layer is formed on its surface. With an increase in the initial concentration of Na2Fumarate the bottom phase is more hydrophilic. Consequently, water is driven from the top phase to the bottom phase and Kcef. is reduced. A recent study by Lin et al. reported the same effect by inorganic salt in IL-based ATPS for protein extraction.53 Therefore, these phenomena indicate the optimum values for feed's initial concentrations.
Salting-in inducing ions usually increase the partition coefficient of biomolecules. High charge density ions (salting-out inducing ions) have lower interaction with biomolecules as they tend to form hydration complexes. Contrarily, the salting-in inducing ions have a lower tendency toward formation of hydration complexes, and with formation of specific ions binding to the solute the partition coefficient is increased.54 The salting-out ability of Citrate−3 is stronger than Tartrate−2 and Fumarate−2. Thus, it is reasonable to observe the system with Na3Citrate having the lowest amount of Cefalexin in its bottom phase compared to others.
3.4.2. Effect of pH.
It is a well known fact that the biomolecule's net charge is dependent on its isoelectric point (pI). Cefalexin is known as an amphoteric compound possessing amino groups and carboxyl groups. Its isoelectric point is generally estimated to be 4.5 to 5. Consequently, as the pH of the ATPS is altered the Cefalexin's partitioning between the two phases is affected. In this work, for all the pH that we considered, Cefalexin is favourably partitioned to the IL-rich phase.
In IL–Na3Citrate and IL–Na2Tartrate ATPSs, the maximum partitioning coefficient is observed at pH = 4.5 (Fig. 6a) and pH = 4.8 (Fig. 6b), respectively. Since the pI of Cefalexin is between 4.5 and 5, it is predominantly a zwitterion (with no net charge) at these pH ranges. At higher pH, which is higher than the isoelectric point of Cefalexin, Cefalexin is negatively charged and therefore it tends to remain in the organic salt-rich phase. A previous study by Li et al.55 validates this result. This could be interpreted by the following reasons: hydrophobic interaction predominantly affects the extraction process and the electrostatic interaction can slightly influence the extraction efficiency.53 At an isoelectric point, strongest hydrophobic interaction and weakest electrostatic interaction are manifested and the optimum Cefalexin's enrichment is observed. The two phases formed in ATPS are of distinct nature. The IL-rich aqueous phase is predominantly a hydrophobic phase, while the organic salt-rich phase is more hydrophilic in nature due to the presence of species with high charge density. As a result, the partition coefficient is controlled by the difference in the phases' polarities along with the net-charge of the Cefalexin. A zwitterion preferentially migrates to the most hydrophobic aqueous phase ([C4mim]BF4-rich phase), while charged Cefalexin tends to partition for the organic rich hydrophilic phase. The hydrophobic nature of [C4mim]BF4 can be validated by the capability of its anions to accept protons in the hydrogen bond between the solute and the solvent. The hydrogen-bond basicity (which is determined by solvatochromic probes) for [C4mim]BF4 is 0.3856 which justifies its higher hydrophobicity.57 However, maximum Kcef. for IL–Na2Fumarate ATPS is observed at pH = 5.5 (see Fig. 6c).
 |
| | Fig. 6 Contour plots of effects of initial concentrations of IL and pH on the partitioning coefficient of Cefalexin (a) Na3Citrate, (b) Na2Tartrate and (c) Na2Fumarate. | |
3.4.3. Development of regression model equation.
A second order polynomial regression equation was developed for the evaluation of the partition coefficient. These equations represent the effect of independent process variables on the response. Furthermore, we selected the confidence level of 95% for the analysis of RSM, and thus the effects with less than 95% significance were not taken into account. Consequently, the following regression models were evaluated, which are tabulated in the coded values:
IL + Na3Citrate ATPS.
|
K
cef. = 1.70 − 0.19x1 + 0.18x2 + 0.47x3 − 0.055x1x2 − 0.049x1x3 − 0.075x2x3 − 0.18x12 + 0.16x22 + 0.28x32 |
| %EEcef. = 88.85 − 1.68x1 − 2.02x2 + 0.59x3 − 0.34x1x2 + 0.40x1x3 + 0.31x2x3 − 3.37x12 + 1.32x22 + 1.80x32 |
IL + Na2Tartrate ATPS.
|
K
cef. = 2.68 − 0.17x1 + 0.69x2 + 0.22x3 − 0.2x1x2 − 0.25x1x3 − 0.089x2x3 + 0.14x12 + 0.3x22 − 0.26x32 |
| %EEcef. = 95.99 − 0.41x1 + 0.099x2 − 0.2x3 − 0.29x1x2 − 0.37x1x3 − 0.014x2x3 − 1.02x12 + 0.36x22 − 0.21x32 |
IL + Na2Fumarate ATPS.
|
K
cef. = 4.25 − 0.16x1 + 0.30x2 + 0.35x3 − 0.048x1x2 − 0.068x1x3 − 0.051x2x3 − 1.20x12 − 0.42x22 + 0.55x32 |
| %EEcef. = 96.69 − 5.02 × 10−3x1 − 1.11x2 − 0.49x3 − 0.049x1x2 − 0.15x1x3 + 0.2x2x3 − 1.94x12 − 0.17x22 + 0.57x32 |
In these regression models, positive sign in front of the term shows that the effect of a factor is positive and consequently the Kcef. increases as the factor is changed from low to high levels. On the other hand, if the effect is negative, a reduction in Kcef. is observed for the high level of the same factor.
Each regression equation has a R2-value, the closer the R2-value to unity, the more promising the model will be. The R2-value for eqn (16), (18) and (20) was 0.9671, 0.9791 and 0.9248, respectively. This indicated that e.g. 96.71% of total variation in Cefalexin's partitioning in IL–Na3Citrate ATPS could be attributed to the experimental variables studied. All regression equations showed a relatively high R2 value, which was a mere indication of a good agreement between the experimental and predicted Kcef..
We employed the analysis of variance (ANOVA) for evaluation of the statistical significance of the regression model. The F-test and p-values for all the linear, quadratic and interaction effects are given in Tables 10–12 for each IL–organic salt ATPS. Based on the ANOVA analysis for all the systems, the model F-values imply the significance of the models.
Table 10 ANOVA table for the partitioning coefficient of Cefalexin in [C4mim]BF4 + Na3Citrate + water ATPS
| Source |
Sum of squares |
DF |
Mean square |
F-value |
p-value |
| Model |
3.32 |
9 |
0.37 |
19.59 |
0.0009 |
| IL |
0.34 |
1 |
0.34 |
18.23 |
0.0053 |
| Salt |
0.32 |
1 |
0.32 |
17.12 |
0.0061 |
| PEG |
2.17 |
1 |
2.17 |
115.51 |
0.0001 |
| IL × salt |
0.024 |
1 |
0.024 |
1.27 |
0.3035 |
| IL × PEG |
0.019 |
1 |
0.019 |
1.01 |
0.3536 |
| Salt × PEG |
0.045 |
1 |
0.045 |
2.40 |
0.1720 |
| IL2 |
0.087 |
1 |
0.087 |
4.61 |
0.0754 |
| Salt2 |
0.066 |
1 |
0.066 |
3.49 |
0.1108 |
| PEG2 |
0.21 |
1 |
0.21 |
11.14 |
0.0157 |
|
|
| Residual |
0.11 |
6 |
0.019 |
|
|
| Lack of fit |
0.11 |
5 |
0.023 |
602.53 |
0.0309 |
| Pure error |
3.748 × 10−5 |
1 |
3.748 × 10−5 |
|
|
| Total |
3.43 |
15 |
|
|
|
Table 11 ANOVA table for the partitioning coefficient of Cefalexin in [C4mim]BF4 + Na2Tartrate + water ATPS
| Source |
Sum of squares |
DF |
Mean square |
F-value |
p-value |
| Model |
6.91 |
9 |
0.77 |
31.26 |
0.0002 |
| IL |
0.30 |
1 |
0.30 |
12.35 |
0.0126 |
| Salt |
4.79 |
1 |
4.79 |
195.09 |
0.0001 |
| PEG |
0.50 |
1 |
0.50 |
20.57 |
0.0040 |
| IL × salt |
0.33 |
1 |
0.33 |
13.41 |
0.0106 |
| IL × PEG |
0.51 |
1 |
0.51 |
20.76 |
0.0039 |
| Salt × PEG |
0.063 |
1 |
0.063 |
2.56 |
0.1607 |
| IL2 |
0.051 |
1 |
0.051 |
2.08 |
0.1992 |
| Salt2 |
0.23 |
1 |
0.23 |
9.51 |
0.0216 |
| PEG2 |
0.18 |
1 |
0.18 |
7.46 |
0.0341 |
|
|
| Residual |
0.15 |
6 |
0.025 |
|
|
| Lack of fit |
0.15 |
5 |
0.029 |
445.70 |
0.0359 |
| Pure error |
6.606 × 10−5 |
1 |
6.606 × 10−5 |
|
|
| Total |
7.05 |
15 |
|
|
|
Table 12 ANOVA table for the partitioning coefficient of Cefalexin in [C4mim]BF4 + Na2Fumarate + water ATPS
| Source |
Sum of squares |
DF |
Mean square |
F-value |
p-value |
| Model |
8.31 |
9 |
0.92 |
8.20 |
0.0093 |
| IL |
0.26 |
1 |
0.26 |
2.34 |
0.1768 |
| Salt |
0.87 |
1 |
0.87 |
7.75 |
0.0319 |
| PEG |
1.24 |
1 |
1.24 |
11.02 |
0.0160 |
| IL × salt |
0.019 |
1 |
0.019 |
0.17 |
0.6980 |
| IL × PEG |
0.037 |
1 |
0.037 |
0.33 |
0.5850 |
| Salt × PEG |
0.020 |
1 |
0.020 |
0.18 |
0.6847 |
| IL2 |
3.82 |
1 |
3.82 |
33.92 |
0.0011 |
| Salt2 |
0.46 |
1 |
0.46 |
4.09 |
0.0896 |
| PEG2 |
0.80 |
1 |
0.80 |
7.13 |
0.0370 |
|
|
| Residual |
0.68 |
6 |
0.11 |
|
|
| Lack of fit |
0.67 |
5 |
0.13 |
70.35 |
0.0903 |
| Pure error |
1.915 × 10−3 |
1 |
1.915 × 10−3 |
|
|
| Total |
8.99 |
15 |
|
|
|
In extraction of Cefalexin using IL–Na3Citrate ATPS, the linear effects of all independent factors were highly significant (p-value < 0.05). On the other hand, for this system, the interaction effects did not appear to be significant and the only significant quadratic effect was for IL's initial concentration. When employing IL–Na2Tartrate, a second order polynomial equation could model Kcef. with significant linear, interaction and quadratic terms (the only insignificant terms were IL × salt and pH2). However, only initial concentration of IL and salt along with the quadratic effect of pH and IL's wt% had a significant effect on Kcef. in Na2Fumarate based ATPSs.
3.5. Optimization procedure
In the optimization procedure we look for a combination of factor levels that satisfy the requirements placed on responses and factors. Hence, the desired goal for each independent variable (pH, feed's initial concentrations) and response (partition coefficient of Cefalexin) should be selected. The possible choices for goals are either maximize, minimize, target, within range or an exact value. Consequently, an overall desirability function is generated by combination of the goals. Finally, the goal seeking is initiated and two or more maximums can be found due to the curvature nature of the response surfaces and their combination into desirability function.
For optimization purposes, the desired goal for the partition coefficient and the extraction efficiency was chosen to a maximum, along with three independent variables to be within range. The optimization results are presented in Table 13.
Table 13 Optimum operating conditions of the process variables for the maximum partitioning coefficient at T = 298.15 K
| Biphasic system |
Optimum level |
| pH |
IL (wt%) |
Salt (wt%) |
K
Cef.
|
%EECef. |
| [C4mim]BF4 + Na3Citrate |
5.15 |
20 |
15 |
2.7935 |
91.0152 |
| [C4mim]BF4 + Na2Tartrate |
4.97 |
24.83 |
8 |
4.1199 |
96.3911 |
| [C4mim]BF4 + Na2Fumarate |
5.45 |
32 |
5.36 |
5.0639 |
97.0062 |
3.6. Conductivity and DLS
It is crucial to investigate the microstructure of the top phase to validate the presence of the aggregates in the IL-rich top phase. The conductivity measurements of various concentrations of IL solution were conducted at 25 ± 1 °C. With the initial increase of concentration a rapid increase in the conductivity was observed, and later the curve tended toward stability. The concentration at which two linear fragments intersect is chosen as the critical aggregation concentration (CAC). Close examination of Fig. 7 gives the CAC value of [C4mim]BF4 to be 0.156 g mL−1. Knowing the fact that CAC was lower than the top phase concentrations of all the studied ATPS, it is reasonable to conclude that IL aggregates were formed in the top phase. Bowers et al.58 have conducted conductivity measurements to evaluate the CAC to be 820 ± 100 mmol dm−3, which is in agreement to our experimental results.
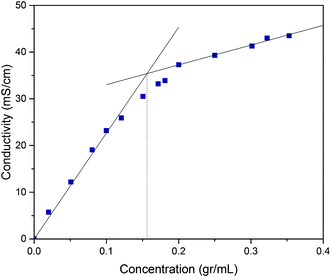 |
| | Fig. 7 The concentration dependence of the conductivity for [C4mim]BF4 in aqueous solutions at 25 ± 1 °C. | |
Fig. 8 illustrates the DLS results of Cefalexin solution along with Cefalexin in the IL rich top phase. A wider aggregation peak appeared in the range of 20–500 nm, which is noticeably wider than the original peak of antibiotic (Fig. 8c). This can be due to the fact that the hydrophobic interactions between the [C4mim]BF4 and Cefalexin can lead to the formation of aggregates which is the main driving force for Cefalexin enrichment in the IL-rich phase.
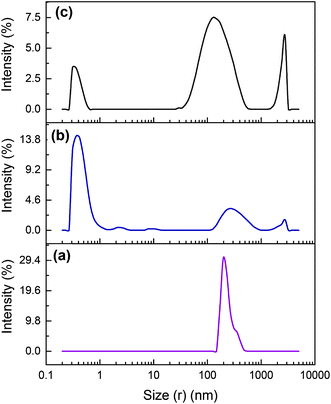 |
| | Fig. 8 DLS graph (a) pure aqueous solution of Cefalexin, (b) IL rich upper phase without Cefalexin and (c) Cefalexin in the IL rich top phase. | |
Furthermore, in the analysis of the top phase, another intensity aggregation was noticed in the range 1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nm. This can be interpreted by the formation of aggregates by excess of ionic liquid.
000 nm. This can be interpreted by the formation of aggregates by excess of ionic liquid.
In order to elucidate the microstructure of Cefalexin in the IL rich top phase, it is essential to study the aggregation behavior of [C4mim]BF4 aqueous solution. Many studies have focused on the aggregation behavior of the aqueous solutions of ILs.58,59 Bowers et al.58 proposed that the aqueous solution of short chain [C4mim]BF4 can be modeled as a dispersion of polydisperse spherical aggregates. They have also stated that [C4mim]BF4 behaves like a short-chain cationic surfactant. Singh et al.59 observed by NMR-measurements that the imidazole ring of [C4mim]BF4 is positioned at the aggregate surface in a configuration favorable for ring stacking through π–π interaction. Consequently, hydrophobic interactions and the π–π conjugation between the imidazole ring of IL and amino groups of Cefalexin led to the formation of aggregates.
3.7. FT-IR spectroscopy
FT-IR spectra are useful tools for identification of functional groups or chemical bonds in a molecule or an interaction system.31,35Fig. 9 shows the FT-IR spectra of pure [C4mim]BF4, pure Cefalexin and Cefalexin in [C4mim]BF4. The major peaks in pure Cefalexin are at 1759.16 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching), 1596.17 (C
O stretching), 1596.17 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bending), 1689.71 (C
C bending), 1689.71 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching), 3420.91 (N–H stretching), 3055.85 (O–H stretching), 2615 cm−1 (S–H stretching), 1195.01 (C–N stretching) and 1280.48 cm−1 (C–O stretching).
O stretching), 3420.91 (N–H stretching), 3055.85 (O–H stretching), 2615 cm−1 (S–H stretching), 1195.01 (C–N stretching) and 1280.48 cm−1 (C–O stretching).
 |
| | Fig. 9 FT-IR spectra of pure Cefalexin, pure [C4mim]BF4 and Cefalexin in [C4mim]BF4. (a) Pure Cefalexin; (b) pure [C4mim]BF4; (c) Cefalexin in [C4mim]BF4. | |
Moreover, the two major absorption bands of Cefalexin (1759.16 and 1596.17 cm−1) have remained unchanged after its enrichment in IL–organic salt ATPSs (Fig. 9c). Thus, it can be concluded that the structural features of Cefalexin before and after extraction are identical. Thereof, by comparison of Fig. 9b and c, it is confirmed that no chemical bonds have been formed between Cefalexin and [C4mim]BF4.
3.8. TEM
Comprehension of the separation process requires close examination of the IL-rich top phase. Consequently, TEM images of Cefalexin in the IL-rich top phase, the top phase of ATPS without the addition of Cefalexin and aqueous solution of Cefalexin have been examined. The IL-rich top phase is not microscopically homogenous, but it forms a polydisperse solution. Fig. 10a demonstrates the conformation of the non-extractive IL-rich top phase and the spot may be attributed to the [C4mim]BF4 without too much aggregation. Moreover, Fig. 10b shows pure Cefalexin aqueous solution and Fig. 10c and d are its TEM images after extraction in the top phase of IL-based ATPSs. New aggregates are formed after the extraction of antibiotic in the [C4mim]BF4-rich top phase. Thereof, there is consistency in size of the aggregates in TEM and DLS. Therefore, it can be stated that the formation of IL aggregates and IL–Cefalexin aggregates is the main driving force in its uptake by IL–organic salt ATPSs.
 |
| | Fig. 10 TEM images (a) IL rich upper phase without Cefalexin, (b) pure aqueous solution of Cefalexin, (c) and (d) Cefalexin in the IL rich top phase. | |
4. Conclusion
Biomolecule extraction and purification with application of IL–inorganic salt ATPSs have been widely exploited; yet the environmental impacts of these high charge density salts make their use unfavourable. For development of more biocompatible systems, organic salts were chosen as the main constituent of IL-based ATPSs. Binodal curves of a common ionic liquid and different organic salts have been studied. The experimental binodal data were satisfactorily correlated by a four parameter equation. It was found that two-phase area would be expanded with an increase in the charge of the anions. In addition, effects of systems' parameters on partition coefficients and extraction efficiencies of Cefalexin were estimated by the use of RSM based on three-variable CCD. We also estimated TLs for each experimental run and confirmed their validity by models. Consequently, the regression models and analysis of variance evaluated the factors' subsequent effects on Kcef.. Hydrophobic interaction along with the salting-out effect and electrostatic interaction govern the transfer process. FT-IR, DLS, conductivity and TEM were used to attain the mechanism of extraction and microscopic structure of the solution. FT-IR spectra validated that no chemical bonds have been formed between Cefalexin and [C4mim]BF4. Withal, DLS, conductivity and TEM results confirmed the formation of some clusters. To sum up, these results gave us some insight into understanding the behavior of antibiotic in IL–organic salt ATPSs.
Notes and references
- H. Passos, A. R. Ferreira, A. Filipa and M. Cláudio, Biochem. Eng. J., 2012, 67, 68–76 CrossRef CAS PubMed.
- S. Abdolrahimi, B. Nasernejad and G. Pazuki, J. Mol. Liq., 2014, 191, 79–84 CrossRef CAS PubMed.
- M. G. Freire, A. Filipa and M. Claudio, Chem. Soc. Rev., 2012, 41, 4966–4995 RSC.
-
R. Hatti-Kaul, Aqueous two-phase systems: methods and protocols, Humana press, Totowa, New Jersey, 2000 Search PubMed.
-
P. A. Albertsson, Partitioning of Cell Particles and Macromolecules, Wiley, New York, 3rd edn, 1986 Search PubMed.
- P. P. Madeira, X. Xu, J. A. Teixeira and E. A. Macedo, Biochem. Eng. J., 2005, 24, 147–155 CrossRef CAS PubMed.
- N. L. P. Dallora, J. G. D. Klemz, P. A. Pessôa Filho, P. P. Madeira, X. Xu, J. A. Teixeira and E. A. Macedo, Biochem. Eng. J., 2007, 34, 92–97 CrossRef CAS PubMed.
- B. K. Vaidya, H. K. Suthar, S. Kasture and S. Nene, Biochem. Eng. J., 2006, 28, 161–166 CrossRef CAS PubMed.
- H. Yue, Q. Yuan and W. Wang, Biochem. Eng. J., 2007, 37, 231–237 CrossRef CAS PubMed.
- G. A. Gomes, A. M. Azevedo, M. R. Aires-Barros and D. M. F. Prazeres, Sep. Purif. Technol., 2009, 65, 22–30 CrossRef CAS PubMed.
- A. M. Azevedo, A. G. Gomes, P. A. J. Rosa, I. F. Ferreira, A. M. M. O. Pisco and M. R. Aires-Barros, Sep. Purif. Technol., 2009, 65, 14–21 CrossRef CAS PubMed.
- K. E. Gutowski, G. A. Broker, H. D. Willauer, J. G. Huddleston, R. P. Swatloski, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2003, 125, 6632–6633 CrossRef CAS PubMed.
- S. P. M. Ventura, S. G. Sousa, L. S. Serafim, A. S. Lima, M. G. Freire and J. A. P. Coutinho, J. Chem. Eng. Data, 2012, 57, 507–512 CrossRef CAS.
- S. P. M. Ventura, S. G. Sousa, L. S. Serafim, A. S. Lima, M. G. Freire and J. A. P. Coutinho, J. Chem. Eng. Data, 2011, 56, 4253–4260 CrossRef CAS.
- S. Dreyer and U. Kragl, Biotechnol. Bioeng., 2008, 99, 1416–1424 CrossRef CAS PubMed.
- M. G. Freire, C. L. S. Louros, L. P. N. Rebelo and J. A. P. Coutinho, Green Chem., 2011, 13, 1536–1545 RSC.
- J. Han, Y. Wang, Y. F. Li, C. L. Yu and Y. S. Yan, J. Chem. Eng. Data, 2011, 56, 3679–3687 CrossRef CAS.
- M. Domınguez-Perez, L. I. N. Tome, M. G. Freire, I. M. Marrucho, O. Cabeza and J. A. P. Coutinho, Sep. Purif. Technol., 2010, 72, 85–91 CrossRef PubMed.
- N. J. Bridges, K. E. Gutowski and R. D. Rogers, Green Chem., 2007, 9, 177–183 RSC.
- Y. C. Pei, J. J. Wang, L. Liu, K. Wu and Y. Zhao, J. Chem. Eng. Data, 2007, 52, 2026–2031 CrossRef CAS.
- C. M. S. S. Neves, S. P. M. Ventura, M. G. Freire, I. M. Marrucho and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 5194–5199 CrossRef CAS PubMed.
- S. P. M. Ventura, C. M. S. S. Neves, M. G. Freire, I. M. Marrucho, J. Oliveira and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 9304–9310 CrossRef CAS PubMed.
- J. Han, C. Yu, Y. Wang, X. Xie, Y. Yan, G. Yin and W. Guan, Fluid Phase Equilib., 2010, 295, 98–103 CrossRef CAS PubMed.
- M. T. Zafarani-Moattar and S. Hamzehzadeh, J. Chem. Eng. Data, 2009, 54, 833–841 CrossRef CAS.
- J. A. Han, R. Pan, X. Q. Xie, Y. Wang, Y. S. Yan, G. W. Yin and W. X. Guan, J. Chem. Eng. Data, 2010, 55, 3749–3754 CrossRef CAS.
- R. Sadeghi, R. Golabiazar and H. Shekaari, J. Chem. Thermodyn., 2010, 42, 441–453 CrossRef CAS PubMed.
- M. T. Zafarani-Moattar and S. Hamzehzadeh, J. Chem. Eng. Data, 2010, 55, 1598–1610 CrossRef CAS.
- M. T. Zafarani-Moattar and S. Hamzehzadeh, Fluid Phase Equilib., 2011, 304, 110–120 CrossRef CAS PubMed.
- K. Ravikumar, S. Ramalingam, S. Krishnan and K. Balu, Dyes Pigm., 2006, 70, 18–26 CrossRef CAS PubMed.
-
G. Box and N. Draper, Empirical Model Building and Response Surfaces, John Wiley and Sons, 1987 Search PubMed.
- Q. Zeng, Y. Wang, N. Li, X. Huang, X. Ding, X. Lin, S. Huang and X. Liu, Talanta, 2013, 16, 409–416 CrossRef PubMed.
- P. Li, Z. Du, X. Ma, G. Wang and G. Li, J. Mol. Liq., 2014, 192, 38–43 CrossRef CAS PubMed.
- X. Wang, X. Wei, J. Liu, J. Liu, D. Sun, P. Du and A. Ping, Fluid Phase Equilib., 2013, 347, 1–7 CrossRef PubMed.
- X. Ding, Y. Wang, Q. Zeng, J. Chen, Y. Huang and K. Xu, Anal. Chim. Acta, 2014, 815, 22–32 CrossRef CAS PubMed.
- J. Chen, Y. Wang, Q. Zeng, X. Ding and Y. Huang, Anal. Methods, 2014, 6, 4067–4076 RSC.
- X. Lin, Y. Wang, Q. Zeng, X. Ding and J. Chen, Analyst, 2013, 138, 6445–6453 RSC.
- J. C. Merchuk, B. A. Andrews and J. A. Asenjo, J. Chromatogr. B: Biomed. Sci. Appl., 1998, 711, 285–293 CrossRef CAS.
- M. Elibol, Process Biochem., 2002, 67, 667–773 CrossRef.
-
R. H. Myers and D. C. Montgomery, Response surface methodology: Process and product optimization using designed experiments, John Wiley and Sons, 2nd edn, 2002 Search PubMed.
-
D. C. Montgomery, Design and analysis of experiments, John Wiley and Sons, 4th edn, 1996 Search PubMed.
- K. D. Collins and M. W. Q. Washbaugh, Q. Rev. Biophys., 1985, 18, 323–422 CrossRef CAS.
- M. G. Cacace, E. M. Landau and J. J. Ramsden, Q. Rev. Biophys., 1997, 30, 241–278 CrossRef CAS.
- M. Holz, R. Grunder, A. Sacco and A. Meleleo, J. Chem. Soc., Faraday Trans., 1993, 89, 1215–1222 RSC.
- M. G. Freire, P. J. Carvalho, A. M. S. Silva, L. M. N. B. F. Santos and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 202–211 CrossRef CAS PubMed.
- M. G. Freire, C. M. S. S. Neves, A. M. S. Silva, L. M. N. B. F. Santos, I. M. Marrucho, L. P. N. Rebelo, J. K. Shah, E. J. Maginn and J. A. P. Coutinho, J. Phys. Chem. B, 2010, 114, 2004–2014 CrossRef CAS PubMed.
- L. I. N. Tome, F. R. Varanda, M. G. Freire, I. M. Marrucho and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 2815–2825 CrossRef CAS PubMed.
- Y. Guan, T. Lilley and T. H. Treffry, Macromolecules, 1993, 26, 3971–3979 CrossRef CAS.
- J. Han, Y. Wang, C. Yu, Y. Li, W. Kang and Y. Yan, J. Chem. Thermodyn., 2012, 45, 59–67 CrossRef CAS PubMed.
- X. Xie, J. Han, Y. Yan, G. Yin and W. Guan, J. Chem. Eng. Data, 2010, 55, 4741–4745 CrossRef CAS.
- J. G. Huddleston, H. D. Willauer and R. D. Rogers, J. Chem. Eng. Data, 2003, 48, 1230–1236 CrossRef CAS.
- D. F. Othmer and P. E. Tobias, J. Ind. Eng. Chem., 1942, 34, 690–692 CrossRef CAS.
- G. Tubio, L. Pellegrini, B. B. Nerli and G. A. Pico, J. Chem. Eng. Data, 2006, 51, 209–212 CrossRef CAS.
- X. Lin, Y. Wang, Q. Zeng, X. Ding and J. Chen, Analyst, 2013, 138, 6445–6453 RSC.
- A. Filipa, M. Claudio, M. G. Freire, C. S. R. Freire, A. J. D. Silvestre and J. A. P. Coutinho, Sep. Purif. Technol., 2010, 75, 39–47 CrossRef PubMed.
- Y. F. Li, J. Han, Y. Wang, J. J. Ma and Y. S. Yan, J. Chem., 2013, 2013, 1–5 Search PubMed.
- A. Filipa, M. Claudio, A. M. Ferreira, S. Shahriari, M. G. Freire and J. A. P. Coutinho, J. Phys. Chem. B, 2011, 115, 11145–11153 CrossRef PubMed.
- A. Filipa, M. Cláudio, A. M. Ferreira, C. S. R. Freire, A. J. D. Silvestre, M. G. Freire and J. A. P. Coutinho, Sep. Purif. Technol., 2012, 97, 142–149 CrossRef PubMed.
- J. Bowers, C. P. Butts, P. J. Martin and M. C. Vergara-Gutierrez, Langmuir, 2004, 20, 2191–2198 CrossRef CAS.
- T. Singh and A. Kumar, J. Phys. Chem. B, 2007, 111, 7843–7851 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp02923b |
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 




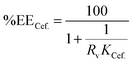



 , Na3Citrate;
, Na3Citrate;  , Na2Succinate;
, Na2Succinate;  , Na2Tartrate; and
, Na2Tartrate; and  , Na2Fumarate.
, Na2Fumarate.






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nm. This can be interpreted by the formation of aggregates by excess of ionic liquid.
000 nm. This can be interpreted by the formation of aggregates by excess of ionic liquid.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching), 1596.17 (C
O stretching), 1596.17 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bending), 1689.71 (C
C bending), 1689.71 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching), 3420.91 (N–H stretching), 3055.85 (O–H stretching), 2615 cm−1 (S–H stretching), 1195.01 (C–N stretching) and 1280.48 cm−1 (C–O stretching).
O stretching), 3420.91 (N–H stretching), 3055.85 (O–H stretching), 2615 cm−1 (S–H stretching), 1195.01 (C–N stretching) and 1280.48 cm−1 (C–O stretching).