Water-mediated interactions between trimethylamine-N-oxide and urea

Abstract

The amphiphilic osmolyte trimethylamine-N-oxide (TMAO) is commonly found in natural organisms, where it counteracts biochemical stress associated with urea in aqueous environments. Despite the important role of TMAO as osmoprotectant, the mechanism behind TMAO's action has remained elusive. Here, we study the interaction between urea, TMAO, and water in solution using broadband (100 MHz–1.6 THz) dielectric spectroscopy. We find that the previously reported tight hydrogen bonds between 3 water molecules and the hydrophilic amine oxide group of TMAO, remain intact at all investigated concentrations of urea, showing that no significant hydrogen bonding occurs between the two co-solutes. Despite the absence of direct TMAO–urea interactions, the solute reorientation times of urea and TMAO show an anomalous nonlinear increase with concentration, for ternary mixtures containing equal amounts of TMAO and urea. The nonlinear increase of the reorientation correlates with changes in the viscosity, showing that the combination of TMAO and urea cooperatively enhances the hydrogen-bond structure of the ternary solutions. This nonlinear increase is indicative of water mediated interaction between the two solutes and is not observed if urea is combined with other amphiphilic solutes.

---

1 Introduction

The biological function of proteins is intimately connected to their hydrated structure¹ and can readily be manipulated using specific co-solutes.² The study of the mechanisms by which co-solutes affect the structure of proteins has constituted an active field within the biochemical sciences over the last decades (see e.g.ref. 3 for a recent overview). Particular attention has been paid to so-called compatible solutes, which tend to stabilize the tertiary structure of biomolecules.⁴ Besides sugars, polyhydric alcohols and amino acids, which induce folding of proteins, considerable attention has been paid to methylamines, which have a remarkably strong stabilizing effect on proteins. Amongst methylamines, trimethylamine-N-oxide (TMAO) is the most commonly used stabilizing agent in biotechnology.⁵ In addition to its technological relevance, TMAO is a ubiquitous, naturally occurring osmolyte (Fig. 1).

Fig. 1 Molecular structure of trimethylamine-N-oxide (left) and urea (right).

The most intensively studied biological function of TMAO is its ability to counter the biochemical stress associated with urea (Fig. 1), which is known to have a strong denaturing activity towards proteins.³ Most remarkably, under physiological conditions the molar ratio between urea and methyl amine is found to be close to 2 : 1 for many marine fish.⁶ Stimulated by this observation several research groups have studied the structure, stability, and functioning of proteins in the presence of TMAO and urea. For several enzymes it was found that TMAO can compensate the urea-induced reduction in activity at a ratio of 2 : 1 (urea : TMAO).⁶ For Ribonuclease A an appreciably higher concentration of TMAO (1 : 1) is required to fully compensate the activity decrease due to the presence of urea.⁷ For other biomolecules the ratio at which TMAO can balance the effect of urea lies between 2 : 1 and 1 : 1.^8,9

The counteraction of urea by TMAO has stimulated many physicochemical studies of solutions with both solutes present. For instance, it has been found that the osmotic coefficient is essentially independent of solute concentration at a molar ratio of 2 : 1.¹⁰ Neutron scattering experiments accompanied by molecular dynamics simulation have indicated that the observed molar ratios can be directly related to a nearly stoichiometric formation of TMAO : urea and TMAO : 2·urea complexes with the NH groups of urea forming hydrogen bonds to the hydrophilic group of TMAO.¹¹ However, this interaction has later been shown to be rather weak¹² or even insignificant¹³ and could be explained from merely statistical contacts due to packing effects.¹⁰ Furthermore, near-infrared spectra¹⁴ and volumetric properties¹⁰ of ternary solutions of TMAO and urea in water suggest that TMAO and urea affect the macroscopic solution properties independently and there seems to be no synergetic effect of both solutes. This is in line with molecular dynamics (MD) simulations performed by Bennion and Daggett,¹⁵ which indicate that the distribution of urea around model peptides is not altered by TMAO. Simulations based on the same force-fields found evidence that TMAO strengthens the hydrogen-bonded structure of the solution and enhances urea–water interactions.^15,16 However, this strengthening of the solution structure was not reproduced by Paul and Patey¹⁷ in a subsequent MD study. In the latter study it has been further suggested that TMAO reduces the number of solvent molecules available to solvate the protein which in turn enhances interactions between different groups in proteins, thereby stabilizing its tertiary structure.¹⁷

In agreement with such a stabilization mechanism, we found, in an earlier combined dielectric relaxation and femtosecond-infrared study, that TMAO strongly binds ∼3 water molecules to its hydrophilic N–O fragment with hydrogen-bond lifetimes exceeding 50 ps.¹⁸ This remarkably strong interaction of TMAO with water also provides a rationale for TMAO stabilizing proteins by reducing the number of available water molecules.¹⁹ As for urea, there is growing evidence that its destabilizing effects on proteins originates from direct urea–protein backbone and urea-side-chain interactions.³ However, the molecular details of how TMAO counteracts the destabilization due to urea have remained elusive.³

In this contribution, we study aqueous solutions of TMAO and urea using broadband dielectric relaxation spectroscopy (DRS), which probes the frequency dependent polarization response of a sample to an external electric field. Dielectric spectra are sensitive to the rotational dynamics of all dipolar molecules in solution, provided that a sufficiently large frequency range can be covered. Thus, DRS is an excellent tool to study the dynamics of the dipolar water, urea, and TMAO molecules. Importantly, it is sensitive to TMAO–water complexes, which have a large electrical dipole moment. Furthermore, the strong hydration of TMAO leads to a marked decrease of the number of water molecules, with rotation times characteristic for bulk water. Thus, DRS is excellently suited to detect potential TMAO–urea interactions. To study the interaction of TMAO with urea in solution, we have performed a DRS study covering frequencies ranging from 100 MHz to 1.6 THz at 23 °C. We report on the dynamics of the binary system urea + water and ternary mixtures containing water, TMAO and urea. The present results are compared to the data from our earlier study on solutions of TMAO in water.¹⁸ We supplement these studies with viscometry of TMAO + urea mixtures and compare these results to other amphiphilic molecules (tetramethylurea or tert-butanol) co-solvated with urea.

2 Experimental section

2.1 Dielectric measurements

In a broadband dielectric spectroscopy experiment we probe the total polarization of a sample as a function of the electric field frequency, ν. In general, the sample polarization is expressed in terms of the sample's complex permittivity, [small epsilon, Greek, circumflex](ν) = ε′(ν) − iε′′(ν), which contains in-phase polarization components described by ε′(ν) and out-of-phase components given by ε′′(ν).

For molecular liquids at ambient conditions the electrical polarization at MHz to THz frequencies predominantly stems from the rotation of permanent molecular dipoles. In the case of a static field (ν = 0) the molecular dipoles in a sample tend to align along the externally applied field against the thermal motion, which results in a polarization according to the static permittivity ε_s (=ε′(ν → 0)) of the sample. With increasing frequency an increasing number of molecular dipoles cannot follow the external field and ε′(ν) decreases and eventually decays to its high frequency limit ε_∞. As the average rotation of the dipoles lags behind the oscillation of the external electric field, a significant portion of the polarization is out-of-phase, which can interfere destructively with the incident field, i.e. the electromagnetic wave is absorbed. As result, molecular rotation leads to a characteristic peak in the dielectric loss, ε′′(ν) at the characteristic rotation frequency of the molecules.

For simple (spherical) dipolar liquids, the step response of the polarization due to an electrical field follows a single exponential decay in the time domain, which corresponds in the frequency domain to a dispersion in ε′(ν) and a peak in ε′′(ν) according to the Debye equation:²⁰

where τ is the relaxation time and S is the relaxation strength (amplitude). For a multi-component system multiple dispersions in ε′(ν) and peaks in ε′′(ν) can be observed,²¹ with each dispersion and corresponding peak being characteristic for the reorientation dynamics of the underlying dipolar species.

To cover the broad frequency range of the present study (0.1 ≲ ν/GHz ≲ 1600), several experimental approaches were combined.²² At 0.4 ≲ ν/THz ≤ 1.6 we use an optical setup based on the propagation of single cycle THz pulses in the sample, generated and detected in non-linear ZnTe crystals (terahertz time-domain spectroscopy). The experimental details can be found elsewhere.^23,24 At frequencies ranging from 25 GHz to 90 GHz we use two variable path length waveguide reflection cells connected to a Vector Network Analyzer (Rhode & Schwarz ZVA67 & ZVA-Z90E).²⁵ To cover frequencies at (0.3 ≲ ν/GHz ≲ 70) we use a Vector Network Analyzer (Rhode & Schwarz ZVA67 & Anritsu MS4647A) to measure the complex reflection coefficient at an open-ended coaxial probe, which is in contact with the sample.²⁴ At frequencies ranging from 0.1 GHz to 2 GHz we measure the permittivity spectra using a coaxial cut-off type measurement cell connected to a Vector Network Analyzer (Rhode & Schwarz ZVA67).²⁶ All measurements were performed in a temperature controlled environment at 23 ± 0.5 °C.

2.2 Samples

Trimethylamine-N-oxide dihydrate (TMAO, Fluka, >99%) and urea (Serva, Germany, molecular biology grade) were used without further purification. All samples were prepared by weighing the appropriate amount of TMAO and urea into volumetric flasks and mixing them with Millipore Milli-Q water (18.2 MΩ cm). For the experiments on aqueous solutions of urea we used samples at molar concentrations ranging from 1 to 4 mol L⁻¹ at increments of 1 mol L⁻¹. For the ternary systems we studied three different trajectories in the ternary phase diagram of the three component system TMAO–urea–water. In the first set of experiments we investigated samples with an equimolar concentration of urea and TMAO at concentrations ranging from 0.47 mol L⁻¹ to 3.53 mol L⁻¹. In a second set of experiments, we kept the concentration of TMAO fixed at a value of 3.53 mol L⁻¹ and vary the urea concentration in the range 0.59 to 3.53 mol L⁻¹. Finally, we performed experiments on the reversed system with a fixed urea concentration (3.53 mol L⁻¹) and a variable concentration of TMAO (0.59 to 3.53 mol L⁻¹).

For selected samples we determined the dynamic viscosities, η, of the solutions using a capillary Ubbelohde viscometer (ViscoSystem AVS 370, Schott Instruments, Germany). We compare the thus obtained viscosities of solutions of TMAO + urea to those of aqueous solutions of other amphiphilic molecules co-solvated with urea, namely equimolar mixtures of urea + tetramethylurea (TMU, Sigma-Aldrich, Germany, >99%) and urea + tert-butanol (Acros Organics, Belgium, for analysis) at concentrations ranging from (0.5 to 3.5 mol L⁻¹).

2.3 Data analysis

For neat water at room temperature the intense relaxation mode (bulk water mode) due to the rotation of the dipolar water molecules is centered at 20 GHz, corresponding to a relaxation τ_H2O of ∼8 ps (Fig. 2, blue component).²⁷ At THz frequencies an additional weak high-frequency mode (fast water mode) is observed that has been assigned to interaction-induced components in the water relaxation mechanism^28,29 or to a small angular rotation preceding a large angle jump.³⁰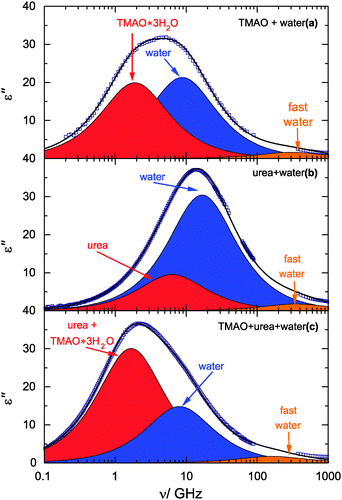

Fig. 2 Dielectric loss spectra for 3 mol L⁻¹ solutions of TMAO in water (a), urea in water (b), and an equimolar solution of TMAO + urea in water (c). Symbols correspond to experimental data and the solid lines show the fits of eqn (2) to the spectra. Shaded areas indicate the contributions of the solute (red), water (blue), and the fast water mode (orange) to the spectra. Data for TMAO in water are taken from ref. 18.

In the present study we investigate aqueous solutions of TMAO and urea. As both solute molecules have a permanent electrical dipole moment their rotation will contribute to the dielectric spectra.^18,31–33 Therefore we fit the experimental spectra with a superposition of three Debye-type relaxation modes

where S_solute and τ_solute are the relaxation strength and relaxation time related to the orientational dynamics of the solute molecules. The second Debye mode (S_H2O, τ_H2O) accounts for the main dipolar relaxation of water, while the third mode (S_fast, τ_fast) models the high frequency relaxation of water. The static permittivity of the samples is given by the sum over all individual contributions to the spectra (ε_s = S_solute + S_H2O + S_fast + ε_∞).

The relaxation strength, S_j of each relaxation process is related to the magnitude of the dipole moment of the relaxing species j in solution, μ_eff,j, and to their corresponding volume concentration, c_j (in mol L⁻¹). We use the Cavell equation, which applies to multi-component mixtures, to relate the observed relaxation strengths to the molecular properties:^21,34

where N_A is Avogadro's constant, ε₀ the vacuum permittivity, k_B the Boltzmann constant, and T the thermodynamic temperature.

3 Results

In Fig. 2 we show dielectric loss spectra for 3 mol L⁻¹ solutions of TMAO, urea, and TMAO + urea in water. All spectra show a rather intense relaxation mode (blue shaded area) at 2–20 GHz and a weak relaxation at 100–400 GHz (orange shaded area). These relaxation modes are reminiscent of those found for neat water and we respectively assign them to the bulk-like and fast water mode as for neat water.²⁷

For the binary solutions of TMAO or urea a separate relaxation mode due to the rotation of the dipolar solutes is expected. Such solute relaxations are indeed observed at lower frequencies in the binary mixtures as indicated by the red shaded areas in Fig. 2a and b, with the rotation of urea centered at higher frequencies (5–8 GHz, depending on concentration) compared to TMAO (0.8–3 GHz), in line with previous studies.^18,31,35 Also for the ternary samples the solute contribution can be excellently modelled with a single Debye relaxation mode (red shaded area in Fig. 2c), as the relaxation times of both solutes are very similar for the ternary systems.³⁶ The solute relaxation mode (S_solute, τ_solute) thus contains both the dipolar rotations of urea and TMAO.

Fig. 3 shows the dielectric spectra of equimolar solutions of TMAO and urea in water. Spectra associated with other paths through the ternary phase diagram can be found in the ESI.† We find the static permittivity to increase monotonously with increasing concentration, for all measurement series. This dielectric increment is, however, significantly higher upon addition of TMAO than upon addition of urea (see ESI†). We have shown previously¹⁸ that the large dielectric increment for solutions of TMAO arises due to pronounced dipole–dipole correlations in solution, which are indicative of the formation of long-lived TMAO·3H₂O complexes.³⁷

Fig. 3 Dielectric permittivity spectra, ε′(ν) (a), and dielectric loss spectra, ε′′(ν) (b) for equimolar solutions of TMAO and urea in water. Symbols show experimental spectra, solid lines show the fits according to eqn (2). The arrows indicate increasing concentration of TMAO and urea.

The dielectric loss peak and the accompanying dispersion in ε′(ν) shift to lower frequencies as the solute concentration is increased (Fig. 3, see also ESI†). This effect is found to be more pronounced when TMAO is added than when the urea concentration is increased. Such a red-shift points at a slow-down of the rotational dynamics. For a quantitative analysis of the contributions from water, TMAO, and urea, we model the experimental data with the relaxation model given by eqn (2).

3.1 Binary solutions

3.1.1 Aqueous solutions of TMAO. In our previous study on aqueous solution of TMAO,¹⁸ we concluded that TMAO rigidly binds ∼3 water molecules for TMAO solutions at high concentration³⁷ and that the TMAO·3H₂O complex has a dipole of μ_{eff,TMAO·3H2O} ≈ 11.5 D, which is significantly larger than the dipole moment of individual TMAO molecules (μ_eff,TMAO ∼ 6.8 D).

The formation of TMAO·3H₂O complex was confirmed by the reduction of the water relaxation amplitude, corresponding to ∼3 water molecules per TMAO. We could show that the water relaxation has two contributions, which are assigned to a bulk-like relaxation centered at 8–20 GHz (depending on the concentration of TMAO) and a second relaxation of water molecules in the vicinity of the hydrophobic fragment of the TMAO molecule. The latter are slowed down with respect to the rotational dynamics of bulk water and their relaxation is centered at 4–9 GHz. These two distinct water modes closely overlap and could only be separated with the help of additional input from time-resolved infrared experiments. In the present study, we model the two water relaxations with a single relaxation mode and do not explicitly consider the contribution of the slowed-down subsensemble of water molecules next to the hydrophobic part of TMAO. Thus, the dynamics of both, bulk-like water and water near hydrophobic groups are modeled by a single relaxation mode (Fig. 2). As a consequence, this relaxation mode represents the weighted average of bulk-like water and water molecules next to hydrophobic groups and an increasing contribution of water close to hydrophobic groups will result in an shift of the overall water amplitude to lower frequencies (longer relaxation times).³⁸

The fast water relaxation mode (orange shaded area at high frequencies in Fig. 2a) did not vary significantly with TMAO concentration, suggesting that the molecular mechanism underlying this mode does not change.

3.1.2 Aqueous solutions of urea. For aqueous solutions of urea, the orientational relaxation of urea is centered at higher frequencies (5–8 GHz) and overlaps with the water relaxation (13–20 GHz, see Fig. 2b). It has been shown previously,^31,35,39,40 that addition of urea has a negligible effect on the water dynamics. Accordingly, for urea solutions, we fix in eqn (2) the amplitude of the water relaxation, S_H2O, to the value expected from the analytical water concentration using eqn (3), assuming the effective dipole moment of the water molecules to be the same as in neat water.¹⁸ This approach allows a reliable separation of both solute and solvent contributions, as shown by others previously.³¹ As can be seen in both Fig. 2b and Fig. S1 (see ESI†), the fits using this assumption are in excellent agreement with the experimental spectra.

We find the relaxation strength of urea, S_solute to increase linearly with increasing concentration of urea (see Fig. S2a, ESI†). From the relaxation strength, S_solute we extract an effective dipole moment of μ_eff,urea = (8.2 ± 1.0) D, which is constant over the entire composition range (see below). It has been shown by Kaatze et al.³¹ that this value can be readily related to the gas-phase dipole moment of urea. As already indicated above, the water relaxation time τ_H2O is becoming only marginally longer as urea is added and at c_urea = 4 mol L⁻¹ it is slowed down by ∼20% compared to bulk water (see Fig. S2, ESI†), confirming previous reports^31,35,39,41 that the urea–water interaction is remarkably similar to the water–water interaction.

The amplitude and timescale of the fast water relaxation increase somewhat with increasing urea concentration, reflecting an increase of the amplitude and time scale of the inertial component of the water reorientation, probably due to a distortion of the hydrogen-bonded structure of water.³⁰

3.2 Ternary solutions

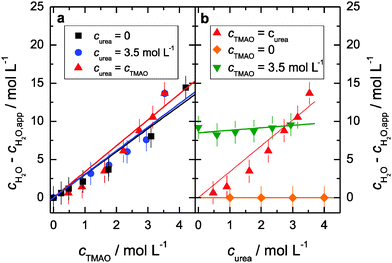
The spectra of all ternary solutions can be well described with three Debye modes (Fig. 3; Fig. S4 and S6, ESI†) with the solute relaxation centered at 0.6–6 GHz (depending on composition), the contribution of the water relaxation centered at 7–20 GHz, and the weak high frequency water relaxation at ∼400 GHz. The extracted fitting parameters are given in Fig. S3, S5 and S6 (see ESI†). For all measurement series, the relaxation strength of the solute mode, S_solute, increases linearly with solute (or co-solute). For equimolar solutions of TMAO and urea the relaxation time τ_fast and the amplitude S_fast increase with increasing solute concentration, similar to what we find for solutions of urea only.

3.2.1 Water relaxation. The relaxation amplitude of the water mode can be related to the apparent concentration of water molecules, c_app,H2O, that contribute to the observed bulk water relaxation (eqn (3)).¹⁸ Note that the thus obtained value of c_app,H2O corresponds to the subensemble of water molecules that reorient with a rotational relaxation time τ_H2O. This concentration may differ from the total (analytical) water concentration c_H2O, if a fraction of water molecules is (tightly) bound to a solute. In Fig. 4a we plot c_H2O − c_app,H2O for the three measurements series where the concentration of TMAO is varied, while Fig. 4b displays the corresponding data upon variation of the urea concentration. Clearly, the number of bound water molecules increases nearly linearly with a slope of ∼3 with the TMAO concentration irrespective of the urea concentration. In contrast, the number of bound water molecules is essentially constant when the urea concentration is varied at a fixed concentration of TMAO (green triangles and orange diamonds in Fig. 4b).

Fig. 4 Concentration of water molecules missing from the water relaxation mode centered at 6–20 GHz in the dielectric spectra. The missing concentration corresponds to the difference between the analytical water concentration, c_H2O, and the apparent water concentration, c_H2O,app, as detected in the bulk water relaxation of the dielectric spectra. Panels a and b show results for measurement series where the concentration of TMAO and urea were varied, respectively. Symbols are experimental data, error bars were estimated assuming ΔS_H2O = 2. Solid lines show linear fits.

Hence, our present results strongly suggest that the hydration structure at the hydrophilic site of TMAO is not altered by the presence of urea, and demonstrate that TMAO·3H₂O complexes remain intact upon co-solvation with urea. This also indicates that urea molecules do not bind to a significant extent to the TMAO hydrophilic group, as this would inevitably lead to a release of water molecules from the TMAO·3H₂O complexes. Therefore, our results confirm that the interaction between the hydrophilic site of TMAO and urea is weak^10,12 and that the hydrogen-bond acceptor sites of TMAO are predominantly occupied by water molecules.

A marked interaction between the solutes is also not apparent from the water dynamics. In Fig. 5 we show the extracted relaxation time τ_H2O of the water molecules not bound in TMAO·3H₂O structures. As can be seen in Fig. 5a, the water relaxation time markedly increases with increasing concentration of TMAO, while we observe only a very modest increase when the urea concentration is increased (green triangles and orange diamonds in Fig. 5b). As mentioned above, we do not distinguish here between bulk-like water and water near hydrophobic groups; we describe both contributions by one effective relaxation time. Hence, the increase of τ_H2O with increasing c_TMAO can be explained from the increasing contribution of water molecules in contact with the hydrophobic CH₃ groups of the TMAO molecules. As in the case of solutions of urea only, τ_H2O is virtually independent of c_urea for the ternary samples. Clearly, also for the ternary samples urea does not significantly affect the water dynamics.

Fig. 5 Relaxation time of the water mode, τ_H2O for samples with varying concentration of TMAO (a) and urea (b), respectively. Symbols correspond to values extracted from fits of eqn (2) to the experimental spectra, lines show linear fits. Error bars correspond to the typical reproducibility Δτ_H2O = 0.3 ps.

3.2.2 Solute relaxation. The solute relaxation strength, S_solute, can be related to its molecular dipole moment using eqn (3). Here S_solute contains contributions from both urea and TMAO. In Fig. 6 we compare the experimentally obtained solute relaxation amplitudes for the different solutions to what would be expected for urea molecules (μ_eff,urea = 8.2 D) and TMAO·3H₂O complexes (μ_{eff,TMAO·3H2O} = 11.5 D at c_TMAO ≳ 3 mol L⁻¹)¹⁸ contributing independently to the solute relaxation mode. The expected values for S_solute (solid lines in Fig. 6) are obtained from the analytical concentrations of both solutes using eqn (3) and show good agreement with the experimental values. We note that ab initio calculations,⁴² analogously to our earlier study on aqueous solutions of TMAO,¹⁸ indicate that TMAO–urea complexes have an electric dipole moment of 12.9–13.3 D. Thus, lower values for S_solute would have been expected for ternary mixtures if long-lived TMAO : urea complexes were formed, as the squared dipole moment of such complexes ((13.1 D)² ≈ 170 D²) is smaller than the sum of the squared dipoles of the individual dipole moments of urea and TMAO·3H₂O ((8.2 D)² + (11.5 D)² ≈ 200 D²; see eqn (3)). In Fig. 6 we show that the measured solute amplitudes are consistently higher than what would be expected for the formation of long-lived TMAO : urea complexes.

Fig. 6 Solute relaxation amplitude, S_solute (symbols). The solid lines show the value that would be expected if TMAO·3H₂O (μ_{eff,TMAO·3H2O} = 11.5 D) complexes and urea (μ_eff,urea = 8.2 D) molecules contribute independently to the solute relaxation mode. The dotted and dashed line correspond to what would be expected for the formation of long-lived TMAO : urea complexes for stoichiometric (1 : 1) association and for an association constant of K = 0.14 L mol⁻¹ (see ref. 12), respectively, assuming μ_{eff,TMAO:urea} = 13.1 D (see text). The error bar represents the typical reproducibility ΔS_solute = 2.

It is instructive to compare the relaxation time of the solute mode, τ_solute to the bulk viscosity η. As can be seen from Fig. 7a, both log τ_solute and log η (Fig. 7b) increase linearly with increasing concentration for aqueous solutions of urea only or TMAO only. This observation indicates that the dipolar rotation is hydrodynamically controlled, as described by the Stokes–Einstein–Debye relation.⁴³ Remarkably, when both TMAO and urea are present in solution, log τ_solute increases in a nonlinear manner (Fig. 7a), which is also reflected in a non-linear increase in the solution viscosities (Fig. 7b). Hence, the results indicate that the solution experiences an enhanced structuring effect if TMAO and urea are both present. While for equimolar solutions of TMAO and urea the relative contribution of both solutes to the observed solute relaxation mode are constant over the entire composition range, this is not the case for our experiments with fixed TMAO or urea concentration. Therefore, log τ_solute values for these systems are intrinsically non-linear due the varying relative amplitude of both solutes. We find also good correlation of the solute relaxation times with the sample viscosities for these ternary samples (Fig. S8, see ESI†).

Fig. 7 (a) Solute relaxation time, τ_solute, for solutions of urea, TMAO and equimolar TMAO + urea solutions obtained from fits of eqn (2) to the dielectric spectra (symbols). (b) Dynamic viscosities, η, of the corresponding aqueous solutions (symbols). Viscosities for solutions of urea⁴⁴ and TMAO⁴⁵ were taken from the literature. Lines are guides to the eye.

4 Discussion

Our present study shows that the measured solute amplitudes do not provide evidence for the formation of TMAO : urea hydrogen-bonds. Instead, the solute amplitudes can be well explained from independent contributions of urea and TMAO·3H₂O complexes to the solute relaxation mode. This contrasts an earlier study¹¹ using neutron scattering and molecular dynamics simulations, which suggested that there is a nearly stoichiometric formation of hydrogen-bonds between urea and TMAO. However, the same authors showed in a subsequent study¹² that this interaction is weak with binding constants of K = c_TMAO:urea/(c_ureac_TMAO) ≈ 0.14 L mol⁻¹. Here, we show that the solute amplitudes are consistently higher than what would be expected for stoichiometric and even for weak (K = 0.14 L mol⁻¹)¹² association (Fig. 6). At this point it should be noted that the observation of TMAO : urea complexes in the dielectric response requires the lifetime of TMAO : urea hydrogen-bonds to be similar to the relaxation time (τ_solute) of these complexes. Thus, the absence of any reduction of S_solute shows that the hydrogen-bond lifetimes of TMAO–urea hydrogen bonds are, if present, short. More importantly, the H-bond lifetimes are significantly shorter than those of TMAO–water hydrogen-bonds.¹⁸

To obtain further information on the formation of short-lived TMAO : urea hydrogen-bonds we consider the hydration of TMAO. We find that three water molecules are strongly bound to the hydrophilic N–O group of TMAO, independent of the urea concentrations (Fig. 4). This indicates that the TMAO·3H₂O complexes formed in aqueous solutions of TMAO remain intact even in the presence of a high concentration of urea. This result shows that the hydrophilic N–O group of TMAO is preferentially solvated by water in solution. The reported binding constants of K = 0.14 L mol⁻¹ (ref. 12) imply that at the highest concentration of our present study (c_TMAO = c_urea = 3.5 mol L⁻¹) approximately 20% of the TMAO molecules form one hydrogen-bond to urea and that 7% of all TMAO molecules have two urea molecules solvating the hydrophilic TMAO group. Hence, at this concentration, the direct interaction of TMAO with urea would lead to a release of ∼0.35 water molecules per TMAO, which is within our experimental accuracy. Based on our experimental accuracy of the c_H2O − c_H2O,app values the equilibrium constant K of the formation of TMAO–urea complexes has a value <0.2 L mol⁻¹. We however find no indications for a reduction of the number of water molecules bound to TMAO upon addition of urea (Fig. 4). Thus, direct binding of TMAO to urea is rare and weak and therefore very likely not the reason for the counteraction of biochemical stress due to urea by TMAO. This is in line with a recent osmometric study that showed that TMAO : urea complexes have a low binding energy and the presence of these complexes can be explained by random contacts between TMAO and urea.¹⁰

While direct interactions are unlikely, the simultaneous presence of TMAO and urea leads to an excess slow down of the measured solute rotation time. This is also reflected in a markedly non-linear increase in log η.⁴⁶ This contrasts the situation for the binary solutions, where the logarithms of the solute relaxation times and the viscosities increase linearly with composition, as expected for an ideal, non-interacting mixture (for TMAO, the TMAO·3H₂O is the non-interacting entity).⁴⁶ To gain insight into the counteraction mechanism of TMAO and urea, we compare the viscosities of the equimolar solutions of TMAO + urea to solutions of similar amphiphilic molecules mixed with urea (tetramethylurea + urea; tert-butanol + urea). Notably, only log η(c_solute) for TMAO + urea exhibits a pronounced positive concavity (∂² log(η)/∂c² = 0.04 L² mol⁻²) while all studied ternary and binary solutions have smaller or even slightly negative second derivatives (<0.01 L² mol⁻², Fig. S9, see ESI†). Thus, we find for TMAO + urea solution an excess increase in viscosity as the concentration of both solutes is increased, indicative of enhanced intermolecular interactions.⁴⁶

In view of the absence of direct interactions between TMAO and urea in aqueous solution, it seems more likely that the excess enhancement in the presence of TMAO and urea is mediated by water. The presence of the hydrophobic methyl groups of TMAO slows down water dynamics significantly,¹⁸ which is reflected in the slow down of τ_H2O (Fig. 5). However, also TBA and TMU have a similar number of methyl groups, which lead to a slow-down of the rotation of the neighboring water molecules.⁴⁷ Thus, we can exclude that the excess slow-down upon co-solvation of TMAO and urea stems from the hydrophobic parts of the molecules. In fact, unlike the solute relaxation times, the water reorientation time in equimolar solutions of TMAO + urea is similar to τ_H2O in solutions of TMAO. This indicates that there is no significant local strengthening of the water hydrogen-bonds. The observed enhancement of the solute rotation and of the sample viscosity must result from a collective effect on longer length scales rather than a local strengthening, i.e. on average more intermolecular bonds are formed in the ternary solutions. Such a long-range interaction may be rationalized by considering the differences in the hydrogen-bonding properties of the two solutes. TMAO has three hydrogen-bond acceptor sites at the hydrophilic N–O fragment. Due to the excess of H-bond acceptor sites at the hydrophilic fragment of TMAO (compared to the two acceptor sites of H₂O), geometrical defects are formed in the three-dimensional hydrogen-bond network of water. Urea, having four hydrogen bond donor sites, can counterbalance these defects. The asymmetric nature of the excess of H-bond acceptors of TMAO and the excess of hydrogen-bond donors of urea, could thus allow for the compensation of their defects imposed on the water structure, as schematically illustrated in Fig. 8. This scenario is supported by earlier time-resolved infrared studies, which probe the rotation of OH (or equivalent OD) groups of water.^18,48 The femtosecond infrared study reported in ref. 48 showed that the defects in the hydrogen-bonded structure of water due to TMAO lead to an enhanced rotational mobility of part of the OH groups in aqueous solutions of TMAO. This enhancement vanished when urea was added.⁴⁸ This would be in line with the proposition that TMAO and urea jointly decrease the number of defects in the hydrogen-bonded structure of water.

Fig. 8 Schematic illustration of the postulated water-mediated interaction between hydrated TMAO·3H₂O and urea. The three hydrogen-bond acceptor sites located at the oxygen atom of TMAO are compensated by the excess of hydrogen-bond donor sites of urea, mediated by 0…n hydration shells of water.

5 Conclusions

We studied the dynamics of aqueous solutions of TMAO and urea using broadband dielectric spectroscopy. The observed amplitude of the solute mode excludes the presence of long-lived TMAO : urea complexes. In addition, we observe stable long-lived TMAO·3H₂O complexes at all studied TMAO and urea concentrations. Accordingly, our results indicate that there are no long-lived TMAO–urea hydrogen-bonds formed and also short-lived interactions between the hydrophilic N–O fragment of TMAO and the hydrogen-bond donor sites of urea are rare. Thus, we conclude that it is highly unlikely that the counteraction by TMAO of biochemical stress due to the presence of urea originates from direct binding of TMAO to urea. The solute rotation times as well as the sample viscosities of TMAO + urea solutions exhibit a remarkable non-linear increase for TMAO + urea, which is not observed for other amphiphilic molecules co-dissolved with urea in water. Thus, our results show that the presence of both TMAO and urea leads to an enhanced structuring of the solution hydrogen-bond network. This is likely because the two solutes balance the defects in the hydrogen-bonded structure of water introduced by the individual solutes. Hence, the anisotropic distribution of hydrogen-bond donor and acceptor sites at TMAO and urea, together with the strong interaction of TMAO with water could provide a mechanistic rationale for the functioning of TMAO as osmoprotectant.

Acknowledgements

This work is part of the research program of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO). N. O. gratefully acknowledges the European Commission (FP7) for funding through the award of a Marie Curie fellowship. The authors gratefully acknowledge H. Schoenmaker and H.-J. Boluijt for technical support and M. Knecht and S. Seywald for performing the viscosity measurements. We thank Dr Yves Rezus and Dr Sapun H. Parekh for helpful discussions.

References

1. K. Teilum, J. G. Olsen and B. B. Kragelund, Biochim. Biophys. Acta, 2011, 1814, 969.
2. S. N. Timasheff, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 67.
3. D. R. Canchi and A. E. García, Annu. Rev. Phys. Chem., 2013, 64, 273.
4. P. H. Yancey, J. Exp. Biol., 2005, 208, 2819.
5. C. C. Mello and D. Barrick, Protein Sci., 2003, 12, 1522.
6. P. H. Yancey and G. N. Somero, J. Exp. Zool., 1980, 212, 205.
7. H. R. Palmer, J. J. Bedford, J. P. Leader and R. A. J. Smith, J. Biol. Chem., 2000, 275, 27708.
8. L. M. Samuelsson, J. J. Bedford, R. A. J. Smith and J. P. Leader, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 2005, 141, 22.
9. T. C. Gluick and S. Yadav, J. Am. Chem. Soc., 2003, 125, 4418.
10. J. Rösgen and R. Jackson-Atogi, J. Am. Chem. Soc., 2012, 134, 3590.
11. F. Meersman, D. Bowron, A. K. Soper and M. H. J. Koch, Biophys. J., 2009, 97, 2559.
12. F. Meersman, D. Bowron, A. K. Soper and M. H. J. Koch, Phys. Chem. Chem. Phys., 2011, 13, 13765.
13. H. Kokubo, C. Y. Hu and B. M. Pettitt, J. Am. Chem. Soc., 2011, 133, 1849–1858.
14. M. Lever, K. Randall and E. A. Galinski, Biochim. Biophys. Acta, 2001, 1528, 135.
15. B. J. Bennion and V. Daggett, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 6433.
16. Q. Zou, B. J. Bennion, V. Dagett and K. P. Murphy, J. Am. Chem. Soc., 2002, 124, 1193.
17. S. Paul and G. N. Patey, J. Am. Chem. Soc., 2007, 129, 4476.
18. J. Hunger, K. J. Tielrooij, R. Buchner, M. Bonn and H. J. Bakker, J. Phys. Chem. B, 2012, 116, 4783–4795.
19. E. S. Courtenay, M. W. Capp, C. F. Anderson and M. T. Record, Biochemistry, 2000, 39, 4455.
20. P. Debye, Polar Molecules, Dover, New York, 1930.
21. E. A. S. Cavell, P. C. Knight and M. A. Sheikh, Trans. Faraday Soc., 1971, 67, 2225–2233.
22. U. Kaatze, Meas. Sci. Technol., 2013, 24, 012005.
23. K. J. Tielrooij, S. van der Post, J. Hunger, M. Bonn and H. J. Bakker, J. Phys. Chem. B, 2011, 115, 12638–12647.
24. W. Ensing, J. Hunger, N. Ottosson and H. J. Bakker, J. Phys. Chem. C, 2013, 117, 12930–12935.
25. J. Hunger, I. Cerjak, H. Schoenmaker, M. Bonn and H. J. Bakker, Rev. Sci. Instrum., 2011, 82, 104703.
26. O. Göttmann, U. Kaatze and P. Petong, Meas. Sci. Technol., 1996, 7, 525.
27. T. Fukasawa, T. Sato, J. Watanabe, Y. Hama, W. Kunz and R. Buchner, Phys. Rev. Lett., 2005, 95, 197802.
28. D. A. Turton, J. Hunger, G. Hefter, R. Buchner and K. Wynne, J. Chem. Phys., 2008, 128, 161102.
29. C. J. Fecko, J. D. Eaves and A. Tokmakoff, J. Chem. Phys., 2002, 117, 1139.
30. A. Y. Zasetsky, Phys. Rev. Lett., 2011, 107, 117601.
31. U. Kaatze, H. Gerke and R. Pottel, J. Phys. Chem., 1986, 90, 5464–5469.
32. Y. Hayashi, Y. Katsumoto, S. Omori, N. Kishii and A. Yasuda, J. Phys. Chem. B, 2007, 111, 1076–1080.
33. M. Freda, H. Onori and A. Santucci, J. Mol. Struct., 2001, 565–566, 153.
34. J. Hunger, A. Stoppa, A. Thoman, M. Walther and R. Buchner, Chem. Phys. Lett., 2009, 471, 85–91.
35. R. Pottel, D. Adolph and U. Kaatze, Ber. Bunsenges. Phys. Chem., 1975, 79, 278–285.
36. Note that the two solutes have a very different effect on the solution viscosities, with TMAO significantly increasing the sample viscosities (e.g. the addition of 3 mol L⁻¹ TMAO results in a 3-fold increase of the solutions viscosity compared to water),⁴⁵ while urea has little impact on the sample viscosity (<15% increase at 3 mol L⁻¹ of urea).⁴⁴ This provides the rationale as to why the relaxation times of TMAO and urea are so similar in the ternary solutions. While the relaxation times differ by a factor of 4–5 in the binary solutions (τ_TMAO·3H2O ≈ 110 ps and τ_urea ≈ 25 ps at c_solute = 3.5 mol L⁻¹), in the ternary samples the presence of TMAO enhances the viscosity, thereby also slowing down the rotation of urea. Thus, the rotation times of urea and TMAO are from the Stokes–Einstein–Debye relation⁴³ expected to be rather similar in the mixture.
37. Note that due to enhanced exchange rates only ∼2 water molecules are on average rigidly bound to TMAO at low concentrations of TMAO.¹⁸ This value is comparable to the solid state, where the dihydrate represents the most stable complex. In the present study we focus on solutions with relatively high concentrations of TMAO (low concentrations of water), where predominantly TMAO·3H₂O contribute to the dielectric spectra.
38. Note that the composite nature may also lead to an asymmetric bandshape of the water relaxation. However, based on the relaxation strengths and amplitudes of bulk-like water and water in the hydrophobic hydration shell,¹⁸ this asymmetry is expected to be weak. Moreover, our present analysis shows that we quantitatively get the same results (formation of TMAO·3H₂O complexes) as for our earlier study,¹⁸ where we could resolve the contribution due to hydrophobic hydration.
39. A. Shimizu, K. Fumino, K. Yukiyasu and Y. Taniguchi, J. Mol. Liq., 2000, 85, 269–278.
40. Y. L. A. Rezus and H. J. Bakker, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18417–18420.
41. Y. L. A. Rezus and H. J. Bakker, J. Chem. Phys., 2006, 125, 144512.
42. Quantum mechanical geometry optimizations were performed using density functional theory^49,50 as provided by the ORCA program package.⁵¹ For all calculations the TZVPP basis set^52,53 was used. Solvation effects were taken into account by the COSMO model⁵⁴ taking the dielectric constant of water ε_s = 80 as the permittivity of the medium.
43. J. L. Dote, D. Kivelson and R. N. Schwartz, J. Phys. Chem., 1981, 85, 2169–2180.
44. K. Kawahara and C. Tanford, J. Biol. Chem., 1966, 241, 3228–3232.
45. R. Sinibaldi, C. Casieri, S. Melchionna, G. Onori, A. L. Segre, S. Viel, L. Mannina and F. De Luca, J. Phys. Chem. B, 2006, 110, 8885.
46. D. S. Viswanath, T. K. Gosh, D. H. L. Prasad, N. V. K. Dutt and K. Y. Rani, Viscosity of Liquids: Theory, Estimation, Experiment, and Data, Springer, Dordrecht, 2007.
47. K. J. Tielrooij, J. Hunger, R. Buchner, M. Bonn and H. J. Bakker, J. Am. Chem. Soc., 2010, 132, 15671–15678.
48. Y. L. A. Rezus and H. J. Bakker, J. Phys. Chem. B, 2009, 113, 4038–4044.
49. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
51. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
52. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
53. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
54. S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235–2245.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp02709d

---