Open Access Article
Open Access ArticleGraphene mediated improved sodium storage in nanocrystalline anatase TiO2 for sodium ion batteries with ether electrolyte†
Shyamal K.
Das
*a,
Birte
Jache
b,
Homen
Lahon
a,
Conrad L.
Bender
b,
Juergen
Janek
*b and
Philipp
Adelhelm
*c
aDepartment of Physics, Tezpur University, Assam, 784028, India. E-mail: skdas@tezu.ernet.in
bInstitute of Physical Chemistry, Justus-Liebig-University Giessen, Heinrich-Buff-Ring 17, 35392 Giessen, Germany. E-mail: Juergen.Janek@phys.Chemie.uni-giessen.de
cFriedrich-Schiller-University Jena, Institute for Technical Chemistry and Environmental Chemistry, Center for Energy and Environmental Chemistry (CEEC Jena), Lessingstraße 12, 07743 Jena, Germany. E-mail: philipp.adelhelm@uni-jena.de
First published on 30th November 2015
Abstract
We report here the synergistic effect of graphene and diglyme electrolyte in significantly improving the sodium insertion electrochemistry of nanocrystalline anatase TiO2.
Since its commercialization in the early 1990s, lithium ion battery technology has found widespread use in portable electronics and nowadays also in stationary energy storage applications.1 Despite a continuous improvement in performance, the technology more and more approaches its limits and therefore a range of alternative concepts is currently being studied.2 It is obvious that different battery types may be used for different applications, depending on whether high energy, high power or low cost are the major target, for example. Moreover, the limited abundance of lithium and other elements such as cobalt might at some later point of massive use become critical to achieve low cost batteries.3 These considerations continuously trigger impetus for new research in alternative affordable electrochemical energy storage and generation technologies.4
Sodium-based batteries, therefore, are gaining renewed interest currently as possible alternative or complement to lithium-based batteries.3 While the research activities on sodium-ion batteries predated to 1970's, both sodium–air and room-temperature sodium–sulfur batteries are the latest additions – following the path in research on lithium-based batteries.5 It is also noted that successful commercialization of sodium–sulfur and sodium–nickel chloride batteries shows confidence on the tremendous potential for not much explored rechargeable sodium-ion/air batteries.3c,5c
The search for suitable high energy density electrode materials and electrolytes for sodium-ion batteries is at an unprecedented acceleration across the globe.3,6 Different research groups successfully proposed several cathode materials for sodium-ion batteries which can be well considered as analogues of lithium-ion battery cathodes, even if there are interesting differences.3,6 However, the success on the anode side is yet comparably limited.6a For example, graphite, the commercially most successful anode in lithium-ion batteries, fails to intercalate Na+ ions under normal operation. It is rather shown that Na+ ions can be intercalated in graphite by co-intercalation phenomena in an ether based electrolyte with capacities in the range of 90–100 mA h g−1 at a current rate of 0.1C.7 Alternatively to carbonaceous materials, few alloys and metal oxides are explored for sodium-ion batteries.3,6a One major concern with most of these materials is their mechanical stability which is affected by drastic volume changes during sodiation/desodiation.
Titanium dioxide (TiO2), of late, is also found to be a promising example of anodes for sodium-ion batteries. Several advantages such as ease in processing, negligible strain, chemical stability, environmentally benign and cost effectiveness attract TiO2 for extensive investigation in sodium cells since two years.8 It is reported that TiO2 electrochemically stores sodium at potentials below 1 V vs. Na+/Na; which is an important requirement for anodes.8a Additionally, exceptionally high cycling stability (>4000 cycles) is shown by graphene coupled TiO2.8b However, it is noticed that the initial Coulombic efficiency is relatively low in most cases (ESI,† Table S1). For example, the initial Coulombic efficiency is only approximately 30% and 39% at 50 mA g−1 and 500 mA g−1 current respectively for the graphene coupled TiO2.8b It is also noteworthy to mention here that the sodium reactivity in TiO2 is quite dissimilar to lithium reactivity.8 Apparently, many unknown subtle parameters ranging from electrolyte composition to TiO2 structures are yet to be explored to wring out the inherent strengths of TiO2. In this communication, we report the synthesis of a nanocrystalline anatase TiO2–graphene composite, and its sodium insertion electrochemistry is investigated utilizing ether and carbonate electrolytes. It is highlighted that graphene and diglyme electrolyte synergistically improve the sodium storage capacities of anatase TiO2. Pristine TiO2 and graphene–TiO2 composite are designated as TiO2 and TiO2–G, respectively.
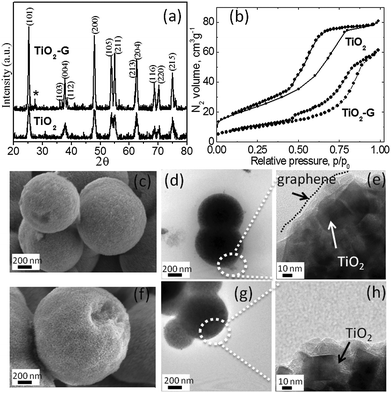
The materials were synthesized by a solvothermal method (details are given in the ESI†). Fig. 1a shows the X-ray diffraction (XRD) patterns of TiO2 and TiO2–G. Both patterns can be indexed to the anatase phase with lattice parameters a = b = 3.7852 Å, c = 9.5139 Å and space group: I41/amd (141) (JCPDS No. 21-1272). The crystallite size is estimated using the Scherrer equation. From the full width at half maximum (FWHM) at the (101) peak (2θ = 25.50°), the crystallite size is determined to be approximately 11 nm for TiO2 and 20 nm for TiO2–G. The XRD pattern of TiO2–G rules out any TiC phase. Generally, a very high temperature (greater than the annealing temperature used here) is required to form Ti–C bond.9a Therefore, graphene and TiO2 in TiO2–G is physically mixed to form three dimensional mixed conducting networks.9b Both the materials possess spherical morphology as characterized by field emission scanning electron microscopy (FESEM) and transmission electron microscopy (TEM). It is shown in Fig. 1(c)–(h). The spherical morphology obtained by carbohydrate mediated hydrothermal synthesis is a well-established phenomenon.9c, d Typical dimension of the TiO2 spheres are in the range of 1–2 μm. The high resolution TEM imaging of the edge of TiO2–G spheres shows the presence of a very thin layer of graphene covering the TiO2 nanocrystals as shown in Fig. 1e. The TEM image of pristine graphene is shown in ESI,† Fig. S1. The presence of graphene is also reflected from the Raman spectra (ESI,† Fig. S2). The typical D and G band of graphene can be observed for TiO2–G. Thermogravimetric analysis confirms the presence of 2.28 wt% of graphene in TiO2–G (ESI,† Fig. S3). It is also well supported by elemental analysis confirming 2.52 wt% of carbon. N2 adsorption/desorption isotherms verify that the materials are mesoporous (Fig. 1b). The BET surface areas of TiO2 and TiO2–G are 80 m2 g−1 and 35 m2 g−1, respectively. The pore diameter is in the range of 2–10 nm (ESI,† Fig. S4).
The sodium storage performance of TiO2 and TiO2–G was evaluated in cells with a sodium metal anode (ESI† for details). The electrolyte compositions were NaPF6 (0.5 M) in diglyme and NaClO4 (0.5 M) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w mixture of ethylene carbonate and dimethyl carbonate (EC/DMC). The choice of different salts in the electrolytes is based on the reported literature.8c,10 It is demonstrated clearly that NaClO4 and NaPF6 are preferred conducting salts in carbonates and diglyme solvents respectively.8c,10a Physico-chemical properties of the solvents are reported elsewhere.10
1 w/w mixture of ethylene carbonate and dimethyl carbonate (EC/DMC). The choice of different salts in the electrolytes is based on the reported literature.8c,10 It is demonstrated clearly that NaClO4 and NaPF6 are preferred conducting salts in carbonates and diglyme solvents respectively.8c,10a Physico-chemical properties of the solvents are reported elsewhere.10
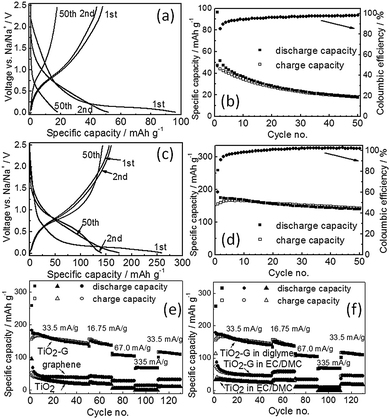
Fig. 2a shows the galvanostatic charge/discharge profiles obtained from pristine TiO2 with diglyme electrolyte at a constant current density of 33.5 mA g−1 in the voltage range of 0.05–2.5 V. Pristine TiO2 spheres deliver a discharge capacity of 96 mA h g−1 in the 1st discharge cycle with an initial Coulombic efficiency of 49%. A potential plateau at much lower voltage (<0.3 V) is observed in the 1st discharge curve. It is noted that the charge/discharge potential profile characteristics are identical to the reported data for anatase TiO2.8 The capacity retention of TiO2 is extremely poor showing a negligible discharge capacity of 18 mA h g−1 at 50th cycle (Fig. 2b).
The graphene–TiO2 composite exhibits significantly improved capacity (Fig. 2c and d) with diglyme electrolyte although the charge/discharge potential profiles are similar to pristine TiO2. It indicates that addition of graphene does not change the fundamental sodium insertion electrochemistry of anatase TiO2. A high discharge capacity of 260 mA h g−1 is obtained in the 1st discharge cycle with a high initial Coulombic efficiency of 60% for TiO2–G at a current density of 33.5 mA g−1. Moreover, stable galvanostatic cycling is also be observed (Fig. 2d). It shows a discharge capacity of 143 mA h g−1 in the 50th cycle. For comparison, the individual contribution from graphene is also separately evaluated with diglyme electrolyte. Pristine graphene delivers in the 1st discharge cycle a capacity of 183 mA h g−1 with an initial Coulombic efficiency of 29% and stores 40 mA h g−1 in the 50th cycle with 33.5 mA g−1 (ESI,† Fig. S5). Since the graphene concentration in TiO2–G is below 3 wt%, therefore, its contribution to the overall capacity of TiO2–G is negligible (below 5 mA h g−1). The rate performance also shows that TiO2–G sustains higher current rates unlike pristine TiO2 and graphene (Fig. 2e). It convincingly demonstrates the beneficial influence of graphene in eight fold enhancement (at 50th cycle, 33.5 mA g−1 current) of the sodium storage capacities of graphene–TiO2. A comparison of initial Coulombic efficiencies of reported TiO2 is given in ESI,† Table S1.
The electrochemical performance of TiO2 and TiO2–G is also evaluated with carbonate (EC/DMC) electrolyte under otherwise identical conditions. All materials show inferior performance in carbonates compared to diglyme. Pristine TiO2 delivers a capacity of 113 mA h g−1 in the 1st discharge cycle with a Coulombic efficiency of 29% with carbonates (ESI,† Fig. S6). Similarly, a 1st discharge cycle capacity of 192 mA h g−1 with a Coulombic efficiency of only 18% is shown by pristine graphene (ESI,† Fig. S7). In terms of Coulombic efficiency, TiO2 and graphene shows relatively poor performance in carbonates unlike in diglyme. On the other hand, it was expected that TiO2–G will show improvement in capacities compared to pristine TiO2 and graphene in carbonates. Surprisingly, no significant improvement is observed. The 1st discharge cycle capacity and Coulombic efficiency are 177 mA h g−1 and 41% respectively for TiO2–G (ESI,† Fig. S8). Moreover, it can retain only 45 mA h g−1 of capacity at 50th cycle. It profoundly indicates that graphene is playing a negligible role in the sodium storage capacity of TiO2 in carbonate electrolytes unlike in diglyme.
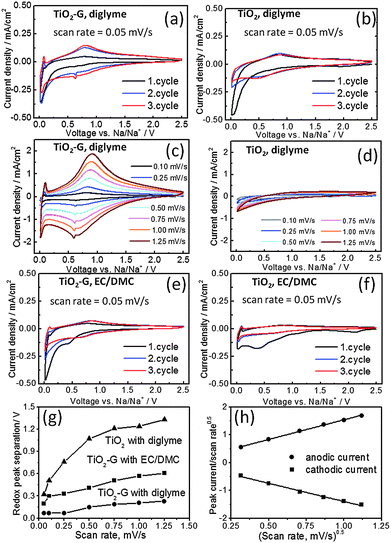
The synergistic effect of graphene and diglyme in improving the cycling stability of TiO2 is also clearly evidenced by cyclic voltammetry (CV). Fig. 3(a) and (b) shows the CV profiles obtained from TiO2–G and TiO2 in diglyme electrolyte at a scan rate of 0.05 mV s−1 at 25 °C. Distinct differences can be observed in both cases (see also ESI,† Fig. S9). A pair of cathodic and anodic redox peaks (depicted from 2nd cycle) at 0.72 V and 0.79 V respectively is detected for TiO2–G in diglyme (Fig. 3a), while these respective peaks are seen at 0.51 V and 0.83 V for pristine TiO2 (Fig. 3b). Typically, these peaks are located in the range of 0.5–0.9 V as according to previous reports.8 Again, TiO2–G shows prominent electrochemical activity at higher scan rates (Fig. 3c), whereas pristine anatase is totally inactive (Fig. 3d). It is interesting to note that the redox peak separation is almost three times smaller in TiO2–G than TiO2 at high scan rates (Fig. 3g). The smaller polarization in TiO2–G (0.07 V at 0.05 mV s−1 and 0.2 V at 1.25 mV s−1) compared to TiO2 (0.32 V at 0.05 mV s−1 and >0.5 V at 1.25 mV s−1) and stability at higher scan rates both strongly suggests that graphene significantly facilitates Na+ insertion kinetics in TiO2. An additional cathodic peak at 0.63 V is also observed for TiO2–G (Fig. 3a). CV profile of graphene in diglyme prominently shows a cathodic peak at 0.52 V and anodic peak at 0.83 V (ESI,† Fig. S10a). Therefore, the additional peak is attributed to the Na+ insertion in graphene/carbon black. The anodic peak is expected to be overlapping with the anodic TiO2 peak. The CV results are further corroborated by the differential capacity plots obtained from the galvanostatic cycling experiments. For example, the anodic and cathodic peaks are prominently seen and they are perfectly overlapping in the voltage range of 0.6–1 V in TiO2–G (ESI,† Fig. S11a). However, these peaks are weakly observed in TiO2 (ESI,† Fig. S11b). The cathodic and anodic peaks at 0.57 V and 0.8 V respectively can also be observed for graphene (ESI,† Fig. S11c).
On the other hand, negligible electrochemical activity is observed in carbonate electrolyte for pristine TiO2 (Fig. 3f) and graphene (ESI,† Fig. S10b), while a certain level of activity (cathodic peak at 0.66 V and anodic peak at 0.85 V) is seen in TiO2–G (Fig. 3e). A broad peak around 0.4 V is also observed in 1st cathodic sweep for both TiO2 and TiO2–G unlike seen in diglyme. Ex situ SEM images (ESI,† Fig. S12) obtained from the discharge products of TiO2–G in diglyme and carbonate electrolytes show that a thick polymeric layer is spread over the microspheres in carbonates while the original spherical structure is retained in diglyme. This layer is probably due to the decomposition of carbonates (8a, c). Interestingly, TiO2–G can also sustain high scan rates in carbonates, although the polarization is higher than in the case of diglyme (Fig. 3g and ESI,† Fig. S13). The polarization in carbonates is almost six times higher than diglyme in TiO2–G. Interestingly, a contrast in electrochemical activity of graphene in diglyme and carbonates can also be figured out (ESI,† Fig. S10 and S14). While certain redox peaks are prominently observed in diglyme, these are totally absent in carbonates. This effect might be simply due to the co-intercalation phenomena which has been demonstrated in the case of graphite.7 It suggests that the beneficial effects of graphene are dependent on the nature of electrolytes. It is also noteworthy to mention here that despite having a lower surface area and larger crystallite size of TiO2–G (35 m2 g−1, 20 nm) than TiO2 (80 m2 g−1, 11 nm), TiO2–G shows better electrochemical stability and sodium storage capacities.11 The coating of TiO2 by graphene might also reduce side reactions and hence will benefit higher coulombic efficiency values. Therefore, considering all these observations, it can be concluded that graphene synergistically couples with diglyme to significantly improve the sodium insertion electrochemistry of TiO2.
To better understand the sodium storage behavior in TiO2–G, the functional dependence of current response (I) at peak potentials (obtained from Fig. 3c) is plotted against scan rates (γ) according to the following equation: I = k1γ + k2γ0.5, k1 and k2 are constants (see Fig. 3h). It combines two separate mechanisms of ion storage, namely surface capacitive effects and diffusion-controlled insertion processes.12 A straight line is observed as shown in Fig. 3h. This indicates that Na+ is stored in TiO2–G both by capacitive and diffusion controlled processes. Additionally, the current response is also plotted against scan rates as per equation I = aγb (Fig. S15, ESI†).8b,10 The obtained b-value of 0.968 and 0.945 for cathodic and anodic peaks respectively suggests that the kinetics is dominated by capacitive process than diffusion controlled process. Further studies are required to clearly understand the storage phenomenon.13
In summary, graphene mediated improvement in sodium storage capacities and cycling stability of anatase TiO2 is convincingly demonstrated in diglyme electrolyte. A high initial Coulombic efficiency of 60% is obtained in graphene–TiO2 composite. Moreover, it is seen that graphene strongly reduces the polarization. The present work suggests that synergy of conductive additives and electrolyte plays pivotal role in improving the performance of sodium-ion batteries.
SKD acknowledges the financial support from German Academic Exchange Service (DAAD), Germany and Science and Engineering Research Board, Department of Science and Technology, Government of India. JJ and PA acknowledge support by STORE-E (LOEWE program, State of Hessen). PA further thanks the ProExzellenz program from the State of Thuringia.
Notes and references
- (a) P. T. Moseley J. Garche Electrochemical Energy Storage for Renewable Sources and Grid Balancing, Elsevier, 2015 Search PubMed; (b) D. Linden and T. B. Reddy, Handbook of Batteries, McGraw Hill, 2002 Search PubMed.
- (a) P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19 CrossRef CAS PubMed; (b) L. Ma, K. E. Hendrickson, S. Wei and L. A. Archer, Nano Today, 2015, 10, 315 CrossRef CAS.
- (a) V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. C. Gonzalez and T. Rojo, Energy Environ. Sci., 2012, 5, 5884 RSC; (b) H. Pan, Y. S. Hu and L. Chen, Energy Environ. Sci., 2013, 6, 2338 RSC; (c) N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636 CrossRef CAS PubMed; (d) C. Wadia, P. Albertus and V. Srinivasan, J. Power Sources, 2011, 196, 1593 CrossRef CAS.
- (a) N. Jayaprakash, S. K. Das and L. A. Archer, Chem. Commun., 2011, 47, 12610 RSC; (b) M. C. Lin, M. Gong, B. Lu, Y. Wu, D. Y. Wang, M. Guan, M. Angell, C. Chen, J. Yang, B. J. Hwang and H. Dai, Nature, 2015, 520, 325 CrossRef PubMed; (c) C. Xu, B. Li, H. Du and F. Kang, Angew. Chem., Int. Ed., 2012, 51, 933 CrossRef CAS PubMed; (d) H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Pour and D. Aurbach, Energy Environ. Sci., 2013, 6, 2265 RSC.
- (a) P. Hartmann, C. L. Bender, M. Vracar, A. K. Dürr, A. Garsuch, J. Janek and P. Adelhelm, Nat. Mater., 2013, 12, 228 CrossRef CAS PubMed; (b) S. K. Das, S. Lau and L. Archer, J. Mater. Chem. A, 2014, 2, 12623 RSC; (c) P. Adelhelm, P. Hartmann, C. L. Bender, M. Busche, C. Eufinger and J. Janek, Beilstein J. Nanotechnol., 2015, 6, 1016 CrossRef CAS PubMed.
- (a) H. Kang, Y. Liu, K. Cao, Y. Zhao, L. Jiao, Y. Wang and H. Yuan, J. Mater. Chem. A, 2015, 3, 17899 RSC; (b) P. Barpanda, G. Oyama, S. Nishimura, S. C. Chung and A. Yamada, Nat. Commun., 2014, 5, 4358 CAS; (c) R. Tripathi, S. M. Wood, M. S. Islam and L. F. Nazar, Energy Environ. Sci., 2013, 6, 2257 RSC; (d) Y. Lu, L. Wang, J. Cheng and J. B. Goodenough, Chem. Commun., 2012, 48, 6544 RSC; (e) J. Qian, X. Wu, Y. Cao, X. Ai and H. Yang, Angew. Chem., Int. Ed., 2013, 52, 4633 CrossRef CAS PubMed; (f) J. Billaud, R. J. Clement, A. R. Armstrong, J. Canales-Vazquez, P. Rozier, C. P. Grey and P. G. Bruce, J. Am. Chem. Soc., 2014, 136, 17243 CrossRef CAS PubMed; (g) L. David, R. Bhandavat and G. Singh, ACS Nano, 2014, 8, 1759 CrossRef CAS PubMed; (h) X. Shu-Yin, W. Xiao-Yan, L. Yun-Ming, H. Yong-Sheng and C. Li-Quan, Chin. Phys. B, 2014, 23, 118202 CrossRef.
- B. Jache and P. Adelhelm, Angew. Chem., Int. Ed., 2014, 53, 10169 CrossRef CAS PubMed.
- (a) Y. Xu, E. M. Lotfabad, H. Wang, B. Farbod, Z. Xu, A. Kohandehghan and D. Mitlin, Chem. Commun., 2013, 49, 8973 RSC; (b) C. Chen, Y. Wen, X. Hu, X. Ji, M. Yan, L. Mai, P. Hu, B. Shan and Y. Huang, Nat. Commun., 2015 DOI:10.1038/ncomms7929; (c) L. Wu, D. Buchholz, D. Bresser, L. G. Chagas and S. Passerini, J. Power Sources, 2014, 251, 379 CrossRef CAS; (d) K. Kim, G. Ali, K. Y. Chung, C. S. Yoon, H. Yashiro, Y. K. Sun, J. Lu, K. Amine and S. T. Myung, Nano Lett., 2014, 14, 416 CrossRef CAS PubMed; (e) G. Qin, X. Zhang and C. Wang, J. Mater. Chem. A, 2014, 2, 12449 RSC; (f) D. Yan, C. Yu, Y. Bai, W. Zhang, T. Chen, B. Hu, Z. Sun and L. Pan, Chem. Commun., 2015, 51, 8261 RSC; (g) Y. Xu, M. Zhou, L. Wen, C. Wang, H. Zhao, Y. Mi, L. Liang, Q. Fu, M. Wu and Y. Lei, Chem. Mater., 2015, 27, 4274 CrossRef CAS; (h) X. Yang, C. Wang, Y. Yang, Y. Zhang, X. Jia, J. Chen and X. Ji, J. Mater. Chem. A, 2015, 3, 8800 RSC; (i) Z. Hong, K. Zhou, J. Zhang, Z. Huang and M. Wei, J. Mater. Chem. A, 2015, 3, 17412 RSC.
- (a) D. W. Flaherty, R. A. May, S. P. Berglund, K. J. Stevenson and C. B. Mullins, Chem. Mater., 2010, 22, 319 CrossRef CAS; (b) Y. G. Guo, Y. S. Hu, W. Sigle and J. Maier, Adv. Mater., 2007, 19, 2087 CrossRef CAS; (c) X. Sun and Y. Li, Angew. Chem., Int. Ed., 2004, 43, 597 CrossRef PubMed; (d) R. D. Cakan, Y. S. Hu, M. Antonietti, J. Maier and M. M. Titirici, Chem. Mater., 2008, 20, 1227 CrossRef.
- (a) Z. W. Seh, J. Sun, Y. Sun and Y. Cui, ACS Cent. Sci., 2015, 1, 449 CrossRef CAS; (b) K. Xu, Chem. Rev., 2004, 104, 4303 CrossRef CAS PubMed; (c) A. Ponrouch, E. Marchante, M. Courty, J.-M. Tarascon and M. R. Palacın, Energy Environ. Sci., 2012, 5, 8572 RSC; (d) H. C. Ku and C. H. Tu, J. Chem. Eng. Data, 2000, 45, 391 CrossRef CAS.
- (a) K. Saravanan, K. Ananthanarayanan and P. Balaya, Energy Environ. Sci., 2010, 3, 939 RSC; (b) S. K. Das, M. Patel and A. J. Bhattacharyya, ACS Appl. Mater. Interfaces, 2010, 2, 2091 CrossRef CAS.
- J. Wang, J. Polleux, J. Lim and B. Dunn, J. Phys. Chem. C, 2007, 111, 14925 CAS.
- (a) L. Wu, D. Bresser, D. Buchholz, G. Giffin, C. R. Castro, A. Ochel and S. Passerini, Adv. Energy Mater., 2014, 5, DOI:10.1002/aenm.201401142; (b) J. Y. Shin, D. Samuelis and J. Maier, Adv. Funct. Mater., 2011, 21, 3464 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, Raman spectra, TGA, various galvanostatic cycling, cyclic voltammetry and incremental plot data, ex situ SEM. See DOI: 10.1039/c5cc09656a |
| This journal is © The Royal Society of Chemistry 2016 |