Uniaxial magnetic anisotropy of square-planar chromium(II) complexes revealed by magnetic and HF-EPR studies

Abstract

Two mononuclear square-planar Cr(II) complexes are reported, exhibiting field-induced slow magnetic relaxation. The axial zero-field splitting parameter was unambiguously determined by both a high-frequency/field electron paramagnetic resonance (HF-EPR) technique and magnetic measurements. This result represents the first observed single-molecule-magnet behavior in the square planar coordination geometry of any metal ions.

---

Molecules that possess the ability to retain magnetization for long periods of time in the absence of an external magnetic field, referred to as single-molecule magnets (SMMs), have received considerable attention due to their promising applications in quantum computing, spintronics and high-density information storage devices.¹ Application of SMMs requires a high blocking temperature (T_B) or a large energy barrier to magnetization reversal (U). U originates from the ground state spin (S) and uniaxial (Ising) magnetic anisotropy. Prior efforts to increase U were concentrated on the enhancement of S. However, recent experimental and theoretical studies have revealed that these two parameters are coupled, which suggests that the enhancement of S would result in the decrease of magnetic anisotropy.² Therefore, the focus has transformed from the synthesis of giant clusters with large S to small compounds with large magnetic anisotropy, especially those molecules containing only one spin centre, known as single-ion magnets (SIMs).³

Since the discovery of slow magnetic relaxation in the double-decker compounds [Ln(III)Pc₂]⁻ (Ln = Tb, Dy) by Ishikawa et al. in 2003,^3a a large number of mononuclear lanthanide complexes have been found to show excellent SMM behavior owing to the large orbital contributions of the lanthanide ions.⁴ In contrast, only a few mononuclear transition metal complexes exhibit such magnetic behavior mainly because the large ligand-field splitting energies of the transition-metal d orbitals are usually expected to suppress orbital contributions to develop magnetic anisotropy.⁵ However, there has been a growing realization in recent years that a low coordination number can ensure a relatively weak ligand field, thereby decreasing the quenching effect in 3d-transition metals. Hence the main attention has begun to focus on coordination-unsaturated 3d transition metal complexes of which the coordination environment can be controlled and manipulated in a rational way.⁶ An example can be found in the work of Long and co-workers⁷ in which a two-coordinate Fe(I) SIM with a record anisotropy barrier of 226(4) cm⁻¹ among transition metal complexes was reported.

The modifications of coordination environments, including the ligand field, coordination number and symmetry, provide a way to tune the magnetic anisotropy of 3d SIMs, which can be monitored by high-frequency/field electron paramagnetic resonance (HF-EPR).⁸ HF-EPR has become a powerful experimental method for investigating a variety of spin systems which cannot be adequately characterized by conventional EPR since the zero-field splitting (ZFS) parameters of many such systems can exceed the microwave quantum energy of 0.3 cm⁻¹ (X-band) or 1.2 cm⁻¹ (Q-band). Typical examples of high-spin species investigated by HF-EPR focus on 3d transition metal complexes because their ZFS parameters fall into the energy range of HF-EPR (∼1–30 cm⁻¹).⁹ In return a targeted design for certain magnetic anisotropy can be achieved.

We found that the coordination geometries of SIMs, including linear coordination, trigonal planar, trigonal pyramid, trigonal prism, tetrahedron, square pyramid, octahedron or those in higher coordination number, have been investigated, while SIMs based on square-planar geometry have not been reported yet.¹⁰ In addition, previous research on 3d-SIMs was mainly based on Fe(I), Fe(II), Mn(III), Co(II) and Ni(I) ions while SIMs based on other 3d transition metal ions have been rarely reported. Among such species the Cr(II) ion may be a good candidate since the dominant Cr isotopes (⁵⁰Cr, ⁵²Cr, ⁵⁴Cr, natural abundance 90.5%) have no nuclear spin, thus enabling us to study a purer SIM without much influence from any hyperfine effects. HF-EPR has been applied to research Cr(II) complexes¹¹ and recently the first Cr(II)-based SMM has been reported, consisting of an extended metal atom chain complex [Cr₅(tpda)₄Cl₂] (H₂tpda = N²,N⁶-di(pyridin-2-yl)pyridine-2,6-diamine). A negative anisotropy value of −1.53(1) cm⁻¹ was determined for this tetragonal pyramid coordination geometry by EPR spectroscopy.¹²

We herein report two mononuclear Cr(II) compounds and their dynamic magnetism, which presents the first example to exhibit SMM behavior of any metal ions based on square-planar coordination geometry. The HF-EPR study indicates that both compounds exhibit unambiguously uniaxial magnetic anisotropy with negative axial ZFS (D) and small rhombic ZFS (E) values, which is found to be consistent with the magnetic studies.

Complex [Cr^II(N(TMS)₂)₂(py)₂] 1 (TMS = SiMe₃, py = pyridine) was obtained by the reaction of CrCl₂, LiN((SiMe₃)₂)₂ and pyridine in THF, while complex [Cr^II(N(TMS)₂)₂(THF)₂] 2 (THF = tetrahydrofuran) was originally reported by D. C. Bradley.¹³ We found that 2 could also be obtained from the reaction of CrCl₃ and LiN((SiMe₃)₂)₂ (1 : 3) in THF. Both crystals were isolated by cooling down the filtrate to −35 °C after extraction with pentane.

Both complexes crystallize in the triclinic space group P1̄ (Fig. 1, Table S1, ESI†). The selected bond distances and angles are provided in the ESI,† Table S2. For 1, the central Cr(II) atom is coordinated by two bis(trimethylsilyl)amido and two pyridine ligands. The Cr–N_py distances (2.099(3) Å) are slightly longer than the other two Cr–N_amido distances (2.040(3)–2.044(3) Å). The N_py–Cr–N_amido angles are around 90° (89.37(14)–90.90(14)°). Both the N_amido–Cr–N_amido and N_py–Cr–N_py angles are close to 180° (178.76(8)–178.85(8)°), which ensures all the nitrogen and chromium atoms in one plane. Thus, the coordination atoms define a square-planar geometry in 1.

Fig. 1 Molecular structures of 1 (left) and 2 (right). Hydrogen atoms are omitted. Color codes: Cr, rose; O, red; C, grey; N, blue; Si, pale blue.

Complex 2 shares a similar structure to that of 1 except that the central Cr(II) atom is coordinated by two THF ligands instead of two pyridines. The crystal data of 2 also reveal a square planar configuration in which the Cr–N distances (2.070(3)–2.078(3) Å) are in close proximity to Cr–O distances (2.087(3)–2.089(3) Å), and all the O–Cr–N angles are around 90° (89.54(12)–90.42(12)°). The N1–Cr–N2 and O1–Cr–O2 angles are 178.89(12)° and 178.31(12)°, respectively. With the shortest Cr ⋯ Cr separation of 8.10 Å for complex 1 and 8.33 Å for complex 2 between adjacent molecules, no available intermolecular magnetic exchange-coupling pathways are apparent in the structures (Fig. S1, ESI†).

The magnetic properties of 1 and 2 were measured on powder samples prepared in a glove box using a MPMS SQUID magnetometer. The purity of samples was confirmed by Powder X-ray Diffraction (Fig. S2, ESI†). Temperature-dependent direct current (dc) susceptibility measurements for 1 and 2 were Å conducted at a magnetic field of 1000 Oe over the temperature range of 2–300 K (Fig. S3, ESI†). The room-temperature χ_MT values of 2.93 cm³ K mol⁻¹ for 1 and 2.86 cm³ K mol⁻¹ for 2 are consistent with the expected χ_MT value of 2.88 cm³ K mol⁻¹ for an isolated high-spin Cr(II) ion (S = 2, g = 1.96).^9d Upon cooling, the χ_MT value drops gradually before a significant decrease at a lower temperature, reaching 2.00 and 2.15 cm³ K mol⁻¹ for 1 and 2 at 2 K, respectively. The decrease at low temperature is possibly attributed to intrinsic magnetic anisotropy of the Cr²⁺ ion, which is indicative of a significant ZFS and g-factor anisotropy resulting from the square-planar crystal field.

To investigate the ground-state properties, the field dependence of the magnetization for complexes 1 and 2 was measured at temperatures ranging from 2 to 5 K under applied magnetic fields of up to 7 T (Fig. S4 and S5, ESI†). The magnetization at 7 T and 2 K reaches 3.06 and 3.08 Nβ for 1 and 2, respectively. The lack of saturation for both complexes also suggests the presence of magnetic anisotropy. As illustrated for 1 and 2 in Fig. 2, the reduced magnetization plots (M vs. B/T) exhibit significant separations between the isofield curves, confirming the existence of magnetic anisotropy. The M vs. B/T plots are further fitted via ANISOFIT 2.0¹⁴ to quantify the anisotropy parameters of the Cr(II) centres. Good quality fits are obtained using the following spin Hamiltonian,

with parameters: D = −2.01 cm⁻¹, E = 0.02 cm⁻¹, g = 1.97 and D = −2.54 cm⁻¹, E = 0.01 cm⁻¹, g = 1.97 for 1 and 2, respectively. The negative sign of D and small rhombicity (|D| ≫ 3|E|) indicate the uniaxial anisotropy of the compounds. Adjusting to a positive D value leads to a worse result. Note that the obtained anisotropy parameters are in proximity to the reported five-coordinate Cr(II) complexes.^12,15

Fig. 2 Reduced magnetization data for 1 (left) and 2 (right). The solid lines represent the best fit to the data.

In order to accurately determine the anisotropy parameters of the Cr(II) centres, a tunable-frequency HF-EPR experiment, varying the frequency between 60 and 200 GHz, was performed at 4.2 K on the polycrystalline powder samples of both complexes (Fig. 3, Fig. S16 and S17, ESI†). The obtained results are plotted in Fig. 3 as a field dependence of the resonances on the sub-THz frequencies. Similarly to the other high-spin systems studied,¹⁶ it is easy to distinguish the allowed (|ΔM_S| = 1) transitions in such plots from the nominally forbidden (|ΔM_S| > 1) ones, since the latter usually have a much less steep slope than the former. In addition, one of the zero-field transitions is clearly observed at about 5.4 cm⁻¹ for 1 and 6 cm⁻¹ for 2. We attribute it to the 3|D| zero field resonance for an axial spin quintet system,^9d,12,15 which then immediately yields an estimate for |D| of ∼1.8 cm⁻¹ and ∼2 cm⁻¹ for 1 and 2, respectively.

Fig. 3 2D field/frequency maps of EPR transitions for 1 and 2 at 4.2 K. The squares are experimental data. Red curves are simulations using best-fitted spin Hamiltonian parameters as in the text with the magnetic field B parallel to the x axis of the ZFS tensor, blue curves with B||y, and black curves with B||z. The green line represents an off-axis turning point. The vertical dash lines indicate the frequencies at which spectra in Fig. 4 were collected.

The full set of spin Hamiltonian parameters, including D, E, and the values of g-matrix, was obtained by a least-square fit to a complete two-dimensional array of the resonances. The best fit was obtained with the parameters: 1: S = 2, |D| = 1.80(1) cm⁻¹, E = 0.020(5) cm⁻¹, g_x = 1.97(1), g_y = 1.98(1); 2: S = 2, |D| = 2.00(1) cm⁻¹, E = 0.025(5) cm⁻¹, g_x = 1.98(1), g_y = 1.99(1). Since only one parallel turning point in each spectrum could be identified (resulting in only four and three points in the 2D map for 1 and 2, respectively, all at very low fields), no dependable g_z values could be obtained from the fits. Single-frequency spectra (Fig. 4) show 1.9 < g_z < 2.0. The D and g values are in reasonable agreement with those obtained by fitting magnetization data. The frequency dependencies simulated using those parameters show the excellent agreement with the experimental points and allow us to unequivocally attribute observed resonances to particular turning points.

Fig. 4 HF-EPR spectra of 1 and 2 (black traces) with their simulations (coloured traces) at indicated frequencies and 4.2 K. Red traces are spectra simulated using positive D values, while blue traces are spectra simulated using negative D values.

To confirm the sign of D, we simulated the single-frequency spectra of 1 (at 190 GHz) and 2 (at 200 GHz) at 4.2 K that are shown in Fig. 4. Their simulations show typical near-axial S = 2 powder patterns. A negative D value matches well the experiment while imposing a positive D parameter results in a much worse fit. The good-quality HF-EPR spectra allow us to extract all the spin parameters in the standard spin Hamiltonian described in eqn (1). Higher order Zeeman interactions are not considered here.¹⁶

As to the identification of particular resonances in the spectra shown in Fig. 4, the low-lying peak (ca. 1.1 T for 1, and 0.85 T for 2) is the parallel turning point of the |S, M_S〉 |2, − 2〉 → |2, − 1〉 transition. No further parallel turning points could be identified in the spectra, which made it difficult to obtain an accurate value of g_z. The other resonances are perpendicular turning points, with the exception of the one occurring at ∼7.9 T for 1 and ∼8.4 T for 2, which is an off-axis (non-canonical) turning point of the same |2, − 2〉 → |2, − 1〉 transition.

The dynamic magnetic properties of complexes 1 and 2 were investigated using alternating current (ac) magnetic susceptibility measurements in the frequency range 1–1500 Hz as shown in the ESI† (Fig. S6–S16). Under a zero dc field no slow magnetic relaxation behavior was observed for both complexes (Fig. S6, ESI†). When applying a dc field, a frequency-dependent behaviour with clear out-of-phase (χ′′) signals was observed for both complexes (Fig. 5, Fig. S9 and S10, ESI†), which indicates that slow relaxation of the magnetization is highly affected by the quantum tunneling effect of magnetization.¹⁷ In order to weaken the tunneling effect, ac measurements were carried out under various dc fields to determine the most suitable field at which much longer relaxation time occurs (Fig. S7 and S8, ESI†). Using the optimized dc field of 1500 Oe for 1 and 2500 Oe for 2, the χ′′ signals shift from 3.8 K to 2.0 K for 1 and from 3.0 K to 2.0 K for 2 (Fig. 5, Fig. S11 and S12, ESI†). These data indicate a significant SIM behavior.

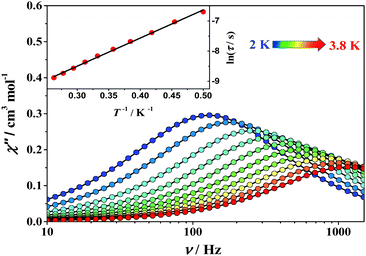Fig. 5 AC susceptibility data obtained for 1 under a 1500 Oe dc field. Solid lines are guides for the eye. Inset: Arrhenius fit of the τ data for 1.

Extraction of the magnetic relaxation times via fitting the field-optimized ac susceptibility data by using the Debye model was performed.^1b The Cole–Cole plots at variable temperatures (Fig. S13 and S14, ESI†) suggest the single thermal relaxation process, as evidenced by the small α values (0.05–0.08 for 1 and 0.08–0.17 for 2, see also ESI,† Table S3). A linear fit to the logarithmic plot of lnτ vs. T⁻¹ over all the available temperature range reveals a thermally activated mechanism and the effective thermal energy barriers to the magnetization reversal (U_eff) are 6.3(4) cm⁻¹ (τ₀ = 1.4 × 10⁻⁵ s) for 1 and 8.2(5) cm⁻¹ (τ₀ = 2.7 × 10⁻⁶ s) for 2 (Fig. S15 and S16, ESI†), where τ₀ is the pre-exponential factor.¹⁸ According to HF-EPR parameters, U_eff is much close to the total splitting of the S = 2 multiplet (U = |D|S² = 7.2(1) cm⁻¹ for 1 and 8.0(1) cm⁻¹ for 2), indicating that the tunneling effect is much suppressed. It is reasonable for the slight difference between the energy barrier obtained from EPR and magnetic data within the fitting error. Theoretical calculations based on state-average CASSCF ab initio and DFT methods were also conducted on complexes 1 and 2 (Fig. S19, Tables S4 and S5, ESI†). As a result, the calculated anisotropy parameters are in good accordance with the HF-EPR data, which yields a further agreement between calculations and experiment.

In summary, the uniaxial magnetic anisotropy and the high spin state of two square-planar Cr(II) complexes have been analysed in detail for the first time. The HF-EPR results unambiguously confirm the negative D values of both complexes, which are consistent with the magnetic analysis as well as calculations. The large ratio of |D/E| is also revealed, indicating that the magnetic anisotropies of square-planar Cr(II) complexes are of the Ising type. Although the magnetic easy-axis cannot be experimentally located, the results significantly increase the magnetometric information of this air-unstable ion. By comparing both complexes we also found that such Ising-type magnetic anisotropy and hence slow magnetic relaxation behavior are less influenced by the substitution of two equatorial solvent ligands such as THF and pyridine though a little difference in bond distance is evidenced. Further investigation into the variation of the donor characteristics is in progress.

This work was supported by “973 projects” (2012CB619401 and 2012CB619402), NSFC (21473129, 21201137, 21103137, 21503155 and IRT13034), the China Postdoctoral Science Foundation (2014M552425), the “National Young 1000-Plan” program, the open funding of Wuhan National High Magnetic Field Centre and the Fundamental Research Funds for Central Universities. This work was also partially supported by the US National Science Foundation (Grant CHE-1152609). The National High Magnetic Field Laboratory is funded by the NSF through a Cooperative Agreement DMR-1157490, the State of Florida and the US Department of Energy. We are grateful to Dr. Andrew Ozarowski, NHMFL, and Dr. Hiroyuki Nojiri, Tohoku University, for the EPR simulation and fitting software SPIN.

Notes and references

1. (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141; (b) D. Gatteschi, R. Sessoli and R. Villain, Molecular Nanomagnets, Oxford University Press, 2006; (c) M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194; (d) R. E. P. Winpenny, Angew. Chem., Int. Ed., 2008, 47, 7992.
2. F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229.
3. (a) N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and S. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694; (b) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078.
4. (a) R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110; (b) H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1.
5. M. Dey and N. Gogoi, Angew. Chem., Int. Ed., 2013, 52, 12780.
6. (a) O. Kahn Molecular Magnetism, VCH, Weinheim, Germany, 1993; (b) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135.
7. J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577.
8. G. M. Smith, P. C. Riedi, B. C. Gilbert, M. J. Davies and D. M. Murphy, Electron Paramagnetic Resonance, Royal Society of Chemistry, Cambridge, UK, 2002, pp. 254–303.
9. (a) T. Taguchi, R. Gupta, B. Lassalle-Kaiser, D. W. Boyce, V. K. Yachandra, W. B. Tolman, J. Yano, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2012, 134, 1996; (b) S. S. Hodgman, R. G. Dall, A. G. Manning, K. G. H. Baldwin and A. G. Truscott, Science, 2011, 331, 1046; (c) J. Krzystek, D. C. Swenson, S. A. Zvyagin, D. Smirnov, A. Ozarowski and J. Telser, J. Am. Chem. Soc., 2010, 132, 5241; (d) J. Telser, L. A. Pardi, J. Krzystek and L. Brunel, Inorg. Chem., 1998, 37, 5769.
10. (a) R. A. Layfield, Organometallics, 2014, 33, 1084; (b) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C. Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125; (c) S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010; (d) S. Jiang, B. Wang, H. Sun, Z. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730.
11. (a) A. Barra, A. Døssing, T. Morsing and J. Vibenholt, Inorg. Chim. Acta, 2011, 373, 266; (b) C. Dobe, C. Noble, G. Carver, P. L. W. Tregenna-Piggott, G. J. McIntyre, A. Barra, A. Neels, S. Janssen and F. Juranyi, J. Am. Chem. Soc., 2004, 126, 16639.
12. A. Cornia, L. Rigamonti, S. Boccedi, R. Clérac, M. Rouzières and L. Sorace, Chem. Commun., 2014, 50, 15191.
13. D. C. Bradley, M. B. Hursthouse, C. W. Newing and A. J. Welch, J. Chem. Soc., Chem. Commun., 1972, 9, 567.
14. M. P. Shores, J. J. Sokol and J. R. Long, J. Am. Chem. Soc., 2002, 124, 2279.
15. J. F. Wang, Z. X. Wang, R. J. Clark, A. Ozarowski, J. V. Tol and N. S. Dalal, Polyhedron, 2011, 30, 3058.
16. J. Krzystek, S. A. Zvyagin, A. Ozarowski, S. Trofimenko and J. Telser, J. Magn. Reson., 2006, 178, 174.
17. (a) L. Lecren, W. Wernsdorfer, Y. Li, O. Roubeau, H. Miyasaka and R. Clérac, J. Am. Chem. Soc., 2005, 127, 11311; (b) J. Tejada, R. F. Ziolo and X. X. Zhang, Chem. Mater., 1996, 8, 1784.
18. R. Carlin, Magnetochemistry, Springer, 1986.

---

Footnotes

† Electronic supplementary information (ESI) available: Physical measurements; additional figures. CCDC 1057925 (1). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5cc07025b

‡ These authors contributed equally to this work.

---