Complex transition metal hydrides: linear correlation of countercation electronegativity versus T–D bond lengths

Abstract

For homoleptic 18-electron complex hydrides, an inverse linear correlation has been established between the T–deuterium bond length (T = Fe, Co, Ni) and the average electronegativity of the metal countercations. This relationship can be further employed towards aiding structural solutions and predicting physical properties of novel complex transition metal hydrides.

---

In recent years, complex transition metal hydrides have become prominent as hydrogen storage materials due to their gravimetric hydrogen capacity and purity of desorbed H₂. Mg₂FeH₆, for instance, has the theoretical capacity to release 5.5 wt% of pure H₂,¹ while its borohydride equivalent (Mg(BH₄)₂) is known to produce toxic B₂H₆ as an impurity during H₂ desorption.² For these materials to achieve technological application,³ reversible desorption of hydrogen is a key requirement. A host of complex transition metal hydrides have been demonstrated to form by the direct reaction with hydrogen gas,⁴ fundamentally making them ideal candidates for energy storage applications.

In the simplest compositions of complex transition metal hydride systems, all hydrogen atoms are bonded to the transition metal centre, T, and are coordinated by alkali, alkali-earth and rare-earth elements, M, achieving the general chemical formula M_m^δ+[TH_n]^δ− (T = 3d, 4d, 5d elements; M = alkali, alkali-earth and rare-earth elements; m, n = 1, 2, 3…).⁵ The transition metals which are known to form these homoleptic mononuclear hydride complexes range from group 7 to group 12; for hydrogen storage research purposes 3d elements retain the majority of the focus. That being said, hydride complexes of the 4d and 5d transition metals have been synthesised, albeit for Ag, Au and Hg.

A host of complex transition metal hydride materials have been structurally characterised by powder X-ray and neutron diffraction, while their physical properties have been probed by a variety of techniques, including multinuclear NMR,⁶ vibrational spectroscopy,⁷ electron microscopy⁸ and ellipsometry.⁹ Vibrational spectroscopic studies of group 8 hydrides have prompted a quest to determine a relationship between the active stretching frequencies of T–H with various physical properties of these complexes. Kritikos and Noréus first reported on the nonlinear inverse correlation of the IR active stretching mode wavenumber in relation to the length of the unit cell (a),^7c revealing that the electropositivity of the metal counterion has secondary importance to its ionic radius. A recent study by Gilson and Moyer suggests a linear relationship between the vibrational wavenumbers and the ionisation potential of the counterion.¹⁰ This relationship provides quantitative support for the charge-transfer mechanism offered by Kritikos and Noréus for explaining the stabilities of these compounds. Hagemann et al. also established an inverse relationship between T–H stretching mode frequencies and T–H bond lengths using experimental and calculated data, observing a decrease in wavenumber as T–H bond length increases.^7d

A recent DFT study by Miwa et al. discussed the thermodynamic stability of established M₂FeH₆ complexes (M = Mg, Ca, and Sr) and compared them to some hypothetical complexes involving M = Mn and Zn.¹¹ It was determined that the electronegativity of the cation elements can be employed to estimate the thermodynamic stability of M₂FeH₆ complexes. Plotting the calculated ΔH_f of the complex metal hydrides against electronegativity using the Allred–Rochow scale, identifies a linear correlation, while the Pauling Scale derives a good fit for the single cation moieties, but not for double cation compounds. These studies were furthered by Takagi et al.¹² who investigated the thermodynamic stability of [FeH₆]⁴⁻ complexes that incorporate H⁻ in their structures (e.g. Na₂Mg₂FeH₈ which has a limiting ionic formula of 2Na⁺·2Mg²⁺·2H⁻·[FeH₆]⁴⁻).¹³ The additional H⁻ significantly increases the number of combinations of countercations that can be incorporated into this class of compounds and opens the possibility for many novel complexes to be synthesised.

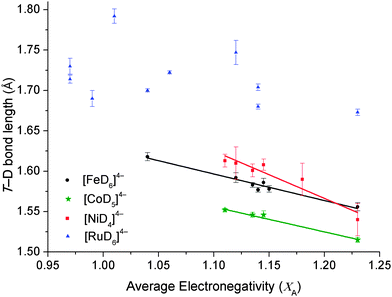
While the recent DFT calculations have enabled researchers to identify the feasibility of forming novel complexes by correlating ΔH_f with the electronegativity of the countercation, a direct link to the physical properties of these compounds is also required. In this study, a linear correlation has been established between the electronegativity of the countercation and the T–D bond length for [FeD₆]⁴⁻, [CoD₅]⁴⁻ and [NiD₄]⁴⁻ complexes and results compared against those of [RuD₆]⁴⁻ and complex hydrides of borohydrides and alanates. As such, not only can the feasibility of forming novel transition metal hydride complexes be determined, but T–D bond lengths can be estimated, allowing for prediction of bond lengths during structural determination of non-deuterated transition metal hydrides.

A variety of complex transition metal hydrides have been structurally characterised by Powder Neutron Diffraction (PND) and this allows a comprehensive comparison of T–D bond lengths to be carried out and correlated with the calculated average countercation electronegativity, X_A. Three equations were identified for the calculation of X_A for binary cation systems. The first:

X_A = (N_iX_i + N_jX_j)(N_i + N_j)⁻¹ (1)

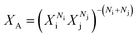where N_i and N_j are the number of each constituent countercations per formula unit and X_i and X_j are their Allred–Rochow electronegativities.¹⁴ The second is the geometric mean of the individual electronegativities of the component atoms as utilised in the Sanderson electronegativity equalisation principle (EEP):¹⁵ The third is the valence averaged cation electronegativities method:¹²

X_A = (N_iV_iX_i + N_jV_jX_j)(N_iV_i + N_jV_j)⁻¹ (3)

where V_i and V_j are the valence states of the individual countercations.

Each of the three equations were tested for suitability using Allred–Rochow¹⁶ and Pauling electronegativity scales.¹⁷ The Allred–Rochow scale has been shown by previous studies to be more suitable for [FeH₆]⁴⁻ complexes,^4b while the Pauling scale is more appropriate to borohydride complexes.¹⁸ Nevertheless, both scales were systematically tested against each equation as possible methods of calculating X_A (Table 1) with the results illustrated in Fig. 1.

Table 1 Methods of calculating average countercation electronegativity (X_A) for complexes of [FeD₆]⁴⁻

Method	Equation	Electronegativity scale	Slope of trendline	R ^2 of trendline
1	1	Allred–Rochow	−2.92	0.962
2	2	Allred–Rochow	−2.91	0.953
3	3	Allred–Rochow	−2.80	0.888
4	1	Pauling	−4.75	0.882
5	2	Pauling	−4.81	0.898
6	3	Pauling	−4.83	0.930

---

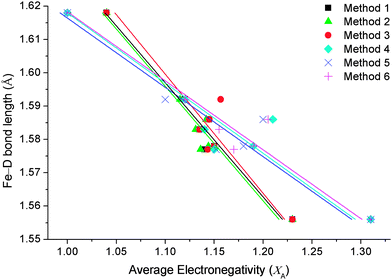Fig. 1 Comparison of Fe–D bond lengths against methods of calculating the average countercation electronegativities (X_A) for complexes of [FeD₆]⁴⁻.

Fig. 1 illustrates how the three equations of calculating X_A (using Pauling and Allred–Rochow electronegativity scales) correlate with Fe–D bond lengths of the known [FeD₆]⁴⁻ compounds in the literature (Table 2). The six methods of calculating X_A (Table 1) have obvious differences that are more dependent on the choice of electronegativity scale than the equation used to calculate average countercation electronegativity. Firstly, X_A calculated using each of the three equations while utilising Allred–Rochow electronegativities have an average slope of the linear trendline of −2.9, whereas the three methods utilising Pauling electronegativities create an average slope of −4.8.

Table 2 T–D lengths of [TD₆]⁴⁻ (T = Fe, Ru, Ni) complexes compared with average atomic Allred–Rochow electronegativity of the cations, X_A. Equatorial T–D lengths used for [FeD₆]⁴⁻, [CoD₅]⁴⁻ and [RuD₆]⁴⁻; average T–D bond lengths of [NiD₄]⁴⁻. Esd's are in parentheses

	Fe–D (Å)	X A		Co–D (Å)	X A		Ni–D (Å)	X A		Ru–D (Å)	X A
Mg2FeD6	1.556(5)^19	1.23	Mg2CoD5	1.515(3)^20	1.23	Mg2NiD4	1.53(2)^21	1.23	Mg2RuD6	1.673(4)^22	1.23
BaMg2FeD8	1.577(3)^23	1.14	Yb4Mg4Co3D19	1.546(5)^24	1.145	LaMg2NiD7	1.59(2)^25	1.18	BaMg2RuD8	1.717(2)^26	1.14
SrMg2FeD8	1.578(4)^27	1.15	Ca4Mg4Co3D19	1.546(3)^24	1.135	CaMgNiD4	1.601(8)^28	1.14	Sr2RuD6	1.69(1)^7c	0.99
Yb4Mg4Fe3D22	1.586(5)^29	1.14	Sr4Mg4Co3D19	1.552(2)^24	1.11	YbMgNiD4	1.608(7)^30	1.15	Ca2RuD6	1.700(2)^31	1.04
Ca4Mg4Fe3D22	1.583(3)^32	1.15				Na2Mg2NiD6	1.61(2)^33	1.12	LiMg2RuD7	1.704(7)^34	1.18
Na2Mg2FeD8	1.592(6)^13b	1.12				SrMgNiD4	1.614(8)^30	1.11	Li4RuD6	1.714(5)^35	0.99
Ca2FeD6	1.618(5)^7d	1.04							Yb2RuD6	1.7223(19)^6b	1.06
									Ba2RuD6	1.73(1)^7c	0.97
									Na2Mg2RuD8	1.749(2)^13b	1.12
									Na4RuD6	1.792(9)^35	1.01

---

The correlation coefficients (R²) of the trendlines were subsequently used to determine the most suitable method. X_A calculated using the Allred–Rochow scale exhibits the highest coefficient values, with Method 1 having an R² of 0.96 and Method 2 of 0.95, while Method 3 had an R² value of 0.89. X_A calculated using the Pauling electronegativity scale produced R² values of 0.93 using Method 6, 0.90 using Method 5 and 0.88 for Method 4. Using these coefficients, Method 1 was chosen as the optimal method.

The complex hydrides of [FeH₆]⁴⁻, [CoD₅]⁴⁻, [NiH₄]⁴⁻ and [RuH₆]⁴⁻ have the greatest number of compounds structurally characterised by PND. X_A of all known crystallographically characterised derivatives of these complexes were calculated and the results tabulated in Table 2 and illustrated in Fig. 2. For the [FeD₆]⁴⁻, [CoD₅]⁴⁻ and [RuD₆]⁴⁻ complexes, the equatorial T–D lengths were used due to the distortion accrued by the axial T–D bonds, whereas the average of all Ni–D bond lengths were used for [NiD₄]⁴⁻ complexes (Fig. S1 in the ESI†).

Fig. 2 T–D bond length as a function of the average atomic Allred–Rochow electronegativity of the cations (T = [FeD₆]⁴⁻ (black circle), [CoD₅]⁴⁻ (green star), [NiD₄]⁴⁻ (red square) and [RuD₆]⁴⁻ (blue triangle)). The trend-lines are obtained by the least-squares fit of the whole data. Error bars are the crystallographically determined esd's of the T–D bond lengths.

As previously observed for [FeH₆]⁴⁻ (R² = 0.962), an inverse linear correlation is also observable for [CoD₅]⁴⁻ and [NiH₄]⁴⁻, with an R² coefficient of 0.983 and 0.903, respectively. [RuD₆]⁴⁻ complexes show only a weak linear correlation, but the general concept that increasing average X_A promotes a decrease in Ru–D bond distance, is still upheld. This correlation implies that for first-row transition metal complex hydrides containing double cations, both metals play an equal part in stabilising the complex anion. The weak correlation of [RuD₆]⁴⁻ complexes are due to the increased stabilisation of the central metal atom attained by the spatially more extensive 4d orbitals of Ru, which are able to overlap with greater effectiveness with the H 1s orbitals than the more compact 3d orbitals of Fe, Co and Ni. This is responsible for the formation of a greater variety of [RuD₆]⁴⁻ complexes³⁶ compared to its 3d analogue and also highlights the importance of the M cations for stabilising the 3d complexes.

As electronegativity is a measure of the degree of electron transfer between atoms, the correlation between X_A and T–D bond length can be justified. As the degree of electronegativity of a cation increases, polarisation of the T–D bond occurs, causing an inherent decrease in the T–D bond length.³⁷ At a certain electronegativity and T–D bond length threshold, [TD_x]⁴⁻ becomes unstable and complexes will not form. For [FeD₆]⁴⁻, the lowest X_A is 1.04 for Ca₂FeD₆ (Fig. 2 and Table 2),^7d,22 while for [CoD₅]⁴⁻ and [NiD₄]⁴⁻, the value is X_A = 1.11. It is notable that the average cation X_A limit at which the 3d T containing compounds are expected to form is higher than that of the 4d [RuD₆]⁴⁻. The lowest X_A for [RuD₆]⁴⁻ is 0.99 for Li₄RuD₆ and Sr₂RuD₆. This is due to the stability of the Ru 4d metal center compared to the 3d metals, Fe, Co and Ni.

It is noted that the synthesis of Li₄FeH₆ has been achieved (X_A = 0.99).³⁸ This compound was synthesised with hydrogen pressures of 6.1 GPa at 900 °C. This compound is metastable and decomposes at room temperature and pressure. Therefore the X_A threshold for [FeD₆]⁴⁻ may be 0.99. Unfortunately, the deutride analogue has not been structurally characterised and as such is not included in this study. This indicates that the X_A threshold designated here may be exceeded under some experimental conditions with a decrease in stability of the product. Hence, based on previous experimental work, this threshold is a suggested guideline to determine which cations can be utilised in the design of novel compounds.

When complex monocation and bication borohydrides are treated using identical methodology, the R² coefficient of the linear trend is below 0.5. If monocation alkali metals are modelled alone, an R² of 0.954 is achieved. The reason why this model works for bication 3d transition metal hydride complexes of Fe, Co and Ni and not borohydrides is due to their atomic configuration and, most importantly, the coordination of the T containing anion by the cations. In fact, the complex anion of 18-electron transition metal hydride complexes is typically encompassed within a cage of eight cations, in turn forming 2D or 3D lattices throughout the structure.^5b,c In this regard, each cation is directly contributing to the coordination of multiple anions with equivalent bond strength. The cation–anion coordination in borohydrides is remarkably different to that of complex transition metal hydrides. In monocation alkali metal borohydrides, the anions coordinate around the cation center, for instance Na⁺ is octahedrally coordinated by BH₄⁻ in NaBH₄.³⁹ In these compounds the electronic distribution to each moiety is equal and thus a linear correlation is observed according to the model described above. In multi-valence and bication borohydride complexes the electronic distribution is often uneven. For example, in hexagonal Mg(BH₄)₂ there are five symmetry independent Mg²⁺ and ten symmetry independent BH₄⁻ anions, whereas in LiK(BH₄)₂ the Li⁺ atoms are tetrahedrally coordinated, while the K⁺ ions are coordinated by seven BH₄⁻ units.^39b As a result, the correlation of bication borohydride complexes using the method reported here is not possible. This phenomenon is also true for multi-valence and bication alanate complexes.

Overall, this study allows for the intuitive design of novel transition metal hydrides, by assessing the X_A of the countercations. If X_A falls within experimentally determined thresholds, the synthesis of new complex hydrides should be feasible but more extreme synthesis temperatures and hydrogen pressures may allow for additional, less-stable, complex hydrides to form. Additionally, the estimation of T–D bond lengths will aid structural determination of new transition metal hydrides and in the prediction of physical properties such as T–H(D) stretching modes in vibrational spectroscopy and relative chemical shifts in NMR spectroscopy.

The authors gratefully acknowledge Ms Keelie Munroe for her scientific discussion. This work was partially funded by the Australian Research Council Linkage project LP120100435 and was partially conducted in conjunction with WPI-Advanced Institute for Materials Research, Tohoku University, Japan.

Notes and references

1. G. Li, M. Matsuo, S. Deledda, R. Sato, B. C. Hauback and S.-i. Orimo, Mater. Trans., JIM, 2013, 54, 1532.
2. C. Pistidda, S. Garroni, F. Dolci, E. G. Bardají, A. Khandelwal, P. Nolis, M. Dornheim, R. Gosalawit, T. Jensen, Y. Cerenius, S. Suriñach, M. D. Baró, W. Lohstroh and M. Fichtner, J. Alloys Compd., 2010, 508, 212.
3. S. Satyapal, J. Petrovic and G. Thomas, Sci. Am., 2007, 296, 80.
4. (a) T. Sato, H. Blomqvist and D. Noréus, J. Alloys Compd., 2003, 356, 494; (b) M. Song, D. Ahn, I. Kwon and H. Ahn, Met. Mater., 1999, 5, 485; (c) A. A. C. Asselli and J. Huot, Metals, 2014, 4, 388.
5. (a) A. Züttel, M. Hirscher, B. Panella, K. Yvon, S.-i. Orimo, B. Bogdanović, M. Felderhoff, F. Schüth, A. Borgschulte, S. Goetze, S. Suda and M. T. Kelly, Hydrogen as a Future Energy Carrier, Wiley-VCH Verlag GmbH & Co. KGaA, 2008, p. 165; (b) K. Yvon, Chimia, 1998, 52, 613; (c) K. Yvon and G. Renaudin, Hydrides: Solid State Transition Metal Complexes, John Wiley & Sons, Ltd, 2006.
6. (a) S. Hayashi, Inorg. Chem., 2002, 41, 2238; (b) R. O. Moyer Jr, D. F. R. Gilson and B. H. Toby, J. Solid State Chem., 2011, 184, 1895; (c) D. E. Linn and S. G. Gibbins, J. Organomet. Chem., 1998, 554, 171.
7. (a) S. F. Parker, Coord. Chem. Rev., 2010, 254, 215; (b) H. Hagemann and R. O. Moyer, J. Alloys Compd., 2002, 330, 296; (c) M. Kritikos and D. Noréus, J. Solid State Chem., 1991, 93, 256; (d) H. Hagemann, V. D'Anna, L. M. Lawson Daku, S. Gomes, G. Renaudin and K. Yvon, J. Phys. Chem. Solids, 2011, 72, 286.
8. (a) M. Danaie, A. A. C. Asselli, J. Huot and G. A. Botton, J. Phys. Chem. C, 2012, 116, 25701; (b) M. Herrich, N. Ismail, A. Handstein, A. Pratt and O. Gutfleisch, Mater. Sci. Eng., B, 2004, 108, 28; (c) R. Martinez-Coronado, M. Retuerto and J. A. Alonso, Int. J. Hydrogen Energy, 2012, 37, 4188.
9. Y. Yamada, K. Tajima, M. Okada, M. Tazawa, A. Roos and K. Yoshimura, Thin Solid Films, 2011, 519, 2941.
10. D. F. R. Gilson and R. O. Moyer, Inorg. Chem., 2012, 51, 1231.
11. K. Miwa, S. Takagi, M. Matsuo and S.-i. Orimo, J. Phys. Chem. C, 2013, 117, 8014.
12. S. Takagi, T. D. Humphries, K. Miwa and S. Orimo, Appl. Phys. Lett., 2014, 104, 203901.
13. (a) T. D. Humphries, M. Matsuo, G. Li and S.-i. Orimo, Phys. Chem. Chem. Phys., 2015, 8276; (b) T. D. Humphries, S. Takagi, G. Li, M. Matsuo, T. Sato, M. H. Sørby, S. Deledda, B. C. Hauback and S. Orimo, J. Alloys Compd., 2015 DOI:10.1016/j.jallcom.2014.12.113.
14. B. Karmakar and R. N. Dwivedi, J. Non-Cryst. Solids, 2004, 342, 132.
15. R. T. Sanderson, Science, 1951, 114, 670.
16. A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264.
17. L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570.
18. (a) G. N. Schrauzer, Naturwissenschaften, 1955, 42, 438; (b) Y. Nakamori, K. Miwa, A. Ninomiya, H. W. Li, N. Ohba, S. I. Towata, A. Zuttel and S. Orimo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045126.
19. J. J. Didisheim, P. Zolliker, K. Yvon, P. Fischer, J. Schefer, M. Gubelmann and A. F. Williams, Inorg. Chem., 1984, 23, 1953.
20. P. Zolliker, K. Yvon, P. Fischer and J. Schefer, Inorg. Chem., 1985, 24, 4177.
21. P. Zolliker, K. Yvon, J. D. Jorgensen and F. J. Rotella, Inorg. Chem., 1986, 25, 3590.
22. B. Huang, F. Bonhomme, P. Selvam, K. Yvon and P. Fischer, J. Less-Common Met., 1991, 171, 301.
23. B. Huang, K. Yvon and P. Fischer, J. Alloys Compd., 1995, 227, 121.
24. H. Fahlquist, K. Kadir and D. Noréus, J. Alloys Compd., 2013, 579, 31.
25. G. Renaudin, L. Guenee and K. Yvon, J. Alloys Compd., 2003, 350, 145.
26. B. Huang, F. Gingl, F. Fauth, A. Hewat and K. Yvon, J. Alloys Compd., 1997, 248, 13.
27. B. Huang, K. Yvon and P. Fischer, J. Alloys Compd., 1992, 187, 227.
28. B. Huang and K. Yvon, J. Alloys Compd., 1992, 178, 173.
29. B. Huang, K. Yvon and P. Fischer, J. Alloys Compd., 1993, 197, 65.
30. B. Huang, K. Yvon and P. Fischer, J. Alloys Compd., 1994, 204, 5.
31. R. O. Moyer Jr, S. M. Antao, B. H. Toby, F. G. Morin and D. F. R. Gilson, J. Alloys Compd., 2008, 460, 138.
32. B. Huang, K. Yvon and P. Fischer, J. Alloys Compd., 1992, 190, 65.
33. M. Orlova, J.-P. Rapin and K. Yvon, Inorg. Chem., 2009, 48, 5052.
34. B. Huang, K. Yvon and P. Fischer, J. Alloys Compd., 1994, 210, 243.
35. M. Kritikos, D. Noréus, A. F. Andresen and P. Fischer, J. Solid State Chem., 1991, 92, 514.
36. K. Kadir and D. Noréus, Inorg. Chem., 2007, 46, 3288.
37. E. Orgaz and A. Aburto, J. Phys. Chem. C, 2008, 112, 15586.
38. H. Saitoh, S. Takagi, M. Matsuo, Y. Iijima, N. Endo, K. Aoki and S. Orimo, APL Mater., 2014, 2, 076103.
39. (a) S. Orimo, Y. Nakamori, J. R. Eliseo, A. Zuttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111; (b) Y. Filinchuk, D. Chernyshov and V. Dmitriev, Z. Kristallogr., 2008, 223, 649.

---

Footnote

† Electronic supplementary information (ESI) available: Supporting figures. See DOI: 10.1039/c5cc03654b

---