Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of intramolecular chemical exchange by initial growth rates of spin saturation transfer difference experiments (SSTD NMR)†
M. Teresa
Quirós
a,
Jesús
Angulo
*b and
María Paz
Muñoz
*a
aSchool of Chemistry, University of East Anglia, Earlham Road, NR4 7TJ, Norwich, UK. E-mail: m.munoz-herranz@uea.ac.uk
bSchool of Pharmacy, University of East Anglia, Earlham Road, NR4 7TJ, Norwich, UK. E-mail: j.angulo@uea.ac.uk
First published on 21st May 2015
Abstract
We report here the Initial Growth Rates SSTD NMR method, as a new powerful tool to obtain the kinetic parameters of intramolecular chemical exchange in challenging small organic and organometallic molecules.
Intramolecular chemical exchange is a common phenomenon in organic molecules, and an important process when studying molecular dynamics.1 The chemical exchange rate is as useful as any other chemical kinetic parameter, as it is related to the thermodynamics of the barrier of the exchange process. Examples of chemical exchanges in organic chemistry are atropoisomerism (e.g. ring flip in biphenyl systems), conformational isomerism in aliphatic compounds or rings, rotation around conjugated bonds (e.g. butadienes), tautomerism, hindered internal rotation (e.g. amide bonds), or redistribution and ligand exchange in metal complexes.
Kinetics of chemical exchange in small molecules have been studied by NMR using mainly two different methods: (i) line-shape analysis,2 and (ii) spin saturation transfer experiments (SST).3 Both of them have, however, a number of drawbacks. Line-shape analysis at very high magnetic field can be experimentally of limited applicability, as the coalescence temperature exceeds the boiling points of most solvents.4 SST experiments require a steady state saturation transfer between the exchanging sites (very long saturation time), and the experimental determination of the longitudinal relaxation time constant, T1, of the monitored spin. The latter measurement can be hampered in spectral regions with significant peak overlap.5
Here we propose a new NMR protocol for the easy determination of the kinetics of molecular systems undergoing mutual-site exchange, based on the SST experiment, but avoiding the need to assure steady state conditions and the determination of T1 values. The method uses difference spectroscopy to measure transient spin saturation transfer along increasing saturation times (build-up curve), and the kinetic rate constant is easily determined from the initial slope from a single set of experiments. The pulse sequence corresponds to that used for protein–ligand interactions by STD NMR spectroscopy.6 On these grounds we have called the experiment spin saturation transfer difference (SSTD NMR).
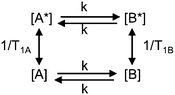
The mutual-site exchange kinetics for two spins A and B (two-site exchange) can be depicted as in Scheme 1 where [A] and [A*], as well as [B] and [B*], are the lower and upper spin-state populations of spins A and B, respectively, T1A and T1B are the longitudinal relaxation time constants of spins A and B, and k is the mutual-site exchange rate constant.7
The rate equation for the magnetization of spin A under saturation of spin B (Scheme 1), taking into account both processes of population exchange, relaxation and chemical exchange, is given by:7
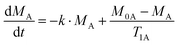 | (1) |
Traditionally, SST experiments have relied on the condition of steady state saturation of spin A, i.e. dMA/dt = 0 (classical “noediff” experiment). Under these conditions, the exchange rate constant, k, is determined using the following equation:7
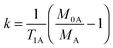 | (2) |
We realized that the method can be reduced to only one type of experiment if we determine the difference spectrum (“equilibrium – saturated” intensity of A) and calculate the fraction of saturation transferred (M0A − MA) over the equilibrium intensity of spin A (M0A). The time evolution of that ratio is given by (see ESI† for details):
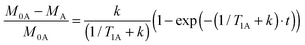 | (3) |
The evolution of ηSSTD for spin A, as a function of the saturation time of spin B is then given by:
| ηSSTD = ηMAXSSTD(1 − exp(−δ·t)) | (4) |
Eqn (4) suggests a more direct way of determining the mutual-site exchange rate constant. The initial slope of the curve of ηSSTDvs. t is given by:
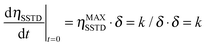 | (5) |
We then propose to use the evolution of the transient saturation transferred to spin A as a function of time to get the kinetic parameters for chemical exchange processes, instead of using the steady state saturation. In this way, the build-up curve of the SSTD factor (ηSSTD) is mathematically fitted to eqn (4), and the fit will yield the parameters ηMAXSSTD and δ. As stated in eqn (5), the product ηMAXSSTD·δ will directly yield the desired rate constant. Additionally, the longitudinal relaxation time constant T1A could also be obtained from these experiments, as δ = R1A + k. Our method improves old transient saturation transfer experiments that involved calibration of a selective 180° pulse, and the measurement of both signals MA and MB.9
Here we demonstrate the applicability of the SSTD NMR method as a powerful and convenient approach to obtain kinetic parameters of intramolecular chemical exchange in small organic molecules and, of particular interest, its straightforward application to organometallic compounds.
One of the most studied chemical exchange process is the rotational barrier in the hindered rotation of N,N-dimethylamides, where the amide bond has partial double bond character developed in the resonance structure (Fig. 1).10 Different NMR methods have been used to study the multi-site exchange kinetics (each methyl is replaced by an equivalent one) on these compounds in different solvents, and much data regarding activation energy, enthalpy and entropy for rotation in many derivatives is available for comparison with our method.7,11 We choose N,N-dimethylacetamide 1 as our model compound, and comparison of the data obtained for 1 with our method and other reported methods is given in Table 1 (see ESI†).
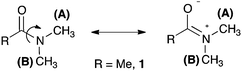 | ||
| Fig. 1 Resonance structure of N,N-dimethylamides showing the hindered rotation around the amide bond. | ||
| Parameter | Method/solvent | ||||
|---|---|---|---|---|---|
| SSTD-NMR (this work)/Tol-d8 | SST-NMR7a/Tol-d8 | Line-shape analysis (1H NMR)11a/CCl4 | Line-shape analysis (1H NMR)11b/(CD3)2CO | Line-shape analysis (13C NMR)11c/neat | |
| E a (kJ mol−1) | 79.7 ± 0.1 | 73.1 ± 1.4 | 70.5 ± 1.7 | 82.0 ± 1.3 | 79.5 ± 0.4 |
| ΔH‡ (kJ mol−1) | 77.2 ± 0.1 | 70.6 ± 1.4 | 68.0 | 79.5 ± 0.4 | 76.6 ± 0.4 |
| ΔS‡ (J mol−1 K−1) | 11.5 ± 0.4 | −10.5 ± 5.0 | −15.0 ± 5.1 | 13 ± 8 | 3 ± 4 |
| ΔG‡298 (kJ mol−1) | 73.8 ± 0.1 | 73.7 ± 2.0 | 72.5 | 75.3 ± 0.4 | 75.7 ± 0.4 |
Our results are in excellent agreement with the reported data using spin saturation transfer techniques and line-shape analysis.12 It is worthy to note that ΔS‡ is very difficult to measure by NMR methods hence the wide range of values reported.7
Given the good results obtained for the model compound 1, we decided to test the method in more challenging substrates in organic and organometallic chemistry.
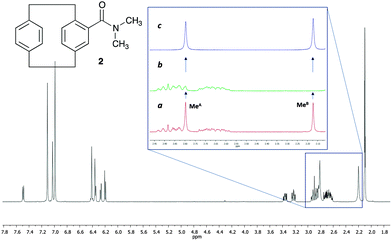
As a challenging compound we decided to analyse 4-N,N-dimethylamido[2.2]paracyclophane 2,13 in which one of the signals of interest is overlapped with the signals from the methylene groups of the paracyclophane system (Fig. 2). As mentioned before, the existence of signal overlap usually makes the analysis of the rotational barriers by SST experiments more complicated, as the T1 is difficult to measure. Using our method, at any saturation time in the difference spectrum, we only observe the exchanging signals and all the other overlapping signals cancel out, making it possible to obtain the k value directly and also the T1 in the same experiment (Note that at least one of the exchanging resonances should be isolated).
In 2, the interconversion of the N-methyl groups takes place through rotation around the amide bond. Since the signal of one of these methyl groups (MeA in Fig. 2) overlaps with other signals in the spectra, the signal chosen for the selective saturation was that corresponding to the isolated methyl group (signal at 2.17 ppm, MeB in Fig. 2). The expansions in Fig. 2 show the spectra without (a), and with (b) saturation of the MeB signal, as well as the difference spectrum (c). As it can be observed in expansion (b), after saturation of MeB its signal disappears, and, due to the saturation transfer process, the signal of MeA decreases its intensity. NOE effects were absent (see ESI† for details).
The ηSSTD factor was calculated dividing the value of the integral of MeA in the SSTD NMR spectrum (c) by the value of the integral of the MeB in spectra (a). The values of ηSSTD were obtained for different saturation times at each temperature and their plot versus saturation time gave exponential curves in which a plateau was reached at long saturation times. The exponential fit allowed us to obtain the values of the rate constants of the process at the different temperatures (see ESI† for details). The values of the rate constants, although obtained at lower temperatures, are higher in this compound than those obtained for the N,N-dimethylamide 1 (see ESI†), suggesting in a first approach, that the rotation through the amide bond is faster in 2. The data obtained was used to calculate the thermodynamic parameters using the Eyring equation (ΔH‡ = 60.0 ± 0.1 kJ mol−1; ΔS‡ = −22.0 ± 0.4 J mol−1 K−1; Ea (298 K) = 62.5 ± 0.1 kJ mol−1; ΔG‡ (298 K) = 66.5 ± 0.1 kJ mol−1). The values of enthalpy, activation energy and Gibbs energy are lower in 2 that in 1 (compare with values in Table 1). This is in agreement with the weaker double-bond character of the amide functionality in 2, due to further conjugation of the carbonyl group with the aromatic system, which makes the rotation of the amide bond easier.14
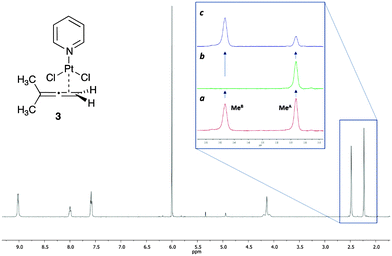
The interest of our group in organometallic chemistry and mechanistic investigations led us to demonstrate the applicability of this new methodology in metal–allene chemistry.15 We used as model compound a platinum–allene complex, already described in the literature and relevant to our current investigations, PtCl2(dimethylallene)(pyridine) 3 (Fig. 3).16 In this complex, the platinum is coordinated with the terminal double bond of the allene (less substituted) in an η2 fashion and the substituents in both terminal positions of the allene are perpendicular to each other. The two methyl substituents therefore are non equivalent, being one closer to the platinum and the other in the opposite face of the allene plane. As a result, in the 1H NMR spectra, both methyl groups appear as different signals (Fig. 3). The chemical exchange in this complex occurs due to the π-face exchange of the coordinated allene around the metal. According to this rotation, the metal could be at the “top” or at the “bottom” of the allene and both methyl groups interconvert between them.
The study of the rotational movement of platinum–allene complexes has been attempted using line-shape analysis for complex 3 and the analogous tetramethylallene–platinum complex.16 Although values for the rate constants could be obtained for the tetramethylallene derivative,17 complex 3 showed a much slower rotation in CDCl3, and no kinetic data could be extracted.
We also observed slow rotation in complex 3, which made the study impossible in the most common deuterated solvents (CDCl3, Tol-d8, THF-d8). The best solvent was 1,1,2,2-tetrachloroethane-d2, which allowed us to study the process at higher temperatures. However, in this solvent, the chemical shift of the signals of the two methyl groups did not change with temperature, with the coalescence temperature too high and in the range of the complex decomposition temperature. This is in agreement with the previous study,16a and it is the reason why analysis of this compound with the line-shape analysis method is not possible. However, the spin saturation transfer process is still efficient enough in the range of temperatures where the complex is stable, which allowed us to apply our SSTD NMR methodology successfully in this challenging system.
The expansion in Fig. 3 shows the spectra of 3 without (a), and with (b) saturation, as well as the difference spectrum (c). The saturation of MeB led to the disappearance of its signal in the 1H NMR, and to the decrease in the intensity of the signal of MeA due to the saturation transfer process (b, Fig. 3). NOE effects were absent (see ESI† for details).
Since the signal of the methyl group under observation, MeA, is isolated from the other signals of the complex, the analysis can be performed by comparing the intensity of its signals in spectra (c) and (a). The values of ηSSTD were obtained and plotted versus the saturation times, and the exponential fit of these curves allowed us to obtain the values of the rate constants of the process at the different temperatures (Fig. 4). The final values for the thermodynamic parameters were calculated using the Eyring equation (ΔH‡ = 77.7 ± 0.4 kJ mol−1; ΔS‡ = −36.0 ± 1 J mol−1 K−1; Ea (298 K) = 80.2 ± 0.4 kJ mol−1; ΔG‡ (298 K) = 88.4 ± 0.4 kJ mol−1). These values are in agreement with a slow rotational movement of the allene on an axis passing through the centre of the coordinated double bond linked to the platinum, as suggested previously.16a,18 Application of this method to an in-depth study of the dynamic behaviour of platinum–allene complexes, including the study of intermolecular exchange processes, is being carried out in our group and will be reported in due course.
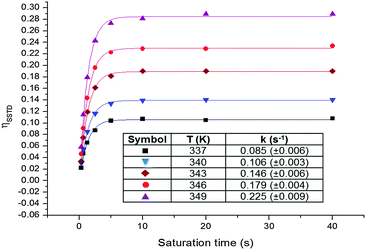 | ||
| Fig. 4 Plots of the ηSSTDvs. saturation time at different temperatures for PtCl2(dimethylallene)(pyridine) 3, and table with the obtained rate constants. | ||
In summary, the Initial Growth Rates SSTD NMR method described here is very robust, and easy to use (it is based on the well-known STD NMR pulse sequence). It presents additional advantages over traditional approaches, and we envision that it will be of wide interest amongst the organic and organometallic community, and that it will be applied in the study of many chemical exchange processes in challenging compounds.19
Authors thank Dr C. J. Richards and R. Arthurs (UEA) for a pure sample of amide 2, and Dr C. Macdonald for his help with the NMR experiments. Funding by the University of East Anglia and the EPSRC (EP/L012855/1) is gratefully acknowledged (MTQ). This work was supported by the A-I Chem Channel program, selected by the European INTERREG IV A France (Channel) – England Cross-border cooperation Programme, co-financed by ERDF.
Notes and references
- (a) A. D. Bain, Prog. Nucl. Magn. Reson. Spectrosc., 2003, 43, 63–103 CrossRef CAS PubMed; (b) A. D. Bain, Mod. Magn. Reson., 2006, 421–427 CAS; (c) A. D. Bain, Annu. Rep. NMR Spectrosc., 2008, 63, 23–48 CAS , and references therein.
- (a) L. Reeves, R. Shaddick and K. Shaw, Can. J. Chem., 1971, 49, 3683–3691 CrossRef CAS; (b) T. Drakenberg, K. Dahlqvist and S. Forsen, J. Phys. Chem., 1972, 76, 2178–2183 CrossRef CAS; (c) F. Fujiwara and C. Airoldi, J. Phys. Chem., 1984, 88, 1640–1642 CrossRef CAS; (d) H. S. Gutowsky and C. H. Holm, J. Chem. Phys., 1956, 25, 1228–1234 CrossRef CAS PubMed.
- (a) S. Forsen and R. A. Hoffman, Acta Chem. Scand., 1963, 6, 1787–1788 CrossRef PubMed; (b) S. Forsen and R. A. Hoffman, J. Chem. Phys., 1963, 39, 2892–2901 CrossRef CAS PubMed.
- J. Sandstrom, Dynamic NMR Spectroscopy, Academic, New York, 1982 Search PubMed.
- L. Castanar, P. Nolis, A. Virgili and T. Parella, J. Magn. Reson., 2014, 244, 30–35 CrossRef CAS PubMed.
- (a) M. Mayer and B. Meyer, Angew. Chem., Int. Ed., 1999, 38, 1784–1788 CrossRef CAS; (b) M. Mayer and B. Meyer, J. Am. Chem. Soc., 2001, 123, 6108–6117 CrossRef CAS PubMed; (c) J. Angulo, P. M. Enriquez-Navas and P. M. Nieto, Chem. – Eur. J., 2010, 16, 7803–7812 CrossRef CAS PubMed.
- (a) R. L. Jarek, R. J. Flesher and S. K. Shin, J. Chem. Educ., 1997, 74, 978–982 CrossRef CAS; (b) H. M. McConnell, J. Chem. Phys., 1958, 28, 430 CrossRef CAS PubMed; (c) K. Ugurbil, J. Magn. Reson., 1985, 64, 207–219 CAS; (d) S. F. Bellon, D. Chen and E. R. Johnston, J. Magn. Reson., 1987, 73, 168–173 CAS.
- S. Kemper, M. K. Patel, J. C. Errey, B. G. Davis, J. A. Jones and T. D. W. Claridge, J. Magn. Reson., 2010, 203, 1–10 CrossRef CAS PubMed.
- F. W. Dahlquist, K. J. Longmuir and R. B. Du Vernet, J. Magn. Reson., 1975, 17, 406–410 CAS.
- W. E. Stewart and T. H. Siddall III, Chem. Rev., 1970, 70, 517–551 CrossRef CAS.
- (a) See ref. 2a; (b) See ref. 2b; (c) See ref. 2c; (d) T. Drakenberg, K.-I. Dahlqvist and S. Forsén, Acta Chem. Scand., 1970, 24, 694–702 CrossRef CAS PubMed; (e) M. T. Rogers and J. C. Woodbrey, J. Phys. Chem., 1961, 66, 540–546 CrossRef; (f) R. C. Neuman, Jr. and V. Jonas, J. Am. Chem. Soc., 1968, 90, 1970–1975 CrossRef CAS; (g) R. C. Neuman, Jr., W. R. Woolfenden and V. Jonas, J. Phys. Chem., 1969, 73, 3177–3180 CrossRef; (h) K. F. Morris and L. E. Erikson, J. Chem. Educ., 1996, 73, 471–473 CrossRef CAS; (i) M. Rabinovitz and A. Pines, J. Chem. Soc. B, 1968, 1110–1111 RSC; (j) M. Rabinovitz and A. Pines, J. Am. Chem. Soc., 1969, 91, 1585–1589 CrossRef CAS.
- The T1 values obtained with this method (see ESI† for details) are in agreement with those obtained with the inversion-recovery experiment. The small differences in the values are due to the different magnetic fields of the spectrometers used (see ref. 7a).
- N. Dendele, F. Bisaro, A.-C. Gaumont, S. Perrio and C. J. Richards, Chem. Commun., 2012, 48, 1991–1993 RSC.
- For amide dissociation enthalpies calculated by DFT, see: I. I. Marochkin and O. V. Dorofeeva, Comput. Theor. Chem., 2012, 991, 182–191 CrossRef CAS PubMed.
- (a) M. P. Muñoz, M. C. de la Torre and M. A. Sierra, Adv. Synth. Catal., 2010, 352, 2189–2194 CrossRef PubMed; (b) M. P. Muñoz, M. C. de la Torre and M. A. Sierra, Chem. – Eur. J., 2012, 18, 4499–4504 CrossRef PubMed; (c) C. Hurtado-Rodrigo, S. Hoehne and M. P. Muñoz, Chem. Commun., 2014, 50, 1494–1496 RSC.
- (a) K. Vrieze, H. C. Volger, M. Gronert and A. P. Praat, J. Organomet. Chem., 1969, 16, P19–P22 CrossRef CAS; (b) K. Vrieze, H. C. Volger and A. P. Praat, J. Organomet. Chem., 1970, 21, 467–475 CrossRef CAS.
- A value of k = 30 s−1 was observed for the tetramethylallene analogue in CDCl3 at −46 °C.
- Line-shape analysis has been applied in the study of the dynamic behaviour of gold-allene complexes in solution: T. J. Brown, A. Sugie, M. G. D. Leed and R. A. Widenhoefer, Chem. – Eur. J., 2012, 18, 6959–6971 CrossRef CAS PubMed . For a general review, see: W. Yang and S. K. Hashmi, Chem. Soc. Rev., 2014, 43, 2941–2955 RSC.
- This method can be extended to multi-site exchange and unequal populations, as long as the equations are properly modified, see: S. Forsen and R. A. Hoffman, J. Chem. Phys., 1964, 40, 1189–1196 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cc02941d |
| This journal is © The Royal Society of Chemistry 2015 |