[V@Ge₈As₄]³⁻ and [Nb@Ge₈As₆]³⁻: encapsulation of electron-poor transition metal atoms

Abstract

[K([2.2.2]crypt)]⁺ salts of [V@Ge₈As₄]³⁻ and [Nb@Ge₈As₆]³⁻ were obtained by extraction of quaternary phases with en/[2.2.2]crypt. The V–Ge–As anion is the first Zintl anion incorporating a (formal) V⁵⁺ cation, thus the smallest cation ever embedded within a main group (semi-)metal cage. It represents the second example of a novel 12-vertex cluster architecture. The bonding situation was elucidated by quantum chemistry, also allowing for a precise assignment of Ge vs. As atoms, being indistinguishable by X-ray diffraction.

---

The research on endohedral clusters, which comprise homo- or heteroatomic main group (semi-)metal cages with interstitial transition metal atoms, is a rapidly advancing field of modern inorganic, materials and theoretical chemistry.¹ This is not only triggered by the beauty of the resulting structures but also by the chemical and physical properties of the compounds that can be viewed as transition metal-doped main group (semi-)metal clusters, thus molecular models to doped (semi-)metals.²

Recent discoveries include clusters that form non-classical, non-deltahedral polyanions with group 14 element atoms³ unexpectedly, since all known classical molecular Zintl anions of group 14 elements are electron deficient and form multicenter-bonded deltahedra. This clearly indicated a great impact of the interstitial atom on the electronic and structural properties of such molecules. The latest addition to this field has been the report on a new non-deltahedral 12-vertex cluster topology by Goicoechea et al.,⁴ which was observed for a paramagnetic cluster [Ru@Ge₁₂]³⁻ and could be shown to be more stable in this system than any further isomeric geometries, such as an icosahedron.

However, most endohedral clusters published to date are based on the inclusion of electron-rich transition metal atoms – most often in a d¹⁰ electronic configuration. Exclusions have been species with interstitial lanthanide ions,^2a,3c,d,5 [Cp₅Ti₄Sn₁₅],^6a and species detected via mass spectrometry, like [V@Si₁₆]⁺.^6b Combining two different main group elements within the cluster shell recently opened up a new direction, as the systems are free to adjust their charge by isolobal substitution of formal (E¹⁴)²⁻ or (E¹⁴)⁻ by (E¹⁵)^±0. This way, many new topologies have been observed that were not accessible with only one of the main group elements involved.⁷

In the present case, formal Ge⁻ besides As atoms served to compensate for the high charge of an interstitial group 5 metal ion M⁵⁺, forming the first endohedral clusters comprising these extremely hard cations of electron-poor transition metals V and Nb. The resultant ternary clusters possess a −3 charge perfect for crystallization with [K([2.2.2]crypt)]⁺ counterions.

The title compounds [K([2.2.2]crypt)]₃[V@Ge₈As₄]·2tol·en (1, 12%) and [K([2.2.2]crypt)]₃[Nb@Ge₈As₆]·tol·en (2, 22%) were obtained by extraction of solid mixtures K–Ge–As–V or K–Ge–As–Nb (with about 3 atom% of the group 5 metal according to EDX measurements) with ethane-1,2-diamine (en)/[2.2.2]crypt; the quoted solids were obtained by fusing equimolar amounts of K, Ge and As with about 0.1 equivalents of V in a silica glass ampoule, or by simply fusing K, Ge, and As in an Nb ampoule, respectively. After 3d at room temperature, the extracts were filtered and layered with toluene. The corresponding extraction of the ampoule material was previously observed for the only further known Nb-containing intermetallic complex within [Rb([2.2.2]crypt)]₂{Rb[NbAs₈]}.⁸

According to X-ray structure analyses,‡ both cluster anions exhibit non-deltahedral topologies (Fig. 1). The one observed in 1 accords with the novel 12-vertex topology of [Ru@Ge₁₂]³⁻,⁴ and the anion in 2 possesses the 14-vertex cage that has so far only been observed with interstitial lanthanide cations.³

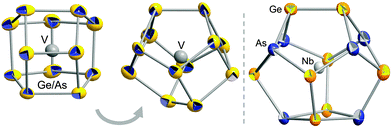Fig. 1 Structures of the cluster anions [V@Ge₈As₄]³⁻ (two views, left and center) and [Nb@Ge₈As₆]³⁻ (right). Ellipsoids shown with 50% probability. Atomic distribution of Ge–As atoms in 2 as determined by perturbation theory calculations.⁹

The persistence of the cluster anions in the two compounds in solution and the gas phase was confirmed by ESI mass-spectrometry on a fresh DMF–en solution (Fig. 2); the spectra further indicate that a complex mixture of species coexists (see ESI†), which explains the relatively low yields of 1 and 2.

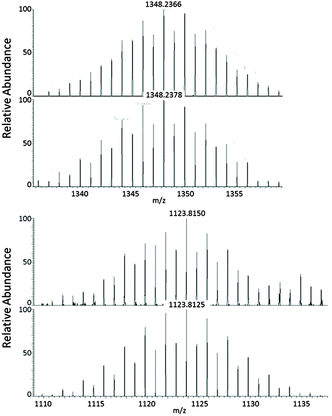Fig. 2 ESI-MS(−) spectra (measured: top versus calculated: bottom) of [K([2.2.2]crypt)][V@Ge₈As₄]⁻ (m/z = 1348.23; top) and [Nb@Ge₈As₆]⁻ (m/z = 1123.81; bottom). The isotopic patterns are well reproduced by simulations, and all measured m/z values agree with the simulated ones within deviations of less than 0.003 m/z. The mass peaks are partially overlaid by mass peaks of further fragments, some of which could be assigned to other anions. The corresponding data are provided in the ESI.†

Perturbation theory treatment⁹ based on DFT calculations^10,11 served to find the energetically most favorable distribution of atoms in the cluster anion in 2, which is by ≥11 kJ mol⁻¹ energetically preferred to other distributions (see ESI†). The result was used for the refinement of the atomic positions in 2 shown in Fig. 1, leading to mean interatomic distances of 2.4965 Å (Ge–As), 2.5011 Å (Ge–Ge), 2.8562 Å (Nb–As), and 2.9654 Å (Nb–Ge).

The [V@Ge₈As₄]³⁻ anion in 1 is disordered over three orientations (82.6%, 9.0%, 8.4%) in the crystal. Additionally, calculations show that several preferable isomers are very close in energy (nine within 4.6 kJ mol⁻¹; see ESI†). Thus, all main group atom positions were refined with a mixed Ge : As occupation (0.67 : 0.33; mean distances (Ge–As)–(Ge–As) 2.515–2.521 Å, mean distances V–(Ge–As) 2.719–2.728 Å within the three orientations), and thermal ellipsoids are given as mixed sites in Fig. 1.

Both anion topologies are highly related: the two Ge–As cages differ only by two atoms, which complete a four-ring in 2 that replaces a two-atom unit in the anion in 1. The close structural relationship might be a hint to both the stepwise formation of such clusters and the ability to adopt a certain cage size in accordance with the size of the interstitial metal atom.

Regarding the sizes of the involved metal atoms in the anions of 1 and 2 as well as in related intermetalloid clusters,¹² it seems plausible to find similar structures for elemental combinations with similar relative atomic sizes, such as for Nb–Ge–As versus Ln–Pb–Bi. However, the structural analogy found for V–Ge–As and Ru–Ge is not intuitive, as the Ru atom was reported to be a formal “Ru²⁻” (d¹⁰ configuration, an atomic radius of Ru: 130 pm), thus being anionic in nature and much larger than formal V⁵⁺ (68 pm).

Inspired by this apparent contradiction, the electronic situation within the cluster anions in 1 and 2 was compared with the situation found at different elemental compositions by means of quantum chemistry.^10,11 For a better understanding of the rather new 12-vertex clusters, the calculations on hypothetical [Rh@Ge₁₂]³⁻ and the diamagnetic analog to [Ru@Ge₁₂]³⁻ were included.⁴

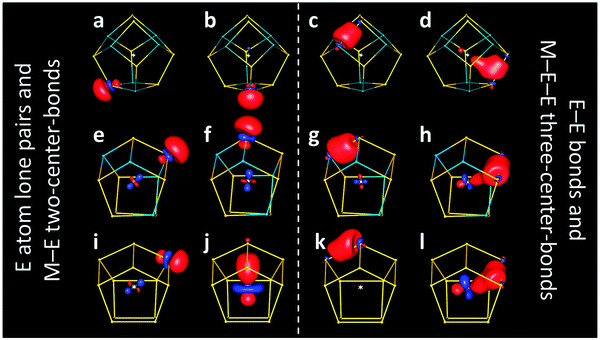
For both the (empty) 12-atom and 14-atom cluster shells, each atom is bonded to three neighbors. For electron precision, five electrons are thus required per atom, three for the bonds and two for the lone pair, which are necessary for the angular local geometry. This results in a 60 (70) electron system for the 12-atom (14-atom) shell, and can be realized, for instance, by 12 (14) Ge⁻ or As atoms in [Ge_nAs_N–n]ⁿ⁻, N = 12, 14 and n = 0, 1, … N. Electron precision, that is the presence of solely two-electron-two-center bonds and lone pairs, corresponds to the result of localization procedures carried out for the orbitals resulting from DFT calculations. These yield localized molecular orbitals (LMOs) that are centered to more than 97% at either one or two atoms.¹³ If n is larger than the total charge q of an intermetalloid cluster anion [M@Ge_nAs_N–n]^q−, electron precision is achieved upon consideration of a maximum formal charge g at the interstitial transition metal atom from group g (g = n − q).

[Nb@Ge₈As₆]³⁻ (n − q = g = 5) thus would be most likely described as a (formally) fivefold charged metal ion in an electron-perfect shell of group 15 or pseudo-group 15 elements. Calculated LMOs (Fig. 3a–d) support this, at least as a rough approximation: they are dominantly located at one or two atoms of the cage, but of course show (Mulliken¹⁴) contributions from the central atom. For LMOs representing lone pairs, these contributions amount to 5–8% (Fig. 3a and b), and for the Ge–As bonds to 5–12%. For the Ge–Ge bonds they are higher, 13–22% for the Ge–Ge bond perpendicular to the two nearly parallel ones with 22% Nb contribution (Fig. 3d). Clearly, the actual charge of the central atom – as far as it can be defined at all – is thus much smaller, but the formal charge of +5 is still justified as all LMOs are dominated by cage contributions.

Fig. 3 Representative localized molecular orbitals for calculated clusters [Nb@Ge₈As₆]³⁻ (top, a–d), [V@Ge₈As₄]³⁻ (center, e–h) and [Rh@Ge₁₂]³⁻ (bottom, i–l). For each type of LMOs, those with the lowest (a, e, i, c, g, and k) or highest (b, f, j, d, h, and l) contribution of the central atom are shown, respectively.

This also holds for the 12-atom-cage cluster [V@Ge₈As₄]³⁻, analyzed at its most stable As : Ge atomic distribution (Fig. 3e–h). The respective numbers of the contribution of the V atom are 3–5% for LMOs representing lone pairs, 3–14% for As–Ge bonds and 12–21% for Ge–Ge bonds. Still, also for these anions, a description of formal M⁵⁺ in an electron-precise shell of solely group 15 and pseudo-group 15 elements with bonds between all neighboring main group atoms, assisted by (or delocalized towards) the valence orbitals of the central metal atom, is still justified, at least as an approximation.

However, this is no longer the case for interstitial transition metal atoms of electron-richer groups, such as presently hypothetical [Rh@Ge₁₂]³⁻ (as the diamagnetic analog of paramagnetic [Ru@Ge₁₂]³⁻ with 59 electrons in sum). For the Rh analog (g = 9), the above description would require a formal oxidation state of 9+ (“Rh⁹⁺”), which is not reasonable. Indeed, LMOs reveal a different picture than found for the group 3 or 5 metal atoms. Here, only eight Ge atoms possess lone pairs (Fig. 3i), while the four remaining Ge atoms (the only ones connecting two four-rings of the cluster shell; Fig. 3j) form a two-center bond with the Rh atom in the center instead, which is polarized towards the latter (Ge : Rh contributions of 1 : 2). Thus, in contrast to the above compounds, four of the LMOs are not dominated by cage contributions, but by the d orbital contributions of the central atom. Accordingly, the respective four Ge atoms cannot be regarded as pseudo-group 15 element atoms anymore. Concerning Ge–Ge bonds, each bond again corresponds to an LMO, as for the compounds discussed above, but the trend towards Ge–Ge–Rh three-center bonds is further enhanced for most of them (Rh contributions up to ca. 27%; Fig. 3l). In analogy to the discussion above, i.e. by neglecting the Rh contributions to the Ge–Ge bonds, the formal charge of Rh is +1 if the four two-center LMOs shown in Fig. 3j are fully assigned to Rh, or even +5 if these are interpreted as bonds between Rh and Ge.

We note in passing that assignment of the formal charge calculated from population analyses based on the total electron density yields negative formal charges for the central atom, both for Rh and Ru.⁴

In conclusion, it was shown that electron-poor V and Nb atoms can be accommodated within endohedral clusters [V@Ge₈As₄]³⁻ and [Nb@Ge₈As₆]³⁻, the first members of an M–Ge–As cluster family. These possess non-deltahedral topologies, described recently for much larger metal ions (La, Ce, Nd, Gd, Tm, and Ru) within cages of either larger main group metal atoms (Sn, Pb, and Bi), or only Ge atoms. In line with the pseudo-element concept (Ge⁻ ≙ As⁰), V is encapsulated as V⁵⁺, making it the hardest cation ever embedded within endohedral Zintl anions. Experiments and complementary DFT calculations showed that (a) an ionic description of the bonding situation within intermetalloid clusters is appropriate for interstitial metal atoms up to group 3 (and Ln), and qualitatively also for formally higher charged and thus more polarizing metal ions, such as M⁵⁺ from group 5. (b) Embedding electron-rich interstitial metal atoms (such as from groups 8 or 9) qualitatively changes the bonding situation: the resulting system does no longer exhibit a classical (pseudo-)group 15, three-bonded situation. Thus, in spite of identical total electron numbers that cause identical overall structures, the bonding situations can exhibit distinct differences.

This work was supported by the Alexander von Humboldt Stiftung and the Friedrich Ebert Stiftung.

Notes and references

1. (a) S. Scharfe, F. Kraus, S. Stegmaier, A. Schier and T. F. Fässler, Angew. Chem., Int. Ed., 2011, 50, 3630; (b) T. F. Fässler, Struct. Bonding, 2011, 140, 91; (c) S. C. Sevov and J. M. Goicoechea, Organometallics, 2006, 25, 5678; (d) F. S. Kocak, P. Zevalij, Y.-F. Lam and B. W. Eichhorn, Inorg. Chem., 2008, 47, 3515; (e) M. Ruck, Angew. Chem., Int. Ed., 2001, 40, 1182.
2. (a) F. Lips, M. Hołyńska, R. Clérac, U. Linne, I. Schellenberg, R. Pöttgen, F. Weigend and S. Dehnen, J. Am. Chem. Soc., 2012, 134, 1181; (b) N. Korber, Angew. Chem., Int. Ed., 2009, 48, 3216.
3. (a) B. Zhou, M. S. Denning, D. L. Kays and J. M. Goicoechea, J. Am. Chem. Soc., 2009, 131, 2802; (b) J.-Q. Wang, S. Stegmaier and T. Fässler, Angew. Chem., Int. Ed., 2009, 48, 1998; (c) F. Lips, R. Clérac and S. Dehnen, Angew. Chem., Int. Ed., 2011, 50, 960; (d) R. Ababei, W. Massa, B. Weinert, P. Pollak, X. Xie, R. Clérac, F. Weigend and S. Dehnen, Chem. – Eur. J., 2015, 1, 386.
4. G. Espinoza-Quintero, J. C. A. Duckworth, W. K. Myers, J. E. McGrady and J. M. Goicoechea, J. Am. Chem. Soc., 2014, 136, 1210.
5. (a) B. Weinert, F. Weigend and S. Dehnen, Chem. – Eur. J., 2012, 18, 13589; (b) B. Weinert, F. Müller, K. Harms, R. Clérac and S. Dehnen, Angew. Chem., Int. Ed., 2014, 53, 11979.
6. (a) C. B. Benda, M. Waibel and T. F. Fässler, Angew. Chem., Int. Ed., 2015, 2, 522; (b) P. Claes, E. Janssens, V. T. Ngan, P. Gruene, J. T. Lyon, D. J. Harding, A. Fielicke, M. T. Nguyen and P. Lievens, Phys. Rev. Lett., 2011, 107, 173401.
7. (a) F. Lips and S. Dehnen, Angew. Chem., Int. Ed., 2009, 48, 6435; (b) F. Lips and S. Dehnen, Angew. Chem., Int. Ed., 2011, 50, 955; (c) F. Lips, R. Clérac and S. Dehnen, J. Am. Chem. Soc., 2011, 133, 14168; (d) R. Ababei, J. Heine, M. Hołyńska, G. Thiele, B. Weinert, X. Xie, F. Weigend and S. Dehnen, Chem. Commun., 2012, 48, 11295.
8. H. G. von Schnering, J. Wolf, D. Weber, R. Ramirez and T. Meyer, Angew. Chem., Int. Ed., 1986, 25, 353.
9. (a) F. Weigend, C. Schrodt and R. Ahlrichs, J. Chem. Phys., 2004, 121, 10380; (b) F. Weigend and C. Schrodt, Chem. – Eur. J., 2005, 11, 3559; (c) F. Weigend, J. Chem. Phys., 2014, 141, 134103.
10. TURBOMOLE Version 6.6, © TURBOMOLE GmbH 2014. TURBOMOLE is developed by the University of Karlsruhe and Forschungszentrum Karlsruhe 1989–2007, TURBOMOLE GmbH since 2007; available from http://www.turbomole.com.
11. (a) D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 33, 8822; (c) K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652; (d) K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119; (e) M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173; (f) H. Stoll, B. Metz and M. Dolg, J. Comput. Chem., 2002, 23, 767; (g) A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805; (h) A. Schäfer, A. Klamt, D. Sattel, J. C. W. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187.
12. (a) B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832; (b) R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
13. (a) S. F. Boys, Rev. Mod. Phys., 1960, 32, 296; (b) J. M. Foster and S. F. Boys, Rev. Mod. Phys., 1960, 32, 300; (c) D. L. Bergman, L. Laaksonen and A. Laaksonen, J. Mol. Graphics Modell., 1997, 15, 301.
14. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of syntheses, X-ray crystallography (SCXRD and PXRD), energy dispersive X-ray spectroscopy (EDX), electrospray ionization mass spectrometry (ESI-MS), and DFT calculations. CCDC 1030791 and 1030792. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4cc10086g

‡ CCDC 1030791 (1) and 1030792 (2). DFT calculations with Turbomole¹⁰ GGA exchange–correlation functional BP86,^11a,b def-SVP basis sets,^11c,d and effective core potentials (ECPs) for Sn, Bi, Nb, Ru, Rh,^11e,f and COSMO.^11g,h Contours drawn at 0.1 a.u. using gOpenMol.^13c

---