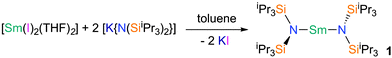Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The first near-linear bis(amide) f-block complex: a blueprint for a high temperature single molecule magnet†
Nicholas F.
Chilton
,
Conrad A. P.
Goodwin
,
David P.
Mills
* and
Richard E. P.
Winpenny
*
School of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: richard.winpenny@manchester.ac.uk; david.mills@manchester.ac.uk
First published on 5th November 2014
Abstract
We report the first near-linear bis(amide) 4f-block compound and show that this novel structure, if implemented with dysprosium(III), would have unprecedented single molecule magnet (SMM) properties with an energy barrier, Ueff, for reorientation of magnetization of 1800 cm−1.
Since their initial discovery,1 single molecule magnets (SMMs) have been lauded as candidates for high density data storage devices.2 A major breakthrough in the field3 occurred in 2003 with the observation of SMM behavior in a monometallic {TbPc2}− complex with an energy barrier, Ueff = 230 cm−1.4 The ensuing decade saw rapid growth in lanthanide SMMs5 with the Ueff barrier to magnetization reversal increased to 652 cm−1 for another derivative of {TbPc2},6 and 585 cm−1 for a polymetallic Dy@{Y4K2} complex.7 The highest blocking temperature TB (i.e. the temperature at which hysteresis is observed) was also increased to 14 K, via an N23−˙ radical bridge in a {Tb2N23−˙} complex.8
Although three of these milestones employ the TbIII ion, by far the most utilized lanthanide ion in SMMs is DyIII by virtue of its unique electronic structure.9 Apart from a radical-bridged {Dy2N23−˙} complex,10 nearly all polymetallic DyIII-based SMMs possess negligible interactions between magnetic spin centres, and instead rely on the single ion anisotropy of DyIII (i.e. the local crystal field environment) to provide the barrier to the reversal of magnetization. Intra- or intermolecular interactions are often detrimental to the performance of DyIII SMMs so that doping a small amount of the paramagnetic ion into a diamagnetic host lattice (usually the YIII analogue) often results in an increased Ueff.7
An electrostatic model for the design of ideal ligand environments to exploit the maximal anisotropy of DyIII has been postulated,11,12 and shown to be in good agreement with multi-configurational complete active space Self consistent field (CASSCF) ab initio calculations12 that are often employed to examine 4f complexes, pioneered by Chibotaru.7,13 Electrostatic approaches suggest that the optimal ligand environment to exploit the oblate spheroidal electron density of DyIII is axial, where rigorously axial systems have the benefit of maintaining a single, unique quantization axis for the total angular momentum mJ states.14 A set of unadulterated mJ states implies that the probability of quantum tunnelling of the magnetization (QTM) is reduced, therefore increasing magnetic relaxation times.2
The simplest axial ligand environment is a linear two-coordinate complex with donor atoms exclusively on a single Cartesian axis; the Ueff barrier is so large for the {Dy5} and {Dy4K2} alkoxide complexes7 because of the strongly axially repulsive crystal field potentials along the local z-direction of each DyIII. Other compounds such as [(C8H8)2Ln]− (ref. 15) or Cloke's bis(arene) lanthanide complexes16 are sometimes described as linear, but lack donor atoms directly on the axis. Linear 3d-metal compounds also show remarkable magnetic behaviour with very high Ueff values.17 A one coordinate lanthanide complex [DyO]+ has been considered theoretically with a very large Ueff predicted,14 however such an entity is not chemically feasible.
Very low coordination numbers for 4f-ions are difficult to achieve as these are large, electropositive ions, which require a sterically demanding ligand. Such a pro-ligand HN(SiiPr3)2 was designed, and synthesised from ClSiiPr3 and LiHN(SiiPr3), and this was converted to the group 1 transfer agent [KN(SiiPr3)2] with KH. Reacting two equivalents of [KN(SiiPr3)2] with samarium(II) diiodide yields the mononuclear homoleptic bis(amide) complex, [(iPr3Si)2N–Sm–N(SiiPr3)2] 1 (Fig. 1, see ESI† for details).
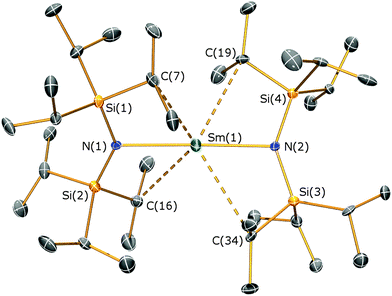
Complex 1 is the first near-linear f-element complex, with an N–Sm–N angle of 175.52(18)° in the solid state (Fig. 2, see ESI† for details); this near-linearity contrasts with the bent C–Ln–C angles of [LnII{C(SiMe3)3}2] complexes (Ln = Sm, Yb, Eu).18–20 The bulky iPr groups are vital for the isolation of a homoleptic complex, as [Sm{N(SiMe3)2}2(THF)2] exhibits additional O-donors.21 The Sm–N distances in 1 [2.483(6) Å] are longer than those observed in [Sm{N(SiMe3)2}2(THF)2] [mean Sm–N 2.433(9) Å] but this is compensated by 1 exhibiting four short Sm⋯Cmethine distances [Sm⋯C 3.082(7)–3.224(7) Å] that are closer than the analogous Sm⋯Cmethyl contacts observed in [Sm{N(SiMe3)2}2(THF)2] [Sm⋯C 3.32(1)–3.46(1) Å].21 The approximately planar SmNSi2 fragments in 1 are staggered with respect to each other (twist angle of 44.42°), with the deviation from 90° attributed to agostic Sm⋯Cmethine interactions.
Formally each nitrogen atom carries a single negative charge and the SmII ion is divalent, with an [Xe]4f6 configuration. The f6 configuration leads to a formally diamagnetic 7F0 ground state, with close lying excited states that provide a non-zero magnetic moment at room temperature. Magnetic measurements on 1 give a room temperature magnetic moment of 3.62 μB that falls towards zero at low temperature (Fig. S2 and S3, ESI†). This is clearly incompatible with interesting low temperature magnetic behaviour. However, the structure of 1 is close to the ideal linear arrangement to stabilize the large angular momentum states of DyIII and produce monstrous uniaxial magnetic anisotropy.
Such a DyIII compound is challenging to make; we believe a route via the heteroleptic [Dy{N(SiiPr3)2}2I] treated with the potassium salt of a large anion might work through precipitation of a potassium iodide. Other routes can be imagined, and here we present predictions of the magnetic properties of such a complex, intending to inspire synthetic work towards the linear DyIII complex, and, more ambitiously, the isoelectronic TbII analogue.
The properties of [(iPr3Si)2N–Dy–N(SiiPr3)2]+2 are predicted by CASSCF/RASSI/SINGLE_ANISO22ab initio calculations (see ESI† for details) employing the structure of 1, where SmII has been replaced by DyIII. The validity of the method was tested by calculating the variable temperature magnetic behavior of 1, where the agreement is excellent (Fig. S2 and S3, ESI†). DyIII has a 6H15/2 ground multiplet, which is split by the crystal field into eight Kramer's doublets with total angular momentum projections mJ = ±1/2, ±3/2,… ±15/2. The ab initio calculations show that the lowest six Kramers doublets are the almost pure mJ states of mJ = ±15/2, ±13/2, ±11/2, ±9/2, ±7/2 and ±5/2, sharing a common quantization axis (Fig. 3 and Tables S1 and S2, ESI†). The two most energetic doublets are strongly mixed; a characteristic of low symmetry complexes due to the lack of a rigorous molecular C∞ axis.14 Along the main magnetic axis these two states can be expressed as |ψab〉 = 64%|±3/2〉 + 26%|∓1/2〉 and |ψcd〉 = 68%|±1/2〉 + 31%|∓3/2〉 and (Table S2, ESI†), giving the most energetic Kramers doublet a large gy value of ∼17.5 perpendicular to the main magnetic axis.
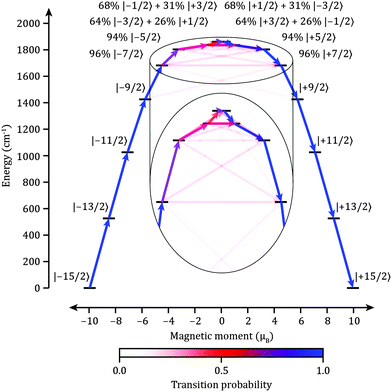 | ||
| Fig. 3 Electronic states and magnetic transition probabilities for the ground 6H15/2 multiplet of 2 in zero field. The x-axis shows the magnetic moment of each state along the main magnetic axis of the molecule. Relaxation commences from the |−15/2〉 state and only includes pathways which reverse the magnetization. Relaxation probabilities are calculated based on a magnetic perturbation and are normalized from each departing state (see ESI† for details). | ||
Magnetic relaxation in lanthanides follows three possible routes: (1) QTM within the ground doublet (e.g. |−15/2〉 → |+15/2〉 in Fig. 3), (2) thermally assisted QTM (TA-QTM) via excited states (e.g. |−15/2〉 → |−13/2〉 → |+13/2〉 → |+15/2〉), or (3) an Orbach process composed of direct and/or Raman mechanisms (e.g. |−15/2〉 → |−13/2〉 → |+15/2〉). The most probable pathway depends on the composition of the states involved and their interactions with phonons. For example, the slow magnetic relaxation for {Dy4K2} was shown to occur via the first or second excited states (TA-QTM), depending on the number and location of neighboring DyIII ions providing a source of transverse magnetic field.7 The states with opposing magnetic projections are mixed proportionally to the product of the transverse field and the transverse g-factors and therefore TA-QTM will occur via the excited state which has transverse g-factors above a certain threshold or where its main magnetic axis is non-collinear with that of the ground state. All non-QTM transitions are induced by the vibrational modes of the lattice (phonons) which create local oscillating magnetic fields through modulation of dipolar fields as well as an oscillating crystal field potential.23 To a first approximation, we can associate the probability of a phonon induced transition with the average magnetic13,14,24 and crystal field perturbation matrix elements (see ESI† for details).
Compared to all known DyIII complexes the calculated properties for 2 are unique with very small transverse g-factors and a common principal axis for the lowest six Kramers doublets. This suggests that both the probability of QTM within the ground doublet and TA-QTM is vanishingly small until the two most energetic doublets. Orbach relaxation is also strongly disfavoured in the low lying states as magnetic transition probabilities due to phonons are miniscule (Fig. 3). Efficient magnetic relaxation will only occur via the highest energy doublets (Fig. 3, Fig. S4 and Tables S4 and S5, ESI†). Therefore the ab initio calculation predicts Ueff ≈ 1800 cm−1 for 2 – far greater than any complex to date. Whilst such calculations may over-estimate the energies of the crystal field states,25,26 we can predict a TB in excess of 77 K as such temperatures are often around 1/20th of the Ueff value if QTM within the ground doublet is disfavored, e.g. the TB/Ueff ratios for {Tb2N23−˙}, {Mn12} and {Mn6} are approximately 1/16, 1/15 and 1/13 cm−1 K−1, respectively. Calculations for the TbII analogue 3, which is also a 4f9 ion, predict analogous behavior to 2 (Table S6, ESI†). The high local symmetry at the DyIII site implies that the nuclear quadrupole and hyperfine interactions will be axially symmetric, preventing efficient QTM within the lower energy doublets.
To examine the stability of 2, we have performed ab initio calculations for modified geometries where the N–Dy–N angle and the Dy–N bond lengths have been altered by ±0.5° and ±0.01 Å, respectively (Fig. S5, ESI†). The results show that 2 is stabilized when the Dy–N bond length is shortened and the N–Dy–N angle is closer to 180° compared to 1, yielding more favorable electronic properties. These calculations do not take into account the inclusion of a counter-ion in the structure, which may have consequences for crystal packing and the local structure of 2.
Compound 1 is the first near-linear bis(amide) 4f-block complex. It allows us to propose a blueprint for the first generation of ‘high-temperature’ SMMs, with blocking temperatures exceeding that of liquid N2 (77 K). The synthesis of the proposed archetypes, viz. the DyIII and TbII analogues of 1, is currently underway in our laboratory, however we believe this is a target many other groups should be pursuing. Calculations on other fn ions suggest that f9 is ideal; even for the oblate f8 TbIII analogue, 4, we find that the pseudo-doublets show strong mixing between the |−mJ〉 and |+mJ〉 projections, (Tables S7 and S8, ESI†), which would lead to strong zero-field QTM.
While 2 would have a huge Ueff, an even higher Ueff barrier might be possible if dianionic monodentate ligands could be incorporated, e.g. [(iPr3Si)2C–Dy–C(SiiPr3)2]−, containing dianionic methanediides. Our preliminary results suggest this could raise Ueff by a factor of 1.2 to 1.3. The incredible advances made in low coordination number metal–organic compounds in the last decade suggest that such hypothetical complexes are now chemically feasible. These metal–organic compounds are becoming of great importance in molecular magnetism.8,10,27,28
This work was supported by the EPSRC (grant number EP/K039547/1) (UK). N.F.C. thanks The University of Manchester for a President's Doctoral Scholarship. R.E.P.W. thanks The Royal Society for a Wolfson research merit award. We would like to thank J. P. S. Walsh for assistance with graphics.
Notes and references
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092 RSC.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed.
- C. R. Ganivet, B. Ballesteros, G. de la Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Chem. – Eur. J., 2013, 19, 1457 CrossRef CAS PubMed.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS PubMed.
- D. Gatteschi, Nat. Chem., 2011, 3, 830 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 RSC.
- L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086 RSC.
- (a) F. Mares, K. Hodgson and A. Streitwieser, Jr., J. Organomet. Chem., 1970, 24, C68 CrossRef CAS; (b) K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952 CrossRef CAS PubMed.
- For example, J. G. Brennan, F. G. N. Cloke, A. A. Sameh and A. Zalkin, Chem. Commun., 1987, 1668 RSC.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577 CrossRef CAS PubMed.
- C. Eaborn, P. B. Hitchcock, K. Izod and J. D. Smith, J. Am. Chem. Soc., 1994, 116, 12071 CrossRef CAS.
- C. Eaborn, P. B. Hitchcock, K. Izod, Z.-R. Lu and J. D. Smith, Organometallics, 1996, 15, 4783 CrossRef CAS.
- G. Qi, Y. Nitto, A. Saiki, T. Tomohiro, Y. Nakayama and H. Yasuda, Tetrahedron, 2003, 59, 10409 CrossRef CAS PubMed.
- W. J. Evans, D. K. Drummond, H. Zhang and J. L. Atwood, Inorg. Chem., 1988, 27, 575 CrossRef CAS.
- (a) G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig and P. Neogrady, et al. , Comput. Mater. Sci., 2003, 28, 222 CrossRef; (b) V. Veryazov, P. Widmark, L. Serrano-Andrés, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626 CrossRef CAS; (c) F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher and B. O. Roos, et al. , J. Comput. Chem., 2010, 31, 224 CrossRef CAS PubMed; (d) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970 Search PubMed.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328 CrossRef CAS PubMed.
- R. Marx, F. Moro, M. Dörfel, L. Ungur, M. Waters, S. D. Jiang, M. Orlita, J. Taylor, W. Frey, L. F. Chibotaru and J. van Slageren, Chem. Sci., 2014, 5, 3287 RSC.
- E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 6243 Search PubMed.
- F. Moro, D. P. Mills, S. T. Liddle and J. van Slageren, Angew. Chem., Int. Ed., 2013, 52, 3430 CrossRef CAS PubMed.
- R. A. Layfield, Organometallics, 2014, 33, 1084 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Full synthetic details, crystallography, NMR spectroscopy, magnetism, and ab initio and magnetic relaxation methodologies. CCDC 1017031. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4cc08312a |
| This journal is © The Royal Society of Chemistry 2015 |