Nanopore analysis of amyloid fibrils formed by lysozyme aggregation

Abstract

The measurement of single particle size distributions of amyloid fibrils is crucial for determining mechanisms of growth and toxicity. Nanopore sensing is an attractive solution for this problem since it gives information on aggregates’ shapes with relatively high throughput for a single particle technology. In this paper we study the translocation of lysozyme fibrils through quartz glass nanopores. We demonstrate that, under appropriate salt and pH conditions, lysozyme fibrils translocate through bare quartz nanopores without causing significant clogging. This enables us to measure statistics on tens of thousands of translocations of lysozyme fibrils with the same nanopore and track their development over a time course of aggregation spanning 24 h. Analysis of our events shows that the statistics are consistent with a simple bulk conductivity model for the passage of rods with a fixed cross sectional area through a conical glass nanopore.

---

Introduction

Nanopores can obtain physical data about individual molecules and larger aggregates in solution and offer the advantage of not needing chemical labels. The basic concept of nanopore sensing is to apply a potential across a single nanoscale pore separating two large electrolyte reservoirs and measure the resulting ionic current. Single molecules can then be identified as they pass through or block the pore thereby transiently altering the flow of ions. Solid-state nanopores are able to measure translocations of proteins in their native state since the pore diameter can be made larger than in common biological pores.¹ This has enabled the detection and characterisation of a wide range of monomeric proteins.^2–7

Solid-state nanopores also have potential as a platform for studying protein aggregation. Amyloids formed by aberrant protein aggregation are implicated in a wide range of diseases such as Alzheimer's and Parkinson's disease.⁸ Amyloid fibrils are the archetypal amyloid state distinguished by their high aspect ratio together with cross β-sheet structure.⁹ Accurate techniques for measuring the kinetics behind the formation of such amyloid fibrils are crucial for understanding the basis of their toxicity.¹⁰ However, the study of amyloid fibrils is complicated due to the heterogeneity of sizes and non-linear rate laws for formation.¹¹ Single molecule techniques can reveal information about these heterogeneous sub-populations. Electron microscopy and atomic force microscopy have been widely used to characterize dimensions of amyloid fibrils but face limits in their statistical throughput and require immobilisation of fibrils onto surfaces. In contrast, nanopores have the potential for high statistical throughput as shown by recent commercial applications of nanopore sequencing methods.

Yusko et al.¹² presented the first measurements of protein aggregates of amyloid beta (Aβ) protein with solid-state nanopores. They were only able to observe translocations of these aggregates when the nanopore was coated with a mobile lipid bilayer since without this fluidic coating the nanopore was quickly clogged.¹³ Using such a bilayer coating, they collected statistics on a total of ∼600 translocations of aggregates over 4 days. An increase in translocation current blockades and dwell times was observed over the course of aggregation and sub-populations of mature amyloid fibrils and protofibrils were assigned from the statistics of the current blockades.

In this work, we analyse the translocation of lysozyme amyloid fibrils through glass nanopores under an applied electric field. Importantly we show that, at low pH and salt concentration, we are able to measure significant statistics on translocations without applying a coating to prevent clogging. Furthermore, we track the translocation statistics at successive time points and observe a characteristic increase in blockade current and translocation time over the course of the aggregation. We simulate translocation statistics using a simple model of a cylindrical rod passing through a conical nanopore at fixed velocity and find good agreement between simulated and experimental data.

Methods

We followed a protocol based on the work of Arnaudov et al.¹⁴ and Hill et al.¹⁵ for formation of lysozyme amyloid fibrils. A 6 wt% solution of hen egg white lysozyme (Sigma-Aldrich) was aggregated by incubation at 60 °C in an aqueous solution of 20 mM NaCl at pH 2 (adjusted using HCl). The solution was seeded with 1% by volume of a previously incubated solution and filtered through a 0.22 μm syringe filter before incubation.

The aggregation was monitored at different time points with atomic force microscopy (AFM) using a Nanosurf Mobile S in tapping mode. The sample was immobilized for AFM by depositing onto a freshly cleaved piece of mica. The aggregation was also confirmed by labelling of diluted samples of the solution with thioflavin T (ThT) (see ESI†). This ensemble measurement is a standard indicator of amyloid fibril formation since ThT fluorescence increases when bound to a fibril.¹⁶

Glass nanopores were fabricated by the laser-assisted pulling of quartz capillaries (Sutter), inner diameter 0.2 mm, outer diameter 0.5 mm, using a commercial laser puller (Sutter P-2000), with cleaning procedure as previously described.² The pulling parameters yield a pointed end (see Fig. 1b) with mean final diameter of 16 nm, as estimated by scanning electron microscopy (SEM). The quartz nanopore is sealed onto a channel between two reservoirs, cis and trans (Fig. 1c), on a polydimethylsiloxane (PDMS) device. The assembled measurement cell is then plasma cleaned and an electrolyte solution with 0.5 KCl, 20 mM NaCl and pH 2 (adjusted using HCl) is added to the reservoirs and degassed in a desiccator. The pH of translocation experiments therefore matches the pH used for the aggregation incubation. An Ag/AgCl electrode is inserted in both reservoirs, the reservoir with the nanopore tip is grounded and a negative voltage applied to the trans reservoir to induce translocations of the positively charged lysozyme (note the current shown in Fig. 2 is the magnitude). The whole chip was placed inside a sealed plastic container to reduce evaporation of the electrolyte. The ionic current through the nanopore was amplified with an Axopatch 200B amplifier, filtered with a 10 kHz 8^th order Bessel low-pass filter and sampled at 100 kHz. The baseline current was recorded before the addition of protein to check for low noise characteristics. The solution in the cis reservoir was then replaced with a solution containing lysozyme fibrils. All ionic current traces were analysed using a custom written program to detect events from the background noise (see ESI†).

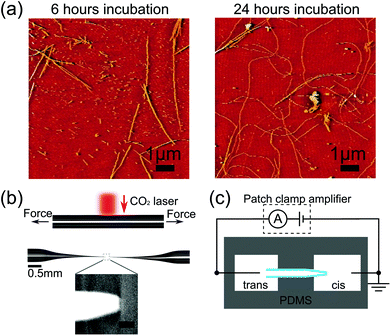Fig. 1 (a) Atomic force microscopy images of lysozyme fibrils, after aggregating for (left) 6 hours, (right) 24 hours. Note these images are from the same samples as those used for nanopore translocations in Fig. 2 and 3. (b) Optical images showing a glass capillary before and after pulling to form a glass nanopore. Inset shows scanning electron micrograph of the tip of a typical glass nanopore. Scale bar represents 50 nm. (c) Schematic of experimental setup with cis (where lysozyme is added) and trans reservoirs.

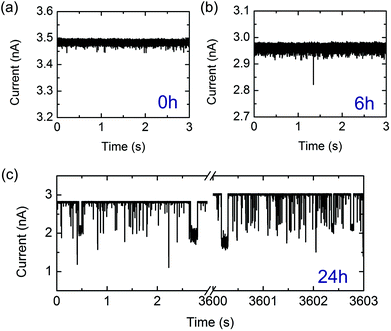Fig. 2 Representative examples of current traces arising from lysozyme monomers and fibrils detected with a nanopore at −500 mV in a 0.5 M KCl solution at pH = 2 (note current is shown as positive magnitude). Note the differences in vertical scaling. (a) Lysozyme monomers detection after t = 0 hours of incubation. (b) Lysozyme fibrils translocating following 6 hours of incubation. (c) Lysozyme fibrils translocating following 24 hours of incubation. Traces from the beginning and end of the experiment are shown and translocations were recorded throughout. The slight increase in baseline current is attributed to electrolyte evaporation (see ESI†).

Results

Fig. 1a and 1b show example AFM images after 6 hours and 24 hours of aggregation. We observe an increase in fibril length over the time scale of incubation so that after 24 hours most fibrils are longer than the field of view which is a limitation of AFM analysis for amyloid fibrils. Ensemble ThT fluorescence measurements also show an increase in fluorescence over several days confirming an increase in the number of β-sheet domains which constitute the fibrils (see ESI†). High resolution AFM studies¹⁵ show that lysozyme aggregation is initiated by thin protofibrils which nucleate and grow to several hundred nanometres in length before assembling into thicker mature fibrils.

Having confirmed the formation of lysozyme fibrils by ThT fluorescence and AFM we investigated their translocation through quartz glass nanopores. We measured the ionic current signals of lysozyme at different stages of aggregation; after 0, 3, 6 and 24 hours of incubation. We took a sample of the incubation solution at every time point and diluted it to a concentration of 0.1 wt% (except t = 0 hour which was diluted to 0.025 wt%). To enable a quantitative comparison of the formation of lysozyme fibrils we used nanopores with similar resistance of around 3 nA of current at −500 mV and with a background noise level of 2.4–2.6 pA RMS at 5 kHz bandwidth. We subjected nanopores with background noise outside this range to 18 V of potential difference to try to reduce noise levels,¹⁷ and if the noise level did not improve to within the range above, the pore was discarded. We carried out each experiment within an hour of the end of the corresponding incubation, and the sample was kept at 4 °C during that time to inhibit further aggregation. Translocations were typically recorded for 1 hour. Whenever the same pore was used for more than one experiment, the cis chamber was washed multiple times with pure electrolyte. We then recorded the current trace for several minutes to ensure there was no remaining lysozyme indicated by the absence of any detectable translocation events. After this we repeatedly washed with the new sample solution to avoid its dilution. The change in resistance of the nanopore after cleaning was consistently found to be comparable to the drift seen during measurements due to slow evaporation (within 10%). In cases where the resistance dramatically decreased or increased, we considered the nanopore to be broken or blocked and excluded it from further experiments.

Initially, we measured the current signals from monomeric lysozyme (at t = 0 hours). In agreement with previous measurements of monomeric proteins with solid-state nanopores, we observe very short translocation times for lysozyme (Fig. 2a with event statistics in Fig. 3a). It is likely that only a small fraction of monomeric proteins are recorded due to the fast translocation timescales of a monomeric protein compared with the bandwidth of the experiment.^2,5 It is also possible that a substantial proportion of these current spikes are due to several proteins passing through the pore in fast succession so they are not resolved independently. To confirm that the monomer signal that we detected was not an artefact, we measured the signal from an empty electrolyte solution over a period of eight hours. This yielded an average of six events per hour, less than one thousandth of the monomer event frequency. After 6 hours of incubation, we measured similarly short and low amplitude translocations (Fig. 2b) occasionally with a larger amplitude event. However after incubation for 24 hours, we observe a high frequency of high amplitude events which reach up to half the baseline current level (Fig. 2c). We assign these large events to the passage of long mature fibrils, as indicated by the AFM image of 24 hours incubation.

Fig. 3 Heat plots of peak current change divided by the baseline current against event duration of monomer/fibril translocation events. Measurements were performed at −500 mV, 0.5 M KCl, pH = 2 using extractions from the same aggregation run (0–24 h). Coloured bars indicate the number of events per bin. Colour scaling is the same in all figures, but relative to the bin with the largest number of points in each plot. (a) Lysozyme monomers (0 h) N (number of events) = 11 177; (b) 1 h incubation N = 44 647; (c) 6 h incubation N = 48 387; (d) 24 h incubation N = 160 551. Different nanopores (but with similar resistance) were used for each time point and the current levels after one hour recording at −500 mV were (a) −3.8 nA, (b) −3.0 nA, (c) −3.0 nA, (d) −3.0 nA. (e) A plot of three simulated current peak traces generated using our simple fibril translocation model. (f) A scatter plot of N = 300 000 simulated events with fibril lengths exponentially distributed in the range 2 to 1000 nm so that there are more events for shorter lengths. The black line is a plot of means of the maximum current change distributions at each value of event duration.

Interestingly, we are able to measure the translocation of thousands of lysozyme fibrils without significant clogging of the nanopore. Fig. 2c shows a measurement where we applied −500 mV for one hour and measured translocations without the signatures of pore clogging (which is a decrease in pore conductance and an increase in baseline noise). In contrast Yusko et al.¹² found that a lipid coating was needed to prevent clogging when measuring translocation of Aβ fibrils through silicon nitride nanopores. We suggest that this is due to the measurement conditions used – Yusko et al. use a pH of 7.4 which is relatively close to the isoelectric point of the Aβ protein (pI ∼ 5.5) and a 2 M KCl electrolyte concentration. Both these factors are likely to promote strong van der Waals attraction of the fibrils to the nanopore walls. In contrast we use a pH of 2 which is significantly below the pI = 11 of lysozyme¹⁸ and also below that of quartz¹⁹ (pI ∼ 2.2). We chose a 0.5 M KCl concentration which provides a trade-off between reduced sticking at lower salt concentrations but also lower signal.

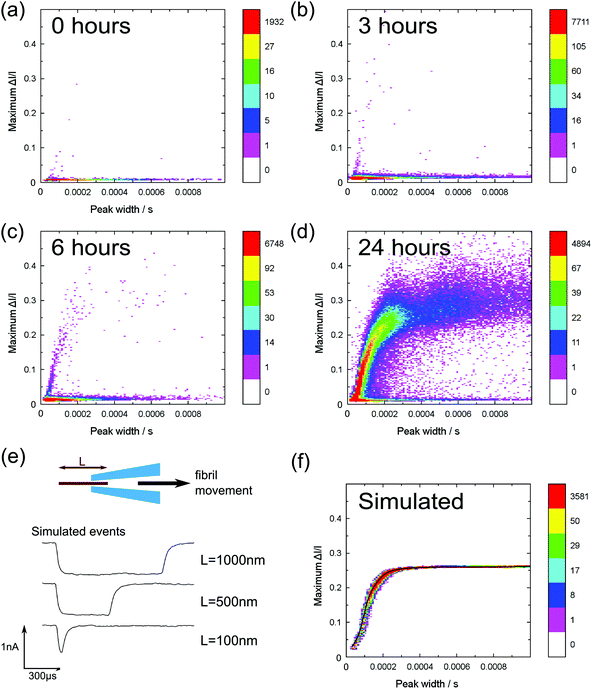
In Fig. 3a–d we show 2D heat map histograms of the translocation statistics at 0, 1, 6 and 24 hours. All timepoints are from the same aggregation run – it is essential to analyse aggregation from the same run since it is well known that small difference in incubation conditions can strongly affect the kinetics of amyloid fibril formation.²⁰ The monomer events are characterized by small event amplitudes and a wide range of event durations, clearly visible in all of the data shown in Fig. 3a–d). With increasing incubation time, Fig. 3b–3d, the events of the incubated lysozyme solutions shows a plateauing growth of event amplitudes with increasing event durations. This plateauing can be easily explained by fibrils which are longer than the effective sensing region of the glass nanopore (∼80% of the voltage is dropped over the final 500 nm from the tip) and the smaller current change values are due to fibrils which do not span the entire sensing region.

In order to rationalise our results, we developed a dynamic model to simulate translocations of fibrils through a conical nanopore for comparison with the experimental data. The fibrils were approximated as rods of fixed diameter, with the diameter taken from calibrated AFM measurements of mature fibrils.¹⁵ We also included the observed values of noise, approximated as Gaussian noise in the model, and the effect of the 8-pole Bessel filter. The full details of the simulation are given in the ESI.† The simulated translocation events were then passed through the same event detection algorithm used for the experimental data so that the results could be directly compared (Fig. 3e and f). In our model we assume that the fibril translocation time scales linearly with the length i.e. all fibrils translocate at constant velocity. Typical simulated example traces for three different fibril lengths are shown in Fig. 3e. The velocity, pore radius and conical angle used in the simulation were calculated by a least squares fit (using the method of steepest descent) of simulation data to the 24 hour incubation experimental data. The result of the simulation is shown in Fig. 3f – the black line represents the mean of the maximum current change distributions at each value of event duration of the simulated data. We note that the simulation likely breaks down for short fibrils a few hundred nanometres in length since, as discussed earlier, there will also be protofibrils in this range. Protofibrils tend to be thinner than mature fibrils. Also the effective sensing length of the glass nanopore is a few hundred nanometres so the velocity will no longer be constant during the translocation when the fibril length is also on the order of a few hundred nanometres. Nevertheless the simulation with fitted parameters captures the essential trend of the data and the expected plateauing in current change for fibrils longer than the sensing length. The spread in experimental data points for long duration translocations is significantly larger than that expected from our simulations which assume only baseline noise. We attribute this to the increased probability of interactions between the pore and fibril for longer fibril lengths which can create an additional spread in current change values and is not present in our simulations.

A central question for further development of the technique is how can we relate the number of observed events to the concentration of the fibril length in the bulk reservoir solution? This requires a detailed understanding of the translocation rate (the number of fibrils passing through the pore per unit time per unit concentration) as a function of fibril length. In general, the translocation rate of polymers into a nanoscale pore is determined by the combined effects of diffusion, electrophoretic forces, electro-osmotic flows and entropic barriers.²¹ In the case of DNA it is possible to characterise translocation rates as a function of length using commercially available DNA ladders. For amyloid fibrils, monodisperse lengths are not readily available but potential methods for generating them are sonication induced scission²² or chromatography based separation. These calibrations are needed so that we can map the event number distribution to a concentration profile and also determine the spread in translocation times for a fibril of fixed length. Further theoretical understanding of capture rates and translocation mechanisms for molecules with high persistence lengths can also help in this regard.

Conclusion

We have demonstrated the ability to generate significant statistics on the translocation of lysozyme fibrils by using a low pH = 2 which helps to increase electrostatic repulsion between the nanopore walls and the fibrils and therefore minimises clogging due to irreversible van der Waals attractions. This demonstrates that simple nanopore systems, without sophisticated surface passivation treatment, can be readily applied to measuring dynamics of protein aggregation by tuning the experimental conditions. We then show that our event distributions agreed with a simple model for the passage of a cylindrical rod through a conical pore and measured a clear increase in large amplitude events over time. The ultimate goal of this research is to map the statistics of nanopore translocations into a distribution of the concentration of different lengths of fibrils in solution. To achieve this, further experiments are needed to provide calibration samples of fibrils with well-defined lengths which will give information on the spread of translocation times for a particular length and also the translocation rate as a function of fibril length.

Acknowledgements

We thank Therese Herling, Alex Buell and Tuomas Knowles for advice on formation of amyloid fibrils. N.A.W.B. acknowledges funding from the EPSRC NanoDTC program and an EPSRC doctoral prize award and U.F.K. acknowledges funding from an ERC starting grant, PassMembrane (261101).

References

1. A. J. Storm, J. H. Chen, X. S. Ling, H. W. Zandbergen and C. Dekker, Nat. Mater., 2003, 2, 537–540.
2. W. Li, N. A. W. Bell, S. Hernández-Ainsa, V. V. Thacker, A. M. Thackray, R. Bujdoso and U. F. Keyser, ACS Nano, 2013, 7, 4129–4134.
3. D. Pedone, M. Firnkes and U. Rant, Anal. Chem., 2009, 81, 9689–9694.
4. M. Firnkes, D. Pedone, J. Knezevic, M. Döblinger and U. Rant, Nano Lett., 2010, 10, 2162–2167.
5. C. Plesa, S. W. Kowalczyk, R. Zinsmeester, A. Y. Grosberg, Y. Rabin and C. Dekker, Nano Lett., 2013, 13, 658–663.
6. L. J. Steinbock, S. Krishnan, R. D. Bulushev, S. Borgeaud, M. Blokesch, L. Feletti and A. Radenovic, Nanoscale, 2014, 6, 14380–14387.
7. N. A. W. Bell and U. F. Keyser, J. Am. Chem. Soc., 2015, 137, 2035–2041.
8. C. A. Ross and M. A. Poirier, Nat. Med., 2004, 10, S10–S17.
9. A. W. P. Fitzpatrick, G. T. Debelouchina, M. J. Bayro, D. K. Clare, M. A. Caporini, V. S. Bajaj, C. P. Jaroniec, L. Wang, V. Ladizhansky, S. A. Müller, C. E. MacPhee, C. A. Waudby, H. R. Mott, A. De Simone, T. P. J. Knowles, H. R. Saibil, M. Vendruscolo, E. V. Orlova, R. G. Griffin and C. M. Dobson, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5468–5473.
10. T. P. J. Knowles, M. Vendruscolo and C. M. Dobson, Nat. Rev. Mol. Cell Biol., 2014, 15, 384–396.
11. T. P. J. Knowles, C. A. Waudby, G. L. Devlin, S. I. A. Cohen, A. Aguzzi, M. Vendruscolo, E. M. Terentjev, M. E. Welland and C. M. Dobson, Science, 2009, 326, 1533–1537.
12. E. C. Yusko, P. Prangkio, D. Sept, R. C. Rollings, J. Li and M. Mayer, ACS Nano, 2012, 6, 5909–5919.
13. E. C. Yusko, J. M. Johnson, S. Majd, P. Prangkio, R. C. Rollings, J. Li, J. Yang and M. Mayer, Nat. Nanotechnol., 2011, 6, 253–260.
14. L. N. Arnaudov and R. de Vries, Biophys. J., 2005, 88, 515–526.
15. S. E. Hill, J. Robinson, G. Matthews and M. Muschol, Biophys. J., 2009, 96, 3781–3790.
16. R. Khurana, C. Coleman, C. Ionescu-Zanetti, S. A. Carter, V. Krishna, R. K. Grover, R. Roy and S. Singh, J. Struct. Biol., 2005, 151, 229–238.
17. E. Beamish, H. Kwok, V. Tabard-Cossa and M. Godin, Nanotechnology, 2012, 23, 405301.
18. K. Rezwan, A. R. Studart, J. Voros and L. J. Gauckler, J. Phys. Chem. B, 2005, 109, 14469–14474.
19. G. Parks, Chem. Rev., 1965, 65, 177–198.
20. B. Morel, L. Varela, A. I. Azuaga and F. Conejero-Lara, Biophys. J., 2010, 99, 3801–3810.
21. M. Muthukumar, J. Chem. Phys., 2010, 132, 195101.
22. Y. Y. Huang, T. P. J. Knowles and E. M. Terentjev, Adv. Mater., 2009, 21, 3945–3948.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5an00530b

---