Electronic and transport properties of carbon and boron-nitride ferrocene nanopeapods

Abstract

Electronic and transport properties of novel ferrocene based carbon nanotube (CNT) and boron-nitride nanotube (BNNT) nanopeapods, including Fe(Cp)₂@CNT, Fe₂(Cp)₃@CNT, Fe(Cp)₂@BNNT, and Fe₂(Cp)₃@BNNT (where Cp refers as cyclopentadiene), are investigated using the density functional theory and non-equilibrium Green's function methods. Computed electronic structures of the Fe(Cp)₂@CNT and Fe₂(Cp)₃@CNT nanopeapods suggest that their electric conductivity is primarily contributed by the CNT π channel while the electron hopping from the core Fe(Cp)₂ or Fe₂(Cp)₃ to the sheath CNT may have some contribution to the transport properties. Encapsulating Fe(Cp)₂ into BNNT is more favorable for the electron conduction, owing to the splitting of the BNNT bandgap by the Fe(Cp)₂ state. In contrast, introducing Fe₂(Cp)₃ into the BNNT is not beneficial to the conduction due to intramolecular electron transfer within the core Fe₂(Cp)₃ which can cause a trap effect. Because the transport channels can be changed by the applied bias voltage, the transport properties cannot be solely predicted from the electronic structures of infinite systems alone. For computing transport properties, we use two-probe device model systems with a finite-sized nanopeapod sandwiched between two CNT electrodes. Again, we find that encapsulating either Fe(Cp)₂ or Fe₂(Cp)₃ into CNTs has little effect on the conductivity owing to the strong metallic character of the CNT sheath. Encapsulating Fe(Cp)₂ into BNNTs can notably enhance electron conducting due to electron hopping from the core Fe(Cp)₂ to the sheath BNNT. Encapsulating Fe₂(Cp)₃ into BNNTs, however, has little effect on the electron conductivity of BNNT nanopeapods due to the trap effect of the longer guest molecules. Hence, the length of guest molecules can effectively tune electronic and transport properties of the BNNT nanopeapods.

---

1 Introduction

Carbon nanotubes are capable of encapsulating guest atoms or molecules into their inner cylindrical space, thus forming a quasi-one-dimensional core–sheath structure of X@CNT, where X denotes the core atoms or molecules. Thus far, a large number of organic and inorganic species, such as fullerenes,^1–6 single elements,^7,8 multimeric thiophene oligomers,^9,10 methyl chloride,¹¹ oxides,¹²etc. have already been introduced into CNT's cylindrical inner space as guest molecules, thereby open exciting possibility of creating new materials that can be tailored to a particular electronic functionality. For example, the iron-fullerene complexes (η⁵-Cp)FeC₆₀R₅ (R = Me and Ph; Cp = C₅H₅) have been successfully encapsulated into CNTs by Nakamura et al.¹³ Li et al. demonstrated “ferrocene nanopeapods” by cramming ferrocene molecules into the CNTs.¹⁴

Boron nitride nanotubes (BNNTs)^15,16 are another prevailing tubular nanomaterials which have also been the subject of extensive studies over the past decade. Like CNTs, BNNTs also possess many intriguing properties such as strong hardness, high thermal conductivity and chemical inertness.^17–19 Indeed, BNNTs are known to be more chemically and thermally stable than CNTs.²⁰ As such, BNNTs are especially suitable for the task of shielding and protecting guest molecules from external chemical attack.²¹ Many previous studies have reported that BNNTs can be used to encapsulate metal nanowires (Ni, Co, Fe, and Cu),^22–26 oxides (α-Al₂O₃ and Al₁₈B₄O₃₃),^27,28 SiC carbides,^29,30 GaN nitrides,^31,32 potassium halide nanowires,³³ or fullerenes.³⁴

Recently, the potential to change electron transport properties of CNTs and BNNTs by encapsulating suitable atoms or molecules has attracted increasing attention from researchers in many fields. However, the specific role of guest molecules inside nanotubes on the electronic and transport properties can be highly system-dependent. For example, a previous study shows that the electric conduction pathway within Fe@CNT is actually through CNT percolation³⁵ while the encapsulated iron nanoparticles have little influence on the CNT conductivity. However, Hsu and coworkers found that the Fe core in CNTs can generate an electromagnetic inductive phase, suggesting some participation in electron transport.³⁶ Therefore, a theoretical study of the one-dimensional (1D) core–sheath structures X@CNT and X@BNNT will be informative for understanding special effects of the core on the electronic and transport properties of endohedral X@CNT and X@BNNT materials.

It is known that CNTs can be either metallic or semiconducting, depending on their diameter and chirality, while the BNNTs are always insulating with bandgaps of 4–5 eV.^37–40 Such a striking difference in electronic properties between CNTs and BNNTs will inevitably lead to different physical properties of the corresponding endohedral X@CNT and X@BNNT. For example, density-functional theory (DFT) calculation suggests that the (η⁶-C₆₀-V)@CNT nanopeapod is metallic with characteristics of multiple carriers contributed from the CNT, C₆₀, and V, while the (η⁶-C₆₀-V)@BNNT nanopeapod is predicted to be semiconducting with a narrow bandgap, and its charge carriers are contributed only by the C₆₀V chain.⁴¹

In the laboratory, many multidecker organometallic sandwich clusters have been synthesized.^42,43 It has been shown that the 1D sandwich compounds can exhibit semiconducting or even conducting properties.^44,45 The Fe_n(Cp)_n+1 nanowires have attracted much attention as they are promising components for nanoelectronic devices, especially in high density storage and quantum computing.⁴⁶ The Fe_n(Cp)_n+1 sandwich clusters have been synthesized in the gas phase and characterized by mass spectroscopy.⁴² Note that ferrocene molecules have already been encapsulated into CNTs to create a class of self-assembled hybrid structures named as “ferrocene nanopeapods”.¹⁴ Thus, we expect that the Fe_n(Cp)_n+1 clusters may also be encapsulated into nanotubes to form “Fe_n(Cp)_n+1 nanopeapods”. In this study, we investigate the electronic and transport properties of Fe_n(Cp)_n+1 nanopeapods and their differences from pure nanotubes. Specifically we select Fe(Cp)₂@CNT (1a), Fe₂(Cp)₃@CNT (1b), Fe(Cp)₂@BNNT (2a), and Fe₂(Cp)₃@BNNT (2b) as prototype nanopeapod systems to compute their electronic structures and transport properties using DFT and non-equilibrium Green's function (NEGF) methods. We find that the length of the core per supercell of CNTs, i.e., Fe(Cp)₂versus Fe₂(Cp)₃, can have notable effects on the electronic and transport properties of the CNT and BNNT nanopeapods.

2 Models and computational methods

Fig. 1 shows optimized structures of nanopeapods 1a, 1b, 2a, and 2b. Here, metallic CNTs (6, 6) and insulating BNNTs (6, 6) are selected as the host nanotubes. For computing electronic structures, the infinite nanotube systems of 1a, 1b, 2a, and 2b are modeled via using the periodic conditions in the axial direction. For computing transport properties, the two-probe devices (a unit cell of the nanopeapod sandwiched between two CNT (6, 6) electrodes) are adopted. For the purpose of the benchmark test, we have computed electronic properties using infinite nanotube systems and transport properties using the two-probe devices for pure CNTs (6, 6) and BNNTs (6, 6).

Fig. 1 Optimized structures of 1a, 1b, 2a, and 2b. 1a and 2a also illustrate the two-probe devices for electron transport computation.

For the periodic systems, the supercell contains 120 atoms for the nanotubes and one Fe(Cp)₂ or Fe₂(Cp)₃ unit inside the nanotube. The Cps of Fe(Cp)₂/Fe₂(Cp)₃ are packed along the axial direction as shown in Fig. 1. The supercell length L is about 12.3 Å in the axial direction (z direction), long enough to neglect intermolecular interactions among core molecules Fe(Cp)₂ or Fe₂(Cp)₃. The nanopeapods are separated by 20.0 Å in two other directions to neglect inter-tube interactions. All the periodic systems are fully optimized until the maximum absolute force is less than 0.02 eV Å⁻¹.

For the two-probe systems, we carve out a supercell for each nanopeapod system as the central scatter region which is sandwiched between two identical CNT (6, 6) electrodes (cf.1a and 2a in Fig. 1). A reason for choosing CNTs (6, 6) as the electrodes is its known metallic character and good matching with the scatter region of peapods. The entire two-probe devices are denoted as CNT/peapod/CNT, i.e., CNT/1a/CNT (CNT/Fe(Cp)₂@CNT/CNT), CNT/1b/CNT (CNT/Fe₂(Cp)₃@CNT/CNT), CNT/2a/CNT (CNT/Fe(Cp)₂@BNNT/CNT), and CNT/2b/CNT (CNT/Fe₂(Cp)₃@BNNT/CNT). The entire system including two electrodes and a scatter region is fully optimized until the maximum absolute force is less than 0.02 eV Å⁻¹. Transport current is computed by changing the applied bias in the step of 0.2 V in the range of −1.0 to 1.0 V.

All the computations for the infinitely long and two-probe systems are performed using an ab initio code package, Atomistix ToolKit (ATK), which is based on the combination of DFT and the NEGF methods.^47–50 A generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) formalism is employed to describe the exchange correlations between electrons. A double-ζ basis functional with polarization (DZP) is used for all atoms. A (1 × 1 × 150) k-point in the string Brillouin zone (x, y, and z directions, respectively) is used. 150 Ry cutoff energy is applied to describe the periodic wave function.

3 Results and discussion

First, we investigate geometrics and band structures of the infinitely long nanopeapods of 1a, 2a, 1b, and 2b, followed by computing transport properties based on the two-probe devices of CNT/nanopeapod/CNT with the metallic CNT (6, 6) electrodes.

3.1 Geometric structures and electronic properties

Stability and geometry. Computed total energies per supercell for the optimized 1a, 1b, 2a, and 2b are listed in Table 1. For the 1b and 2b nanopeapods, we consider two spin states of the two Fe atoms, i.e., the antiferromagnetic (AFM) state and the ferromagnetic (FM) state. It is noteworthy that both 1b and 2b favor the FM ground state, indicating the ferromagnetic Fe–Fe coupling. Hereafter, we mainly focus on the FM state for 1b and 2b and associated electronic and transport properties.

Table 1 Optimized total energies of unit cells of peapods 1a, 1b, 2a, and 2b

Species	Total energies (in unit of eV)
1a Fe(Cp)2@CNT	−21 307.81607
1b Fe2(Cp)3@CNT (FM)	−22 925.03092
1b Fe2(Cp)3@CNT (AFM)	−22 924.98010
2a (Cp)2@BNNT	−23 612.79319
2b Fe2(Cp)3@BNNT (FM)	−25 267.18630
2b Fe2(Cp)3@BNNT (AFM)	−25 267.11294

---

Chemical stability for encapsulating either Fe(Cp)₂ or Fe₂(Cp)₃ into nanotubes is evaluated by computing the reaction energy per supercell for the net reaction [nanotube (NT) + Fe(Cp)₂ or Fe₂(Cp)₃ → peapod − ΔE_r]. Here, the computed reaction energies ΔE_r are −3.27, −7.18, −1.89, and −2.93 eV for 1a, 1b, 2a, and 2b, respectively. The negative values indicate exothermic energies. Hence, incorporation of Fe(Cp)₂ or Fe₂(Cp)₃ into either CNTs or BNNTs is energetically favorable.

The optimized supercell length in the axial direction (L), the radii of the nanotube (R), the face-to-face distances between adjacent Cps (r₁), the average C–C bond lengths in Cp (r₂), and the distances between the H atom of Cp and the nearest atom of the nanotube (r₃) for 1a, 1b, 2a and 2b are given in Table 2. Incorporation of Fe(Cp)₂ or Fe₂(Cp)₃ into nanotubes induces a slight expansion of the host nanotube as reflected from the larger values of R compared to the pristine nanotube. The distances r₁ are within the range of 3.188–3.280 Å, very close to the Cp-to-Cp separation in the Fe(Cp)₂ molecule (3.32 Å)^51–53 but slightly shorter than that (3.40 Å) in the ferrocene dimer.⁵⁴ The computed C–C bond lengths in Cp r₂ are in the range of 1.447–1.463 Å for both CNT and BNNT nanopeapods, very close to the experimentally measured bond lengths for ferrocene (1.440 Å).⁵⁵ The shortest distances between the H atom of Cp and the nearest atom of the nanotube (r₃) are in the range of 1.998–2.094 Å. Similar to the ferrocene, the H atoms on the terminal Cp rings tilt inward (toward the Fe atoms) by 6–9°.

Table 2 Computed geometric parameters for 1a, 1b, 2a, and 2b. Those for the pure CNT and BNNT are listed for comparison (in unit of Å)

Species	L	R	r 1	r 2	r 3
Pure CNT	12.310	8.298
1a Fe(Cp)2@CNT	12.302	8.352	3.280	1.447	2.016
1b Fe2(Cp)3@CNT	12.313	8.328	3.258	1.458	1.998
Pure BNNT	12.315	8.147
2a Fe(Cp)2@BNNT	12.304	8.452	3.188	1.452	2.094
2b Fe2(Cp)3@BNNT	12.313	8.489	3.248	1.463	2.078

---

Electronic band structures. Computed band structures and the projected density of states (PDOS) for the nanopeapods 1a, 1b, 2a, and 2b are given in Fig. 2–4. For the purpose of comparison, the results of pure CNTs and BNNTs are also given in Fig. 2–4. It is known that for the ferrocene molecule Fe(Cp)₂, the ligand field splitting of the Fe d orbitals results in five molecular orbitals mainly consisting of Fe d_xy, d_x²−y², d_z², d_xz, and d_yz, where the former three are occupied while the latter two are unoccupied.

Fig. 2 Computed band structures (left panels) of (a) the pure CNT, (b) 1a, and (c and d) 1b nanopeapod systems and the Kohn–Sham orbitals (middle and right panels) corresponding to the energy levels (highlighted in color lines) near E_f at the Γ point. The iso-surface value is 0.05 (e Å⁻³).

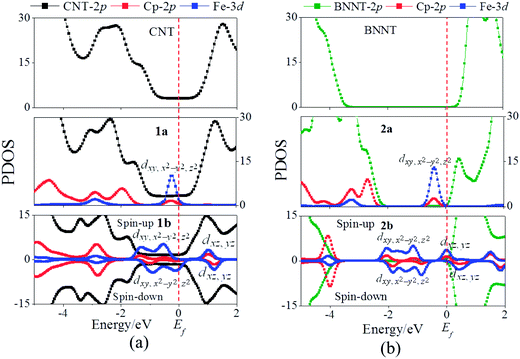
Fig. 2 displays the band structures of the CNT nanopeapods 1a and 1b, as well as the Kohn–Sham orbitals near the Fermi level (E_f). For pure CNTs, the valence band I (red line in Fig. 2(a)) and the conduction band II (blue line in Fig. 2(a)) cross at E_f with large dispersion, suggesting a typical metallic character. In 1a, two nearly degenerate and flat levels, the Fe d_xy and d_x²−y² bands (cyan and wine lines in Fig. 2(b)), are located just below E_f. The Kohn–Sham orbital shows that the Fe d_z² state is coupled with the Cp π state (denoted as a d_z²(Fe)-π(Cp) state). Notably, this d_z²(Fe)-π(Cp) state hybridizes with the CNT π state, giving rise to a band just below E_f with modest dispersion (dark yellow line in Fig. 2(b)). Hence, the core–sheath interaction occurs when Fe(Cp)₂ is encapsulated into the CNT. The CNT band I (red line in Fig. 2(b)) is located just below the d_z²(Fe)-π(Cp) state and crosses with the d_z²(Fe)-π(Cp) state. The unoccupied Fe d_xz and d_yz states are far away from E_f and hence not displayed in Fig. 2(b). The conduction band still includes the CNT band II in 1a (blue line in Fig. 2(b)). Thus, there may be two conducting pathways in 1a: one through the CNT and another through electron hopping from the core Fe(Cp)₂ to the sheath CNT.

For nanopeapod 1b, the spin-up state clearly shows different features from the spin-down state, which results in a magnetic moment of 0.81 μ_B per supercell (with two Fe atoms), close to 1.0 μ_B per supercell for the Fe_n(Cp)_n+1 nanowire.⁵⁶ The Kohn–Sham orbitals plotted in Fig. 2(c) and (d) show the strong core–sheath interaction in 1b as in 1a. More bands, originated mainly from the Fe d_xy, d_x²−y², and d_z² states, are introduced below E_f in both spin-up and spin-down states. Again, the unoccupied Fe d_xz and d_yz orbitals are far away from E_f and thus not plotted in Fig. 2(c) and (d). Compared to pure CNTs, one can see that the CNT bands II and III (blue and green lines in Fig. 2(c)) in the spin-up state of 1b downshift considerably, and both bestride E_f. As such, the CNT π state in the spin-up state behaves like half-filled and dominates the electron transport. In the spin-down state, the CNT band II (blue line in Fig. 2(d)) crosses E_f and the CNT band III (green line in Fig. 2(d)) is located just above E_f. Therefore, the CNT π state in the spin-down state still serves as a major transport pathway. One occupied band originated mainly from the Fe d orbital of the spin-down state upshifts across E_f, turned into a half-filled band, which suggests that electrons could transfer to the core Fe₂(Cp)₃. Hence, the core Fe₂(Cp)₃ may also serve as a localized trap-state in the process of electron transport, which is not beneficial to the conducting. Overall, the conductivity of 1b is likely contributed from multiple factors: (1) the CNT π channel dominates the conductivity; (2) electron hopping from core Fe₂(Cp)₃ to CNTs may have appreciable effects on the transport properties; and (3) Fe₂(Cp)₃ may entails a trap effect on the electron transport.

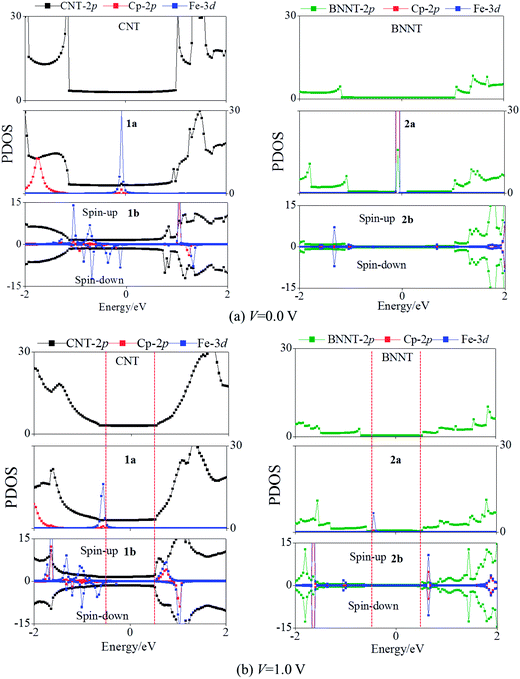
Fig. 3(a) plots the PDOS of pure CNTs, 1a, and 1b. Evidently, the CNT π states of pure CNTs, 1a, and 1b exhibit similar PDOS peaks and broad valley feature around E_f. Thus, the CNT π states are still the main transport channels even with the core Fe(Cp)₂ or Fe₂(Cp)₃. In 1a, the PDOS peaks of Fe d_xy, d_x²−y², and d_z² states are located below E_f, hybridized with the CNT π state. The unoccupied Fe d_xz and d_yz PDOS peaks do not arise even up to 2.0 eV (Fig. 3(a)). The conduction band of 1a is dominated by the CNT π state. The core Fe(Cp)₂ may participate in the electron tunneling through electron hopping to the CNT. In the case of 1b, a similar Fe₂(Cp)₃–CNT hopping channel also arises in the spin-up state. Compared to 1a, the PDOS peak of the unoccupied Fe d_xz and d_yz states moves to the lower energy region, but is still located at about 1.0 eV. The splitting of the spin states of 1b results in an asymmetric PDOS distribution for the spin-up and spin-down states. The Fe d_xy, d_x²−y², and d_z² orbitals in the spin-down state are shifted toward the higher energy region compared to the spin-up state, so that the Fe d orbital of the spin-down state crosses E_f with a half-filled character, again a manifestation of the trap effect due to the core Fe₂(Cp)₃.

Fig. 3 Computed projected density of states (PDOS) of 1a, 1b, 2a, and 2b nanopeapod systems. For comparison, PDOS of the pure CNT and BNNT systems are also presented.

In summary, electronic structures of the 1a and 1b systems suggest that the electric conductivity is primarily contributed by the CNT π channel, while electron hopping from the core Fe(Cp)₂ or Fe₂(Cp)₃ to the sheath CNT may have some contribution to the transport properties. On the other hand, the core Fe₂(Cp)₃ may also have a trap effect on the electron transport. Comparison with transport properties obtained based on the two-probe devices of CNT/1a/CNT and CNT/1b/CNT will be discussed in Section 3.2.

In Fig. 4, computed band structures of the pure BNNT, 2a, and 2b are plotted, so are the Kohn–Sham orbitals near E_f. For pure BNNTs, as expected, the valence band I (red line in Fig. 4(a)) and the conduction band II (green line in Fig 4(a)) are separated by a large bandgap of 4.52 eV. In 2a, the core Fe(Cp)₂ introduces three flat bands (cyan, wine, and dark yellow lines in Fig. 4(b)) in the range of −0.37 to −0.43 eV and these bands are mainly contributed from the occupied Fe d_xy, d_x²−y², and d_z² orbitals. The unoccupied orbitals stem mainly from Fe d_xz and d_yz are far away from E_f and thus not shown in Fig. 4(b). Unlike 1a which entails strong core–sheath interactions, in 2a little FeCp₂–BNNT interaction occurs as reflected from the Kohn–Sham orbitals and the flat feature of the Fe(Cp)₂ bands in Fig. 4(b). The three nearly degenerate Fe(Cp)₂ bands split the native BNNT band gap into two subgaps. As a result, the Fe(Cp)₂ state turns into the valence band and the BNNT band II is the conduction band. As such, the bandgap is reduced to 0.73 eV for 2a from 4.52 eV of the pristine BNNT. This notable band reduction indicates that electron hopping from the core Fe(Cp)₂ to the sheath BNNT is significant in 2a.

Fig. 4 Computed band structures (left panels) of the pure BNNT, 2a, and 2b nanopeapod systems and the Kohn–Sham orbitals (middle and right panels) corresponding to the energy levels (highlighted in color lines) near E_f at the Γ point. The iso-surface value is 0.05 (e Å⁻³).

For 2b, more orbitals originated from the core Fe₂(Cp)₃ appear in the bandgap region of BNNTs. Clearly, the spin-up and the spin-down states are different, leading to a magnetic moment of 0.98 μ_B per supercell. In the spin-up state, the Fe d_xz and d_yz orbitals, due to coupling with the Cp π orbital, are downshifted and across E_f (cyan and wine lines in Fig. 4(c)), showing a half-filled character and a trap-state. This case differs from 1a, 1b, and 2a for which the Fe d_xz and d_yz orbitals are located far away from E_f. For the spin-down state, the conduction band is contributed by Fe d_xz and d_yz orbitals coupled with certain BNNT π orbitals as can be seen from the Kohn–Sham orbitals shown in Fig. 4(d) (cyan and wine lines). The valence band (dark yellow and dark cyan lines in Fig. 4(d)) stems only from Fe d_xy and d_x²−y² orbitals. Hence, the core Fe₂(Cp)₃ can also have a trap effect on the electron transport in the spin-down state.

Fig. 3(b) shows computed PDOS of the pure BNNT, 2a, and 2b. The BNNT retains the insulating properties in 2a and 2b, as the BNNT π PDOS are largely separated above and below E_f. In 2a, the Fe d_xy, d_x²−y², and d_z² orbitals contribute a peak below E_f, resulting in a valence state, while the BNNT π orbitals also contribute to the conduction state. Thus, electrons can be transported by hopping from the core Fe(Cp)₂ to the sheath BNNT, consistent with the conclusion based on computed band structures. Like in 1a, the unoccupied Fe d_xz and d_yz PDOS are far away from E_f (Fig. 3(b)). No PDOS hybridization between the BNNT and the FeCp₂ is seen near E_f, suggesting little Fe(Cp)₂–BNNT interaction in 2a. This result is consistent with the Kohn–Sham orbital diagram in Fig. 4(b). In 2b, the Fe d_xz and d_yz orbitals, coupled with the Cp π orbital, are downshifted less substantially compared with 1a, 1b, and 2a. As a result, the Fe d_xz and d_yz PDOS peaks appear just across E_f in the spin-up state, showing a half-filled feature and a trap state. Overall, the Fe d PDOS in the spin-up and spin-down states are asymmetric. In the spin-down state, the Fe d_xz and d_yz orbitals are located just above E_f while hybridized with the BNNT π state, resulting in the conduction band; the valence band originates from the Fe d_xy, d_x²−y², and d_z² orbitals. Therefore, the trap effect could also exist in the spin-down state. These results are in line with the band structure analysis.

From the above analysis for 2a and 2b, it seems that encapsulating Fe(Cp)₂ is more favorable for the electron conduction, owing to the splitting of the BNNT bandgap by the Fe(Cp)₂ state. Electrons could transport through hopping from the core Fe(Cp)₂ to the sheath BNNT. In contrast, introducing Fe₂(Cp)₃ into the BNNT is not beneficial to the conduction due to intramolecular electron transfer within the core Fe₂(Cp)₃ which can cause a trap effect. More related discussions are given in Section 3.2.

3.2 Two-probe devices

To obtain more quantitative transport properties of the nanopeapods and analyze the effect of core Fe(Cp)₂ or Fe₂(Cp)₃ on the transport properties, we construct a model system such that a supercell of 1a, 1b, 2a, or 2b is sandwiched between two CNT (6, 6) electrodes to form two-probe devices (denoted as CNT/nanopeapod/CNT). Calculation results based on this model system suggest that electric conductivities of the two-probe devices are mostly consistent with the electronic structures of the corresponding infinitely long nanopeapod systems, although the computed electronic structures can be influenced by applied external bias voltage.

The computed I–V curves based on the two-probe devices are given in Fig. 5. It can be seen that pure CNTs, 1a, and 1b show a metallic feature and give nearly the same I–V curves (Fig. 5(a)), suggesting that the conductivity is entirely contributed by the CNT (π state) in the two-probe devices, consistent with the conclusion based on the computed electronic structures. Moreover, conductivities of the CNT/1b/CNT and CNT/2b/CNT devices appear independent of the spin state within the considered bias range of −1.0 to 1.0 V, although the band structures and PDOS distributions are dependent on the spin state. Fig. 5(b) shows that the pure BNNT, 2a, and 2b exhibit features of insulators. Their conductivities follow the sequence 2a > pure BNNT > 2b, again consistent with the predication based on computed electronic structures, that is, encapsulation of Fe(Cp)₂ into BNNTs would enhance conductivity while encapsulating Fe₂(Cp)₃ into BNNTs would lower the conductivity.

Fig. 5 Computed I–V curves of two-probe devices with finite-sized 1a, 1b, 2a, and 2b between the two electrodes. For comparison, the I–V curves of the pure CNT and BNNT two-probe devices are also presented.

In general, computed electric conductivity is dependent on multiple factors, including, for examples, energy spectra, the molecular projected self-consistent Hamiltonian (MPSH) states, the PDOS, the transmission spectra (TS), and electrostatic potentials, among others. Next, we analyze the extent to which these factors affect the transport properties of each two-probe CNT/nanopeapod/CNT devices. Results are depicted in Fig. 6–10, from which one can see that the applied external bias voltage can alter the transport channel.

Fig. 6 Computed energy spectra (left panels) of (a and b) the pure CNT; (c and d) 1a; and (e–h) 1b two-probe devices. The MPSH states (middle and right panels) correspond to the energy levels (highlighted in color lines) near E_f. The iso-surface value is 0.05 (e Å⁻³).

CNT/1a/CNT. As shown in Fig. 6(c), at zero bias (V = 0), the Fe d_xy, d_x²−y², and d_z² states contribute to three frontier occupied orbitals, namely, the highest occupied molecular orbital (HOMO), HOMO−1, and HOMO−2. The CNT valence π orbital is located just below the Fe d_z² state and contributes to the HOMO−3. The lowest unoccupied molecular orbital (LUMO) of CNT/1a/CNT stems from the unoccupied CNT π orbital. The energy spectrum of CNT/1a/CNT is in line with the band structures of the infinite 1a system. At 1.0 V bias, the CNT valence π orbital (HOMO−3) is shifted upward and becomes the HOMO (Fig. 6(d)), while the LUMO is still originated from the unoccupied CNT π state. This result demonstrates that the external electric field can induce orbital rearrangement of CNT/1a/CNT, which can be further reflected from the PDOS in Fig. 7. The Fe d_xy, d_x²−y², and d_z² states yield a sharp peak below E_f at 0.0 V bias voltage (left panel in Fig. 7(a)), while this peak is pushed to the lower energy region and even out of the bias window when the bias V = 1.0 V is applied (left panel in Fig. 7(b)). Here, the bias window refers to [−V/2, V/2]. Generally, only states within the bias window contribute to the total current. More importantly, the HOMO and LUMO MPSH states spread over the entire CNT, which suggests an effective transport path. Therefore, the conductivity of 1a is fully determined by the CNT while the core Fe(Cp)₂ plays little role in the conductivity. This is why the I–V curves shown in Fig. 5(a) between pure CNTs and 1a exhibit little difference. The transmission spectra (left panels in Fig. 8) also show that pure CNTs and 1a should have the same conductivity as they have almost the same transmission spectral distributions at 1.0 V bias. To evaluate the efficiency of the electron transport through the nanopeapod we compute the molecular electrostatic potentials at 0.0 and 1.0 V bias voltages. The calculation result can also provide atomic-level information about the electron transfer barrier. In any case, the CNT should serve as a major transport path. The application of bias greatly changes the potential distribution due to the external electric field. By comparing results of 1a and those of pure CNTs, one can see that the core Fe(Cp)₂ leads to two major effects. First, it acts as a barrier for the transport (blue part in Fig. 9 for systems CNT/1a/CNT at V = 1.0 V bias), and second, it enhances electron transport (red part in Fig. 9 for systems CNT/1a/CNT at V = 1.0 V bias). The charge carriers can effectively permeate from the left electrode to the right electrode as can be seen from the contour plot of the electrostatic potential along the tube (Fig. 9).

Fig. 7 Computed projected density of states (PDOS) of 1a, 1b, 2a, and 2b two-probe devices at biases of (a) 0.0 and (b) 1.0 V. For comparison, PDOS of the pure CNT and BNNT two-probe devices are also given. The vertical red lines in (b) refer to the bias window.

Fig. 8 Transmission spectra (TS) of 1a, 1b, 2a, and 2b two-probe devices. For comparison, transmission spectra of pure CNT and BNNT two-probe devices are also given. The vertical red lines in (b) refer to the bias window.

Fig. 9 Computed contour plot of potential distribution for 1a, 1b, 2a, and 2b at 0.0 and 1.0 V. For comparison, potential distribution of the pure CNT and BNNT are also given. Blue (red) represents low (high) potential.

CNT/1b/CNT. At V = 0.0 V bias and in the spin-up state of the scatter region 1b both the HOMO and LUMO stem from the CNT π states (Fig. 6(e)), while in the spin-down state, the HOMO stems from the Fe d orbital and the LUMO originates from the CNT π state (Fig. 6(g)). This is consistent with the electronic structure of the infinite 1b system. Importantly, under 1.0 V bias, both the HOMO and LUMO, either in the spin-up state or in the spin-down state, are dominated by the CNT π states (Fig. 6f and h). Clearly, no Fe d PDOS appear within the bias window and the bias window exhibits only the CNT π PDOS at the 1.0 V bias (left panel in Fig. 7(b)). Therefore, the conductivity of 1b is contributed by the CNT π channel in the two-probe device. This is why 1b has the same I–V curve as pure CNTs and 1a. Moreover, the spin-up and spin-down states give the same HOMO–LUMO gap of ∼0.53 eV and the same transition spectrum at E_f and at 1.0 V bias voltage (left panel in Fig. 8(b)), indicating that the conductivity of 1b is independent of the spin state, consistent with the I–V curves shown in Fig. 5(a). Distributions of electrostatic potential in Fig. 9 also suggest that the core Fe₂Cp₃ does not participate in the electron transport.

CNT/2a/CNT. For pure BNNTs, the MPSH states shown in Fig. 10(a) indicate that the HOMO and LUMO are located at two ends of the finite-size BNNT at V = 0.0 V bias. At V = 1.0 V bias, the HOMO is located on the right side of the BNNT while the LUMO is located on the left side (Fig. 10(b)). With Fe(Cp)₂ encapsulation, the Fe d state becomes the HOMO and the BNNT π state is still the LUMO at 0.0 V bias (Fig. 10(c)), consistent with the computed electronic structure of the infinite 2a system. Note that the BNNT valence π state is upshifted and turns into the HOMO at 1.0 V bias (Fig. 10(d)), indicating that the external bias can induce orbital rearrangement. Consequently, the HOMO and LUMO of CNT/2a/CNT are both controlled by the BNNT π state. Meanwhile, the occupied Fe d PDOS is relocated to the lower energy region at 1.0 V bias but still lies within the bias window (Fig. 7). The TS distributions of 2a in Fig. 8 clearly show that 2a is an insulator. Evidently, the MPSH states indicate that the HOMO of CNT/2a/CNT becomes more delocalized than the pure BNNT (Fig. 10(b)vs.10(d)), thereby becoming a more effective transport channel. The electrostatic potential distributions shown in Fig. 9 indicate that the core Fe(Cp)₂ can offer a transport path at 1.0 V bias. In fact, by comparing the electrostatic potential with that of other nanopeapods, the efficiency of electron transport through the core Fe(Cp)₂ in CNT/2a/CNT is the highest at 1.0 V bias. Therefore, the conductivity is improved by encapsulating Fe(Cp)₂ into BNNTs, as demonstrated by the I–V curve in Fig. 5(b).

Fig. 10 Computed energy spectra (left panels) of (a and b) the pure BNNT; (c and d) 2a; and (e–h) 2b two-probe devices and the MPSH states (middle and right panels) corresponding to the energy levels (highlighted in color lines) near E_f. The iso-surface value is 0.05 (e Å⁻³).

CNT/2b/CNT. Note also that regardless of the bias voltage, no obvious difference in the energy spectra, the PDOS, and the TS between the spin-up state and the spin-down state when the unit of Fe₂(Cp)₃@BNNT is sandwiched between two CNT electrodes. This is clearly different from the case of the infinite systems which show distinctly different band structures between the spin-up state and the spin-down state. Confirmation of 2b can be made through the TS distributions in Fig. 8. At 0.0 V bias, the HOMO is controlled by the BNNT π state and the LUMO is dominated by a coupling state of Fe₂(Cp)₃–BNNT (Fig. 10(e) and (g)). At 1.0 bias, the HOMO and LUMO both stem from the BNNT π state (Fig. 10(f) and (h)), suggesting that the orbital rearrangement occurs under external bias. Through comparison, one can find that the π-delocalization of the HOMO and LUMO is shrunk if an external bias is applied. At 0.0 V bias, the HOMO and LUMO states are located at both ends of the system, while at 1.0 V bias, they are off just to one side of the system. No Fe₂(Cp)₃ PDOS appears within the bias window (Fig. 7). The potential distribution in Fig. 9 also indicates that the core Fe₂Cp₃ acts as a barrier in the electron transport. Therefore, the conductivity of CNT/2b/CNT should be weaker than the pure BNNT and 2a.

4 Conclusions

We have investigated the electronic and transport properties of a novel form of Fe(Cp)₂@CNT, Fe₂(Cp)₃@CNT, Fe(Cp)₂@BNNT, and Fe₂(Cp)₃@BNNT by means of DFT and NEGF methods. We have found that endohedral encapsulation of Fe(Cp)₂/Fe₂(Cp)₃ into CNTs (6, 6) or BNNTs (6, 6) is energetically favorable. In Fe₂(Cp)₃@CNT and Fe₂(Cp)₃@BNNT nanopeapods the spin of Fe is coupled ferromagnetically. Conductivities of Fe₂(Cp)₃@CNT and Fe₂(Cp)₃@BNNT nanopeapods appear to be independent of the spin state within the bias range of −1.0 to 1.0 V, even though the band structures and PDOS distributions of the spin-up state and the spin-down state of the infinite structures are different. Characteristics of computed electric conductivities based on the two-probe devices are qualitatively consistent with the computed electronic structures of the corresponding infinite nanopeapod systems.

Encapsulating either Fe(Cp)₂ or Fe₂(Cp)₃ into the CNT has little effect on the conductivity owing to the strong metallic character of the CNT sheath. Encapsulating Fe(Cp)₂ into the BNNT however can notably enhance electron conduction due to added electron hopping from the core Fe(Cp)₂ to the sheath BNNT. Encapsulating Fe₂(Cp)₃ into the BNNT does not assist electron conduction due to the trap effect. Hence, the electronic and transport properties of the BNNT nanopeapods are very sensitive to the length of guest molecules while those of the CNT nanopeapods are insensitive to the length of guest molecules. These properties of BNNT and CNT nanopeapods can be exploited for nanoelectronic and sensor applications.

Acknowledgements

XCZ is supported by grants from the NSF (EPS-1010674) and ARL (W911NF1020099), and by the University of Nebraska Holland Computing Center. GLZ is supported by grants from the NSFC (51073048 and 51473042), the NSF of Heilongjiang Province of China (B201102), the SF for leaders in the academy of Harbin City of China (2013RFXXJ024), and foundation for Scientist Leaders of Heilongjiang Provincial Talent Echelon.

References

1. B. W. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323.
2. A. Burteaux, B. Claye, W. Smith, M. Monthoioux, D. E. Luzzi and J. E. Fischer, Chem. Phys. Lett., 1999, 310, 21.
3. J. Sloan, R. E. Dunin-Borkowski, J. L. Hutchison, K. S. Coleman, V. C. Williams, J. B. Claridge, A. P. E. York, C. Xu, S. R. Bailey, G. Brown, S. Friedrichs and M. L. H. Green, Chem. Phys. Lett., 2000, 316, 191.
4. Y. Kataura, T. Maniwa, K. Kodama, K. Kikuchi, K. Hirahara, S. Suenaga, S. Iijima, Y. Suzuki, Y. Achiba and W. Krätschmer, Synth. Met., 2001, 121, 1195.
5. K. Hirahara, S. Bandow, K. Suenaga, H. Kato, T. Okazaki, H. Shinohara and S. Iijima, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 115420.
6. K. Masatoshi, K. Haruka, S. Takuya, I. Toru, S. Hironori, O. Toshiya, K. Hiromichi, M. Yutaka and Y. J. Kazuhiro, J. Am. Chem. Soc., 2012, 134, 9545.
7. P. M. Ajayan and S. Iijima, Nature, 1993, 361, 333.
8. R. S. Lee, H. J. Kim, J. E. Fischer, A. Thess and R. E. Smalley, Nature, 1997, 388, 255.
9. M. Milko, P. Puschnig, P. Blondeau, E. Menna, J. Gao, M. A. Loi and C. Draxl, J. Phys. Chem. Lett., 2013, 4, 2664.
10. Y. Takashi and Y. Hiroki, J. Phys. Chem. C, 2014, 118, 5510.
11. G. Pietro, B. Andrea, C. Matteo and Z. Francesco, J. Phys. Chem. C, 2014, 118, 5032.
12. H. Jiang, Y. Hu, S. Guo, C. Yan, P. S. Lee and C. Li, ACS Nano, 2014, 8, 6038.
13. E. Nakamura, M. Koshino, T. Saito, Y. Niimi, K. Suenaga and Y. Matsuo, J. Am. Chem. Soc., 2011, 133, 14151.
14. N. Sun, L. Guan, Z. Shi, N. Li, Z. Gu, Z. Zhu, M. Li and Y. Shao, Anal. Chem., 2006, 78, 6050.
15. A. Rubio, J. L. Corkill and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5081.
16. N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Science, 1995, 269, 966.
17. E. Hernandez, C. Goze, P. Bernier and A. Rubio, Phys. Rev. Lett., 1998, 80, 4502.
18. C. W. Chang, A. M. Fennimore, A. Afanasiev, D. Okawa, T. Ikuno, H. Garcia, L. Deyu, A. Majumdar and A. Zettl, Phys. Rev. Lett., 2006, 97, 085901.
19. D. Golberg, X. D. Bai, M. Mitome, C. C. Tang, C. Y. Zhi and Y. Bando, Acta Mater., 2007, 55, 1293.
20. Y. Chen, J. Zhou, S. J. Campell and G. L. Caer, Appl. Phys. Lett., 2004, 84, 2430.
21. P. Ravinder and V. Subramanian, J. Phys. Chem. C, 2013, 117, 5095.
22. K. B. Shelimov and M. Moskovits, Chem. Mater., 2000, 12, 250.
23. D. Golberg, Y. Bando, K. Kurashima and T. Sato, J. Nanosci. Nanotechnol., 2001, 1, 49.
24. C. C. Tang, Y. Bando, D. Golberg, X. X. Ding and S. R. Qi, J. Phys. Chem. B, 2003, 107, 6539.
25. R. Z. Ma, Y. Bando and T. Sato, Chem. Phys. Lett., 2004, 350, 1.
26. A. L. M. Reddy, B. K. Gupta, T. N. Narayanan, A. A. Martí, P. M. Ajayan and G. C. Walker, J. Phys. Chem. C, 2012, 116, 12803.
27. R. Z. Ma, Y. Bando and T. Sato, Adv. Mater., 2002, 14, 366.
28. H. S. Song, J. Zhang, J. Lin, S. J. Liu, J. J. Lou, Y. Huang, E. M. Elssfah, A. Elsanousi, X. X. Ding, J. M. Gao and C. Tang, J. Phys. Chem. C, 2007, 111, 1136.
29. C. C. Tang, Y. Bando, T. Sato and K. Kurashima, J. Mater. Chem., 2002, 12, 1910.
30. Y. B. Li, P. S. Dorozhkin, Y. Bando and D. Golberg, Adv. Mater., 2005, 17, 545.
31. W. Q. Han and A. Zettl, Appl. Phys. Lett., 2002, 81, 5051.
32. J. Zhang, L. D. Zhang, F. H. Jiang and Z. H. Dai, Chem. Phys. Lett., 2004, 383, 423.
33. W. Q. Han, C. W. Chang and A. Zettl, Nano Lett., 2004, 4, 1355.
34. W. Mickelson, S. Aloni, W. Q. Han, J. Cumings and A. Zettl, Science, 2003, 300, 467.
35. P. C. P. Watts, W. K. Hsu, G. Z. Chen, D. J. Fray, H. W. Kroto and D. R. M. Walton, J. Mater. Chem., 2001, 11, 2482.
36. P. C. P. Watts, W. K. Hsu, D. P. Randall, V. Kotzeva and G. Z. Chen, Chem. Mater., 2002, 14, 4505.
37. A. Rubio, J. L. Corkill and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5081.
38. X. Blase, A. Rubio, S. G. Louie and M. L. Cohen, Europhys. Lett., 1994, 28, 335.
39. J. Cumings and A. Zettl, Chem. Phys. Lett., 2000, 316, 211.
40. W. Q. Han, W. Mickelson, J. Cumings and A. Zettl, Appl. Phys. Lett., 2002, 81, 1110.
41. G. Zhang, R. Zhou and X. C. Zeng, J. Mater. Chem. C, 2013, 1, 4518.
42. S. Nagao, A. Kato and A. Nakajima, J. Am. Chem. Soc., 2000, 122, 4221.
43. P. Kruse, E. R. Johnson, G. A. DiLabio and R. A. Wolkow, Nano Lett., 2002, 2, 807.
44. T. Kuhlmann, S. Roth, J. Rozière and W. Siebert, Angew. Chem., Int. Ed. Engl., 1986, 25, 105.
45. M. Y. Lavrentiev, H. Köppel and M. C. Böhm, Chem. Phys., 1993, 169, 85.
46. N. J. Long, Metallocenes, Blackwell Science Press, Oxford, 1998.
47. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407.
48. M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
49. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
50. ATK, Version 13.8, atomistix a/s, 2013, http://www.quantumwise.com.
51. J. C. Wu, X. F. Wang, L. P. Zhou, H. X. Da, K. H. Lim, S. W. Yang and Z. Y. Li, J. Phys. Chem. C, 2009, 113, 7913.
52. H. X. Da, H. M. Jin, S. W. Yang and K. H. Lim, J. Phys. Chem. C, 2009, 113, 21422.
53. J. F. Yang, L. P. Zhou, Q. Han and X. F. Wang, J. Phys. Chem. C, 2012, 116, 19996.
54. K. Peter, R. J. Erin, A. D. Gino and A. W. Robert, Nano Lett., 2002, 2, 807.
55. M. Lein, J. Frunzke, A. Timoshkin and G. Frenking, Chem.–Eur. J., 2001, 7, 4155.
56. L. Shen, S. Yang, M. Ng, V. Ligatchev, L. Zhou and Y. J. Feng, J. Am. Chem. Soc., 2008, 130, 13956.

---