Phase behavior and superprotonic conductivity in the Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ systems

Abstract

The solid acid compound CsH₂PO₄ (CDP) adopts a cubic structure of high conductivity above 228 °C, rendering it attractive as a fuel cell electrolyte for intermediate temperature operation. This superprotonic phase is stable from the phase transition temperature, T_s, to the dehydration temperature, T_d, where the latter depends on water vapor pressure (e.g. T_d = 290 °C at p_H2O = 0.8 atm). In this work we examine the possibility of modifying these temperatures and thereby, amongst other characteristics, fuel cell operating conditions by introduction of Rb and K as substituents for Cs in CDP. The phase behavior of the Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ pseudo-binary systems are determined by in situ X-ray diffraction (XRD) and thermal analysis. It is found that RbH₂PO₄ (RDP) and CDP are entirely miscible both below and above the transition to the cubic phase. With increasing Rb concentration, T_s increases and T_d decreases. In contrast, K has limited solubility in CDP, with a 27 at.% solubility limit in the cubic phase, and both T_s and T_d decrease with K content. The eutectoid temperature in the Cs_1−xK_xH₂PO₄ system is 208 ± 2 °C and the K solubility decreases sharply below this temperature. In both systems, conductivity decreases monotonically with increasing substituent concentration. Furthermore, even after normalization for cation size, the impact of K is greater than that of Rb, suggesting local disruptions to the proton migration pathway, beyond global changes in unit cell volume. Although this investigation shows unmodified CDP to remain the optimal fuel cell electrolyte material, the study provides a possible framework for elucidating proton transport mechanisms in superprotonic conductors.

---

1. Introduction

At moderate temperatures and under sufficient humidity, CsH₂PO₄ adopts the CsCl structure type with orientationally disordered oxyanion groups and has high protonic conductivity (∼10⁻² S cm⁻¹). As such, it is attractive as a fuel cell electrolyte for operation in the intermediate temperature range of 230 to 280 °C.^1–3 In an earlier publication we reported the thermodynamic phase stability of cubic CsH₂PO₄ and the kinetic characteristics of its dehydration.⁴ The lower temperature limit for operation of CsH₂PO₄-based fuel cells corresponds to the phase transition temperature, T_s = 228 °C, from the monoclinic to the cubic phase. This polymorphic phase transition is independent of p_H2O. The upper temperature limit corresponds to the dehydration temperature, T_d, which, in contrast to T_s, depends strongly on p_H2O. For example, at p_H2O = 0.8 atm T_d is 290 °C, whereas at p_H2O = 0.15 atm it is 230 °C. The relatively narrow stability window for cubic CsH₂PO₄ presents challenges for fuel cell operation. While these are not insurmountable, increasing T_d and lowering T_s are technologically desirable.³ In this work we evaluate phase behavior in the Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ pseudo-binary systems and explore the possibility of manipulating the stability window of the cubic phase through chemical modification. Beyond near-term implications for fuel cell operation, such a study has the potential to provide broad insight into the crystal-chemical factors governing superprotonic behavior.

At ambient conditions, CsH₂PO₄ and RbH₂PO₄ have distinct structures (the former monoclinic, P2₁/m,⁵ the latter tetragonal, I4̄2d⁶), precluding the possibility of complete solid solubility. It has been shown, however, that Rb is highly soluble in monoclinic CsH₂PO₄, with a solubility limit in the vicinity of 80 at.% at ambient temperatures.^7–9 In addition, it has recently been shown that, upon heating, RbH₂PO₄ transforms to a monoclinic phase isostructural to that of CsH₂PO₄, with the transition occurring gradually over the temperature range from 90 to 130 °C.¹⁰ In the case of the intermediate compositions, a sharp increase in conductivity on heating to somewhat higher temperatures,^7–9,11 as well as observation of a thermal anomaly of appropriate magnitude,^8,12 has suggested that Cs_1−xRb_xH₂PO₄ can adopt the cubic CsCl-type structure of superprotonic CsH₂PO₄. Direct high-temperature diffraction studies are limited to the work of Martsinkevich,¹³ who was able to show that for compositions up to 40 at.% Rb the high-temperature phase is indeed cubic. In parallel with these ambient pressure experiments, Botez examined RbH₂PO₄ under high pressure and reported the occurrence of monoclinic and cubic phases of RbH₂PO₄, isostructural with those of CsH₂PO₄.¹⁴ This collection of prior results suggests the possibility of complete miscibility between CsH₂PO₄ and RbH₂PO₄ at temperatures in the vicinity of T_s, below it in the form of the monoclinic phase and above in the form of the cubic phase. Studies of the impact of Rb substitution on the temperature of the transition between these two phases generally indicate an increase in T_s with increasing Rb,^7–9,12,15 although Lavrova et al. have reported a 20 °C reduction in T_s when the Rb content is 3 at.%.¹¹ Little has been documented with respect to the influence of Rb on dehydration behavior. We reported previously that Cs_0.75Rb_0.25H₂PO₄ has a slightly lower T_d than CsH₂PO₄.¹² Again, Lavrova et al. have reported opposite behavior, claiming enhanced stability for Cs_0.97Rb_0.03H₂PO₄ over CsH₂PO₄.¹¹ These discrepancies signify a clear need to resolve the phase behavior of the Cs_1−xRb_xH₂PO₄ system and quantify the influence of Rb content on T_s and T_d.

In contrast to the case with Rb, there are no known studies of the Cs_1−xK_xH₂PO₄ system. At ambient temperatures, KH₂PO₄ is tetragonal¹⁶ and isostructural to the ambient temperature form of RbH₂PO₄. Recent high-temperature synchrotron X-ray studies¹⁷ have revealed a transition at ∼190 °C to a monoclinic phase (P2₁/m), isostructural to that of RbH₂PO₄ (above 130 °C) and CsH₂PO₄ (ambient temperature). However, further heating apparently results in melting or dehydration prior to any transition to a superprotonic phase, even under high pressure.¹⁸ Because K is only slightly smaller than Rb and the phosphates share two isomorphous structures, non-negligible solubility of K into CsH₂PO₄ can be anticipated, suggesting another chemical means of manipulating T_s and T_d in CsH₂PO₄-based materials.

To meet the objective of elucidating phase behavior we perform, in this work a careful examination of the Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ pseudo-binary systems using in situ X-ray powder diffraction (XRD), differential scanning calorimetry (DSC) and alternating current (AC) impedance spectroscopy. Key to the success of this study is the active control of humidity in order to clearly distinguish between polymorphic phase transitions and dehydration reactions,¹⁹ as well as acquisition of data over long periods to ensure system equilibration. This approach enables reliable determination of (i) solubility limits, (ii) T_s, and (iii) T_d, all of which are embodied in the phase diagrams constructed from these measurements.

2. Experimental details

2.1. Sample preparation

Polycrystalline powders of CsH₂PO₄ and RbH₂PO₄ were synthesized by combining the starting reagents Cs₂CO₃ (Alfa Aesar, 99.99%) or Rb₂CO₃ (Alfa Aesar, 99.99%) and H₃PO₄ (ACS, 85% w/w aqueous solution) in a molar ratio of 1 : 2 in aqueous solution. The resulting solutions were gently heated and the end-member solid acid phosphates obtained upon evaporation of water. Samples of overall composition Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ were synthesized from these starting materials. Stoichiometric aqueous solutions of target overall composition were prepared and again solid precipitates obtained upon inducing water evaporation. For further experimentation the resulting materials were ground in a mortar and pestle to yield to powders with particle size of ∼10 μm.

Chemical compositions were measured by X-ray energy dispersive spectroscopy (EDS), performed using an Oxford INCA 300 in conjunction with a scanning electron microscope (LEO 1550 VP) at an accelerating voltage of 15 kV. For the Cs_1−xRb_xH₂PO₄ system, slight differences were determined between the nominal and actual compositions, Table 1, and all results are presented in terms of the actual (measured compositions). In the case of the Cs_1−xK_xH₂PO₄ system, the solubility of K into CsH₂PO₄ was found to be extremely limited, and the multi-phase nature of the resulting materials prevented acquisition of meaningful EDS data. Consequently, for these materials we refer only to the nominal compositions.

Table 1 Rb concentration in Cs_1−xRb_xH₂PO₄ samples as determined by EDS

Sample	Nominal (at.%)	Measured (at.%)
19%Rb	20	19.4 ± 1.2
50%Rb	50	50.1 ± 1.3
78%Rb	75	77.8 ± 1.8

---

2.2. In situ XRD measurements

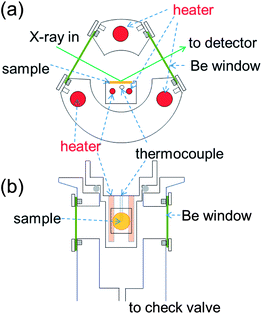
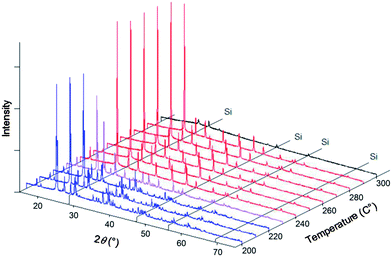
XRD measurements were carried out using an X'pert MD (Panalytical) diffractometer equipped with an in-house constructed sealed, high-temperature stage, Fig. 1. Two resistive heaters in the sample stage provide heat to the sample, the temperature of which is monitored and controlled using a thermocouple (K-type) also embedded in the stage. Three additional resistive heaters, typically set to ∼150 °C, are embedded in the walls of the chamber and are utilized to prevent water condensation. The chamber is further equipped with a check valve to limit the system pressure to 2 atm. Be windows permit incident and diffracted X-rays to enter and exit the chamber. A thin glass plate was placed on the sample stage to prevent possible reaction between the sample and stage material. The sample powder was combined, by light mechanical milling, with 20 at.% Si (Alfa Aesar, 99.9%), which served as an internal 2θ reference. No reaction between Si and the materials investigated was observed. Measurements were typically carried out in the temperature range 150 to 300 °C in 10 °C increments. Samples were held at each temperature for at least 30 minutes prior to data acquisition to allow for equilibration.

Fig. 1 Schematic illustration of the sealed, high-temperature X-ray powder diffraction stage constructed for data collection under high p_H2O, up to 2 atm: (a) cross-sectional view, and (b) top-down view.

Exemplary diffraction data obtained from this system are presented in Fig. 2 for the parent compound CsH₂PO₄. Consistent with the widely confirmed phase transformation behavior, the data show CsH₂PO₄ to remain entirely in the monoclinic phase to 220 °C. A two-phase mixture of the monoclinic and cubic phases is obtained at 230 °C, and from 240 to 290 °C only diffraction peaks from the cubic phase are evident. The material becomes entirely amorphous at 300 °C, corresponding to the occurrence of a liquid phase, likely as a result of direct melting. Based on the retention of the cubic phase to such high temperature,¹⁹ we estimate that a water partial pressure of ∼1 atm was attained in the sealed chamber. Crystallographic parameters were determined by Rietveld refinement using the RIETAN-FP software package.²⁰ The known thermal expansion behavior of Si (ref. 21) provided an internal 2θ standard to ensure accurate lattice parameter refinement. To facilitate refinement of atomic positions, the P–O distance was fixed (at 1.52 Å (ref. 8)) irrespective of temperature. The refined parameters for cubic CsH₂PO₄ (Pm3̄m) are presented in Table 2.

Fig. 2 XRD patterns of CsH₂PO₄ with Si (as an internal standard) at several temperatures showing wide temperature range of stability of the cubic phase (red patterns) under sufficiently high humidity, estimated to be ∼1 atm.

Table 2 Rietveld refinement fit parameters for cubic CsH₂PO₄ (Pm3̄m, CsCl structure type) at several temperatures

T (°C)	a 0 (Å)	Cs1					P1					O1					S	R P
		sof	x	y	z	B	sof	x	y	z	B	sof	x	y	z	B
230	4.9673(9)	1	0	0	0	8.2	1	1/2	1/2	1/2	4.4	0.1667	1/2	0.221	0.374	4.4	—	—
240	4.9683(2)	1	0	0	0	8.2(1)	1	1/2	1/2	1/2	4.4(2)	0.1667	1/2	0.221(1)	0.374(1)	4.4(2)	1.38	3.94
250	4.9707(2)	1	0	0	0	8.7(1)	1	1/2	1/2	1/2	4.9(2)	0.1667	1/2	0.222(1)	0.374(2)	4.9(2)	1.32	3.79
260	4.9728(2)	1	0	0	0	8.7(1)	1	1/2	1/2	1/2	4.8(2)	0.1667	1/2	0.222(1)	0.373(2)	4.8(2)	1.34	3.80
270	4.9748(2)	1	0	0	0	8.9(1)	1	1/2	1/2	1/2	4.7(2)	0.1667	1/2	0.223(1)	0.374(1)	4.7(2)	1.30	3.77
280	4.9764(2)	1	0	0	0	9.3(1)	1	1/2	1/2	1/2	4.9(2)	0.1667	1/2	0.223(1)	0.367(2)	4.9(2)	1.31	3.80
290	4.9777(2)	1	0	0	0	9.4(1)	1	1/2	1/2	1/2	6.0(2)	0.1667	1/2	0.222(1)	0.374(1)	6.0(2)	1.18	3.49

---

2.3. Thermal measurements

Thermal analysis was performed using an in-house constructed differential thermal analyzer, shown schematically in Fig. 3, capable of accessing temperatures as high as 350 °C (with 0.1 °C stability) under water partial pressures as high as 0.9 atm. The system is a modification to an apparatus described previously as part of our earlier study of the phase behavior of CsH₂PO₄.⁴ In the present design, the sample stage is constructed of constantan alloy, the reference and sample are placed on the stage as shown in the figure, and directly beneath each (on the opposite side of the stage) is welded the junction of an E-type thermocouple. The temperatures of the sample and thermocouple are measured directly using the thermocouples, whereas the differential thermal signal between the sample and the reference is additionally recorded via measurement of the voltage generated between the two chromel leads. The voltage data are collected using a nanovolt meter (Keithley 182) with ±100 nV accuracy, corresponding to a precision of 0.02 mW. The electrical paths for measuring absolute temperature (the voltage between chromel–constantan couples) and that for measuring the differential temperature (voltage between two chromel leads) were electrically isolated during measurements by switching from one circuit to the other using a by Keithley 7001. The magnitude of the differential thermal signal was calibrated for measurement of heat using the melting reactions of Sn and of Pd at 232 and 327 °C, respectively. The heating and humidification schemes are unchanged relative to the previous configuration.⁴

Fig. 3 Schematic illustration of the in-house constructed DSC cell used for thermal studies under high p_H2O.

Prior to examination, the sample powders were combined with 20 wt% amorphous silica powder (Alfa Aesar, S.A 330–410, 325 mesh), homogenized by mechanical agitation, and then annealed under high humidity (p_H2O = 0.6–0.85 atm) at high temperature (2 h at 350 °C followed by 6 h at 250 °C). This treatment creates a composite sample with a fine structure, which accelerates dehydration and hydration kinetics⁴ and enables access to equilibrium behavior on laboratory time scales.

Thermal data were collected at a heating rate of 0.5 K min⁻¹ using samples typically 60 mg in mass. Under these conditions, the enthalpy for the superprotonic phase transition, with a reported value of 11.6 kJ mol,¹⁹ is detected as 11.5 ± 0.6 kJ mol⁻¹. Due to the excellent quantitative agreement, the method can be considered functionally identical to differential scanning calorimetry (DSC).

2.4. AC impedance measurements

Conductivity of the materials was determined by AC impedance spectroscopy (HP 4284A). Samples were formed into discs, 9.3 mm in diameter and typically 2 mm in thickness, by uniaxial pressing of ground powders at 491 MPa for 10 min to achieve a relative density of 99% as determined from direct measurements of mass and physical dimensions. Sputtered films of Pt or Ag, approximately 100 nm in thickness, served as electrodes. Samples were placed in a horizontal tube furnace and held in place using Pt wire current collectors. Measurements were carried out in the temperature range 180 to 280 °C under humidified N₂, p_H2O = 0.9 atm, achieved by passing the inlet gas through a water bubbler held at 98 °C prior to its entrance to the measurement zone. Step changes in temperature of 5 to 10 °C were applied and the system allowed to equilibrate for at least 30 minutes or until the impedance response had stabilized before recording the final data. The temperature was measured using an alumina sheathed E-type thermocouple placed in direct contact with the sample.

3. Results and discussion

3.1. Overall phase characteristics

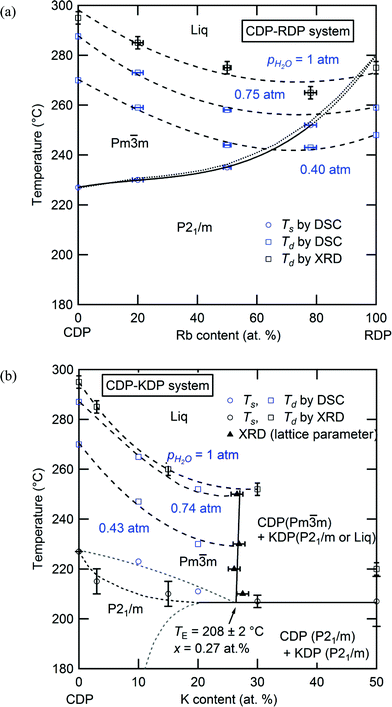
Integration of the results of the comprehensive structural, thermal and transport measurements of the materials yielded the phase diagrams presented in Fig. 4, part (a) showing the CsH₂PO₄–RbH₂PO₄ system and (b) the CsH₂PO₄–KH₂PO₄ system. Circles designate phase transition temperatures, squares dehydration temperatures, and triangles phase boundaries, where data in blue were acquired by DSC measurements and those in black by in situ XRD measurements. The CsH₂PO₄–RbH₂PO₄ system has simple isomorphous phase behavior. The end-members are entirely miscible at temperatures above 150 °C in both the monoclinic and cubic phases. The superprotonic transition temperature increases monotonically and the dehydration temperature largely decreases with increasing Rb content, resulting in a narrowing of the superprotonic region. At ambient temperature (not shown) the solubility limit of Rb into CsH₂PO₄ is ∼80 at.%,⁸ and the transformation of RbH₂PO₄ into the CsH₂PO₄-like monoclinic phase at 117 °C (ref. 22) facilitates complete solid solubility at the temperatures probed in this study. While compositions with very low Rb content were not explicitly studied here, the generally smooth manner in which the phase boundaries vary with composition suggest that the remarkable stabilization observed by Lavrova¹¹ for Cs_0.97Rb_0.03H₂PO₄ may have been an artifact due to kinetic effects.

Fig. 4 Phase diagrams of the (a) CsH₂PO₄–RbH₂PO₄, and (b) CsH₂PO₄–KH₂PO₄ systems. The dashed curves indicate the dehydration temperatures at the given values of p_H2O. The solid and dotted curves are phase boundaries.

In sharp contrast to the CsH₂PO₄–RbH₂PO₄ system, the CsH₂PO₄–KH₂PO₄ system displays eutectoid behavior with limited solubility of K in either phase of CsH₂PO₄. On introduction of K, the superprotonic transition temperature shifts downward until the eutectoid temperature of ∼208 °C (20 °C lower than the superprotonic temperature of neat CsH₂PO₄) is reached. The solubility of K into cubic CsH₂PO₄ is 27 at.% and is surprisingly temperature insensitive above the eutectoid point. Due to the challenges of determining composition in situ at high temperature, the solidus and solvus lines, however, could not be accurately determined; the dotted and dashed lines are approximate locations for these boundaries based on the requirements of the Gibbs phase rule.²³ At ambient temperature (not shown in the phase diagram) the solubility of K into monoclinic CsH₂PO₄ is just 7.2 ± 0.8 at.%, significantly lower than the 27 at.% at the eutectoid point. Above the eutectoid temperature, compositions with greater than 27 at.% K form a mixture of a cubic CDP-rich phase and a KH₂PO₄-rich phase. At moderate temperatures the latter adopts the crystalline monoclinic structure recently reported for neat KH₂PO₄ (ref. 17) and transforms to a liquid at higher temperatures. The precise transformation temperature, which was found to be sensitive to humidity, could not be determined as a result of sluggish kinetics. Overall, the dehydration temperature in this system decreases notably on introduction of K, particularly so within the single-phase superprotonic region. Accordingly, there is an overall shift of the stable cubic region to lower temperature with increasing K content, along with a slight narrowing of the stability window.

3.2. Determination of phase behavior in the Cs_1−xRb_xH₂PO₄ system: 0 ≤ x ≤ 1

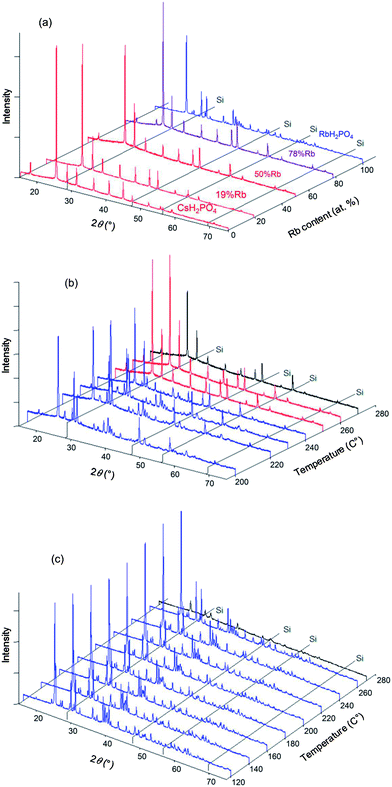
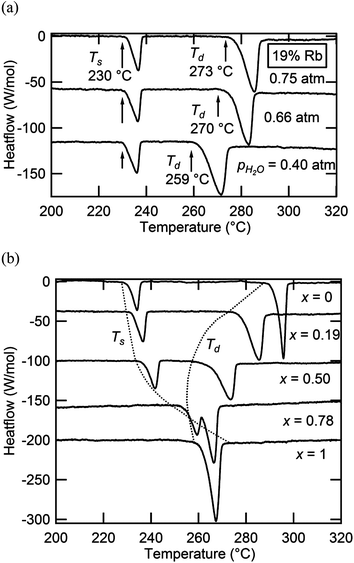
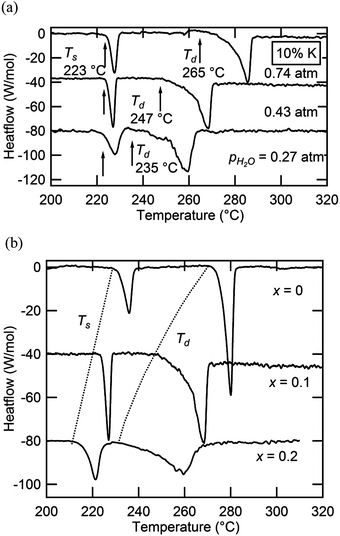
In situ XRD data were collected for the specific compositions in the Cs_1−xRb_xH₂PO₄ system of x = 0.19, 0.5, 0.78 (the actual compositions, Table 1) and for the end-member RbH₂PO₄, in addition to CsH₂PO₄ as reported above. Example diffraction results are presented in Fig. 5 both as a function of composition (part a) at high temperature (T = 260 °C) and as a function of temperature (parts b and c) for given compositions (x = 0.5, 1, respectively). The data show that the Cs_1−xRb_xH₂PO₄ compounds transform from the CDP-type monoclinic phase to the cubic CsCl-type phase of superprotonic CsH₂PO₄. Furthermore, the monoclinic P2₁/m phase reported to occur above 130 °C in RbH₂PO₄ is confirmed (and is even found to exist at 120 °C). However, no cubic phase was observed in the absence of Cs. The diffraction peaks are lost from RbH₂PO₄ at 270 °C, suggesting the occurrence of a liquid phase. It is possible the cubic superprotonic phase may be accessible under p_H2O values higher than the ∼1 atm estimated for the sealed diffraction chamber, as it is under high total pressure (1 GPa).¹⁴ Such conditions were not examined here. For all the compounds, at sufficiently high temperatures, the XRD data are marked by the absence of diffraction peaks. By analogy to CsH₂PO₄, this behavior is taken to reflect the presence of a partially dehydrated liquid (MH_2−2xPO_4−x(l), M = alkali metals), and the temperature at which the crystalline phase is no longer observed is taken to be the decomposition temperature. Weight loss at this temperature was not independently confirmed, but the DSC measurements, as discussed below, are consistent with such an interpretation.

Fig. 5 Selected XRD patterns obtained in the Cs_1−xRb_xH₂PO₄ system with Si (as internal standard). (a) Results at 260 °C with various x; and results at (b) x = 0.5 and (c) x = 1.0 (RbH₂PO₄), as functions of temperature. Red patterns correspond to the cubic phase (Pm3̄m), blue patterns to the monoclinic phase (P2₁/m) and purple patterns to 2-phase mixtures. Patterns shown in black are those with lower intensity due to amorphization and/or melting. Selected XRD patterns obtained in the Cs_1−xRb_xH₂PO₄ system.

Selected DSC profiles for compounds in the Cs_1−xRb_xH₂PO₄ system are presented in Fig. 6, part a for fixed x = 0.19 and part b for fixed p_H2O. Two thermal events are evident in all cases. At fixed stoichiometry, the first event occurs at a given temperature, 230 °C in this example, whereas the second depends on the water partial pressure. This behavior is consistent with the identification of the first transition as a polymorphic transformation, involving no change in sample composition, and of the second transition as a dehydration or partial dehydration event, involving loss of H₂O from the structure. With increasing Rb content (Fig. 6b), the temperature of the polymorphic transition monotonically increases, whereas the decomposition temperature generally decreases but finally increases slightly for the RbH₂PO₄ end-member. At x = 0.78 and p_H2O = 0.75 atm, for example, the polymorphic transition just precedes the dehydration, and the two events are almost indistinguishable. These trends are reflected in the phase diagram presented in Fig. 4(a), for which T_s and T_d are defined in terms of the onset of the respective thermal anomalies.

Fig. 6 Selected DSC profiles of materials in the Cs_1−xRb_xH₂PO₄ system: (a) results as a function of p_H2O at fixed composition (x = 0.19); and (b) results as a function of composition at fixed p_H2O (0.75 atm).

In principle, the monoclinic to cubic phase transition should pass through a two-phase region. The relatively sharp DSC peaks, spanning no more than ∼9 K, indicate that the two-phase region is rather narrow, as displayed in the phase diagram. No attempt was made in the diffraction measurements to capture the compositional breadth of the two phase region, a rather subtle feature of the phase diagram. Similar to the superprotonic transition, the dehydration anomaly displays a relatively sharp peak, despite the likely transformation to a partially dehydrated liquid and continuous weight loss at high temperature.⁴ Such behavior is similar to that observed in CsH₂PO₄ in which the dehydration is confirmed to occur over a wide temperature range but with a relatively sharp thermal signal, reflecting the fact that the majority of the weight loss occurs shortly after the onset of dehydration. The breadths, magnitudes, and onset temperatures for the superprotonic transformation and dehydration peaks are summarized in Table 3. The enthalpies of transformation/dehydration are largely independent of composition, with a typical value of 11.5 kJ mol⁻¹ for the superprotonic transition and 31.4 kJ mol⁻¹ for dehydration (comparable to the thermal properties of CsH₂PO₄ (ref. 4)). It has been suggested that the entropy of the superprotonic transition can be accounted for in terms of the configurational disorder of the oxygen atoms and protons in the cubic phase.^19,24 In light of the almost constant T_s, an almost constant ΔH is consistent with this interpretation and suggests the absence of any local ordering effects between Cs and Rb.

Table 3 Features of the peaks detected in the DSC profiles of Cs_1−xRb_xH₂PO₄ alloys

Composition	Superprotonic transition			Dehydration
	ΔH (kJ mol^−1)	T onset (°C)	FWHM (°C)	ΔH (kJ mol^−1)	T onset (°C)	FWHM (°C)
CsH2PO4	11.5 ± 0.6	227.2 ± 0.4	2.9 ± 0.1	31.0 ± 1.6	288.5 ± 0.5	2.6 ± 0.1
19%Rb	11.8 ± 0.5	230.6 ± 0.3	3.6 ± 0.1	30.2 ± 1.3	273.5 ± 0.4	5.7 ± 0.1
50%Rb	11.8 ± 0.9	234.9 ± 0.4	3.7 ± 0.1	29.0 ± 3.1	258.1 ± 0.5	6.3 ± 0.1
78%Rb	—	251.6 ± 0.2	4.2 ± 0.1	—	258 ± 3	4.2 ± 0.1
RbH2PO4	—	—	—	—	258.9 ± 0.6	4.3 ± 0.1

---

3.3. Determination of phase behavior in the Cs_1−xK_xH₂PO₄ system: 0 ≤ x ≤ 0.5

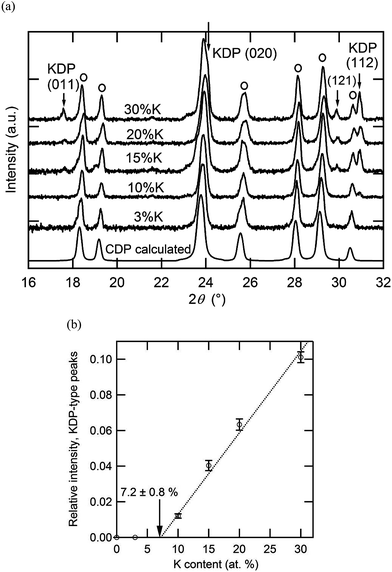
The room temperature XRD patterns of the Cs_1−xK_xH₂PO₄ system have not been previously reported and are accordingly provided here in Fig. 7. The patterns with x = 0 and 0.03 are almost identical, indicating a minimum K solubility of 3 at.%. At higher x (10 at.% and higher), the patterns reflect the presence of a two-phase mixture of a CsH₂PO₄-type monoclinic phase (P2₁/m) and a KH₂PO₄-type tetragonal phase. From an analysis of the intensity of the diffraction peaks of the latter and extrapolation to the composition at which these peaks would have zero intensity, we estimate the K solubility in monoclinic CsH₂PO₄ to be 7.2 ± 0.8 at.% (Fig. 7b). Within the two-phase region, the lattice constants of the KH₂PO₄-type tetragonal phase are, within error, equal to that of neat KH₂PO₄ (specifically, respective cell volumes of 386.1 (ref. 16) and 384 ± 1 ų at room temperature), indicating that the solubility of Cs into this phase is no more than a few at. %.

Fig. 7 Room temperature X-ray diffraction analysis of Cs_1−xK_xH₂PO₄: (a) XRD patterns from compositions with x as specified, and (b) summed intensity of KDP-type peaks {(011), (121) and (112) peaks} relative to the summed intensity of CDP-type peaks identified in (a) by the label O.

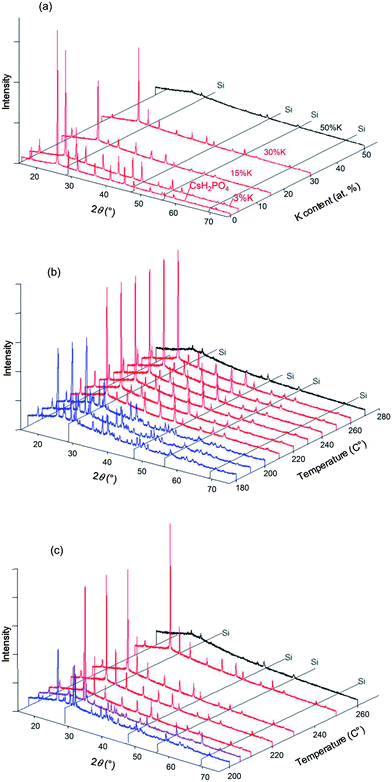
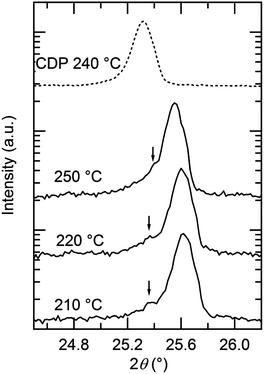
In situ high-temperature XRD experiments were performed in the Cs_1−xK_xH₂PO₄ system for the specific compositions x = 0.03, 0.15, 0.3, and 0.5, with higher potassium concentrations being of less interest with respect to superprotonic behavior. Selected diffraction results are presented in Fig. 8. At 250 °C, the data show that the cubic CsCl-type phase is the only crystalline phase present for all compositions (Fig. 8a), but in the case of x = 0.5, a broad amorphous background, indicative of a liquid phase, is the most significant feature, and the peaks from the crystalline phase are barely detectable. That the amorphous phase is liquid rather than solid was deduced on the basis of the transformation of the loose powder sample placed in the diffraction chamber into a coagulated, shiny agglomerate by the conclusion of the experiments. The temperature-dependent diffraction data reveal the x = 0.15 composition to be composed in the temperature range from 180 to 200 °C of a mixture of isostructural CsH₂PO₄-type and KH₂PO₄-type monoclinic phases (Fig. 8b). Lower temperatures were not examined, but this result indicates that, as with the Rb system, dissolution of Cs into KH₂PO₄ stabilizes the monoclinic form otherwise observed at slightly higher temperatures¹⁷ (190 °C and higher). At temperatures between 210 and 260 °C only peaks from the CsCl-type cubic phase are evident, and finally at 270 °C all diffraction peaks disappear and only the liquid is present. This behavior is generally reproduced for the x = 0.3 composition (Fig. 8c). In this case, however, an additional peak was observed around 2θ = 25° at temperatures at which the cubic phase is stable, as shown more clearly in Fig. 9. The peak location coincides with that of the (1 1 1̄) peak of monoclinic KH₂PO₄. At 205 °C after cooling from 210 °C, peaks from the cubic CsH₂PO₄-type phase, the monoclinic CsH₂PO₄-type phase and the monoclinic KH₂PO₄-type phase were observed. This co-existence suggests that the lower boundary of the cubic CsH₂PO₄-type phase lies between 205 and 210 °C. Slow equilibration kinetics prevented acquisition of diffraction data that would have provided more definitive identification of the phase boundaries.

Fig. 8 Selected XRD patterns obtained in the Cs_1−xK_xH₂PO₄ system with Si (as internal standard). (a) Results at 250 °C with various x; and results at (b) x = 0.15 and (c) x = 0.30 as functions of temperature. Red patterns correspond to the cubic phase (Pm3̄m), blue patterns to the monoclinic phase (P2₁/m) and purple patterns to 2-phase mixtures. Patterns shown in black are those with lower intensity due to amorphization and/or melting. Selected XRD patterns obtained in the Cs_1−xK_xH₂PO₄ system.

Fig. 9 Exploded view of high-temperature diffraction patterns of Cs_0.7K_0.3H₂PO₄ in the vicinity of the (1 1 1̄) peak of the KDP-type monoclinic phase, shown in comparison to the pattern of neat CsH₂PO₄ (top).

Given the challenges of direct determination of the equilibrium phase assemblage at high temperature, an evaluation of the lattice parameter dependence on composition was used as a secondary means of estimating the solubility limit of K into cubic Cs_1−xK_xH₂PO₄. In Fig. 10 this parameter is shown as a function of potassium content at 230 and 250 °C. At low K content, the cell constant decreases linearly, in accord with Vegard's empirical law. The data points for the x = 0.3 composition, however, deviate from the linear relationship. Extrapolation of the lattice parameter trendline to the measured values at x = 0.3 suggests an actual composition (i.e., solubility limit) of 27 at.% at both temperatures. This method of analysis is justified by the observation of a linear dependence of lattice parameter on dopant content in the superprotonic cubic phase within the Cs_1−xRb_xH₂PO₄ system (as discussed below).

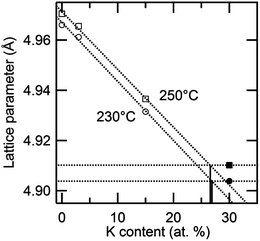Fig. 10 Variation of the high temperature lattice parameter of cubic Cs_1−xK_xH₂PO₄ as a function of x at 230 and 250 °C.

Selected DSC measurements in the Cs_1−xK_xH₂PO₄ system are presented in Fig. 11, showing both (a) isocompositional and (b) isobaric results. Thermal measurements in this case were limited to compositions of x = 0.1 and 0.2. As evidenced from Fig. 11(a), a lower temperature transition occurs that is independent of p_H2O and is followed by a higher temperature one that shifts to lower temperature on decrease of p_H2O. These events are consequently interpreted as a polymorphic transition and a dehydration reaction, respectively. The behavior is analogous to that of the Cs_1−xRb_xH₂PO₄ system, with the dehydration similarly resulting in a product phase that is a liquid. In contrast to the first system, however, a slight discrepancy was observed with respect to the temperature of the polymorphic transition as determined by diffraction and by calorimetry. For example, for x = 0.15, one observes a fully cubic pattern at 210 °C, Fig. 8b, whereas the x = 0.10 composition has an onset for the polymorphic transition, T_s, of 223 °C. Furthermore, on introduction of K, the thermal signatures widen, particularly for x = 0.2 for the superprotonic transition and for both compositions for the dehydration event. These features in the Cs_1−xK_xH₂PO₄ system are tentatively assigned to wider compositional differences between phases in the two-phase regions. During the transformation from the monoclinic to cubic phase at small x, the finite heating rate used in the DSC experiments may, as a consequence of the necessary solid state diffusion, retard the transition and shift it to higher temperature than observed under the quasi-equilibrium conditions of the diffraction experiment. Similarly, gradual and continuous phase separation into distinct monoclinic and cubic phases or a potassium-rich liquid dehydrate [MH_2−2xPO_4−x(l)] and a cesium-rich solid may be responsible for the broadening observed in the thermal peaks.

Fig. 11 Selected DSC profiles of materials in the Cs_1−xK_xH₂PO₄ system: (a) results as a function of p_H2O at fixed composition (x = 0.10) and (b) results as a function of composition at fixed p_H2O (0.43 atm).

3.4. Structural and transport properties

The thermal expansion behavior of the cubic phase in the Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ systems is summarized in Fig. 12 and Table 4, where the coefficients of thermal expansion, α, are of the form Δa/a₀ = α(T − T₀), with T₀ = 260 °C. These coefficients are approximately 4 × 10⁻⁵ K⁻¹ for each of the compounds with negligible impact from the introduction of substituents. The volumetric expansion coefficient (3α) for CsH₂PO₄ in the cubic phase, determined here to be 1.57(3) × 10⁻⁴ K⁻¹, is slightly smaller than that, 1.98(2) × 10⁻⁴ K⁻¹, reported by Louie.⁷ The lattice parameters measured in this work agree well with Louie's values and are slightly larger than those of other reports.^25–27 The influence of material composition, specifically, the weighted mean ionic radii,²⁸ on the cubic lattice parameter (at 260 °C) is summarized in Fig. 13. The data from the two systems show good agreement, indicating that the lattice constant of the solid-solution cubic phase depends simply on the averaged ionic radius of cations in the alkali ion site rather than the nature of the specific cation. Again, the behavior is in accord with Vegard's empirical law.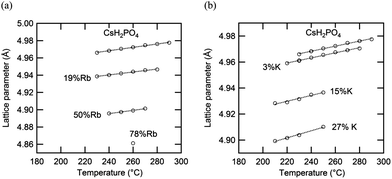

Fig. 12 Lattice parameters of cubic (a) Cs_1−xRb_xH₂PO₄ and (b) Cs_1−xK_xH₂PO₄ as functions of temperature under p_H2O ∼ 1 atm (the estimated errors lie within the size of the data markers).

Table 4 Thermal expansion coefficients (Δa/a₀ = α(T − T₀) with T₀ = 260 °C) of cubic Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄

Composition	α (10^−5 K^−1)	a 0 (Å)	T (°C)	Composition	α (10^−5 K^−1)	a 0 (Å)	T (°C)
CsH2PO4	3.92(11)	4.9724(2)	230–290
19%Rb	3.42(17)	4.9440(2)	230–280	3%K	3.95(13)	4.9675(2)	220–280
50%Rb	3.85(19)	4.8991(2)	240–270	15%K	4.54(48)	4.9388(8)	210–250
78%Rb	—	4.8612(3)	260	30%K	4.65(10)	4.9107(6)	210–250

---

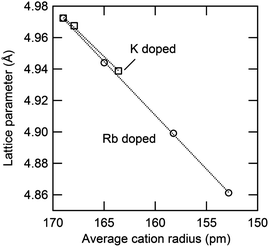Fig. 13 Relationship between averaged ionic radius and lattice parameter in cubic Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ at 260 °C. For the latter, the values are extrapolated from measurements at slightly lower temperatures using the measured thermal expansion coefficient (Table 4).

The AC impedance measurements revealed that the solid solution cubic phase has high conductivity in both the CsH₂PO₄–RbH₂PO₄ and the CsH₂PO₄–KH₂PO₄ systems. The impedance spectra at high temperature displayed typical features¹⁹ in which the response appears as a straight line with a real intercept at the high frequency limit corresponding to the resistance of the polycrystalline solid electrolyte, Fig. 14. In the case of the Rb containing compositions, the low temperature spectra were also typical of CsH₂PO₄, as shown for example for Cs_0.81Rb_0.19H₂PO₄, Fig. 14(a), in which the spectrum appears as a single, high-frequency arc, the diameter of which corresponds to the resistance of the electrolyte. The difference in conductivity at 200 and at 240 °C is almost four orders of magnitude, similar to the reported impact of the superprotonic transition on the transport properties of neat CsH₂PO₄. In contrast, the K containing compositions displayed surprisingly high conductivity even at temperatures below the transition, with the difference in conductivity between 202 and 243 °C being only about a factor of six for Cs_0.90K_0.10H₂PO₄. Although such enhancement is intriguing and results in spectra that are similar in the high and low temperature phases, Fig. 14(b), it was not explored further due to the overall low conductivity of the monoclinic phase. Moreover, measurements in the CsH₂PO₄–KH₂PO₄ system were limited to compositions lying within the solubility limit of potassium into monoclinic CsH₂PO₄ so as to eliminate any influence of ensemble microstructure. For comparative purposes, the conductivity of CsH₂PO₄ was also measured and was found to be in excellent agreement with literature values.^1,2,19,29

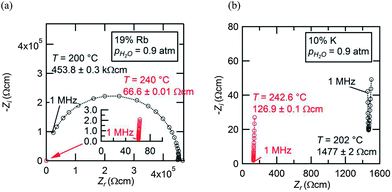Fig. 14 AC impedance spectra collected from (a) Cs_0.81Rb₁₉H₂PO₄ and (b) Cs_0.90K_0.10H₂PO₄ at temperatures just below (black) and just above (red) the respective T_s values with p_H2O = 0.9 atm. The behavior of Cs_0.81Rb₁₉H₂PO₄ is entirely analogous to that of neat CsH₂PO₄.¹⁹ In the case of Cs_0.90K_0.10H₂PO₄, the surprisingly high conductivity below T_s results in a spectrum that has similar general characteristics to that above T_s, appearing as an almost vertical straight line with real intercept that corresponds to the bulk electrolyte conductivity.

Focusing on transport in the high temperature phase, Fig. 15, it is apparent that introduction of both Rb and K leads to a monotonic reduction of the conductivity of CsH₂PO₄. A similar result was observed by Matsuo,⁹ but was reported without comment. Here, it is further observed that potassium has a stronger impact than rubidium. A close examination of the Arrhenius representation of the conductivity data reveals that, although the conductivity decreases on with increasing concentration of Rb or K, the activation energy for transport also decreases, and hence it is the reduction in the pre-exponential factor, A, in the expression 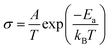that correlates with the reduction in conductivity. A detailed investigation of the role of cation chemistry on proton transport characteristics is beyond the scope of the present work, which is instead focused on exploration of phase stability. Nevertheless, it is noteworthy that changes to the averaged structure apparently do not account for the change in transport properties. Specifically, although the cell volumes of Cs_0.81Rb_0.19H₂PO₄ and Cs_0.90K_0.10H₂PO₄ are almost identical, the latter has a conductivity that is less than half that of the former and an activation energy that is also almost halved in comparison, Table 5. Elucidation of the origins of this intriguing phenomenon awaits a future study.

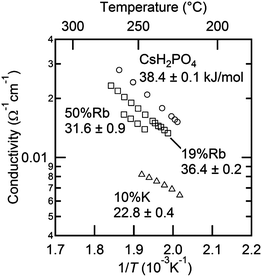Fig. 15 Arrhenius representation of the conductivities of cubic Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄ as functions of temperature.

Table 5 Activation energy and pre-exponential factor for proton transport in cubic Cs_1−xRb_xH₂PO₄ and Cs_1−xK_xH₂PO₄

Composition	E a (eV)	log(A) Ω^−1 cm^−1 K
CsH2PO4	38.4 ± 0.1	11.32 ± 0.02
19%Rb	36.4 ± 0.2	10.60 ± 0.05
50%Rb	31.6 ± 0.9	9.31 ± 0.20
10%K	22.8 ± 0.4	6.73 ± 0.08

---

4. Conclusions and summary

The results of this work are summarized as follows. The CsH₂PO₄–RbH₂PO₄ system displays complete solid solubility at all temperatures above 180 °C. The transformation from the monoclinic phase (P2₁/m) to the superprotonic cubic phase (Pm3̄m) shifts to higher temperatures with increasing Rb content. Simultaneously, the dehydration temperature largely decreases, resulting in a narrowing of the region of stability of the cubic phase. In the case of the end-member RbH₂PO₄ compound, this phase cannot be observed under 1 atm p_H2O. While a two-phase region is expected between the monoclinic and cubic phases at intermediate composition, the width of this region is too small for detection in this study. In contrast, CsH₂PO₄–KH₂PO₄ forms a eutectoid system, with a eutectoid temperature of ∼208 °C. The solubility limit of K into cubic CDP is 27 at.% and is surprisingly temperature insensitive above the eutectoid temperature up to 260 °C. Below the eutectoid point the solubility drops steeply. Within the single-phase cubic region, the transition temperature decreases monotonically, but is accompanied by a simultaneous decrease in the dehydration temperature. Thus, the phase stability width of the superprotonic phase is relatively unchanged upon introduction of K. The phase boundaries could not be accurately determined due to the challenges of high temperature, in situ composition measurements and the slow equilibration kinetics. A wider two-phase region between monoclinic and cubic phases than the Rb system is inferred on the basis of the broader DSC signals.

In both systems, the cubic cell volume decreases in proportion to the substituent concentration. The reduction is independent of the nature of the element, instead being given by the average cation radius. The thermal expansion coefficient in the cubic phase is, within the limits of measurement, independent of composition.

The most significant finding is the substantial reduction in conductivity in the high-temperature cubic phase upon introduction of substituent elements. This reduction occurs as a result of a dramatic decrease in the pre-exponential factor. Furthermore, the influence of K on the conductivity exceeds that of its influence on the cell volume, suggesting that the impact on transport must be due to local rather than global or averaged effects. The reduction in conductivity due to the introduction of substituent elements, though undesirable from a technological perspective, provides a possible avenue for elucidating and ultimately tuning the rate-limiting step in charge transport in superprotonic crystals. At this stage, unmodified CsH₂PO₄ remains the most feasible composition for fuel cell development.

Acknowledgements

The authors gratefully acknowledge financial support from U.S. National Science Foundation, Division of Materials Research (DMR-0906543) and the Army Research Office MURI Program (W911NF-07-1-0410).

References

1. D. A. Boysen, T. Uda, C. R. I. Chisholm and S. M. Haile, Science, 2004, 303, 68–70.
2. J. Otomo, T. Tamaki, S. Nishida, S. Q. Wang, M. Ogura, T. Kobayashi, C. J. Wen, H. Nagamoto and H. Takahashi, J. Appl. Electrochem., 2005, 35, 865–870.
3. T. Uda, D. A. Boysen, C. R. I. Chisholm and S. M. Haile, Electrochem. Solid-State Lett., 2006, 9, A261–A264.
4. A. Ikeda and S. M. Haile, Solid State Ionics, 2012, 213, 63–71.
5. Y. Uesu and J. Kobayashi, Phys. Status Solidi A, 1976, 34, 475–481.
6. A. R. Al-Karaghouli, B. Abdul-Wahab, E. Ajaj and A. Sequeira, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 1040–1042.
7. M. W. Louie, M. Kislitsyn, K. Bhattacharya and S. M. Haile, Solid State Ionics, 2010, 181, 173–179.
8. L. Cowan, Ph.D. Thesis, California Institute of Technology, Pasadena, California, 2007.
9. Y. Matsuo, J. Hatori, Y. Yoshida and S. Ikehata, Solid State Ionics, 2012, 213, 42–44.
10. C. E. Botez, H. Martinez, R. J. Tackett, R. R. Chianelli, J. Z. Zhang and Y. S. Zhao, J. Phys.: Condens. Matter, 2009, 21, 325401.
11. G. V. Lavrova, V. V. Martsinkevich and V. G. Ponomareva, Inorg. Mater., 2009, 45, 795–801.
12. A. Ikeda and S. M. Haile, Solid State Ionics, 2010, 181, 193–196.
13. V. V. Martsinkevich, V. G. Ponomareva, T. N. Drebushchak, G. V. Lavrova and S. S. Shatskaya, Inorg. Mater., 2010, 46, 765–769.
14. C. E. Botez, R. J. Tackett, J. D. Hermosillo, J. Z. Zhang, Y. S. Zhao and L. P. Wang, Solid State Ionics, 2012, 213, 58–62.
15. H. Naili, N. Zouari, T. Mhiri and A. Daoud, J. Mol. Struct., 2000, 519, 143–151.
16. K. Itoh and M. Uchimoto, Ferroelectrics, 1998, 217, 155–162.
17. C. E. Botez, D. Carbajal, V. A. K. Adiraju, R. J. Tackett and R. R. Chianelli, J. Phys. Chem. Solids, 2010, 71, 1576–1580.
18. D. A. Boysen, S. M. Haile, H. J. Liu and R. A. Secco, Chem. Mater., 2004, 16, 693–697.
19. S. M. Haile, C. R. I. Chisholm, K. Sasaki, D. A. Boysen and T. Uda, Faraday Discuss., 2007, 134, 17–39.
20. F. Izumi and K. Momma, Applied Crystallography XX, 2007, 130, 15–20.
21. B. N. Dutta, Phys. Status Solidi B, 1962, 2, 984–987.
22. M. Komukae, K. Kawashima and T. Osaka, J. Phys. Soc. Jpn., 2000, 69, 2076–2081.
23. P. W. Atkins and J. de Paula, Physical chemistry, Oxford University Press, 8th edn, 2006.
24. C. R. I. Chisholm, Ph.D. Thesis, California Institute of Technology, 2003.
25. K. Yamada, Solid State Ionics, 2004, 175, 557–562.
26. W. Bronowska, Mater. Sci.-Pol., 2006, 24, 229–236.
27. A. Preisinger, K. Mereiter and W. Bronowska, Mater. Sci. Forum, 1994, 166, 511–516.
28. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, 1960.
29. A. Ishikawa, H. Maekawa, T. Yamamura, Y. Kawakita, K. Shibata and M. Kawai, Solid State Ionics, 2008, 179, 2345–2349.

---