Open Access Article
Open Access ArticleFluctuation spectra in polymer nematics and Frank elastic constants: a coarse-grained modelling study
Patrick
Gemünden
and
Kostas Ch.
Daoulas
*
Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: daoulas@mpip-mainz.mpg.de
First published on 12th November 2014
Abstract
Monte Carlo simulations of uniaxial nematic polymer melts are performed, based on a discrete worm-like chain model combined with soft, anisotropic non-bonded potentials. Different chain lengths are considered, the contour length of the longest being an order of magnitude larger than the persistence length. From equilibrated melt configurations, density and director fluctuation spectra are calculated and compared with analytical predictions available in literature. The latter typically correspond to hydrodynamic treatments of correlations and assume that there is no chain backfolding along the nematic director. Nevertheless, it is demonstrated that the analytical theories capture several features of the spectra obtained in the current simulations, where moderate backfolding of polymer chains is observed. Based on the available analytical expressions for density and director fluctuation spectra, material properties, such as Frank elastic constants, are extracted. Their dependence on polymerisation degree is studied and found to reproduce theoretically expected trends. For example, evidence is provided that the splay constant increases linearly with chain length, when effects of hairpins are negligible.
1 Introduction
In nematic liquid crystals (LC), the thermodynamic cost of changes in the orientation of the director on the mesoscale, away from the core of topological defects,1,2 can be expressed through the Frank-Oseen free energy.3 The latter presents a volume integral of a free-energy density, corresponding to a quadratic expansion with respect to the gradient of the director field. For bulk LC this expansion reduces to a sum of three distortion modes (splay, twist, and bend) of the director field, coupled to an appropriate elastic constant.4–6Elastic properties of LC are significant for various technological applications, including opto-electronics,7,8 pattern formation in colloids,9 chemical detection,10,11 and microfluidics.12 In polymeric LC, elastic properties are a major factor affecting texture.13 Examples where the latter is important include manufacturing high strength materials14,15 and applications in organic electronics.16–23 There it has been suggested22 that thermotropic LC mesophases of conjugated polymers can facilitate manipulation of their morphology in solid state through appropriate thermal annealing protocols.
Linking mesogenes into long molecules increases for polymeric LC the complexity of elastic behaviour. For instance, changes in orientational order and density variations are coupled, affecting splay deformation. Several analytical theories were formulated24–31 predicting fluctuation spectra and associated material properties (including Frank constants) within a hydrodynamic treatment of correlations. The “bow-tie” shape of the density structure factor27–31 is one of the representative theoretical results. At the same time, analytical theories differ in certain predictions depending on the underlying assumptions and approximations. One of the most known examples is the effect of chain length on the splay elastic constant, where both linear26 and quadratic dependences24,25 have been predicted. The former stems from an entropic penalty for an inhomogeneous distribution of chain ends required for a splay deformation, as assumed by Meyer.26 The alternative result is due to de Gennes, assuming that the splay deformation is achieved through density variations, while chain ends are randomly distributed.24,25 Interestingly, for lyotropic LC, taking into account the dependence of the osmotic compressibility on chain length (inversely proportional to leading order) eliminates32 the discrepancy between the results of de Gennes and Meyer, i.e., they both yield a linear dependence. For polymer melts (i.e., thermotropic LC), however, the controversy remains. Notably, other theoretical studies reproduce the result of Meyer.27–29,31
There have been very few5 experimental measurements of elastic constants in thermotropic polymeric LC.33–35 Lyotropic systems have been investigated to a somewhat larger extent,5 considering effects of concentration and chain length on elastic properties. For instance, results supporting a linear dependence of the splay constant on chain length have been reported.32 In the same work evidence was provided that in the limit of long, semiflexible chains, the bending constant becomes independent of chain length, as predicted theoretically.26,30,36–38
In particle-based computer simulations of LC composed of small molecules, several approaches have been developed for a “first principle” determination of elastic constants corresponding to a given microscopic model. Their evaluation from director fluctuations has been particularly popular,39–42 while relationships between elastic constants and orientation-dependent pair-correlation functions known from density functional theory43–45 have been also utilised.41,46,47 Recently a new method based on free-energy perturbations was proposed.48 However, these techniques have been rarely applied to polymeric LC. For example, an early work49 discussed properties of elastic constants in lyotropic nematics, describing them as two dimensional semi-flexible chains with hard excluded volume interactions. Later,50 the bow-tie shape of the density structure factor in lyotropic polymer nematics was confirmed without addressing, however, director fluctuations and related material properties.
Here, coarse-grained computer simulations are employed to study density and orientational order fluctuations, as well as related material properties in thermotropic polymer nematics in a unified way. The main-chain LC polymers are represented with discrete worm-like chains (WLCs), while non-bonded interactions are described through soft anisotropic potentials.51,52 To obtain a realistic model and facilitate possible comparison with future experiments, the potentials are parameterised to reproduce persistence length and density typical for poly(3-alkylthiophenes). This is a representative family of conjugated polymers where LC mesophases have been reported.20,21,53 With this model, Monte Carlo (MC) simulations are conducted to equilibrate monodisperse nematic melts with different chain lengths. Due to softness of interactions, polymers with contour lengths up to an order of magnitude larger than the persistence length (as defined from a disordered melt) could be studied.
Equilibrated configurations are analysed to obtain density and director-fluctuation spectra. We verify that the spectra can be described by generic functional forms proposed theoretically,27–31,54 treating material constants (e.g., compressibility and Frank constants) entering these expressions as adjustable parameters. Material constants extracted independently from density and director-fluctuation spectra are compared with each other, while their dependence on chain length is also discussed. The results are compared with theoretical predictions, taking into account that they assume absence of hairpins as opposed to moderate chain backfolding in the simulations of the longest WLCs. For example, evidence is provided supporting the arguments of Meyer26 regarding a linear dependence of the splay constant on chain length, when there is no significant chain backfolding.
The paper is organised as follows. Section 2 describes the simulation strategy and the modelled systems. Section 3 recapitulates the theoretical predictions in the “zero-hairpin” limit in terms of the molecular model employed in the simulations. In Section 4 the strength of ordering and chain backfolding are quantified. Density and director fluctuation spectra are discussed. Material properties such as Frank elastic constants are extracted and their dependence on chain length is compared with theoretical predictions. Our conclusions follow in the last section.
2 Modelling approach
2.1 Coarse-grained description
Studying fluctuations in polymer nematics and comparing with related analytical theories requires the consideration of large systems. In particular, it is desirable that the dimensions of the system substantially exceed the largest possible molecular scale of the problem – the length of a fully stretched polymer chain. This motivates us to combine a drastically coarse-grained representation of polymer architecture with soft non-bonded interactions (i.e. on the order of the thermal energy, kBT). The latter relaxes excluded volume constraints, increasing significantly the computational efficiency. At the same time, comparing to models with “microscopic” hard sphere excluded volume,50 achieving nematic polymer order with isotropic soft potentials (as those in standard Dissipative Particle Dynamics55) is more complicated.56 In contrast, it has been demonstrated56–61 that it is straightforward to describe LC mesophases with anisotropic soft potentials. This strategy will be employed here, using a special form of anisotropic potentials51,52 inspired by field theoretical approaches to polymeric liquid crystals,62–66 which facilitates parameterisation.Each of the n polymers is represented51 by a discrete WLC chain with N segments (bonds) so that the bonded interactions are described by:
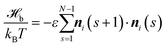 | (1) |
In principle, within the current strategy models closer to the original chemical structure of specific polymers can be also implemented. For example, in ref. 52 liquid crystalline mesophases of P3HT were addressed employing less drastic coarse-graining, where each effective monomer represented one atomistic hexylthiophene (thus in that model b = 0.4 nm which expresses the distance of two neighbouring repeat units). Bonded interactions were described by torsional and angular potentials obtained in a bottom-up fashion from systematic coarse-graining of atomistic chains. In this case, describing the geometric zigzag of the backbone was necessary for developing soft anisotropic potentials leading to biaxial nematic mesophases and considering effects of morphology on charge transport.52 At the same time, for the purposes of the current study focusing on the long wavelength limit, the WLC model which neglects microscopic details presents a more natural choice. The implementation of the discrete WLC in the simulations simplifies the comparison with analytical theoretical predictions, which were obtained on the basis of the continuum WLC model (see Section 3). The WLC model is also computationally more advantageous: to address the same magnitude of chain lengths (in terms of persistence length) the more detailed description would involve twice as many coarse-grained particles.
The anisotropic soft potential describing the non-bonded interactions is defined51,52 as:
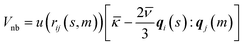 | (2) |
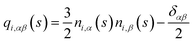 expresses the segment orientation with respect to the laboratory coordinate frame. The soft core u(rij(s, m)) is proportional52 to the overlap of two spherical density distributions set to ω(r) = 3/4πσ3 for r ≤ σ and zero otherwise, placed at ri(s) and rj(m). Thus the following form is obtained:70
expresses the segment orientation with respect to the laboratory coordinate frame. The soft core u(rij(s, m)) is proportional52 to the overlap of two spherical density distributions set to ω(r) = 3/4πσ3 for r ≤ σ and zero otherwise, placed at ri(s) and rj(m). Thus the following form is obtained:70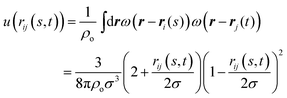 | (3) |
Since the density distributions can be seen as representations of the microscopic degrees of freedom underlying the coarse-grained units,51,52,71,72 we choose for the interaction range σ = 0.79 nm which is comparable to the length of a hexyl chain in all-trans configuration. Combined with the density clouds, the WLC can be considered as a soft tube encasing the backbone of the poly(3-hexylthiophene) together with the attached side chains.51ρo is a reference bulk density; since the bulk density of P3HT is ∼4 hexylthiophenes per nm3 and each segment in our model represents two hexylthiophenes we choose ρo = 2 segments per nm3. The parameter κ controls the compressibility and we choose κ = 7.58kBT, which is comparable to the values used in earlier studies.51,52 To obtain nematic ordering, the strength of the orientation coupling between segments is set to ν = 3.33kBT. All simulations are performed at temperature T = 500 K.
2.2 Systems studied and simulation details
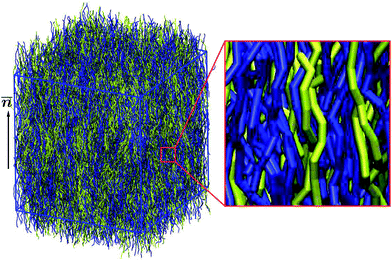
Monodisperse melts of coarse-grained chains with N = 16, 32, 48 and 64 segments were equilibrated using Monte Carlo (MC) simulations in the nVT ensemble. Cubic simulation cells with periodic boundary conditions in all directions were considered. For the three largest N the length of the cell-edges, Lbox, was chosen to be two times larger than the end-to-end distance of a fully stretched WLC (which equals the contour length, L = bN). For the shortest chains, N = 16, simulations in cells with Lbox = 8L were conducted, while smaller systems, Lbox = 4L, were also considered to estimate finite system size effects. The number of chains in each melt was chosen so that the average segment density reproduced the reference bulk density of P3HT, i.e., nN/V = ρo. This requirement leads to systems with a large number of particles (e.g., for N = 64 there are more than 2 × 106 segments in the cell), which nevertheless can be equilibrated due to the softness of the interactions. For each of the longest melts eight independent simulations were performed, to allow for an error estimation of the extracted properties (cf. Section 4). For melts with N = 16 chains the number of independent simulations was larger – sixteen.All chains are initially fully stretched and aligned along the z-axis of the laboratory frame, while their centres-of-mass are randomly distributed. A MC algorithm based on a combination of standard random monomer displacement (DIS) and slithering snake (REP) MC moves is employed to equilibrate the system. The mix of moves contains 30% DIS and 70% REP. A representative snapshot of an equilibrated nematic melt of chains with N = 32 is presented in Fig. 1.
3 Theoretical background (zero-hairpin limit)
In this section, earlier theoretical predictions regarding density and director fluctuations in polymer nematics will be recapitulated in terms of the discrete WLC model employed in the simulations. For a nematic mesophase with n continuum WLCs, it is straightforward to introduce a local areal density of chains intersecting a plane normal to the average director of the mesophase,![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) . Without loosing generality, it is convenient to assume that
. Without loosing generality, it is convenient to assume that ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) is parallel to the z-axis of the laboratory coordinate frame. Then zp sets the position of such a plane and r⊥ is a two dimensional vector defining a point on the plane. In this setup chains, when oriented without backfolding, can be described27,29–31 as curves which are single-valued functions of z. The local areal density becomes:
is parallel to the z-axis of the laboratory coordinate frame. Then zp sets the position of such a plane and r⊥ is a two dimensional vector defining a point on the plane. In this setup chains, when oriented without backfolding, can be described27,29–31 as curves which are single-valued functions of z. The local areal density becomes: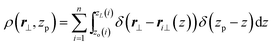 | (4) |
In the above, zo(i) and zL(i) are z-projections of the two ends of the i-th chain (L is the contour length of the WLC). Within a hydrodynamic treatment of correlations, local fluctuations δρ(r⊥, zp) and δn(r⊥, zp) of density and director fields can be penalised through a free energy:27,29,31
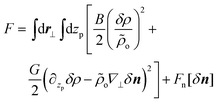 | (5) |
The first term in eqn (5) stands for a simple equation-of-state, with ρo and B being the average areal chain density and the two-dimensional bulk modulus, respectively. The latter does not depend on chain length, up to a ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (L−1) term29 due to translational entropy. For a chain to intersect a plane, the average distance of its centre from zp must be smaller than l/2 below or above the surface,73 where l is the average length of the chain projection on the z axis. Thus it follows that ρo = nl/V. The second term in eqn (5) expresses the constraint that changes in areal density and director fields are coupled, hence G can be seen as a Lagrange multiplier enforcing this constraint. In particular4,26 ∂zpδρ − ρo∇⊥δn = ρH − ρT, where ρH and ρT are the local densities of chain “head” and “tail” ends. In the limit of infinitely long chains there are no chain ends present, thus the differential form in eqn (5) is strictly zero. Hence in this case G → ∞. For finite chains, to penalise deviations of ρH − ρT from zero (as happens in the case of splay deformation26), analytical theories26,27,29,31 typically assume G = lkBT/2ρo. This corresponds to the concentration susceptibility of a mixture of “head” and “tail” ends, considering them as noninteracting ideal gases. Recently it was recognised that this constraint applies in fact to polar nematic ordering and care is required when it is implemented in nonpolar nematics73,74 (i.e. quadrupolar ordering). For the latter, an alternative tensorial conservation law has been developed.74 However, to the best of our knowledge this constraint has not yet been employed when describing fluctuations. The last term, Fn, is a “bare” Frank free energy with splay, K1, twist, K2, and bend, K3, elastic constants approximately equal to those of a system of unpolymerised mesogenes.29
(L−1) term29 due to translational entropy. For a chain to intersect a plane, the average distance of its centre from zp must be smaller than l/2 below or above the surface,73 where l is the average length of the chain projection on the z axis. Thus it follows that ρo = nl/V. The second term in eqn (5) expresses the constraint that changes in areal density and director fields are coupled, hence G can be seen as a Lagrange multiplier enforcing this constraint. In particular4,26 ∂zpδρ − ρo∇⊥δn = ρH − ρT, where ρH and ρT are the local densities of chain “head” and “tail” ends. In the limit of infinitely long chains there are no chain ends present, thus the differential form in eqn (5) is strictly zero. Hence in this case G → ∞. For finite chains, to penalise deviations of ρH − ρT from zero (as happens in the case of splay deformation26), analytical theories26,27,29,31 typically assume G = lkBT/2ρo. This corresponds to the concentration susceptibility of a mixture of “head” and “tail” ends, considering them as noninteracting ideal gases. Recently it was recognised that this constraint applies in fact to polar nematic ordering and care is required when it is implemented in nonpolar nematics73,74 (i.e. quadrupolar ordering). For the latter, an alternative tensorial conservation law has been developed.74 However, to the best of our knowledge this constraint has not yet been employed when describing fluctuations. The last term, Fn, is a “bare” Frank free energy with splay, K1, twist, K2, and bend, K3, elastic constants approximately equal to those of a system of unpolymerised mesogenes.29
From eqn (5), structure factors of areal density and director fluctuations were obtained27,29,31 in the hydrodynamic limit and found in agreement with a more elaborated “microscopic” description, mapping polymer trajectories on wordlines of two dimensional bosons.27,29,31 To cast these results in context of discrete WLCs, it is helpful to parameterise the continuum WLC through the arc length t of the curve. Since there is no backfolding, z will be a single-valued function of t, that is, z = zi(t) and ri⊥(zi(t)) = ri⊥(t). Thus eqn (4) becomes:
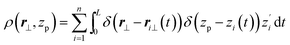 | (6) |
Considering that z′i = dzi/dt is the direction cosine of the tangent vector of the curve at arc length t with the z-axis, a discrete analog of eqn (6) can be introduced as:
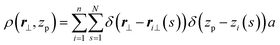 | (7) |
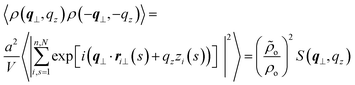 | (8) |
Angular brackets denote an average in the canonical ensemble and l = aN was substituted into ρo = nl/V to obtain a = ρo/ρo. The scattering function S(q⊥, qz) is normalised by V and not the number of scatterers, nN, as is more common. Direct substitution of theoretical results27,29,31 for 〈ρ(q⊥, qz)ρ(−q⊥, −qz)〉 into eqn (8) leads to the following prediction for the discrete WLC model:
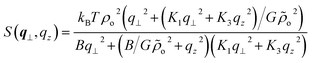 | (9) |
This corresponds to highly asymmetric scattering, where the contour lines of constant S(q⊥, qz) create the characteristic “bow-tie” pattern.27,29–31 As an illustration, it is helpful to consider the behaviour of S(q⊥, qz) along the qz = 0 and q⊥ = 0 axes:
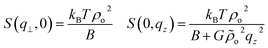 | (10) |
S(0, qz) has an Ornstein–Zernike form with 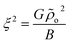 being the analog of a correlation length (squared). Indeed the above demonstrate that for infinitely long chains, l → ∞ (that is, G → ∞), there should be no scattering30 along q⊥ = 0 while constant scattering is still obtained for qz = 0. According to eqn (10), chains of finite length scatter also for q⊥ = 0. This scattering however decays as one moves from the origin of the axes (more detailed discussion of the predicted contour plots of the structure factor can be found, for example, in ref. 31).
being the analog of a correlation length (squared). Indeed the above demonstrate that for infinitely long chains, l → ∞ (that is, G → ∞), there should be no scattering30 along q⊥ = 0 while constant scattering is still obtained for qz = 0. According to eqn (10), chains of finite length scatter also for q⊥ = 0. This scattering however decays as one moves from the origin of the axes (more detailed discussion of the predicted contour plots of the structure factor can be found, for example, in ref. 31).
To compare with simulations, it is convenient to address director fluctuations in melts of discrete WLCs in terms of the nematic tensor,39,40,54,75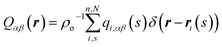 . The Fourier transform of this quantity is given by:
. The Fourier transform of this quantity is given by:
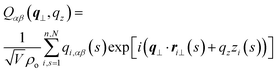 | (11) |
For ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) oriented along the z-axis and small distortions of the director field, one has:54,76δnα(r) = 2Qαz(r)/3〈S〉 (here α = x, y and 〈S〉 is the average order parameter). Thus the theoretical predictions27,29,31 for 〈δnα(q⊥, qz)2〉 transform to:
oriented along the z-axis and small distortions of the director field, one has:54,76δnα(r) = 2Qαz(r)/3〈S〉 (here α = x, y and 〈S〉 is the average order parameter). Thus the theoretical predictions27,29,31 for 〈δnα(q⊥, qz)2〉 transform to:
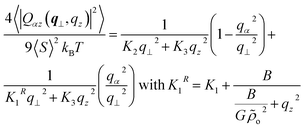 | (12) |
As in the case of S(q⊥, qz) angular brackets denote an average in the canonical ensemble.
The form of the spectrum of the orientation tensor in eqn (12) is generic and typical54 for nematic LC described by a Frank free energy, albeit here the splay constant K1R is q-dependent. The limit of K1R for qz2 → 0 is 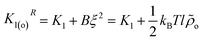 . It can be seen27,29,31 that K1(o)R ∼ N, which agrees with a more qualitative treatment by Meyer. On the contrary, in the same limit, an alternative approach by de Gennes24,25 leads to a different scaling, K1(o)R ∼ N2. Notably, for infinite chains all analytical theories24,27,29,31 are consistent with each other, predicting K1R = K1 + B/qz2.
. It can be seen27,29,31 that K1(o)R ∼ N, which agrees with a more qualitative treatment by Meyer. On the contrary, in the same limit, an alternative approach by de Gennes24,25 leads to a different scaling, K1(o)R ∼ N2. Notably, for infinite chains all analytical theories24,27,29,31 are consistent with each other, predicting K1R = K1 + B/qz2.
4 Results
4.1 Data analysis
During the discussion of the theoretical predictions, for simplicity it was assumed that the laboratory and the macroscopic nematic director frames match. In simulations, this takes place in the starting configurations where![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) is oriented along the z-axis of the simulation box. However, it is important to monitor
is oriented along the z-axis of the simulation box. However, it is important to monitor ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) during the entire MC run since it can reorient40,77 due to fluctuations. Thus in each melt configuration the maximum eigenvalue, S, and the corresponding eigenvector of the tensor
during the entire MC run since it can reorient40,77 due to fluctuations. Thus in each melt configuration the maximum eigenvalue, S, and the corresponding eigenvector of the tensor 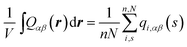 were calculated. This analysis demonstrates that for the two shortest melts, N = 16 and 32, the changes in the orientation of
were calculated. This analysis demonstrates that for the two shortest melts, N = 16 and 32, the changes in the orientation of ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) are indeed substantial. For example, for the N = 16 melt angles as large as θ = 7.5° between
are indeed substantial. For example, for the N = 16 melt angles as large as θ = 7.5° between ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) and the z-axis of the laboratory frame were observed. At the same time, for the two longest melts N = 48 and 64 the re-orientations of
and the z-axis of the laboratory frame were observed. At the same time, for the two longest melts N = 48 and 64 the re-orientations of ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) were found insignificant, i.e., the observed angles were at most θ ≃ 1°. During the analysis of the fluctuation spectra, the differences between the laboratory and the nematic director frames are taken into account40,77 as described below.
were found insignificant, i.e., the observed angles were at most θ ≃ 1°. During the analysis of the fluctuation spectra, the differences between the laboratory and the nematic director frames are taken into account40,77 as described below.
To calculate fluctuation spectra, the scattering vectors must comply with periodic boundary conditions78 and it is more convenient to introduce them in the laboratory frame. There their components are given by qαL = 2πiα/Lbox, where iα are integers and α = x, y, z. For each configuration of the N = 16 and 32 melts a density structure factor S(qL) is calculated in the Fourier space of the laboratory frame via the definition in eqn (8) but replacing q = {q⊥, qz} with qL (ri(s) are by default in the laboratory frame). To define the vectors we use −15 ≤ iα ≤ 15. Subsequently, a qL-dependent 123-frame is introduced.40,77 The z-axis of this frame in every configuration is set along the corresponding ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) . The y-axis is placed in the plane defined by qL and
. The y-axis is placed in the plane defined by qL and ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) , while orthonormality determines the x-axis. The scattering vector in 123-frame is obtained as q =
, while orthonormality determines the x-axis. The scattering vector in 123-frame is obtained as q = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) qL, where
qL, where ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the rotation matrix transforming between the two frames. From the definition of the 123-frame it follows that q = {0, qy, qz}, with qy ⊥
is the rotation matrix transforming between the two frames. From the definition of the 123-frame it follows that q = {0, qy, qz}, with qy ⊥ ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) and qz ∥
and qz ∥ ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) . Transforming all available qL into {qy, qz}-pairs, the values of S(qL) can be assigned to a two dimensional spectrum S(qy, qz) in the director-based frame. Since the θ angle between the director and the z-axis of the laboratory frame changes during the run, the discrete set of vectors qL generates a continuum set of q-vectors in 123-frames. In practice, these continuum values of qy and qz are coarse-grained into bins.40 In this work the width of the bins is chosen equal to the resolution 2π/Lbox of the Fourier space in the laboratory frame and final density fluctuation spectra are obtained as averages of the S(qy, qz) accumulated in each bin over all configurations.
. Transforming all available qL into {qy, qz}-pairs, the values of S(qL) can be assigned to a two dimensional spectrum S(qy, qz) in the director-based frame. Since the θ angle between the director and the z-axis of the laboratory frame changes during the run, the discrete set of vectors qL generates a continuum set of q-vectors in 123-frames. In practice, these continuum values of qy and qz are coarse-grained into bins.40 In this work the width of the bins is chosen equal to the resolution 2π/Lbox of the Fourier space in the laboratory frame and final density fluctuation spectra are obtained as averages of the S(qy, qz) accumulated in each bin over all configurations.
The calculation of the spectrum of the orientation tensor is similar. Namely, for the two shortest melts the Fourier transform Qαβ(qL) is first calculated replacing in eqn (11)q = {q⊥, qz} with qL. The Fourier image is transformed to a qL-dependent 123-frame to obtain ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) (qy, qz) =
(qy, qz) = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) (qL)
(qL)![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −1. Then |Qαβ(qy, qz)|2 are calculated and assigned to the bins of the yz-plane in 123-frame which correspond to the rotated qL. After considering all configurations, the final spectra are obtained as averages of the values accumulated in each bin.
−1. Then |Qαβ(qy, qz)|2 are calculated and assigned to the bins of the yz-plane in 123-frame which correspond to the rotated qL. After considering all configurations, the final spectra are obtained as averages of the values accumulated in each bin.
For the longest N = 48 and 64 melts, where the variations in the orientation of ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) are small, we assume that the director frame coincides with the laboratory frame, so that q = qL. In these melts q is placed in the yz-plane of the laboratory frame so that q = {0, qy, qz}, where qy,z = 2πiy,z/Lbox with −20 ≤ iy,z ≤ 20. Thus S(qy, qz) and |Qαβ(qy, qz)|2 are directly calculated from eqn (8) and (11) respectively, and the final spectra are obtained as averages of the values accumulated for each discrete {qy, qz}-pair for all configurations.
are small, we assume that the director frame coincides with the laboratory frame, so that q = qL. In these melts q is placed in the yz-plane of the laboratory frame so that q = {0, qy, qz}, where qy,z = 2πiy,z/Lbox with −20 ≤ iy,z ≤ 20. Thus S(qy, qz) and |Qαβ(qy, qz)|2 are directly calculated from eqn (8) and (11) respectively, and the final spectra are obtained as averages of the values accumulated for each discrete {qy, qz}-pair for all configurations.
4.2 Strength of nematic order and director orientation
In Table 1 we summarise the values of configurational averages of the maximum eigenvalues, 〈S〉, as a function of chain length N. It can be seen that the strength of nematic orientation increases with chain length, saturating for longer molecules. This behaviour stems from orientational correlations along chain backbone induced by bending rigidity51 and is qualitatively similar to the shift of the isotropic-nematic transition to higher temperatures as molecular weight increases.51,53,79| N | 16 | 32 | 48 | 64 |
| 〈S〉 | 0.62(4) | 0.65(1) | 0.66(0) | 0.66(7) |
4.3 Chain backfolding
For the following discussion of fluctuation spectra and material constants, it is important to quantify the amount of backfolded chains as a function of polymer length. To comply with the theoretical description in Section 3, in every configuration, for each chain the number of intersections with a sequence of planes normal to the axis of the director,![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) , was calculated. The distance between the planes was chosen with fine step (significantly smaller than the bond length). A chain was considered as backfolded if found to intersect a plane more than once.
, was calculated. The distance between the planes was chosen with fine step (significantly smaller than the bond length). A chain was considered as backfolded if found to intersect a plane more than once.
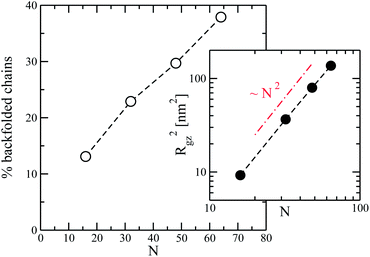
Fig. 2 presents the percentage of backfolded chains (averaged over all configurations) as a function of the number of segments in the chain. It can be seen that the amount of these molecules increases substantially with chain length so that for N = 64 almost 40% of polymers have at least one backfolding. The apparent linearity of the plot is due to the still moderate chain lengths. Theoretical arguments based on the continuum WLC model80 within mean-field approximation predict that the fraction of backfolded chains should eventually saturate to unity as 1 − exp(−Γ) with Γ = (L/lo)exp(−Uh/kBT). The characteristic scales of length, lo, and energy, Uh, are functions of chain stiffness, strength of orientational coupling, order parameter, and temperature. L stands for the contour length. The small number of backfolding events per chain in our case is demonstrated by the inset of Fig. 2. The figure presents a logarithmic plot of the component of the average radius of gyration (squared) along the nematic director, Rgz2, as a function of N. It can be seen that it still obeys a rod-like scaling Rgz2 ∼ N2; in a regime with many hairpins it should be37,80Rgz2 ∼ N.
4.4 Density fluctuation spectra
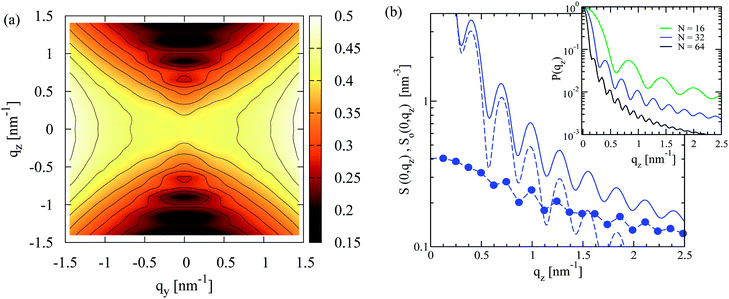
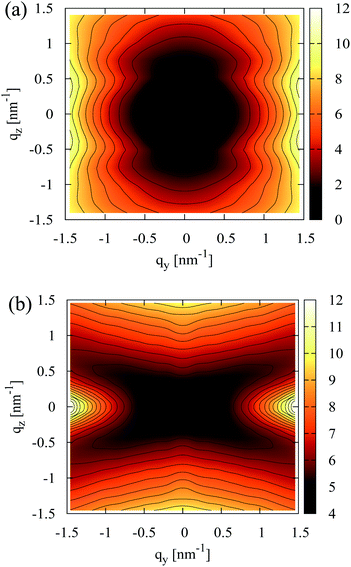
A representative contour plot of S(qy, qz) for a nematic N = 32 melt, calculated in the director frame as described in Section 4.1, is presented in Fig. 3a. It agrees qualitatively with the theoretically predicted bow-tie shape (see previous section), while similar scattering patterns have been reported in earlier simulations of lyotropic polymer nematics.50Fig. 3a demonstrates that near the origin, the scattering decreases moving along the qy = 0 axis as predicted theoretically. However, in simulations this decay is not monotonous and for higher qz, a sequence of scattering minima is observed.The additional scattering features in Fig. 3a do not signify smectic ordering but stem from intramolecular scattering. For a nematic N = 32 melt, this is shown in Fig. 3b by comparing S(0, qz) with the contribution from intramolecular scattering, So(0, qz), along the z-axis of the director frame (for clarity only the region qz > 0 is shown). The intramolecular scattering is first calculated in the laboratory frame from:
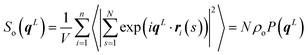 | (13) |
Angular brackets denote an average over chain conformations and P(qL) stands for the molecular form factor.81 Subsequently, the 123-frame transformation is employed to obtain from So(qL) the So(0, qz) in the director frame. Fig. 3b highlights that S(0, qz) is already affected by the second of the subsidiary maxima of So(0, qz). The apparent difference in the location of some of the maxima of S(0, qz) and So(0, qz) stems from the binning of the qz vectors used to calculate the former.
The oscillations of So(0, qz) manifest the strong stretching of polymers along the nematic director and are observed in all melts modelled in the current work. This is illustrated in the inset of Fig. 3b presenting P(0, qz) for systems with N = 16, 32 and 64. It is instructive to compare the intramolecular scattering with the following estimate. In a melt configuration, for each i-th chain the component of the radius of gyration (squared) along the nematic director, Rgz(i)2, is obtained. Each i-th chain is assigned the form factor of a rod, Prod(i)(qz) = [2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(qzlr(i)/2)/qzlr(i)]2 (qz is taken parallel to the rod axis). The length of the rod, lr(i), is chosen so that it has the same radius of gyration (squared) as the chain, that is,
sin(qzlr(i)/2)/qzlr(i)]2 (qz is taken parallel to the rod axis). The length of the rod, lr(i), is chosen so that it has the same radius of gyration (squared) as the chain, that is, 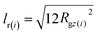 . The approximate intramolecular scattering follows from So(0, qz) ≃ (Nρo)〈Prod(qz)〉, where angular brackets denote an average over all chains and configurations. It is presented in the main panel of Fig. 3b with dashed line and follows roughly the shape of So(0, qz) calculated exactly viaeqn (13). As illustrated in the inset, the loss of structuring in P(0, qz) increases with chain length, e.g., due to larger variations in chain conformations.
. The approximate intramolecular scattering follows from So(0, qz) ≃ (Nρo)〈Prod(qz)〉, where angular brackets denote an average over all chains and configurations. It is presented in the main panel of Fig. 3b with dashed line and follows roughly the shape of So(0, qz) calculated exactly viaeqn (13). As illustrated in the inset, the loss of structuring in P(0, qz) increases with chain length, e.g., due to larger variations in chain conformations.
It is interesting to explore whether S(qy, 0) and S(0, qz) can be described by a constant and an Ornstein–Zernike form respectively, as suggested by eqn (10). For this purpose Fig. 4 presents ρo2S−1(qy, 0) (lower panel) and ρo2S−1(0, qz) (upper panel) as a function of qy and qz respectively, for N = 32 (blue solid symbols) and N = 64 (black open symbols) melts. The structure factor presented in the figure is the average of eight S(qy, qz) calculated from the corresponding number of independent runs. Accordingly, errorbars are equal to the standard deviation 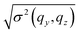 of the structure factor at every scattering mode.
of the structure factor at every scattering mode.
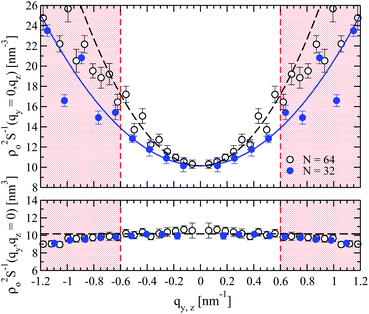 | ||
| Fig. 4 Examples of the inverse density structure factor for N = 32 (solid circles) and N = 64 (open circles) melts. The bottom panel presents ρo2S−1(qy, 0) as a function of qy and the approximation (cf.eqn (10)) with a constant (dashed line) which is practically the same for both N. The upper panel presents ρo2S−1(0, qz) as a function of qz. The parabolic fits for N = 32 and N = 64 are shown with solid and dashed lines, respectively. In both panels, broken red lines mark the boundaries of q-space used for the fit. | ||
The bottom panel of Fig. 4 demonstrates that for small wavevectors, the density structure factor normal to the nematic director can be indeed approximated by a constant, which should equal B/kBT (cf.eqn (10)). The constant is marked by the horizontal black dashed line, obtained from a linear least squares fit82 of ρo2S−1(qy, 0) in q2-space, for |qy| ≤ 0.6 nm−1. The extracted B/kBT is presented as a function of N in Fig. 5 (open squares). The errorbars correspond to approximately 1% error in the estimation of B. They characterise the spread of the values obtained after splitting the independent runs for each chain length into groups with four simulations each, and calculating the B constant separately for each group as described above. The data in Fig. 5 demonstrate that, for the considered chain lengths, the two-dimensional bulk modulus B does not depend on N. In principle, a weak reduction of B as N becomes larger is expected mainly because of the smaller translational entropy of chains (cf., Section 3). Such effects however are not discernible in the plot.
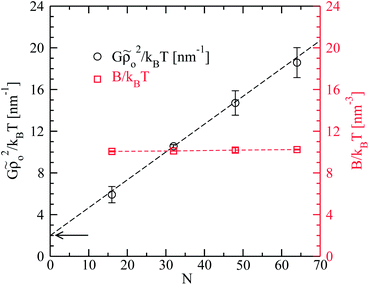 | ||
| Fig. 5 Simulation results for Gρo2/kBT (black circles, left axis) and B/kBT (red squares, right axis) as a function of number of chain segments, N. The arrow marks the constant offset of Gρo2/kBT. | ||
A parabolic approximation to ρo2S−1(0, qz), motivated by the Ornstein–Zernike form of eqn (10), is demonstrated in the upper panel of Fig. 4 for melts with N = 32 and N = 64 (solid blue and dashed black lines, respectively). The curves shown in the figure were obtained through a linear least squares fit of ρo2S−1(0, qz) in q2-space, with Gρo2/kBT as a free parameter while fixing B/kBT to the values calculated from the analysis of ρo2S−1(qy, 0). As a test, we have fitted the spectra allowing also for variations of B/kBT and no significant differences were observed. Moreover, the B/kBT calculated in this way, match the data obtained from the analysis of ρo2S−1(qy, 0) (see Fig. 5). For all melts the choice of the region where the fit was performed is empirical. Namely, as suggested by the similarity between the So(0, qz) and the approximate intramolecular scattering calculated from the rod system, the natural choice to avoid the “jagginess” of ρo2S−1(0, qz) would be to consider length scales larger than the characteristic chain dimension dominating scattering. This would correspond to 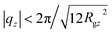 (Rgz2 follows from Fig. 2). Indeed for the shortest N = 16 chains, where effects from intramolecular scattering are the strongest, we follow this condition and fit ρo2S−1(0, qz) by a parabola for |qz| < 2π/l ≃ 0.5 nm−1. At the same time, we have observed that Gρo2/kBT extracted from the parabolic approximation does not change substantially when the fit regime is expanded beyond |qz| = 0.5 nm−1 to incorporate periods of oscillations in ρo2S−1(0, qz) (presumably because of cancellation effects). For longer chains, where effects from intramolecular scattering are less pronounced, ρo2S−1(0, qz) is approximated by a parabola for |qz| ≃ 0.6 nm−1. In this case, the fitting region includes several multiples of
(Rgz2 follows from Fig. 2). Indeed for the shortest N = 16 chains, where effects from intramolecular scattering are the strongest, we follow this condition and fit ρo2S−1(0, qz) by a parabola for |qz| < 2π/l ≃ 0.5 nm−1. At the same time, we have observed that Gρo2/kBT extracted from the parabolic approximation does not change substantially when the fit regime is expanded beyond |qz| = 0.5 nm−1 to incorporate periods of oscillations in ρo2S−1(0, qz) (presumably because of cancellation effects). For longer chains, where effects from intramolecular scattering are less pronounced, ρo2S−1(0, qz) is approximated by a parabola for |qz| ≃ 0.6 nm−1. In this case, the fitting region includes several multiples of 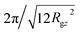 .
.
Fig. 5 presents the Gρo2/kBT obtained from the above procedure as a function of N (open circles). As in the case of B/kBT, errorbars characterise the spread of the values for Gρo2/kBT obtained after splitting the independent runs for each chain length into groups with four simulations each. Notably, the Gρo2/kBT calculated from fits where B/kBT was also allowed to vary, are within these errorbars. The results can be well described by linear dependence of Gρo2/kBT on chain length (dashed black line). This observation supports the theoretical assumption26,27,31G ∼ l (since l = aN) with the difference that in simulations the linear dependence has a constant offset (marked by the arrow in Fig. 5). It is interesting that there are no clear deviations from the dependence Gρo2/kBT ∼ N which was predicted in the zero-hairpin limit, even in the case of the longer melts, N = 64, where almost 40% of molecules have at least one backfolding “defect”.
4.5 Director fluctuation spectra and Frank constants
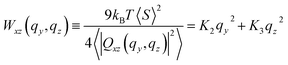 | (14) |
The theoretical result can describe the simulation data in a rather broad range of wavevectors, for all modelled chain lengths. This conclusion follows after fitting the right-hand side of eqn (14) to Wxz(qy, qz) calculated from melt configurations. We perform this fit in q2-space for |qy,z| ≤ 1 nm−1 using linear least squares. The statistical error estimate for the individual modes of Wxz(qy, qz) was obtained as described in Section 4.4. The elliptic shape of the twist-bend fluctuation spectrum is illustrated in Fig. 6a, presenting for N = 64 a contour plot of Wxz(qy, qz). An example of the accuracy of the fit is provided in Fig. 6b presenting a subset of simulation data for Wxz(qy, qz) as a function of qy2 at two representative values, qz = 0 and 1 nm−1 (squares and circles, respectively). For these qz, dashed lines show the approximation by K2qy2 + K3qz2 (where K2 and K3 originate from the fit in the whole region |qy,z| ≤ 1 nm−1) and, within errorbars, are close to the data. Fig. 6c presents a similar plot, considering Wxz(qy, qz) now as a function of qz2 at qy = 0 and 1 nm−1.
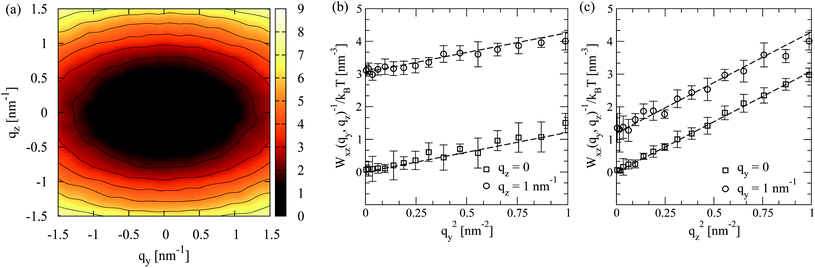 | ||
| Fig. 6 (a) Contour plot of the inverse director fluctuation spectrum, Wxz(qy, qz), corresponding to twist-bend modes for N = 64 melt. (b) A subset of simulation data for Wxz(qy, qz) as a function of qy2 at two representative values, qz = 0 and 1 nm−1 (squares and circles, respectively) is presented. Dashed lines show the approximation by the analytical expression of eqn (14). (c) Same as (b) but considering Wxz(qy, qz) as a function of qz2 at fixed qy = 0 and 1 nm−1. | ||
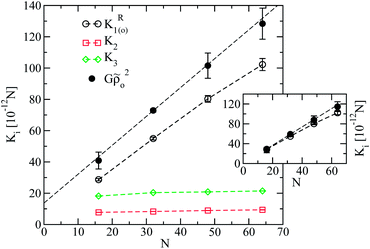
The twist and bend elastic constants calculated from the fit for all modelled chain lengths are presented in Fig. 7. Errorbars were obtained from the standard deviation of elastic constants calculated by fitting the fluctuation spectra in each of the available independent runs, separately. We emphasise the robustness of the results regarding the choice of the fitting region. Namely, choosing smaller limits, for example |qz,y| ≤ 0.5 nm−1, yields for K2 and K3 very similar results. Fig. 7 demonstrates that both K2 and K3 tend to constant values as chain length increases, which is in agreement with theoretical arguments.26K3 is roughly twice as large as K2, while the order of magnitude of both constants is 10−11 N. For thermotropic nematic polymers, experiments have reported for K2 and K3 a rather broad range of order of magnitudes, from33,34 10−12 N to35 10−10 N. Interestingly, the order of magnitude of the twist and bend constants obtained in the simulations falls within this window. The magnitudes of K2 and K3 in the above experiments were found to be comparable to each other.
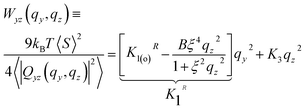 | (15) |
In the above expression an equivalent form for the splay constant K1R(qz) (comparing to eqn (12)) is employed, to facilitate fitting. It follows from eqn (15) that, in theory, for small wavevectors the isolines of Wyz(qy, qz) should form an ellipse in the yz-plane of the director frame. As qy and qz increase, the contour plot of Wyz(qy, qz) should transform into a figure-of-eight shape with the long axis oriented along the director.
In contrast to twist-bend fluctuations, the shapes of splay-bend spectra Wyz(qy, qz) in the simulations of melts with shorter chains (N = 16 and N = 32) do not completely match the corresponding theoretical predictions. As an illustration Fig. 8a presents a contour plot of Wyz(qy, qz) for a N = 16 melt. While the general shape of the plot follows the theoretical expectations, the isolines exhibit a sequence of “wiggles”. Contrary to the case of density structure factors (cf.Fig. 3a) these additional features stem from intermolecular correlations and not directly from intramolecular scattering. This conclusion follows after considering the contribution of intramolecular scattering, obtained by calculating for each i-th molecule first the Fourier transform of its nematic tensor in the laboratory frame according to:
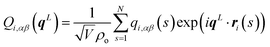 | (16) |
For each chain the Fourier image of the molecular nematic tensor is transformed to a qL-dependent 123-frame to obtain ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) i(qy, qz) =
i(qy, qz) = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) i(qL)
i(qL)![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −1 so that the total part of intramolecular scattering is given by
−1 so that the total part of intramolecular scattering is given by 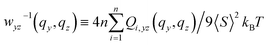 .
.
Fig. 8b presents the contour plot of wyz(qy, qz) for N = 16 demonstrating that it has a different pattern comparing to Wyz(qy, qz). For short chains, the cross-like shape of minima in wyz(qy, qz), not observed in total scattering, stems from strong correlations in the orientation of segments along the same molecule due to stiffness. The instantaneous polar angle θs between a segment and ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) is nonnegative and has an average value 〈θs〉 > 0. In Fig. 8b the angles between the branches of the cross and the qy-axis depend on the magnitude of 〈θs〉. Indirectly however the intermolecular correlations leading to the distortions in Fig. 8a are still coupled to chain connectivity. This follows from the observation that they are located at wavevectors roughly corresponding to the contour length of the polymer chains. For longer polymers the distortions of the isolines not only shift to smaller wavevectors but become also less pronounced. Fig. 9a presents the contour plot of Wyz(qy, qz) for the longest N = 64 melt, which is in very good agreement with the shape predicted by eqn (15). This can be quantified by fitting the Wyz(qy, qz) obtained in the simulations for |qy,z| ≤ 1 nm−1 by the functional form suggested by eqn (15). Fig. 9b considers two representative values qz = 0 and 1 nm−1 to demonstrate that the fitted function (dashed lines) describes the original data (squares and circles, respectively) closely at different values of qz. Fig. 9c provides a similar comparison, now considering Wyz(qy, qz) as a function of qz2 at two representative values, qy = 0 and 1 nm−1. Notably, the value of the bend constant K3 obtained from this fit matches the value extracted from the twist-bend fluctuations.
is nonnegative and has an average value 〈θs〉 > 0. In Fig. 8b the angles between the branches of the cross and the qy-axis depend on the magnitude of 〈θs〉. Indirectly however the intermolecular correlations leading to the distortions in Fig. 8a are still coupled to chain connectivity. This follows from the observation that they are located at wavevectors roughly corresponding to the contour length of the polymer chains. For longer polymers the distortions of the isolines not only shift to smaller wavevectors but become also less pronounced. Fig. 9a presents the contour plot of Wyz(qy, qz) for the longest N = 64 melt, which is in very good agreement with the shape predicted by eqn (15). This can be quantified by fitting the Wyz(qy, qz) obtained in the simulations for |qy,z| ≤ 1 nm−1 by the functional form suggested by eqn (15). Fig. 9b considers two representative values qz = 0 and 1 nm−1 to demonstrate that the fitted function (dashed lines) describes the original data (squares and circles, respectively) closely at different values of qz. Fig. 9c provides a similar comparison, now considering Wyz(qy, qz) as a function of qz2 at two representative values, qy = 0 and 1 nm−1. Notably, the value of the bend constant K3 obtained from this fit matches the value extracted from the twist-bend fluctuations.
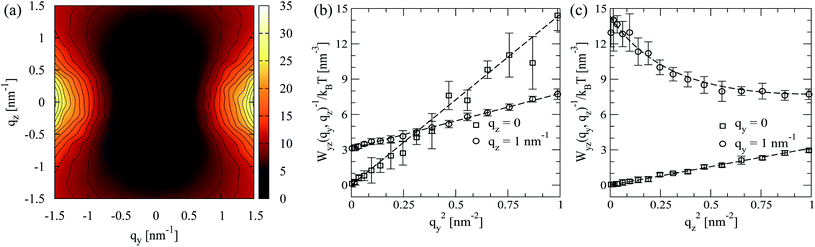 | ||
| Fig. 9 (a) Contour plot of the inverse director fluctuation spectrum, Wyz(qy, qz), corresponding to splay-bend modes for N = 64 melt where no “wiggles” are observed. (b) A subset of simulation data for Wyz(qy, qz) as a function of qy2 at two representative values, qz = 0 and 1 nm−1 (squares and circles, respectively) is presented. Dashed lines show the approximation by the analytical expression of eqn (15). (c) Same as (b) but considering Wyz(qy, qz) as a function of qz2 at fixed qy = 0 and 1 nm−1. | ||
For all chain lengths, the small wavelength behaviour of the splay constant, K1(o)R, is presented in Fig. 7 (open circles). It was extracted from linear fits to Wyz(qy, qz) as a function of qy2, while setting qz = 0. For melts without significant hairpin effects, the plot suggests a linear dependence of K1(o)R on N as first predicted by Meyer. For polymer nematics with a large number of hairpins per chain, it has been predicted theoretically37 that K1(o)R should reach a finite value as a function of N. Thus, for longer chains with moderate backfolding (such as N = 64) the onset of saturation, i.e., sublinear dependence of K1(o)R on N, might be expected. In fact for N = 64 our results suggest the appearance of such effects, manifested by the slight, within errorbars, “bending” of the K1(o)R plot.
An important question refers to the extent to which the above results are affected by finite system size effects. For N = 16 the splay constant obtained from test simulations in smaller cells, Lbox = 4L, matched the K1(o)R in Fig. 7 (obtained at Lbox = 8L). However, in simulations of longest melts where Lbox = 2L is employed, fluctuations could be more suppressed, resulting into Frank constants that are larger comparing to those of an “infinite” system. Therefore, in larger samples of these melts splay constants might reduce, leading to more pronounced saturation effects.
In Fig. 7 the quantity Gρo2 previously calculated from density fluctuations (cf.Fig. 5) is also reproduced as a function of N. According to the theoretical prediction K1(o)R = K1 + Gρo2 one expects that: (a) K1(o)R has the same slope comparing to Gρo2 as a function of N and (b) K1(o)R ≥ Gρo2, since K1 is nonnegative. In Fig. 7 for short chains, Gρo2 has a similar slope with K1(o)R which agrees with the first expectation. At the same time in simulations Gρo2 is larger than K1(o)R. One can argue that this difference from the theoretical result is due to the constant offset in the linear dependence of Gρo2 on N observed in Fig. 5. The inset of Fig. 7 compares K1(o)R and Gρo2, subtracting from the latter the offset 1.99kBT obtained in Fig. 5. In this case the two curves are very close to each other, for short chains.
5 Conclusions and outlook
In this work Monte Carlo simulations of nematic polymer melts described by a soft model were performed to study equilibrium density and director fluctuation spectra, as well as related material constants. The model is generic but incorporates features important for the qualitative study of the above properties. The polymer architecture is represented by the discrete WLC model, accounting for two characteristic molecular scales: the persistence and the contour length. Pairwise non-bonded potentials have two components. The first is isotropic and limits the compressibility of the polymeric liquid, while the second depends on the relative orientation of the segments, inducing nematic ordering. Nematic WLC melts for four different chain lengths were considered, their contours being up to an order of magnitude longer than the persistence length (as defined in the state of a disordered melt).Some generic characteristics (such as the bow-tie pattern) of the shape of density and director fluctuations spectra were found to agree with theoretical predictions.27–29,31 At the same time, at length scales roughly comparable with the extension of polymer chains along the nematic director, the density and the splay-bend spectra exhibited additional scattering features. These features were evident in melts with short WLC (only a few persistence lengths long). In such systems, the spectra of the density fluctuations parallel and normal to nematic director were well described by the theoretical predictions only for wavelengths comparable or larger than the contour length. For short WLC, in contrast to density fluctuations, the secondary scattering features did not allow us to fit the splay-bend spectra by the theoretical functional forms. For melts with longer chains effects from secondary scattering features diminish. Thus the shape of the density and director fluctuation spectra (including splay-bend modes) is well approximated by the theoretical predictions in a broad range of wavevectors. This is noteworthy since the population of backfolded chains in these melts is substantial (up to 40%), while the theoretical results were obtained in the zero-hairpin limit.
Two material constants controlling (for large wavelengths) density fluctuations normal and parallel to the nematic director were extracted and their dependence on chain length was investigated. For all melts, this dependence was found to be consistent with the theoretical predictions in the zero-hairpin limit,26–29,31 despite the increasing amount of backfolding with chain length. For the shorter melts, within the accuracy of the data and the considered system sizes, the splay Frank constant obtained from director fluctuations was found to increase linearly with chain length, in agreement with the arguments of Meyer26 and later theories.27–29,31,37 For larger chains (an order of magnitude longer than the persistence length) our data suggest the onset of a sub-linear dependence due to larger amount of backfolded molecules.37 Twist and bend Frank constants were found to saturate with chain length, in agreement with theoretical expectations.26
Although the interactions are soft, the order of magnitude of bend and twist constants was found to be 10−11 N which is within the window of magnitudes 10−12 N to 10−10 N reported in some experiments.33–35 Both constants were found to be significantly smaller than the splay constant. Taking into account that the model was mapped on a real family of polymers (i.e. poly(3-alkylthiophenes)), these observations are encouraging for a possible comparison of our results with future experiments in these materials.
In the current study, no strong effects of chain backfolding on the dependence of material constants on the length of polymer chains were observed. This behaviour can be rationalised by the fact that the number of hairpins per molecule remained small. To address in detail how material constants are affected by chain backfolding, modelling nematic melts with longer chains would be required. Varying chain stiffness offers additional possibilities for changing conformational properties and such effects should be also explored in the future.
Acknowledgements
We are grateful to Kurt Kremer, Marcus Müller, and Harald Pleiner for carefully reading our manuscript, their valuable comments, and stimulating discussions. Financial support by the German Federal Ministry for Education and Research BMBF within the MORPHEUS Project (FKZ 13N11704) is gratefully acknowledged.References
- N. Schopohl and T. J. Sluckin, Phys. Rev. Lett., 1987, 59, 2582–2584 CrossRef.
- A. K. A. Sonnet and S. Hess, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 718–722 CrossRef CAS.
- F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19–28 RSC.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 1995 Search PubMed.
- M. Kléman and O. D. Lavrentovich, Soft Matter Physics: An Introduction, Springer, 2002 Search PubMed.
- S. Chandrasekhar, Rep. Prog. Phys., 1976, 39, 613–692 CrossRef CAS.
- E. K. Fleischmann and R. Zentel, Angew. Chem., Int. Ed., 2013, 52, 8810–8827 CrossRef CAS PubMed.
- S. M. Kelly and M. O'Neill, in Handbook of Advanced Electronic and Photonic Materials and Devices, ed. H. S. Nalwa, Academic Press, New York, 2000, vol. 7 Search PubMed.
- I. I. Smalyukh, S. Chernyshuk, B. I. Lev, A. B. Nych, U. Ognysta, V. G. Nazarenko and O. D. Lavrentovich, Phys. Rev. Lett., 2004, 93, 117801-1–117801-4 CrossRef.
- J. K. Gupta, S. Sivakumar, F. Caruso and N. L. Abbott, Angew. Chem., Int. Ed., 2009, 48, 1652–1655 CrossRef CAS PubMed.
- I. H. Lin, D. S. Miller, P. J. Bertics, C. J. Murphy, J. J. Pablo and N. L. Abbott, Science, 2011, 332, 1297–1300 CrossRef CAS PubMed.
- A. Sengupta, T. Uroš, M. Ravnik, J. M. Yeomans, C. Bahr and S. Herminghaus, Phys. Rev. Lett., 2013, 110, 048303-1–048303-5 Search PubMed.
- T. De Nève, M. Kléman and P. Navar, Liq. Cryst., 1994, 18, 67–71 CrossRef.
- E. T. Samulski, Phys. Today, 1982, 35, 40–46 CrossRef CAS PubMed.
- X. J. Wang and Q.-F. Zhou, Liquid Crystalline Polymers, World Scientific, Singapore, 2004 Search PubMed.
- R. Xia, M. Campoy-Quiles, G. Heliotis, P. Stavrinou, K. S. Whitehead and D. D. C. Bradley, Synth. Met., 2005, 155, 274–278 CrossRef CAS PubMed.
- H. Sirringhaus, R. J. Wilson, R. H. Friend, M. Inbasekaran, W. Wu, E. P. Woo, M. Grell and D. D. C. Bradley, Appl. Phys. Lett., 2000, 77, 406–408 CrossRef CAS PubMed.
- D. Neher, Macromol. Rapid Commun., 2001, 22, 1365–1385 CrossRef CAS.
- I. McCulloch, M. Heeney, C. Bailey, K. Genevicius, I. MacDonald, M. Shkunov, D. Sparrowe, S. Tierney, R. Wagner, W. Zhang, M. L. Chabinyc, R. J. Kline, M. D. McGehee and M. F. Toney, Nat. Mater., 2006, 5, 328–333 CrossRef CAS PubMed.
- S. Hugger, R. Thomann, T. Heinzel and T. Thurn-Albrecht, Colloid Polym. Sci., 2004, 282, 932–938 CAS.
- M. L. Chabinyc, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2008, 26, 445–457 CrossRef CAS.
- N. Stingelin, Polym. Int., 2012, 61, 866–873 CrossRef CAS.
- I. McCulloch, M. Heeney, M. L. Chabinyc, D. DeLongchamp, R. J. Kline, M. Cölle, W. Duffy, D. Fischer, D. Gundlach, B. Hamadani, R. Hamilton, L. Richter, A. Salleo, M. Shkunov, D. Sparrowe, S. Tierney and W. Zhang, Adv. Mater., 2009, 21, 1091–1109 CrossRef CAS.
- P. G. de Gennes, Mol. Cryst. Liq. Cryst., 1977, 34, 177–182 CrossRef CAS.
- P. G. de Gennes, in Polymer Liquid Crystals, eds. A. Ciferri and W. R. Kringbaum, Academic Press, New York, 1982, ch. 5 Search PubMed.
- R. B. Meyer, in Polymer Liquid Crystals, ed. A. Ciferri and W. R. Kringbaum, Academic Press, New York, 1982, ch. 6 Search PubMed.
- P. Le Doussal and D. R. Nelson, Europhys. Lett., 1991, 15, 161–166 CrossRef CAS.
- R. D. Kamien, P. Le Doussal and D. R. Nelson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 4116–4117 CrossRef CAS.
- R. D. Kamien, P. Le Doussal and D. R. Nelson, Phys. Rev. A, 1992, 45, 8727–8750 CrossRef CAS.
- J. V. Selinger and R. F. Bruinsma, Phys. Rev. A, 1991, 43, 2910–2921 CrossRef.
- D. R. Nelson, Phys. A, 1991, 177, 220–232 CrossRef.
- S.-D. Lee and R. B. Meyer, Liq. Cryst., 1990, 7, 15–29 CrossRef CAS.
- S. Zheng-Min and M. Kléman, Mol. Cryst. Liq. Cryst., 1984, 111, 321–328 CrossRef CAS.
- M. Kléman, Faraday Discuss. Chem. Soc., 1985, 79, 215–224 RSC.
- D. Frezzato, G. J. Moro, M. Tittelbach and G. Kothe, J. Chem. Phys., 2003, 119, 4060–4069 CrossRef CAS PubMed.
- K. Odijk, Liq. Cryst., 1986, 1, 553–559 CrossRef.
- G. J. Vroege and K. Odijk, Macromolecules, 1988, 21, 2849–2858 CrossRef.
- A. Y. Grosberg and A. V. Zhestkov, Polymer Sci., 1986, 28, 97–104 Search PubMed.
- M. P. Allen and D. Frenkel, Phys. Rev. A, 1988, 37, 1813–1816 CrossRef.
- M. P. Allen, M. A. Warren, M. R. Wilson, A. Sauron and W. Smith, J. Chem. Phys., 1996, 105, 2850–2858 CrossRef CAS PubMed.
- N. H. Phuong, G. Germano and F. Schmid, J. Chem. Phys., 2001, 115, 7227–7234 CrossRef CAS PubMed.
- D. Andrienko and M. P. Allen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 021704-1–021704-11 Search PubMed.
- A. Poniewierski and J. Stecki, Mol. Phys., 1979, 38, 1931–1940 CrossRef CAS.
- Y. Singh, Phys. Rev. A, 1984, 30, 583–593 CrossRef CAS.
- Y. Singh, Phys. Rep., 1996, 277, 284–384 Search PubMed.
- J. Stelzer, M. A. Bates, L. Longa and G. R. Luckhurst, Proc. SPIE, 1998, 3318, 175–178 CrossRef CAS PubMed.
- A. Zakharov and A. Maliniak, Eur. Phys. J. E, 2001, 4, 85–91 CrossRef CAS.
- A. A. Joshi, J. K. Whitmer, O. Guzmán, N. L. Abbott and J. J. de Pablo, Soft Matter, 2014, 10, 882–893 RSC.
- M. Dijkstra and D. Frenkel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 349–357 CrossRef CAS.
- R. D. Kamien and G. S. Grest, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 1197–1200 CrossRef CAS.
- K. C. Daoulas, V. Rühle and K. Kremer, J. Phys.: Condens. Matter, 2012, 24, 284121-1–284121-15 CrossRef PubMed.
- P. Gemünden, C. Poelking, D. Andrienko, K. Kremer and K. C. Daoulas, Macromolecules, 2013, 46, 5762–5774 CrossRef.
- V. Ho, B. W. Boudouris and R. A. Segalman, Macromolecules, 2010, 43, 7895–7899 CrossRef CAS.
- D. Foster, Ann. Phys., 1974, 85, 505–534 Search PubMed.
- P. Warren, Curr. Opin. Colloid Interface Sci., 1998, 3, 620–624 CrossRef CAS.
- A. Polimeno, A. Gomes and A. Martins, in Computer Simulations of Liquid Crystals and Polymers, ed. P. Pasini, C. Zannoni, and S. Žumer, Kluwer Academic Publishers, 2005 Search PubMed.
- R. Berardi, C. Fava and C. Zannoni, Chem. Phys. Lett., 1995, 236, 462–468 CrossRef CAS.
- R. L. C. Vink and T. Schilling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051716-1–051716-7 Search PubMed.
- S. Prestipino and F. Saija, J. Chem. Phys., 2007, 126, 194902-1–194902-9 CrossRef PubMed.
- Z. E. Hughes, L. M. Stimson, H. Slim, J. S. Lintuvuori, J. M. Ilnytskyi and M. R. Wilson, Comput. Phys. Commun., 2008, 178, 724–731 CrossRef CAS PubMed.
- M. R. Wilson, Int. Rev. Phys. Chem., 2005, 24, 421–455 CrossRef CAS.
- R. Hołyst and T. A. Vilgis, Macromol. Theory Simul., 1996, 5, 573–643 CrossRef.
- M. Hamm, G. Goldbeck-Wood, A. V. Zvelindovsky, G. J. A. Sevink and J. G. E. M. Fraaije, J. Chem. Phys., 2002, 116, 3152–3161 CrossRef CAS PubMed.
- V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2004, 120, 5824–5838 CrossRef CAS PubMed.
- N. A. Kumar and V. Ganesan, J. Chem. Phys., 2012, 136, 101101-1–101101-4 Search PubMed.
- Q. Wang, Soft Matter, 2011, 7, 3711–3716 RSC.
- K. Tashiro, K. Ono, Y. Minagawa, M. Kobayashi, T. Kawai and K. Yoshino, J. Polym. Sci., Part B: Polym. Phys., 1991, 29, 1223–1233 CrossRef CAS.
- L. Livandaru, R. R. Netz and H. J. Kreuzer, Macromolecules, 2003, 36, 3732–3744 CrossRef.
- B. McCulloch, V. Ho, M. Hoarfrost, C. Stanley, C. Do, W. T. Heller and R. A. Segalman, Macromolecules, 2013, 46, 1899–1907 CrossRef CAS.
- M. Müller, J. Stat. Phys., 2011, 145, 967–1016 CrossRef.
- T. Vettorel, G. Besold and K. Kremer, Soft Matter, 2010, 6, 2282–2292 RSC.
- G. Zhang, L. A. Moreira, T. Stuehn, K. C. Daoulas and K. Kremer, ACS Macro Lett., 2014, 3, 198–203 CrossRef CAS.
- G. Svenšek, G. Veble and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 011708-1–011708-14 CrossRef.
- D. Svenšek, G. M. Grason and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052603-1–052603-7 CrossRef.
- T. C. Lubensky, Phys. Rev. A, 1970, 2, 2497–2514 CrossRef.
- P. M. Allen and A. J. Masters, J. Mater. Chem., 2001, 11, 2678–2689 RSC.
- P. A. O'Brien, M. P. Allen, D. L. Cheung, M. Dennison and A. Masters, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 051705-1–051705-7 Search PubMed.
- E. Vives and P. A. Lindgård, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 1318–1328 CrossRef.
- V. V. Rusakov and M. I. Shliomis, J. Phys., Lett., 1985, 46, 935–943 CrossRef CAS.
- D. R. M. Williams and A. Halperin, J. Phys. II, 1993, 3, 69–89 CrossRef CAS.
- J. S. Higgins and H. C. Benoît, Polymers and Neutron Scattering, Clarendon Press, Oxford, 1994 Search PubMed.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in Fortran, Cambridge University Press, Cambridge, 1986 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |