Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantitative mechanical analysis of thin compressible polymer monolayers on oxide surfaces†
Qian
Huang
a,
Ilsun
Yoon
a,
Josh
Villanueva
a,
Kanguk
Kim
b and
Donald J.
Sirbuly
*ab
aDepartment of NanoEngineering, University of California, La Jolla, San Diego, CA 92093, USA. E-mail: dsirbuly@ucsd.edu
bMaterials Science and Engineering, University of California, La Jolla, San Diego, CA 92093, USA
First published on 13th August 2014
Abstract
A clear understanding of the mechanical behavior of nanometer thick films on nanostructures, as well as developing versatile approaches to characterize their mechanical properties, are of great importance and may serve as the foundation for understanding and controlling molecular interactions at the interface of nanostructures. Here we report on the synthesis of thin, compressible polyethylene glycol (PEG) monolayers with a wet thickness of <20 nm on tin dioxide (SnO2) nanofibers through silane-based chemistries. Nanomechanical properties of such thin PEG films were extensively investigated using atomic force microscopy (AFM). In addition, tip–sample interactions were carefully studied, with different AFM tip modifications (i.e., hydrophilic and hydrophobic) and in different ionic solutions. We find that the steric forces dominate the tip–sample interactions when the polymer film is immersed in solution with salt concentrations similar to biological media (e.g., 1× phosphate buffer solution), while van der Waals and electrostatic forces have minimal contributions. A Dimitriadis thin film polymer compression model shows that the linear elastic regime is reproducible in the initial 50% indentation of these films which have tunable Young's moduli ranging from 5 MPa for the low molecular weight films to 700 kPa for the high molecular weight PEG films. Results are compared with the same PEG films deposited on silicon substrates which helped quantify the structural properties and understand the relationship between the structural and the mechanical properties of PEG films on the SnO2 fibers.
Introduction
Oxide nanomaterials such as silicon oxide, iron oxide and titanium oxide offer a broad range of physical and chemical properties that make them excellent candidates for novel biotechnological applications in medical diagnostics and therapeutics.1–3 For example, colloidal suspensions of oxide nanoparticles are currently being investigated for enhanced in vivo imaging contrast agents, drug vehicular systems and mammalian toxicity study targets.4,5 However, without a chemically robust and benign outer coating, these oxide materials can often interfere with biological functions, or their efficacy in vivo can be reduced due to promoted particle aggregation and/or reduced retention/circulation time. To overcome the difficulty of the high reactive surface of oxide nanomaterials and their sensitivity to adsorbates, the oxide surfaces are typically modified to reduce the surface energy and allow for more chemical neutrality in biological environments. Due to the low surface charge density, tunable surface coverage, long-term stability, and non-toxicity properties of polymers such as polyethylene glycol (PEG), these materials have been extensively used as passivating films on nanomaterials for biological applications.6–8Besides the chemical properties of PEG films there is also of significant interests in tuning their mechanical properties, particularly in the case of extremely thin (<20 nm) polymer films. It is not only important to control the thickness and mechanical properties of thin polymer films for understanding molecular interactions with target materials in vitro and in vivo, but compressible films can also be used for mechanical feedback in novel nanoscale sensor designs for biological applications.9,10 There are several methods to study the mechanical properties of ultrathin polymer films in the dry state;11–14 however, there are currently few reports on the stiffness of thin, uniform polymer monolayers deposited on oxide nanoparticles and/or oxide nanofiber structures in the liquid state, which is likely rooted in the challenges associated with synthesizing conformal, uniform monolayer films and the difficulties in accurately quantifying the mechanical properties at the nanometer scale at the same time.15–18 Many theories have been proposed to explain the interaction forces involved in nanometer thickness polymer deformations.19–24 For example, Spencer et al. reported on the absorption of a copolymer consisting of PEG chains grafted on the poly(L-lysine) backbone on niobium oxide substrates, and studied the mechanical properties of different PEG grafting densities via colloid-probe atomic force microscopy (AFM) under varying ionic strength.25–28 There are also many reports on how salt, temperature and approach velocity influence the mechanical properties of PEG brushes.29–32 However, the absolute stiffness values have not been reported, which makes the comparison between different studies difficult. Also, there is a substantial amount of work on developing force–indentation models and characterizing micron thick films,33–36 but these models tend to break down for nanoscale films with thicknesses < 20 nm because many interaction forces, such as van der Waals interactions, electric double layer (EDL) forces, and attractive hydrophobic interactions, complicate the mechanical response of the films at these scales.37
Here we investigate synthetic approaches to creating thin, mechanically compliant PEG monolayer films on single crystalline tin dioxide (SnO2) nanofibers38 and characterize their elastic properties using AFM. Silane-based chemistries are exploited to generate smooth, conformal brush structures with a thickness of <20 nm in solution. The strength of the tip–sample interactions are extensively examined with different AFM tip modifications and in different ionic solutions, which lays the foundation for accurate characterization of the mechanical properties. Our results show that there exists a highly reproducible linear elastic regime that spans the initial 50% indentation and that the mechanical properties of the PEG films can be tuned from 5 MPa to 700 kPa by altering the molecular weight (MW) of the polymer chains.
Experimental
Materials
PEG-silanes (MW = 2000 Da, 5000 Da, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da) were purchased from Laysan Bio. All the other reagents and solvents were purchased from Fisher Scientific.
000 Da) were purchased from Laysan Bio. All the other reagents and solvents were purchased from Fisher Scientific.
Nanofiber chip fabrication
Silicon wafers (111) were first cleaned in a piranha solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 30% H2O2/conc. H2SO4, Caution: piranha solution is a strong oxidant and can cause explosions when mixed with organic solvents) at 90 °C for 10 min. The silicon substrates were then immersed in HF for 5 min to completely remove the surface oxide followed by a soak in an RCA 1 solution (NH4OH
3 30% H2O2/conc. H2SO4, Caution: piranha solution is a strong oxidant and can cause explosions when mixed with organic solvents) at 90 °C for 10 min. The silicon substrates were then immersed in HF for 5 min to completely remove the surface oxide followed by a soak in an RCA 1 solution (NH4OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2
H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1
H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) and RCA 2 solution (HCl
5) and RCA 2 solution (HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2
H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 1
H2O 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5), each at 70 °C for 10 min, to grow a clean native oxide layer. The silicon substrates were rinsed with deionized water (18 ΩM, MilliQ) then blown dry with nitrogen. The SnO2 nanofibers were synthesized via a thermal vaporization process as described elsewhere.39,40 The cross-sectional dimensions of the nanofibers range from 200–700 nm. The clean SnO2 nanofibers were then transferred to the silicon substrates using a 3-axis micromanipulator. After a 10 min oxygen plasma treatment, the nanofiber chips were rinsed with water and dried under nitrogen.
5), each at 70 °C for 10 min, to grow a clean native oxide layer. The silicon substrates were rinsed with deionized water (18 ΩM, MilliQ) then blown dry with nitrogen. The SnO2 nanofibers were synthesized via a thermal vaporization process as described elsewhere.39,40 The cross-sectional dimensions of the nanofibers range from 200–700 nm. The clean SnO2 nanofibers were then transferred to the silicon substrates using a 3-axis micromanipulator. After a 10 min oxygen plasma treatment, the nanofiber chips were rinsed with water and dried under nitrogen.
PEG films
The high MW PEG silanes are insoluble in the toluene solutions at room temperature. To improve solubility and promote the reaction to occur between the PEG silane and nanofibers, the nanofiber chips were allowed to react overnight at 50 °C with 0.2 mM PEG silane in an anhydrous toluene solution in a dry air protected glove box. A 0.1% v/v HCl catalyst was added to drive the reaction.41–43 Afterwards, the chips were rinsed thoroughly with toluene, acetone, and methanol. The wafers were then blown dried and kept in the dry box until testing. For TEM analysis, the SnO2 nanofibers were suspended over 50 μm wide × 3 μm deep trenches etched in silicon to allow the PEG to deposit around the entire fiber and simplify the transfer of the fiber to the TEM grids using the micromanipulator.AFM characterization
A multimode AFM (Veeco Nanoscope IV) was used to carry out the imaging and force–indentation experiments. The dry thickness and dry imaging was measured using silicon probes in tapping mode. The incompressible wet thickness was measured in contact mode under an applied force of 5.5 nN. The force–indentation measurements were conducted in contact mode in 1× phosphate buffered solution (PBS) to reduce electrostatic interactions between the tip and surface except when electric double layer forces were purposefully being probed. The AFM was programmed to indent on the PEG films with a maximum force of 5.5 nN during a 100 nm approach at a speed of 0.1 Hz. Each force curve consisted of 1024 points along the AFM approach and retraction sections. Force mapping was used for indenting the PEG films on SnO2 nanofibers at a speed of 1 Hz for each force curve with a resolution of 512 points at each node of a square grid (16 × 16) distributed in a 500 nm × 500 nm area. The AFM probes used for the fluidic measurements were triangular SiN MLCT probes (Bruker, Santa Barbara, CA) with a tip radius r = 30 nm and a spring constant k = 0.14 ± 0.02 N m−1. The tip radius was calibrated by scanning electron microscopy (Fig. S1†) and imaging (under contact mode) sharp features on a standard RS-12M sample from Bruker (Fig. S2†).44,45 The spring constant of the tip was quantified using the thermal tune method on a separate Veeco Nanoscope V controller AFM.46 The optical sensitivity of the AFM system was assessed by indenting on a clean silicon surface in 1× PBS.Tip functionalization
To render the tips hydrophilic, and get rid of the silicone oil and contaminations on the commercial SiN tips,47 the tips were cleaned by first exposing the tips to a UV/ozone plasma for 15 min, then dipping in a hot freshly prepared piranha solution for 15 min, followed by rinsing with copious amounts of deionized water and nitrogen drying. To render the tips hydrophobic, the clean tips were reacted with a 5 mM solution of trimethoxy(propyl) silane in toluene overnight. After chemical modification, the tips were rinsed thoroughly with toluene, acetone, methanol, and dried with nitrogen.48Results and discussion
PEG films and thickness characterization
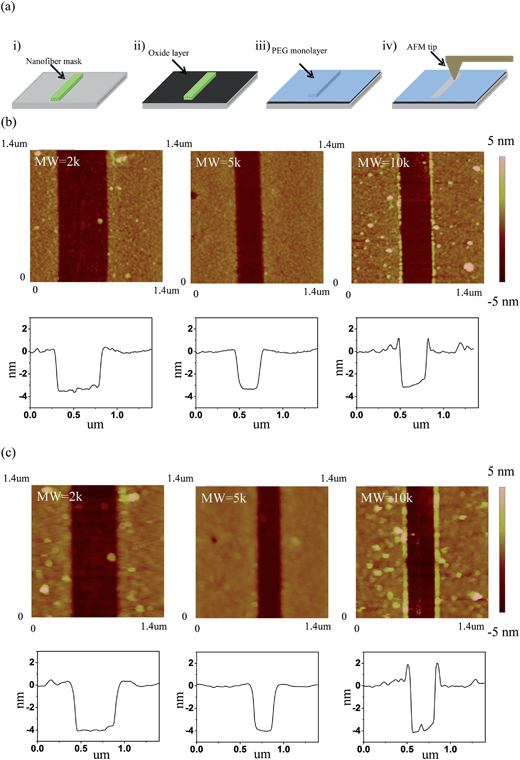
A favorable approach to coat a polymer on the surface of an oxide material is a silane coupling reaction. Fig. 1 illustrates the chemical reaction scheme for the PEG grafting. A silane coupling reaction was chosen to covalently link PEG on the oxide surface of silicon and SnO2 nanofibers since the chemical approach produces higher density, and more stable, PEG monolayer films compared to other reported methods.49,50 To optimize the synthetic condition, we introduced an oxygen plasma etch to hydroxylate the surface,51 rather than the typical piranha treatment followed by sonication, since the bubbles formation during piranha cleaning can dislodge the nanofibers from the substrate. Our silane reactions used much lower PEG concentrations compared to other synthetic processes, but even with the smaller reactant amounts our films showed thicknesses similar to other oxide surfaces.49 To determine the roughness of the PEG films on the silicon in an aqueous environment, AFM topography images were captured and the rms roughness was extracted. The roughness of the unmodified silicon surface was found to be around 1 Å and after modifying the surface with PEG films, all of the measured roughness values were less than 2 Å (Fig. 2). The AFM images also revealed that the PEG monolayers were continuous and pit-free. We converted the raw data with tip deconvolution technique (provided by Gwyddion52 software) and found there to be no difference before and after surface reconstruction (Fig. S3†), indicating that the image captures the true morphology of the PEG film. Our wet rms roughness values are lower than the dry roughness (≈3 Å) (Fig. S4†) which is similar to the dry reported roughness for lower molecular weight PEG-silanes (MW ≈ 500 Da) deposited on silicon.42,53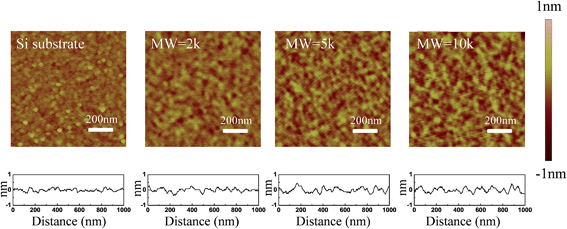 | ||
| Fig. 2 AFM topographic images of PEG films (on silicon) of varying molecular weight (2k, 5k, 10k) along with line profiles across the film in 1× PBS buffer. | ||
The thicknesses of the as-deposited PEG films on silicon substrates were then analyzed using a nanofiber mask method. With this procedure nanofibers were used as masks to protect the underlying silicon substrate (Fig. 3a) from the grafting chemistry. After depositing the PEG films on the substrates, the nanofiber masks were removed using a 3-axis micromanipulator so we could image the dry thickness of the PEG film (Fig. 3b) and incompressible wet thickness when the materials are immersed in solution (Fig. 3c). The thickness of the step in the AFM image is a combination of the PEG film thickness and the oxide layer thickness (ca. 1 nm) formed during the oxygen plasma step (Fig. S5†).54–57Table 1 lists the corrected thicknesses extracted from the AFM images on the silicon substrates. The data shows that the dry thickness and the incompressible wet thickness are very similar for all the different MWs. This implies that the longer PEG chains graft to the surface with a lower density, compared to the lower MW chains, so that all the MWs end up with roughly the same thickness in the dry state. PEG films deposited on the SnO2 nanofibers were also characterized using high-resolution transmission electron microscopy (TEM). As shown in Fig. 4, the PEG deposition creates smooth and conformal coatings on the SnO2 nanofiber with a dry thickness of around 2 nm.
| MW (Da) | h dry (nm) | h incompressible (nm) | h compressible (nm) | h 0 (nm) | h wet /hdry | s (nm) | R F (nm) |
|---|---|---|---|---|---|---|---|
| a Average thicknesses of the PEG monolayer, hdry, were obtained from multiple AFM images in the dry state (Fig. 3b). b Incompressible thicknesses, hincompressible, were obtained from the AFM images of the PEG monolayers at around 5.5 nN force in 1× PBS (Fig. 3c). c Compressible thicknesses, hcompressible, were obtained from the indentation distance during the force–indentation curves with a maximum force of 5.5 nN. d The polymer equilibrium thickness, h0, was calculated from Milner's polymer brush theory.23 e Wet thickness, hwet, is the sum of hincompressible and hcompressible. f Average separation between chains sites, s, was calculated from Milner's polymer brush theory. g Flory radius, Rf = l(MWPEG/MWEG)3/5, where l is length of the PEG monomer (l = 0.358 nm),8 and MWPEG and MWEG are the MWs of PEG and ethylene glycol (44 Da), respectively. | |||||||
| 2k | 2.42 ± 0.05 | 3.01 ± 0.04 | 3.45 ± 0.35 | 4.43 ± 0.16 | 2.67 | 2.59 ± 0.14 | 3.54 |
| 5k | 2.32 ± 0.03 | 2.95 ± 0.05 | 6.37 ± 0.32 | 9.02 ± 0.27 | 4.02 | 3.59 ± 0.16 | 6.13 |
| 10k | 2.20 ± 0.05 | 3.01 ± 0.08 | 10.36 ± 1.96 | 15.39 ± 0.81 | 6.08 | 4.55 ± 0.37 | 9.29 |
Tip–sample interactions and ionic effects
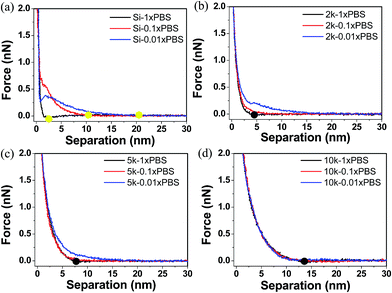
When using AFM probes to characterize the mechanic properties of a thin film, there exists several surface interaction forces that need to be understood to properly quantify the true mechanical response of the polymer. For example, local tip–sample interaction forces such as electrostatic and van der Waals forces have to be decoupled from steric interactions between the tip and polymer chains to minimize the errors during the mechanical characterization. Feldman et al. have shown that oligo(ethylene glycol) single monolayers formed on gold and silver substrates have different grafting densities, and therefore exhibit different hydrophilic and hydrophobic properties.58 In this work we compared the force–separation curves of PEG films on silicon surfaces using both hydrophilic and hydrophobic functionalized tips to see if there are any dominant surface interactions that can contribute to the measured mechanical resistance of the films.59Fig. 5 shows that the responses for all MWs are fairly similar, indicating there are no attractive hydrophobic interactions that have been previously reported for high density oligo(ethylene glycol) monolayers on silver surfaces.58 Our data also suggests that the short propyl groups used to render the tips hydrophobic do not interfere with the mechanical properties of the PEG film. Therefore, we chose to use the hydrophobic tips for mechanical measurements since they are less susceptible to fouling and contaminations, which could complicate the mechanical measurements by introducing unknown tip–sample interactions.The majority of tip–sample interactions are due to EDL forces that arise when two charged surfaces are brought in close proximity of each other. These surface effects strongly depend on the ionic strength of the surrounding medium, in which counter ions in the solution screen the surface charge and alter the repulsive or attractive forces between the surfaces. To analyze EDL forces, we carried out numerous nanoindentation experiments in different salt concentrations and monitored the local interactions that occurred as the tip was brought in close proximity to the substrate. It was found that all the force curves, independent of the MW of the PEG, were identical for ionic strengths ranging from 1–10× PBS. At these salt concentrations the Debye length is <3 nm and has minimal effects on the compression of the films. Importantly, slight variations in salt concentration around 150 mM (equivalent to 1× PBS and similar to that found in biological media) did not influence the AFM force curves. However, in the case of lower ionic strengths, the Debye length exceeds that of the film thicknesses and starts to alter the nanoindentation curves. The effect from low ionic strength on the nano-indentation curves is translated to premature force signatures during the AFM approach curves, making it hard to assign the contact point. Properly assigning the contact point is critical for accurately deriving the mechanical properties of the film. In our data the contact point was identified as the point where the force is higher than twice of the standard deviation of the noise level compared to when the tip is in free space. Overall, when the contact point (Fig. 6b–d, black dots) occurs at a distance larger than the electrostatic interaction distance determined from the bare substrates (Fig. 6a, yellow dots), the force–separation response is generated from steric repulsion; otherwise the indentation curves are a convolution of both steric and tip–sample electrostatic interactions. Similar results are also discussed by Pasche et al. where they investigated the force indentation curve of PLL-g-PEG copolymers in different buffer concentration and showed that PEG layers thicker than the Debye length can shield the electrostatic forces.25,26
Structural properties of the PEG films
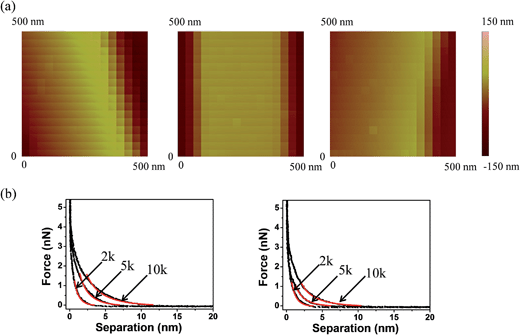
Multiple force–indentation curves were measured at different film locations on the SnO2 nanofibers dispersed on the silicon substrates (Fig. 7a), and for a given MW they all showed similar elastic behavior at various cycling frequencies (0.1–4 Hz). However, to decrease the noise of the force curves the approach speeds were kept low (≤1 Hz). Fig. 7b shows representative force–indentation curves for PEG 2k, 5k, and 10k, on silicon substrates and tin dioxide nanofibers in 1× PBS. An important structural parameter for the PEG films is the inter-chain spacing, s, which could be calculated from the dry thickness of the film. However, we wanted to investigate the spacing between chains when the film is in the uncompressed or elastic regime. It is found from the indentation experiments that the incompressible thickness (once the film is fully collapsed under force) did not contribute much to the elastic properties of the initial compression, but if the incompressible thickness is used to quantify the inter-chain spacing the stiffness values were overestimated. A more reasonable approach is to fit the force–separation curve with a polymer compression model and use the model to calculate the distance between the chains. The de Gennes model assumes a uniform density throughout the film,19,20 whereas Milner and colleagues use a mean-field theory to show that the self-similar concentration profile of the polymer brush is parabolic.21–24 Milner's theory provides a better description of our polymer material and can be represented by the following expressions:60–62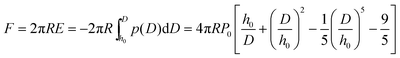 | (1) |
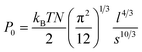 | (2) |
| h0 = (12/π2)1/3N(l)5/3/D2/3 | (3) |
| MW (Da) | h compressible (nm) | h 0 (nm) | s (nm) |
|---|---|---|---|
| 2k | 3.57 ± 0.50 | 4.36 ± 0.16 | 2.66 ± 0.15 |
| 5k | 6.38 ± 1.06 | 8.43 ± 0.25 | 3.98 ± 0.18 |
| 10k | 11.16 ± 1.31 | 14.45 ± 0.41 | 4.99 ± 0.22 |
To get a more detailed understanding of the packing geometry of the PEG, we compared the chain spacing with the Flory radius in different conformations. All of our films obey the condition of s < RF, where RF is the Flory radius.64 Therefore, all PEG chains in our system have a brush-like structure where the total wet thickness hwet is a summation of the incompressible wet thickness hincompressible and the probe indentation distance hcompressible. Knowing that the monomer length is about 0.36 nm for all-trans PEG chains, and 0.28 nm for PEG chains in the helical conformation,8,65 our films with hwet < 0.28N nm (where N is the number of monomers) indicates that the PEG films are all in a helical brush geometry. Comparing Tables 1 and 2, it is clear that the chain spacing of the PEG monolayer on the nanofiber is larger than that on the silicon substrate with the same MW. This is in agreement with the thinner dry thicknesses observed in the TEM images (Fig. 4). The lower SnO2 grafting density is likely due to reduced binding sites on the (010) or (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) side planes of SnO2 compared to the amorphous SiO2 surface on the silicon substrate. For the PEG films on silicon, we also observe that hwet/hdry increases as the MW increases which is reasonable and predicted for the SnO2 nanofibers as well, even though it is much more difficult to measure the absolute value of the film thickness on the SnO2 nanofibers in solution.
) side planes of SnO2 compared to the amorphous SiO2 surface on the silicon substrate. For the PEG films on silicon, we also observe that hwet/hdry increases as the MW increases which is reasonable and predicted for the SnO2 nanofibers as well, even though it is much more difficult to measure the absolute value of the film thickness on the SnO2 nanofibers in solution.
Nanomechanical properties of the PEG films
During compression of the PEG film, the force measured by the AFM is a combination of an elastic force (the conformational entropy of the PEG chains) and the osmotic force (due to the solvation of the PEG chains).61 Therefore it is reasonable to model the films as elastic materials bonded on the substrate with a finite thickness. Since these PEG films are extremely thin, the substrate would constrain the deformation of PEG films at high degrees of compression. We are interested in understanding how the substrate affects the stiffness of the film. To investigate this we compare the Sneddon spherical probe model66 for indentation on infinite thickness films (which does not consider substrate effects) with the Dimitriadis model67 (which include substrate effects).In Dimitriadis' model, the force F varies with the indentation δ through the following expression:
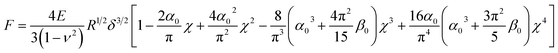 | (4) |
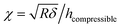 | (5) |
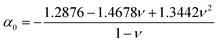 | (6) |
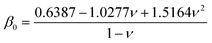 | (7) |
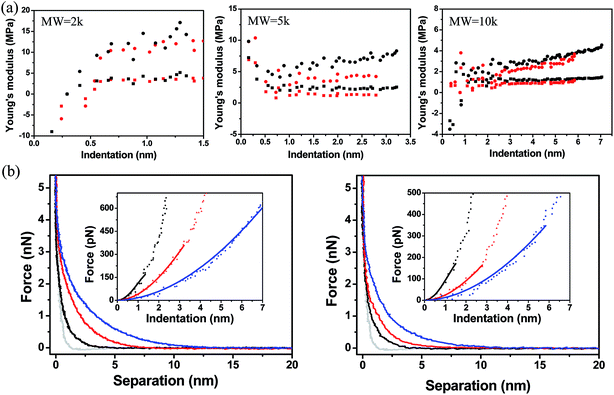
The model derives the force–indentation relationship for a microsphere tip indentation on a film with micron thickness and considers substrate effects that can artificially stiffen the film. The term outside the bracket is Sneddon's spherical probe model and the asymmetric series inside the bracket is a correction term for the finite thickness. Even though the tips in our experiments have much sharper indenters (radii ∼ 30 nm, determined by SEM and a scanning calibration method – see Experimental section and Fig. S1 and S2†), we can still use the model to calculate the Young's modulus since the tip radius is more than 2× larger than the thicknesses of the PEG films in the wet state (the indentation depth δ lies in the spherical range of the tip). To meet the boundary condition in the model, χ is set to ≤1 which limits the indentation δ to be used in the Dimitriadis model to the radius of the tip (as χ increases with δ, the asymmetric series expansion loses accuracy). This allows the Young's modulus, E, to be calculated from indentation data points that fall between the contact point and the boundary condition as shown in Fig. 8a. It is apparent that with the Dimitriadis model the calculated modulus is stable after the initial indentation even for MWs down to 2k. The instability of the Young's modulus at the beginning of the indentation arises since we are at the lower force limit (∼10 pN) of the AFM. In contrast, the calculated E values from the Sneddon model show a gradual increase as the tip indents into the films, which is indicative of substrate effects for such thin films.
Fig. 8b shows the force vs. separation as well as the least-squares fit for representative force–indentation curves (insets) using Dimitriadis' model within the boundary condition. The average Young's moduli extracted from the Dimitriadis model are compared in Table 3. The moduli range from 700 kPa to 5 MPa depending on the MW and substrate. There are currently only a few studies that have investigated the stiffness of PEG brushes with a thickness < 100 nm, and none have measured the stiffness of sub-20 nm thick films in liquid. Sue et al. reported on the synthesis of drendritic PEG monolayer structures deposited on silicon nitride, and carried out force–indentation curves on 5k PEG films in KCl solutions.68 By dividing the curves into three regions, and fitting the first two with Hertzian theory, they were able to back out stiffness values of 5 ± 2.5 MPa for the initial 17 nm of indentation and an increase to 45 MPa when indented by an additional 9 nm. Stan et al. reported on the nanomechanical properties of multilayer sparse brush-like thiolated PEG 20k deposited on gold.15 In their experiments they used Xu and Pharr's model36 to correct for substrate effects and also showed two different stiffness regions: EregionI = 0.09 MPa at a thickness tregionI = 75 nm and EregionII = 1 MPa at a thickness tregionII = 5 nm. These elastic moduli were over an order of magnitude smaller than the values reported by Sue et al. due to the consideration of substrate effects. Our monolayer films showed higher moduli mainly due to the higher packing densities. Tranchida et al. reported on the surface-initiated polymerization synthesis of uniform poly(diethylene glycol methylether methacrylate) (PDEGMA) brushes deposited on gold with a thickness of ∼80 ± 20 nm and elastic modulus of 0.76 ± 0.2 MPa in a buffered solution using Sneddon's model.69 In addition, they synthesized poly(oligoethylene glycol methylether methacrylate) (POEGMA) brushes on gold and extracted an elastic modulus of ∼3.24 ± 0.2 MPa. Our stiffness values were calculated on much thinner (<20 nm) PEG monolayer films, and are comparable to what Tranchida et al. have calculated for much thicker brush structures. Furthermore, we have taken extreme care in isolating the substrate effects from the pure elastic behavior of the films. Part of this process also includes properly assigning the contact point. If the contact point is altered even by 15% of the compressible thickness the extracted moduli fluctuate by up to 50% (Fig. S6†). Considering all these factors, we are confident that our procedures provide accurate values for the stiffness of PEG monolayers and can be leveraged to probe the mechanical properties of other thin, compressible layers.
| MW (Da) | 2k | 2k nanofiber | 5k | 5k nanofiber | 10k | 10k nanofiber |
|---|---|---|---|---|---|---|
| a Young's moduli are calculated from the Dimitriadis fit. b Linear stiffness length ratio is the ratio of the length where the Young's modulus is linear over the total compressible thickness. | ||||||
| Young's modulusa (MPa) | 4.99 ± 1.61 | 4.65 ± 2.78 | 2.57 ± 0.68 | 1.43 ± 0.82 | 1.52 ± 0.35 | 0.69 ± 0.32 |
| Linear stiffness length ratiob | 0.40 ± 0.003 | 0.40 ± 0.006 | 0.46 ± 0.008 | 0.46 ± 0.028 | 0.58 ± 0.059 | 0.60 ± 0.040 |
In the previous section we showed that the expansion ratio hwet/hdry increases as the MW increases. The data in Table 3 also validates this trend by showing that longer chains (larger MW) produce a larger compressibility of the PEG brushes (Fig. 9). We also observe a slight softening of the PEG coatings when grafted to the SnO2 surface. As indicated earlier, when discussing the grafting density differences, this is likely caused by the lower number of binding sites on the single crystalline side surfaces of the SnO2 nanofibers compared to the amorphous silica surface. Besides the expansion ratio, it is interesting to find that the linear stiffness length ratios, defined as the compression length where the Young's modulus is linear over the total compressible thickness, are all over 40% of the total indentation thickness (Table 3). As the molecular weight increase to 10k, the linear stiffness length ratio increases to 60%. This finding is similar to what Tranchida et al. observe for their thicker spin coated films, where they modeled the films as a mattress of non-interacting springs and verified that the Young's modulus of their 90 nm thick films are linear up to a compression of ∼50%.70 The linear regime of our thin films is much larger than what has been reported in literature (∼10%) which indicates that the PEG brush monolayers behave more like a bed of springs instead of a continuous film up to an indentation of ∼50%. We attempted to fit our force curves using the graded model,11 but this failed likely due to the large difference in stiffness between the polymer monolayer and underlying substrate.
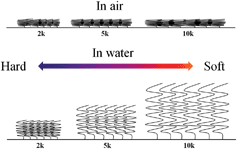 | ||
| Fig. 9 A cartoon showing the different states of the PEG monolayers as a function of molecular weight and local environment (air vs. water). | ||
To understand why the fitting model breaks down at higher forces and compression, we have to consider several properties of the system including the conformational changes in the polymer, as well as solvent exclusion mechanisms. Since the PEG brushes are in a helical structure they allow strong hydrogen bonding between the oxygen atoms of the PEG chains and the water molecules. Therefore, it is expected that higher compressions will force water to be excluded from the chains, leading to an increase in the effective stiffness. The initial 50% of the indentation fits well using Dimitriadis' model and can be considered as a linear elastic regime, which is minimally affected by local solvation shells and intermolecular interactions. As the film is compressed further by the AFM tip, the PEG chains are subject to solvent exclusion effects and inter- and intra-chain interactions. These effects are difficult to incorporate into the model which breaks down at higher indentation. Importantly, the linear elastic regime is highly predictable and reproducible, which is shown throughout our data.
Conclusion
We have demonstrated a facile route to grafting thin, compressible PEG monolayers on SnO2 nanofibers and have described a universal method for quantifying their structural and nanomechanical properties in liquid using AFM. The nanomechanical properties of the PEG films were isolated from other interactions including electrostatic and van der Waals interactions using hydrophobic modified AFM tips. All of the tested PEG MWs (2k, 5k, 10k) show that the dominant forces measured by the AFM stem from steric interaction in solutions when the ionic strength is equal to or greater than that found in biological media. The dry and wet states of the PEG films on silicon were probed using a nanofiber masking technique which allowed us to directly extract thicknesses of the thin films. AFM force–indentation curves showed wide tunability in the nanomechanical properties of the PEG chains by simply controlling the MW of the starting materials. The higher MW PEG exhibited smaller Young's moduli due to a higher expansion ratio. The physical properties of the films deposited on the nanofiber surfaces also showed softer mechanical properties compared to silicon-supported films due to slightly lower densities. Our method for quantifying the stiffness of thin polymer films is valid when the indentation and film thickness is constrained to dimensions less than the tip radius. These findings not only provide impactful information for oxide systems designed to control molecular interactions on surfaces, but these films could play a significant role in the develop of novel optomechanical instrumentation that utilizes the mechanical feedback from polymer films to transduce molecular level forces.Acknowledgements
The authors acknowledge the National Science Foundation (NSF, contract no. 1150952) and the University of California, Office of the President (UC-LFRP, contract no. 130585-001). We would like to thank Dr Fernando Arce and Mr Joon Lee for help with the AFM probe calibration and insightful discussions.References
- T. Gillich, C. Acikgoz, L. Isa, A. D. Schluter, N. D. Spencer and M. Textor, ACS Nano, 2013, 7(1), 316–329 CrossRef CAS PubMed.
- C. L. Lay, H. Q. Liu, D. C. Wu and Y. Liu, Chem.–Eur. J., 2010, 16(10), 3001–3004 CrossRef CAS PubMed.
- J. Peyre, V. Humblot, C. Methivier, J. M. Berjeaud and C. M. Pradier, J. Phys. Chem. B, 2012, 116(47), 13839–13847 CrossRef CAS PubMed.
- S. Sharma, R. W. Johnson and T. A. Desai, Langmuir, 2004, 20(2), 348–356 CrossRef CAS.
- S. Sharma, R. W. Johnson and T. A. Desai, Biosens. Bioelectron., 2004, 20(2), 227–239 CrossRef CAS PubMed.
- H. Xu, F. Yan, E. E. Monson and R. Kopelman, J. Biomed. Mater. Res., Part A, 2003, 66(4), 870–879 CrossRef PubMed.
- I. M. Rio-Echevarria, F. Selvestrel, D. Segat, G. Guarino, R. Tavano, V. Causin, E. Reddi, E. Papini and F. Mancin, J. Mater. Chem., 2010, 20(14), 2780–2787 RSC.
- S. Upadhyayula, T. Quinata, S. Bishop, S. Gupta, N. R. Johnson, B. Bahmani, K. Bozhilov, J. Stubbs, P. Jreij, P. Nallagatla and V. I. Vullev, Langmuir, 2012, 28(11), 5059–5069 CrossRef CAS PubMed.
- I. Yoon, S. E. Baker, K. Kim, Y. M. Wang, S. C. Esener and D. J. Sirbuly, Nanoscale, 2013, 5(2), 552–555 RSC.
- I. Yoon, S. E. Baker, K. Kim, N. O. Fischer, D. Heineck, Y. M. Wang, S. C. Esener and D. J. Sirbuly, Nano Lett., 2013, 13(4), 1440–1445 CAS.
- H. Shulha, A. Kovalev, N. Myshkin and V. V. Tsukruk, Eur. Polym. J., 2004, 40(5), 949–956 CrossRef CAS PubMed.
- C. M. Stafford, C. Harrison, K. L. Beers, A. Karim, E. J. Amis, M. R. Vanlandingham, H. C. Kim, W. Volksen, R. D. Miller and E. E. Simonyi, Nat. Mater., 2004, 3(8), 545–550 CrossRef CAS PubMed.
- C. M. Stafford, B. D. Vogt, C. Harrison, D. Julthongpiput and R. Huang, Macromolecules, 2006, 39(15), 5095–5099 CrossRef CAS.
- Y. J. Sun, B. Akhremitchev and G. C. Walker, Langmuir, 2004, 20(14), 5837–5845 CrossRef CAS.
- G. Stan, F. W. DelRio, R. I. MacCuspie and R. F. Cook, J. Phys. Chem. B, 2012, 116(10), 3138–3147 CrossRef CAS PubMed.
- G. Duner, E. Thormann, A. Dedinaite, P. M. Claesson, K. Matyjaszewski and R. D. Tilton, Soft Matter, 2012, 8(32), 8312–8320 RSC.
- J. L. Cuellar, I. Llarena, S. E. Moya and E. Donath, Macromolecules, 2013, 46(6), 2323–2330 CrossRef CAS.
- I. M. Nnebe and J. W. Schneider, Macromolecules, 2006, 39(10), 3616–3621 CrossRef CAS.
- P. G. de Gennes, Adv. Colloid Interface Sci., 1987, 27(3–4), 189–209 CrossRef CAS.
- S. Alexander, J. Phys. (Paris), 1977, 38(8), 983–987 CrossRef CAS.
- S. T. Milner, T. A. Witten and M. E. Cates, Macromolecules, 1988, 21(8), 2610–2619 CrossRef CAS.
- S. T. Milner, T. A. Witten and M. E. Cates, Macromolecules, 1989, 22(2), 853–861 CrossRef CAS.
- S. T. Milner, Science, 1991, 251(4996), 905–914 CrossRef CAS PubMed.
- S. T. Milner, T. A. Witten and M. E. Cates, Europhys. Lett., 1988, 5(5), 413–418 CrossRef CAS.
- S. Pasche, J. Voros, H. J. Griesser, N. D. Spencer and M. Textor, J. Phys. Chem. B, 2005, 109(37), 17545–17552 CrossRef CAS PubMed.
- S. Pasche, M. Textor, L. Meagher, N. D. Spencer and H. J. Griesser, Langmuir, 2005, 21(14), 6508–6520 CrossRef CAS PubMed.
- M. Heuberger, T. Drobek and N. D. Spencer, Biophys. J., 2005, 88(1), 495–504 CrossRef CAS PubMed.
- T. Drobek, N. D. Spencer and M. Heuberger, Macromolecules, 2005, 38(12), 5254–5259 CrossRef CAS.
- A. S. Lea, J. D. Andrade and V. Hlady, Colloids Surf., A, 1994, 93, 349–357 CrossRef CAS.
- S. C. McLean, H. Lioe, L. Meagher, V. S. J. Craig and M. L. Gee, Langmuir, 2005, 21(6), 2199–2208 CrossRef CAS PubMed.
- H. J. Butt, M. Kappl, H. Mueller, R. Raiteri, W. Meyer and J. Ruhe, Langmuir, 1999, 15(7), 2559–2565 CrossRef CAS.
- C. Dicke and G. Hahner, J. Phys. Chem. B, 2002, 106(17), 4450–4456 CrossRef CAS.
- D. Tranchida, S. Piccarolo and M. Soliman, Macromolecules, 2006, 39(13), 4547–4556 CrossRef CAS.
- H. J. Gao, C. H. Chiu and J. Lee, Int. J. Solids Struct., 1992, 29(20), 2471–2492 CrossRef.
- N. Gavara and R. S. Chadwick, Nat. Nanotechnol., 2012, 7(11), 733–736 CrossRef CAS PubMed.
- H. T. Xu and G. M. Pharr, Scr. Mater., 2006, 55(4), 315–318 CrossRef CAS PubMed.
- D. C. Lin and F. Horkay, Soft Matter, 2008, 4(4), 669–682 RSC.
- M. Law, D. J. Sirbuly, J. C. Johnson, J. Goldberger, R. J. Saykally and P. D. Yang, Science, 2004, 305(5688), 1269–1273 CrossRef CAS PubMed.
- Z. W. Pan, Z. R. Dai and Z. L. Wang, Science, 2001, 291(5510), 1947–1949 CrossRef CAS PubMed.
- D. J. Sirbuly, M. Law, H. Q. Yan and P. D. Yang, J. Phys. Chem. B, 2005, 109(32), 15190–15213 CrossRef CAS PubMed.
- Z. H. Yang, J. A. Galloway and H. U. Yu, Langmuir, 1999, 15(24), 8405–8411 CrossRef CAS.
- A. Papra, N. Gadegaard and N. B. Larsen, Langmuir, 2001, 17(5), 1457–1460 CrossRef CAS.
- M. Q. Zhang, T. Desai and M. Ferrari, Biomaterials, 1998, 19(10), 953–960 CrossRef CAS.
- J. S. Villarrubia, Surf. Sci., 1994, 321(3), 287–300 CrossRef CAS.
- J. S. Villarrubia, J. Res. Natl. Inst. Stand. Technol., 1997, 102(4), 425–454 CrossRef.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64(11), 3342 CrossRef CAS PubMed.
- Y. S. Lo, N. D. Huefner, W. S. Chan, P. Dryden, B. Hagenhoff and T. P. Beebe, Langmuir, 1999, 15(19), 6522–6526 CrossRef CAS.
- Z. Q. Wei, C. Wang and C. L. Bai, Surf. Sci., 2000, 467(1–3), 185–190 CrossRef CAS.
- R. Schlapak, D. Armitage, N. Saucedo-Zeni, M. Hohage and S. Howorka, Langmuir, 2007, 23(20), 10244–10253 CrossRef CAS PubMed.
- M. Cerruti, S. Fissolo, C. Carraro, C. Ricciardi, A. Majumdar and R. Maboudian, Langmuir, 2008, 24(19), 10646–10653 CrossRef CAS PubMed.
- A. U. Alam, M. M. R. Howlader and M. J. Deen, ECS J. Solid State Sci. Technol., 2013, 2(12), 515–523 CrossRef PubMed.
- Gwyddion– Free SPM data analysis software, http://gwyddion.net/ Search PubMed.
- F. Cecchet, B. De Meersman, S. Demoustier-Champagne, B. Nysten and A. M. Jonas, Langmuir, 2006, 22(3), 1173–1181 CrossRef CAS PubMed.
- S. Yamamoto, M. Ejaz, Y. Tsujii, M. Matsumoto and T. Fukuda, Macromolecules, 2000, 33(15), 5602–5607 CrossRef CAS.
- J. Fick, R. Steitz, V. Leiner, S. Tokumitsu, M. Himmelhaus and M. Grunze, Langmuir, 2004, 20(10), 3848–3853 CrossRef CAS.
- B. Bilen, Y. Skarlatos, G. Aktas, M. N. Inci, T. Dispinar, M. M. Kose and A. Sanyal, J. Appl. Phys., 2007, 102(7), 073534 CrossRef PubMed.
- S. Acikgoz, B. Bilen, M. M. Demir, Y. Z. Menceloglu, Y. Skarlatos, G. Aktas and M. N. Inci, Opt. Rev., 2008, 15(2), 84–90 CrossRef CAS PubMed.
- K. Feldman, G. Hahner, N. D. Spencer, P. Harder and M. Grunze, J. Am. Chem. Soc., 1999, 121(43), 10134–10141 CrossRef CAS.
- J. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 1997, 94(16), 8378–8379 CrossRef CAS.
- K. Hristova and D. Needham, J. Colloid Interface Sci., 1994, 168(2), 302–314 CrossRef CAS.
- A. K. Kenworthy, K. Hristova, D. Needham and T. J. Mcintosh, Biophys. J., 1995, 68(5), 1921–1936 CrossRef CAS.
- P. Hamilton-Brown, T. Gengebach, H. J. Griesser and L. Meagher, Langmuir, 2009, 25(16), 9149–9156 CrossRef CAS PubMed.
- S. J. Oshea, M. E. Welland and T. Rayment, Langmuir, 1993, 9(7), 1826–1835 CrossRef CAS.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic press, 2011 Search PubMed.
- P. Harder, M. Grunze, R. Dahint, G. M. Whitesides and P. E. Laibinis, J. Phys. Chem. B, 1998, 102(2), 426–436 CrossRef CAS.
- I. N. Sneddon, Int. J. Eng. Sci., 1965, 3(1), 47–57 CrossRef.
- E. K. Dimitriadis, F. Horkay, J. Maresca, B. Kachar and R. S. Chadwick, Biophys. J., 2002, 82(5), 2798–2810 CrossRef CAS.
- Z. Y. Suo, F. T. Arce, R. Avci, K. Thieltges and B. Spangler, Langmuir, 2006, 22(8), 3844–3850 CrossRef CAS PubMed.
- D. Tranchida, E. Sperotto, T. Staedler, X. Jiang and H. Schonherr, Adv. Eng. Mater., 2011, 13(10), B369–B376 CrossRef PubMed.
- D. Tranchida, I. Lilge and H. Schonherr, Polym. Eng. Sci., 2011, 51(8), 1507–1512 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tip radius determination and image reconstruction, thickness of oxide layer, and Young's moduli dependence on contact point assignment. See DOI: 10.1039/c4sm01530d |
| This journal is © The Royal Society of Chemistry 2014 |