Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of micellization-induced deprotonation on the associative behavior of a carboxyl modified Pluronic P85†
Adriana
Šturcová
*,
Jiří
Dybal
,
Alexander
Zhigunov
,
Nikolay
Kotov
and
Alena
Braunová
Institute of Macromolecular Chemistry, Academy of Sciences of the Czech Republic, Heyrovsky Sq. 2, 162 06 Prague 6, Czech Republic. E-mail: sturcova@imc.cas.cz
First published on 5th August 2014
Abstract
Thermoresponsive polymeric surfactant CAE85 is a telechelic carboxyl group derivative of Pluronic P85 and its carboxyl end-groups undergo deprotonation into carboxylate groups upon micellization. Micelle formation and disintegration were studied here by means of small angle X-ray scattering, FTIR and Raman spectroscopy, quantum mechanical calculations and dynamical mechanical analysis. The deprotonation was observed in aqueous solutions of CAE85 for concentrations from 5 wt% to 30 wt% at temperatures above the corresponding critical micellization temperature (CMT). The most likely cause is a difference between the proton dissociation constant of the micelle (pKm) and the proton dissociation constant of the unimers in solution (pKa); our observations indicate that pKm < pKa. For concentrations up to 15 wt%, the presence of carboxylate groups in CAE85 lowered the CMT in comparison with P85. In addition, the behavior of CAE85 was generally not thermo-reversible and reproducible upon cooling. Quantum chemical calculations showed that, in the dense micelle corona, the deprotonated states were more stable than hydrogen-bonded states of neutral molecules, which is likely to affect the equilibrium processes in the micelle. In contrast to the unmodified P85, no gelation was observed in the case of CAE85. By studying the processes at all the levels of organization from nanoscale charge formation through micellization to the macroscale process of gelation, our understanding of polymeric micelle formation may be advanced.
Introduction
Pluronics are tri-block co-polymers consisting of poly(ethylene oxide) and poly(propylene oxide) blocks (PEO–PPO–PEO). They have partially hydrophobic and partially hydrophilic character. Hydrophobic interactions of non-polar methyl groups in the PPO block compete with the solvation of polar ether groups in PEO and in PPO. These interactions change with temperature and make Pluronics respond to it: they are soluble in aqueous media at low temperatures; with the increase of temperature above a certain critical value, desolvation of the macromolecular chain takes place. The desolvation results in formation of micelles—thermodynamically stable poly-molecular aggregates. The formation of a micelle is described by the critical micellization temperature (CMT) or critical micellization concentration (CMC). Micellization is driven by the hydrophobic interactions and by the difference in energy gain from association and from solvation. At higher concentration and elevated temperatures such block copolymers can transform from a low viscosity solution into a gel. Both processes are thermoreversible and dependent on many factors, such as molecular weight, relative block size, and concentration.1Temperature-induced micellization of carboxyl-end modified Pluronic P85 (denoted as CAE85, HOOC–CH2–CH2–CO–O–(EO)26–(PO)39–(EO)26–CO–CH2–CH2–COOH) has been reported by Custers et al.2 In our previous work,3 an observation has been made, that upon and after micellization and at pH values below the value of the acid dissociation constant pKa of the unimer solution, the CAE85 macromolecules undergo a two-stage deprotonation process. As a result, the degree of deprotonation significantly exceeds the degree of deprotonation of unimers in solution. The first stage of deprotonation follows immediately after micelle formation at the CMT and it is in agreement with models elaborated for low-molecular-weight surfactants.4 The second stage was suggested to appear only in micelles with sufficiently high density of chains in the corona, which can be achieved by an increase in temperature and by allowing sufficient time for equilibration. The observed deprotonation was not ascribed to a temperature-induced change of pH, since only very small changes of pH of the solution were detected. In addition, Chang et al. have found that the degree of ionization of weak acid groups in a solution of an amphiphilic polymer is small and the temperature has little effect when working at a pH below the acid dissociation constant pKa of unimer solution.5 The study of aqueous solutions of three low-molecular-weight carboxylic acids by Cistola et al. has also shown that at a low pH of 2.5, the temperature has a negligible effect on the ionization of these acids.6 The behavior of CAE85 in aqueous solutions is thus in agreement with the predictions about the acid dissociation constant made for low-molecular-weight surfactants: it has been argued that the acid dissociation constant of a micelle pKm is a property different from that of surfactant monomers pKa.4,7 In a micelle, pKm is lower than pKa if working at pH values lower than pKa. The decrease of the acid dissociation constant when going from unimer solution to an aggregate explains the increased deprotonation of CAE85 macromolecules in comparison with their unimer solution.
Since the macromolecules of CAE85 can exist both in non-ionic (protonated) form and in ionic (deprotonated) form, behavior of such solutions corresponds to the behavior of binary mixtures of surfactants. The micelles formed from the CAE85 polymer are therefore mixed micelles, which have been studied extensively and which include neutral surfactants, charged surfactants and polymers.8 The control of acid–base properties of this macromolecular surfactant is important for applications, in which ion-binding processes take place.2 In general, the use of surfactant mixtures is advantageous in cosmetics, pharmacology and biological systems.8,9
The mixed micelles are often assumed to behave like a homogenous mixture of solvents, which is dispersed in a solution and is in equilibrium with it. Following this assumption, phenomenological thermodynamic models such as regular solution theory, originally developed for mixtures of solvents, are applied also to the mixed micelles.10 However, when a charged surfactant is a part of the solvent mixture, it can dissociate (deprotonate in our case) and, consequently, it may be difficult to choose an appropriate definition of the concentration (molar fraction) of the surfactant in the bulk and in the micelle.8 Therefore, other approaches to modelling of the mixed micelles must be considered.11 Letellier et al.11 have shown that a model of adsorption originally invented by Brunauer, Emmett and Teller12 in 1938 and later modified by Stokes and Robinson13 can be applied to mixtures of ionic and non-ionic surfactants. This model was initially intended for very concentrated water solutions of electrolytes. Letellier et al.11 viewed the micelles (the pseudo-phase) as a mixed medium, in which the non-ionic amphiphile was considered as the molecular solvent and the ionic amphiphile represented the electrolyte (the salt).11 The properties (e.g. CMC, micelle aggregation number, pH of solution) of micelles and solutions of binary mixtures of surfactants are studied also by molecular thermodynamic theories.7
In all of the thermodynamic models mentioned above, that deal with the mixture of low-molecular-weight surfactants, the CMC is used to characterize the process of micellization. The influence of temperature on the value of the CMC is weak. In polymeric surfactants, the effects of temperature on the CMC are strong14 and thus the formation of micelles is characterized also by the CMT. The CMT of mixtures of surfactants in which at least one component is a polymer is studied less frequently.15
The aim of the present work was to investigate the charge formation during the temperature-induced micellization of the CAE85 co-polymer at various concentrations. Small angle X-ray scattering (SAXS), vibrational (infrared and Raman) spectroscopy, quantum chemical calculations and dynamical mechanical analysis (DMA) were used for the comparison of association and gelation behavior of modified CAE-85 with the behavior of the unmodified Pluronic P85, (EO)26–(PO)39–(EO)26. The presence of charge in a micelle can also affect the kinetics of association to and dissociation from micelles.16 Even though equilibrium mechanisms in polymer micelles are not well understood yet, it has been established that polymer micelles have generally slower equilibration kinetics than low-molecular-weight surfactants. The kinetics is slower due to the polymer long chains being subjected to additional thermodynamic and dynamic constraints.17 It is demonstrated here, that ionization of the CAE85 micellar aggregates significantly affects the dissociation process of the micelles.
Experimental
Materials
Pluronic P85 was obtained from BASF and succinic anhydride was purchased from Fluka. All other chemicals and solvents used were of analytical grade. Usual procedures were used for solvents' purification and drying. Reagents were used without further purification. Modification of Pluronic P85 was first described by Custers and co-workers.2 In this work, the modified method of Custers et al.2 was used for the introduction of terminal COOH groups and this method was previously described.3 The sample preparation procedure was the same as in our previous work: aqueous solutions of the polymers were prepared gravimetrically and stirred magnetically in an ice bath.3 Water used for the solutions was obtained from Sigma Aldrich (LCMS CHROMASOLV quality).Small angle X-ray scattering (SAXS)
SAXS experiments were performed using a pinhole camera (Molecular Metrology SAXS System) attached to a microfocused X-ray beam generator (Osmic MicroMax 002) operating at 45 kV and 0.66 mA (30 W). The camera was equipped with a multiwire gas-filled area detector with an active area diameter of 20 cm (Gabriel design). The experimental setup covered a scattering vector (q) range of 0.004–0.25 Å−1, q = (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where λ = 1.54 Å is the wavelength and 2θ is the angle between the incident X-ray beam and the detector measuring the scattered intensity.
θ, where λ = 1.54 Å is the wavelength and 2θ is the angle between the incident X-ray beam and the detector measuring the scattered intensity.
Attenuated total reflectance infrared (ATR FTIR) spectroscopy
A Nicolet Nexus 870 FTIR spectrometer purged with dry air and equipped with a cooled mercury–cadmium–telluride (MCT) detector, a KBr beam splitter and a horizontal micro-ATR Golden Gate unit (SPECAC) was used for ATR FTIR spectra collection. The ATR accessory had a diamond prism and controlled heating of the accessory top plate was employed. When processing the spectra, a spectrum of atmosphere surrounding the empty diamond crystal was subtracted from the sample ATR FTIR spectra; the spectra were then baseline corrected and advanced ATR corrected using OMNIC software version 7.1a or 8. The position on the wavenumber axis of the bands for the CH3 group deformation vibration and for the stretching vibration of the C–O bond were found using the “Find Peaks” tool in the OMNIC™ software package. The resultant wavenumber vs. temperature curves were differentiated using the Origin™ software in order to determine the inflection point. The solution under investigation was kept covered in the course of the whole experiment.Raman spectroscopy
Ambient-pressure Raman spectra at various temperatures were obtained on a Renishaw in-Via Raman micro-spectrometer with an Ar+ ion laser with an excitation wavelength of 514.5 nm. A cuvette (closed with a lid) with a sample was placed into a temperature cell from Linkam Scientific Instruments Ltd. (a THMS600 stage, a TMS94 temperature programmer, a LNP cooling pump and a Dewar vessel). Spectra in the temperature range from 10 °C to 50 °C were obtained. Prior to the accumulation of the spectra at the low temperature of 10 °C, it was necessary to manipulate with the polymer solutions at ambient temperature. Peak assignments in the C–H stretching vibration region were made according to Guo et al.:18 in the neat Pluronic P85, the CH3 symmetric stretching of the PPO block is located at around 2935 cm−1 and the CH2 symmetric stretching vibration in the same block takes place at about 2875 cm−1. The positions of these bands were obtained from the second derivative spectra. In the spectra of aqueous solutions, the water spectra were subtracted before the second differentiation was carried out. The position of the bands (in wavenumber) was plotted against temperature and these dependences in aqueous solutions were fitted with the sigmoidal Boltzmann function of the form, | (1) |
Even though the precise physical principle for this dependence is not known yet, the parameters have a physical interpretation: A1 and A2 are the initial and the end limit values, respectively. The parameter x0 is the center (the inflection point) of the dependence and was used to determine the critical micellization temperature and Δx denotes the width of the transition from unimers to micelles. In the neat co-polymer, the wavenumber vs. temperature curves were fitted with a third order polynomial only to guide the eye.
Quantum chemical calculations
The model quantum chemical calculations were carried out at the density functional theory (DFT) level with the B3LYP functional and the 6311++G(2d,2p) basis set employing the Gaussian 09 program package.19 In order to verify the reliability of the DFT results, all the stable structures were reoptimized at the Møller–Plesset (MP2) level of theory (MP2/6-31+G(d)). The optimizations were fully unconstrained and vibrational frequencies were used to characterize the stationary points as minima. The Gibbs free energy G298 was calculated at room temperature using the Gaussian 09 software package in which G is computed as the sum of the electronic energy E and the thermal correction of the Gibbs free energy Gcorr.19pH measurement
The temperature dependence of pH was measured in a cryostat Haake F8 using a pH-meter (Radiometer Copenhagen).Dynamical mechanical analysis (DMA)
Dynamic mechanical measurements were made for Pluronic P85 and CAE85 concentrated solutions over a wide range of temperatures. A Bohlin Gemini Rheometer with cone–plate geometry with 40 mm diameter and 1° angle was used. The heating rate was set to 0.5 °C min−1; the DMA analysis on cooling was not carried out. During the oscillatory measurements, the frequency was fixed to 1 Hz.Results
Scattering
The scattering curve obtained from a small-angle X-ray scattering (SAXS) experiment on a 10 wt% solution of modified Pluronic P85 (denoted as CAE85) at the temperature of 40 °C is presented in Fig. 1A. The SANS results of P85 can be found elsewhere.20,21 The curve was fitted using the SASFit software (package for fitting small-angle scattering curves: https://kur.web.psi.ch/sans1/SANSSoft/sasfit.html) with a model of a micelle consisting of the homogenous spherical core and Gaussian chains attached to the surface of the core. The scattering intensity is proportional to the form factor and the structure factor. The form factor of such micelles contains four different terms: the self-correlation term of the core, the self-correlation term of the chains, the cross-term between the core and chains, and the cross term between different chains.22 The best-fit parameters were determined to be R = 214 Å (radius of core) and Rg = 18 Å (gyration radius of chains). The value of the gyration radius was slightly larger than that calculated by Pedersen,22 who estimated Rg for the flexible chain model to be 13.7 Å. This could be explained by a longer chain due to carboxyl-end modification. The fit was obtained without any contribution of the structure factor. Usually the effect of the structure factor appears at higher concentrations as an additional peak in the scattering curve of micelles and it is related to the effect of intermicellar interactions.23,24 This peak was not present in our system, apparently due to the increased radius of the micelles, which led to the larger intermicellar distance compared to the results obtained by Pedersen.25A good fit to the experimental scattering curve could be achieved also by a linear combination of two form factors corresponding to models of hard spheres and Gaussian chains. The model of hard spheres is represented by the equation
 | (2) |
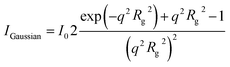 | (3) |
A good average overview of the structure can be obtained by the pair distribution function (PDF) method. The method is based on the Fourier transformation of the experimental scattering data according to the equation:
 | (4) |
The results are displayed in Fig. 1B where two maxima are visible. The greater one corresponded to the core of the micelle, while the less intensive one to the corona. The gyration radius in real space was calculated to be 139 Å from p(r) using the following equation:
 | (5) |
This result was in a good agreement with the parameters obtained by the Guinier approximation, which gave Rg = 127 ± 10 Å.
Infrared spectroscopy
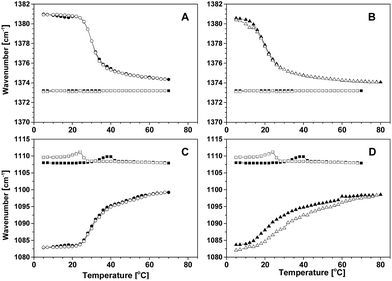
The deformation vibration mode of the CH3 group is sensitive to the changes in the structure and interactions experienced by the poly(propylene oxide) block of Pluronic P85 and of modified Pluronic CAE85.28,29 The wavenumber shift of this mode was used to follow the process of micellization induced by the increase in temperature (Fig. 2A and B, 3A and B and S1 in the ESI†). In the neat polymers, the position of this mode did not change significantly with temperature – it fluctuated between 1373.1 cm−1 and 1373.2 cm−1 in P85 and between 1373.9 cm−1 and 1374.3 cm−1 in CAE85. Upon dissolution of both polymers in water at a low temperature of 5 °C, the wavenumber of the CH3 group vibration was blue-shifted (to a higher wavenumber) due to the hydrophobic interaction with water. The magnitude of the shift displayed slight variation with the copolymer type and concentration. For all solutions, upon an increase of temperature, the wavenumber of the CH3 deformation mode was red-shifted and approached values close to the values found in neat polymers. The inflection point on the wavenumber vs. temperature curve determined the critical micellization temperature in all solutions (Table 1). The CAE85/water solution of concentration 30 wt% was the exception – a steady red-shift corresponding to a gradual transition was finalized at a temperature of about 58 °C (data not shown).| Co-polymer | Concentration (wt%) | Critical micellization temperaturea (°C) | Widthb (°C) | |||||
|---|---|---|---|---|---|---|---|---|
| IR | Raman | IR | ||||||
| CH3 def. | C–O str. | CH3 sym. str. | CH2 sym. str. | CH3 def. | ||||
| Heating | Cooling | Heating | Cooling | Heating, 2nd cycle | Heating, 2nd cycle | Heating | ||
| a CMT determined from the inflection point of the wavenumber vs. temperature curve of the respective vibration bands in the IR and Raman spectra, using the fit to the sigmoidal Boltzmann function in eqn (1). b Width of the transition determined as the parameter Δx in eqn (1). c Data published in ref. 3. | ||||||||
| P85 | 5 | 29 | 29 | 31 | 28 | — | — | 1.0 |
| 10 | 30 | 30 | 29 | 29 | 3.3 | |||
| 15 | 29 | 28 | 28 | 30 | 25 | 29 | 3.1 | |
| 30 | 20 | 20 | 19 | 29 | 15 | 22 | 5.2 | |
| CAE85 | 5 | 26 | — | 26 | — | — | — | 1.0 |
| 10 | 17 | 17 | 1.3 | |||||
| 15 | 12c | 12c | 13c | 9c | 33 | 37 | 0.7 | |
| 30 | Broad | Broad | 20 | Broad | — | |||
The band of the stretching vibrations of the C–O bonds is another band significant for investigation of changes in the structure and interactions in polymer–water solutions upon micellization. The temperature dependence of the position of this band for various systems studied is shown in Fig. 2C and D and 3C and D. Upon solubilization of the polymer in water at a temperature of 5 °C, the C–O stretching band was red-shifted with respect to the position in neat P85 and CAE85. The shift was caused by the hydrophilic interaction of the ether oxygen with water molecules. As the temperature of solutions was increased, the band moved to a higher wavenumber, but did not reach the position obtained for neat polymers. This indicated that especially the PEO segments in the corona of the micelle remained hydrated. The absolute value of the initial red shift and the consequent blue shift was slightly dependent on the concentration and polymer type.
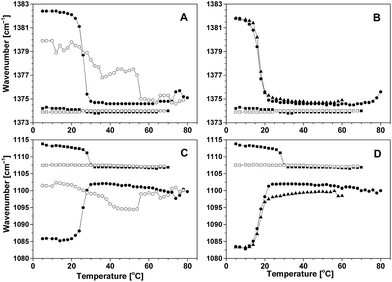
After completing the heating part of the temperature cycle, the P85/water solutions were cooled. For both the CH3 and C–O vibrational bands, shifts in their position opposite to the shifts induced on heating were observed (Fig. 2 and S1 in the ESI†). This behavior was concentration dependent: at the concentrations of 5 wt% and 10 wt%, the position of both modes displayed a fully reversible change with temperature; at concentrations of 15 wt% and 30 wt%, the position of the methyl deformation mode was reversible, but a slight hysteresis was present in the position of the C–O stretching vibration mode. The CMT (∼30 °C) did not change significantly when the concentration was within the range from 5 wt% to 15 wt%; it decreased by about 10 °C upon a concentration increase to 30 wt%. The width of the transition increased with concentration from 1.0 °C to 5.2 °C (Table 1).
The shifts of the CH3 and C–O vibrational bands in CAE85 solutions at concentrations of 5, 10 and 30 wt% upon cooling did not show a reversible change with temperature (Fig. 3A and C). In addition, the wavenumber vs. temperature curves were not reproducible even at the same average cooling rate: in some cases, the band position returned to the (fully) hydrated state and the charged groups either remained present or they underwent re-protonation. In other cases, there were fluctuations in the band position with eventual return to the dehydrated state and with the charged groups present even at 5 °C and after prolonged equilibration at this temperature (concentration 15 wt%; data not shown). Therefore, the CMT was determined only from the heating curves at the concentration of 5, and 10 wt% (Table 1). The CMT values decreased with increasing concentration of CAE85 and they were lower than the CMT in P85 solutions at the corresponding concentration. At all concentrations, the width of the transition was around 1.0 °C, a lower value than in the aqueous solutions of P85 (Table 1).
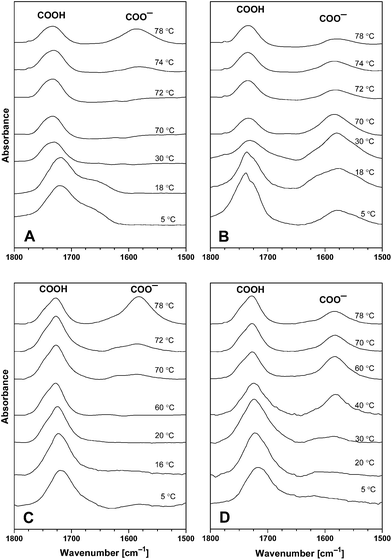
Infrared spectroscopy is used to study acid–base equilibriums of compounds containing the carboxyl group exploiting the fact that the stretching vibration of the carboxyl and the carboxylate group have well-separated bands.3,30 The absorption band due to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration in the carboxyl group of the CAE85 macromolecules was identified at around 1717 cm−1 when CAE85 was dissolved in water (concentrations 5 wt%, 10 wt% and 30 wt%; temperature 5 °C; Fig. 4 and 5). The –CO–O– linkage between an EO block and the end group of the CAE85 macromolecule also contributed to this band. In addition, the water deformation vibration band at around 1640 cm−1 partially overlapped with the C
O stretching vibration in the carboxyl group of the CAE85 macromolecules was identified at around 1717 cm−1 when CAE85 was dissolved in water (concentrations 5 wt%, 10 wt% and 30 wt%; temperature 5 °C; Fig. 4 and 5). The –CO–O– linkage between an EO block and the end group of the CAE85 macromolecule also contributed to this band. In addition, the water deformation vibration band at around 1640 cm−1 partially overlapped with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration region. In order to gain better access to the spectral changes, the water subtraction procedure was used as described in the previous paper.3 In this procedure, it was assumed that the polymer solute affected some of the water molecules (interacting water) while the remaining water molecules retained properties of bulk (or non-interacting) water. It was possible to fully subtract the band corresponding to the bulk water, but the interacting water molecules created characteristic difference band patterns in the difference spectra. At the concentration of 15 wt%,3 water molecules interacting with the solubilized CAE85 unimers were detected only up to the respective CMT of 12 °C. Likewise, at 5 wt% and 10 wt% (Fig. 4), some interacting water was detected up to 24 °C and 16 °C, respectively, which was close to the corresponding CMT of 26 °C and 17 °C, respectively. Upon a further increase of the temperature, the behavior at 5 wt% and 10 wt% closely followed the behavior reported for 15 wt%: above the critical micellization temperature, a spectral shoulder at about 1745 cm−1 appeared and it corresponded to hydrogen bonded dimers COO−…COOH, indicating that some of the carboxyl groups were deprotonated and carboxylate groups were formed.31 At the temperature of approximately 74 °C and 72 °C, respectively – well above the CMTs corresponding to 5 wt% and 10 wt% solutions, formation of a new band at 1580 cm−1 was observed. The band corresponded to more extensive deprotonation and the newly formed carboxylate groups did not enter into interaction with the carboxyl groups. Upon cooling the 5 wt% solution, the carboxylate band went through a maximum intensity and decreased towards the temperature of 5 °C, but did not disappear completely. In addition, a band around 1740 cm−1 significantly increased in intensity, indicating the presence of hydrogen bonded dimers between carboxylate and carboxyl groups even at 5 °C. Upon cooling the 10 wt% solution to a temperature of 30 °C, the intensity of the carboxylate band at 1580 cm−1 was significantly decreased and at a temperature of 5 °C, this band and the shoulder at 1745 cm−1 were not present at all indicating complete re-protonation of the carboxylate groups. Thus, the effect of cooling on the 10 wt% solution differed from the effect on the 5 wt% and 15 wt% solution: charge formation at the concentration of 10 wt% was reversible, while at the concentrations of 5 wt% and 15 wt% it was not. Fig. 5 shows the evolution of the carboxyl and carboxylate bands in the 30 wt% aqueous solution of CAE-85. At this concentration, the interacting water did not disappear from the spectra until the temperature was raised to 40 °C (the spectrum not shown) – indicating that CAE-85 molecules were not in the associated state. A spectral shoulder at 1740 cm−1 (corresponding to dimers COO−…COOH) developed at around 50 °C (the spectrum not shown). The carboxylate band at about 1580 cm−1 was first detected at 70 °C – this was above the temperature of 58 °C, at which the association process of CAE85 unimers was assumed to reach completion according to the position of CH3 deformation vibration (data not shown). The charged COO− groups remained present upon cooling (Fig. 5) – behavior similar to that reported for a concentration of 15 wt%.3
O stretching vibration region. In order to gain better access to the spectral changes, the water subtraction procedure was used as described in the previous paper.3 In this procedure, it was assumed that the polymer solute affected some of the water molecules (interacting water) while the remaining water molecules retained properties of bulk (or non-interacting) water. It was possible to fully subtract the band corresponding to the bulk water, but the interacting water molecules created characteristic difference band patterns in the difference spectra. At the concentration of 15 wt%,3 water molecules interacting with the solubilized CAE85 unimers were detected only up to the respective CMT of 12 °C. Likewise, at 5 wt% and 10 wt% (Fig. 4), some interacting water was detected up to 24 °C and 16 °C, respectively, which was close to the corresponding CMT of 26 °C and 17 °C, respectively. Upon a further increase of the temperature, the behavior at 5 wt% and 10 wt% closely followed the behavior reported for 15 wt%: above the critical micellization temperature, a spectral shoulder at about 1745 cm−1 appeared and it corresponded to hydrogen bonded dimers COO−…COOH, indicating that some of the carboxyl groups were deprotonated and carboxylate groups were formed.31 At the temperature of approximately 74 °C and 72 °C, respectively – well above the CMTs corresponding to 5 wt% and 10 wt% solutions, formation of a new band at 1580 cm−1 was observed. The band corresponded to more extensive deprotonation and the newly formed carboxylate groups did not enter into interaction with the carboxyl groups. Upon cooling the 5 wt% solution, the carboxylate band went through a maximum intensity and decreased towards the temperature of 5 °C, but did not disappear completely. In addition, a band around 1740 cm−1 significantly increased in intensity, indicating the presence of hydrogen bonded dimers between carboxylate and carboxyl groups even at 5 °C. Upon cooling the 10 wt% solution to a temperature of 30 °C, the intensity of the carboxylate band at 1580 cm−1 was significantly decreased and at a temperature of 5 °C, this band and the shoulder at 1745 cm−1 were not present at all indicating complete re-protonation of the carboxylate groups. Thus, the effect of cooling on the 10 wt% solution differed from the effect on the 5 wt% and 15 wt% solution: charge formation at the concentration of 10 wt% was reversible, while at the concentrations of 5 wt% and 15 wt% it was not. Fig. 5 shows the evolution of the carboxyl and carboxylate bands in the 30 wt% aqueous solution of CAE-85. At this concentration, the interacting water did not disappear from the spectra until the temperature was raised to 40 °C (the spectrum not shown) – indicating that CAE-85 molecules were not in the associated state. A spectral shoulder at 1740 cm−1 (corresponding to dimers COO−…COOH) developed at around 50 °C (the spectrum not shown). The carboxylate band at about 1580 cm−1 was first detected at 70 °C – this was above the temperature of 58 °C, at which the association process of CAE85 unimers was assumed to reach completion according to the position of CH3 deformation vibration (data not shown). The charged COO− groups remained present upon cooling (Fig. 5) – behavior similar to that reported for a concentration of 15 wt%.3
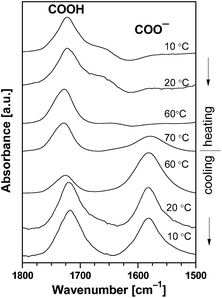 | ||
| Fig. 5 Corrected and normalized ATR FTIR spectra of the 30 wt% aqueous solution of CAE85 at the corresponding temperatures. Spectra of water at the corresponding temperature were subtracted. | ||
Apart from temperature-dependent behavior, a time-dependent evolution of charge was also followed. A solution of concentration 10 wt% was heated to the temperature of 60 °C, which is above the CMT of 17 °C, but below the temperature of about 70 °C at which the COO− groups were first observed (Fig. 4C). The start of the deprotonation of carboxyl groups was observed after about 5 minutes, but the intensity of bands corresponding to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration in both COOH and COO− groups was not stable even at the end of a 300 minute observation (data not shown). In another time-dependent experiment, a solution of concentration 15 wt% was heated to 80 °C, then cooled to 5 °C, and kept at this low temperature for 180 minutes. During the heating part of the cycle, COO− groups were formed and they did not fully re-protonate upon cooling or upon the subsequent equilibration at 5 °C (data not shown).
O stretching vibration in both COOH and COO− groups was not stable even at the end of a 300 minute observation (data not shown). In another time-dependent experiment, a solution of concentration 15 wt% was heated to 80 °C, then cooled to 5 °C, and kept at this low temperature for 180 minutes. During the heating part of the cycle, COO− groups were formed and they did not fully re-protonate upon cooling or upon the subsequent equilibration at 5 °C (data not shown).
Raman spectroscopy
Similar to ATR FTIR spectra, wavenumber shifts in Raman spectra can be used to detect changes in the conformation and/or association state of Pluronic block copolymers.18 The temperature dependence of the C–H stretching vibrations located in the region between 3000–2800 cm−1 was followed (Fig. S2 in the ESI†).In neat P85, the symmetric CH3 stretching vibration of the PPO block was located at 2936 cm−1 at a temperature of 10 °C and remained stable up to 40 °C; it decreased to 2935 cm−1 at 50 °C (Fig. 6). The symmetric CH2 stretching vibration also in the PPO block was found at 2874 cm−1 from 10 °C to 40 °C and shifted to 2873 cm−1 at 50 °C.
In the aqueous solution of P85 at a concentration of 15 wt%, the CH3 vibration was blue-shifted to 2944 cm−1 compared to neat P85 at a temperature of 10 °C. Upon a second heating of the solution (see Experimental), the vibration was red-shifted to approximately 2937 cm−1 at 50 °C. This was a value close to that of neat Pluronic. The CMT was determined to be 25 °C – a temperature that is 4 °C lower than the CMT estimated from the wavenumber vs. temperature curve obtained by ATR FTIR spectroscopy (Fig. 2 and Table 1). The CH2 vibration was also blue shifted to 2884 cm−1 when P85 was dissolved in water and the temperature was 10 °C. As the temperature was increased to 50 °C, a red-shift to 2876 cm−1 was observed and the transition (CMT) temperature was 29 °C (Fig. 6) – in agreement with the narrow range from 28 °C to 30 °C found by ATR FTIR spectroscopy (Fig. 2 and Table 1); the CMT from the CH2 vibration mode is 4 °C higher than that from the curve for the CH3 vibration mode (Fig. 6).
At 30 wt% (Fig. 6), the behavior of the two vibrational modes, CH3 symmetric and CH2 symmetric stretching in the PPO block, during the heating process was qualitatively similar to the behavior at 15 wt%. The corresponding CMT values, determined as 15 °C and 22 °C from the CH3 and from the CH2 mode, respectively, were lower than those determined by Raman spectroscopy for 15 wt% as expected. In addition, the CMT values determined by Raman spectroscopy at 30 wt% agreed well with those determined from the cooling curves of the first temperature cycle obtained by ATR FTIR spectroscopy (Fig. 2 and Table 1). Similar to 15 wt%, the CMT determined from the CH3 vibration mode was lower than the CMT determined from the CH2 mode, even though both types of groups were located in the same block (PPO).
The two above-used C–H stretching vibrations were found to be the most responsive to the changes in temperature. Other vibrations, e.g. the antisymmetric CH3 stretching in the PPO block and the antisymmetric CH2 stretching in the PEO block, did show variation with temperature, but it was not possible to determine the CMT from the wavenumber vs. temperature curves due to fluctuations in the actual values of the wavenumber. It was most likely due to the fact that these two modes were very sensitive not only to changes in polarity of the polymer environment induced by dehydration but also to the conformation of the macromolecular chains. The effects of these two processes on the frequency of the vibration might have counteracted each other. Therefore, in the analysis of Raman spectra of the CAE85 macromolecules, only the symmetric CH3 stretching vibration and the symmetric CH2 vibration both in the PPO block were used.
The temperature dependent positions of the symmetric CH3 stretching vibration and the symmetric CH2 vibration of the 15 wt% and 30 wt% solutions of CAE85 in water are shown in Fig. 7. These positions were obtained from Raman spectra recorded upon a second heating of the solutions (see Experimental). The CMT values determined from the CH3 and CH2 curves for the 15 wt% concentration were 33 °C and 37 °C respectively, which are 21 °C and 25 °C degrees higher than the CMT determined from the CH3 deformation mode in the ATR FTIR spectra obtained from the heating part of the first temperature cycle (Table 1).
In the case of the 30 wt% aqueous solution of CAE85, it was possible to determine the transition temperature from the position vs. temperature curve for the symmetric CH3 stretching vibration – the transition took place at 20 °C and was relatively sharp compared to the transition observed by ATR FTIR (data not shown). On the other hand, the symmetric CH2 stretching vibration gave a gradual and very broad transition in the position vs. temperature curve – in agreement with the behavior obtained by ATR FTIR spectroscopy (data not shown).
Quantum chemical calculations
To get deeper insight into hydration and hydrogen bonding interactions of the carboxyl end-groups in the modified Pluronic, we carried out model quantum chemical calculations. The hydrogen bonded structures of acetic acid molecules and their hydrates were fully optimized without any geometrical constraint. In our previous paper,3 we presented a model study of deprotonation in hydrated dimers of acetic acid using the quantum chemical methods DFT and MP2. It was found that, for dimers hydrated with three or more water molecules two stable structures existed, either the dimer of two neutral molecules of acetic acid or the deprotonated structure with one of the carboxyl groups dissociated and a released proton stabilized in the forming hydroxonium ion H3O+. The deprotonated structure was stable; nevertheless, compared to the neutral aggregate it was energetically much less favored. For the acetic acid dimer hydrated with four water molecules the stabilization energy of the deprotonated state was −6.01 kcal mol−1 and −7.07 kcal mol−1 according to the B3LYP/6-311++G(2d,2p) and MP2/6-31 + G(d) calculations, respectively.To support the hypothesis that the deprotonation of carboxyl end-groups is enhanced by the formation of hydrogen bonded aggregates stabilized by hydration, in this paper we performed model calculations on higher aggregates of acetic acid. The final structures of the acetic acid trimer hydrated with three water molecules are displayed in Fig. 8. Analogously to the case of acetic acid dimers, two stable structures were found. While the first structure is formed by the hydrogen bonded aggregate of neutral molecules (Fig. 8A), in the second structure (Fig. 8B) the acetic acid positioned in the middle is dissociated and the released proton is transferred to the newly-formed hydroxonium ion H3O+. The geometry of the hydroxonium ion H3O+ is asymmetric, with O–H bond lengths 1.00, 1.01 and 1.11 Å; the longest O–H bond is aimed at the adjacent water molecule. No stable structure with dissociated carboxyl groups was found in the case of acetic acid trimers hydrated with less than three water molecules.
Deprotonated structures of the acetic acid trimer hydrated with higher number of water molecules (4, 5, and 6) are shown in Fig. S3 (ESI†). Stabilization energies of the deprotonated structures in acetic acid dimers and trimers calculated with respect to the initial aggregates of neutral molecules are summarized in Table 2. It is seen that when going from dimers to trimers the energy balance was significantly shifted in favor of the dissociated carboxyl group and the population of the deprotonated states may be comparable to or even higher than the population of the neutral states. The results of calculations therefore clearly demonstrate that deprotonated states are more stable in higher aggregates of carboxyl groups (trimers) and at the same time progressive hydration contributes to increasing stabilization.
| B3LYP/6-311++G(2d,2p) | MP2/6-31+G(d) | |||
|---|---|---|---|---|
| ΔE | ΔG298 | ΔE | ΔG298 | |
| a Stabilization electronic energies and Gibbs free energies were calculated as the differences between the respective values obtained for the protonated and deprotonated structures: ΔE = ΔEprotonated − ΔEdeprotonated, ΔG = ΔGprotonated − ΔGdeprotonated. | ||||
| 2AA·3H2O | −6.96 | −9.23 | −7.53 | −9.73 |
| 2AA·4H2O | −6.01 | −7.59 | −7.07 | −7.44 |
| 3AA·3H2O | 0.41 | −1.89 | −1.40 | −3.15 |
| 3AA·4H2O | 0.04 | −3.33 | −0.11 | −2.33 |
| 3AA·5H2O | 2.34 | 0.49 | 1.26 | −0.04 |
| 3AA·6H2O | 1.92 | 0.18 | −0.24 | 0.86 |
In the quantum chemical calculations of the model aggregates, we studied optimized geometries corresponding to the frozen local energetic minima appearing in the dynamic arrangements of the carboxyl end groups. In the micelle corona with the chain aggregates being continuously restructured, the layer of H3O+ will also be dynamic while remaining dissociated.
In the above calculations, the effective concentration of acetic acid was higher than the experimentally used concentrations of the CAE85 polymer. The high effective concentration used in these calculations was chosen to approximate the local concentration of the carboxylic groups after micellization, i.e. after the acid groups were brought into close proximity due to the hydrophobic interaction.
Dynamical mechanical analysis
Temperature dependences of the storage (G′) and loss (G′′) moduli in the aqueous solution of P85 at a concentration of 30 wt% are shown in Fig. S4 (ESI†). The experimental rheological curve could be divided into two regions. Newtonian behavior was observed for a temperature below 13 °C and, under these conditions, the loss modulus (G′′) exceeded the storage modulus. At 13 °C, the storage modulus (G′) was very small (∼2 × 10−2 Pa) and the phase angle was close to 90°. Thus the system was qualified as a viscoelastic liquid. Micelle formation started at 12 °C, which was indicated by a slight increase in the loss modulus. Upon further increasing the temperature, a simultaneous increase of the loss and storage moduli by several orders of magnitude was observed and at the temperature of 13 °C of the storage modulus crossed the curve of the loss modulus. Usually, the crossover temperature (G′ = G′′ at the chosen frequency of measurement), defines the gel point.32 The crossover temperature and the gel point are not necessarily equal,33 but in the case of narrow temperature transition, a point of equilibrium can still be defined.34In the case of aqueous solutions of CAE85, the observed values of moduli for 15 wt% were reasonably lower than those for 30 wt% and the obtained values were very close to the limit of instrument resolution (Fig. S5 and S6 in the ESI†). When modified Pluronic CAE85 solutions were compared to the same concentrations of P85 solutions, the loss and storage moduli were the same at the lower temperatures. However, in the higher temperature range, the carboxyl acid end modified Pluronic CAE85 did not exhibit gel transition behavior anywhere in the measured temperature interval for either of the two concentrations used (15 wt% and 30 wt%; Fig. S5 and S6 in the ESI†), contrary to P85.
The viscosity (η) of the 30 wt% aqueous solution of P85 decreased slightly when temperature increased (Fig. 9A). The tendency was the same as for pure water; this means that the solution viscosity was dominated by the underlying solvent and no enhancement due to micelles was visible (Fig. 9A). The solution remained Newtonian until formation of the crystalline structure, because micelles interacted only through repulsive forces. The gelation temperature could be defined as the onset of the viscosity increase on the η versus temperature plot, this temperature was somewhat lower than that reported,24 but those authors used a higher heating rate. The η versus temperature behavior depended on the concentration of the polymer and was in agreement with other researchers. Similar to Arztner et al.,24 the gelation followed after the micellization – these were not simultaneous processes. For high enough concentrations, there was a visible change in the slope in viscosity vs. temperature dependence corresponding to the unimer-to-micelle offset temperature above which micellar dynamics began to markedly influence the solution viscosity.35
 | ||
| Fig. 9 Dependence of viscosity on temperature shown for (A) the 30 wt% aqueous solution of P85 (■) and (B) the 15 wt% and 30 wt% solutions of modified CAE85 in water (▲ and □, respectively). | ||
In the case of 15 wt% and 30 wt% solutions of CAE85, the viscosity decreased with increasing temperature (Fig. 9B) – the same behavior as observed for unmodified Pluronic P85. Such a process could be described using the Arrhenius equation with the temperature coefficient of viscosity ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J. The value of the temperature coefficient was slightly higher than the activation energy of viscous flow of the water within the same temperature range.36 A curve fitted to the data agreed with the experimental data only in the limited temperature range – up to 15 °C. At higher temperatures, the slope of the curve changed due to other processes involved in the dynamics. At the temperature of about 60 °C for the concentration of 30 wt% and at 65 °C for 15 wt%, the viscosity started increasing (sharply in the case of 30 wt% solution) – probably indicating a dehydration of PEO chains in the corona.37 After the increase, an equally sharp decrease of viscosity followed – most likely indicating the presence of repulsive forces between the micelles due to the charge formed. These phenomena apparently prevented the gel formation.
000 J. The value of the temperature coefficient was slightly higher than the activation energy of viscous flow of the water within the same temperature range.36 A curve fitted to the data agreed with the experimental data only in the limited temperature range – up to 15 °C. At higher temperatures, the slope of the curve changed due to other processes involved in the dynamics. At the temperature of about 60 °C for the concentration of 30 wt% and at 65 °C for 15 wt%, the viscosity started increasing (sharply in the case of 30 wt% solution) – probably indicating a dehydration of PEO chains in the corona.37 After the increase, an equally sharp decrease of viscosity followed – most likely indicating the presence of repulsive forces between the micelles due to the charge formed. These phenomena apparently prevented the gel formation.
Discussion
As in other polymeric surfactants, the micellization behavior of Pluronic copolymers in aqueous solutions is strongly dependent on the temperature and concentration: the critical micellization concentration decreases with the increase in temperature and the critical micellization temperature decreases with the increase in copolymer concentration.38 The behavior of Pluronic P85 described in this work is in accordance with the general trends observed for this group of copolymers and with the previously published behavior of P85 specifically.21 For example, the CMT value of 29 °C for the concentration of 5 wt% found in this work is in good agreement with the CMC value of 5 wt% at the temperature of 25 °C found by Hammouda.21 Values of CMC at 25 °C similar to Hammouda21 were reported by Mortensen39 (approx. 7 wt%), and by Alexandridis40 (approx. 4 wt%).Using the SAXS technique, it was shown for the 10 wt% solution of CAE85 at 40 °C, spherical particles were present, indicating the formation of micelles. The SAXS data were measured above the CMT to avoid the presence of Gaussian chains. By comparison of the temperature dependent behavior of certain molecular vibration bands in Pluronic P85 obtained by ATR FTIR spectroscopy with the behavior of CAE85, it can be concluded that micellar associates form also at the other concentrations used in this study: in 5 wt%, 15 wt% and 30 wt% solutions of CAE85 above a transition temperature – the critical micellization temperature.
The response to a concentration increase of the critical micellization temperature of the modified P85 (CAE85) follows a path different from that of P85. The CMT does decrease from 26 °C to 17 °C and to 12 °C with the increase of the concentration from 5 wt% through 10 wt% to 15 wt% (Table 1); however, after that the CMT rises to about 37 °C at 30 wt%. With the exception of the solution of 30 wt% concentration, the CMT values of CAE85 solutions at each concentration are lower than those of the P85 solutions at the corresponding concentration. In addition, the width of the transition region (from the start of micellization to its completion) is concentration dependent in P85 solutions: with increasing concentration, the width increases from 1.0 °C to 5.2 °C. In CAE85 solutions, the transition width does not change significantly and it fluctuates around 1.0 °C (Table 1) for concentrations between 5 wt% and 15 wt%. The micellization parameters obtained in this work compare favorably with the report of Lauw et al.:41 the CMT of approx. 20 °C for the concentration of about 2 wt% at ionic strength of 5 × 10−3 M and at pH = 7.
Similar to our previous report,3 deprotonation of the carboxyl ends of CAE85 upon an increase of temperature above the CMT was also observed in this work at all the concentrations studied (Fig. 4 and 5). The process of proton dissociation is not likely to be a result of pH drifts due to the temperature increase or intake of carbon dioxide from the air: at 5 wt%, the pH of the solution varied only between 2.36 and 2.68 (Fig. S7 in the ESI†) when the solution was heated and cooled in the same regime as the solutions investigated by ATR FTIR spectroscopy. This range is similar to that observed in the previous work3 at 15 wt% – the pH was between 2.37 and 2.51. The most probable explanation for the extensive dissociation of carboxyl groups into carboxylate groups is the difference between the proton dissociation constant of the micelle (pKm) and the proton dissociation constant of the unimers in solution (pKa). Our data suggest that pKm < pKa. Using different approaches, Goldsipe and Blankschtein7 and Maeda42 have developed further the concept of the proton dissociation constant of micelles of low-molecular-weight surfactants suggested by Tokiwa and Ohki.43 They have shown that pKm may differ from pKa.7,42 In addition, a model proposed by Lair et al.4 predicts that pKm will be lower than pKa when the pH of the surfactant monomer solution is lower than pKa (and the opposite: pKm > pKa for pH > pKa). The origin of the difference between pKm and pKa may lie in a change of the energy of the system upon micellization: especially the energy change that is associated with the formation of the micelle interfacial region and which results from the electrostatic interactions that are present at the micelle interface between the ionic and non-ionic surfactants and bound counterions.7 Hydrogen bonding interactions have also been proposed to be the cause of the shift in proton dissociation equilibrium when the solution of surfactant monomers undergoes micellization.44 The above-mentioned molecular thermodynamic theory7 and phenomenological thermodynamic models45 have been originally developed for low-molecular-weight surfactants that are sensitive to pH and the models may not be directly applied to the polymeric surfactant such as CAE85. However, it was shown that the proton dissociation processes of CAE85 unimer solutions and CAE85 micelles follow the trends predicted for the low-molecular-weight surfactants. It is thus very likely, that the expressions for free energy contributions associated with micelle formation (or with formation of the micelle interfacial region) can be adapted also to CAE85 polymeric micelles. This work has therefore provided experimental data that may advance our understanding of the polymeric micelle formation.
The deprotonation of CAE85 and the presence of charge in the CAE85 micelles will affect the equilibrium processes and micelle stability.44 In polymeric micelles, the same equilibrium/relaxation processes as in low-molecular-weight surfactants are present: (1) a fast exchange of monomers between the micelle and the monomer solution; (2) a slower process of micelle formation and disintegration that determines the lifetime of the micelle. When the dynamics of polymer micelles is in equilibrium or close to it, the fast single-chain insertion–expulsion mechanism dominates over the micelle fusion–fission, which is 106 times slower.46 On the other hand, it was shown that at the beginning of the micellization (i.e., far from equilibrium), a combination of micelle fusion–fission with unimer/single chain insertion–expulsion was the most effective way of reaching equilibrium.16 The lower CMT values observed for the 5 wt%, 10 wt% and 15 wt% solutions of CAE 85 when compared to Pluronic P85 are most likely caused by longer average lifetime of the coupled unimers and of the submicellar aggregates formed from CAE85 – independent of the mechanism by which they were formed. The longer average lifetime results from additional stabilization of hydrogen bonds between the telechelic carboxyl and carboxylate groups by the hydroxonium ions as seen from the quantum mechanical calculations. The calculations showed that in trimers of acetic acid, the deprotonated states were more stable than hydrogen-bonded states of neutral molecules when the hydration was three or more water molecules per one hydrogen-bonded aggregate (Table 2).
So far, the behavior on heating and during micelle formation was discussed – a reproducible dependence of infrared vibrational bands position on temperature could be obtained at a given concentration. While P85 solutions exhibited reproducible and reversible behavior also upon cooling, the behavior during cooling of the CAE85 solutions was not fully reproducible even at the same average cooling rate (Fig. 3A and C). The slightest variations in the cooling rate and in the addition of cooling medium into the ATR FTIR appliance were reflected in the cooling paths. Either the band position returned to the (fully) hydrated state or there were fluctuations in the hydration (band position) – a return to the dehydrated state with the charged groups present even at 5 °C and after prolonged equilibration at this temperature was detected (data not shown). In the case of full re-hydration, the temperature of micelle disintegration could be determined, but the charged groups either remained present or they underwent re-protonation. When re-hydration occurs without re-protonation, it could suggest that the micelles do not disintegrate fully. Most likely, some structures (analogous to multi-tail low-molecular-weight surfactants) are formed which are stabilized by the still existing hydrogen bonds, which were initially formed at high temperatures and these structures have propylene oxide segments that are accessible to water. The fact, that upon cooling, the CAE85/water systems did not return to their initial state on the timescale of the experiment, caused the differences between the CMT values obtained from wavenumber shifts in the Raman spectra (obtained from a second heating of the solutions, Fig. 7) and from wavenumber shifts in the ATR FTIR spectra (obtained from the first heating, Fig. 3 and 7). In aqueous solutions of P85, the agreement between the CMT values determined by both, Raman and ATR FTIR, spectroscopies was observed.
It was reported earlier, that the 30 wt% solution of P85 undergoes gelation upon a temperature increase.24 However, in the aqueous solution of CAE85 with concentrations of 15 wt% and 30 wt%, it was demonstrated by means of the dynamical mechanical analysis that gelation did not take place. This is most likely caused by repulsive forces between micelles caused by the charge due to the deprotonation of carboxyl groups located at the ends of the PEO blocks and/or caused by the physical size of carboxylate groups and the surrounding layer of hydroxonium cations (a steric repulsion). The mesoscale and nanoscale events such as micellization and the charge formation in polymeric micelles, respectively, affect the macroscale phenomenon of gelation.
Conclusions
Modified tri-block co-polymer Pluronic P85 denoted as CAE85 has carboxyl groups at each end of the macromolecule. Similar to P85, CAE85 undergoes micellization and the critical micellization temperature (CMT) is lower than the CMT of the original Pluronic P85 for concentrations between 5 wt% and 15 wt%. Micellization of CAE85 is accompanied by deprotonation of the carboxyl groups into carboxylate groups. The extensive deprotonation is explained in terms of a decreased proton dissociation constant of micelles in comparison with the proton dissociation constant of the unimer solution. It is also suggested that hydrogen bonds COO−…COOH are formed and that CAE85 micelles are stabilized by the presence of the hydrogen bonded structures, which affect the kinetics of micelle formation and dissociation. Unlike P85, CAE85 does not form gel under any of the conditions used in this study. The experimental data show that the mesoscale event of micellization can alter the nanoscale process of charge formation as well as the macroscale process of gelation.Acknowledgements
The authors gratefully acknowledge the financial support from the Grant Agency of the Czech Republic (grant number P108/12/0703).Notes and references
- P. Alexandridis and T. A. Hatton, Colloids Surf., A, 1995, 96, 1–46 CrossRef CAS.
- J. P. A. Custers, P. Kelemen, L. J. P. van den Broeke, M. A. Cohen Stuart and J. T. F. Keurentjes, J. Am. Chem. Soc., 2005, 127, 1594–1595 CrossRef CAS PubMed.
- A. Šturcová, J. Dybal, A. Braunová and M. Pechar, Vib. Spectrosc., 2011, 57, 300–305 CrossRef PubMed.
- V. Lair, S. Bouguerra, M. Turmine and P. Letellier, Langmuir, 2004, 20, 8490–8495 CrossRef CAS PubMed.
- G. Chang, L. Yu, Z. Yang and J. Ding, Polymer, 2009, 50, 6111–6120 CrossRef CAS PubMed.
- D. P. Cistola, D. M. Small and J. A. Hamilton, J. Lipid Res., 1982, 23, 795–799 CAS.
- A. Goldsipe and D. Blankschtein, Langmuir, 2006, 22, 3547–3559 CrossRef CAS PubMed.
- P. Letellier, A. Mayaffre and M. Turmine, J. Colloid Interface Sci., 2011, 354, 248–255 CrossRef CAS PubMed.
- S. Soontravanich, J. A. Munoz, J. F. Scamehorn, J. H. Harwell and D. A. Sabatini, J. Surfactants Deterg., 2008, 11, 251–261 CrossRef CAS PubMed.
- K. D. Danov, P. A. Kralchevsky and K. P. Ananthapadmanabhan, Adv. Colloid Interface Sci., 2014, 206, 17–45 CrossRef CAS PubMed.
- P. Letellier, A. Mayaffre and M. Turmine, J. Colloid Interface Sci., 2009, 337, 234–239 CrossRef CAS PubMed.
- S. Bruanuer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef.
- R. H. Stokes and R. A. Robinson, J. Am. Chem. Soc., 1948, 70, 1870–1878 CrossRef CAS.
- J. Eastoe, Surfactant Aggregation and Adsorption at Interfaces, in Colloid science: principles, methods and applications, ed. T. Cosgrove, John Wiley & Sons Ltd., UK, 2nd edn, 2010, ch. 4, pp. 61–89 Search PubMed.
- C. Brinatti, L. Bissoli Mello and W. Loh, Langmuir, 2014, 30, 6002–6010 CrossRef CAS PubMed.
- E. E. Dormidontova, Macromolecules, 1999, 32, 7630–7644 CrossRef CAS.
- J. Lu, F. S. Bates and T. P. Lodge, ACS Macro Lett., 2013, 2, 451–455 CrossRef CAS.
- C. Guo, J. Wang, H.-z. Liu and J.-y. Chen, Langmuir, 1999, 15, 2703–2708 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- S. Pedersen and M. C. Gerstenberg, Colloids Surf., A, 2003, 213, 175–187 CrossRef.
- B. Hammouda, Eur. Polym. J., 2010, 46, 2275–2281 CrossRef CAS PubMed.
- J. S. Pedersen and M. C. Gerstenberg, Macromolecules, 1996, 29, 1363–1365 CrossRef CAS.
- O. Glatter, G. Scherf, K. Schillen and W. Brown, Macromolecules, 1994, 27, 6046–6054 CrossRef CAS.
- F. Artzner, S. Geiger, A. Olivier, S. Finet and F. Agnely, Langmuir, 2007, 23, 5085–5092 CrossRef CAS PubMed.
- J. S. Pedersen and M. C. Gerstenberg, Colloids Surf., A, 2003, 213, 175–187 CrossRef CAS.
- P. Debye, J. Phys. Chem., 1947, 51, 18–32 CrossRef CAS.
- C. Perreur, J.-P. Habas, J. Peyrelasse, A. Lapp and J. Francois, Macromol. Symp., 2001, 166, 127–137 CrossRef CAS.
- Y. Su, J. Wang and H. Z. Liu, Langmuir, 2002, 18, 5370–5376 CrossRef CAS.
- P. Schmidt, J. Dybal and A. Šturcová, Vib. Spectrosc., 2009, 50, 218–225 CrossRef CAS PubMed.
- D. Aureau, F. Ozanam, P. Allounge and J.-N. Chazalviel, Langmuir, 2008, 24, 9440–9448 CrossRef CAS PubMed.
- M. Sedlák, Č. Koňák and J. Dybal, Macromolecules, 2009, 42, 7439–7446 CrossRef.
- T. Y. M. Tung and P. J. Dynes, J. Appl. Polym. Sci., 1982, 27, 569–574 CrossRef PubMed.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef CAS.
- S. Hvidt, E. B. Jorgensen, W. Brown and K. Schillen, J. Phys. Chem., 1994, 98, 12320–12328 CrossRef CAS.
- D. Meng and Q. Wang, J. Chem. Phys., 2009, 130, 134904 CrossRef PubMed.
- R. A. Horne, R. A. Courant, D. S. Johnson and F. F. Margosian, J. Phys. Chem., 1965, 69, 3988–3991 CrossRef CAS.
- R. K. Prud'homme, G. Wu and D. K. Schneider, Langmuir, 1996, 12, 4651–4659 CrossRef.
- B. Chu and Z. Zhou, Physical chemistry of Polyoxyalkylene Block Copolymer Surfactants, in Nonionic Surfactants: Polyoxyalkylene Block Copolymer Studies, ed. V. M. Nace, Marcel-Dekker, Inc., NY, 1996, ch. 3, pp. 67–143 Search PubMed.
- K. Mortensen and J. S. Pedersen, Macromolecules, 1993, 26, 805–812 CrossRef CAS.
- P. Alexandridis, J. F. Holzwarth and T. A. Hatton, Macromolecules, 1994, 27, 2414–2425 CrossRef CAS.
- Y. Lauw, F. A. M. Leermakers, M. A. Cohen Stuart, J. P. Pinheiro, J. P. A. Custers, L. J. P. van den Broeke and J. T. F. Keurentjes, Langmuir, 2006, 22, 10931–10941 Search PubMed.
- H. Maeda, J. Colloid Interface Sci., 2003, 263, 277–287 CrossRef CAS.
- F. Tokiwa and K. Ohki, J. Phys. Chem., 1966, 70, 3437–3441 CrossRef CAS.
- H. Maeda, S. Muroi, M. Ishii, R. Kakehashi, H. Kaimoto, T. Nakahara and K. Motomura, J. Colloid Interface Sci., 1995, 175, 497–505 CrossRef CAS.
- H. Maeda, Adv. Colloid Interface Sci., 2010, 156, 70–82 CrossRef CAS PubMed.
- Y. Rharbi, Macromolecules, 2012, 45, 9823–9826 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm01337a |
| This journal is © The Royal Society of Chemistry 2014 |