 Open Access Article
Open Access ArticleOsmotic buckling of spherical capsules
Sebastian
Knoche
and
Jan
Kierfeld
*
TU Dortmund University, Department of Physics, 44221 Dortmund, Germany. E-mail: Jan.Kierfeld@tu-dortmund.de
First published on 18th August 2014
Abstract
We study the buckling of elastic spherical shells under osmotic pressure with the osmolyte concentration of the exterior solution as a control parameter. We compare our results for the bifurcation behavior with results for buckling under mechanical pressure control, that is, with an empty capsule interior. We find striking differences for the buckling states between osmotic and mechanical buckling. Mechanical pressure control always leads to fully collapsed states with opposite sides in contact, whereas uncollapsed states with a single finite dimple are generic for osmotic pressure control. For sufficiently large interior osmolyte concentrations, osmotic pressure control is qualitatively similar to buckling under volume control with the volume prescribed by the osmolyte concentrations inside and outside the shell. We present a quantitative theory which also captures the influence of shell elasticity on the relationship between osmotic pressure and volume. These findings are relevant for the control of buckled shapes in applications. We show how the osmolyte concentration can be used to control the volume of buckled shells. An accurate analytical formula is derived for the relationship between the osmotic pressure, the elastic moduli and the volume of buckled capsules. This also allows use of elastic capsules as osmotic pressure sensors or deduction of elastic properties and the internal osmolyte concentration from shape changes in response to osmotic pressure changes. We apply our findings to published experimental data on polyelectrolyte capsules.
1 Introduction
Elastic capsules consist of an elastic spherical shell enclosing a fluid phase. They are commonly found in nature, prominent examples exhibiting elastic properties similar to elastic shells are red blood cells,1 virus capsules,2 and pollen grains.3 Artificial capsules can be fabricated by various methods,4–6 for example by interfacial polymerization of liquid droplets7 or by multilayer deposition of polyelectrolytes,8 and have numerous applications as delivery systems. Capsules are easily deformed by mechanical forces and their deformation behavior exhibits buckling instabilities upon decreasing the interior pressure or the enclosed volume.5,9–15 These deformation modes can potentially be used to infer material properties of the enclosing shell material6,16–18 or to control the shapes of capsules for applications.14Theoretically, the buckling instability of a spherical shell can be described within classical shell theory,19–24 which identifies a critical pressure where the spherical shape becomes unstable with respect to decreasing volume and develops a finite dimple. Beyond the critical mechanical pressure buckled shapes with a small dimple remain unstable with respect to further spontaneous growth of the dimple20,22 until opposite sides get into contact, and the shells snap-through into a fully collapsed state.16
Despite this theoretical prediction of a spontaneous snap-through into a collapsed state for buckling under mechanical pressure, buckled shapes with a finite dimple, i.e., without contact of opposite capsule sides, are usually observed in microcapsule experiments performed under osmotic pressure control.5,9,14,15 Buckling by osmotic pressure is intimately related to buckling by controlled volume reduction because an applied external osmotic pressure defines an osmotically preferred volume. The capsule volume can also be considered as fixed when it is filled with an incompressible fluid that cannot leave the capsule, or leaves the capsule on a very slow time scale like in dissolving or drying mechanisms.10–13,25,26 In such volume controlled experiments, buckled shapes with finite dimples are also stable configurations. This raises the questions to what extent buckling under osmotic pressure control with the osmolyte concentration of the exterior solution as a control parameter differs from buckling under mechanical pressure control, where we assume an “empty” capsule interior, and to what extent it differs from buckling under volume control with the volume prescribed by the conditions of equal interior and exterior osmolyte concentrations. A precise theoretical answer to these questions is highly relevant for the control and analysis of buckled shapes in applications. Eventually, the shape of osmotically buckled capsules can also be used to sense the osmotic pressure and to deduce elastic material parameters based on quantitative theoretical modeling.
2 Model for axisymmetric shells
We analyze axisymmetric shapes by the use of non-linear shell theory27,28 from which we can derive axisymmetric shape equations.16 Solutions of these equations can represent stable, metastable, or even unstable capsules shapes. Shape transitions or bifurcations between different axisymmetric solution branches can be investigated using general results from bifurcation theory.29 If a spherical shell develops a dimple, we naively expect relevant shapes to be axisymmetric. However, non-axisymmetric shapes are relevant both at the onset of the buckling instability21,22 and for heavily deflated thin shells that undergo a secondary buckling transition.13,30–33 Here, we aim for a classification of the transition from the spherical to the axisymmetric buckled shape under osmotic pressure, under mechanical pressure, and under volume control. Our analysis will reveal important differences in the resulting buckling pathway between these three types of control.2.1 The elastic energy functional
We start with an elastic shell that is spherical in its relaxed state, with a radius R0. This shape can be parametrized in polar cylindrical coordinates (r0, z0) by | (1) |
Nonlinear shell theory can be used to calculate the parametrization r(s0) of the deformed shape from which the strains and stresses in the shell can be deduced. Appropriate shape equations have been introduced in ref. 16, to which the reader is referred for the full mathematical treatment.
For the stability discussion that will be presented in the next sections, the essential feature of the shape equations is that they can be derived from an energy functional by the calculus of variations. The elastic energy that is stored in the deformed shell depends on the meridional and circumferential stretches λs and λφ and the bending strains Ks = λsκs − 1/R0 and Kφ = λφκφ − 1/R0 which measure the change of curvature in the meridional and circumferential direction, with κs and κφ being the principal curvatures of the deformed midsurface.16,28 They can be calculated from the parametrizations r0(s0) and r(s0) of the reference shape and deformed shape, respectively.
The surface energy density wS measures the elastic energy per undeformed area,16,28
 | (2) |
The elastic energy functional can now be written as the integral of the energy density over the undeformed shape with surface element dA0 = 2πr0ds0.
 | (3) |
2.2 Mechanical pressure control and volume control
In order to describe the deflation of the shell, additional terms must be incorporated in the energy functional that account for the external loads. When there is a prescribed mechanical pressure difference p between the inside and the outside, the appropriate load potential is −pV[r] where the volume is a functional of the shape.16,28 Then the shape equations follow from minimizing the enthalpy functional H[r] = U[r] − pV[r] for given p, which means that the first variation must vanish.
is a functional of the shape.16,28 Then the shape equations follow from minimizing the enthalpy functional H[r] = U[r] − pV[r] for given p, which means that the first variation must vanish.| δH = δU − pδV = 0, | (4) |
This minimization can be interpreted in two ways: either as an unconstrained minimization of the enthalpy functional H or, alternatively, as a minimization of the functional U under the constraint that the functional V[r] equals some given volume. The pressure p is then merely a Lagrange multiplier to control the shell volume. These two cases, termed (mechanical) pressure control and volume control, respectively, produce the same shapes as solutions of the shape equations. However, the shapes show very different stability properties in the two cases: while buckling under volume control will start with relatively small (but finite) dimples and the size of the dimple is precisely controlled by the prescribed volume; buckling under mechanical pressure control will lead to a complete collapse of the shell, so that opposite sides are in contact with each other.16 A detailed discussion follows below. Both cases are idealized and hard to achieve in actual experiments: as long as capsules are filled with some internal medium, there is feedback between the volume change and the internal pressure, so that the pressure difference p is not fixed but varies with the capsule volume, which is in conflict with our notion of pressure control. Also in a typical volume control experiment, e.g., when an enclosed incompressible liquid evaporates, volume control is only an approximation whose quality depends on how large the time scale for evaporation is in comparison to the time scale for elastic shape relaxation.
2.3 Osmotic pressure control
Many deformation experiments with microcapsules are based on osmosis.5,9,14,15 In osmotic buckling, the solvent diffuses through the semi-permeable capsule membrane because of an osmolyte concentration gradient between the inside and outside. Osmosis tends to decrease the concentration gradient and deflation of the capsule stops when the concentrations in the inside and outside are sufficiently matched. This is an important difference to mechanical pressure control with an “empty” interior, where the deflation only stops when the opposite sides of the capsule are in contact and the capsule volume is virtually zero.Ideal dilute solutions of osmotically active particles can be treated like ideal gases.34 The appropriate energy functional that is to be minimized in the case of osmosis must take into account the osmotic free energy of the inner and outer solutions,35
 | (5) |
In this expression, kB is the Boltzmann constant, T the temperature of the solutions, and 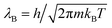 is the thermal de Broglie wavelength with Planck constant h and particle mass m. Nin and Nex are the number of osmotically active particles inside and outside the shell, respectively, V is the volume inside the shell and Vex − V is the outside volume. The osmotically active particles cannot diffuse through the shell wall, such that Nin is fixed during the deflation; the experimental control parameter for osmotic pressure control is the number Nex of osmotically active molecules in the outside solution via their concentration Nex/(Vex − V) ≈ Nex/Vex (assuming V ≪ Vex). Furthermore, the temperature T is considered to affect only the ideal solutions; we do not incorporate thermal fluctuations in the elastic shell, which is a good approximation unless shells are extremely thin.36
is the thermal de Broglie wavelength with Planck constant h and particle mass m. Nin and Nex are the number of osmotically active particles inside and outside the shell, respectively, V is the volume inside the shell and Vex − V is the outside volume. The osmotically active particles cannot diffuse through the shell wall, such that Nin is fixed during the deflation; the experimental control parameter for osmotic pressure control is the number Nex of osmotically active molecules in the outside solution via their concentration Nex/(Vex − V) ≈ Nex/Vex (assuming V ≪ Vex). Furthermore, the temperature T is considered to affect only the ideal solutions; we do not incorporate thermal fluctuations in the elastic shell, which is a good approximation unless shells are extremely thin.36
For V ≪ Vex, the second logarithm in Fos can be expanded and simplifies to
 | (6) |
| pos = −∂Fos/∂V = kBT(Nin/V − Nex/Vex) ≡ pin − pex. | (7) |
The first term represents the internal osmotic pressure pin and the second term represents the external osmotic pressure pex, which also occurs in eqn (6) as the prefactor of the term linear in V. The external pressure pex is proportional to the external concentration of osmotically active particles, and thus it is the experimentally controlled pressure component. The osmotic free energy Fos in eqn (6) is minimized by volume V = NinVex/Nex indicating that the preferred state of the system has equal concentrations of osmotically active particles inside and outside the capsule.
The total energy functional accounts for the elastic energy of the deformed shell and the free energies of the solutions, and reads
G[r] = U[r] − kBTNin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V[r] + pexV[r]. V[r] + pexV[r]. | (8) |
Also for the experimental situation of a shell containing an ideal gas, the same energy functional (8) is obtained. The internal gas has a free energy Fgas = −kBTNin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V, where Nin is the number of gas atoms. According to the ideal gas equation pV = NkBT, the prefactor can also be written as kBTNin = pinV with an internal gas pressure pin. For isothermal processes, the left-hand side of the equation is constant during the deflation, and we may choose the initial state as the reference, where the shell volume is V0 and the internal pressure equals some ambient pressure pa, and so we have Fgas = −paV0
V, where Nin is the number of gas atoms. According to the ideal gas equation pV = NkBT, the prefactor can also be written as kBTNin = pinV with an internal gas pressure pin. For isothermal processes, the left-hand side of the equation is constant during the deflation, and we may choose the initial state as the reference, where the shell volume is V0 and the internal pressure equals some ambient pressure pa, and so we have Fgas = −paV0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V. For the applied external pressure pex, an energy contribution pexV must be included. The total energy functional is thus G = U − paV0
V. For the applied external pressure pex, an energy contribution pexV must be included. The total energy functional is thus G = U − paV0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V + pexV, which is of the same form as in eqn (8). Note that in the undeformed configuration, the force balance requires pex = pa. The buckling of spherical shells with an internal ideal gas has in part been studied numerically in ref. 37.
V + pexV, which is of the same form as in eqn (8). Note that in the undeformed configuration, the force balance requires pex = pa. The buckling of spherical shells with an internal ideal gas has in part been studied numerically in ref. 37.
3 Bifurcation diagrams, stability discussion, and capsule collapse (snap-through)
The shape equations are solved numerically as described in ref. 16 with the mechanical pressure p as the control parameter. For the numerical analysis, it is convenient to choose a length unit R0 and a tension unit E2D. The shape equations then depend only on the dimensionless pressure pR0/E2D, the Poisson ratio ν and the dimensionless bending stiffness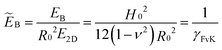 | (9) |
Solutions for given elastic moduli and over a wide range of pressures p have been computed. From this dataset, bifurcation diagrams can be obtained from which the stability in the three load cases – mechanical pressure control, volume control and osmotic pressure control – can be derived. They contain different solution branches,16 and we concentrate here on the two most relevant ones: one with uniformly contracted spherical shapes and one with buckled shapes with a single dimple. A third solution branch are top-down symmetric shapes with two dimples; they have been shown to be less favorable for mechanical pressure control and volume control,16 and it will be shown in Section 4 that this is also true for osmotic pressure control.
The buckled branch with a single dimple develops from the spherical branch by flattening a region around one pole of the shell, then creating a dimple by inverting the region around the pole that subsequently grows until it finally leads to self-intersecting shapes. We suppress unphysical self-intersecting shapes by replacing them by shapes with opposite sides in contact, for which a simplified model has been developed in ref. 16. However, not all of the calculated shapes are stable. We split the buckled solution branch with a single dimple into parts A, B, C and C′, see Fig. 1, according to their stability under pressure and volume control as obtained from bifurcation theory. Branches A, B, and C represent buckled shapes without opposite sides in contact, branch C′ is the continuation of branch C after opposite sides make contact.
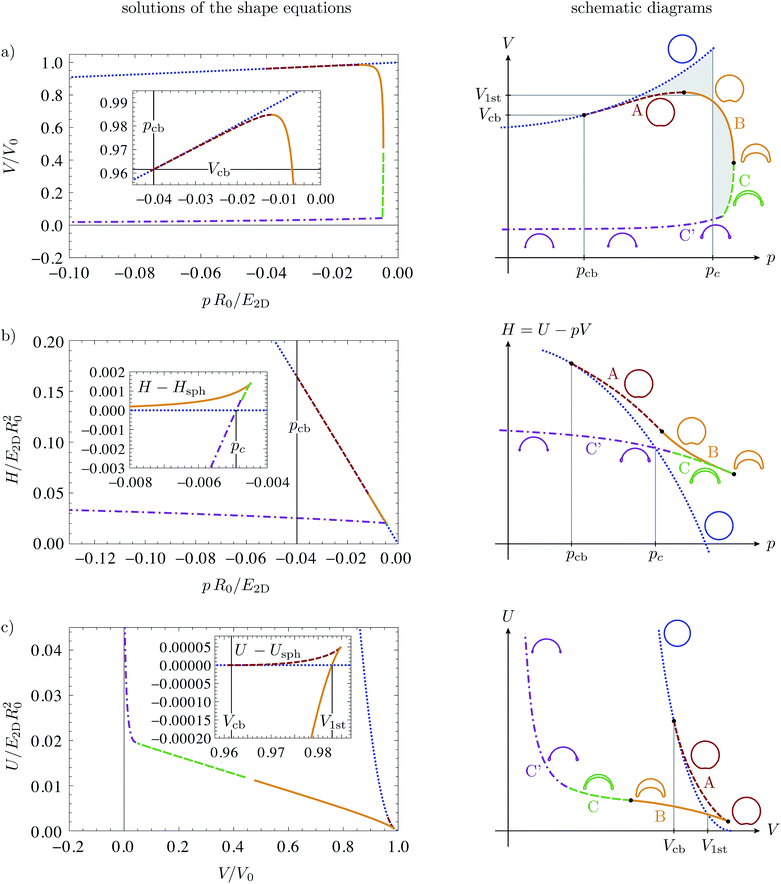 | ||
| Fig. 1 Bifurcation diagrams for buckling by mechanical pressure and volume control: (a) volume–pressure relationship, (b) enthalpy as a function of pressure, (c) elastic energy as a function of volume. The dotted blue line represents the spherical solution branch; the other colored lines represent buckled solution branches A, B, C and C′ according to the labels and pictograms on the right. The insets in the energy diagrams in (b and c) show the differences between buckled and spherical branches. In all plots, the elastic moduli are ẼB = 10−4 and ν = 1/3, and the same qualitative behavior has been obtained for all bending stiffness under consideration, from ẼB = 10−6 to 10−2, see also ref. 16. On the right, schematic diagrams clarify the qualitative course of the solution branches. | ||
3.1 Theorems from bifurcation theory
We exploit very general mathematical theorems about the stability of the solution branches in bifurcation diagrams due to Maddocks29 in order to characterize the stability of the different parts of the buckled solution branches. A solution of the shape equations is only stable when it represents a local minimum of the energy functional (and not a maximum or saddle point). The theorems from bifurcation theory allow us to infer stability from the slope of the volume–pressure relations and can be applied both to mechanical and osmotic pressure.For the reader's convenience we will briefly summarize the relevant results of ref. 29 concerning the stability of solution branches in a bifurcation diagram. The solution branches shall originate from the variational problem of minimizing a functional ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [r, λ] with respect to the function r, while λ is a bifurcation parameter. For our buckling problems,
[r, λ] with respect to the function r, while λ is a bifurcation parameter. For our buckling problems, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) represents the total energy functional, i.e., the above functional H for mechanical pressure control and G for osmotic pressure control, respectively, and the bifurcation parameter λ is the mechanical pressure p or the external osmotic pressure pex, respectively. The function r contains the parametrization of the capsule shape. Specifically, we consider the case that the bifurcation parameter enters the functional linearly in the form
represents the total energy functional, i.e., the above functional H for mechanical pressure control and G for osmotic pressure control, respectively, and the bifurcation parameter λ is the mechanical pressure p or the external osmotic pressure pex, respectively. The function r contains the parametrization of the capsule shape. Specifically, we consider the case that the bifurcation parameter enters the functional linearly in the form ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [r, λ] =
[r, λ] = ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) [r] − λV[r], which applies both to mechanical and osmotic pressure, where
[r] − λV[r], which applies both to mechanical and osmotic pressure, where ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) is the corresponding energy of the shape r and V its volume, cf.eqn (4) and (8).
is the corresponding energy of the shape r and V its volume, cf.eqn (4) and (8).
The solution branches r(λ) of this minimization problem are best visualized in the distinguished bifurcation diagram in which the functional −∂λ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , evaluated at a solution r(λ), is plotted against the bifurcation parameter λ, see Fig. 2. Points of vertical tangency are called folds, in our example this is the point between branches B and C.
, evaluated at a solution r(λ), is plotted against the bifurcation parameter λ, see Fig. 2. Points of vertical tangency are called folds, in our example this is the point between branches B and C.
A solution branch is called stable when it represents minima of the functional ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) . Mathematically, this is related to the second variation of
. Mathematically, this is related to the second variation of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) : if it is positive definite in a solution r, i.e., has only positive eigenvalues, r is a minimum and, thus, a stable solution of the minimization problem. We quote two results from ref. 29 concerning the stability of solution branches: (i) the slope of a stable solution branch in the distinguished bifurcation diagram is non-negative, and (ii) the upper branch of a simple fold opening to the left has one more negative eigenvalue than the lower branch. In the example of Fig. 2, branches A and C are candidates for stable branches according to (i). However, (ii) states that the upper branch (consisting of A and B) of the fold has one more negative eigenvalue than C. If C is stable, i.e., has no negative eigenvalues, then A and B are unstable and have precisely one negative eigenvalue.
: if it is positive definite in a solution r, i.e., has only positive eigenvalues, r is a minimum and, thus, a stable solution of the minimization problem. We quote two results from ref. 29 concerning the stability of solution branches: (i) the slope of a stable solution branch in the distinguished bifurcation diagram is non-negative, and (ii) the upper branch of a simple fold opening to the left has one more negative eigenvalue than the lower branch. In the example of Fig. 2, branches A and C are candidates for stable branches according to (i). However, (ii) states that the upper branch (consisting of A and B) of the fold has one more negative eigenvalue than C. If C is stable, i.e., has no negative eigenvalues, then A and B are unstable and have precisely one negative eigenvalue.
Maddocks also discusses the variational problem to minimize the functional ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) [r] under the constraint that V[r] = const. He calls branches that are stable in this constrained problem c-stable. Stability in the constrained problem is a weaker condition than stability in the unconstrained problem, because only variations that leave V constant can give rise to instabilities. Mathematically speaking, the second variation must be non-negative on the tangent space to the constraint surface V(r) = const.29 Maddocks shows that (iii) all stable branches are also c-stable, and (iv) the branches that are c-stable but not stable are those with precisely one negative eigenvalue and negative slope in the distinguished bifurcation diagram. In our example of Fig. 2, where we assume that A and B have one negative eigenvalue, this means that branch B is c-stable.
[r] under the constraint that V[r] = const. He calls branches that are stable in this constrained problem c-stable. Stability in the constrained problem is a weaker condition than stability in the unconstrained problem, because only variations that leave V constant can give rise to instabilities. Mathematically speaking, the second variation must be non-negative on the tangent space to the constraint surface V(r) = const.29 Maddocks shows that (iii) all stable branches are also c-stable, and (iv) the branches that are c-stable but not stable are those with precisely one negative eigenvalue and negative slope in the distinguished bifurcation diagram. In our example of Fig. 2, where we assume that A and B have one negative eigenvalue, this means that branch B is c-stable.
The criteria (i–iv) can now be applied to study stability under mechanical pressure control or osmotic pressure control and to study c-stability under volume control.
3.2 Mechanical pressure control
Let us start with the case of mechanical pressure control, which requires unconstrained minimization of the enthalpy H = U − pV. This case has already been discussed in ref. 16, we include it here for completeness. The bifurcation parameter is p, and the distinguished bifurcation diagram is the V(p) diagram of Fig. 1(a). Branches A, B, and C/C′ of the V(p) diagram have the same structure as our example in Fig. 2. The H(p) diagram in Fig. 1(b) reveals that the branches C and C′ are stable: C′ seems to be the global enthalpy minimum over a large pressure range, and if C′ is stable, C must also be stable because the stability only changes at folds. Thus, branch C/C′ has only positive eigenvalues in the second variation, and A and B have precisely one negative eigenvalue, and are therefore unstable under pressure control.The bifurcation behavior under mechanical pressure control can thus be summarized as follows. When spherical shells are loaded with a negative internal pressure they remain spherical for small loads because the spherical branch is the global enthalpy minimum. At a critical pressure pc, the branch C′ (consisting of buckled shapes with self-contact) crosses the spherical branch in the H(p) diagram. Beyond this pressure, branch C′ is the global energy minimum. Although it is energetically preferable for the shell to change from the spherical into a fully buckled shape at pc, this will not happen spontaneously because both branches are metastable energy minima, and an energy barrier must be overcome. Spontaneous buckling is possible only at the classical buckling pressure19
 | (10) |
3.3 Volume control
Stability under volume control corresponds to c-stability of shapes. Since we have seen that branches A and B have precisely one negative eigenvalue of the second variation and B has a negative slope ∂pV < 0, we can conclude that branch B is stable under volume control, but A is not. C and C′ are, of course, also stable under volume control. This is in accordance with the U(V) diagram, from which we see that branch B is the global energy minimum when the volume is lowered beyond a critical volume V1st. As in the case of pressure control, buckling at this point involves overcoming an energy barrier which can be read off from the inset in Fig. 1(c). This barrier vanishes at the classical buckling volume32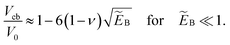 | (11) |
This behavior is analogous to the case of pressure control but, for volume control, the first stable shapes after buckling are those of branch B, with a medium large dimple, and not the completely collapsed ones of branch C′ as for pressure control.
Branch B, which contains the buckled shapes with small to medium sized dimples that are frequently observed in microcapsule experiments,5,10,11,13,14 has thus a very interesting property: it changes from stable to unstable when the mechanical pressure is controlled instead of the volume. We will see that for osmotic pressure control parts of branch B will become stabilized again.
Legendre transformations provide a link between the three bifurcation diagrams in Fig. 1. The function H(p) stems from the functional H[r, p] = U[r] − pV[r] by inserting the numerical solutions r(p) of the shape equations for a given pressure p, i.e.,
| H(p) = U[r(p)] − pV[r(p)]. | (12) |
Taking the derivative with respect to p, we must consider that the shape changes by δr when the pressure is changed by dp. We thus obtain
 | (13) |
| U(V) = H(p(V)) + p(V)V, | (14) |
The Maxwell construction from thermodynamics16,34 can therefore be applied to the V(p) diagram, in order to construct the critical pressure pc and volume V1st of the buckling transition. They are defined as the points in the energy diagrams H(p) and U(V), respectively, where the buckled solution branch crosses the spherical one. In the V(p) diagram, the critical pressure pc thus fulfills the condition of equal shaded areas in Fig. 1(a). The critical volume V1st can be constructed analogously, with equal enclosed areas between the horizontal line V1st and the spherical and buckled branches.
3.4 Osmotic pressure control
Let us now turn to the stability analysis for osmotically induced buckling, or buckling under pressure control with an internal gas. Now, the bifurcation parameter is the external part of the osmotic pressure pex = kBTNex/Vex, because this quantity can be controlled in experiments by changing the concentration of osmotically active particles outside the shell. In order to study stability under osmotic pressure control we can use the available solutions of the shape equations for mechanical pressure control, which have already been used to draw the bifurcation diagram Fig. 1. For each solution of the shape equations for a given mechanical pressure p and with a volume V, a corresponding external osmotic pressure can be obtained as pex = pin − p if a value for kBTNin is chosen.Fig. 3 shows the resulting bifurcation diagrams: on the left, the energy diagram G(pex) and, on the right, the reduced volume V(pex)/V0. The latter one is related to Maddock's distinguished bifurcation diagram, since −∂pexG = −V, and his stability discussion can be applied to the V(pex) diagram when the minus sign is kept in mind. From both bifurcation diagrams it is evident that, compared to pressure control without internal gas, some of the buckled shapes of branch B are stabilized. To illustrate this, we use the same color code for the shapes as in Fig. 1, i.e., a shape corresponding to an orange point in Fig. 1 also gives an orange point in Fig. 3. Fig. 3 immediately shows that the buckled shape at the critical external pressure is for osmotic pressure control on a shape on branch B, with a medium large dimple, rather than a collapsed state with opposite sides in contact.
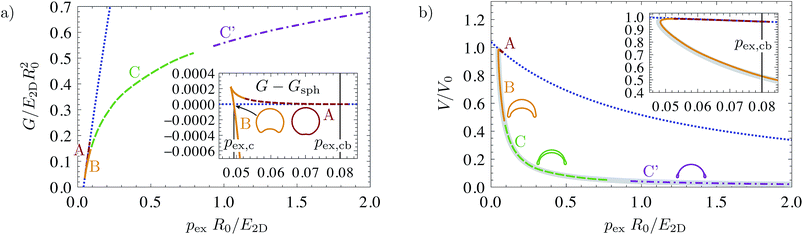 | ||
| Fig. 3 Bifurcation diagrams for osmotically induced buckling or buckling under pressure control with an internal gas. (a) Energy G as a function of the external osmotic pressure. (b) Volume–pressure relationship. The diagrams were created from the same dataset used for Fig. 1 (with ẼB = 10−4, ν = 1/3 and kBTNin = −pcbV0), and the color code of the different branches is also the same. In comparison with Fig. 1(a) and (b) it should be noted that p and pex have different signs, and that a part of the orange branch B is stable now. The thick gray line in the background of diagram (b) represents the analytical result (23) derived below. | ||
As for mechanical pressure control, there are also two critical external osmotic pressures, pex,c corresponding to the point where the buckled and spherical branches cross in the energy diagram, and pex,cb corresponding to the classical buckling threshold, where the spherical shape becomes unstable and the buckled branch separates from the spherical one. Again, the threshold pex,c where buckling becomes energetically favorable (but is only accessible by overcoming an energy barrier, see the inset in Fig. 3) is much smaller than the classical threshold pex,cb where the spherical branch loses its stability. The latter value can be calculated as
| pex,cb = kBTNin/Vcb − pcb = pin(Vcb) − pcb | (15) |
How much of branch B becomes stabilized under osmotic pressure control and whether branch B (as in the example shown in Fig. 3) or branch C or the snap-through branch C′ cross the spherical branch in the G(pex) diagram depends on the number of osmotically active particles Nin or the initial internal osmotic pressure: in the limit Nin → 0, where there are no osmotically active particles (or gas particles) enclosed in the shell, the behavior for mechanical pressure control is recovered in which the whole branch B is unstable and the first buckled shape after the instability is a collapsed snap-through state on branch C′. For an increasing number Nin, we first find buckling into shapes C and, then, a stabilization of and buckling into branch B. Further increasing Nin then further extends the stabilized part of branch B. The bifurcation behavior under osmotic pressure control becomes qualitatively similar to buckling under volume control if Nin is sufficiently large such that the spherical branch exchanges stability with branch B as in the example shown in Fig. 3.
4 Enthalpy landscape for buckled shapes: osmotic pressure control and stabilization of non-collapsed shapes
The stabilizing effect of an internal medium on the non-collapsed shapes can be shown more explicitly by considering the energy landscape during the buckling process. The “reaction coordinate” that describes the progress of buckling is ΔV = V0 − V. An analytical estimate of the elastic energy in a shell with one dimple has been given by Pogorelov,38 | (16) |
 | ||
| Fig. 4 (a) Enthalpy landscape for the buckling transition under mechanical pressure control (blue line) and osmotic pressure control (red line). After the enthalpy barrier has been overcome, mechanically pressurized shells can lower their enthalpy on and on by reducing the volume, but osmotically pressurized shells will end up in the enthalpy minimum at finite ΔV. (b) Effect of a second dimple in the shape (dashed line): the enthalpy function is raised, with the effect that the minimum of the function, where the stationary shape resides, is also lifted to higher enthalpy. (c) Numerical demonstration (for the same parameters as in Fig. 3) that the branch with two dimples is energetically less favorable than the branch with one dimple. We plot the enthalpy difference to the spherical branch in order to better resolve the differences in the branches. | ||
The global minimum of H(ΔV) becomes a boundary minimum at ΔV = V0 for pressure values |p| > |pc|. The criterion H(0) = H(V0) thus provides an estimate for the critical pressure pc
 | (17) |
We checked with our numerical results the accuracy of this estimate over a large range of bending stiffness, from ẼB = 2 × 10−6 to 10−3, and found that also the numerical prefactor is in reasonable agreement with the numerical results, despite the simplicity of the enthalpy landscape.
Pogorelov's model also becomes inaccurate for very small dimples.30,31 For the energy landscape, this has the effect that the energy barrier is always present. The height of the energy barrier is Hbarrier ∼ E2D4ẼB3/|p|3R0(1 − ν2). The barrier is even present for pressures p exceeding the critical buckling threshold pcb, where buckling should become spontaneous and a barrier should be absent. Therefore, one can simply assume that small barriers Hbarrier ∼ E2D4ẼB3/|pcb|3R0(1 − ν2) ∼ E2DẼB3/2R02/(1 − ν2) can be overcome spontaneously. For an isotropic shell material, with E2D = EH0 and ẼB = EH03/(12(1 − ν2), this barrier height corresponds to an indentation of the order of the shell thickness H0 at the barrier. This argument is similar to a corresponding argument in ref. 20, where it is assumed that the buckling threshold pcb can be identified with the necessary pressure for an indentation of the order of the shell thickness H0 to grow spontaneously. Apart from this problem for pressures p close to the buckling threshold pcb, the energy landscape is qualitatively correct for |p| < |pcb|.
When we consider the appropriate energy functional for osmotic pressure or pressure control with an internal gas, a term ∝ − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V must be added to the energy functional. It penalizes small volumes and, therefore, prevents the shell volume from approaching ΔV → V0. The total energy (or free enthalpy) reads
V must be added to the energy functional. It penalizes small volumes and, therefore, prevents the shell volume from approaching ΔV → V0. The total energy (or free enthalpy) reads
G(ΔV) = UPog(ΔV) − pexΔV − kBTNin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(V0 − ΔV) ln(V0 − ΔV) | (18) |
It remains to justify why we concentrated our investigations on buckled shapes with a single dimple only, and disregarded all other solution branches that can be obtained from the shape equations.16 Numerical solutions of the shape equations in ref. 16 have shown that all other solution branches are less favorable for volume control and mechanical pressure control. Here we present an analytical argument, which confirms these findings and also covers osmotic pressure control. The most promising candidates that could become energetically favorable for osmotic buckling are shapes with multiple dimples. We can consider symmetric shapes with two dimples within the Pogorelov model and within the axisymmetric shape equations to show that their free enthalpy is larger than for one dimple. The volume reduction ΔV of the shell is divided between the two dimples which have ΔV/2 each. According to the Pogorelov model, the elastic energy of a double buckled shell is thus UPog 2 (ΔV) = 2UPog(ΔV/2) = 21/4UPog(ΔV), where the last equation holds because UPog ∼ ΔV3/4. Thus, for given volume difference it is energetically unfavorable to create multiple dimples.16,32
Now we have to clarify how this translates to the free enthalpy G(pex) for osmotic pressure control where a change of variables from ΔV to pex is necessary. The branch with a single dimple has a free enthalpy
 | (19) |
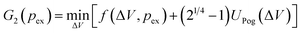 | (20) |
The additional term (21/4 − 1)UPog(ΔV) is positive for all ΔV. The volume-dependent enthalpy function whose minimum we are searching is thus shifted to higher values, see Fig. 4(b). As a consequence, the stationary shape that resides in the minimum is shifted to a higher enthalpy when there are two dimples on the shell instead of one; and also the transition states at the enthalpy maximum lie at higher enthalpy. This result is confirmed by the enthalpy diagram Fig. 4(c) that was generated from the shape equations.
5 Applications: shape control, shape analysis and osmotic pressure sensing
In osmotic buckling, both the external part pex = kBTNex/Vex of the osmotic pressure, which is given by the external concentration of osmotically active particles and the internal particle number Nin, which is enclosed in the capsule during synthesis, are relevant experimental control parameters. The external pressure pex allows to control the final buckled shape experimentally, and the internal particle number Nin allows to control the final buckled shape and the buckling threshold pex,cb itself. Both of these controls provide interesting applications, which can be analyzed using the energy landscape (18).We can determine the energy minimum analytically and quantify the concentration of osmotically active particles, which is needed inside and outside the shell in order to stabilize buckled shapes of a desired volume reduction. Particularly interesting is the buckled shape that is obtained at the buckling threshold (15), pex = pex,cb, where the shell can buckle spontaneously. The condition for an extremum of the free enthalpy is
 | (21) |
This equation can be solved for the internal osmolyte concentration Nin/V0 and simplifies considerably if only the leading order in ẼB is retained. The value of kBTNin also determines the external pressure pex,cb needed to induce buckling, see eqn (15). For both values, the simplified results are
 | (22) |
Both results can be directly translated into concentrations of osmotically active particles inside and outside the shell. The classical buckling pressure  occurs as the relevant scale in eqn (22). In order to obtain buckled shapes with ΔV = V0/2, for example, one should adjust the internal osmolyte concentration to Nin/V0 = −pcb/kBT and the external osmolyte concentration to Nex/Vex = −2pcb/kBT. These are exactly the values used in Fig. 3, and the inset in the V(pex) diagram confirms that the buckling at the classical threshold indeed results in a shape close to V = V0/2.
occurs as the relevant scale in eqn (22). In order to obtain buckled shapes with ΔV = V0/2, for example, one should adjust the internal osmolyte concentration to Nin/V0 = −pcb/kBT and the external osmolyte concentration to Nex/Vex = −2pcb/kBT. These are exactly the values used in Fig. 3, and the inset in the V(pex) diagram confirms that the buckling at the classical threshold indeed results in a shape close to V = V0/2.
Because the external osmotic pressure determines the volume of the buckled capsule, we can also use the shape or volume of osmotically buckled capsules as an indicator for the applied osmotic pressure. Solving the equation G′(ΔV) = 0, for pex we find the relationship between capsule volume and external osmotic pressure as
 | (23) |
The relationship (23) matches the numerical results with a striking accuracy as can be seen in the bifurcation diagram Fig. 3 (gray line). Because the free enthalpy landscape is based on the approximate Pogorelov model, which is inaccurate for large dimples, we would expect our analytical estimate also to become inaccurate for large ΔV. Surprisingly, this is not the case. For large ΔV, the position of the free enthalpy minimum is primarily determined by the competition of the osmotic terms −pexΔV and −kBTNin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(V0 − ΔV) in eqn (18); the elastic energy UPog plays a subordinate role. Indeed, the purely osmotic approximation pex = kBTNin/(V0 − ΔV), where the elastic contribution is completely neglected, is in good agreement with the numerical pressure–volume-relationship for ΔV ≳ 0.5. Neglecting the elastic contribution in eqn (23) is justified for small ẼB (and not too small ΔV) because kBTNin =
ln(V0 − ΔV) in eqn (18); the elastic energy UPog plays a subordinate role. Indeed, the purely osmotic approximation pex = kBTNin/(V0 − ΔV), where the elastic contribution is completely neglected, is in good agreement with the numerical pressure–volume-relationship for ΔV ≳ 0.5. Neglecting the elastic contribution in eqn (23) is justified for small ẼB (and not too small ΔV) because kBTNin = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (pcb) ∼ ẼB1/2 and the elastic term is ∼ẼB3/4.
(pcb) ∼ ẼB1/2 and the elastic term is ∼ẼB3/4.
Eqn (23) provides the basis for measurements of the external osmotic pressure by using elastic capsules as pressure sensors. The capsules must be “calibrated” in the sense that their elastic properties, size and internal osmolyte concentration are known. When they are embedded in a bath with a larger, unknown osmolyte concentration and buckle consequently, their volume difference can be measured and inserted into eqn (23) to obtain pex or the external osmolyte concentration Nex/Vex = pex/kBT. The volume measurement could be achieved through a microscopy image analysis, in the simplest version by measuring the shell depth d and original radius R0 (see Fig. 5) and using the geometrical relationship for shapes whose dimple is an exact mirror-reflection of a spherical cap31 to obtain ΔV/V0 = (1 − d/2R0)2(2 + d/2R0)/2. While the relationship (23) for pex(ΔV) is very precise, this relationship ΔV(d) acquires some errors, but Fig. 5(a) shows that these errors are only significant for d ≲ R0/2.
 | ||
| Fig. 5 Using a buckled shell as an osmotic pressure sensor: from a measurement of the depth d and original shell radius R0, the external osmotic pressure pex can be determined. (a) The data points are generated from the dataset already used in Fig. 1 and 3, with ẼB = 10−4, ν = 1/3 and kBTNin = −pcbV0, and the solid line represents the analytical approximation based on eqn (23). (b) Analysis of experimental results published in ref. 9. The data points from the experiments are fitted using eqn (23) with the internal osmotic pressure as a fitting parameter. The open points were excluded from the fit because the experimental images looked conspicuous that they may not represent centered cross-sections. | ||
Vice versa, eqn (23) or the resulting relationship for pex as a function of d/R0, see Fig. 5, can be used to determine the capsule's material parameters by fitting experimental data for d/R0 at different external osmotic pressures pex. Specifically, eqn (23) can be used to determine the parameter combination E2DẼB3/4/R0 and the internal osmotic pressure pin,0. In combination with an analysis of the maximal edge curvature of buckled shapes as proposed in ref. 16 and experimentally realized in ref. 17, which allows to determine the reduced bending modulus ẼB, both elastic moduli and the internal osmotic pressure can be obtained from relatively simple shape analyses of osmotically pressurized shells. To this end, accurate measurements of the external osmotic pressure and images of cross-sections along the axis of symmetry of the shells must be provided.
We tested such an analysis using the data published in ref. 9 for polyelectrolyte capsules with radius R0 = 2 × 10−6 m and wall thickness H0 = 2 × 10−8 m. The polyelectrolyte capsules were then deflated osmotically, by adding poly(styrene sulfonate, sodium salt) (PSS) to the exterior solution. The osmotically active particles are the counter-ions surrounding the PSS molecules, and they exert an external osmotic pressure pex on the capsules. In the experiments, the values of pex were measured with a Vapor Pressure Osmometer. In view of the few available data points, which can be obtained from the confocal microscopy capsule images in ref. 9, we use the value for the shear modulus of the shell material G = 500 MPa given in ref. 9, which corresponds to a Young modulus of E = 1500 MPa if ν = 0.5. Using also the measured values for capsule radius and thickness this leads to E2D = 30 N m−1 and ẼB = 1.11 × 10−5. Inside the capsule we also expect a certain concentration of ions, because the capsule was fabricated from polyelectrolytes. This gives rise to a nonzero but unknown internal osmotic pressure pin,0 = kBTNin/V0 (in the undeformed state) which serves as the only fitting parameter in the following in order to explain the observed shapes after osmotic buckling.
The value for G obtained in ref. 9 might be questionable because its determination relied on a measurement of the buckling pressure using the classical buckling pressure |pcb|, see eqn (10). This determination assumes a vanishing internal pressure, i.e., pin ≈ 0 in eqn (15) and, moreover, the classical buckling pressure (15) only represents an upper bound for the buckling pressure. Real imperfect shells buckle already at considerably weaker pressures,21,39 between the classical osmotic buckling pressure pex,cb, where the spherical shape becomes unstable and the much smaller critical osmotic pressure pex,c, where buckling becomes energetically favorable as discussed above. As already pointed out, values for E2D and ẼB could also be obtained from a shape analysis, in principle, if shape images for more external osmotic pressures pex were available.
From five confocal microscopy images, Fig. 2(B) and (C) in ref. 9, we measured the ratio d/R0. An uncertainty arises because we are not sure if the cross-sections imaged by the confocal microscopy cut through the center of the capsules and if they are oriented along the axis of symmetry of the capsules. For each image, the external osmotic pressure is given in ref. 9. The resulting data points are plotted in Fig. 5(b), together with the fit using eqn (23). For the fit parameter we obtained kBTNin = 5.4 × 10−12 J, which corresponds to an internal osmotic pressure (in the undeformed state) of pin,0 = kBTNin/V0 = 1.6 × 105 Pa and to a concentration of Nin/V0 = 65 mol m−3. eqn (23) describes the experimental results with reasonable accuracy.
6 Discussion and conclusion
We have shown that the stability of buckled spherical shells (with respect to axisymmetric deformation modes) depends on the specific system that generates the pressure difference between the inside and outside. If a simple mechanical pressure difference is prescribed, the enclosed volume will not affect the applied mechanical pressure, and the shell will collapse completely after the buckling has set in. This is known as snap-through buckling in the shell theory literature. On the other hand, when the system is constructed so that the shell must have a given volume, the first stable shapes after buckling have a small, but finite dimple.In most experiments, there will be feedback between the deformation and the pressure difference exerted on the shell, for example, for osmotic buckling or if the shell encloses a gas. The feedback by an internal medium will stop the snap-through buckling at a finite volume, thus stabilizing buckled shapes with medium volume. Our findings explain why these are the shapes that are usually observed in experiments, although they are unstable from the simple viewpoint of pressure control.
The stabilizing effect of an internal medium is quite generic as long as the force density exerted on the shell is still a normal pressure that is spatially constant. We checked that the same qualitative results could be obtained by including a compressible fluid in the shell, with an energy contribution F ∝ (V − V0).2 The reason for this generic behavior is that the enthalpy landscape, see Fig. 4, is qualitatively identical, no matter how exactly the energies that penalize large volume differences look like.
Within this paper we specifically discussed buckling under (i) volume control, (ii) mechanical pressure control and (iii) osmotic pressure control. Yet, even more experimental situations are conceivable, which give rise to feedback between volume and pressure difference: (iv) as already mentioned, the shell can be filled with a compressible fluid. (v) The elastic properties of the shell could depend on the concentration of an enclosed substance, e.g., if the substance chemically reacts with the shell material. This will give rise to capsule volume dependent elastic properties. (vi) One frequently used mechanism in volume controlled experiments is to slowly dissolve the interior liquid of the capsule by the external liquid, thus reducing the internal volume.12,13,26 This procedure will involve feedback as soon as the exterior volume is no longer much larger than the internal capsule volume. If reducing the capsule volume increases the internal pressure or stiffens the capsule material, such feedback mechanisms will stabilize non-collapsed buckled shapes. If a reduced capsule volume increases the external pressure or softens the capsule material, complete collapse upon buckling will be the generic behavior.
For osmotic pressure control, the capsule tends to assume a preferred volume which is prescribed by the osmolyte concentrations. Therefore, the observed shape bifurcation behavior for osmotic pressure control becomes typically qualitatively similar to buckling under volume control, see Fig. 1 and 3. In particular, snap-through buckling is suppressed. This requires, however, that the initial osmolyte concentration in the capsule interior is sufficiently large. We presented a quantitative theory which also captures the influence of shell elasticity on the resulting relationship (23) between external osmotic pressure and capsule volume. Buckling under osmotic pressure is indeed intermediate between buckling under volume control and buckling under mechanical pressure: in the limit of a small number Nin of osmotically active molecules in the capsule interior, buckling under mechanical pressure control is recovered; for increasing Nin, the behavior effectively approaches buckling under volume control.
We have shown that these findings can be relevant for the control of buckled shapes in applications by controlling the osmolyte concentration. Conversely, we can use elastic capsules as osmotic pressure sensors, and an accurate analytical formula is derived that allows deduction of the osmotic pressure from the observed volume of buckled capsules using eqn (23). This relationship can also be used to obtain elastic moduli of the capsule and its internal osmotic pressure from shape changes of the capsule if the external osmotic pressure is experimentally controlled. We applied this procedure to published experimental data from Gao et al.9 on polyelectrolyte capsules. Our findings are also relevant for stabilizing buckled shapes of a desired volume in applications by choosing the osmolyte concentrations according to eqn (22) to realize a desired ΔV.
References
- D. E. Discher, D. H. Boal and S. K. Boey, Biophys. J., 1998, 75, 1584–1597 CrossRef CAS.
- J. P. Michel, I. L. Ivanovska, M. M. Gibbons, W. S. Klug, C. M. Knobler, G. J. L. Wuite and C. F. Schmidt, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6184–6189 CrossRef CAS PubMed.
- E. Katifori, S. Alben, E. Cerda, D. R. Nelson and J. Dumais, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7635–7639 CrossRef CAS PubMed.
- W. Meier, Chem. Soc. Rev., 2000, 29, 295 RSC.
- A. Fery, F. Dubreuil and H. Möhwald, New J. Phys., 2004, 6, 18 CrossRef.
- M. P. Neubauer, M. Poehlmann and A. Fery, Adv. Colloid Interface Sci., 2013, 207, 65–80 CrossRef PubMed.
- H. Rehage, M. Husmann and A. Walter, Rheol. Acta, 2002, 41, 292 CrossRef CAS.
- E. Donath, G. Sukhorukov, F. Caruso, S. Davis and H. Möhwald, Angew. Chem., Int. Ed., 1998, 37, 2201 CrossRef.
- C. Gao, E. Donath, S. Moya, V. Dudnik and H. Möhwald, Eur. Phys. J. E, 2001, 5, 21–27 CrossRef CAS.
- M. Okubo, H. Minami and K. Morikawa, Colloid Polym. Sci., 2001, 279, 931–935 CAS.
- M. Okubo, H. Minami and K. Morikawa, Colloid Polym. Sci., 2003, 281, 214–219 CAS.
- C. I. Zoldesi, I. L. Ivanovska, C. Quilliet, G. J. L. Wuite and A. Imhof, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 1–8 CrossRef.
- C. Quilliet, C. Zoldesi, C. Riera, A. van Blaaderen and A. Imhof, Eur. Phys. J. E, 2008, 27, 13–20 CrossRef CAS PubMed.
- S. Sacanna, W. T. M. Irvine, L. Rossi and D. J. Pine, Soft Matter, 2011, 7, 1631 RSC.
- S. S. Datta, S.-H. Kim, J. Paulose, A. Abbaspourrad, D. Nelson and D. Weitz, Phys. Rev. Lett., 2012, 109, 1–5 CrossRef.
- S. Knoche and J. Kierfeld, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 046608 CrossRef.
- J. Jose, M. Kamp, A. van Blaaderen and A. Imhof, Langmuir, 2014, 30, 2385–2393 CrossRef CAS PubMed.
- S. Knoche, D. Vella, E. Aumaitre, P. Degen, H. Rehage, P. Cicuta and J. Kierfeld, Langmuir, 2013, 29, 12463–12471 CrossRef CAS PubMed.
- E. Ventsel and T. Krauthammer, Thin Plates and Shells, CRC Press, 2001 Search PubMed.
- L. Landau and E. Lifshitz, Theory of Elasticity, Pergamon Press, Oxford, 2nd edn, 1970 Search PubMed.
- J. W. Hutchinson, J. Appl. Mech., 1967, 34, 49 CrossRef.
- W. Koiter, Proc., K. Akad. Wet. Amsterdam, 1969, 72, 40 Search PubMed.
- S. P. Timoshenko and S. Woinowsky-Krieger, Theory of Plates and Shells, McGraw-Hill, New York, 2nd edn, 1959 Search PubMed.
- S. P. Timoshenko and J. M. Gere, Theory of Elastic Stability, McGraw-Hill, New York, 2nd edn, 1961 Search PubMed.
- L. Pauchard and Y. Couder, EPL, 2004, 66, 667–673 CrossRef CAS.
- S. S. Datta, H. C. Shum and D. A. Weitz, Langmuir, 2010, 26, 18612–18616 CrossRef CAS PubMed.
- C. Pozrikidis, Modeling and Simulation of Capsules and Biological Cells, Chapman and Hall/CRC, 2003 Search PubMed.
- A. Libai and J. G. Simmonds, The Nonlinear Theory of Elastic Shells, Cambridge University Press, 1998 Search PubMed.
- J. H. Maddocks, Arch. Ration. Mech. Anal., 1987, 99, 301 CrossRef.
- S. Knoche and J. Kierfeld, EPL, 2014, 106, 24004 CrossRef.
- S. Knoche and J. Kierfeld, Eur. Phys. J. E, 2014, 37, 62 CrossRef PubMed.
- C. Quilliet, Eur. Phys. J. E, 2012, 35, 48 CrossRef CAS PubMed.
- G. A. Vliegenthart and G. Gompper, New J. Phys., 2011, 13, 045020 CrossRef.
- H. B. Callen, Thermodynamics, John Wiley & Sons, New York, 1960 Search PubMed.
- R. Lipowsky, M. Brinkmann, R. Dimova, T. Franke, J. Kierfeld and X. Zhang, J. Phys.: Condens. Matter, 2005, 17, S537–S558 CrossRef CAS.
- J. Paulose, G. A. Vliegenthart, G. Gompper and D. R. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19551–19556 CrossRef CAS PubMed.
- N. Pelekasis and A. Lytra, Fluid Dynam. Res., 2014, 46, 041422 CrossRef.
- A. V. Pogorelov, Bendings of Surfaces and Stability of Shells, American Mathematical Society, 1988, p. 77 Search PubMed.
- R. L. Carlson, R. L. Sendelbeck and N. J. Hoff, Exp. Mech., 1967, 281–288 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |

