DOI:
10.1039/C4SM00770K
(Paper)
Soft Matter, 2014,
10, 5894-5904
Effects of thermal fluctuations and fluid compressibility on hydrodynamic synchronization of microrotors at finite oscillatory Reynolds number: a multiparticle collision dynamics simulation study
Received
8th April 2014
, Accepted 23rd June 2014
First published on 24th June 2014
Abstract
We investigate the emergent dynamical behavior of hydrodynamically coupled microrotors by means of multiparticle collision dynamics (MPC) simulations. The two rotors are confined in a plane and move along circles driven by active forces. Comparing simulations to theoretical results based on linearized hydrodynamics, we demonstrate that time-dependent hydrodynamic interactions lead to synchronization of the rotational motion. Thermal noise implies large fluctuations of the phase-angle difference between the rotors, but synchronization prevails and the ensemble-averaged time dependence of the phase-angle difference agrees well with analytical predictions. Moreover, we demonstrate that compressibility effects lead to longer synchronization times. In addition, the relevance of the inertia terms of the Navier–Stokes equation are discussed, specifically the linear unsteady acceleration term characterized by the oscillatory Reynolds number ReT. We illustrate the continuous breakdown of synchronization with the Reynolds number ReT, in analogy to the continuous breakdown of the scallop theorem with decreasing Reynolds number.
1 Introduction
Cell motility is a remarkable accomplishment of evolution, being fundamental for a variety of cellular activities. Microorganisms such as spermatozoa, bacteria, protozoa, or algae use flagella for their propulsion.1–3 Furthermore, flagellar motion plays a major role in eukaryotes,1,2 where they transport fluid in the respiratory system in form of cilia,4 are involved in cellular communications,5 and even determine the morphological left–right asymmetry in the embryo.6
The various types of collective flagella and cilia motions require a synchronization of their beating pattern. The two flagella of Chlamydomonas beat synchronously during straight swimming, while asynchronous beating causes tumbling.7–13 The helical filaments of bacteria, e.g., E. coli, synchronize their rotational motion during bundling.14–18 Multi-ciliated and multi-flagellated objects such as unicellular Paramecia19 or Volovoxes20 exhibit periodic spatio-temporal surface patterns known as metachronal waves (MCW).20–28
The synchronized beating of nearby swimming spermatozoa was first modeled and analyzed in ref. 29, suggesting that hydrodynamic interactions lead to synchronization. Since then, the hydrodynamics of active systems at low Reynolds numbers has become a subject of major interest.3,30 Indeed, recent experimental results on the fluid-mediated interactions between flagella of two Volvox carteri cells unambiguously reveal the importance of hydrodynamic interactions on their synchronized motion.31 However, synchronization is not easily achieved for systems at zero Reynolds number,15,16,30,32–34 where the fluid dynamics is described by Stokes equations. The presence of kinematic reversibility of these equations combined with swimmer symmetries may prevent synchronization.15,16,30,32,34 To overcome this fundamental limitation of Stokes equations and to generate a non-reciprocal dynamics, various alternatives have been suggested. This comprises inclusion of additional degrees of freedom such as system flexibility,7,15–18,20,23,25,33,35,36 a specific coupling,37e.g., via surfaces,38 or nonreversible driving forces.13,36,39,40 In addition, specific system designs combined with hydrodynamic interactions lead to synchronization as has been shown for sheets32,41 and models of Chlamydomonas.13,39 For the latter, synchronization of flagella beating can even be achieved without hydrodynamic interactions.42–44 Alternatively and more general, the linear unsteady Stokes equation can be adopted to describe the fluid properties.34,45 Here, the time reversibility of the underlying dynamical equation is broken.
The described lack of synchronization due to kinematic reversibility is equivalent to Purcell's scallop theorem46 for locomotion at zero Reynolds numbers. The same type of symmetry arguments apply for both effects. Hence, the two examples belong to a more general class of physical phenomena, which are all based on the specificities of the time independent, linear, and zero Reynolds number Stokes equations, which are identical under time reversal. Hence, any insight into a particular phenomenon has implications for a broader range of physical effects. Recently, it has been shown45,47 that even for oscillatory reciprocal forcing of a solid body at arbitrary small Reynolds numbers Re > 0 a net translational motion is obtained. The effect disappears for zero Reynolds number in agreement with the scallop theorem.45–47 The consideration demonstrates, however, that the scallop theorem breaks down in a continuous way and no critical inertia is required for the onset of motion.47 Implications for other phenomena, e.g., synchronization need to be resolved.
For a theoretical understanding of the mechanisms governing synchronization in complex (biological) systems, computer simulations are particularly beneficial, since they capture potential non-linear effects, hydrodynamic interactions, and thermal fluctuations.17,18,48,49 The latter have been recently shown to markedly effect the dynamics of E. coli bacteria.50 Thereby, mesoscale hydrodynamic simulation techniques such as the multiparticle collision dynamics (MPC) method51–54 are particularly valuable. MPC is a particle-based simulation approach, which captures hydrodynamic interactions and thermal fluctuations.51–56 It has successfully been applied to a broad range of soft matter systems such as colloids, polymers, vesicles and blood cells, and, in particular, microswimmers.17,18,28,57–68
In this article, we apply the MPC approach to study the time-dependent, correlated dynamics of two hydrodynamically coupled microrotors. We adopt the rotor model proposed in ref. 23. As we have shown analytically, the rotational dynamics of such coupled rotors is synchronized by time-dependent hydrodynamic interactions.34 MPC simulations are performed to verify the previous results, to elucidate the influence of thermal fluctuations and that of fluid compressibility. Moreover, we discuss the importance of the inertia terms of the Navier–Stokes equation—the linear unsteady acceleration term and the non-linear advection term—by introducing corresponding Reynolds numbers45,47 and demonstrate that the two can be comparable for micrometer-size objects. From a simulation technical point of view, we establish a link between the Landau–Lifshitz Navier–Stokes fluctuating hydrodynamic equations and the MPC approach in terms of stress tensors for angular and non-angular momentum conserving simulations. Specifically, we present the respective dissipation fluctuation relations.
The paper is organized as follows. The fluid and the rotor model are described in Sec. 2. In Sec. 3, relevant basic hydrodynamic equations are discussed. Theoretical results for synchronization and the flow field are presented in Sec. 4, and simulation results are shown in Sec. 5. Finally, Sec. 6 summarizes our findings.
2 Fluid and rotor model
2.1 Multiparticle collision dynamics
The MPC fluid consists of N point particles of mass m with the positions ri and velocities vi (i = 1, …, N), which interact with each other by a stochastic, momentum-conserving process. The particle dynamics proceed in two steps—streaming and collision. In the ballistic streaming step, the particle positions are updated via| | | ri(t + h) = ri(t) + hvi(t), | (1) |
where h is the collision time step. In the collision step the simulation box is partitioned into cubic cells of length a, in which multiparticle collisions are performed. In the SRD version of MPC,51–53 the relative velocity of each particle, with respect to the center-of-mass velocity of the cell, is rotated by a fixed angle α around a randomly oriented axis. Hence, the new velocities are| | | vi(t + h) = vcm(t) + R(α)[vi(t) − vcm(t)], | (2) |
where R(α) is the rotation matrix,69| | 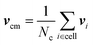 | (3) |
is the center-of-mass velocity, and Nc the total number of particles in the cell. In its original version, MPC violates Galilean invariance. It is restored by a random shift of the collision grid at every step.70
The collision rule (2) violates angular momentum conservation,71 which is associated with a non-symmetric stress tensor.54,72,73 Angular momentum conservation is reestablished on the cell level by a solid-body type rotation of relative velocities after a collision according to71
| | 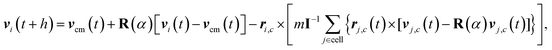 | (4) |
where
I is the moment of inertia tensor of the particles in the center-of-mass reference frame;
ri,c(
t) and
vi,c(
t) are the respective relative positions and velocities after streaming,
i.e.,
ri,c =
ri −
rcm and
vi,c =
vi −
vcm, with the center-of-mass position
rcm.
In order to simulate an isothermal fluid, a collision-cell-based, local Maxwellian thermostat is applied, where the relative velocities of the particles in a cell are scaled according to the Maxwell–Boltzmann scaling (MBS) method.74
2.2 Microrotor
We adopt the rotor model of ref. 23: two beads of radius RH move along circles of radius R, each driven by an active force Fi (cf.Fig. 1). The two circles are centered at Ri0 = (−1)i(d/2)ex (i = 1, 2), where êx is the unit vector along the x-axis and d the center-to-center distance; both beads are confined in the xy-plane. The trajectories of the bead centers can be expressed as| | Ri(t) = Ri0 + (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), R φi(t), R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), 0)T, φi(t), 0)T, | (5) |
in terms of the phase angles φi(t). The driving forces| | Fi(t) = F![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t) i(t) | (6) |
are of equal magnitude and point along the tangents ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t) of the trajectories, where
i(t) of the trajectories, where| | ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t) = (−sin i(t) = (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), cos φi(t), cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), 0)T. φi(t), 0)T. | (7) |
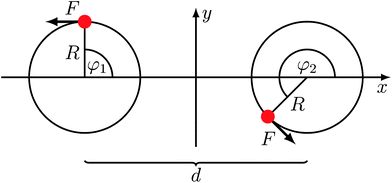 |
| | Fig. 1 Model system of hydrodynamically coupled rotors.23 Two beads move along fixed circular trajectories, each driven by a constant tangential force F. | |
The coupling of the beads with the MPC solvent is established in the collision step.53,75–78 Thereby, the beads are treated as fluid particles with the mass M. Thus, in cells with a bead the center-of-mass velocity is given by
| | 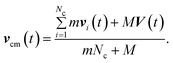 | (8) |
The velocity V(t + h) of the bead after a collision follows according to eqn (2) or (4), respectively, taking into account the appropriate mass M.
Hence, the phase angles evolve as
| | 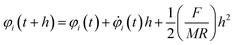 | (9) |
between MPC collisions. In a collision, the angular velocities change. The new values after a collision follow from the relation
| | 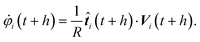 | (10) |
2.3 Parameters
All simulations are performed with the rotation angle α = 130°, the mean number of particles per collision cell 〈Nc〉 = 10, and the collision step 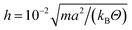 , where Θ is the temperature and kB the Boltzmann constant. This yields the viscosity
, where Θ is the temperature and kB the Boltzmann constant. This yields the viscosity 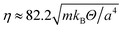 for the non-angular momentum conserving MPC variant (2).79 For a rotor, we choose M = 10m, which yields the bead diffusion coefficient
for the non-angular momentum conserving MPC variant (2).79 For a rotor, we choose M = 10m, which yields the bead diffusion coefficient 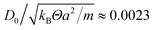 and the hydrodynamics radius RH = kBΘ/(6πηD0) ≈ 0.28a assuming no-slip boundary conditions.80 The radius of a circle is set to R = 2a and the distance to d = 5a in terms of the MPC length scale. In simulations, forces in the range F/(kBΘ/a) = 10–100 are considered, which corresponds to the Péclet numbers Pe = FR/(kBΘ) = 20–200.
and the hydrodynamics radius RH = kBΘ/(6πηD0) ≈ 0.28a assuming no-slip boundary conditions.80 The radius of a circle is set to R = 2a and the distance to d = 5a in terms of the MPC length scale. In simulations, forces in the range F/(kBΘ/a) = 10–100 are considered, which corresponds to the Péclet numbers Pe = FR/(kBΘ) = 20–200.
Periodic boundary conditions are applied for the fluid, with a rectangular square–cuboid box of side lengths Lx = Ly = 100a and Lz = 20a.
All results presented in the following have been obtained with the non-angular momentum conserving collision rule (2). However, simulations confirm that these results are independent of the applied MPC variant and they agree very well with each other.
3 Hydrodynamics
As is well established, the hydrodynamic properties of the MPC fluid are excellently described by the linearized Navier–Stokes equations on sufficiently large length and time scales.51,52,54,72,73 Moreover, the dynamics of the coupled rotors of Sec. 2.2 can be described analytically within the linearized Navier–Stokes equations.34 In order to establish a link between simulation results and analytical considerations, we will briefly describe the basic hydrodynamic background.
3.1 Navier–Stokes equations and MPC fluid
Mass and momentum conservation of an isothermal fluid are expressed by the continuity and the Navier–Stokes equation81–83| | 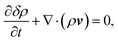 | (11) |
| | 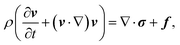 | (12) |
respectively. Here, ρ + δρ(r, t) denotes the mass density with its mean value ρ and its (small) fluctuations δρ(r, t) at the position r in space and the time t. v = v(r, t) is the fluid velocity field, f(r, t) a volume force, and σ(r, t) the stress tensor. Note that only the mean density ρ will appear throughout the rest of the paper.
For the MPC fluid, the explicit form of the stress tensor depends on the lack or presence of angular momentum conservation during collision. In general, the stress tensor can be expressed as
| | 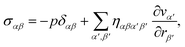 | (13) |
with the pressure
p and the Cartesian indices
α,
β,
α′,
β′ ∈ {
x,
y,
z}.
(i) For angular momentum conserving fluids, the standard symmetric stress tensor is obtained81
| | 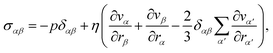 | (14) |
with
| | 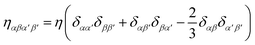 | (15) |
in three dimensions.
η denotes the shear viscosity. Note, we assume that the bulk viscosity is zero.
54,84
(ii) For the non-angular momentum conserving variant of the MPC approach of Sec. 2.1, the non-symmetric tensor is given by73,84,85
| | 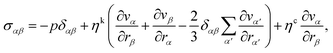 | (16) |
with
| | 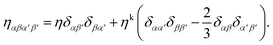 | (17) |
Here,
ηk and
ηc are the kinetic and collisional contribution to the viscosity
η =
ηk +
ηc.
52,53,71–73,79,86,87 Alternative expressions for the stress tensor have been used, which differ from
eqn (16) by a term with vanishing divergence only and thus yield the same Navier–Stokes equation.
54,71,72,84
With the stress tensor (16), eqn (12) turns into
| | 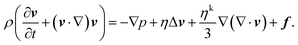 | (18) |
For angular momentum conserving fluids ηk is replaced by η in eqn (18).
3.2 Inertia and Reynolds numbers
In order to asses the relevance of the various terms in eqn (18), in particular the time-dependent and non-linear inertia terms, we scale the velocity field by a typical value V, length by L, and time by T, as usual,88 which yields the equation| | 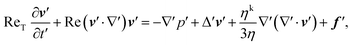 | (19) |
where the primed quantities are dimensionless and of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). Furthermore, we introduced the Reynolds numbers
(1). Furthermore, we introduced the Reynolds numbers| | 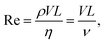 | (20) |
| | 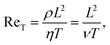 | (21) |
with the kinematic viscosity ν = η/ρ. Typically, T is defined as T = L/V which yields ReT = Re, and for Re ≪ 1 the left hand side of eqn (19) is neglected. In particular, Re = 0 is assumed for microswimmers, which leads to peculiarities in their locomotion as expressed by the well-known scallop theorem.46
The oscillatory Reynolds number ReT can be written as ReT = τν/T, with τν = L2/ν. Hence, ReT is the ratio of the viscose time scale τν for shear wave propagation over the distance L and the characteristic system time T. In order to establish proper hydrodynamic interactions, τν/T < 1 and, hence, ReT < 1.
In ref. 45 and 47, it is assumed that ReT ≪ Re, which may apply for the systems considered there, but may not be valid in general. Alternatively to the proposed breakdown of the scallop theorem due to the nonlinear advection term, the linear unsteady acceleration term implies such a breakdown even at zero Reynolds number Re, because the term breaks time reversibility.
A priori, the relevance of the various Reynolds numbers is not evident. As far as the rotor model of Fig. 1 is concerned, the relevant length scale is the distance between the two beads L = d, the characteristic time is the rotational period, and the relevant velocity is V = ωR ≈ R/T, with the rotational frequency ω. Hence, Re/ReT ≈ R/d ≪ 1, since typically R ≪ d. Thus, ReT is at least as important as Re itself.
For a quantitative estimation of the Reynolds number, we consider the beating of the flagella of Chlamydomonas.39,42 With L ≈ 15 μm, R ≈ 4 μm, and T ≈ 15 ms, we find Re ≈ 10−3 and ReT ≈ 10−2 in water.
The emergent dynamical behavior due to the presence of the unsteady acceleration term has recently been studied experimentally and theoretically for a colloidal particle confined in an optical trap.89 Here, the characteristic time is the trap relaxation time τK = 6πηRH/K, which depends on the trap stiffness K. The studies reveal strong hydrodynamic correlations for ReT = τν/τK ≳ 0.1. More precisely, the studies show the self-interaction of a single colloid mediated by its surrounding fluid. This fundamentally changes the particle's thermal fluctuations, which are mediated by hydrodynamic self-interactions.90 A similar type of coupling can be achieved for two simple colloidal rotors. This might open opportunities to exploit hydrodynamic phenomena for novel sensing applications.
3.3 Fluctuating hydrodynamics
In the following, we focus on the linearized Navier–Stokes equation and neglect the advection term, i.e., we set Re = 0, but keep the unsteady acceleration term. Moreover, to account for thermal fluctuations inherent in the MPC fluid, we introduce a random stress tensor σR(r, t). Then, eqn (18) turns into (Landau–Lifshitz Navier–Stokes equation)54,56| | 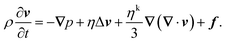 | (22) |
The volume force f now consists of a deterministic force fD and the random force fR = ∇·σR. The stress tensor σR is assumed to be a Gaussian and Markovian stochastic process with the moments54
| | 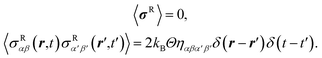 | (23) |
ηαβα′β′ is either given by
eqn (15) or
(17) depending on the applied MPC procedure.
Taking the divergence of eqn (22) and using the linearized continuity eqn (11) together with the ideal gas equation of state with the velocity of sound 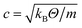 for an isothermal system, we obtain the wave equation
for an isothermal system, we obtain the wave equation
| | 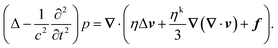 | (24) |
In Fourier space, eqn (22) and (24) read as54,56
| | 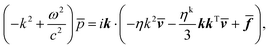 | (25) |
| | 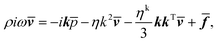 | (26) |
with
k = |
k| and the argument (
k,
ω) of all variables with a bar. In order to solve
eqn (25) and
(26) we define the longitudinal and transverse projection operators
PL(
k) =
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
, with the unit vector
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
and the dyadic product
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
, and
PT(
k) = 1 −
PL(
k) along with
![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) L
L =
PL![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif)
and
![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) T
T =
PT![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif)
. Using these projection operators, we obtain the solution
| | ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) (k,ω) = (k,ω) = ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) T(k,ω) + T(k,ω) + ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) L(k,ω) = L(k,ω) = ![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) (k,ω) (k,ω)![[f with combining macron]](https://www.rsc.org/images/entities/b_i_char_0066_0304.gif) = ( = (![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) T(k,ω) + QL(k,ω)) T(k,ω) + QL(k,ω))![[f with combining macron]](https://www.rsc.org/images/entities/b_i_char_0066_0304.gif) , , | (27) |
where
| | ![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) T(k,ω) = [iρω + ηk2]−1PT = T(k,ω) = [iρω + ηk2]−1PT = ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) T(k,ω)PT, T(k,ω)PT, | (28) |
and
| | 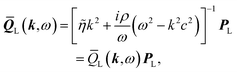 | (29) |
with
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif)
=
η +
ηk/3. The transverse part of the velocity
![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) T
T describes shear waves, whereas the longitudinal part
![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) L
L represents sound waves. Fourier transformation with respect to frequency yields the time-dependent tensors
QT(
k,
t) =
QT(
k,
t)
PT and
QL(
k,
t) =
QL(
k,
t)
PL,
54 where
| | 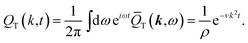 | (30) |
For the longitudinal part, we find
| | 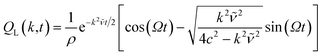 | (31) |
for 4
c2 >
k2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2
2, and
| | 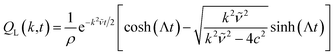 | (32) |
for
k2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2
2 > 4
c2. Here, we defined
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
=
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif)
/
ρ,
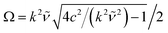
,
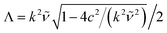
, and assume
t ≥ 0. We obtain the velocity field
v(
r,
t) by Fourier transformation of
eqn (27) and using the convolution theorem
| | 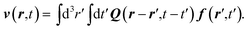 | (33) |
The Green's function
| | 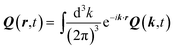 | (34) |
is known as the dynamical Oseen tensor. In general, the matrix elements of
Q(
r,
t) can be expressed as (
r = |
r|)
| | 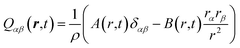 | (35) |
in real space, for both, the transversal and longitudinal part,
i.e.,
A =
AT +
AL and
B =
BT +
BL. For the transverse part, the closed expressions
| | 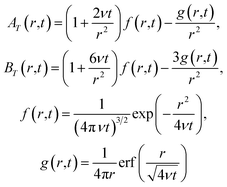 | (36) |
have been derived.
34,91 For the longitudinal part, we obtain the integral representation
AL =
I2 and
BL = 3
I2 − 2
I1, with
| | 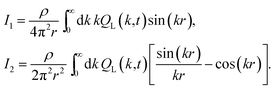 | (37) |
4 Theoretical results
4.1 Rotor equations of motion
We consider the limit of point particles and assume a balance between the driving and the hydrodynamic friction forces acting on the beads, i.e.,| | | Fi(t) − γ(Ṙi − v(ri)) = 0, | (38) |
where γ = 6πηRH is the friction coefficient and v(r, t) is given by eqn (33). The forces Fi and FRi are related with the respective force densities fD and fR according to| | 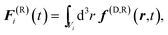 | (39) |
with the volume Vi of particle i. Hence, we obtain the equations of motion| | 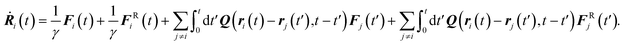 | (40) |
The restriction to a circular trajectory of a bead implies a constraining force. In the following considerations, we neglect this constraining force, as it leads to terms of quadratic order in RH/d. Moreover, for an analytical solution of the equations of motion (40), we apply the mean-field approximation R2(t) − R1(t′) ≈ d = dêx, which is strictly valid for d/R ≫ 1,34 and neglect the random force, i.e., we set FRi ≡ 0.
Using the position vectors (5) and forces (6), eqn (40) yield the coupled integro-differential equations
| | 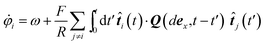 | (41) |
for the phase angles
φi. Here,
ω =
F/(
γR) = 2π/
T is the intrinsic angular frequency with the rotation period
T.
34
The creeping-flow limit studied previously23,30,36,40 follows, when we assume that ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) j(t′) under the integral is changing much more slowly in time than the hydrodynamic tensor Q. Then, integration of the transverse hydrodynamic tensor QT(r, t) yields the asymptotic expression for t → ∞
j(t′) under the integral is changing much more slowly in time than the hydrodynamic tensor Q. Then, integration of the transverse hydrodynamic tensor QT(r, t) yields the asymptotic expression for t → ∞
| | 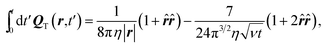 | (42) |
with the unit vector
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
=
r/|
r| and the dyadic product
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
. The first term on the right hand side is the well-known Ossen tensor.
88,92 The long-range hydrodynamic correlations yield a leading time-dependent term, which decays slowly as
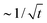
. The sound contribution decays much faster,
54 since it includes an exponentially decaying factor and is thus irrelevant for the asymptotic behavior.
4.2 Synchronization and flow field
To characterize the rotor dynamics, we solve eqn (41) numerically by a combination of Euler's integration scheme and the trapezoidal rule.93 In eqn (41), Q(r, t) = QL(r, t) + QT(r, t) is required in position space. In contrast to the transversal component QT, for which a closed expression is given in eqn (35) and (36), the longitudinal component QL has to be computed numerically for each time step by evaluating the integrals (37).
Fig. 2 shows numerically obtained phase-angle differences Δ(t) = φ1(t) − φ2(t) for various initial differences Δ(0). The phase-angle differences exhibit an exponential decay for long times, except for the initial value Δ(0) = π, which is a metastable state as discussed in ref. 34. Hence, the phase difference vanishes with time and the rotors exhibit an inphase synchronized rotation.
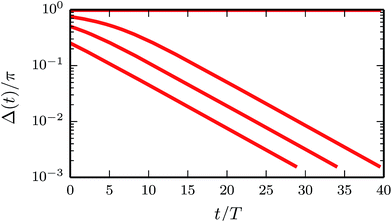 |
| | Fig. 2 Phase-angle differences Δ(t) = φ1(t) − φ2(t) determined by a numerical solution of eqn (41) for the initial conditions Δ(0) = π, 3π/4, π/2, and π/4 (top to bottom) and the Péclet number Pe = 200. Note that Δ(0) = π is an unstable fixed point. Time is scaled by the intrinsic period T = 2πγR/F. Other relevant parameters are provided in Sec. 2.3. | |
As discussed in ref. 34, the equation of motion for the phase difference is well approximated by
| | 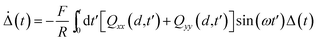 | (43) |
for
t ≫
τν =
d2/
ν. Hence, Δ(
t) decays exponentially in the asymptotic limit
t →
∞ with the characteristic time
| | 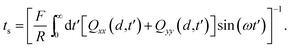 | (44) |
Neglecting compressibility effects by setting Q = QT, we find34
| | 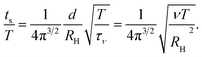 | (45) |
The analytical result (45) agrees very well with numerically determined characteristic decay times for the full numerical solution of eqn (41), with Q = QT, as long as T ≫ τν.34
The synchronized rotation is energetically favorable, as can be visualized by the velocity field. For pointlike particles, it can be computed according to
| | 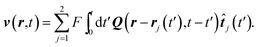 | (46) |
Fig. 3 depicts examples for an asynchronous and synchronous state. The velocity profile decays very fast with separation from a beat. Thereby, it is anisotropic—of Stokeslet shape — with a slower decay in the tangential forward and backward direction. In the synchronous state, the overall flow field is smoother, which minimizes dissipation.
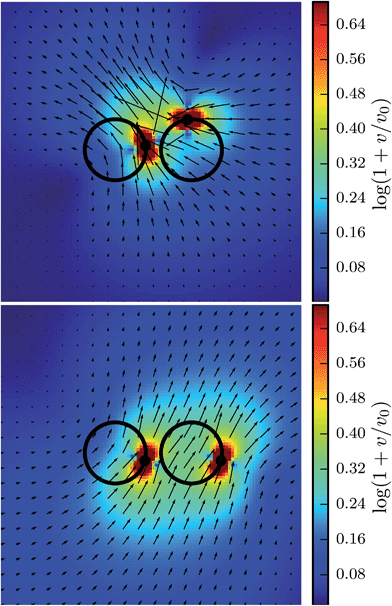 |
| | Fig. 3 Flow fields of hydrodynamically coupled rotors for an asynchronous (top) and a synchronized (bottom) state for the Péclet number Pe = 120. The flow field of a point particle diverges, hence, we introduce the maximum cut-off velocity v0. | |
4.3 Discussion
The linear unsteady acceleration term leads to synchronization of the rotational motion of the rotors (cf. Sec. 3.2 and 4.2). Interestingly, the ratio of the synchronization time and the rotational period ts/T is proportional to the inverse of the square root of the Reynolds number ReT = τν/T. This implies that synchronization appears for any non-zero Reynolds number ReT. However, a vanishing Reynolds number leads to an infinitely long synchronization time. This is in agreement with the fact that there is no synchronization in the Stokes limit.23 Hence, we get a continuous crossover from a synchronizing to a non-synchronizing system. This is similar to the considerations in ref. 45 and 47 for the non-linear inertia term, with the continuous breakdown of the scallop theorem with inertia due to the unsteady acceleration term.
The dependence on the radio d/RH is characteristic for synchronization and has been found for other synchronization mechanisms.25,36,40 Interestingly, in our case ts can solely be expressed by the ratio of the viscous time scale RH2/ν and the period T. Hence, synchronization is determined by shear wave propagation over the size RH of the sphere rather than the distance between the two rotors. However, we have to keep in mind that the approximate expression (45) applies for T ≫ τν only, i.e., shear waves traversed the distance between the beads. In the limit t′ ≫ τν, the integrand of eqn (44) reduces to (4πνt′)−3/2 sin(ωt′), and the integral is determined by the fluid long-time tail only.54 The details of the set-up become irrelevant on time-scales longer than the viscous time-scale τν. This is similar to the polymer center-of-mass velocity auto-correlation function, which is also independent of polymer properties on respective long time scales and is solely determined by the fluid long-time tail.56 On short time scales (t/T ≲ 10 in Fig. 2), however, there is naturally a significant dependence of synchronization on d due to the finite shear-wave propagation time.
For a quantitative estimation of the synchronization time of a biological system, we return to Chlamydomonas. In Sec. 3.2, we estimated the Reynolds number to be ReT ≈ 10−2. Taking as radius of a flagellum RH ≈ 0.1 μm, we find ts/T ≈ 50, i.e., 50 periods would be required to synchronize the beating between the two flagella. Hence, the provided mechanism is definitely too slow to be effective for synchronization of Chlamydomonas flagella. An important factor here is the thin flagellum.
Synthetic systems, such as colloids driven along circular trajectories, may provide more control over the relevant parameters. Consider two colloids dissolved in water with a radius of RH = 2 μm driven along a circle with the rotation period T = 10−2 s. The distance between the rotors and the radius of their trajectories does not really matter. We will assume values adopted in ref. 94, i.e., R ≈ 3 μm and d ≈ 20 μm, which yields ts/T ≈ 2 and τν/T = d2/(νT) ≪ 1. Hence, within about two cycles the colloids synchronize their rotation. As indicated in ref. 90 for colloids confined in optical traps, we expect that the rotor setup can be exploited for novel sensing applications for colloidal particles of various shape or living cells due to hydrodynamic phenomena.
5 Simulations
5.1 Co-rotating beads
MPC simulation results for the time dependence of the phase-angle difference Δ(t) = φ1(t) − φ2(t) of co-rotating beads are displayed in Fig. 4. The three phase-angle differences decay initially, but there is no clear asymptotic value. In contrast, the variations due to thermal fluctuations are rather large. To extract the average behavior, we performed up to 103 independent simulation runs for a parameter set. The average Δ indeed shows synchronization of the bead rotation despite strong thermal fluctuations as displayed in Fig. 5 for various Péclet numbers. As is evident from the figure, the simulation results compare well with the theoretical predictions according to eqn (41) when taking into account compressibility effects, although there are small differences for Pe = 140 and 160.
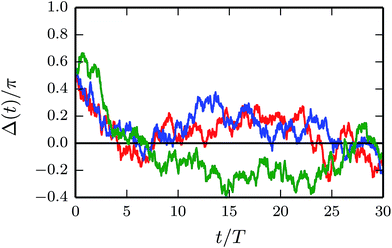 |
| | Fig. 4 Time dependence of phase-angle differences for three realizations with the initial value Δ(0) = π/2 and Pe = 180. | |
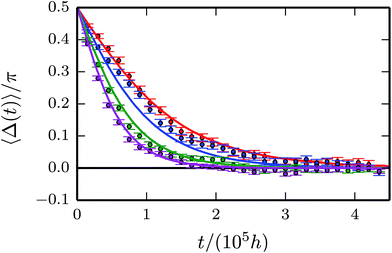 |
| | Fig. 5 Average phase-angle difference Δ(t) for the Péclet numbers Pe = 120, 140, 160, and 180 (top to bottom). Symbols represent simulation results and the solid lines are obtained by numerical integration of eqn (41) including transversal and longitudinal modes of the hydrodynamic tensor. | |
The distribution of phase-angle differences in the synchronized state are shown in Fig. 6 in a polar representation. The simulation data are well described by a wrapped normal distribution, where the mean μ and standard deviation σ of a set of phase differences Δn are calculated according to
| | 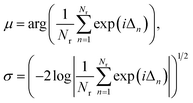 | (47) |
for
Nr realizations.
95
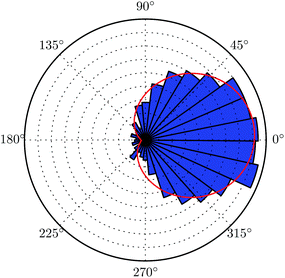 |
| | Fig. 6 Distribution of the phase-angle difference in the synchronized state for Pe = 100. The red line indicates a wrapped normal distribution with parameters estimated according to eqn (47). | |
The time dependence of the standard deviations σ for the systems of Fig. 5 are presented in Fig. 7. We find a significant dependence of σ on the applied force. Thereby, the fluctuations decrease with increasing Pe. For the considered range of Péclet numbers, the ratio of the standard deviations (≈0.4/0.2 = 2) decreases faster with increasing Pe than the ratio of the Pe decreases (120/180 = 2/3). The increase of the fluctuations with decreasing Pe implies very large σ on the order of π.
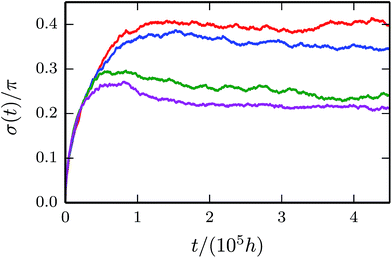 |
| | Fig. 7 Standard deviations (eqn (47)) for the Péclet numbers Pe = 120, 140, 160 and 180 (top to bottom). | |
We like to stress that synchronization reveals a strong dependence on periodic boundary conditions, as illustrated in Fig. 8 and already reported in ref. 25 for a similar, but time-independent rotor model. The synchronization time is evidently significantly shorter for smaller simulation boxes, increases with increasing box size Lx and approaches an asymptotic value. Within the accuracy of the simulations, the curves for Lx = 100a and 150a are similar and are therefore close to the asymptotic limit. The following results are obtained for the box length Lx = Ly = 100a and Lz = 20a.
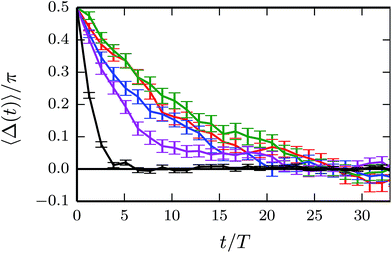 |
| | Fig. 8 Average phase-angle differences for the simulation box sizes Lx/a = 25, 50, 75, 100 and 150 (bottom to top). The box dimension Lz = 20a is fixed and the Pécelt number is Pe = 100. | |
The influence of compressibility on the decay of the phase-angle difference is illustrated in Fig. 9, where simulations are compared with analytical results for incompressible and compressible fluids. Interestingly, for the selected parameters, compressibility slows down synchronization considerably.
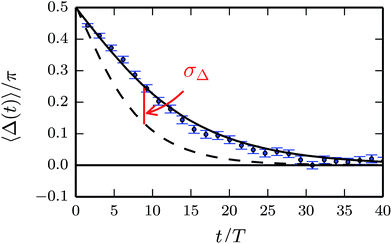 |
| | Fig. 9 Phase-angle difference Δ(t) for Pe = 120. The solid line follows by numerical integration of eqn (41) including transversal and longitudinal modes of the hydrodynamic tensor, whereas the dashed line includes transverse modes only. Symbols are ensemble-averaged simulation results and the vertical line indicates the definition of σΔ. | |
In order to quantify the effects of compressibility, we define the maximum deviation
| | 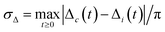 | (48) |
of the phase-angle differences and the difference
| | 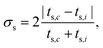 | (49) |
of the synchronization times between a compressible (index
c) and an incompressible (index
i) fluid. Results for these quantities obtained from the theoretical description of Sec. IV are presented in
Fig. 10 for various Péclet numbers. Evidently, there is little qualitative difference between
σΔ and
σs. Compressibility matters most in the range Pe = 40–120. For smaller and larger Pe, the effect of sound diminishes.
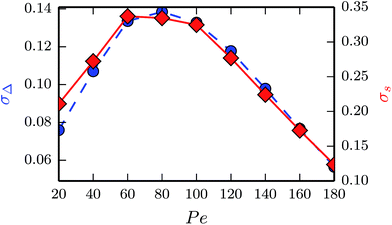 |
| | Fig. 10 Maximum deviations σΔ (eqn (48), bullets) of the phase-angle difference and deviations σs (eqn (49), diamonds) between synchronization times for various Pécelt numbers of compressible and incompressible fluids. | |
The influence of compressibility on synchronization also depends on the separation d. It can be rationalized by comparing the viscous time scale τν = d2/ν with the sound time scale τc = d/c. Since τν increases much faster than τc with d, the relevance of sound for hydrodynamics decreases with increasing d, until eventually τc ≪ τν and compressibility effects can be neglected.
5.2 Counter-rotating beads
The time-dependent hydrodynamic properties of counter-rotating beads can also be studied. Here, the driving forces in eqn (40) are given by| | Fi(t) = (−1)iF![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t). i(t). | (50) |
Similar mean field calculations as for the co-rotating beads can be employed and suggest a slow exponential decay of φ1 + φ2 → 0. Numerical investigations of eqn (40) without random forces and sound modes qualitatively agree with this prediction, although the dynamics of the rotors are not well described quantitatively by the mean-field approach.
Interestingly, in our MPC simulations, the rotors exhibit an anti-synchronized stationary state, i.e., φ1 + φ2 → π, in contrast to the theoretical results. Whether this is due to the multiplicative noise term in eqn (40), or due to sound modes remains unclear, since a mean-field approach is not applicable. In any case, the stationary synchronized state is reached at markedly longer time scales, i.e., the synchronization times increase considerably.
6 Summary and conclusions
We have performed analytical calculations and computer simulations to elucidate the influence of time-dependent hydrodynamic interactions, thermal fluctuations, and fluid compressibility on the synchronization of the rotational motion of microrotors. We find that the presence of the linear unsteady acceleration term in the Navier–Stokes equation leads to synchronization of the rotational motion. Synchronization even prevails in the presence of thermal fluctuations, as shown by our mesoscale simulations exploiting the MPC method. Thereby, the simulation results are well described by our mean-field analytical theory. Fluid compressibility affects the synchronization time over a certain range of Péclet numbers. Thereby, compressibility implies larger synchronization times compared to incompressible fluids. This is related to the instantaneous propagation of hydrodynamics in incompressible fluids.91
Naturally, synchronization by time-dependent hydrodynamic interactions is possible, because the time reversibility of the underlying dynamical equations is broken, despite a time-reversible cyclic rotor motion. Our studies show that the synchronization time exhibits the dependence 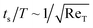 on the oscillatory Reynolds number ReT = τν/T, with τν the viscous time scale and T the period. Hence, ts approaches infinity for ReT → 0, i.e., for systems where the period is far larger than the viscous time. However, the transition is gradual, which implies a continuous breakdown of synchronization in analogy to the continuous breakdown of the scallop theorem with decreasing Reynolds number Re.45,47 Only for ReT = 0, there is no synchronization anymore, again in analogy with the scallop theorem.
on the oscillatory Reynolds number ReT = τν/T, with τν the viscous time scale and T the period. Hence, ts approaches infinity for ReT → 0, i.e., for systems where the period is far larger than the viscous time. However, the transition is gradual, which implies a continuous breakdown of synchronization in analogy to the continuous breakdown of the scallop theorem with decreasing Reynolds number Re.45,47 Only for ReT = 0, there is no synchronization anymore, again in analogy with the scallop theorem.
Our MPC simulations emphasize the importance of time-dependent hydrodynamic interactions as a synchronization mechanism. Aside from physical aspects, this is also important from a simulational point of view. In mesoscale simulations, such as MPC, a clear separation of time scales, e.g., τc ≪ τν ≪ T, is often not possible and Reynolds numbers are rather on the order of 10−1 to 10−2 than zero. Thus, time-dependent hydrodynamic interactions are present and relevant, and results have to be interpreted with care when compared with results of the Stokes equation. In this context, we would like to mention that the present finite Reynolds number has very little effect on synchronization, as is evident by the agreement between simulations and analytical theory.
The simulations reveal a strong dependence of synchronization on the size of the simulation box. Thereby, the finite size effect becomes more pronounced for smaller Péclet numbers and the determination of the asymptotic behavior becomes increasingly demanding. The box-size dependence can be understood as follows. No box-size effect appears when the rotors synchronized their motion before the sound traversed the box length L, which requires the time τLc = L/c, hence, ts/τLc < 1. With eqn (45) and the intrinsic frequency ω ∼ F, we obtain ts/τLc ∼ (R/RH)3/2/(LF3/2). Thus, a reduction of the force has to be compensated by an increase of the box size in order to maintain a small ratio ts/τLc.
Moreover, thermal fluctuations are significantly more pronounced for small Pe, which impedes the extraction of the average synchronization behavior. We emphasize, however, that the rotor motion synchronizes even for small Péclet numbers; only the numerical effort increases.
A critical comparison with typical values of microswimmers, e.g., Chlamydomonas, reveals that time-dependent hydrodynamic interactions are present, but are most likely not the dominant mechanisms for synchronization of their flagella motion. In contrast, systems of micrometer-size objects, e.g., colloids or biological cells, can be tailored such that hydrodynamic interactions are most relevant. This might open opportunities to exploit hydrodynamic phenomena for novel sensing applications with tailored set-ups.
Acknowledgements
Financial support by the VW Foundation (VolkswagenStiftung) within the program Computer Simulation of Molecular and Cellular Bio-Systems as well as Complex Soft Matter is gratefully acknowledged.
References
- R. Stocker and W. M. Durham, Science, 2009, 325, 400–402 CrossRef PubMed.
- M. Polin, I. Tuval, K. Drescher, J. P. Gollub and R. E. Goldstein, Science, 2009, 325, 487–490 CrossRef CAS PubMed.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- B. Afzelius, Science, 1976, 193, 317–319 CAS.
- Q. Wang, J. Pan and W. J. Snell, Cell, 2006, 125, 549 CrossRef CAS PubMed.
- J. H. E. Cartwright, O. Piro and I. Tuval, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 7234–7239 CrossRef CAS PubMed.
- B. Qian, H. Jiang, D. A. Gagnon, K. S. Breuer and T. R. Powers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061919 CrossRef.
- R. E. Goldstein, M. Polin and I. Tuval, Phys. Rev. Lett., 2009, 103, 168103 CrossRef.
- K. Drescher, R. E. Goldstein, N. Michel, M. Polin and I. Tuval, Phys. Rev. Lett., 2010, 105, 168101 CrossRef.
- J. S. Guasto, K. A. Johnson and J. P. Gollub, Phys. Rev. Lett., 2010, 105, 168102 CrossRef.
- R. E. Goldstein, M. Polin and I. Tuval, Phys. Rev. Lett., 2011, 107, 148103 CrossRef.
- E. Lauga and R. E. Goldstein, Phys. Today, 2012, 65, 30 CrossRef PubMed.
- R. R. Bennett and R. Golestanian, Phys. Rev. Lett., 2013, 110, 148102 CrossRef.
- M. J. Kim, J. C. Bird, A. J. Van Parys, K. S. Breuer and T. R. Powers, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 15481 CrossRef CAS PubMed.
- M. Kim and T. R. Powers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 061910 CrossRef.
- M. Reichert and H. Stark, Eur. Phys. J. E, 2005, 17, 493 CrossRef CAS PubMed.
- S. Y. Reigh, R. G. Winkler and G. Gompper, Soft Matter, 2012, 8, 4363 RSC.
- S. Y. Reigh, R. G. Winkler and G. Gompper, PLoS One, 2013, 8, e70868 CAS.
- E. W. Knight-Jones, Q. J. Microsc. Sci., 1954, 95, 503 Search PubMed.
- D. R. Brumley, M. Polin, T. J. Pedley and R. E. Goldstein, Phys. Rev. Lett., 2012, 109, 268102 CrossRef.
-
M. A. Sleigh, The Biology of Cilia and Flagella, Pergamon Press, Oxford, 1962 Search PubMed.
- S. Gueron, K. Levit-Gurevich, N. Liron and J. J. Blum, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6001 CrossRef CAS.
- P. Lenz and A. Ryskin, Phys. Biol., 2006, 3, 285 CrossRef CAS PubMed.
- B. Guirao and J. Joanny, Biophys. J., 2007, 92, 1900–1917 CrossRef CAS PubMed.
- T. Niedermayer, B. Eckhardt and P. Lenz, Chaos, 2008, 18, 037128 CrossRef PubMed.
- N. Osterman and A. Vilfan, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15727–15732 CrossRef CAS PubMed.
- C. Wollin and H. Stark, Eur. Phys. J. E, 2011, 34, 42 CrossRef PubMed.
- J. Elgeti and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4470 CrossRef CAS PubMed.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1951, 209, 447 CrossRef.
- R. Golestanian, J. M. Yeomans and N. Uchida, Soft Matter, 2011, 7, 3074–3082 RSC.
-
D. R. Brumley, K. Y. Wan, M. Polin and R. E. Goldstein, 2014, arXiv:1403.2100.
- G. J. Elfring and E. Lauga, Phys. Rev. Lett., 2009, 103, 088101 CrossRef.
- R. Di Leonardo, A. Búzás, L. Kelemen, G. Vizsnyiczai, L. Oroszi and P. Ormos, Phys. Rev. Lett., 2012, 109, 034104 CrossRef CAS.
- M. Theers and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023012 CrossRef.
- J. Kotar, M. Leoni, B. Bassetti and M. C. Lagomarsino, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7669 CrossRef CAS PubMed.
- N. Uchida and R. Golestanian, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–14 Search PubMed.
- M. Leoni and T. B. Liverpool, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 040901 CrossRef CAS.
- A. Vilfan and F. Jülicher, Phys. Rev. Lett., 2006, 96, 058102 CrossRef.
- R. R. Bennett and R. Golestanian, New. J. Phys., 2013, 15, 075028 CrossRef.
- N. Uchida and R. Golestanian, Phys. Rev. Lett., 2011, 106, 058104 CrossRef.
- G. J. Elfring and E. Lauga, Phys. Fluids, 2011, 23, 011902 CrossRef PubMed.
- B. M. Friedrich and F. Jülicher, Phys. Rev. Lett., 2012, 109, 138102 CrossRef.
- A. A. Polotsky, F. A. Plamper and O. V. Borisov, Macromolecules, 2013, 46, 8702 CrossRef CAS.
- V. F. Geyer, F. Jülicher, J. Howard and B. M. Friedrich, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18058–18063 CrossRef CAS PubMed.
- E. Lauga, Soft Matter, 2011, 7, 3060 RSC.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- E. Lauga, Phys. Fluids, 2007, 19, 061703 CrossRef PubMed.
- P. J. A. Janssen and M. D. Graham, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011910 CrossRef CAS.
- N. Watari and R. G. Larson, Biophys. J., 2010, 98, 12–17 CrossRef CAS PubMed.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 10940, 108 Search PubMed.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605 CrossRef CAS PubMed.
- R. Kapral, Adv. Chem. Phys., 2008, 140, 89 CrossRef CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Adv. Polym. Sci., 2009, 221, 1 CAS.
- C.-C. Huang, G. Gompper and R. G. Winkler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056711 CrossRef.
- K. Mussawisade, M. Ripoll, R. G. Winkler and G. Gompper, J. Chem. Phys., 2005, 123, 144905 CrossRef CAS PubMed.
- C. C. Huang, G. Gompper and R. G. Winkler, J. Chem. Phys., 2013, 138, 144902 CrossRef PubMed.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef.
- L. F. Valadares, Y.-G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Small, 2010, 6, 565–572 CrossRef CAS PubMed.
- M. Yang and M. Ripoll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061401 CrossRef.
- J. Elgeti, U. B. Kaupp and G. Gompper, Biophys. J., 2010, 99, 1018 CrossRef CAS PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef.
- Y.-G. Tao and R. Kapral, Soft Matter, 2010, 756 RSC.
- D. A. P. Reid, H. Hildenbrandt, J. T. Padding and C. K. Hemelrijk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021901 CrossRef.
- S. B. Babu and H. Stark, New J. Phys., 2012, 14, 085012 CrossRef.
- M.-J. Huang, H.-Y. Chen and A. Mikhailov, Eur. Phys. J. E, 2012, 35, 1 CrossRef PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2012, 108, 218104 CrossRef.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef.
- M. Yang and M. Ripoll, Soft Matter, 2014, 10, 1006 RSC.
- E. Westphal, S. P. Singh, C.-C. Huang, G. Gompper and R. G. Winkler, Comput. Phys. Comm., 2014, 185, 495 CrossRef CAS PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 066705 CrossRef CAS.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 016706 CrossRef.
- T. Ihle, E. Tüzel and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 046707 CrossRef CAS.
- C. M. Pooley and J. M. Yeomans, J. Phys. Chem. B, 2005, 109, 6505 CrossRef CAS PubMed.
- C.-C. Huang, R. G. Winkler, G. Sutmann and G. Gompper, Macromolecules, 2010, 43, 10107 CrossRef CAS.
- M. Ripoll, K. Mussawisade, R. G. Winkler and G. Gompper, Europhys. Lett., 2004, 68, 106 CrossRef CAS.
- R. G. Winkler, K. Mussawisade, M. Ripoll and G. Gompper, J. Phys.: Condens. Matter, 2004, 16, S3941–S3954 CrossRef CAS.
- A. Malevanets and J. M. Yeomans, Europhys. Lett., 2000, 52, 231–237 CrossRef CAS.
- C.-C. Huang, A. Chatterji, G. Sutmann, G. Gompper and R. G. Winkler, J. Comput. Phys., 2010, 229, 168 CrossRef CAS PubMed.
- R. G. Winkler and C.-C. Huang, J. Chem. Phys., 2009, 130, 074907 CrossRef PubMed.
- B. Kowalik and R. G. Winkler, J. Chem. Phys., 2013, 138, 104903 CrossRef PubMed.
-
L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon Press, London, 1960 Search PubMed.
-
J. P. Boon and S. Yip, Molecular Hydrodynamics, Dover, New York, 1980 Search PubMed.
-
J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, London, 1986 Search PubMed.
- E. Tüzel, T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 056702 CrossRef.
- T. Ihle, Phys. Chem. Chem. Phys., 2009, 11, 9667 RSC.
- T. Ihle and D. M. Kroll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 020201(R) CrossRef.
- N. Kikuchi, C. M. Pooley, J. F. Ryder and J. M. Yeomans, J. Chem. Phys., 2003, 119, 6388–6395 CrossRef CAS PubMed.
-
J. K. G. Dhont, An Introduction to Dynamics of Colloids, Elsevier, Amsterdam, 1996 Search PubMed.
- T. Franosch, M. Grimm, M. Belushkin, F. M. Mor, G. Foffi, L. Forró and S. Jeney, Nature, 2011, 478, 85 CrossRef CAS PubMed.
- U. F. Keyser, Nature, 2011, 478, 45 CrossRef CAS PubMed.
- P. Español, A. P. Miguel and I. Zúñiga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 803 CrossRef.
-
M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1986 Search PubMed.
- C. Lubich, Numer. Math., 1982, 40, 119–135 CrossRef.
- J. Kotar, L. Debono, N. Bruot, S. Box, D. Phillips, S. Simpson, S. Hanna and P. Cicuta, Phys. Rev. Lett., 2013, 111, 228103 CrossRef.
-
K. V. Mardia and P. E. Jupp, Directional statistics, Wiley, Chichester, 2000 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article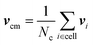
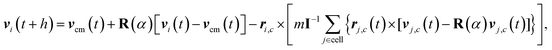
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), R
φi(t), R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), 0)T,
φi(t), 0)T,![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t)
i(t)![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t) of the trajectories, where
i(t) of the trajectories, where![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t) = (−sin
i(t) = (−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), cos
φi(t), cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φi(t), 0)T.
φi(t), 0)T.
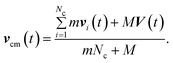
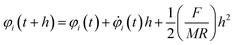
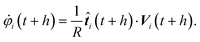
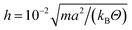 , where Θ is the temperature and kB the Boltzmann constant. This yields the viscosity
, where Θ is the temperature and kB the Boltzmann constant. This yields the viscosity 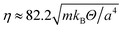 for the non-angular momentum conserving MPC variant (2).79 For a rotor, we choose M = 10m, which yields the bead diffusion coefficient
for the non-angular momentum conserving MPC variant (2).79 For a rotor, we choose M = 10m, which yields the bead diffusion coefficient 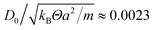 and the hydrodynamics radius RH = kBΘ/(6πηD0) ≈ 0.28a assuming no-slip boundary conditions.80 The radius of a circle is set to R = 2a and the distance to d = 5a in terms of the MPC length scale. In simulations, forces in the range F/(kBΘ/a) = 10–100 are considered, which corresponds to the Péclet numbers Pe = FR/(kBΘ) = 20–200.
and the hydrodynamics radius RH = kBΘ/(6πηD0) ≈ 0.28a assuming no-slip boundary conditions.80 The radius of a circle is set to R = 2a and the distance to d = 5a in terms of the MPC length scale. In simulations, forces in the range F/(kBΘ/a) = 10–100 are considered, which corresponds to the Péclet numbers Pe = FR/(kBΘ) = 20–200.
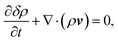
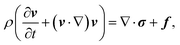
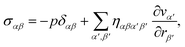
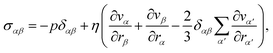
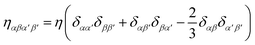
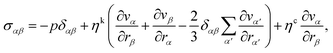
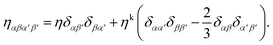
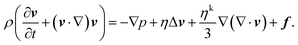
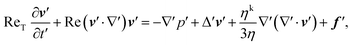
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). Furthermore, we introduced the Reynolds numbers
(1). Furthermore, we introduced the Reynolds numbers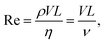
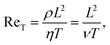
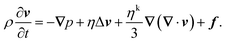
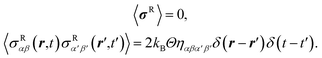
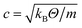 for an isothermal system, we obtain the wave equation
for an isothermal system, we obtain the wave equation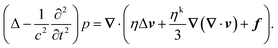
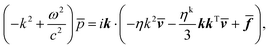
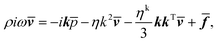
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) , with the unit vector
, with the unit vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) and the dyadic product
and the dyadic product ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif)
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) , and PT(k) = 1 − PL(k) along with
, and PT(k) = 1 − PL(k) along with ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) L = PL
L = PL![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) and
and ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) T = PT
T = PT![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) . Using these projection operators, we obtain the solution
. Using these projection operators, we obtain the solution![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) (k,ω) =
(k,ω) = ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) T(k,ω) +
T(k,ω) + ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) L(k,ω) =
L(k,ω) = ![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) (k,ω)
(k,ω)![[f with combining macron]](https://www.rsc.org/images/entities/b_i_char_0066_0304.gif) = (
= (![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) T(k,ω) + QL(k,ω))
T(k,ω) + QL(k,ω))![[f with combining macron]](https://www.rsc.org/images/entities/b_i_char_0066_0304.gif) ,
,![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) T(k,ω) = [iρω + ηk2]−1PT =
T(k,ω) = [iρω + ηk2]−1PT = ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) T(k,ω)PT,
T(k,ω)PT,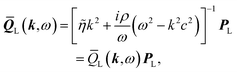
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = η + ηk/3. The transverse part of the velocity
= η + ηk/3. The transverse part of the velocity ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) T describes shear waves, whereas the longitudinal part
T describes shear waves, whereas the longitudinal part ![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) L represents sound waves. Fourier transformation with respect to frequency yields the time-dependent tensors QT(k, t) = QT(k, t)PT and QL(k, t) = QL(k, t)PL,54 where
L represents sound waves. Fourier transformation with respect to frequency yields the time-dependent tensors QT(k, t) = QT(k, t)PT and QL(k, t) = QL(k, t)PL,54 where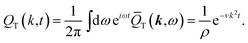
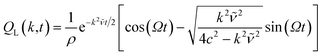
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2, and
2, and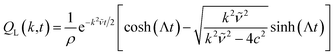
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 > 4c2. Here, we defined
2 > 4c2. Here, we defined ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) =
= ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) /ρ,
/ρ, 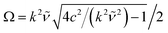 ,
, 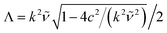 , and assume t ≥ 0. We obtain the velocity field v(r, t) by Fourier transformation of eqn (27) and using the convolution theorem
, and assume t ≥ 0. We obtain the velocity field v(r, t) by Fourier transformation of eqn (27) and using the convolution theorem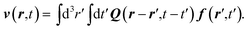
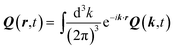
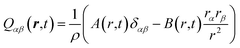
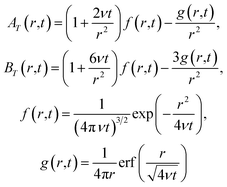
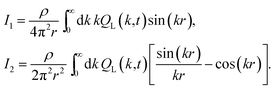
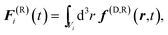
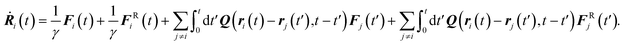
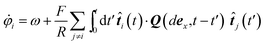
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) j(t′) under the integral is changing much more slowly in time than the hydrodynamic tensor Q. Then, integration of the transverse hydrodynamic tensor QT(r, t) yields the asymptotic expression for t → ∞
j(t′) under the integral is changing much more slowly in time than the hydrodynamic tensor Q. Then, integration of the transverse hydrodynamic tensor QT(r, t) yields the asymptotic expression for t → ∞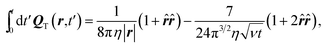
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) = r/|r| and the dyadic product
= r/|r| and the dyadic product ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif)
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) . The first term on the right hand side is the well-known Ossen tensor.88,92 The long-range hydrodynamic correlations yield a leading time-dependent term, which decays slowly as
. The first term on the right hand side is the well-known Ossen tensor.88,92 The long-range hydrodynamic correlations yield a leading time-dependent term, which decays slowly as 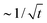 . The sound contribution decays much faster,54 since it includes an exponentially decaying factor and is thus irrelevant for the asymptotic behavior.
. The sound contribution decays much faster,54 since it includes an exponentially decaying factor and is thus irrelevant for the asymptotic behavior.

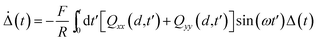
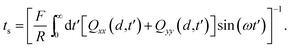
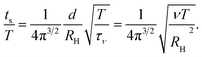
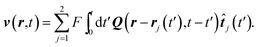


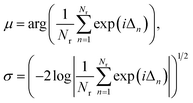




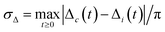
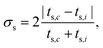

![[t with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0074_0302.gif) i(t).
i(t).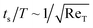 on the oscillatory Reynolds number ReT = τν/T, with τν the viscous time scale and T the period. Hence, ts approaches infinity for ReT → 0, i.e., for systems where the period is far larger than the viscous time. However, the transition is gradual, which implies a continuous breakdown of synchronization in analogy to the continuous breakdown of the scallop theorem with decreasing Reynolds number Re.45,47 Only for ReT = 0, there is no synchronization anymore, again in analogy with the scallop theorem.
on the oscillatory Reynolds number ReT = τν/T, with τν the viscous time scale and T the period. Hence, ts approaches infinity for ReT → 0, i.e., for systems where the period is far larger than the viscous time. However, the transition is gradual, which implies a continuous breakdown of synchronization in analogy to the continuous breakdown of the scallop theorem with decreasing Reynolds number Re.45,47 Only for ReT = 0, there is no synchronization anymore, again in analogy with the scallop theorem.
