 Open Access Article
Open Access ArticleCritical Casimir interactions around the consolute point of a binary solvent
T. F.
Mohry
ab,
S.
Kondrat
cd,
A.
Maciołek
*abe and
S.
Dietrich
ab
aMax-Planck-Institut für Intelligente Systeme, Heisenbergstraße 3, 70569 Stuttgart, Germany. E-mail: mohry@is.mpg.de; maciolek@is.mpg.de; dietrich@is.mpg.de
bIV. Institut für Theoretische Physik, Universität Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany
cDepartment of Chemistry, Imperial College London, SW7 2AZ, UK
dIBG-1: Biotechnology, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: s.kondrat@fz-juelich.de
eInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, PL-01-224 Warsaw, Poland
First published on 8th May 2014
Abstract
Spatial confinement of a near-critical medium changes its fluctuation spectrum and modifies the corresponding order parameter distribution, resulting in effective, so-called critical Casimir forces (CCFs) acting on the confining surfaces. These forces are attractive for like boundary conditions of the order parameter at the opposing surfaces of the confinement. For colloidal particles dissolved in a binary liquid mixture acting as a solvent close to its critical point of demixing, one thus expects the emergence of phase segregation into equilibrium colloidal liquid and gas phases. We analyze how such phenomena occur asymmetrically in the whole thermodynamic neighborhood of the consolute point of the binary solvent. By applying field-theoretical methods within mean-field approximation and the semi-empirical de Gennes–Fisher functional, we study the CCFs acting between planar parallel walls as well as between two spherical colloids and their dependence on temperature and on the composition of the near-critical binary mixture. We find that for compositions slightly poor in the molecules preferentially adsorbed at the surfaces, the CCFs are significantly stronger than at the critical composition, thus leading to pronounced colloidal segregation. The segregation phase diagram of the colloid solution following from the calculated effective pair potential between the colloids agrees surprisingly well with experiments and simulations.
I. Introduction
Finite-size contributions to the free energy of a spatially confined fluid give rise to an excess pressure, viz., an effective force per unit area acting on the confining surfaces. This so-called solvation force depends on the geometry of the confinement, the surface separation, the fluid–fluid interactions, the substrate potentials exhibited by the surfaces, and on the thermodynamic state of the fluid.1 The solvation force acquires a universal, long-ranged contribution upon approaching the bulk critical point of the fluid, as first pointed out by Fisher and de Gennes.2 This is due to critical order parameter fluctuations which led to the notion of ‘critical Casimir forces’, in analogy with the quantum-mechanical Casimir forces which are due to quantum fluctuations of confined electromagnetic fields.3The important role of critical Casimir forces (CCFs) for colloidal suspensions has implicitly been first recognized while studying experimentally aggregation phenomena in binary near-critical solvents.4 Numerous other experimental studies followed aiming to clarify important aspects of the observed phenomenon, such as its reversibility and the location of its occurrence in the temperature – composition phase diagram of the solvent (see, for example, ref. 5–7 and references therein). Measurements were performed mostly in the homogeneous phase of the liquid mixture. They have demonstrated that the temperature–composition (T, c) region within which colloidal aggregation occurs is not symmetric about the critical composition cc of the solvent mixture. Strong aggregation occurs on that side of the critical composition which is rich in the component disfavored by the colloids. More recently, reversible fluid–fluid and fluid–solid phase transitions of colloids dissolved in the homogeneous phase of a binary liquid mixture have been observed.8–10 These experiments also show that the occurrence of such phase transitions is related to the affinity of the colloidal surfaces for one of the two solvent components as described above.
Various mechanisms for attraction between the colloids, which can lead to these phenomena, have been suggested. The role of dispersion interactions, which are effectively modified in the presence of an adsorption layer around the colloidal particles, has been discussed in ref. 11. A “bridging” transition, which occurs when the wetting films surrounding each colloid merge to form a liquid bridge,12 provides a likely mechanism sufficiently off the critical composition of the solvent. However, in the close vicinity of the bulk critical point of the solvent, in line with the prediction by Fisher and de Gennes,2 attraction induced by critical fluctuations should dominate.
In the original argument by Fisher and de Gennes, the scaling analysis for off-critical composition of the solvent has not been carried out. Due to the lack of explicit results for the composition dependence of CCFs, for a long time it has not been possible to quantitatively relate the aggregation curves to CCFs. Rather, it was expected that CCFs play a negligible role for off-critical compositions because away from cc the bulk correlation length, which determines the range of CCFs, shrinks rapidly. However, to a certain extent the properties of an aggregation region can be captured by assuming the attraction mechanism to be entirely due to CCFs. This has been shown in a recent theoretical study which employs an effective one-component description of the colloidal suspensions.13 Such an approach is based on the assumption of additivity of CCFs and requires the knowledge of the critical Casimir pair potential in the whole neighborhood of the critical point of the binary solvent, i.e., as a function of both temperature and solvent composition close to (Tc, cc). In ref. 13, it was assumed that colloids are spherical particles all strongly preferring the same component of the binary mixture such that they impose symmetry breaking (+, +) boundary conditions14 on the order parameter of the solvent. Further, the pair potential between two spherical particles has been expressed in terms of the scaling function of the CCFs between two parallel plates by using the Derjaguin approximation.15 The dependence of the CCFs on the solvent composition translates into the dependence on the bulk ordering field hb conjugate to the order parameter [see eqn (A4) in the first part of ref. 13]. For the parallel-plate (or film) geometry in spatial dimension D = 3, the latter has been approximated by the functional form obtained from Ginzburg–Landau theory in the mean-field approximation (i.e., for D = 4). The scaling functions of the CCFs resulting from these approximations have not yet been reported in the literature. We present them here for a wide range of parameters. In order to assess the quality of the approximations adopted in ref. 13 we calculate the scaling functions of the CCFs by using alternative theoretical approaches and compare the corresponding results.
In this spirit, one can estimate how well the mean-field functional form, which is exact in D = 4 (up to logarithmic corrections), approximates the dependence on hb of CCFs for films in D = 3 by comparing it with the form obtained from the local-functional approach16 in D = 3. We use the semi-empirical free energy functional developed by Fisher and Upton16 in order to extend the original de Gennes–Fisher critical-point ansatz.2 Upon construction, this functional fulfills the necessary analytic properties as function of T and a proper scaling behavior for arbitrary D. The extended de Gennes–Fisher functional provides results for CCFs in films with (+, +) boundary conditions at hb = 0, which are in a good agreement with results from Monte Carlo simulations.17 A similar local-functional approach proposed by Okamoto and Onuki18 uses a renormalized Helmholtz free energy instead of the Helmholtz free energy of the linear parametric model used in ref. 17. Such a version does not seem to produce better results for the Casimir amplitudes.18 This ‘renormalized’ local-functional theory has been recently applied to study the bridging transition between two spherical particles.19 Some results for the CCFs with strongly adsorbing walls and hb ≠ 0 obtained within mean-field theory and within density functional theory in D = 3 have been presented in ref. 20 and 21, respectively. These results are consistent with the present ones.
We also explore the validity of the Derjaguin approximation for the mean-field scaling functions of the CCFs, focusing on their dependence on the bulk ordering field. For that purpose, we have performed bona fide mean-field calculations for spherical particles, the results of which can be viewed as exact for hypercylinders in D = 4 or approximate for two spherical particles in D = 3.
This detailed knowledge of the CCFs as function of T and hb is applied in order to analyze recently published experimental data for the pair potential and the segregation phase diagram10 of poly-n-isopropyl-acrylamide microgel (PNIPAM) colloidal particles immersed in a near-critical 3-methyl-pyridine (3MP)–heavy water mixture.
Our paper is organized such that in Section II we discuss the theoretical background. In Section IIIA, results for CCFs for films are presented. These results as obtained from the field-theoretical approach within mean-field approximation are compared with those stemming from the local functional approach. We discuss how the dependence of the CCFs on the bulk ordering field hb changes with the spatial dimension D. Section IIIB is devoted to the CCF between spherical particles, where we also probe the reliability of the Derjaguin approximation. In Section IV our theoretical results are confronted with the corresponding experimental findings and simulations. We provide a summary in Section V.
II. Theoretical background
For the demixing phase transition of a binary liquid mixture, the order parameter ϕ is proportional to the deviation of the concentration c = ϱA − ϱB from its value cc at the critical point, i.e., ϕ ∼ c − cc; here ϱα, α ∈ {A, B}, are the number densities of the particles of species A and B, respectively. The bulk ordering field hb, conjugate to this order parameter, is proportional to the deviation of the difference Δμ = μA − μB of the chemical potentials μα, α ∈ {A, B}, of the two species from its critical value, i.e., hb ∼ Δμ − Δμc. We note, that the actual scaling fields for real fluids are linear combinations of hb and the reduced temperature t = (Tc − T)/Tc [t = (T − Tc)/Tc] for a lower [upper] critical point.Close to the bulk critical point, the bulk correlation length attains the scaling form
| ξ(t, hb) = ξtI(D)±(|Σ| = ξt/ξh), | (1) |
| ξt = ξ(0)±|t|−ν | (2) |
| ξh = ξ(0)h|hb|−ν/(βδ) | (3) |
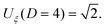 The values of ξ(0)± and ξ(0)h depend on the definition of ξ which we take to be the true bulk correlation length governing the exponential decay of the two-point correlation function of the bulk order parameter.
The values of ξ(0)± and ξ(0)h depend on the definition of ξ which we take to be the true bulk correlation length governing the exponential decay of the two-point correlation function of the bulk order parameter.
A. Film geometry
A generalized, solvent mediated force f(‖) between two parallel planar walls a distance L apart is given by1 | (4) |
 is the bulk free energy density,
is the bulk free energy density,  is the free energy of the film, and
is the free energy of the film, and  where
where  is the macroscopically large surface area of one wall.
is the macroscopically large surface area of one wall.  is the excess pressure over the bulk value of the solvent. Upon approaching the bulk critical point of the confined medium f(‖) acquires the universal long-ranged contribution f(∥)C, known as the critical Casimir force.25–27 Due to its particular spatial variation and dependence on temperature, f(∥)C is a well defined and distinct contribution to f(∥).28
is the excess pressure over the bulk value of the solvent. Upon approaching the bulk critical point of the confined medium f(‖) acquires the universal long-ranged contribution f(∥)C, known as the critical Casimir force.25–27 Due to its particular spatial variation and dependence on temperature, f(∥)C is a well defined and distinct contribution to f(∥).28
Finite-size scaling29 predicts that2
 | (5) |
 is an universal scaling function. Its functional form depends on the bulk universality class and on the surface universality classes of the confining walls. Here we focus on walls with the same adsorption preferences (expressed in terms of surface fields conjugate to the order parameter at the surfaces) in the so-called strong adsorption limit in which ϕ(r) → ∞ for the spatial coordinate r approaching the walls. Note that
is an universal scaling function. Its functional form depends on the bulk universality class and on the surface universality classes of the confining walls. Here we focus on walls with the same adsorption preferences (expressed in terms of surface fields conjugate to the order parameter at the surfaces) in the so-called strong adsorption limit in which ϕ(r) → ∞ for the spatial coordinate r approaching the walls. Note that ![[small variant theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e1ec.gif) (D) depends on the sign of hb because the surface fields at the confining walls break the bulk symmetry hb → −hb. Depending on the particular thermodynamic path under consideration, other representations of the scaling function of the critical Casimir force might be more convenient. For example, the scaling function
(D) depends on the sign of hb because the surface fields at the confining walls break the bulk symmetry hb → −hb. Depending on the particular thermodynamic path under consideration, other representations of the scaling function of the critical Casimir force might be more convenient. For example, the scaling function 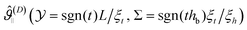 lends itself to describe the dependence of the CCFs on hb at fixed temperature. We will discuss the following representations
lends itself to describe the dependence of the CCFs on hb at fixed temperature. We will discuss the following representations | (6) |
B. Colloidal particles
We consider two spherical colloids, or more generally two hypercylinders, in spatial dimension D. A hypercylinder HD,d = {r = (r⊥, r∥) ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d ×
d × ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) D−d
D−d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ||r⊥| ≤ R} has a finite extension R in d dimensions and is infinitely elongated in the remaining (D − d) dimensions. In particular, spherical colloids in D = 3 are H3,3-particles; our numerical results are approximate for H3,3, but exact in D = 4, i.e. for H4,3. Here, the two hypercylinders are assumed to be geometrically identical and aligned parallel to each other. We denote this geometry by ∘∘. The solvent-mediated force f(∘∘) between two hypercylinders a closest surface-to-surface distance L apart is defined by the right hand side of eqn (4) with
||r⊥| ≤ R} has a finite extension R in d dimensions and is infinitely elongated in the remaining (D − d) dimensions. In particular, spherical colloids in D = 3 are H3,3-particles; our numerical results are approximate for H3,3, but exact in D = 4, i.e. for H4,3. Here, the two hypercylinders are assumed to be geometrically identical and aligned parallel to each other. We denote this geometry by ∘∘. The solvent-mediated force f(∘∘) between two hypercylinders a closest surface-to-surface distance L apart is defined by the right hand side of eqn (4) with  as the free energy of the binary solvent in the macroscopically large volume V with two suspended colloids.
as the free energy of the binary solvent in the macroscopically large volume V with two suspended colloids.
In analogy to the film geometry, f(∘∘) acquires the scaling contribution f(∘∘)C, which is given by
 | (7) |
Within the Derjaguin approximation15 the total force between two spherical objects, H3,3 or H4,3, is taken to be  where
where ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (∥)C is the force per area and
(∥)C is the force per area and  , leading to the scaling function [compare with eqn (5) and (7)] for d = 3 and D ∈ {3, 4}
, leading to the scaling function [compare with eqn (5) and (7)] for d = 3 and D ∈ {3, 4}
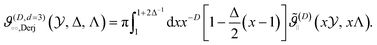 | (8) |
Note, that for (D, d) = (4, 4) in the expression for ϑ(4,4)∘∘,Derj there is an additional factor of 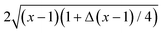 multiplying the integrand in eqn (8). Commonly,20,30–33 in this context [i.e., eqn (8)] Δ is set to zero. Thus, within the Derjaguin approximation, f(∘∘)C ∼ Δ−(d−1)/2 [eqn (7)]. We adopt this approximation except of, cf., Fig. 3(b), where we shall discuss the full dependence on Δ given by eqn (8).
multiplying the integrand in eqn (8). Commonly,20,30–33 in this context [i.e., eqn (8)] Δ is set to zero. Thus, within the Derjaguin approximation, f(∘∘)C ∼ Δ−(d−1)/2 [eqn (7)]. We adopt this approximation except of, cf., Fig. 3(b), where we shall discuss the full dependence on Δ given by eqn (8).
 | ||
Fig. 1 Behavior of the normalized scaling function ϑ(D=4)∥(Y = sgn(t)L/ξ(t, hb), Σ = sgn(thb)ξt/ξh) of the CCF from Landau theory along lines of constant scaling variable |Y| = 4, 5, …, 10 (from the inner to the outermost ring) in the thermodynamic state space of the solvent spanned by ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = (L/ξ(0)+)1/νt and ĥb = (L/ξ(0)h)βδ/νhb. The color along the lines of constant |Y| indicates the absolute value |ϑ(D=4)∥|. The bulk critical point of the solvent ( = (L/ξ(0)+)1/νt and ĥb = (L/ξ(0)h)βδ/νhb. The color along the lines of constant |Y| indicates the absolute value |ϑ(D=4)∥|. The bulk critical point of the solvent (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) , ĥb) = (0, 0) is indicated by •. The region shown here lies above the capillary transition critical point (Y‖,c = −11, Σ‖,c = 1.3),20 where the film coexistence line ends. For (+, +) boundary conditions, the capillary condensation transition occurs for , ĥb) = (0, 0) is indicated by •. The region shown here lies above the capillary transition critical point (Y‖,c = −11, Σ‖,c = 1.3),20 where the film coexistence line ends. For (+, +) boundary conditions, the capillary condensation transition occurs for ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) < 0 and ĥb < 0. The dash-dotted lines indicate the thermodynamic paths Σ = 1 and = 3 and the dashed line the path of constant order parameter < 0 and ĥb < 0. The dash-dotted lines indicate the thermodynamic paths Σ = 1 and = 3 and the dashed line the path of constant order parameter 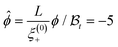 . Within Landau theory ν = 1/2 and ν/(βδ) = 1/3. Δ(D=4)∥ = |ϑ(D=4)∥(Y = 0, Σ)|, which is independent of Σ. . Within Landau theory ν = 1/2 and ν/(βδ) = 1/3. Δ(D=4)∥ = |ϑ(D=4)∥(Y = 0, Σ)|, which is independent of Σ. | ||
 | ||
Fig. 2 Two representations of the scaling function of the critical Casimir force for the film geometry with (+, +) boundary conditions [eqn (6)]: (a)  plotted versus plotted versus and (b) and (b) ![[small variant theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e1f3.gif) (D=3)∥(Λ, Σ) plotted versus Λ = sgn(hb)L/ξh for several values of the scaling variable Σ = sgn(thb)ξt/ξh. The full lines are the results obtained from the local functional approach together with the linear parametric model [eqn (18)], and the dashed lines correspond to the dimensional approximation [eqn (19)]. In (b) the symbols are Monte Carlo data from ref. 43 for Σ = −∞. We note that thermodynamic states corresponding to Σ = −∞ and Σ = ∞ are the same; they form the critical isotherm. (D=3)∥(Λ, Σ) plotted versus Λ = sgn(hb)L/ξh for several values of the scaling variable Σ = sgn(thb)ξt/ξh. The full lines are the results obtained from the local functional approach together with the linear parametric model [eqn (18)], and the dashed lines correspond to the dimensional approximation [eqn (19)]. In (b) the symbols are Monte Carlo data from ref. 43 for Σ = −∞. We note that thermodynamic states corresponding to Σ = −∞ and Σ = ∞ are the same; they form the critical isotherm. | ||
 | ||
Fig. 3 The critical Casimir force between two like colloids in zero bulk field (Λ = 0) as obtained from Landau theory. (a) The normalized scaling function ϑ(D=4,d=3)∘∘versus for five values of Δ = L/R, where L is the surface-to-surface distance between two H4,3-particles of radius R. The curve Δ = 0 corresponds to the Derjaguin approximation. (b) The normalized scaling function ϑ(4,3)∘∘versus Δ for three values of for five values of Δ = L/R, where L is the surface-to-surface distance between two H4,3-particles of radius R. The curve Δ = 0 corresponds to the Derjaguin approximation. (b) The normalized scaling function ϑ(4,3)∘∘versus Δ for three values of 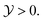 The results of the Derjaguin approximation as given by eqn (8) are shown by dashed lines (Δ → 0, next to leading order) and by crosses (Δ = 0). We recall the relation The results of the Derjaguin approximation as given by eqn (8) are shown by dashed lines (Δ → 0, next to leading order) and by crosses (Δ = 0). We recall the relation  For comparison, the scaling function ϑ(D=4,d=4)∘∘ at the critical point For comparison, the scaling function ϑ(D=4,d=4)∘∘ at the critical point  for H4,4-particles20 is shown by the grey dash-dotted line. Interestingly, the full dependence on Δ of the Derjaguin approximation for H4,4 (grey dotted line emerging from the grey cross) displays a trend opposite to the result ϑ(D=4,d=4)∘∘ of ref. 20, obtained from the full calculation. for H4,4-particles20 is shown by the grey dash-dotted line. Interestingly, the full dependence on Δ of the Derjaguin approximation for H4,4 (grey dotted line emerging from the grey cross) displays a trend opposite to the result ϑ(D=4,d=4)∘∘ of ref. 20, obtained from the full calculation. | ||
C. Landau theory
In the spirit of an expansion in terms of ε = 4 − D, for the lowest order contribution we use the mean-field Landau–Ginzburg–Wilson theory (hereafter called ‘Landau theory’ for brevity) in order to study the universal CCF in the film geometry (Section IIIA) and between two colloidal particles (Section IIIB). The Hamiltonian, in units of kBT, is given by14,34,35 | (9) |
Within Landau theory, the bulk correlation lengths [eqn (1), (2) and (3)] are20
| ξt (t > 0) = τ−1/2, ξt (t < 0) = |2τ|−1/2, | (10) |
 | (11) |
| ξ(t, hb) = {[ξt(|t|)]−2sgn(t) + (u/2)ϕb2(t, hb)}−1/2, | (12) |
 so that
so that  can be expressed in terms of ξt and ξh and inserted into eqn (12). Within Landau theory τ = [ξ(0)+]−2t.
can be expressed in terms of ξt and ξh and inserted into eqn (12). Within Landau theory τ = [ξ(0)+]−2t.
The minimum of eqn (9) gives the mean-field profile ϕmf (r; t, hb). With this the critical Casimir force is
 | (13) |
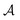 is an arbitrary (D − 1)-dimensional surface enclosing a colloid or separating two planes,
is an arbitrary (D − 1)-dimensional surface enclosing a colloid or separating two planes,  is its (d − 1)-dimensional subset in the subspace in which the colloids have a finite extent, n is its unit outward normal, and
is its (d − 1)-dimensional subset in the subspace in which the colloids have a finite extent, n is its unit outward normal, and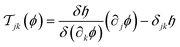 | (14) |
 is the integrand in eqn (9), and ∂kϕ = ∂ϕ/∂xk. For the film geometry with chemically and geometrically uniform surfaces, the integration in eqn (13) amounts to the evaluation of
is the integrand in eqn (9), and ∂kϕ = ∂ϕ/∂xk. For the film geometry with chemically and geometrically uniform surfaces, the integration in eqn (13) amounts to the evaluation of 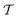 at an arbitrary point between the two surfaces. The force between two colloids is fC = fCe, where e is a unit vector along the line connecting their centers. We have minimized the Hamiltonian
at an arbitrary point between the two surfaces. The force between two colloids is fC = fCe, where e is a unit vector along the line connecting their centers. We have minimized the Hamiltonian  numerically using the finite element method.36
numerically using the finite element method.36
Within Landau theory, the scaling functions of the critical Casimir force carry the undetermined prefactor 1/u, which is dimensionless in D = 4. In order to circumvent this uncertainty and to facilitate the comparison with experimental or other theoretical results, we shall normalize our mean-field results by the critical Casimir amplitude for the film geometry [see eqn (5)]  25 where K is the complete elliptic integral of the first kind. This normalization eliminates the prefactor
25 where K is the complete elliptic integral of the first kind. This normalization eliminates the prefactor  . For the sphere–sphere geometry, one has20,30
. For the sphere–sphere geometry, one has20,30 note that Σ = sgn(thb)ξt/ξh = const defines implicitly various thermodynamic paths hb(t) which, however, all pass through the critical point (t = 0, hb = 0), i.e., Y = 0 [see Fig. 1]. Accordingly, ϑ(D) (Y = 0, Σ) does not depend on Σ. This normalization scheme holds also for nonzero values of
note that Σ = sgn(thb)ξt/ξh = const defines implicitly various thermodynamic paths hb(t) which, however, all pass through the critical point (t = 0, hb = 0), i.e., Y = 0 [see Fig. 1]. Accordingly, ϑ(D) (Y = 0, Σ) does not depend on Σ. This normalization scheme holds also for nonzero values of  , Δ, and Λ as well as beyond the Derjaguin approximation.
, Δ, and Λ as well as beyond the Derjaguin approximation.
D. Extended de Gennes–Fisher functional
For the film geometry, we consider the ansatz for the free energy functional proposed by Fisher and Upton16 | (15) |
Minimizing the functional given by eqn (15) leads to an Euler–Lagrange equation, which can be formally integrated. One then proceeds by taking the scaling limit of this latter first integral and by using the scaling forms of the following bulk quantities:
| W(Φ; t, hb) = |Φ|δ+1Y±(Ψ, Σ) | (16) |
| ξ2/(2χ) = |Φ|ην/βZ±(Ψ), | (17) |
 . The (dimensionless) non-universal amplitude
. The (dimensionless) non-universal amplitude  of the bulk order parameter Φb can be expressed via universal amplitude ratios in terms of the non-universal amplitudes ξ(0)+ and ξ(0)h of the bulk correlation length;23 the functions Ỹ±(Ψ, Σ) = Y±(Ψ, Σ)/Y+(∞, 0) and
of the bulk order parameter Φb can be expressed via universal amplitude ratios in terms of the non-universal amplitudes ξ(0)+ and ξ(0)h of the bulk correlation length;23 the functions Ỹ±(Ψ, Σ) = Y±(Ψ, Σ)/Y+(∞, 0) and ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) ±(Ψ) = Z±(Ψ)/Z+(∞) are universal. This procedure determines (even without knowing the explicit functional forms of Ỹ± and
±(Ψ) = Z±(Ψ)/Z+(∞) are universal. This procedure determines (even without knowing the explicit functional forms of Ỹ± and ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) ±) a formal expression for the scaling function
±) a formal expression for the scaling function ![[small variant theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1e2.gif) (D)‖ of the CCF.17,37 Here we take into account the additional dependence on the scaling variable Σ ≠ 0 and obtain38 for
(D)‖ of the CCF.17,37 Here we take into account the additional dependence on the scaling variable Σ ≠ 0 and obtain38 for 
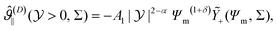 | (18) |
In order to calculate the critical Casimir force from eqn (18) one has to evaluate the functions Y± and Z± in eqn (16) and (17). The analytical expressions of these functions can be obtained by using the so-called linear parametric model.17,23,39 For given  and Σ the scaling function of the critical Casimir force is then computed numerically (for details see ref. 38).
and Σ the scaling function of the critical Casimir force is then computed numerically (for details see ref. 38).
III. Numerical results
A. Critical Casimir forces in films
In Fig. 1, we have plotted several lines of constant scaling variable |Y| = L/ξ(t, hb) = 4, 5,…,10 in the thermodynamic space of the solvent spanned by ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = (L/ξ(0)+)1/νt and ĥb = (L/ξ(0)h)βδ/νhb. The shape of the lines |Y| = const is determined by the bulk correlation length ξ(t, hb). Therefore it is symmetric about the
= (L/ξ(0)+)1/νt and ĥb = (L/ξ(0)h)βδ/νhb. The shape of the lines |Y| = const is determined by the bulk correlation length ξ(t, hb). Therefore it is symmetric about the ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) -axis. A break of slope occurs at the bulk coexistence line (
-axis. A break of slope occurs at the bulk coexistence line (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) < 0, ĥb = 0) because ξ(t, hb) depends on the bulk order parameter ϕb [see eqn (12)] which varies there discontinuously. We use the color code to indicate the strength |ϑ(D=4)∥| of the scaling function of the CCF along these lines. For (+, +) boundary conditions the critical Casimir force in a slab is attractive and accordingly ϑ(D=4)∥ < 0 for all values of t and hb.
< 0, ĥb = 0) because ξ(t, hb) depends on the bulk order parameter ϕb [see eqn (12)] which varies there discontinuously. We use the color code to indicate the strength |ϑ(D=4)∥| of the scaling function of the CCF along these lines. For (+, +) boundary conditions the critical Casimir force in a slab is attractive and accordingly ϑ(D=4)∥ < 0 for all values of t and hb.
The main message conveyed by Fig. 1 is the asymmetry of the critical Casimir force around the critical point of the solvent with the maximum strength occurring at hb < 0. This asymmetry is due to the presence of surface fields which break the bulk symmetry hb → −hb of the system and shift the phase coexistence line away from the bulk location hb = 0. In the film with (+, +) boundary conditions the shifted, so-called capillary condensation transition, occurs for negative values of hb.1,40 At capillary condensation, the solvation force (which within this context is a more appropriate notion than the notion of the critical Casimir force) exhibits a jump from a large value for thermodynamic states corresponding to the (+) phase to a vanishingly small value for those corresponding to the (−) phase. Above the two-dimensional plane spanned by (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) , ĥb), the surface ϑ(D=4)∥ forms a trough which is the remnant of these jumps extending to the thermodynamic region above the capillary condensation critical point, even to temperatures higher than Tc. This trough, reflecting the large strengths visible in Fig. 1 for ĥb < 0, deepens upon approaching the capillary condensation point.
, ĥb), the surface ϑ(D=4)∥ forms a trough which is the remnant of these jumps extending to the thermodynamic region above the capillary condensation critical point, even to temperatures higher than Tc. This trough, reflecting the large strengths visible in Fig. 1 for ĥb < 0, deepens upon approaching the capillary condensation point.
Along the particular thermodynamic path of zero bulk field (i.e., Σ = 0) the minimum is located above Tc and has the value ϑ(4)∥(Ymin = 3.8, Σ = 0) = 1.4 × ϑ(4)∥(0, 0). Along the critical isotherm (i.e., |Σ| = ∞) one has ϑ(4)∥(Ymin = 8.4, Σ = −∞) = 10 × ϑ(4)∥(0, 0). Interestingly, along all lines |Y| = L/ξ(t, hb) = const the strength |ϑ(4)∥(Y = const, Σ)| takes its minimal value at the bulk coexistence curve hb = 0+. For |Y| ≷ 6.3 the maximal value of |ϑ(4)∥(Y = const, Σ)| is located at hb < 0 and t ≶ 0.
It is useful to consider the variation of the scaling function of the CCF along the thermodynamic paths of fixed Σ. As examples, such paths are shown for Σ = 1 and Σ = 3 in Fig. 1 by dash-dotted lines. Thermodynamic paths corresponding to 0 < Σ ≲ 1.3 cross the phase boundary of coexisting phases in the film at certain values Ycx(Σ), which lie outside the range of the plot in Fig. 1. Along the paths corresponding to 0 < Σ ≲ 3, ϑ(4)∥(Y, Σ = const < 3) as function of Y has two minima. The local minimum occurs above Tc, whereas the global one occurs below Tc. For all other fixed values of Σ, the scaling function ϑ(4)∥, as function of Y, exhibits a single minimum; for negative Σ it is located above Tc (i.e., Y > 0), whereas for Σ ≳ 3 below Tc (i.e., Y < 0). Results for ϑ(D=4)∥ as function of Y = sgn(t)L/ξ(t, hb) for constant values of Σ = sgn(thb) ξt/ξh are shown in ref. 38.
Thermodynamic paths of constant order parameter ϕ ≠ 0 are particularly experimentally relevant, because they correspond to a fixed off-critical composition of the solvent. As an example Fig. 1 shows the case  as indicated by the dashed line. Within mean-field theory this path varies linearly with t.
as indicated by the dashed line. Within mean-field theory this path varies linearly with t.
 | (19) |
 is taken from Monte Carlo simulation data.41 This “dimensional approximation” is inspired by the observation that the trends and qualitative features of
is taken from Monte Carlo simulation data.41 This “dimensional approximation” is inspired by the observation that the trends and qualitative features of ![[small variant theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1e2.gif) (D)∥ are the same for different values of D.41,42 The characteristics of this approximation are as follows: (i) For D → D' = 4, the right hand side of eqn (19) turns into the correct expression for the full range of all scaling variables. (ii) For hb → 0 (i.e., Σ → 0) the right hand side of eqn (19) reduces exactly to
(D)∥ are the same for different values of D.41,42 The characteristics of this approximation are as follows: (i) For D → D' = 4, the right hand side of eqn (19) turns into the correct expression for the full range of all scaling variables. (ii) For hb → 0 (i.e., Σ → 0) the right hand side of eqn (19) reduces exactly to  for all values D, D′, and
for all values D, D′, and  . In this sense the approximation is concentrated on the dependence on hb. (iii) For D′ = 4 the approximation can be understood as the lowest order contribution in an ε = 4 − D expansion of
. In this sense the approximation is concentrated on the dependence on hb. (iii) For D′ = 4 the approximation can be understood as the lowest order contribution in an ε = 4 − D expansion of  which carries the whole dependence of the CCFs on Σ. Since
which carries the whole dependence of the CCFs on Σ. Since  is a ratio, the prefactor of
is a ratio, the prefactor of ![[small variant theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1e2.gif) (D′=4)∥, which cannot be determined within Landau theory (see Section IIC), drops out. In eqn (19), the scaling variables
(D′=4)∥, which cannot be determined within Landau theory (see Section IIC), drops out. In eqn (19), the scaling variables  and Σ are taken to involve the critical bulk exponents in spatial dimension D so that the approximation concerns only the shape of the scaling function. The use of bulk critical exponents in spatial dimension D for scaling variables which, however, are arguments of the scaling function in spatial dimension D′ ≠ D, may lead to a deviation from the proper asymptotic behavior. However, this potential violation of the proper asymptotic behavior of the scaling function of the CCFs is expected to occur for large values of the arguments of the scaling function for which its value is exponentially small. Thus, the potential violation should not matter quantitatively in the range of the values of
and Σ are taken to involve the critical bulk exponents in spatial dimension D so that the approximation concerns only the shape of the scaling function. The use of bulk critical exponents in spatial dimension D for scaling variables which, however, are arguments of the scaling function in spatial dimension D′ ≠ D, may lead to a deviation from the proper asymptotic behavior. However, this potential violation of the proper asymptotic behavior of the scaling function of the CCFs is expected to occur for large values of the arguments of the scaling function for which its value is exponentially small. Thus, the potential violation should not matter quantitatively in the range of the values of  and Σ for which the scaling function
and Σ for which the scaling function ![[small variant theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1e2.gif) (D)∥ attains noticeable values. Here we compare this approximation with the results obtained from the extended de Gennes-Fisher functional using the linear parametric model.
(D)∥ attains noticeable values. Here we compare this approximation with the results obtained from the extended de Gennes-Fisher functional using the linear parametric model.
In Fig. 2(a) we plot 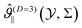 as a function of
as a function of  for several values of Σ. For large values of |Σ| the relevant part of the corresponding thermodynamic path is close to the critical isotherm and accordingly the scaling variable
for several values of Σ. For large values of |Σ| the relevant part of the corresponding thermodynamic path is close to the critical isotherm and accordingly the scaling variable 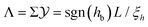 is more appropriate than the scaling variable
is more appropriate than the scaling variable 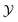 . Therefore, in Fig. 2(b) we show
. Therefore, in Fig. 2(b) we show ![[small variant theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e1f3.gif) (D=3)‖(Λ, Σ) =
(D=3)‖(Λ, Σ) = ![[small variant theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1e2.gif) (D=3)‖(Λ/Σ, Σ) as a function of Λ for several fixed values of Σ ≤ −2.
(D=3)‖(Λ/Σ, Σ) as a function of Λ for several fixed values of Σ ≤ −2.
As can be inferred from Fig. 2 the dimensional approximation in eqn (19) works well for weak bulk fields (such that |Σ| < 3). Although the minima of the scaling functions are slightly shifted relative to each other, the depths of these minima compare well with the results of the local functional approach. For all |Σ| < ∞, the value 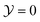 corresponds to the bulk critical point and thus at
corresponds to the bulk critical point and thus at  the curves
the curves ![[small variant theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1e2.gif) (D)∥ attain the same value [see Fig. 2(a)].
(D)∥ attain the same value [see Fig. 2(a)].
For strong bulk fields, i.e., Σ < −4 the dimensional approximation [eqn (19)] fails [see Fig. 2(b)]. For example, |![[small variant theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e1f3.gif) (D=3)∥| of the approximative curve becomes smaller for more negative values of Σ, which is in contrast to the results of Landau theory and of the local functional approach. This wrong trend of the results of the dimensional approximation is explained in detail in ref. 38.
(D=3)∥| of the approximative curve becomes smaller for more negative values of Σ, which is in contrast to the results of Landau theory and of the local functional approach. This wrong trend of the results of the dimensional approximation is explained in detail in ref. 38.
We note that the scaling functions ϑ(D=3)∥ of the critical Casimir force as obtained from the local functional exhibit the same qualitative features as the ones calculated within Landau theory. For example, the position Ymin(Σ) of the minimum as obtained from the present local functional theory changes from  at the thermodynamic path hb = 0 towards Ymin(Σ = −∞) = −Λmin(Σ = −∞) = 9.4 at the critical isotherm. These values are similar to the ones obtained from Landau theory. The results of the local functional approach are peculiar with respect to the cusp-like minimum for curves close to the critical isotherm [for |Σ| = ∞, i.e., t = 0, see Fig. 2(b)]. Such a behavior is also reported for the similar approach used in ref. 18. However, there is no such cusp in the Monte Carlo data43 for t = 0, i.e., |Σ| = ∞, [see the symbols in Fig. 2(b)]. As compared with the results of the local functional, the minimum of
at the thermodynamic path hb = 0 towards Ymin(Σ = −∞) = −Λmin(Σ = −∞) = 9.4 at the critical isotherm. These values are similar to the ones obtained from Landau theory. The results of the local functional approach are peculiar with respect to the cusp-like minimum for curves close to the critical isotherm [for |Σ| = ∞, i.e., t = 0, see Fig. 2(b)]. Such a behavior is also reported for the similar approach used in ref. 18. However, there is no such cusp in the Monte Carlo data43 for t = 0, i.e., |Σ| = ∞, [see the symbols in Fig. 2(b)]. As compared with the results of the local functional, the minimum of ![[small variant theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e1f3.gif) (D=3)∥(Λ, |Σ| = ∞) obtained from Monte Carlo simulations is less deep and is positioned at a more negative value of Λ. For Λ > 0 [not shown in Fig. 2(b)],
(D=3)∥(Λ, |Σ| = ∞) obtained from Monte Carlo simulations is less deep and is positioned at a more negative value of Λ. For Λ > 0 [not shown in Fig. 2(b)], ![[small variant theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e1f3.gif) (D=3)∥(Λ, |Σ| = ∞) as obtained from the local functional is less negative than the corresponding scaling function obtained from the Monte Carlo simulations.
(D=3)∥(Λ, |Σ| = ∞) as obtained from the local functional is less negative than the corresponding scaling function obtained from the Monte Carlo simulations.
We observe that upon decreasing the spatial dimension D the ratio of the strengths |ϑ(D)∥| at its two extrema, the one located at the critical isotherm and the other located at hb = 0, increases, from 7 in D = 4 to 11.5 (local functional) or 8 (Monte Carlo simulations) in D = 3, and to 15 in D = 2.44
B. Critical Casimir forces between spherical colloids
The CCF between two spherical colloids takes the form given by eqn (7); here we take d = 3 and D = 4. In order to calculate ϑ(4,3)∘∘, we use the stress tensor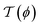 [see eqn (13) and (14)] with the mean-field profile ϕ(r) which has been determined by minimizing the Hamiltonian in eqn (9) numerically using F3DM.36 To this end we have put two spherical particles inside a sufficiently large rectangular box and divided the physical space into a mesh of finite elements using TETGEN.45 We have used linear basis functions to approximate ϕ(r) on the mesh elements, and transformed the functional [eqn (9)] into a function of values of ϕ on the mesh nodes; this function has been minimized numerically using GSL.46 In order to account for the strong adsorption boundary conditions on the surfaces of the colloids, we have applied a short-distance expansion and have determined ϕ(r) at a certain small distance away from each colloid; this amounts to applying fixed boundary conditions at spheres surrounding the colloids. (Note, however, that this approach is only valid for sufficiently large colloid separations.) At all sides of the computational box ϕ(r) is taken to exhibit a vanishing gradient.
[see eqn (13) and (14)] with the mean-field profile ϕ(r) which has been determined by minimizing the Hamiltonian in eqn (9) numerically using F3DM.36 To this end we have put two spherical particles inside a sufficiently large rectangular box and divided the physical space into a mesh of finite elements using TETGEN.45 We have used linear basis functions to approximate ϕ(r) on the mesh elements, and transformed the functional [eqn (9)] into a function of values of ϕ on the mesh nodes; this function has been minimized numerically using GSL.46 In order to account for the strong adsorption boundary conditions on the surfaces of the colloids, we have applied a short-distance expansion and have determined ϕ(r) at a certain small distance away from each colloid; this amounts to applying fixed boundary conditions at spheres surrounding the colloids. (Note, however, that this approach is only valid for sufficiently large colloid separations.) At all sides of the computational box ϕ(r) is taken to exhibit a vanishing gradient.
CCFs between spherical colloids in zero bulk field have been widely studied in the literature.20,31,33,47,48 Within Landau theory, so far only the critical Casimir interaction between two HD≥4,3 particles in the presence of a wall has been reported; the dependence of the CCFs on the bulk field hb has been considered only for HD=4,d=4 particles. Here we focus on three-dimensional spherical particles, i.e., on hypercylinders H3,3 or HD≥4,3. We recall that we consider (+, +) boundary conditions only.
The scaling function  , as a function of
, as a function of  , has a shape which is typical for like boundary conditions [see Fig. 3(a)]. Interestingly, the magnitude of ϑ(4,3)∘∘ depends non-monotonically on Δ. This is shown explicitly in Fig. 3(b), where the scaling function is plotted versus Δ for three values of
, has a shape which is typical for like boundary conditions [see Fig. 3(a)]. Interestingly, the magnitude of ϑ(4,3)∘∘ depends non-monotonically on Δ. This is shown explicitly in Fig. 3(b), where the scaling function is plotted versus Δ for three values of  In Fig. 3(b), ϑ(4,3)∘∘ approaches the scaling function of the Derjaguin approximation from above when Δ → 0, but decreases upon increasing Δ > Δm, where Δm ≈ 1/2 seems to be almost independent of
In Fig. 3(b), ϑ(4,3)∘∘ approaches the scaling function of the Derjaguin approximation from above when Δ → 0, but decreases upon increasing Δ > Δm, where Δm ≈ 1/2 seems to be almost independent of  (in the range of
(in the range of 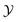 shown). This non-monotonic behavior is unlike the case of H4,4 hypercylinders, for which the scaling function approaches its value at Δ = 0 from below and exhibits no maxima (grey dash-dotted line in Fig. 3(b) reproduced from ref. 20). For the wall-sphere geometry, such a non-monotonic behavior of the scaling function of the CCF for Δ → 0 has been found for a sphere H3,3 using Monte Carlo simulations,33 but not for (hyper)cylinders H4,d, d ∈ {2, 3}, treated within Landau theory.32
shown). This non-monotonic behavior is unlike the case of H4,4 hypercylinders, for which the scaling function approaches its value at Δ = 0 from below and exhibits no maxima (grey dash-dotted line in Fig. 3(b) reproduced from ref. 20). For the wall-sphere geometry, such a non-monotonic behavior of the scaling function of the CCF for Δ → 0 has been found for a sphere H3,3 using Monte Carlo simulations,33 but not for (hyper)cylinders H4,d, d ∈ {2, 3}, treated within Landau theory.32
The behavior of ϑ(4,3)∘∘ for large Δ ≫ 1 is not quite clear due to technical difficulties associated with large mesh sizes and the increasing numerical inaccuracy; moreover, in this limit, the force attains very small values.
Results for nonzero bulk fields hb are shown in Fig. 4. For fixed sphere radii R and fixed surface-to-surface distance L, the curves in Fig. 4(a) for fixed Λ correspond to varying the temperature along the thermodynamic paths of iso-fields hb = const. For fixed L, the curves in Fig. 4(b) compare the scaling function of the CCF as function of hb along the supercritical isotherm Tc < T = const for various sphere sizes.
 | ||
Fig. 4 Effect of the bulk field (Λ ≠ 0) on the scaling function ϑ(D=4,d=3)∘∘ of the critical Casimir force [eqn (7)] as obtained from Landau theory. (a) Normalized ϑ(4,3)∘∘ shown as a function of 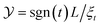 for Δ = L/R = 1 (full lines) and within the Derjaguin approximation (Δ = 0, dashed lines) for four values of Λ = sgn(hb)L/ξh. (b) Normalized ϑ(4,3)∘∘ shown as a function of Λ for for Δ = L/R = 1 (full lines) and within the Derjaguin approximation (Δ = 0, dashed lines) for four values of Λ = sgn(hb)L/ξh. (b) Normalized ϑ(4,3)∘∘ shown as a function of Λ for 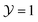 and for four values of Δ. The curves are normalized with the critical Casimir amplitude Δ(4)∥ for the film. and for four values of Δ. The curves are normalized with the critical Casimir amplitude Δ(4)∥ for the film. | ||
For hb > 0 the variation of ϑ(4,3)∘∘ with 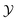 resembles the features observed for vanishing hb in the case of the sphere–sphere or film geometry, i.e., ϑ(4,3)∘∘ exhibits a minimum located above Tc (
resembles the features observed for vanishing hb in the case of the sphere–sphere or film geometry, i.e., ϑ(4,3)∘∘ exhibits a minimum located above Tc ( ) [compare Fig. 4(a) with Fig. 2 and 3(a)]. Upon increasing the bulk field, the magnitude of the scaling function decreases and the position of the minimum shifts towards larger
) [compare Fig. 4(a) with Fig. 2 and 3(a)]. Upon increasing the bulk field, the magnitude of the scaling function decreases and the position of the minimum shifts towards larger 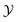 . This is in line with the behavior for the film geometry (Fig. 1).
. This is in line with the behavior for the film geometry (Fig. 1).
The behavior of the scaling function for negative bulk fields is different. For positive 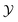 , there is still a residual minimum of the scaling function located very close to
, there is still a residual minimum of the scaling function located very close to  , which disappears upon decreasing hb. This is already the case for Λ = −2 in Fig. 4(a). This disappearance is in line with the results for film geometry. For negative
, which disappears upon decreasing hb. This is already the case for Λ = −2 in Fig. 4(a). This disappearance is in line with the results for film geometry. For negative  , at a certain value Λ < 0, in films capillary condensation occurs whereas between spherical colloids a bridging transition takes place.12,19,49 Near these phase transitions, the effective force acting between the confining surfaces is attractive and becomes extremely strong; the depth of the corresponding effective interaction potentials can reach a few hundred kBT. This concomitant enormous increase of the strength of the force is also reflected in the universal scaling function [see the green line Λ = −2 in Fig. 4(a) for
, at a certain value Λ < 0, in films capillary condensation occurs whereas between spherical colloids a bridging transition takes place.12,19,49 Near these phase transitions, the effective force acting between the confining surfaces is attractive and becomes extremely strong; the depth of the corresponding effective interaction potentials can reach a few hundred kBT. This concomitant enormous increase of the strength of the force is also reflected in the universal scaling function [see the green line Λ = −2 in Fig. 4(a) for  ]. (For the film geometry this issue has been discussed in detail in ref. 20; in particular, Fig. 11 in ref. 20 exhibits a cusp in the scaling function in the vicinity of the capillary condensation; similarly, upon decreasing
]. (For the film geometry this issue has been discussed in detail in ref. 20; in particular, Fig. 11 in ref. 20 exhibits a cusp in the scaling function in the vicinity of the capillary condensation; similarly, upon decreasing 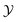 , called Θ− in ref. 20, to negative values the magnitude of the scaling function increases strongly.)
, called Θ− in ref. 20, to negative values the magnitude of the scaling function increases strongly.)
It is also interesting to note a non-monotonic dependence of the scaling function ϑ(4,3)∘∘ on Δ = L/R [Fig. 4(b)]. For positive bulk fields, |ϑ(4,3)∘∘| is stronger for larger Δ. This is different, however, for negative bulk fields, for which |ϑ(4,3)∘∘| is stronger for smaller Δ. Such an increase of |ϑ(4,3)∘∘| upon decreasing Δ holds also for zero bulk field [see Fig. 3(b) for Δ ≳ 1/2].
Finally, for larger values of Δ = L/R the deficiencies of the Derjaguin approximation are clearly visible in Fig. 3 and 4.
IV. Comparison with experimental data
A. Effective interaction potentials
In ref. 10, the pair distribution function g(r) of poly-n-isopropyl-acrylamide microgel (PNIPAM) colloidal particles immersed in a near-critical 3-methyl-pyridine (3MP)–heavy water mixture has been determined experimentally for various deviations ΔT = Tc − T from the lower critical temperature Tc ≈ 39 °C (of the miscibility gap of the bulk 3MP–heavy water mixture without colloidal particles). Here we analyze the experimental data for the 3MP mass fraction ω = 0.28 which is close to the critical value (see below).We assume that the solvent-mediated interaction between the PNIPAM colloids is the sum of a background contribution Ubck and the critical Casimir potential Uc. This assumption is valid for small salt concentrations50 which is the case for the samples studied in ref. 10. Accordingly, one has
| Ubck(r) = Uexp(r; ΔT) − Uc(r; ΔT), | (20) |
Within the studied temperature range ΔT < 1 K this ‘background’ contribution is expected to depend only weakly on temperature and hence we consider it to be temperature independent. We use the potential of mean-force in order to extract the experimentally determined interaction potential Uexp(r) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[g(r)]. This relation is reliable for small solute densities, as they have been used in the experiments. Therefore only small deviations are expected to occur by using more accurate expressions for the potential, such as the hypernetted chain or the Percus–Yevick closures.
ln[g(r)]. This relation is reliable for small solute densities, as they have been used in the experiments. Therefore only small deviations are expected to occur by using more accurate expressions for the potential, such as the hypernetted chain or the Percus–Yevick closures.
Since the numerical calculation of the critical Casimir potential in the bona fide sphere–sphere geometry for all parameters which are needed for comparison with experiment is too demanding, here we resort to the Derjaguin approximation. Within this approximation the critical Casimir potential Uc between two colloids of radius R [eqn (7) and (8)] is15,31,32
 | (21) |
 and Σ = sgn(thb)ξt/ξh. The dependence of Uc on temperature and on the mass fraction of the solvent is captured by the bulk correlation lengths ξt and ξh of the solvent, respectively [eqn (2) and (3)]. In order to calculate the scaling function
and Σ = sgn(thb)ξt/ξh. The dependence of Uc on temperature and on the mass fraction of the solvent is captured by the bulk correlation lengths ξt and ξh of the solvent, respectively [eqn (2) and (3)]. In order to calculate the scaling function ![[small variant theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1e2.gif) (D=3)∥ of the critical Casimir force between two planar walls we use the local functional approach (see Section IID).
(D=3)∥ of the critical Casimir force between two planar walls we use the local functional approach (see Section IID).
For the amplitude of the thermal bulk correlation length we take ξ(0)+ = 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm, which we extracted from the experimental data presented in ref. 51. However, in the literature there are no well established data for the critical mass fraction ωc of the 3MP-heavy water binary liquid mixtures. In ref. 52, the value ωc = 0.28 is quoted while the scaling analysis of the data shown in Fig. 1 in ref. 52 suggests the value ωc ≈ 0.29. The inaccuracy of the value for ωc enters into the reduced order parameter
nm, which we extracted from the experimental data presented in ref. 51. However, in the literature there are no well established data for the critical mass fraction ωc of the 3MP-heavy water binary liquid mixtures. In ref. 52, the value ωc = 0.28 is quoted while the scaling analysis of the data shown in Fig. 1 in ref. 52 suggests the value ωc ≈ 0.29. The inaccuracy of the value for ωc enters into the reduced order parameter  ;
; ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) t is the non-universal amplitude of the bulk coexistence curve
t is the non-universal amplitude of the bulk coexistence curve  . Thus, via the equation of state one obtains
. Thus, via the equation of state one obtains  [see eqn (A4) in the first part of ref. 13] so that the critical Casimir potential Uc [eqn (21)] depends sensitively on the value of ωc. The function E is determined by using the equation of state within the linear parametric model.39 Note, that as long as we consider the reduced order parameter
[see eqn (A4) in the first part of ref. 13] so that the critical Casimir potential Uc [eqn (21)] depends sensitively on the value of ωc. The function E is determined by using the equation of state within the linear parametric model.39 Note, that as long as we consider the reduced order parameter ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) we do not have to know the non-universal amplitude
we do not have to know the non-universal amplitude  (or ξ(0)h which is related to
(or ξ(0)h which is related to  via universal amplitude ratios.)
via universal amplitude ratios.)
Fig. 5(a) shows the experimentally determined potentials and the extracted background contributions Ubck for the critical composition being ωc = 0.28 = ω, as stated in ref. 10. In view of the uncertainty in the value of ωc, we used ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) as a variational parameter for achieving the weakest variation of the background potential Ubck with temperature. For example, for
as a variational parameter for achieving the weakest variation of the background potential Ubck with temperature. For example, for ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = −0.088 the variation of Ubck as function of T is smaller than 0.5kBT and thus comparable with the experimentally induced inaccuracy [see Fig. 5(b)]. Adopting the value
= −0.088 the variation of Ubck as function of T is smaller than 0.5kBT and thus comparable with the experimentally induced inaccuracy [see Fig. 5(b)]. Adopting the value  (which can be inferred from the experimental data of ref. 52)
(which can be inferred from the experimental data of ref. 52)  corresponds to a critical mass fraction ωc ≃ 0.236. This value of ωc differs significantly from the value given in ref. 10. We conclude that either the solvent used in these experiments was indeed at the critical composition, but Uc does not capture the whole temperature dependence of Uexp [case (a)]; or that Uc does capture the whole temperature dependence of Uexp, but ω = 0.28 is not the critical composition [case (b)]. For all tested values of
corresponds to a critical mass fraction ωc ≃ 0.236. This value of ωc differs significantly from the value given in ref. 10. We conclude that either the solvent used in these experiments was indeed at the critical composition, but Uc does not capture the whole temperature dependence of Uexp [case (a)]; or that Uc does capture the whole temperature dependence of Uexp, but ω = 0.28 is not the critical composition [case (b)]. For all tested values of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) , the potential Ubck, which corresponds to ΔT/K = 0.2, deviates the most from the other three curves. Theses deviations might be attributed to the invalidity of the Derjaguin approximation (compare Section IIIB) or to the overestimation of the CCFs within the local functional approach (compare Fig. 2). The calculated Uc may suffer from these approximations, and accordingly the obtained Ubck; this may thus also be the cause of the attractive part in Ubck. Moreover, also other physical effects, such as a coupling of the critical fluctuations to electrostatic interactions or the structural properties of the soft microgel particles, which we have not included in our analysis [see eqn (20)], might be of importance for the considered system.
, the potential Ubck, which corresponds to ΔT/K = 0.2, deviates the most from the other three curves. Theses deviations might be attributed to the invalidity of the Derjaguin approximation (compare Section IIIB) or to the overestimation of the CCFs within the local functional approach (compare Fig. 2). The calculated Uc may suffer from these approximations, and accordingly the obtained Ubck; this may thus also be the cause of the attractive part in Ubck. Moreover, also other physical effects, such as a coupling of the critical fluctuations to electrostatic interactions or the structural properties of the soft microgel particles, which we have not included in our analysis [see eqn (20)], might be of importance for the considered system.
 | ||
Fig. 5 Effective interaction potential Uexp as determined experimentally in ref. 10 (symbols, dashed lines as a guide to the eye) and its background contribution Ubck (full lines). The experimental system consists of colloidal particles of radius R ≈ 250 nm immersed in a near critical binary liquid mixture. The effective potential was determined for various deviations ΔT = Tc − T from the lower critical point Tc, at ΔT/K = 0.6 (×, magenta), 0.5 (□, green), 0.4 (○, orange), and 0.3 (△, blue). Upon approaching Tc the minimum of the potential U deepens due to the attractive Casimir interaction. The ‘background’ part of the potential is obtained by subtracting the critical Casimir potential Uc [see eqn (20) and (21)]. If Ubck was temperature independent the various full lines would collapse. In (a) the binary liquid mixture used in the experiments (mass fraction ω = 0.28) is assumed to be at its critical composition ω = ωc = 0.28, whereas (b) corresponds to a slightly off-critical composition 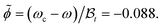 In (b) one observes a better collapse of the full lines than in (a). The critical Casimir potential Uc depends on Σ, which is directly related to In (b) one observes a better collapse of the full lines than in (a). The critical Casimir potential Uc depends on Σ, which is directly related to ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) via the equation of state Σ = E(|t|β via the equation of state Σ = E(|t|β![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) ) (see the main text). The curves correspond to the value ξ(0)+ = 1.5 ) (see the main text). The curves correspond to the value ξ(0)+ = 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm [eqn (2)]. The colloidal particles are soft, so that Uexp(r < 2R) > 0 and very large but not infinite. nm [eqn (2)]. The colloidal particles are soft, so that Uexp(r < 2R) > 0 and very large but not infinite. | ||
B. Segregation phase diagram
The experiments of ref. 10 indicate that, upon approaching the critical point of the solvent, a colloidal suspension segregates into two phases: poor (I) and rich (II) in colloids. Ref. 10 also provides the experimental data for the colloidal packing fractions (η(I,II)cx) in the coexisting phases I and II. In order to calculate η(I,II)cx, we use the so-called ‘effective approach,’ within which one considers a one-component system of colloidal particles interacting with each other through an effective, solvent-mediated pair potential U. Thus this approach ignores that the solvent itself may ‘participate’ in the phase separation of the colloidal suspension. This approximation allows us, however, to make full use of the known results of standard liquid state theory (for more details and concerning the limitations of this approach see ref. 13 and 53).Within the random-phase approximation, the free energy  of the effective one-component system is given by13,54
of the effective one-component system is given by13,54
 | (22) |
 is the volume of the system. For the hard-sphere reference free energy
is the volume of the system. For the hard-sphere reference free energy  we adopt the Percus–Yevick expression
we adopt the Percus–Yevick expression | (23) |
 with η being the packing fraction of the colloids, ϱ their number density, and λ is the thermal wavelength. We use for the effective hard-sphere diameter
with η being the packing fraction of the colloids, ϱ their number density, and λ is the thermal wavelength. We use for the effective hard-sphere diameter  , with U(r = r0) = 0. One can adopt also other definitions of σ (for a discussion see ref. 55 and 56). Using the present definition renders a slightly better agreement with the experimental data than using the one given in ref. 56.
, with U(r = r0) = 0. One can adopt also other definitions of σ (for a discussion see ref. 55 and 56). Using the present definition renders a slightly better agreement with the experimental data than using the one given in ref. 56.
In eqn (22), one has 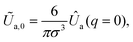 where Ûa(q = |q|) = ∫exp(−iqr)Ua(r)d3r is the Fourier transform of the attractive part (Ua) of the interaction potential,
where Ûa(q = |q|) = ∫exp(−iqr)Ua(r)d3r is the Fourier transform of the attractive part (Ua) of the interaction potential,
 | (24) |
In order to calculate the phase diagram of the effective one-component system within the RPA approximation, we use the pair potential U(r) = Ubck(r) + Uc(r), where Uc is given by eqn (21), and where the background contribution Ubck is extracted from the experimental data of ref. 10. As discussed in Section IVA, there is some inaccuracy in determining the background potential Ubck. Following ref. 10 and assuming ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = 0, we have to consider four different Ubck. The resulting corresponding segregation phase diagrams differ from each other qualitatively. Interestingly, the attractive part of the background potentials Ubck(r; ΔT,
= 0, we have to consider four different Ubck. The resulting corresponding segregation phase diagrams differ from each other qualitatively. Interestingly, the attractive part of the background potentials Ubck(r; ΔT, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) ) corresponding to ΔT/K = 0.4 and 0.2 [see Fig. 5(a)] is so strong, that for these potentials alone (i.e., for U = Ubck without Uc) the RPA free energy predicts already a phase segregation. For the background potential Ubck(r; ΔT,
) corresponding to ΔT/K = 0.4 and 0.2 [see Fig. 5(a)] is so strong, that for these potentials alone (i.e., for U = Ubck without Uc) the RPA free energy predicts already a phase segregation. For the background potential Ubck(r; ΔT, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) ) corresponding to ΔT = 0.6 K and
) corresponding to ΔT = 0.6 K and ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = 0, the presence of Uc is necessary for the occurrence of phase segregation within RPA. However, the resulting relative value of the critical temperature (ΔT)c,eff ≃ 0.39K is much smaller than the experimentally observed one. On the other hand, for
= 0, the presence of Uc is necessary for the occurrence of phase segregation within RPA. However, the resulting relative value of the critical temperature (ΔT)c,eff ≃ 0.39K is much smaller than the experimentally observed one. On the other hand, for ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = −0.088, which renders the best expression for Ubck out of the experimental data of ref. 10 (see Fig. 5), the resulting RPA phase segregation diagrams are consistent with each other. This is visible in Fig. 6(a), where we compare the coexistence curves ηcx(T) resulting from the four potentials Ubck of Fig. 5(b), as well as from Ubck obtained by averaging these four potentials Ubck. Although these five background potentials look very similar, they nonetheless lead to coexistence curves the critical temperatures of which differ noticeably [see Fig. 6(a)]. However, away from their critical point, the various coexistence curves merge; see the region ΔT < 0.4 K in Fig. 6(a). This indicates that for small ΔT the critical Casimir potential dominates the background potential, so that the details of the latter (and thus its inaccuracy) become less important.
= −0.088, which renders the best expression for Ubck out of the experimental data of ref. 10 (see Fig. 5), the resulting RPA phase segregation diagrams are consistent with each other. This is visible in Fig. 6(a), where we compare the coexistence curves ηcx(T) resulting from the four potentials Ubck of Fig. 5(b), as well as from Ubck obtained by averaging these four potentials Ubck. Although these five background potentials look very similar, they nonetheless lead to coexistence curves the critical temperatures of which differ noticeably [see Fig. 6(a)]. However, away from their critical point, the various coexistence curves merge; see the region ΔT < 0.4 K in Fig. 6(a). This indicates that for small ΔT the critical Casimir potential dominates the background potential, so that the details of the latter (and thus its inaccuracy) become less important.
 | ||
Fig. 6 Segregation phase diagram from theory (RPA), experiment, and simulations (MC). (a) The phase diagram obtained within RPA using the four available background potentials Ubck from Fig. 5, and their average. The critical Casimir potential is calculated within the Derjaguin approximation using the local functional approach (see Section IVA) for a reduced solvent order parameter ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = −0.088. The background contributions Ubck have been extracted from the experimentally determined effective potentials [compare eqn (20)] at ΔT/K = 0.6 (magenta), 0.5 (green), 0.4 (orange), and 0.3 (blue). The thick brown curve corresponds to the average of the four potentials Ubck. The solid lines show the phase boundaries in terms of the packing fraction η of the colloids, the dashed lines correspond to the spinodals, and dots represent critical points. (b) Comparison of the theoretical predictions for the phase boundaries (based on the average Ubck) with Monte Carlo simulations (⊡) and experiments (×, with error bars) of ref. 10. On the temperature axis ΔT = Tc − T increases from top to bottom in order to mimic a lower critical point Tc (of the solvent) as observed experimentally. = −0.088. The background contributions Ubck have been extracted from the experimentally determined effective potentials [compare eqn (20)] at ΔT/K = 0.6 (magenta), 0.5 (green), 0.4 (orange), and 0.3 (blue). The thick brown curve corresponds to the average of the four potentials Ubck. The solid lines show the phase boundaries in terms of the packing fraction η of the colloids, the dashed lines correspond to the spinodals, and dots represent critical points. (b) Comparison of the theoretical predictions for the phase boundaries (based on the average Ubck) with Monte Carlo simulations (⊡) and experiments (×, with error bars) of ref. 10. On the temperature axis ΔT = Tc − T increases from top to bottom in order to mimic a lower critical point Tc (of the solvent) as observed experimentally. | ||
Fig. 6(b) compares the RPA predictions for the segregation phase diagram with the experimental data and with the Monte Carlo simulation data provided by ref. 10. The pair potentials used in these MC simulations are the sum of an attractive and a repulsive exponential function and thus they differ from the ones used here. At high colloidal densities, the RPA is in surprisingly good agreement with the experimental data. On the other hand, at low densities the RPA agrees well with the Monte Carlo simulations, but both theoretical results underestimate the experimental values which, in turn, agree well with the low-η branch of the RPA-spinodal (an observation also observed for ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = 0). While this latter ‘agreement’ might be accidental, it nevertheless raises the question whether the experimental system has actually been fully equilibrated at the time of the measurements.
= 0). While this latter ‘agreement’ might be accidental, it nevertheless raises the question whether the experimental system has actually been fully equilibrated at the time of the measurements.
V. Summary
Critical Casimir forces act between surfaces confining a near-critical medium. For instance, colloidal particles suspended in a binary liquid mixture act as cavities in this solvent. Thus near its critical point of demixing the suspended colloids interact via an effective, solvent-mediated force, the so-called critical Casimir force (CCF). We have analyzed the dependence of the CCFs on the bulk ordering field (hb) conjugate to the order parameter of the solvent. For a binary liquid mixture, hb is proportional to the deviation of the difference of the chemical potentials of the two species from its critical value. In the presence of hb, we have used the mean-field approximation for the Landau–Ginsburg–Wilson theory to calculate the CCFs between parallel plates and between two spherical colloids, as well as the local functional approach of Fisher and de Gennes for parallel plates. We have shown that the CCF is asymmetric around the consolute point of the solvent, and that it is stronger for compositions slightly poor in that species of the mixture which preferentially adsorbs at the surfaces of the colloids [see Fig. 1, 2(a), (b) and 4].For two three-dimensional spherical particles posing as hypercylinders (H4,3) in spatial dimension D = 4 we observe a non-monotonic dependence of the scaling function of the CCF on the scaling variable Δ = L/R, where L is the surface-to-surface distance and R is the radius of monodisperse colloids [see Fig. 3(b) as well as Fig. 4]. Unlike four-dimensional spherical particles (H4,4) in D = 4, the scaling functions for H4,3 exhibit a maximum at Δ ≈ 1/2 before decreasing upon increasing Δ [see Fig. 3(b)]. This different behavior may be attributed to the extra macroscopic extension of the hypercylinders H4,3. This raises the question whether H4,3 or H4,4 is the better mean-field approximation for the physically relevant case of three-dimensional particles H3,3 in D = 3. Due to this uncertainty, and in view of the limited reliability of the Derjaguin approximation (see Fig. 3 and 4), more accurate theoretical approaches are highly desirable. Because the local functional approach is computational less demanding than Monte Carlo simulations and it is reliable for hb = 0, it would be very useful to improve this approach for hb ≠ 0 and to generalize it to more complex geometries, in particular to spherical objects.
In addition, due to numerical difficulties the behavior of the scaling function of the CCF for Δ → ∞ remains as an open issue. Since one faces similar numerical difficulties for Δ → 0, we conclude that within Landau theory, the numerical solution finds its useful place in between small and large colloid separations. The small separations are captured well by the Derjaguin approximation. For HD,d-particles with d > βD/ν, the large separations can be investigated by the so-called small radius expansion. However, the case H4,3 represents a ‘marginal’ perturbation for which the small radius expansion is not valid.57 Therefore, it would be interesting to study the asymptotic behavior of the scaling function of the CCF for large colloid separations by other means.
We have compared our theoretical results for the critical Casimir potential [within the Derjaguin approximation and the local functional approach, see eqn (21)] with experimental data taken from ref. 10 (see Fig. 5). Concerning the potentials we find a fair agreement, however their detailed behavior calls for further, more elaborate experimental and theoretical investigations.
As a consequence of the emergence of CCFs, a colloidal suspension thermodynamically close to the critical point of its solvent undergoes phase separation into a phase dense in colloids and a phase dilute in colloids. Using the random phase approximation for an effective one-component system, we have calculated the phase diagram for this segregation in terms of the colloidal packing fraction and of the deviation of temperature from the critical temperature of the solvent. Surprisingly, despite resorting to these approximations, the calculated phase diagram agrees fairly well with the corresponding experimental and Monte Carlo data (Fig. 6). Both the RPA calculations and the Monte Carlo simulations are based on the so-called effective approach and compare similarly well with the experimental data. However, in order to achieve an even better agreement with the experimental data, it is likely that models have to be considered which take into account the truly ternary character of the colloidal suspension.
Acknowledgements
We thank M. T. Dang, V. D. Nguyen, and P. Schall for interesting discussions about their experiments and for providing us their data.References
- R. Evans, J. Phys.: Condens. Matter., 1990, 2, 8989 CrossRef.
- M. E. Fisher and P. G. de Gennes, C. R. Seances Acad. Sci., Ser. B, 1978, 287, 207 CAS.
- H. B. G. Casimir, Proc. K. Ned. Akad. Wet., 1948, 51, 793 Search PubMed , online available at the KNAW digital library, http://www.dwc.knaw.nl/DL/publications/PU00018547.pdf.
- D. Beysens and D. Estève, Phys. Rev. Lett., 1985, 54, 2123 CrossRef CAS PubMed.
- D. Beysens and T. Narayanan, J. Stat. Phys., 1999, 95, 997 CrossRef CAS; P. D. Gallagher, M. L. Kurnaz and J. V. Maher, Phys. Rev. A, 1992, 46, 7750 CrossRef; T. Narayanan, A. Kumar, E. S. R. Gopal, D. Beysens, P. Guenoun and G. Zalczer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 1989 CrossRef; M. L. Kurnaz and J. V. Maher, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 572 CrossRef.
- D. Bonn, J. Otwinowski, S. Sacanna, H. Guo, G. Wegdam and P. Schall, Phys. Rev. Lett., 2009, 103, 156101 CrossRef PubMed; A. Gambassi and S. Dietrich, Phys. Rev. Lett., 2010, 105, 059601 CrossRef PubMed; D. Bonn, G. Wegdam and P. Schall, Phys. Rev. Lett., 2010, 105, 059602 CrossRef.
- S. J. Veen, O. Antoniuk, B. Weber, M. A. C. Potenza, S. Mazzoni, P. Schall and G. H. Wegdam, Phys. Rev. Lett., 2012, 109, 248302 CrossRef PubMed.
- H. Guo, T. Narayanan, M. Sztuchi, P. Schall and G. H. Wegdam, Phys. Rev. Lett., 2008, 100, 188303 CrossRef PubMed.
- V. D. Nguyen, S. Faber, Z. Hu, G. H. Wegdam and P. Schall, Nat. Commun., 2013, 4, 1584 CrossRef PubMed.
- M. T. Dang, A. V. Verde, V. D. Nguyen, P. G. Bolhuis and P. Schall, J. Chem. Phys., 2013, 139, 094903 CrossRef PubMed.
- B. M. Law, J.-M. Petit and D. Beysens, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 5782 CrossRef CAS.
- A. J. Archer, R. Evans, R. Roth and M. Oettel, J. Chem. Phys., 2005, 122, 084513 CrossRef CAS PubMed.
- T. F. Mohry, A. Maciołek and S. Dietrich, J. Chem. Phys., 2012, 136, 224902 CrossRef CAS PubMed; T. F. Mohry, A. Maciołek and S. Dietrich, J. Chem. Phys., 2012, 136, 224903 CrossRef PubMed.
- H. W. Diehl, Int. J. Mod. Phys. B, 1997, 11, 3503 CrossRef.
- B. Derjaguin, Kolloid-Z., 1934, 69, 155 CrossRef.
- M. E. Fisher and P. J. Upton, Phys. Rev. Lett., 1990, 65, 2402 CrossRef CAS PubMed; M. E. Fisher and P. J. Upton, Phys. Rev. Lett., 1990, 65, 3405 CrossRef PubMed.
- Z. Borjan and P. J. Upton, Phys. Rev. Lett., 2008, 101, 125702 CrossRef CAS PubMed.
- R. Okamoto and A. Onuki, J. Chem. Phys., 2012, 136, 114704 CrossRef PubMed.
- R. Okamoto and A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022309 CrossRef.
- F. Schlesener, A. Hanke and S. Dietrich, J. Stat. Phys., 2003, 110, 981 CrossRef CAS.
- S. Buzzaccaro, J. Colombo, A. Parola and R. Piazza, Phys. Rev. Lett., 2010, 105, 198301 CrossRef PubMed; R. Piazza, S. Buzzaccaro, A. Parola and J. Colombo, J. Phys.: Condens. Matter., 2011, 23, 194114 CrossRef PubMed.
- M. E. Fisher, Rep. Prog. Phys., 1967, 30, 615 CAS.
- A. Pelissetto and E. Vicari, Phys. Rep., 2002, 368, 549 CrossRef CAS.
- Note, that in ref. 23 the universal amplitude ratios are defined in terms of the amplitudes of the bulk correlation length ξ(2nd) (t, hb) defined via the second moment of the two-point correlation function of the bulk order parameter, whereas here we consider the so-called true bulk correlation length ξ(t, hb) defined by the exponential decay of the two-point correlation function of the bulk order parameter. The corresponding amplitude ratios are related by universal amplitude ratios23Q+ξ = ξ(0)+/ξ(2nd,0)+ ≈ 1 and Qcξ = ξ(0)h/ξ(2nd,0)h ≈ 1.
- M. Krech, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 1642 CrossRef CAS.
- J. G. Brankov, D. M. Danchev and N. S. Tonchev, Theory of critical phenomena in finite-size systems: scaling and quantum effects, Series in modern condensed matter physics, World Scientific, Singapore, 2000, vol. 9 Search PubMed.
- A. Gambassi, J. Phys.: Conf. Ser., 2009, 161, 012037 CrossRef.
- D. Dantchev, M. Krech and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 066120 CrossRef; D. Dantchev, F. Schlesener and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011121 CrossRef.
- M. N. Barber, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1983, vol. 8, p. 145 Search PubMed.
- S. Kondrat, L. Harnau and S. Dietrich, J. Chem. Phys., 2009, 131, 204902 CrossRef CAS PubMed.
- A. Hanke, F. Schlesener, E. Eisenriegler and S. Dietrich, Phys. Rev. Lett., 1998, 81, 1885 CrossRef CAS.
- M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, EPL, 2009, 88, 40004 CrossRef CAS; M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, J. Chem. Phys., 2010, 133, 074702 CrossRef PubMed; M. Labbe-Laurent, M. Tröndle, L. Harnau and S. Dietrich, Soft Matter, 2014, 10, 2270 RSC.
- M. Hasenbusch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022130 CrossRef.
- K. Binder, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1983, vol. 8, p. 2 Search PubMed.
- H. W. Diehl, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1986, vol. 10, p. 75 Search PubMed.
- S. Kondrat and M. Tröndle, F3DM library and tools, to be publicly released; the F3DM library can be downloaded from http://sourceforge.net/projects/f3dm/ Search PubMed.
- Z. Borjan, Application of local functional theory to surface critical phenomena, Ph.D. thesis, University of Bristol, Bristol, 1999.
- T. F. Mohry, Phase behavior of colloidal suspensions with critical solvents, Ph.D. thesis, University Stuttgart, Stuttgart, 2013, online available at OPUS the publication server of the University of Stuttgart, http://elib.uni-stuttgart.de/opus/volltexte/2013/8282/.
- P. Schofield, Phys. Rev. Lett., 1969, 22, 606 CrossRef CAS; B. D. Josephson, J. Phys. C: Solid State Phys., 1969, 2, 1113 Search PubMed; M. E. Fisher, in Fenomeni critici: Corso 51, Varenna sul Lago di Como, 1970, pp. 27.7.–8.8 Search PubMed; Proceedings of the International School of Physics “Enrico Fermi”, ed. M. S. Green, Academic, London, 1971, p. 1 Search PubMed.
- H. Nakanishi and M. E. Fisher, J. Chem. Phys., 1983, 78, 3279 CrossRef CAS.
- O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 041142 CrossRef CAS; O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 039902 CrossRef; O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, EPL, 2007, 80, 60009 CrossRef.
- T. F. Mohry, A. Maciołek and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061117 CrossRef CAS.
- O. A. Vasilyev and S. Dietrich, EPL, 2013, 104, 60002 CrossRef.
- A. Drzewiński, A. Maciołek and A. Ciach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5009 CrossRef.
- H. Si, http://wias-berlin.de/software/tetgen/.
- Gnu Scientific Library, http://www.gnu.org/software/gsl/.
- T. W. Burkhardt and E. Eisenriegler, Phys. Rev. Lett., 1995, 74, 3189 CrossRef CAS PubMed.
- T. G. Mattos, L. Harnau and S. Dietrich, J. Chem. Phys., 2013, 138, 074704 CrossRef CAS PubMed.
- C. Bauer, T. Bieker and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5324 CrossRef CAS.
- F. Pousaneh and A. Ciach, J. Phys.: Condens. Matter, 2011, 23, 412101 CrossRef PubMed; M. Bier, A. Gambassi, M. Oettel and S. Dietrich, EPL, 2011, 95, 60001 CrossRef; F. Pousaneh, A. Ciach and A. Maciolek, Soft Matter, 2012, 8, 3567 RSC.
- C. M. Sorensen and G. A. Larsen, J. Chem. Phys., 1985, 83, 1835 CrossRef CAS.
- J. D. Cox, J. Chem. Soc., 1952, 1952, 4606 RSC.
- A. A. Louis, J. Phys.: Condens. Matter, 2002, 14, 9187 CrossRef CAS.
- J. P. Hansen and I. R. McDonald, Theory of simple liquidsAcademic, London, 1976 Search PubMed.
- H. C. Andersen, J. D. Weeks and D. Chandler, Phys. Rev. A, 1971, 4, 1597 CrossRef.
- We have also considered the definition
 , where Ur(r) = U(r) − U(rmin) with U(r) attaining its minimum at rmin.
, where Ur(r) = U(r) − U(rmin) with U(r) attaining its minimum at rmin. - A. Hanke and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5081 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |
