Interplay between microdynamics and macrorheology in vesicle suspensions

Abstract

The microscopic dynamics of objects suspended in a fluid determines the macroscopic rheology of a suspension. For example, as shown by Danker and Misbah [Phys. Rev. Lett., 2007, 98, 088104], the viscosity of a dilute suspension of fluid-filled vesicles is a non-monotonic function of the viscosity contrast (the ratio between the viscosities of the internal encapsulated and the external suspending fluids) and exhibits a minimum at the critical point of the tank-treading-to-tumbling transition. By performing numerical simulations, we recover this effect and demonstrate that it persists for a wide range of vesicle parameters such as the concentration, membrane deformability, or swelling degree. We also explain why other numerical and experimental studies lead to contradicting results. Furthermore, our simulations show that this effect even persists in non-dilute and confined suspensions, but that it becomes less pronounced at higher concentrations and for more swollen vesicles. For dense suspensions and for spherical (circular in 2D) vesicles, the intrinsic viscosity tends to depend weakly on the viscosity contrast.

---

I. Introduction

Rheological properties of complex fluids (e.g. suspensions or emulsions) are not yet fully understood. Their macroscopic behavior is tightly coupled in a non-trivial way to the dynamics of their components at the microscale. Understanding this interplay is of importance for many fundamental and practical applications. Many constitutive laws have been proposed since the pioneering works of Einstein¹ and Batchelor² for the rheology of suspensions, in particular for rigid particles. Suspensions of fluid-filled deformable objects are a sub-class of complex fluids for which rheology depends on the deformability of the suspended particles and on the nature of the fluid they encapsulate. The most known and studied case is blood. How blood flows results from the micro-structuration of its components, mainly red blood cells (RBCs). For example, the Fåhræus–Lindqvist³ effect in blood vessels – the blood viscosity decreases with the vessel width is reduced – is caused by the lateral migration of RBCs towards the center of the vessel. Another example is the effect first proposed by Danker and Misbah⁴ which is observed for dilute suspensions of vesicles: following from the dynamical state of each vesicle at the microscale, the shear viscosity of the suspension varies in a non-monotonic way as a function of the viscosity contrast Λ (the ratio between the viscosities of the suspending and the encapsulated fluids).

Vesicles undergo mainly two states of motion under shear flow: either tank-treading (the particle assumes a steady angle with the flow direction, while its membrane undergoes a tank-treading-like motion) or tumbling (the particle rotates around its center of mass).⁵ At lower viscosity contrasts, a particle tank-treads (TT) and at higher viscosity contrasts it tumbles (TB). One way to trigger the transition from TT to TB is by solely increasing Λ beyond a threshold Λ_C. At this critical point, the viscosity of the suspension changes from a decreasing to an increasing function of Λ. Danker and Misbah predicted this effect theoretically⁴ and it was later confirmed experimentally⁶ and numerically using the boundary integral method.^7–10 A similar trend was also observed for RBCs⁶ and capsules.¹¹ However, recent numerical simulations by Lamura and Gompper¹² (based on the multi-particle collision dynamics method) did not capture this effect. Instead, the viscosity is found to be a monotonically increasing function of the viscosity contrast in the range 1 ≤ Λ ≤ 10, somehow similar to the rheological behavior of an emulsion.^7,13 In the same range of Λ, experiments of Kantsler et al.¹⁴ revealed also a monotonic behavior of the viscosity, but as a purely decreasing function of Λ. Thus, there is an apparent contradiction between different studies regarding the dependency of the vesicle suspension viscosity on the viscosity contrast.

In the present paper we recheck independently for the existence of the Danker–Misbah effect using an alternative simulation technique based on the lattice-Boltzmann and the immersed boundary methods.^15,16 As in ref. 12 we consider a confined geometry and a non-zero Reynolds number. The main observable is the intrinsic viscosity η and the main control parameter is the viscosity contrast Λ. We study how the dependence of η on Λ changes when varying the concentration ϕ, the capillary number Ca (via the membrane rigidity) and the swelling degree Δ. We capture the non-monotonic behavior of the viscosity as proposed by Danker and Misbah and find that it persists even when varying ϕ, Ca or Δ. It only becomes less pronounced for denser suspensions or for very swollen vesicles, but it does not show a monotonically increasing/decreasing behavior with Λ as reported in ref. 12 and 14. We explain this disagreement and provide insight into the origins that lead to this apparent contradiction.

II. Simulation method

We only give a short overview on the algorithm and refer to our previous articles for more details.^15–17

Fluid dynamics

The dynamics of the involved fluids is simulated using the lattice-Boltzmann method (LBM).^18,19 The LBM is based on a discrete version of Boltzmann's equation and recovers the solutions of the Navier–Stokes equations in the limit of small Knudsen and Mach numbers. Our implementation combines the standard nine velocity model in two dimensions (D2Q9) with a single relaxation time Bathnagar–Gross–Krook collision scheme. The computational domain is a channel with length L_x and height L_y. At the inlet and outlet of the channel, periodic boundary conditions are imposed. At the bottom a mid-grid bounce back no-slip boundary is set. The top no-slip boundary is translated from left to right with a steady velocity u_tw = L_yγ, where γ is the shear rate.

Vesicles

Vesicles are closed lipid membranes. They encapsulate an internal fluid and are suspended in an external fluid. Their membrane experiences resistance towards bending and compressing/stretching deformation modes. This gives rise to a restorative force which in 2D is given byHere, c is the local membrane curvature, κ is the bending modulus (the membrane rigidity), and s is the arclength coordinate along the membrane. n and t are the normal and tangential unit vectors, respectively. ζ is the effective tension field that enforces the local inextensible character of the membrane, which leads to the conservation of the vesicle perimeter P. A detailed derivation of the membrane force can be found in ref. 20. In addition, we consider that the fluids, inside and outside the vesicles, to be incompressible Newtonian fluids. This latter leads to the conservation of the vesicle enclosed area A.

Viscosity contrast

The viscosity contrast Λ is defined as the ratio of the internal to the external fluid viscosities. Here, we restrict ourselves to 1 ≤ Λ ≤ 20. In order to achieve this numerically, the LBM relaxation time, that is related to the viscosity,¹⁹ is adjusted depending on whether a fluid node is located inside or outside a vesicle using the even-odd rule.¹⁶

Vesicle-fluid coupling

We couple the fluid flow and the vesicle dynamics using the immersed boundary method (IBM):²¹ an Eulerian regular fixed mesh represents the fluid, while the vesicles are modeled as Lagrangian moving meshes. The first step consists in computing the fluid flow with the LBM, as if the membrane does not exist. Then, the velocity of each membrane point is computed by interpolation of the velocities of its surrounding fluid nodes. The membrane is advected, deformed and adopts a new out-of-equilibrium shape. Afterwards, the restoring membrane force (eqn (1)) is evaluated and exerted on the surrounding fluid. These two steps provide a fluid-structure two-way coupling causing the motion of the vesicles and the disturbance of the externally applied flow.

Rheology

The effective viscosity η* of a suspension – consisting of the suspending fluid and its suspended vesicles – under shear flow is calculated usingwhere 〈σ_xy(t)〉 are the hydrodynamic stresses averaged on the bounding walls,¹⁵

We introduce the dimensionless quantity,

where η₀ is the viscosity of the external suspending fluid and ϕ the concentration of the vesicles. η(t) measures the deviation of η* (the viscosity of the fluid in the presence of the vesicles) from η₀ (the viscosity of the fluid in the absence of vesicles) normalized by the quantity η₀ϕ. Following ref. 6 and 12, we call this quantity the intrinsic viscosity, even though we use it not only in the very dilute limit. Other authors rather call it the normalized effective viscosity¹⁰ or the normalized suspension viscosity.¹⁴ We further use the average of η(t) over time

The first t_s = 3 × 10⁵ timesteps (γt_s = 62.49) are ignored in order to assure that the system has reached a quasi-steady regime. Data is then taken until the final timestep t_f = 10⁶ (γt_f = 208.3). In this time interval [t_s, t_f] the system is in the quasi-steady regime in all simulations – independent of the chosen values of the input parameters. This quasi-steady regime is characterized by fluctuations of the instantaneous intrinsic viscosity around an average value.

Parameters

We consider a simulation box with size L_x = L_y = 200 (lattice units) that represents the suspending fluid and boundary conditions as introduced above. In all simulations, we generate a linear shear flow with a fixed shear rate γ = 2.083 × 10⁻⁴ (lu). N vesicles which are characterized by their effective radius R₀ = 20 (lu) and their swelling degree Δ = 4πA/P² (in 2D) are placed inside the box. The swelling degree is kept at Δ = 0.8 if not stated otherwise. The conservation of P and A in our numerical scheme is achieved using: (i) the Lagrangian multiplier field in eqn (1): ζ(s, t) = κ_P[Δs(s, t) − Δs(s, t₀)], where Δs(s, t) and Δs(s, t₀) are the distance between two adjacent membrane nodes at time t and t₀, respectively (ii) even though the enclosed fluid is to good approximation an incompressible Newtonian fluid, slight variations of A are observed because of numerical errors.¹⁵ To further ensure the conservation of A an additional term κ_A(A − A₀)n is introduced in eqn (1), where A₀ is the initial area of a vesicle. We set κ_P = 3 (lu) and κ_A = 0.01 (lu).

Below we present our results as a function of six dimensionless control parameters:

(1) The Reynolds number Re = ρ₀γR₀²/η₀, which quantifies the importance of the inertial forces versus the viscous forces; ρ₀ is the density of the suspending fluid. We keep Re = 0.5 in all simulations.

(2) The capillary number Ca = η₀γR₀³/κ, which gives the ratio between viscous and bending forces. Ca is a measure for the deformability of a vesicle. Larger Ca leads to larger deformations.

(3) The viscosity contrast Λ.

(4) The concentration ϕ of the vesicles in a suspension ϕ = NA/L_xL_y.

(5) The swelling degree Δ.

(6) The degree of confinement χ = 2R₀/L_y = 0.2. For this degree of confinement, the tank-treading-to-tumbling transition is expected to take place at a value of Λ_C = 7.8.¹⁶

III. Results

A. Rheology of a fluid containing a single vesicle

We validated our computational method against the case of a single isolated vesicle (N = 1) which corresponds to the limit of a very dilute suspension (ϕ → 0). This case was previously studied numerically by Ghigliotti et al.^7,22 in 2D and in the limit of unbounded flow (χ = 0).

Here, we place a vesicle with Δ = 0.8 in a channel with confinement χ = 0.2. We use the inclination angle θ – the angle between the flow direction and the main long axis of the vesicle – as an order parameter to classify if a vesicle is in the TT (θ is steady in time) or in the TB state (θ varies periodically in time). Fig. 1a shows the evolution in time (γt) of the inclination angle θ of a vesicle in the TT state (Λ = 4) and another one in the TB state (Λ = 16). We compute the instantaneous intrinsic viscosity η(t) of the fluid suspending each of these two vesicles using eqn (4) and we show in Fig. 1b how η(t) evolves in time. The vesicle in the TT state performs a steady motion, therefore, the hydrodynamic stresses exerted on the bounding walls remain also steady in time. This is why η(t) does not change in time for a tank-treading vesicle. For the tumbling vesicle, the hydrodynamic stresses on the walls vary periodically in time with the same frequency as the inclination angle θ. This is the reason for the viscosity exhibiting a time-dependent behavior for a tumbling vesicle. The rheological behavior and its correlation with the dynamics reported in Fig. 1 are consistent with the results of ref. 7.

Fig. 1 (a) Evolution in time (rescaled time γt) of the inclination angle θ (in degrees) of two vesicles: one in the TT state (Λ = 4) and the other one in the TB state (Λ = 16). The tank-treading vesicle assumes a steady inclination angle while the tumbling vesicle assumes a periodic angle. (b) The corresponding evolution in time of the instantaneous intrinsic viscosity η(t) in the TT state (Λ = 4) and in the TB state (Λ = 16). The vesicle in the TT regime performs steady motion and so does its viscosity. For the TB vesicle, the viscosity evolves in a periodic manner in time. The two figures recover qualitatively the same behavior as reported in ref. 7 computed with 2D boundary integral method simulations, in the limit of an unbounded suspending fluid (χ = 0). Here, the confinement is set to χ = 0.2. Other parameters are: Re = 0.5, Ca = 10, Δ = 0.8.

Using eqn (5) we obtain the average intrinsic viscosity η which is reported as a function of Λ in Fig. 2. The horizontal line at η = 2 is the Einstein coefficient ref. 1 in 2D (ref. 7) (the intrinsic viscosity of an unbounded fluid suspending a single rigid spherical particle). We see that η behaves differently depending on whether the vesicle performs TT or TB. η decreases with Λ in the TT regime, because θ decreases with Λ. The vesicle aligns with the flow direction and thus its surrounding fluid experiences less resistance. η continues to decrease with Λ until it drops down to a minimum at exactly Λ_C, the critical viscosity contrast at which the TT–TB transition occurs. Beyond this critical point, in the tumbling regime, η increases again with Λ. For a tumbling vesicle, the viscous dissipation and the stresses on the walls increase with Λ. This leads to the increase of η with Λ. Fig. 2 clearly shows that the intrinsic viscosity η of a fluid containing a single vesicle is a non-monotonic function of the viscosity contrast Λ. It is a decreasing function in the TT regime and an increasing function in the TB regime. It changes its behavior at a minimum that coincides with the critical transition point of the TT–TB transition. This observation agrees (qualitatively) with the previous analytical work of Danker and Misbah⁴ and the numerical work of Ghigliotti et al.⁷ In contrast to the work of those authors our Reynolds number Re = 0.5 is not zero and the vesicle is confined (χ = 0.2), but we also recover the predicted non-monotonic behavior of η versus Λ.

Fig. 2 The intrinsic viscosity η of a fluid suspending a single vesicle versus the viscosity contrast Λ. As Λ increases in the TT regime η decreases until it reaches a minimum at a value of Λ that corresponds to the point of the transition from TT to TB. Beyond this critical value, η increases with Λ in the TB regime. This non-monotonic behavior of η towards increasing Λ agrees with the analytical and numerical works performed in the unbounded limit (χ = 0) and for a single vesicle (dilute limit ϕ → 0).^4,7 The horizontal line at η = 2 is the Einstein coefficient in 2D.^1,7 Other parameters: Re = 0.5, Ca = 10, Δ = 0.8 and χ = 0.2.

B. Effect of concentration ϕ

The concentration ϕ of a suspension is varied by increasing/decreasing the number of its vesicles N, while keeping the size of the simulation box constant. We consider three suspensions with concentrations ϕ = 7.5%, 15.1% and 22.6% corresponding to 3, 6 and 9 vesicles, respectively. After the system has reached a quasi steady state, we measure the intrinsic viscosity η(t). Fig. 3 depicts how η(t) evolves in time for two suspensions having the same ϕ = 15.1%, but different viscosity contrast: Λ = 4 and 16. For both cases, η(t) evolves in an unsteady way, even for the non-tumbling vesicles (for Λ = 4). It largely fluctuates and sometimes shows higher sharp peaks. These fluctuations are correlated with how the vesicles rearrange themselves in response to the applied flow. Fig. 4 shows snapshots taken at equal time intervals displaying the motion of vesicles with Λ = 4. For this low viscosity contrast, vesicles are in the tank-treading state. They pass each other while assuming almost the same steady inclination angle. Collisions of hydrodynamic nature occur occasionally and become more frequent upon increasing concentration ϕ. When two vesicles collide, as is the case for the red- and the blue-colored vesicles in Fig. 4, their respective inclination angle reaches a maximum at the moment of the collision (see Fig. 4c and d) as observed also experimentally.^14,23 This event increases the flow resistance, which is amplified by the presence of the bounding walls. Here, the two interacting vesicles have no way to move farther away from each other, in contrast to the case of unbounded suspensions. Thus, they collide later with other neighboring vesicles or with the walls. This latter effect results in exerting firm stresses upon the walls and causes the peaks of η(t) observed in Fig. 3. In Fig. 5, we show snapshots for the suspension with Λ = 16, a higher value for which vesicles are expected to undergo tumbling. However, we can clearly see that vesicles do not have sufficient free space around them to tumble. Each vesicle is surrounded and hindered by others. Thus, vesicles are forced to undergo the tank-treading motion, although they would tumble in free space. The area available for vesicles to tumble reduces dramatically when increasing ϕ. In the time window represented in Fig. 5 only one vesicle is tumbling (the red-colored vesicle in the top-half of the simulation box). Another observed feature in Fig. 5 is the formation of a rouleau-like structure of a given number of vesicles that performs a collective tumbling motion. When the main axis (dashed line) of this chain of vesicles is perpendicular to the bounding walls it results in an increased effective viscosity. The formation of the rouleau-like structure is not a usual behavior. For example, it has not taken place in the simulation presented in Fig. 4.

Fig. 3 Evolution in time of the instantaneous intrinsic viscosity η(t) of two suspensions with the same concentration ϕ = 15.1% (that corresponds to 6 vesicles), but with different viscosity contrast: Λ = 4 and Λ = 16. η(t) fluctuates because of the motion and the ordering of the vesicles in response to the applied external shear flow. The large peaks in η(t) are caused by the events of the vesicle–vesicle and vesicle–wall hydrodynamic collisions. Other parameters: Re = 0.5, Ca = 10, Δ = 0.8 and χ = 0.2.

Fig. 4 Snapshots taken at equal time intervals showing the motion of six vesicles (ϕ = 15.1%) with a viscosity contrast Λ = 4 in shear flow. The flow direction is from left to right. The background color map shows the pressure field that develops around the vesicles. Red-colored regions correspond to regions with higher pressure, while blue-colored ones corresponds to lower pressure. The two blue- and red-colored vesicles undergo a hydrodynamic collision. All vesicles perform TT with a steady prolate shape and assume almost the same steady positive inclination angle. Only the angles of the colliding vesicles vary and reach a maximum at the moment of the collision (d). Other parameters: Re = 0.5, Ca = 10, Δ = 0.8 and χ = 0.2.

Fig. 5 Snapshots taken at equal time intervals showing the motion of six vesicles (ϕ = 15.1%) with viscosity contrast Λ = 16 in shear flow. The background color map shows the pressure field that develops around the vesicles. In the time window shown here, all vesicles undergo TT except the one colored in red. For Λ = 16, vesicles are expected to tumble, but because of the confinement and the vesicle–vesicle hydrodynamical interaction, the tumbling motion is inhibited. All vesicles adhere to shapes which largely deviate from the prolate shape a free vesicle would adopt. These shapes result on the one hand from the collisions that lead to deformations and on the other hand from the long time they require to recover their equilibrium shape. Another observed feature is the formation of a rouleau-like structure of a given number of vesicles that performs a collective tumbling motion. When the main axis (dashed line) of this chain of vesicles is perpendicular to the bounding walls it results in an increased effective viscosity.

In Fig. 6 we report the intrinsic viscosity η versus the viscosity contrast Λ for three different concentrations: ϕ = 7.5%, 15.1% and 22.6%. Further, we provide the data corresponding to the case of a single vesicle (ϕ = 2.5%) as a reference. We observe that by increasing the concentration, the intrinsic viscosity increases. The curve of η versus Λ shifts towards higher values of η. The more vesicles we have, the higher is the chance for vesicle–vesicle and vesicle–wall collisions, which leads to an increase of the flow resistance. By increasing ϕ, Λ at which η reaches a minimum changes the value without a clear trend. This is not consistent with the observation in ref. 9 stating that the minimum of η occurs at higher Λ with increasing ϕ. However, Fig. 1 in ref. 6 clearly demonstrates that the minimum of the viscosity of red blood cell suspensions occurs at lower Λ with increasing ϕ. The non-increasing behavior of η as a function of ϕ observed here and in ref. 6 maybe attributed to the low swelling degree of our vesicles Δ = 0.8 and of the red blood cells Δ = 0.65, in contrast to the vesicles used in ref. 9 which have Δ = 0.90.

Fig. 6 The intrinsic viscosity η versus the viscosity contrast Λ of four suspensions with concentrations ϕ = 2.5%, 7.5%, 15.1% and 22.6%. The vertical lines denote the minima of the curves. For every given value of Λ, a suspension becomes more and more viscous with increasing ϕ. For the dense suspension (ϕ = 22.6%), the non-monotonic behavior of η with Λ is less pronounced. Furthermore, the viscosity contrast of the minimum of η does not vary in a monotonic way with ϕ. Other parameters: Re = 0.5, Ca = 10, Δ = 0.8 and χ = 0.2.

The transition from decreasing to increasing behavior of η as a function of Λ becomes less pronounced for larger ϕ. If we extrapolate the trend of η versus Λ to higher values of ϕ (the limit of dense suspensions) we expect η to be an almost constant function that does not depend on Λ. At a higher concentration (ϕ = 22.6%), we observe a continuous cross-over from vesicles with lower to the ones with higher viscosity contrast. For denser suspensions, the tumbling is inhibited because of the vesicle–vesicle and vesicle–wall hydrodynamic interactions (collisions) that become more frequent. In this limit, the details of the dynamics of each individual vesicle are irrelevant to the rheology of vesicle suspensions.

For each concentration, we also measure the thickness of the vesicle-free boundary layer δ defined as the thickness of the gap that develops between the wall and the core vesicle-rich region of a suspension. The vesicle-free boundary layer is due to the wall-induced lift force that pushes vesicles away from the wall and results in their complete absence close to the wall. In Fig. 7 we report δ (averaged in time and scaled by the vesicle size) versus the viscosity contrast Λ for three suspensions with concentrations ϕ = 7.5%, 15.1% and 22.6%. For these three concentrations, δ/R₀ is a non-monotonic function of Λ. It increases for low Λ and then decreases for high Λ. Its maximum increases with increasing ϕ and it does shift towards lower values of Λ. The maximum of δ coincides neither with the critical viscosity contrast of the tank-treading-to-tumbling transition nor with the minimum of the intrinsic viscosity. This means that the intrinsic viscosity and the vesicle-free layer thickness are not correlated. Therefore, the non-monotonic behavior of η with Λ, which we capture in our study, is tightly correlated with the vesicle dynamics and not with the vesicle-free boundary layer thickness as is the case in ref. 12.

Fig. 7 The rescaled vesicle-free boundary layer δ/R₀versus the viscosity contrast Λ of three suspensions with concentrations ϕ = 7.5%, 15.1% and 22.6%. For all three concentrations, δ/R₀ increases for low Λ and then decreases for high Λ. Its maximum coincides neither with the critical viscosity contrast of the tank-treading-to-tumbling transition nor with the minimum of the intrinsic viscosity. It does shift towards lower values of Λ with increasing ϕ. Other parameters: Re = 0.5, Ca = 10, Δ = 0.8 and χ = 0.2.

C. Effect of deformability Ca

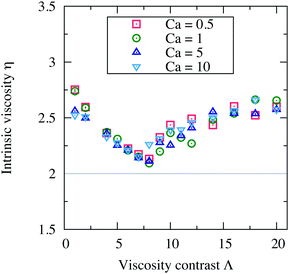
The capillary number, Ca = η₀γR₀³/κ, controls how the shape of a vesicle deforms in response to an applied external flow. Vesicles deform less when Ca ≪ 1 (limit of stiffer vesicles) and undergo larger deformation when Ca ≫ 1. We vary Ca by varying only the membrane rigidity κ. In this way, all other parameters and in particular the shear rate γ are hold constant assuring also a constant Reynolds number (Re = 0.5).

In Fig. 8, we report the intrinsic viscosity η versus the viscosity contrast Λ, for suspensions with concentration ϕ = 15.1% and with different capillary numbers: Ca = 0.5, 1, 5 and 10. It appears that the vesicle deformability (Ca) does not have any substantial effect on the viscosity of a suspension. η still varies in a non-monotonic way with Λ, but without any significant quantitative change when varying Ca. This is consistent with the results of ref. 7 and 9. Stiffer vesicles assume almost a similar steady inclination angle as deformable vesicles when tank-treading. For deformable vesicles, they tumble in an almost similar manner as stiffer vesicles; their tumbling period is less affected by the shape deformability. Ca affects the shape deformation but not as much the dynamics. Moreover, in 2D simulations, perfectly inextensible vesicles (the perimeter is kept constant) do not exhibit vacillating-breathing motion (trembling) observed theoretically and numerically for their 3D counterparts. The absence of this dynamical state of motion in 2D (direct transition from TT to TB even at higher Ca) is a further explanation of why η is insensitive to variations in Ca. That η does not depend on Ca means that the vesicle suspensions we study behave like a Newtonian fluid. A Ca-induced dynamical transition or Ca-induced variation of the free-vesicle boundary thickness are expected to lead to non-Newtonian behavior. For example, the vesicle suspensions studied in ref. 12 are non-Newtonian fluids exhibiting shear-thinning behavior.

Fig. 8 The intrinsic viscosity η versus the viscosity contrast Λ of four suspensions with different capillary numbers Ca: 0.5, 1, 5 and 10. The deformability of the vesicles does not have any notable effect on the macroscopic viscosity of the suspension. Other parameters: Re = 0.5, Δ = 0.8, χ = 0.2 and ϕ = 15.1%.

D. Effect of the swelling degree Δ

To investigate how the rheology of a suspension of vesicles is affected by varying the swelling degree Δ, we consider monodisperse suspensions consisting of 6 vesicles with size R₀. The swelling degree Δ = 4πA/P² is varied by swelling (deflating) vesicles, that is in 2D, by increasing (decreasing) A while holding the perimeter P of the vesicles constant. This change in the enclosed area effectively leads to a slight modification of the concentration: ϕ = 0.13% for Δ = 0.7, ϕ = 0.15% for Δ = 0.8, ϕ = 0.17% for Δ = 0.9 and ϕ = 0.19% for Δ = 1. All other parameters are similar to the above sections, except for Ca. Here, we opt for a smaller value (Ca = 0.5) in order to be able to capture the effect of vesicle shape (via Δ) while excluding the contribution of the shape deformation (induced by larger Ca).

In Fig. 9 the intrinsic viscosity η versus the viscosity contrast Λ is reported for various swelling degrees Δ: 0.7, 0.8, 0.9 and 1. Again, we observe the same non-monotonic trend of η as a function of Λ with a minimum. Here, η shifts upwards when increasing Δ. This is due to the increase of the flow resistance for more swollen vesicles Δ → 1 (the limit of circular-shaped vesicles in 2D). This observation agrees perfectly with the rheology of a single vesicle without viscosity contrast (Λ = 1): η is an increasing function of Δ.²² This was explained by the fact that the steady inclination of a tank-treading vesicle increases with Δ. However, for tumbling vesicles with viscosity contrast (see Fig. 9), the increase in η for larger Δ maybe attributed to the high tumbling frequency of less deflated vesicles, which favors rotation of vesicles and thus decreases the flow resistance. Moreover, we observe that the point of the minimum shifts to the right for larger Δ: deflated vesicles are more subject to tumbling motion than swollen vesicles. This agrees with the fact that the critical viscosity for a single vesicle increases with Δ.⁵ For Δ = 1 (circular vesicles in 2D), vesicles behave like rigid (circular) particles for which TT or TB states are meaningless, therefore, η does not exhibit the non-monotonic behavior with Λ. Instead, it assumes a constant value that is larger than the Einstein coefficient (η = 2), because of the influence of confinement and interaction between particles.

Fig. 9 The intrinsic viscosity η versus the viscosity contrast Λ of four suspensions with swelling degrees Δ = 0.7, 0.8, 0.9 and 1. η increases with Δ and its minimum shifts towards higher values of Λ. For Δ = 1, η is a constant and does not depend on Λ. Other parameters: Re = 0.5, Ca = 0.5, and χ = 0.2.

IV. Discussions and conclusions

In this article, we presented numerical simulations of the rheological behavior of vesicle suspensions under shear flow as a function of the viscosity contrast (the ratio between the viscosities of the encapsulated and the suspending fluids). Our two-dimensional fluid-structure simulations are based on a combination of the lattice-Boltzmann and the immersed boundary methods. The method has been benchmarked against previous works performed for the case of a single isolated vesicle suspended in unbounded creeping flow.^4,7 As those authors, we recover the non-monotonic behavior of the intrinsic viscosity versus the viscosity contrast – even in the presence of bounding walls and at non-zero Reynold number. In contrast to a recent work by Lamura and Gompper¹² we found that the effect proposed by Danker and Misbah⁴ persists even for non-dilute suspensions of vesicles and when we vary the deformability and the swelling degree of the vesicles. The effect becomes less pronounced at higher swelling degrees and at higher concentrations (limit of dense suspensions) where the tumbling motion is inhibited. This can be understood by means of the vesicle–vesicle and vesicle–wall hydrodynamic collisions that then become more important.

Let us now close the question about the origin of the apparent contradicting behaviors of the intrinsic viscosity versus the viscosity contrast (1 ≤ Λ ≤ 10) reported in different studies:^{4,6–10,12,14} if we disregard errors in the measurements, numerical artifacts or the contribution of thermal fluctuations, the influence of the wall confinement remains the main possible origin. Weak confinements, for example, χ = 0 in ref. 7 and 9 or χ = 0.2 in the present work, allow for the tank-treading-to-tumbling transition to take place. This dynamical transition, triggered solely by increasing the viscosity contrast, is the main responsible mechanism for the non-monotonic behavior of the intrinsic viscosity we observe. Increasing confinement delays the transition to the tumbling motion,¹⁶ as for example, in cone-plate rheometers.²⁴ This explains why in ref. 14 the intrinsic viscosity does not show an increasing behavior. The minimum (the transition point) is in fact expected to occur at higher values of the viscosity contrast. The authors even mentioned that their last data point, taken at Λ = 10, deviates from the decreasing monotonic behavior of the viscosity. For these experiments, one would capture the minimum and the increasing behavior of the intrinsic viscosity just by further increasing the viscosity contrast beyond Λ = 10. However, the data in ref. 12 are obtained at higher degrees of confinement (χ = 0.30 and 0.35). The walls are so close that they strongly influence the dynamics and the microstructures formed by the vesicles. In our case, such higher confinements do not even allow for the tank-treading-to-tumbling transition to take place at Λ < 7.8.¹⁶ In ref. 12 the interplay between the wall-induced lift force and increasing the viscosity contrast causes the vesicle-free boundary layer to become narrower, and results in higher intrinsic viscosity. This is similar to the Fåhræus–Lindqvist effect.³ Therefore, the observed monotonic increasing behavior of the intrinsic viscosity with the viscosity contrast in ref. 12 is mainly due to the variation of the vesicle-free boundary layer thickness, and not due to the vesicle dynamical transition as is the case for the Danker–Misbah effect. For these simulations, the wall effects are dominant and hide the contribution of the vesicle dynamical transition. Thus, in order to capture the Danker–Misbah effect one should decrease confinement to lower values, as is done in the present work.

Acknowledgements

We thank Chaouqi Misbah and the anonymous referees for valuable comments, and NWO/STW for financial support (VIDI grant 10787 of J. Harting).

References

1. A. Einstein, Ann. Phys., 1906, 19, 289.
2. G. K. Batchelor, J. Fluid Mech., 1970, 41, 545.
3. R. Fåhræus and T. Lindqvist, Am. J. Phys., 1931, 96, 562.
4. G. Danker and C. Misbah, Phys. Rev. Lett., 2007, 98, 088104.
5. J. Beaucourt, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 011906.
6. V. Vitkova, et al. , Biophys. J., 2008, 95, 33.
7. G. Ghigliotti, T. Biben and C. Misbah, J. Fluid Mech., 2010, 653, 489.
8. H. Zhao and E. S. G. Shaqfeh, J. Fluid Mech., 2011, 674, 578.
9. H. Zhao and E. S. G. Shaqfeh, J. Fluid Mech., 2013, 725, 709.
10. M. Thiébaud and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062707.
11. P. Bagchi and R. M. Kalluri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 056320.
12. A. Lamura and G. Gompper, EPL, 2013, 102, 28004.
13. M. R. Kennedy, C. Pozrikidis and R. Skalak, Comput. Fluids, 1994, 23(2), 251.
14. V. Kantsler, E. Serge and V. Steinberg, EPL, 2008, 82, 58005.
15. B. Kaoui, J. Harting and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 066319.
16. B. Kaoui, T. Krüger and J. Harting, Soft Matter, 2012, 8, 9246.
17. B. Kaoui, T. Krüger and J. Harting, Soft Matter, 2013, 9, 8057.
18. R. Benzi, S. Succi and M. Vergassola, Phys. Rep., 1992, 222, 145.
19. D. Raabe, Modell. Simul. Mater. Sci. Eng., 2004, 12, 13.
20. B. Kaoui, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 021903.
21. C. S. Peskin, Acta Numerica, 2002, 11, 479.
22. G. Ghigliotti, et al. , ESAIM: Proceedings, 2009, 28, 211.
23. M. Levant, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 056306.
24. T. M. Fischer and R. Korzeniewski, J. Fluid Mech., 2013, 736, 351.

---