Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mode-coupling analysis of residual stresses in colloidal glasses
S.
Fritschi
a,
M.
Fuchs
a and
Th.
Voigtmann
*abc
aFachbereich Physik, Universität Konstanz, 78457 Konstanz, Germany. E-mail: thomas.voigtmann@dlr.de
bZukunftskolleg, Universität Konstanz, 78457 Konstanz, Germany
cInstitut für Materialphysik im Weltraum, Deutsches Zentrum für Luft- und Raumfahrt (DLR), 51170 Köln, Germany
First published on 1st April 2014
Abstract
We present results from computer simulation and mode-coupling theory of the glass transition for the nonequilibrium relaxation of stresses in a colloidal glass former after the cessation of shear flow. In the ideal glass, persistent residual stresses are found that depend on the flow history. The partial decay of stresses from the steady state to this residual stress is governed by the previous shear rate. We rationalize this observation in a schematic model of mode-coupling theory. The results from Brownian-dynamics simulations of a glassy two-dimensional hard-disk system are in qualitative agreement with the predictions of the theory.
1 Introduction
Amorphous soft solids that are produced by flowing them into shape (entailing a quench into a nonequilibrium glassy state) display residual stresses.1,2 The internal stresses that build up during flow do not relax fully, so that some part of them persists in the solid that is formed by kinetic arrest in the fluid; indefinitely, in the ideal-glass case. This was recently demonstrated qualitatively for a simple setup where glass-forming colloidal suspensions of nearly-hard-sphere particles were observed after cessation of steady shear from their nonequilibrium stationary state (NESS), combining macroscopic and microscopic experiment, computer simulation, and mode-coupling theory of the glass transition (MCT).1In fact, the appearance of persistent residual stresses is known empirically since centuries, and is neither restricted to soft solids, nor to amorphous ones. An early demonstration involves small drops of molten (ordinary window) glass that fall into cold water and thus solidify very rapidly. These drops, known as Prince Rupert's drops or Dutch tears since the 17th century,3 have a surprisingly shock-resistant body (capable of withstanding the blow of a hammer) but explode dramatically upon the slightest damage done to their tail. The high mechanical stability arises from a shield of compressive residual stresses along the drop's surface that compensates high tensile stresses in the less rapidly cooled inner material and acts to stop crack formation.3–5 Clipping the tail releases this frozen-in network of residual stresses, rendering the material less strong, and in this case even unstable.6 Under normal conditions, the residual-stress network on the other hand is stable over decades in time. Safety glass and modern smartphone cover glasses (where chemical processes are used to impose residual stresses) exploit this effect to fine-tune the desired mechanical properties of the product.7–9 Aside from the amorphous state, residual stresses are decisive for the fatigue crack growth and hence the long-term stability of railway rails under the strong external forces caused by trains.10,11 One encounters residual-stress related material phenomena even in biophysics. For example the cytoskeleton of cells is prestressed (mainly due to the action of myosin motors).12 The unsurpassed material properties of spider silk are attributed to residual stresses.13 The control of residual stresses during the production stage is decisive in tuning the long-term stability of certain thin polymer films.14
Shear cessation experiments15,16 arguably provide the cleanest setup to investigate residual stresses. Close to kinetic arrest, cessation experiments have addressed the relaxation of stresses17 and the evolution of linear viscoelastic moduli after the cessation of flow18,19 in laponite gels, and aging effects in depletion gels.20 We consider even simpler model systems with hard-sphere like interactions, at fixed temperature and density, initially subject to homogeneous, stationary simple-shear flow. Residual stresses arise when the system does not relax back to equilibrium after cessation of the flow, but gets trapped in a nonergodic state on the way. This is the case for (ideal) glasses, the quiescent state of which is nonergodic, but which fluidize under shear, allowing the start of the cessation experiment from a well-defined, unique NESS.
We seek to improve the first-principles theoretical understanding of residual stresses: they are definitely a nonequilibrium and nonlinear-response effect, and are found to depend strongly on the history of past material deformation. For colloidal suspensions as model soft solids, the combination of an integration-through transients (ITT) approach to the nonlinear response with the mode-coupling theory of the glass transition (MCT)21–24 allows us to address such issues starting from a particle-based microscopic description. The theory predicts shear-rate dependent residual stresses after the cessation of steady shear,1 in qualitative agreement with experiment and simulation.
It should be stressed that the theoretical modeling of residual stresses is far from trivial. A successful model used to describe the nonlinear time-dependent rheology of soft materials is the soft glassy rheology (SGR) model.25 Although it explicitly addresses the aging dynamics of kinetically arrested solids, it implies the relaxation of stresses back to zero after cessation of flow.26
In this article, we discuss residual stresses in model hard-sphere like glasses as explained by MCT. The theory predicts the persistence of a non-relaxing component of the stress after flow cessation and captures its strong dependence on past flow history and on the mechanism of yielding. We compare with Brownian dynamics computer simulations on a two-dimensional hard-sphere glass to test the predictions of the theory, finding qualitative agreement.
This paper is organized as follows: we describe in Section 2 the schematic-MCT model and give details of the event-driven Brownian-dynamics (ED-BD) simulations we performed. In Section 3, the main results for the partial relaxation of stresses, and their analysis using the schematic-MCT model is given. Section 4 presents conclusions and outlook.
2 Methods
We discuss the evolution of the shear stress σ(t) after the cessation of steady simple-shear flow with shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , instantaneously switched off at time t = 0. The time is measured in units of the free-particle Brownian relaxation time τ0 = d2/D0, where d is the diameter of the particles (the unit of length) and D0 is their free diffusion coefficient. Stresses are reported in these natural units, kBT/dD, where kBT is the energy associated with thermal fluctuations and D is the dimensionality (D = 2 for our BD simulations, and D = 3 for the theory, although this difference in dimensionality is not borne out in the schematic-MCT model).
, instantaneously switched off at time t = 0. The time is measured in units of the free-particle Brownian relaxation time τ0 = d2/D0, where d is the diameter of the particles (the unit of length) and D0 is their free diffusion coefficient. Stresses are reported in these natural units, kBT/dD, where kBT is the energy associated with thermal fluctuations and D is the dimensionality (D = 2 for our BD simulations, and D = 3 for the theory, although this difference in dimensionality is not borne out in the schematic-MCT model).
Flow cessation is implemented in the theory by assuming that instantaneously, for all t > 0, the (assumed) homogeneous velocity-gradient field vanishes everywhere. In our Brownian-dynamics simulations, this is reflected, but in comparison with molecular-dynamics (MD) computer simulations in general, and with experiment, one has to keep in mind that this is a simplification. If shear flow is imposed by moving boundaries, our discussion refers to the case where these boundaries are suddenly fixed at their current position, and held there so that no further strain relaxation is allowed. This is to be distinguished from zero-stress boundary conditions, where stress relaxation by adjusting the total strain would occur in addition.27,28 We also neglect the effect of transiently inhomogeneous flow fields as they might arise shortly after stopping the flow.29 The transients should be associated with a comparatively short timescale of transverse-momentum diffusion, as confirmed by thermostatted MD simulations.30,31
2.1 Theory
The integration-through transient32,33 approach to colloidal rheology assumes that the system is at rest and in Boltzmann equilibrium for the infinitely distant past, t → −∞. The flow is subsequently switched on and causes a nonequilibrium perturbation of the Smoluchwoski operator describing the temporal evolution of the N-particle distribution function. A formal manipulation allows us to derive the nonequilibrium, nonlinear generalization of the Green–Kubo relationship for the stress tensor.23,24 MCT inspires the subsequent approximation in terms of density fluctuations to wave vector![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . For the shear stress in simple shear flow along the x-direction and with gradient in the y-direction, one gets
. For the shear stress in simple shear flow along the x-direction and with gradient in the y-direction, one gets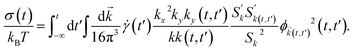 | (1) |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (t, t′) =
(t, t′) = ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) + kx
+ kx![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) yγtt′ is the shear-advected wave vector, describing the affine deformation of a plane-wave fluctuation through the accumulated strain
yγtt′ is the shear-advected wave vector, describing the affine deformation of a plane-wave fluctuation through the accumulated strain  between two points in time, t′ ≤ t. For the case of shear cessation, we set
between two points in time, t′ ≤ t. For the case of shear cessation, we set ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) =
(t) = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Θ(−t) with the Heaviside step function Θ. Eqn (1) consists of a history integral over transient density-correlation functions ϕ
Θ(−t) with the Heaviside step function Θ. Eqn (1) consists of a history integral over transient density-correlation functions ϕ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (t,t′)(t, t′) involving strain-dependent density–stress coupling vertices that are given in terms of the quiescent static structure factor Sk. The transient correlation function is defined as the equilibrium average of fluctuations evolved with the nonequilibrium dynamics. An important asset is that transient correlation functions only depend on the flow history between their two time arguments t′ and t, and are oblivious of any changes in the flow before t′.
(t,t′)(t, t′) involving strain-dependent density–stress coupling vertices that are given in terms of the quiescent static structure factor Sk. The transient correlation function is defined as the equilibrium average of fluctuations evolved with the nonequilibrium dynamics. An important asset is that transient correlation functions only depend on the flow history between their two time arguments t′ and t, and are oblivious of any changes in the flow before t′.
Eqn (1), together with the ITT-MCT equations for ϕ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (t, t′), allows us in principle to calculate the time-dependent shear stress in response to an arbitrary time-dependent shear flow
(t, t′), allows us in principle to calculate the time-dependent shear stress in response to an arbitrary time-dependent shear flow ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t), given the static structural factors of the system. To reduce the computational effort, one often employs an additional isotropic approximation; in ref. 1 such an isotropically sheared hard-sphere model (ISHSM) was solved for the case of shear cessation.
(t), given the static structural factors of the system. To reduce the computational effort, one often employs an additional isotropic approximation; in ref. 1 such an isotropically sheared hard-sphere model (ISHSM) was solved for the case of shear cessation.
In schematic-MCT models, the full equations of motion of the theory are simplified ad hoc, dropping the dependence on wave vectors. This emphasizes the temporal correlations as the main origin for nonlinear rheology close to the mode-coupling glass transition. One possible schematic simplification of eqn (1), in the following referred to as model A, reads34
 | (2) |
| G(t, t′) = vσϕ(t, t′)2. | (3) |
The dynamic shear modulus G(t, t′) entering eqn (1) is in the schematic model replaced by the square of the density correlation function. As a consequence, the integrand in eqn (2) is manifestly positive under steady shear. Yet, in many dense glass-forming systems, so-called stress overshoots are observed after the startup of steady shear for accumulated strains γ = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t of a few percentage (assuming shear flow to be started at t′ = 0). The resulting stress–strain curves σ(γ) display an intermediate maximum before decreasing towards the steady-state value, at about γ ≈ 0.1 for hard-sphere systems. The position and strength of this overshoot depend on the details of the interaction and the sample preparation and age.30,35,36 The overshoot corresponds to stress-over relaxation visible as a negative dip in G(t, 0) during the structural-relaxation process. It describes the capability of the viscoelastic system to transiently store more elastic energy than is maintained during plastic flow, and an elastic recoil process during yielding. Comparing the ITT Green–Kubo relationship, eqn (1), with its schematic simplification, eqn (2), one recognizes that reduction of the coupling coefficients driven by shear advection is missing from the schematic model. In the microscopic MCT model, a certain amount of negative coupling of density fluctuations into the stress can occur. One can interpret this reversible suppression as the effect of anelasticity on the average structure, rather than that of plasticity, which is expressed through the strain-induced irreversible decay of the correlation function.
t of a few percentage (assuming shear flow to be started at t′ = 0). The resulting stress–strain curves σ(γ) display an intermediate maximum before decreasing towards the steady-state value, at about γ ≈ 0.1 for hard-sphere systems. The position and strength of this overshoot depend on the details of the interaction and the sample preparation and age.30,35,36 The overshoot corresponds to stress-over relaxation visible as a negative dip in G(t, 0) during the structural-relaxation process. It describes the capability of the viscoelastic system to transiently store more elastic energy than is maintained during plastic flow, and an elastic recoil process during yielding. Comparing the ITT Green–Kubo relationship, eqn (1), with its schematic simplification, eqn (2), one recognizes that reduction of the coupling coefficients driven by shear advection is missing from the schematic model. In the microscopic MCT model, a certain amount of negative coupling of density fluctuations into the stress can occur. One can interpret this reversible suppression as the effect of anelasticity on the average structure, rather than that of plasticity, which is expressed through the strain-induced irreversible decay of the correlation function.
For the purpose of quantitative fits to such stress–strain curves, a schematic model (here referred to as model B) has been proposed, including an empirical term that captures the strain dependence of density-fluctuation–stress couplings by setting,37 with G(t, t′) = vσ(t, t′)ϕ(t, t′)2,
| vσ(t, t′) = v0σ(1 − (γtt′/γ*)4)exp[−(γtt′/γ**)4]. | (4) |
We denote here the obvious generalization of ref. 37 to non-steady shear. The parameters γ* and γ** model the position and width of the overshoot, and are adjusted to fit the experimental data. They show a weak dependence on the shear rate themselves in fits of the steady-shear rheology of a hard-sphere suspension.37 To keep the discussion simple, we neglect this and set γ* = 0.105γc and γ** = 0.14γc. This produces a pronounced stress overshoot in startup flow, allowing us to discuss the influence of the elastic-recoil effect on the stress relaxation after cessation in a qualitative way. The scale parameter v0σ is adjusted to match the dynamic yield stress with that of model A with a fixed vσ.
The equation of motion for the transient density correlation functions in the schematic MCT (for both models) reads34
 | (5) |
| m(t, t′′, t′) = h(t, t′)h(t, t′′)[v1ϕ(t, t′′) + v2ϕ(t, t′′)2]. | (6) |
Here, h(t, t′) is a function describing the suppression due to shear of the memory effects that cause the slow structural relaxation. v1 and v2 are the coupling coefficients of the model. They describe the thermodynamic state of the system. For small coupling coefficients, the quiescent solution of the F12 model is liquid like, where density fluctuations fully relax: ϕ(t, t′) → 0 as t − t′ → ∞. There is a line of critical coupling coefficients (v1c, v2c) identified as the ideal glass transition of the model, where a nonergodic solution ϕ(t, t′) → f > 0 first appears.38 Choosing the point determined by v2c = 2 ensures that the asymptotic dynamics of the F12 model matches with that expected for hard-sphere-like suspensions. For simplicity, we set v2 = 2 throughout. We introduce a separation parameter ε to indicate the distance to the glass transition: 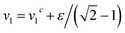 , where ε > 0 indicates glassy states with v1 > v1c, and ε < 0 liquid states with v1 < v1c.
, where ε > 0 indicates glassy states with v1 > v1c, and ε < 0 liquid states with v1 < v1c.
Accumulated strain decorrelates the MCT memory kernel; this is described by the empirical strain-reduction function h(t, t′) = 1/[1 + (γtt′/γc)2]. Here, γc = 0.1 is a parameter that sets the scale for the elastic limit of the solid.
The ITT-MCT equations of motion are solved numerically. We need to keep the full dependence of correlation functions on their two time arguments. However, for the transient correlation functions the calculation is eased by noting that for cessation of steady flow at t = 0, the time half-plane (t, t′ < t) can be split into three regions. In particular, for the two regions t > t′ > 0 and t′ < t < 0, the equations for the transient correlation functions restore time-translational invariance since the shear rate is constant between any pair (t′, t) there. The nontrivial predictions of the model all stem from the behavior of the two-time correlation functions spanning the cessation point, t′ < 0 < t. A numerical scheme to deal with these correlation functions in the case of step changes in shear rate has been devised.39
2.2 Simulation
We perform event-driven Brownian dynamics simulations40 for a 2D binary mixture of hard disks. The system consists of NA = 500 particles with diameter d = 1, and NB = 500 particles with diameter dB = 1.4, and has been widely studied as a model glass former,41,42 including its nonlinear rheology in the steady state, large-amplitude oscillatory shear, and the transient dynamics after shear startup.37,43–46 The only control parameter is the packing fraction φ giving the ratio of the volume occupied by all the disks to the volume of the system. The mode-coupling glass transition point of this binary mixture has been determined from extensive simulations,41φc ≈ 0.795. For comparison, jamming in this system occurs around φrcp ≈ 0.84,47 significantly above the density regime we are interested in.In this contribution, we focus on the shear-cessation dynamics of a glassy state, and set φ = 0.81 throughout. Brownian dynamics is approximated by a sequence of event-driven simulation steps of length τB, ensuring that no particle overlaps occur, after which the particles are assigned to new Gaussian random displacement vectors.40 For times t ≫ τB, the dynamics reflects that expected from the N-particle diffusion equation for hard spheres with a free-diffusion coefficient D0 = τB/2 in simulation units. We set τB = 0.01. The shear flow is imposed on the simulation by Lees–Edwards periodic boundary conditions,48 and by imposing a corresponding deterministic bias for the random displacements. The resulting stationary state is homogeneous for all the shear rates considered below.
Stresses are measured in ED-BD by associating with each “collision” of two Brownian particles i and j a momentum transfer Δ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) ij, where each Brownian displacement Δ
ij, where each Brownian displacement Δ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i is assigned to a velocity
i is assigned to a velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i = Δ
i = Δ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i/τB. The shear stress is then given by
i/τB. The shear stress is then given by
 | (7) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij(tc) is the separation vector between two particles during their collision. The sum runs over all collision times tc in a small time interval Δt used to smoothen the result. We choose Δt in the range [25τB, 150τB] ≡ [0.00125τ0, 0.75τ0] depending on the shear rate, and the time after startup and cessation (using smaller time intervals close to the points where the shear rate changes). To improve statistics at the largest shear rates (
ij(tc) is the separation vector between two particles during their collision. The sum runs over all collision times tc in a small time interval Δt used to smoothen the result. We choose Δt in the range [25τB, 150τB] ≡ [0.00125τ0, 0.75τ0] depending on the shear rate, and the time after startup and cessation (using smaller time intervals close to the points where the shear rate changes). To improve statistics at the largest shear rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 ≥ 4 × 10−1), averaging intervals up to Δt = 10τ0 have been used.
τ0 ≥ 4 × 10−1), averaging intervals up to Δt = 10τ0 have been used.
After startup of shear from a well-aged glassy configuration, the simulations were run up to an accumulated strain of γ = 1 to ensure that a steady state had been reached. The final steady-state configuration is used to set the origin of time thereafter. After cessation, runs were performed with up to 5 × 106 BD simulation steps, corresponding to a time t/τ0 = 2.5 × 104. To obtain sufficient statistics for the stresses, a large number Nr of independent simulation runs is required. We have used Nr = 393 (524, 801, 615, 392) runs for the calculation of σ(t) after cessation from shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 4 × 10−n with n = 0 (1, 2, 3, 4), supplemented with 359 (200, 187, 193) shorter runs (with 1 × 106 BD steps) for n = 1 (2, 3, 4).
τ0 = 4 × 10−n with n = 0 (1, 2, 3, 4), supplemented with 359 (200, 187, 193) shorter runs (with 1 × 106 BD steps) for n = 1 (2, 3, 4).
The results for σ(t) from the ED-BD simulations are shown in Fig. 1. The region ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t < 0 corresponds to simulations of startup shear, as discussed previously for this system37 and for MD simulations of similar model glass formers.30 This initial part of the σ-versus-
t < 0 corresponds to simulations of startup shear, as discussed previously for this system37 and for MD simulations of similar model glass formers.30 This initial part of the σ-versus-![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t curves reflects the stress–strain curves σ(γ) discussed in these references. They exhibit pronounced stress overshoot phenomena, a fact that will be related to the stress relaxation after cessation below. At the highest shear rate,
t curves reflects the stress–strain curves σ(γ) discussed in these references. They exhibit pronounced stress overshoot phenomena, a fact that will be related to the stress relaxation after cessation below. At the highest shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 4, one notices a small undershoot after the maximum in the stress–strain curve, and some smaller oscillations in σ(t) until the point where the shear was switched off. Therefore, some care has to be taken to interpret the results for this shear rate, and we will only discuss generic features that are qualitatively identical also for the lower shear rates. While the present ED-BD simulation algorithm remains a well-defined, overlap-free, rejection-free Monte Carlo scheme,40 its approximation of the Smoluchowski equation for the Brownian-particle motion becomes questionable for shear rates much larger than
τ0 = 4, one notices a small undershoot after the maximum in the stress–strain curve, and some smaller oscillations in σ(t) until the point where the shear was switched off. Therefore, some care has to be taken to interpret the results for this shear rate, and we will only discuss generic features that are qualitatively identical also for the lower shear rates. While the present ED-BD simulation algorithm remains a well-defined, overlap-free, rejection-free Monte Carlo scheme,40 its approximation of the Smoluchowski equation for the Brownian-particle motion becomes questionable for shear rates much larger than ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 ≈ 4.
τ0 ≈ 4.
3 Results and discussion
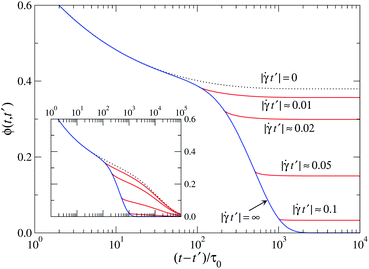
We first present results for the stress relaxation after simple-shear cessation in our two-dimensional Brownian dynamics simulation. Fig. 2 shows the shear stress σ(t) as a function of time t since cessation, for various shear rates. With increasing shear rate, the steady-state shear stress σss(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) increases; this is seen as the initial value of the σ(t) curves in Fig. 2. Some of this shear stress relaxes after cessation of flow, on a time scale set by the past shear rate. This is evidenced by the lower panel in the figure, where scaling of the normalized σ(t)/σss-versus-
) increases; this is seen as the initial value of the σ(t) curves in Fig. 2. Some of this shear stress relaxes after cessation of flow, on a time scale set by the past shear rate. This is evidenced by the lower panel in the figure, where scaling of the normalized σ(t)/σss-versus-![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t curves onto an apparent master curve is observed for an initial time window,
t curves onto an apparent master curve is observed for an initial time window, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t ≲ 0.1. Curves for lower pre-shear rates deviate from the master curve at previous rescaled times. For the highest shear rates, the decay at intermediate times is approximately described by a 1/
t ≲ 0.1. Curves for lower pre-shear rates deviate from the master curve at previous rescaled times. For the highest shear rates, the decay at intermediate times is approximately described by a 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t form (dash-dotted line in the figure).
t form (dash-dotted line in the figure).
 | ||
Fig. 2 Upper panel: stress relaxation σ(t) after cessation of shear flow from the nonequilibrium stationary state, for a two-dimensional Brownian dynamics simulation of a binary hard-disk system, at packing fraction φ = 0.81, for the shear rates from Fig. 1 as indicated. Dotted lines: results from a schematic-MCT model with a strain-dependent stress–density coupling vertex (model B, see text) for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 4 × 10−4 and 4 × 10−3 and separation from the glass transition ε = 0.0001. Dashed lines indicate the residual stress σ∞ (shown in Fig. 5) estimated from the simulation, see text. Lower panel: the same data, normalized to the steady-state stress (flowcurve) and as a function of rescaled time τ0 = 4 × 10−4 and 4 × 10−3 and separation from the glass transition ε = 0.0001. Dashed lines indicate the residual stress σ∞ (shown in Fig. 5) estimated from the simulation, see text. Lower panel: the same data, normalized to the steady-state stress (flowcurve) and as a function of rescaled time ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t. The dash-dotted line indicates a 1/ t. The dash-dotted line indicates a 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t law. t law. | ||
For long times, a nonzero plateau value is indicated in the simulations. Note that large fluctuations hamper the exploration of the long-time regime in the simulation; this is in particular true for the larger shear rates shown in Fig. 2. Here, the initial part of the relaxation covers around two orders of magnitude in stress, and hence reaches the noise limit of the statistical sampling. Nevertheless, the simulation data are compatible with the emergence of a finite long-time limit in the ideal glass, σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = limt→∞σ(
) = limt→∞σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ;t) > 0 i.e., a persistent residual stress. To demonstrate this, we have shown in Fig. 2 as dashed lines the time-averaged stress
;t) > 0 i.e., a persistent residual stress. To demonstrate this, we have shown in Fig. 2 as dashed lines the time-averaged stress ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) over the interval t/τ0 ∈ [9800, 25
over the interval t/τ0 ∈ [9800, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000] for the simulations with shear rates
000] for the simulations with shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 ≤ 4 × 10−2. For these cases,
τ0 ≤ 4 × 10−2. For these cases, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is significantly different from zero. Dotted lines in the upper panel of Fig. 2 show exemplary results from schematic MCT, discussed in more detail below, to highlight the expected behavior in the ideal glass. The theory result overestimates the amount of residual stress that persists in the glass, but describes the partial relaxation from the steady state. Our result corroborates previous MD simulation results for a binary Yukawa mixture with a dissipative-particle-dynamics thermostat and temperature as the control variable.1
is significantly different from zero. Dotted lines in the upper panel of Fig. 2 show exemplary results from schematic MCT, discussed in more detail below, to highlight the expected behavior in the ideal glass. The theory result overestimates the amount of residual stress that persists in the glass, but describes the partial relaxation from the steady state. Our result corroborates previous MD simulation results for a binary Yukawa mixture with a dissipative-particle-dynamics thermostat and temperature as the control variable.1
In MCT, a finite residual stress emerges since σ(t) is determined from the past flow history, and infinitely long-lasting memory effects in the ideal glass cause a nonvanishing contribution to the generalized dynamical modulus G(t, t′) from times t′ < 0 (i.e., before cessation) even as t → ∞. We will investigate the shape of these correlation functions in more detail below. Fig. 3 demonstrates the stress relaxation after the cessation of flow in the schematic-MCT models introduced above. A state in the ideal glass (distance parameter ε = 0.01; solid lines) was chosen. For comparison, we also show stress relaxation curves for a state point in the liquid (ε = −0.01; dashed lines). There, stresses ultimately relax to zero as the system reaches an equilibrium state again. This final relaxation is determined by the structural-relaxation time scale τα of the quiescent equilibrium correlation function, which is independent of the pre-shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Since the simulation data shown in Fig. 2 show relaxation essentially only on a time scale connected with
. Since the simulation data shown in Fig. 2 show relaxation essentially only on a time scale connected with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , this can be taken as an indicator that they are not connected with equilibrium-liquid like relaxation.
, this can be taken as an indicator that they are not connected with equilibrium-liquid like relaxation.
 | ||
Fig. 3 Stress relaxation σ(t) following cessation of stationary shear flow, calculated within schematic MCT for a state in the ideal glass (distance parameter ε = 0.01; solid lines), and in the liquid (ε = −0.01; dashed lines). Shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 10−4, 4 × 10−4, 4 × 10−3, and 4 × 10−2, as indicated by labels. Upper panel: with a strain-independent coupling coefficient in the schematic Green–Kubo relationship (model A). Lower panel: with strain-dependent coupling vσ(t, t′), eqn (4), as discussed in the text (model B). τ0 = 10−4, 4 × 10−4, 4 × 10−3, and 4 × 10−2, as indicated by labels. Upper panel: with a strain-independent coupling coefficient in the schematic Green–Kubo relationship (model A). Lower panel: with strain-dependent coupling vσ(t, t′), eqn (4), as discussed in the text (model B). | ||
Comparing with the simulation results, Fig. 2, one recognizes two main differences from schematic model A: in the simulation, the initial transient stress relaxation is stronger, so that the final residual-stress plateau is hardly discernible in a semi-log representation (upper panel of Fig. 2); only in a double-logarithmic representation (lower panel), the finite residual stress becomes apparent. The second difference concerns the dependence of the residual stress on the pre-shear rate: in the simulations, we observe σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) to be a decreasing function of increasing
) to be a decreasing function of increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . In schematic model A with fixed vertex vσ, the residual stress σ∞ instead increases with increasing pre-shear rate; this is also the case in the isotropic approximation to the microscopic ITT-MCT.1
. In schematic model A with fixed vertex vσ, the residual stress σ∞ instead increases with increasing pre-shear rate; this is also the case in the isotropic approximation to the microscopic ITT-MCT.1
The trend exhibited by the simulation results typically leads to a crossing of σ(t)-versus-t curves belonging to different ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Stronger shear causes higher steady-state stresses (so that the initial value of the σ(t) curve increases), but a larger amount of these stresses can relax after cessation from strong pre-shear, than from weaker pre-shear. Intuitively, stronger shear fluidizes the glassy structure more severely, allowing for more effective particle rearrangements in order to relax stresses after the driving is switched off. Note however that the decrease of σ∞ with increasing pre-shear rate is a general, but not a universal effect; it is observed in the MD simulations mentioned above, in experiments on hard-sphere-like suspensions of core–shell PS-PNIPAM particles, and also for hard-sphere suspensions of PMMA particles close to the glass transition.1 However, these PMMA suspensions at higher packing fraction displayed an increase of the residual stress with increasing pre-shear rate. Coincidentally, the systems for which a decreasing σ∞(
. Stronger shear causes higher steady-state stresses (so that the initial value of the σ(t) curve increases), but a larger amount of these stresses can relax after cessation from strong pre-shear, than from weaker pre-shear. Intuitively, stronger shear fluidizes the glassy structure more severely, allowing for more effective particle rearrangements in order to relax stresses after the driving is switched off. Note however that the decrease of σ∞ with increasing pre-shear rate is a general, but not a universal effect; it is observed in the MD simulations mentioned above, in experiments on hard-sphere-like suspensions of core–shell PS-PNIPAM particles, and also for hard-sphere suspensions of PMMA particles close to the glass transition.1 However, these PMMA suspensions at higher packing fraction displayed an increase of the residual stress with increasing pre-shear rate. Coincidentally, the systems for which a decreasing σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) was observed are also those with strong stress overshoot phenomena under startup flow.
) was observed are also those with strong stress overshoot phenomena under startup flow.
The different trends of σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) can indeed be connected to the amount of elastic recoil that causes the stress overshoots under startup flow. As explained above, schematic model A does not contain this mechanism. It only describes the relaxation of stresses due to irreversible, plastic rearrangements, in the theory identified as those that cause strain-induced decorrelation of advected density fluctuations. The introduction of a time-dependent coupling between stresses and those density modes, introduced into the schematic model by a time-dependent vertex vσ(t, t′), accounts for a further relaxation caused by anelastic deformation due to the affine effects of shear. Including this mechanism of stress overshoots indeed has the effect of reducing the residual stress σ∞(
) can indeed be connected to the amount of elastic recoil that causes the stress overshoots under startup flow. As explained above, schematic model A does not contain this mechanism. It only describes the relaxation of stresses due to irreversible, plastic rearrangements, in the theory identified as those that cause strain-induced decorrelation of advected density fluctuations. The introduction of a time-dependent coupling between stresses and those density modes, introduced into the schematic model by a time-dependent vertex vσ(t, t′), accounts for a further relaxation caused by anelastic deformation due to the affine effects of shear. Including this mechanism of stress overshoots indeed has the effect of reducing the residual stress σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) such that it becomes a decreasing function of increasing
) such that it becomes a decreasing function of increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The lower panel of Fig. 3 demonstrates this for model B with the time-dependent vertex with parameters γ* and γ** from eqn (4). With this choice, schematic model B reproduces the crossing of σ-versus-t curves observed in the simulation. Curves from model B corresponding to two shear rates used in the simulation,
. The lower panel of Fig. 3 demonstrates this for model B with the time-dependent vertex with parameters γ* and γ** from eqn (4). With this choice, schematic model B reproduces the crossing of σ-versus-t curves observed in the simulation. Curves from model B corresponding to two shear rates used in the simulation, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 4 × 10−4 and 4 × 10−3, albeit at a smaller distance parameter ε = 0.0001 (corresponding to the simulated state which is rather close to the glass transition), have also been added to the simulation results for comparison (the dotted line in Fig. 2). Note that we did not attempt to fit the simulation data by adjusting the model parameters.
τ0 = 4 × 10−4 and 4 × 10−3, albeit at a smaller distance parameter ε = 0.0001 (corresponding to the simulated state which is rather close to the glass transition), have also been added to the simulation results for comparison (the dotted line in Fig. 2). Note that we did not attempt to fit the simulation data by adjusting the model parameters.
The qualitative similarity between the MCT model and the simulation results becomes clearer in a double-logarithmic representation of σ(t) as a function of t or rescaled time ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t. This is shown for the schematic-MCT models in Fig. 4. As in the simulation results, one notes reasonably good data collapse for the normalized stress σ(t)/σss for intermediate rescaled times
t. This is shown for the schematic-MCT models in Fig. 4. As in the simulation results, one notes reasonably good data collapse for the normalized stress σ(t)/σss for intermediate rescaled times ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t: all liquid- and glass-state curves for the shear rates shown almost coincide with their initial relaxation from the steady-state value. It should however be noted that in the schematic-MCT models, this scaling does not hold strictly. This can in particular be noted for model B with the strain-dependent vertex, shown in the lower panel of Fig. 4. The relative amount of stress relaxation after cessation, Δσ∞ = (σss − σ∞)/σss, is described qualitatively and correctly by both variants of the schematic model: Δσ∞ increases as a function of increasing pre-shear rate, in agreement with all known experimental and simulation data.
t: all liquid- and glass-state curves for the shear rates shown almost coincide with their initial relaxation from the steady-state value. It should however be noted that in the schematic-MCT models, this scaling does not hold strictly. This can in particular be noted for model B with the strain-dependent vertex, shown in the lower panel of Fig. 4. The relative amount of stress relaxation after cessation, Δσ∞ = (σss − σ∞)/σss, is described qualitatively and correctly by both variants of the schematic model: Δσ∞ increases as a function of increasing pre-shear rate, in agreement with all known experimental and simulation data.
While the simulation results shown in Fig. 2 show indications of a decay ∼1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t, the schematic-MCT curves are significantly less steep. In model A with a fixed vσ, the initial decay approximately follows σ ∼ t−a with a ≈ 0.33 as expected from the asymptotic power law for relaxation onto the nonergodic plateau derived in MCT.38 The σ(t)/σss-versus-
t, the schematic-MCT curves are significantly less steep. In model A with a fixed vσ, the initial decay approximately follows σ ∼ t−a with a ≈ 0.33 as expected from the asymptotic power law for relaxation onto the nonergodic plateau derived in MCT.38 The σ(t)/σss-versus-![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t curves from the experimental data of ref. 1 similarly show a power-law-like relaxation regime, σ(t) ∼ (
t curves from the experimental data of ref. 1 similarly show a power-law-like relaxation regime, σ(t) ∼ (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t)−x. For the PS-PNIPAM system, one estimates x ≈ 0.5, while the PMMA suspension is described by an exponent x ≳ 0.67 close to the glass transition (φ = 0.587), and x ≈ 0.4 for the state that was investigated deeper in the glass (φ = 0.614).
t)−x. For the PS-PNIPAM system, one estimates x ≈ 0.5, while the PMMA suspension is described by an exponent x ≳ 0.67 close to the glass transition (φ = 0.587), and x ≈ 0.4 for the state that was investigated deeper in the glass (φ = 0.614).
It is worth noting that the soft glassy rheology model predicts such power law decay, with an exponent x that is identical to the SGR's effective temperature parameter,26 and independent of the shear rate. In the SGR model, one thus expects the stress relaxation to be slower and deeper in the glass, with x ≈ 1 close to the transition. In this respect, the initial decay of σ(t) observed in our simulations and in the PMMA suspensions follow this expectation, while the value x ≈ 0.5 observed for the PS-PNIPAM system is lower than expected (given that these experimental data correspond to a state not too far from the glass transition). The ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) -dependent slowing down of the stress relaxation (visible, e.g., in the lower panel of Fig. 2) interpreted as the approach to a finite residual stress is a feature that differs significantly from SGR.
-dependent slowing down of the stress relaxation (visible, e.g., in the lower panel of Fig. 2) interpreted as the approach to a finite residual stress is a feature that differs significantly from SGR.
Fig. 5 shows the dependence of the residual stress σ∞ = σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ;t = ∞) as a function of the previous shear rate
;t = ∞) as a function of the previous shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Symbols show experimental and simulation data. Values for σ∞ for three different hard-sphere-like colloidal suspensions were taken from ref. 1, where they had been determined as the stress reached at a fixed time towards the end of the measurement. We add our results from ED-BD computer simulations of the 2D hard-disk mixture (square symbols in the figure). Here, to determine σ∞, the simulated σ(t) curves have been averaged over a certain time window, as explained in connection with Fig. 2 (dashed lines here). In line with the discussion above, the residual stress values σ∞(
. Symbols show experimental and simulation data. Values for σ∞ for three different hard-sphere-like colloidal suspensions were taken from ref. 1, where they had been determined as the stress reached at a fixed time towards the end of the measurement. We add our results from ED-BD computer simulations of the 2D hard-disk mixture (square symbols in the figure). Here, to determine σ∞, the simulated σ(t) curves have been averaged over a certain time window, as explained in connection with Fig. 2 (dashed lines here). In line with the discussion above, the residual stress values σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) decrease with increasing pre-shear rate for most experimental and simulation data, with the exception of the highest-density PMMA suspension where an increase is observed. Note again that this latter result is a direct consequence of the experimental protocol, i.e., of keeping the overall strain fixed after flow cessation. Otherwise, the system should start to flow since the frozen-in residual stress σ∞ exceeds the dynamic yield stress – and hence likely also the static yield stress that determines the maximum stress the solid can sustain. Even for the cases where σ∞ < σss, slow creep should be the result of free-strain boundary conditions, leading to additional relaxation phenomena.36,49
) decrease with increasing pre-shear rate for most experimental and simulation data, with the exception of the highest-density PMMA suspension where an increase is observed. Note again that this latter result is a direct consequence of the experimental protocol, i.e., of keeping the overall strain fixed after flow cessation. Otherwise, the system should start to flow since the frozen-in residual stress σ∞ exceeds the dynamic yield stress – and hence likely also the static yield stress that determines the maximum stress the solid can sustain. Even for the cases where σ∞ < σss, slow creep should be the result of free-strain boundary conditions, leading to additional relaxation phenomena.36,49
 | ||
Fig. 5 Residual stress σ∞ as a function of pre-shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , in thermal units kBT/dD (D is the spatial dimension, separation parameters ε as labeled). Solid lines are σ∞( , in thermal units kBT/dD (D is the spatial dimension, separation parameters ε as labeled). Solid lines are σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) including a strain-dependent vertex in the Green–Kubo relationship (model B, separation parameters ε as labeled); dashed lines correspond to model A with a fixed vertex vσ. Dotted lines are the flow curves (steady-state stress σss as a function of shear rate) for model A. Filled symbols: σ∞ from experiment in D = 3 (PMMA suspensions at φ = 0.587: diamonds; at φ = 0.614: triangles; PS-PNIPAM suspensions close to the glass transition: circles), all from ref. 1, and from ED-BD simulations in D = 2 (squares). For the PS-PNIPAM data at the four lowest shear rates, open circles indicate σss. ) including a strain-dependent vertex in the Green–Kubo relationship (model B, separation parameters ε as labeled); dashed lines correspond to model A with a fixed vertex vσ. Dotted lines are the flow curves (steady-state stress σss as a function of shear rate) for model A. Filled symbols: σ∞ from experiment in D = 3 (PMMA suspensions at φ = 0.587: diamonds; at φ = 0.614: triangles; PS-PNIPAM suspensions close to the glass transition: circles), all from ref. 1, and from ED-BD simulations in D = 2 (squares). For the PS-PNIPAM data at the four lowest shear rates, open circles indicate σss. | ||
Lines in Fig. 5 show the results for the schematic-MCT model for several state points in the ideal glass as labeled by their distance parameter ε. As observed above, model A with a constant vσ predicts an increase of the residual stress with increasing pre-shear rate (dashed lines). Including the strain-dependent correction to the vertex according to eqn (4), model B predicts the observed decrease of σ∞ as a function of increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (solid lines). Note that with our choice of model parameters γ* and γ**, eqn (4) produces a marked stress overshoot in startup flow. As the density increases beyond the glass transition, the magnitude of this stress overshoot in hard-sphere colloidal suspensions diminishes;36 a feature that is likely connected to the approach to random-close packing in these systems. Hence, γ* and γ** should acquire a density dependence that we have not accounted for. Let us further note that with our choice of fixed γ* and γ**, the integral in eqn (2) together with eqn (4) is no longer guaranteed to be positive at large shear rates. The corresponding σ∞ curves in Fig. 5 have thus been restricted to
(solid lines). Note that with our choice of model parameters γ* and γ**, eqn (4) produces a marked stress overshoot in startup flow. As the density increases beyond the glass transition, the magnitude of this stress overshoot in hard-sphere colloidal suspensions diminishes;36 a feature that is likely connected to the approach to random-close packing in these systems. Hence, γ* and γ** should acquire a density dependence that we have not accounted for. Let us further note that with our choice of fixed γ* and γ**, the integral in eqn (2) together with eqn (4) is no longer guaranteed to be positive at large shear rates. The corresponding σ∞ curves in Fig. 5 have thus been restricted to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 < 0.05. The agreement between the schematic-MCT model and the available experimental and simulation data is surprisingly good, although this may be fortuitous.
τ0 < 0.05. The agreement between the schematic-MCT model and the available experimental and simulation data is surprisingly good, although this may be fortuitous.
Independent of quantitative details, there are two asymptotic regimes for σ∞(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) that are predicted by schematic MCT. As
) that are predicted by schematic MCT. As ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0, the residual stress approaches the yield stress σy = lim
→ 0, the residual stress approaches the yield stress σy = lim![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) →0σss(
→0σss(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) > 0. This is also indicated in the experiment (cf. open and filled circles in Fig. 5). For large pre-shear rates, on the other hand, σss is predicted to reach a second plateau as
) > 0. This is also indicated in the experiment (cf. open and filled circles in Fig. 5). For large pre-shear rates, on the other hand, σss is predicted to reach a second plateau as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → ∞. Experimental data for the PS-PNIPAM suspension are compatible with these predictions. But note that the high-shear limit entails physics of particle contacts and solvent-induced interactions that are not captured in the present MCT. For the cases where σ∞ grows with increasing
→ ∞. Experimental data for the PS-PNIPAM suspension are compatible with these predictions. But note that the high-shear limit entails physics of particle contacts and solvent-induced interactions that are not captured in the present MCT. For the cases where σ∞ grows with increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , this growth is much slower than that of the corresponding flow curve. The latter (dotted lines in Fig. 5) approaches a high-shear Newtonian regime (σss ∼
, this growth is much slower than that of the corresponding flow curve. The latter (dotted lines in Fig. 5) approaches a high-shear Newtonian regime (σss ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for
for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → ∞) in the schematic-MCT model. As a result, after the cessation of stronger shear flow, a larger amount of stress is released than for weak flow.
→ ∞) in the schematic-MCT model. As a result, after the cessation of stronger shear flow, a larger amount of stress is released than for weak flow.
The fact that the residual stress σ∞ approaches a constant for both ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0 and
→ 0 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → ∞ can be understood on the basis of the ITT formula and an asymptotic consideration of the schematic-MCT correlation functions. For this, note that the ITT-MCT description is based on transient correlation functions ϕ(t, t′) that are modified solely by deformations occurring between their two time arguments t′ ≤ t. This is in distinct difference to the waiting-time dependent correlation functions Φ(t + tw, tw) measured in nonequilibrium since there, the nonequilibrium distribution function at time tw determines the ensemble average, while for the transient correlators it is always the (deformation-independent) equilibrium distribution function.
→ ∞ can be understood on the basis of the ITT formula and an asymptotic consideration of the schematic-MCT correlation functions. For this, note that the ITT-MCT description is based on transient correlation functions ϕ(t, t′) that are modified solely by deformations occurring between their two time arguments t′ ≤ t. This is in distinct difference to the waiting-time dependent correlation functions Φ(t + tw, tw) measured in nonequilibrium since there, the nonequilibrium distribution function at time tw determines the ensemble average, while for the transient correlators it is always the (deformation-independent) equilibrium distribution function.
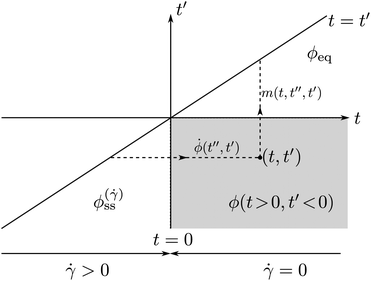
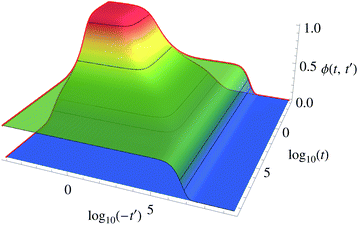
In the integral determining σ(t) after cessation, eqn (2), only the regime t′ < 0 t enters. Schematically, this is represented as the shaded area in Fig. 6. The MCT equation of motion for ϕ(t, t′) is dominated by the history-dependent contribution arising through the memory-kernel integral involving m(t, t′′, t′) and ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) (t′′, t′) for t′′ ∈ [t′, t], eqn (5). The paths for t′′ followed in this integral are indicated in Fig. 6 by dashed lines for the two functions. Fig. 7 shows the two-time “cessation correlator” ϕ(t, t′) for t > 0 and t′ < 0 for an exemplary case.
(t′′, t′) for t′′ ∈ [t′, t], eqn (5). The paths for t′′ followed in this integral are indicated in Fig. 6 by dashed lines for the two functions. Fig. 7 shows the two-time “cessation correlator” ϕ(t, t′) for t > 0 and t′ < 0 for an exemplary case.
The qualitative behavior of this correlation function can be understood from the structure of the memory-kernel equation and from the boundary conditions. Note that correlation functions are at least continuous, so that for t′ = 0 the cessation correlator equals the quiescent equilibrium one (cf.Fig. 6), ϕ(t, 0) = ϕeq(t). For t = 0, on the other hand, ϕ(0, t′) = ϕss(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )(|t′|), the transient correlation function under steady shear rate
)(|t′|), the transient correlation function under steady shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . These two boundary cases are shown in Fig. 7 as the red lines towards the back of the plot.
. These two boundary cases are shown in Fig. 7 as the red lines towards the back of the plot.
The MCT expression for σ(t) suggests discussion of correlation functions at fixed first argument t, as a function of −t′ > 0. Exemplary results are shown in Fig. 8. Since the accumulated strain that decorrelates the MCT memory kernel increases with increasing |t′|, one expects the correlation functions to monotonically decay from their initial value for each t with increasing |t′|. (The situation may be different when, say, considering cessation of a large-amplitude oscillatory flow, where the transient correlation functions are nonmonotonic.43)
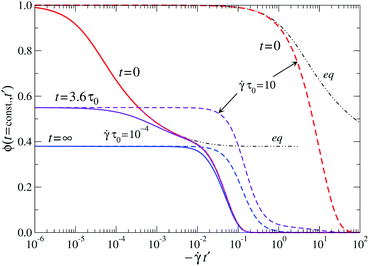 | ||
Fig. 8 Constant-t cuts through Fig. 7: transient two-time correlation function ϕ(t, t′) of the schematic-MCT model for t′ < 0 < t, as a function of −![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t′ for fixed t for a distance parameter ε = 0.01. Solid lines correspond to t′ for fixed t for a distance parameter ε = 0.01. Solid lines correspond to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 10−4, at t = 0 (identical to the nonequilibrium-steady-state correlator), t = 3.6τ0, and t = ∞ (numerically obtained for t/τ0 > 109) as labeled. Dashed lines: the same curves for τ0 = 10−4, at t = 0 (identical to the nonequilibrium-steady-state correlator), t = 3.6τ0, and t = ∞ (numerically obtained for t/τ0 > 109) as labeled. Dashed lines: the same curves for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 10. τ0 = 10. | ||
For liquid states (ε < 0 in the model), the equilibrium correlation function decays to zero on a structural-relaxation time scale τα. Hence, for t ≫ τα, the transient correlator ϕ(t, t′) for t′ < 0 vanishes, and there is no contribution to σ(t) in eqn (2). This explains the observation shown in Fig. 3 that in the liquid, stresses relax back to zero after cessation on the time scale τα, independent of the previous shear rate.
In the glass, the quiescent correlator decays to a finite plateau, the nonergodicity parameter f = limt→∞ϕeq(t). For a sufficiently large t, the cessation correlator ϕ(t, t′), viewed as a function of |t′|, hence has an initial value f. To understand its decay to zero, note first that the steady-state transient correlation function in the shear-melted glass features a decay to zero on a time scale τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 1/
∼ 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (up to a prefactor set in the model by γc), as long as
(up to a prefactor set in the model by γc), as long as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 ≪ 1.
τ0 ≪ 1.
For ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0, a scaling limit is approached where ϕss(t) ∼
→ 0, a scaling limit is approached where ϕss(t) ∼ ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) ss(
ss(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t) for t → ∞. In this scaling limit, the short-time decay of the correlator on the time scale τ0 becomes irrelevant, and the scaling function obeys
t) for t → ∞. In this scaling limit, the short-time decay of the correlator on the time scale τ0 becomes irrelevant, and the scaling function obeys ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) ss(s) = f for s → 0. Since the steady-state stress σss is then determined essentially only by the integral over
ss(s) = f for s → 0. Since the steady-state stress σss is then determined essentially only by the integral over ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) ss(
ss(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t), a dynamic yield stress arises that is qualitatively given by vσf2.
t), a dynamic yield stress arises that is qualitatively given by vσf2.
For times ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t′ ≪ 1, ϕss(t′) (or eqiuvalently ϕ(0, −t′)) remains close to the equilibrium curve. The decay of ϕ(t, t′) for t → ∞ can now be understood considering the structure of the MCT memory integral shown in Fig. 6. At large t and small |t′|, the integral is dominated by equilibrium-correlator contributions, and extends the latter. The contributions only change significantly once |t′| = O(τ
t′ ≪ 1, ϕss(t′) (or eqiuvalently ϕ(0, −t′)) remains close to the equilibrium curve. The decay of ϕ(t, t′) for t → ∞ can now be understood considering the structure of the MCT memory integral shown in Fig. 6. At large t and small |t′|, the integral is dominated by equilibrium-correlator contributions, and extends the latter. The contributions only change significantly once |t′| = O(τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), since then the contribution to the memory kernel arising from
), since then the contribution to the memory kernel arising from ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) (t′′, t′) (the horizontal dashed line in Fig. 6) starts to decay. Therefore, also ϕ(t, t′) decays to zero on a time scale τ′
(t′′, t′) (the horizontal dashed line in Fig. 6) starts to decay. Therefore, also ϕ(t, t′) decays to zero on a time scale τ′![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = O(τ
= O(τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). If t ≫ τ0, the two-time correlator hence resembles the scaling curve
). If t ≫ τ0, the two-time correlator hence resembles the scaling curve ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) ss(
ss(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t) that determines the yield stress. This is visualized in Fig. 7 where we show ϕ(t, t′) as a function of the two time arguments t > 0 and t′ < 0. At t′, t → 0, the microscopic relaxation from unity to f can be seen. For the small pre-shear rate chosen in the figure, this microscopic relaxation has a small weight in the integral determining σ(t). For a large |t′|, the correlator becomes effectively independent of t, featuring decay on the time scale τ
t) that determines the yield stress. This is visualized in Fig. 7 where we show ϕ(t, t′) as a function of the two time arguments t > 0 and t′ < 0. At t′, t → 0, the microscopic relaxation from unity to f can be seen. For the small pre-shear rate chosen in the figure, this microscopic relaxation has a small weight in the integral determining σ(t). For a large |t′|, the correlator becomes effectively independent of t, featuring decay on the time scale τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . This explains that for
. This explains that for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0, both the residual stress σ∞ and the steady-state stress σss approach the dynamic yield stress.
→ 0, both the residual stress σ∞ and the steady-state stress σss approach the dynamic yield stress.
For large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0, the shear-induced relaxation of the steady-state correlator no longer obeys τ
τ0, the shear-induced relaxation of the steady-state correlator no longer obeys τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 1/
∼ 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . In the schematic model, it instead approaches τ
. In the schematic model, it instead approaches τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → ∞ ∼ τ0. As a result, σss ∝
→ ∞ ∼ τ0. As a result, σss ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , and the flowcurve exhibits a high-shear Newtonian regime. The two-time cessation correlator ϕ(t, t′) is still governed by the same qualitative argument as given above: the initial value for t → ∞ is still f, and the memory integral is still cut off by the decay of the steady-state correlator on a time scale O(1/
, and the flowcurve exhibits a high-shear Newtonian regime. The two-time cessation correlator ϕ(t, t′) is still governed by the same qualitative argument as given above: the initial value for t → ∞ is still f, and the memory integral is still cut off by the decay of the steady-state correlator on a time scale O(1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) (the horizontal dashed line in Fig. 6). Thus, σ∞ is still determined by the integral over a function whose decay scales as 1/
) (the horizontal dashed line in Fig. 6). Thus, σ∞ is still determined by the integral over a function whose decay scales as 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , resulting in a constant expression in eqn (2). The numerical value of σ∞ will differ somewhat from the yield stress σy, since the shape of the cessation correlator for t → ∞ changes somewhat with changing
, resulting in a constant expression in eqn (2). The numerical value of σ∞ will differ somewhat from the yield stress σy, since the shape of the cessation correlator for t → ∞ changes somewhat with changing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
The situation is demonstrated for two different shear rates, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 10−4 and
τ0 = 10−4 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 = 10, in Fig. 8 (solid and dashed lines). Here, the cessation correlator ϕ(t, t′) is shown for fixed t > 0 as a function of rescaled second time argument, |
τ0 = 10, in Fig. 8 (solid and dashed lines). Here, the cessation correlator ϕ(t, t′) is shown for fixed t > 0 as a function of rescaled second time argument, |![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t′|. For the lower shear rate, the final decay to zero is set by τ
t′|. For the lower shear rate, the final decay to zero is set by τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for all t, which is also the case demonstrated in Fig. 7. For
for all t, which is also the case demonstrated in Fig. 7. For ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ0 ≫ 1, the steady-shear correlation function decays on the microscopic time scale τ0, and hence does not scale with
τ0 ≫ 1, the steady-shear correlation function decays on the microscopic time scale τ0, and hence does not scale with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . As however t increases, the microscopic contributions disappear from ϕ(t, t′), and a decay on a shear-induced time scale, τ′
. As however t increases, the microscopic contributions disappear from ϕ(t, t′), and a decay on a shear-induced time scale, τ′![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 1/
∼ 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) re-emerges. In this case one notices that τ′
re-emerges. In this case one notices that τ′![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > τ
> τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , since the memory integral picks up microscopic transients that are, in the case of strong shear, no longer negligible. As a result, the irreversible plastic relaxation described by the transient correlation functions describe a residual stress that increases with increasing
, since the memory integral picks up microscopic transients that are, in the case of strong shear, no longer negligible. As a result, the irreversible plastic relaxation described by the transient correlation functions describe a residual stress that increases with increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , as noted above, but becomes independent of the pre-shear rate as
, as noted above, but becomes independent of the pre-shear rate as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → ∞.
→ ∞.
So far, we have discussed constant-t cuts of the transient correlation functions, i.e., those that determine the shear stress within ITT-MCT. On discussing two-time-dependent correlation functions, it is often more convenient to consider cuts for the fixed second argument, i.e., constant-t′ cuts, since this facilitates the interpretation of t′ as a waiting time from which correlations into the future are measured. For the case of shear cessation, the transient correlation functions are of interest only for t′ < 0. Fig. 9 shows an exemplary case for the schematic-MCT model. The qualitative behavior can again be understood from Fig. 7. For |t′| ≈ 0, the quiescent correlator is recovered, while for |t′| → ∞, one approaches the steady-shear correlation function. Since this steady-state correlator decays on the time scale τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , the region of nontrivial t′-dependence is |
, the region of nontrivial t′-dependence is |![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t′| ≲ 0.1. By continuity, the transient correlator then follows the steady-state correlator initially (for t < 0). Since for t > 0, no further relaxation mechanisms contribute to its decay, the transient two-time correlator then quickly crosses over to a t′-dependent plateau where ϕ(t, t′) is independent of t. In Fig. 7, this is exhibited by the fact that for a |t′| large enough such that the transient correlation function assumes a value less than the plateau f, it is independent of t in the glass. The curves shown in the main panel of Fig. 9 hence obey ϕ(t, t′) →
t′| ≲ 0.1. By continuity, the transient correlator then follows the steady-state correlator initially (for t < 0). Since for t > 0, no further relaxation mechanisms contribute to its decay, the transient two-time correlator then quickly crosses over to a t′-dependent plateau where ϕ(t, t′) is independent of t. In Fig. 7, this is exhibited by the fact that for a |t′| large enough such that the transient correlation function assumes a value less than the plateau f, it is independent of t in the glass. The curves shown in the main panel of Fig. 9 hence obey ϕ(t, t′) → ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (t′) < f for t → ∞ and fixed t′ < 0. In the non-ideal glass, one expects this plateau to ultimately decay due to relaxation processes that are not captured in the MCT approximation. In the liquid, the curves are modulated by the final decay on the structural-relaxation time scale τα. This is demonstrated in the inset of Fig. 9, where we show the same constant-t′ cuts as in the main panel, but for the liquid state with separation parameter ε = −0.01.
(t′) < f for t → ∞ and fixed t′ < 0. In the non-ideal glass, one expects this plateau to ultimately decay due to relaxation processes that are not captured in the MCT approximation. In the liquid, the curves are modulated by the final decay on the structural-relaxation time scale τα. This is demonstrated in the inset of Fig. 9, where we show the same constant-t′ cuts as in the main panel, but for the liquid state with separation parameter ε = −0.01.
The transient cessation correlators are not straightforwardly accessible in molecular-dynamics simulations, since they require averaging over the equilibrium distribution function while the trajectories correspond to those influenced by the past shear rate. In the simulation, the averaging is performed over a set of configurations that one assumes to be representative of the statistical ensemble as it evolves over time. This a priori only gives access to the waiting-time dependent correlation function Φ(t + tw, tw). Evaluating this quantity within ITT-MCT involves additional approximations (see ESI of ref. 1) and is outside the scope of the present discussion.
4 Conclusions
We have analyzed the transient decay of the shear stress after the cessation of steady shear flow in an ideal-glass model using schematic models of the mode-coupling theory combined with the integration-through transients framework (ITT-MCT). The theory predicts the partial relaxation of stresses to a long-time plateau value: a flow-history dependent residual stress σ∞ emerges that is sustained by the glass produced from the shear-melted initial steady state. Brownian-dynamics computer simulations of a two-dimensional hard-disk mixture in the glass confirm this picture qualitatively. Our simulation results further corroborate similar results from previous experiments and 3D molecular-dynamics simulations.1The residual stress depends on the preparation history of the glass, in our case exemplified by its dependence on the pre-shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Two variants of the schematic-MCT model have been discussed that differ by whether or not they take account of anelastic strain-induced decorrelation of the overlap between stress and density fluctuations. Taking into account only the relaxation of stresses through irreversible decorrelation of density fluctuations caused by thermal noise (model A), residual stresses remain that are larger than the dynamical yield stress σy. Further stress relaxation is provided by reduction of stress–density couplings that originate in the affine shear advection and is also the cause of pronounced stress overshoots in startup flow. In the schematic model, it needs to be captured empirically (model B), guided by a numerical discussion of the full, wave-vector dependent ITT-MCT.37
. Two variants of the schematic-MCT model have been discussed that differ by whether or not they take account of anelastic strain-induced decorrelation of the overlap between stress and density fluctuations. Taking into account only the relaxation of stresses through irreversible decorrelation of density fluctuations caused by thermal noise (model A), residual stresses remain that are larger than the dynamical yield stress σy. Further stress relaxation is provided by reduction of stress–density couplings that originate in the affine shear advection and is also the cause of pronounced stress overshoots in startup flow. In the schematic model, it needs to be captured empirically (model B), guided by a numerical discussion of the full, wave-vector dependent ITT-MCT.37
The yield stress is the smallest stress the shear-melted glassy state needs to maintain in order to flow homogeneously. In the limit of infinitesimally slow flow, none of this stress can relax. For faster flow, the steady-state stress rises above the dynamic yield stress, and for models with no or sufficiently weak startup-stress-overshoot phenomena, these additional stresses only relax partially, due to the effect of irreversible thermal motion. A further stress-relaxation mechanism is provided by the same mechanism that is responsible for stress overshoots in flow startup: the capability of cages to transiently store a large amount of elastic energy that is released under plastic deformation. In the case of shear cessation, this mechanism allows for a further relaxation of past-flow-induced stresses, so that the remaining residual stresses decrease with increasing shear rate. Nevertheless, a certain amount of stresses never relaxes in the arrested glass, signalling the nonequilibrium nature of the amorphous solid that is being produced.
From the point of view of statistical physics, the appearance of persistent residual stresses is a clear deviation from Onsager's regression hypothesis, and hence a genuine nonlinear-response effect. Consider Onsager's reasoning in the present context:50 if an external perturbing field h0 coupling to the dynamical variable X, is switched on adiabatically in the infinite past, h(t) = h0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[εt] (with ε → 0+), the normalized deviation in X obeys: 〈ΔX(t)〉ne/〈ΔX(t = 0)〉ne = Φx(t) + O(h0), where the relaxation function, Φx(t), is the normalized correlation function of the fluctuations of the variable X in the unperturbed system. It is thus independent of the external field. In our case, the imposed shear flow with the rate
exp[εt] (with ε → 0+), the normalized deviation in X obeys: 〈ΔX(t)〉ne/〈ΔX(t = 0)〉ne = Φx(t) + O(h0), where the relaxation function, Φx(t), is the normalized correlation function of the fluctuations of the variable X in the unperturbed system. It is thus independent of the external field. In our case, the imposed shear flow with the rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) couples to the shear stress, yet we find that the normalized deviatoric shear stress σ(t)/σss sensitively depends on small shear rates, even in the asymptotic long-time limit. The origin of the violation of Onsager's result lies in the time-dependence of the initial stationary state. Its decay is shear-induced and thus becomes arbitrarily slow in the limit of
couples to the shear stress, yet we find that the normalized deviatoric shear stress σ(t)/σss sensitively depends on small shear rates, even in the asymptotic long-time limit. The origin of the violation of Onsager's result lies in the time-dependence of the initial stationary state. Its decay is shear-induced and thus becomes arbitrarily slow in the limit of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0. In ITT-MCT this slow decay is the origin of a dynamic yield stress in the steady state, and of the persistent residual stress after flow cessation.
→ 0. In ITT-MCT this slow decay is the origin of a dynamic yield stress in the steady state, and of the persistent residual stress after flow cessation.
The ITT-MCT theory describes time-dependent single-point averages (such as the macroscopic stress σ(t)) in nonequilibrium through Green–Kubo-like integrals, based on two-point transient correlation functions ϕ(t, t′). The latter are a convenient tool for theoretical analysis, but one has to keep in mind that they do not correspond to the correlation functions accessible in experiment or simulation. Since they are formed with the Boltzmann equilibrium distribution by definition, they describe the nonequilibrium evolution contingent on only those external fields that are present between their two time arguments t′ and t. In ordinary correlation functions, averaging is performed with the time-dependent nonequilibrium distribution function at time t′, which is then denoted as a waiting time tw. The nonequilibrium distribution function contains a further flow-history dependence, so that the correlation functions Φ(t + tw, tw) seen in experiment and simulation depend also on perturbations at times t′′ < tw. The ITT formalism can in principle be extended to describe these waiting-time dependent correlators, as has been demonstrated for the case of the MSD at tw = 0 after cessation.1 We leave a more in-depth discussion of waiting-time dependences for a future publication.51
Since glassy states contain internal stresses caused by past perturbations, they are no longer characterized solely in terms of the thermodynamic state variables. One expects them to show material properties that again depend on the past flow history; for example, the Maxwell shear modulus depends on the pre-strain applied to the glass,18,52,53 and also on the thermal history of the glass.54 The time-dependent changes observed in the (frequency-dependent) dynamical shear moduli after cessation provide a rheological probe of aging-like phenomena.55 Understanding the dependence of material coefficients on the previous strain history is of great conceptual importance for applications. The further development of first-principles microscopic theory will provide a basis for improving the predictability of materials-design processes.
Acknowledgements
This work was partially supported by Deutsche Forschungsgemeinschaft, FOR1394 project P3. ThV thanks for funding from Helmholtz-Gemeinschaft (HGF Hochschul-Nachwuchsgruppe VH-NG 406), and Zukunftskolleg der Universität Konstanz.References
- M. Ballauff, J. M. Brader, S. U. Egelhaaf, M. Fuchs, J. Horbach, N. Koumakis, M. Krüger, M. Laurati, K. J. Mutch, G. Petekidis, M. Siebenbürger, Th. Voigtmann and J. Zausch, Phys. Rev. Lett., 2013, 110, 215701 CrossRef CAS.
- L. Mohan, R. T. Bonnecaze and M. Cloitre, Phys. Rev. Lett., 2013, 111, 268301 CrossRef.
- L. Brodsley, C. Frank and J. W. Steeds, Notes and Records of the Royal Society, 1986, 41, 1–26 CrossRef.
- D. J. Green, R. Tandon and V. M. Sglavo, Science, 1999, 283, 1295–1297 CrossRef.
- L. Wondraczek, J. C. Mauro, J. Eckert, U. Kühn, J. Horbach, J. Deubener and T. Rouxel, Adv. Mater., 2011, 23, 4578–4586 CrossRef CAS.
- S. Chandrasekar and M. M. Chaudhri, Philos. Mag. B, 1994, 70, 1195–1218 CAS.
- (a) J. P. Withers and H. K. D. H. Bhadeshia, Mater. Sci. Technol., 2001, 17, 355–365 CrossRef PubMed; (b) J. P. Withers and H. K. D. H. Bhadeshia, Mater. Sci. Technol., 2001, 17, 366–375 CrossRef PubMed.
- P. J. Withers, Rep. Prog. Phys., 2007, 70, 2211–2264 CrossRef.
- D. Walton, J. Amin and N. Shashidhar, electronic design, 2010, 58, 70–73 Search PubMed.
- P. J. Webster, D. J. Hughes, G. Mills and G. B. M. Vaughan, Mater. Sci. Forum, 2002, 404–407, 767–772 CrossRef CAS.
- T. Sasaki, S. Takahashi, Y. Kanematsu, Y. Satoh, K. Iwafuchi, M. Ishida and Y. Morii, Wear, 2008, 265, 1402–1407 CrossRef CAS PubMed.
- X. Trepat, G. Lenormand and J. J. Fredberg, Soft Matter, 2008, 4, 1750–1759 RSC.
- P. Papadopoulos, J. Sölter and F. Kremer, Colloid Polym. Sci., 2009, 287, 231–236 CAS.
- G. Reiter, M. Hamieh, P. Damman, S. Sclavons, S. Gabriele, T. Vilmin and E. Raphaël, Nat. Mater., 2005, 4, 754–758 CrossRef CAS PubMed.
- K. Dullaert and J. Mewis, J. Rheol., 2005, 49, 1213–1230 CrossRef CAS.
- K. Dullaert and J. Mewis, J. Colloid Interface Sci., 2005, 287, 542–551 CrossRef CAS PubMed.
- A. S. Negi and C. O. Osuji, J. Rheol., 2010, 54, 943–958 CrossRef CAS.
- A. S. Negi and C. O. Osuji, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031404 CrossRef.
- A. S. Negi, C. G. Redmon, S. Ramakrishnan and C.O. Osuji, arXiv:1401.8018.
- B. Chung, S. Ramakrishnan, R. Bandyopadhyay, D. Liang, C. F. Zukoski, J. L. Harden and R. L. Leheny, Phys. Rev. Lett., 2006, 96, 228301 CrossRef CAS.
- J. M. Fuchs and M. E. Cates, Phys. Rev. Lett., 2002, 89, 248304 CrossRef.
- J. M. Brader, Th. Voigtmann, M. E. Cates and M. Fuchs, Phys. Rev. Lett., 2007, 98, 058301 CrossRef CAS.
- J. M. Brader, M. E. Cates and M. Fuchs, Phys. Rev. Lett., 2008, 101, 138301 CrossRef CAS.
- M. Fuchs and M. E. Cates, J. Rheol., 2009, 53, 957–1000 CrossRef CAS.
- P. Sollich, F. Lequeux, P. Hébraud and M. E. Cates, Phys. Rev. Lett., 1997, 78, 2020–2023 CrossRef CAS.
- M. E. Cates and P. Sollich, J. Rheol., 2004, 48, 193–207 CrossRef CAS.
- G. Petekidis, D. Vlassopoulos and P. N. Pusey, Faraday Discuss., 2003, 123, 287–302 RSC.
- G. Petekidis, D. Vlassopoulos and P. N. Pusey, J. Phys.: Condens. Matter, 2004, 16, S3955 CrossRef CAS.
- S. Papenkort and Th. Voigtmann, J. Chem. Phys., 2014, 140, 164507 CrossRef CAS PubMed.
- J. Zausch, J. Horbach, M. Laurati, S. Egelhaaf, J. M. Brader and Th. Voigtmann, J. Phys.: Condens. Matter, 2008, 20, 404210 CrossRef.
- J. Zausch, Ph.D. thesis, Universität Mainz, Germany, 2008.
- K. Kawasaki and J. D. Gunton, Phys. Rev. A, 1973, 8, 2048–2064 CrossRef CAS.
- G. P. Morriss and D. J. Evans, Phys. Rev. A, 1987, 35, 792–797 CrossRef.
- J. M. Brader, Th. Voigtmann, M. Fuchs, R. G. Larson and M. E. Cates, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15186–15191 CrossRef CAS PubMed.
- N. Koumakis, M. Laurati, S. U. Egelhaaf, J. F. Brady and G. Petekidis, Phys. Rev. Lett., 2012, 108, 098303 CrossRef CAS.
- M. Siebenbürger, M. Ballauff and Th. Voigtmann, Phys. Rev. Lett., 2012, 108, 255701 CrossRef.
- C. P. Amann, M. Siebenbürger, M. Krüger, F. Weysser, M. Ballauff and M. Fuchs, J. Rheol., 2013, 57, 149–175 CrossRef CAS.
- W. Götze, Complex Dynamics of Glass-Forming Liquids, Oxford University Press, Oxford, 2009 Search PubMed.
- Th. Voigtmann, J. M. Brader, M. Fuchs and M. E. Cates, Soft Matter, 2012, 8, 4244–4253 RSC.
- A. Scala, Th. Voigtmann and C. De Michele, J. Chem. Phys., 2007, 126, 134109 CrossRef CAS PubMed.
- F. Weysser and D. Hajnal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041503 CrossRef.
- R. Seyboldt, D. Hajnal, F. Weysser and M. Fuchs, Soft Matter, 2012, 8, 4132–4140 RSC.
- J. M. Brader, M. Siebenbürger, M. Ballauff, K. Reinheimer, M. Wilhelm, S. J. Frey, F. Weysser and M. Fuchs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061401 CrossRef CAS.
- O. Henrich, F. Weysser, M. E. Cates and M. Fuchs, Philos. Trans. R. Soc., A, 2009, 367, 5033–5050 CrossRef PubMed.
- M. Krüger, F. Weysser and Th. Voigtmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061506 CrossRef.
- M. Krüger, F. Weysser and M. Fuchs, Eur. Phys. J. E, 2011, 34, 88 CrossRef PubMed.
- P. Olsson and S. Teitel, Phys. Rev. Lett., 2007, 99, 178001 CrossRef.
- A. W. Lees and S. F. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921–1929 CrossRef.
- R. C. Welch, J. R. Smith, M. Potuzak, X. Guo, B. F. Bowden, T. J. Kiczenski, D. C. Allan, E. A. King, A. J. Ellison and J. C. Mauro, Phys. Rev. Lett., 2013, 110, 265901 CrossRef.
- W. Brenig, Statistical Theory of Heat, Springer-Verlag, Berlin, 1989 Search PubMed.
- S. Fritschi, et al., in preparation.
- S. Karmakar, E. Lerner and I. Procaccia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 026104 CrossRef.
- F. Frahsa, A. K. Bhattacharjee, J. Horbach, M. Fuchs and Th. Voigtmann, J. Chem. Phys., 2013, 138, 12A513 CrossRef PubMed.
- J. Ashwin, E. Bouchbinder and I. Procaccia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 83, 042310 Search PubMed.
- P. Moldenaers and J. Mewis, J. Rheol., 1986, 30, 567–584 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |