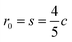Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crystalline order and topological charges on capillary bridges†
Verena
Schmid
a and
Axel
Voigt
*ab
aInstitute of Scientific Computing, TU Dresden, 01062 Dresden, Germany
bCentre of Advanced Modeling and Simulation, TU Dresden, 01062 Dresden, Germany. E-mail: axel.voigt@tu-dresden.de
First published on 7th April 2014
Abstract
We numerically investigate crystalline order on negative Gaussian curvature capillary bridges. In agreement with the experimental results in [W. Irvine et al., Nature, Pleats in crystals on curved surfaces, 2010, 468, 947] we observe for decreasing integrated Gaussian curvature, a sequence of transitions, from no defects to isolated dislocations, pleats, scars and isolated sevenfold disclinations. We especially focus on the dependency of topological charge on the integrated Gaussian curvature, for which we observe, again in agreement with the experimental results, no net disclination for an integrated curvature down to −10, and an approximately linear behavior from there on until the disclinations match the integrated curvature of −12. In contrast to previous studies in which ground states for each geometry are searched for, we here show that the experimental results, which are likely to be in a metastable state, can be best resembled by mimicking the experimental settings and continuously changing the geometry. The obtained configurations are only low energy local minima. The results are computed using a phase field crystal approach on catenoid-like surfaces and are highly sensitive to the initialization.
When soft materials assemble in the presence of geometric and topological constraints, the regular order favored by local interactions is frustrated, which leads to defect structures in the ground state. The capsid of a spherical virus provides an example. Here proteins form subunits, which arrange in an icosahedral shape, constructed from varying numbers of hexamers and 12 pentamers. On more general surfaces with spatially varying positive and negative curvature the geometric and topological constraints lead to more complex defect structures. These defects can be chemically functionalized1,2 and provide the key to self-assembly into complex hierarchical structures with emergent novel macroscopic properties. Geometric and topological constraints thus provide a route to control the self-assembly process and an understanding of the interplay of geometry, topology and defects is therefore of utmost importance, if this route to design novel materials will be explored. See e.g. the themed collection on The geometry and topology of soft materials3 for a broader discussion.
Besides this practical motivation, crystalline order on curved surfaces is also a rich academic problem. Various theoretical results are known. Topological constraints are considered in a classic theorem of Euler, which shows for a triangulation of the surface that  , with vi as the number of vertices with i nearest neighbors and ξ as the Euler characteristic of the surface. Thus for surfaces with the topology of a sphere (ξ = 2) the total charge must be 12. One realization is again the spherical virus, considered as a triangular lattice with sixfold coordination, with 12 fivefold disclinations present. However, there are many other possibilities to fulfill the theorem of Euler and it is energetics that determines the number, type and arrangement of defects. With each disclination a stretching energy is associated (relative to a perfect triangular lattice in flat space) which grows proportional to R2, with R as the radius of the sphere. For a fixed lattice constant a we have N ∼ (R/a)2, where N is the number of particles. Thus for large N, mechanisms are expected which reduce this extra energy by changing the ground-state configuration. This can be done by surface buckling as considered e.g. in ref. 4 and 5. However, in cases where buckling is limited, the energy is reduced by introducing dislocations and grain-boundary scars, see ref. 6. Realizations of water droplets in oil, which are coated with colloidal particles7 show that these excess dislocations grow linearly with the system size.
, with vi as the number of vertices with i nearest neighbors and ξ as the Euler characteristic of the surface. Thus for surfaces with the topology of a sphere (ξ = 2) the total charge must be 12. One realization is again the spherical virus, considered as a triangular lattice with sixfold coordination, with 12 fivefold disclinations present. However, there are many other possibilities to fulfill the theorem of Euler and it is energetics that determines the number, type and arrangement of defects. With each disclination a stretching energy is associated (relative to a perfect triangular lattice in flat space) which grows proportional to R2, with R as the radius of the sphere. For a fixed lattice constant a we have N ∼ (R/a)2, where N is the number of particles. Thus for large N, mechanisms are expected which reduce this extra energy by changing the ground-state configuration. This can be done by surface buckling as considered e.g. in ref. 4 and 5. However, in cases where buckling is limited, the energy is reduced by introducing dislocations and grain-boundary scars, see ref. 6. Realizations of water droplets in oil, which are coated with colloidal particles7 show that these excess dislocations grow linearly with the system size.
The same arguments hold for toroidal crystals and capillary bridges with the topology of a cylinder (ξ = 0). In these cases, there is no topological need for disclinations and all defects are introduced to relieve the strain induced by the curvature. For toroidal geometries it is found that excess disclinations are energetically favorable for fat torii8 and that the number of excess disclinations is controlled primarily by the aspect ratio of the torus.9 Experiments for colloidal particles on oil–glycerol capillary bridges10 show a more complex behavior. No net topological charge is found on the surface for an integrated Gaussian curvature down to Ω = −10, with  and Gaussian curvature G. For Ω beyond the threshold of −10, disclinations rapidly fill the surface until 12 disclinations approximately match the integrated curvature of −12. A sequence of transitions is observed, from no defects to isolated dislocations, which organize into pleats, and finally form scars and isolated sevenfold disclinations, see Fig. 1 for an explanation of the various defect types.
and Gaussian curvature G. For Ω beyond the threshold of −10, disclinations rapidly fill the surface until 12 disclinations approximately match the integrated curvature of −12. A sequence of transitions is observed, from no defects to isolated dislocations, which organize into pleats, and finally form scars and isolated sevenfold disclinations, see Fig. 1 for an explanation of the various defect types.
 | ||
| Fig. 1 Defect types: (a) sevenfold disclination, (b) dislocation, (c) pleat consisting of two dislocations, and (d) scar with topological charge of −1. The colour coding corresponds to the number of neighbors: green (5), yellow (6) and red (7), within Fig. 3 we will find dark blue (3) and light blue (4) at the boundary. | ||
If the presence of topological grain-boundary scars for spheres and torii is surprising and unexpected, the occurrence of pleats on capillary bridges is even more surprising. It has been explained in ref. 11 in terms of a curvature screening provided by the stress free boundary.
While the linear increase of excess dislocations and the formation of scars on a sphere and a torus is well understood and reproduced quantitatively by various theoretical approaches and simulation techniques, see e.g., ref. 9 and 12–16 and the review, ref. 17, the behavior on capillary bridges is less understood. In ref. 18 the problem is addressed by mapping the microscopic interacting particle problem to the problem of discrete interacting defects in a continuum elastic background. The critical value for the transition between configurations with and without disclinations or scars is deduced for catenoids. Three different ways are considered. In the first approach the critical value corresponds to the catenoid for which the integrated Gaussian curvature of the geodesic disc matches the curvature, which would be screened by a sevenfold disclination. Using the definition in ref. 10, in which the integrated Gaussian curvature is defined in units of disclinations as above, the obtained critical waist size c* = 0.85 corresponds to Ω* = −6.3. The second approach uses an effective screened disclination charge, for which c* = 0.87, corresponding to Ω* = −6.0. The third approach uses an energetic argument. The transition point for the emergence of a disclination in the interior is found to be c* = 0.8, corresponding to Ω* = −7.2. All values are significantly larger than the experimentally obtained Ω* = −10. The same approach is used in ref. 11 and validated against a numerical energy minimization of a discrete spring model. The results are in qualitative agreement with ref. 10 but no quantitative estimate for Ω* is given. Simulation results for electrostatically charged particles are obtained for a wide range of system sizes, curvature and interaction potentials, including Yukawa, Coulomb and Lennard-Jones in ref. 19 and 20. The results qualitatively agree with the continuum theory and the experimental data. Depending on Ω dislocations, pleats, scars and sevenfold disclinations are found, independent of the used potential. The supplemental material in ref. 19 also provides tabulated numbers of positive and negative topological charges and a critical waist size c*, which here correspond to the transition to isolated sevenfold disclinations. It seems to be only weakly dependent on the number of particles, but sensitive to the considered potential. For the Coulomb potential, a critical waist size c* = 0.55 is found, corresponding to Ω* = −10.01. However, the tabulated charges indicate the presence of charged defects as scars already above that value, in disagreement with the experimental results in ref. 10. The data also strongly depend on the considered constant mean curvature (Delaunay) surface. Within the experiments, the capillary bridge is obtained through a sequence of Delaunay surfaces (unduloids, catenoids and nodoids) each with different geometrical parameters, such as aspect ratio, mean curvature and maximal Gaussian curvature. Such different Delaunay surfaces are considered in ref. 20. However, quantitative results for Ω* are not given.
Here, instead of a coarse grained elasticity problem for the defects or a discrete particle simulation for the position of N particles, we consider a continuous optimization problem for a number density, with N maxima representing the N particles. The idea is to find a free energy, which is minimized for a configuration, which corresponds to the minimum of the original problem. We consider the Swift–Hohenberg free energy on the surface Γ with ∇Γ and ΔΓ the corresponding surface gradient and surface Laplacian. We define
 | (1) |
Thereby ρ denotes a number density of the particles and 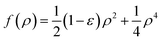 can have a double-well structure, depending on the parameter ε. Within various parameter regimes, the minimizers of this energy are periodic solutions with a hexagonal structure in a flat space, which are geometrically frustrated in the considered setting on Γ. We here have an interplay between the tendency to form periodic solutions and the geometric frustration which prevents such a periodicity. We consider the H−1 gradient flow of this energy, which can be viewed as an extension of the phase-field-crystal (PFC) model, introduced in ref. 21 to surfaces. From
can have a double-well structure, depending on the parameter ε. Within various parameter regimes, the minimizers of this energy are periodic solutions with a hexagonal structure in a flat space, which are geometrically frustrated in the considered setting on Γ. We here have an interplay between the tendency to form periodic solutions and the geometric frustration which prevents such a periodicity. We consider the H−1 gradient flow of this energy, which can be viewed as an extension of the phase-field-crystal (PFC) model, introduced in ref. 21 to surfaces. From
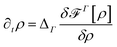 | (2) |
| ∂tρ = ΔΓμ | (3) |
| μ = 2ν + ΔΓν + f′(ρ) | (4) |
| ν = ΔΓρ | (5) |
The system is solved towards the steady state and each maximum in the computed number density is identified with a particle. In ref. 16 this phenomenological approach is validated for the Thomson problem22 by computing minimal energy configurations for various numbers of N and comparing the resulting configurations and Coulomb energies, which are computed as  with i-th particle position pi and the distance measured in
with i-th particle position pi and the distance measured in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, with known results for N ∈ [12, 2790]. However, the approach is also quantitatively related to discrete particle simulations. In ref. 23 the equations are derived from a discrete particle setting via classical dynamic density functional theory, following the derivation in ref. 24 for the flat space. Numerical results on a sphere have shown that the obtained minimal energy configurations are insensitive to the specific underlying interparticle potential. These results are in agreement with ref. 19 where five different potentials are considered and qualitatively the same defect motifs are found. Both results indicate that the geometric frustration is much stronger than the influence of the interparticle potential. We therefore stick to the phenomenological model above. Besides this qualitative and quantitative comparison of the phase field crystal approach with discrete particle simulation results, questions concerning reachable size and efficiency can be asked. The largest problem considered in ref. 23 accounts for N = 99
3, with known results for N ∈ [12, 2790]. However, the approach is also quantitatively related to discrete particle simulations. In ref. 23 the equations are derived from a discrete particle setting via classical dynamic density functional theory, following the derivation in ref. 24 for the flat space. Numerical results on a sphere have shown that the obtained minimal energy configurations are insensitive to the specific underlying interparticle potential. These results are in agreement with ref. 19 where five different potentials are considered and qualitatively the same defect motifs are found. Both results indicate that the geometric frustration is much stronger than the influence of the interparticle potential. We therefore stick to the phenomenological model above. Besides this qualitative and quantitative comparison of the phase field crystal approach with discrete particle simulation results, questions concerning reachable size and efficiency can be asked. The largest problem considered in ref. 23 accounts for N = 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 602 maxima on a sphere and finds in energy E1 which is only 0.0004% above the lower bound 0.5N2 − 0.553051N3/2 from ref. 25. The simulation took about 1.5 days on a single processor with 12 GB RAM. The computational approach certainly is more involved than discrete particle simulations, but allows for simple coupling with other fields, such as surface buckling of the underlying surface, as considered for viral capsided in ref. 26 or fluid flow in the surrounding medium, as e.g. considered for bijels27 and particle stabilized emulsions.28,29
602 maxima on a sphere and finds in energy E1 which is only 0.0004% above the lower bound 0.5N2 − 0.553051N3/2 from ref. 25. The simulation took about 1.5 days on a single processor with 12 GB RAM. The computational approach certainly is more involved than discrete particle simulations, but allows for simple coupling with other fields, such as surface buckling of the underlying surface, as considered for viral capsided in ref. 26 or fluid flow in the surrounding medium, as e.g. considered for bijels27 and particle stabilized emulsions.28,29
Different numerical approaches have been considered in ref. 23 to solve the system of surface partial differential equations. We here adapt a parametric finite element setting, which is realized within the simulation toolbox AMDiS.30 The approach is thereby based on the stable finite element discretization for the PFC model in ref. 31 and is described in detail in ref. 23. The key idea is to use the surface operators on the discrete surface which consists of triangles T. To do the integration on these triangles a parameterization FT: ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) → T is used, with
→ T is used, with ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) the standard element in
the standard element in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2. These allow transformation of all integrations onto the standard element using the finite element basis defined also in
2. These allow transformation of all integrations onto the standard element using the finite element basis defined also in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2. The parameterization FT is given by the coordinates of the surface mesh elements and provides the only difference between solving equations on surfaces and on planar domains. For a surface we have to allow FT:
2. The parameterization FT is given by the coordinates of the surface mesh elements and provides the only difference between solving equations on surfaces and on planar domains. For a surface we have to allow FT: ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2 →
2 → ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, whereas for a planar domain FT:
3, whereas for a planar domain FT: ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2 →
2 → ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2. With this tiny modification any code to solve partial differential equations on Cartesian grids can be used to solve the same problem on a surface, providing a surface triangulation is given. It is essentially this modification which induces the geometric frustration to the problem.
2. With this tiny modification any code to solve partial differential equations on Cartesian grids can be used to solve the same problem on a surface, providing a surface triangulation is given. It is essentially this modification which induces the geometric frustration to the problem.
Our surface is given as an approximation of a catenoid and obtained through a rotation around the x3-axis. The parametric equation of the surface is given by
 | (6) |
The surface area is computed as  , the Gaussian curvature follows as
, the Gaussian curvature follows as  and
and  . Using this approximation, we can scale the surface area by varying the waist radius r0, without changing the height s, the vertical curvature radius at the waist c and the integrated Gaussian curvature Ω. The approach allows for changing the surface to scatter (Ω ∈ (−12, 0)) by keeping the surface area A and the outer radius R fixed.
. Using this approximation, we can scale the surface area by varying the waist radius r0, without changing the height s, the vertical curvature radius at the waist c and the integrated Gaussian curvature Ω. The approach allows for changing the surface to scatter (Ω ∈ (−12, 0)) by keeping the surface area A and the outer radius R fixed.
The surface is discretized using triangular elements with a sufficient mesh size h ∼ a/10. We use the parameters ε = 0.4 and the average particle density as ρ0 = −0.3,‡ which correspond to a point in the two-dimensional phase diagram within the hexagonal region.
The boundary conditions are crucial, as they have to be stress free. This is accounted for by specifying Dirichlet conditions using a one-mode approximation, see ref. 32. Choosing the outer radius R in accordance with the distance between neighboring particles allows for a stress free boundary.
We consider four different initializations. We either specify different initial conditions and use (a) random initialization with ρ = ρ0 + η, with white noise η, (b) initialization at the boundary, with the one-mode approximation specified at the boundary, (c) initialization at the waist, with the one-mode approximation specified at the waist or as in ref. 10 start with a cylinder and subsequently change the surface to decrease Ω. Within this last approach we use a sequence of 42 geometries and compute the steady state on each, with the one from the previous surface as the initial condition. An animation is provided in the ESI.†
The simulation results are postprocessed in the following way. We identify the maxima of the computed particle density ρ, interpret them as particle positions and define their neighborship based on their two-dimensional Voronoi regions. These data are used to evaluate the number of dislocations, scars, pleats, five- and sevenfold disclinations, as well as the number of three- and fivefold disclinations on the boundary. Within colliding defect structures, clusters are separated preferring dislocations and pleats over disclinations and scars, larger defects over smaller defects and oriented defects over unoriented defects. The visualization is done using the software Ovito.33
Fig. 3 shows selected results for the evolving surface. For all initializations, also for the not shown random initialization and the initialization from the boundary or the waist, we observe the whole spectrum of defects: dislocations, pleats, scars, five- and sevenfold disclinations and the expected sequence of transitions to dislocations, pleats, scars and isolated sevenfold disclinations. Table 1 summarizes their first appearance.
 | ||
| Fig. 3 Front, top and perspective view of four configurations for selected values of Ω of the evolving surface. The configurations are selected to show characteristic features: for 0 > Ω > −7.75 the configuration is defect free, at Ω = −7.75 dislocations are formed at the boundary, at Ω = −9.41 pleats are formed. First charged defects are formed at Ω = −10.44 in terms of scars and at Ω = −10.87 five- and sevenfold disclinations are present. An animation through all considered 42 surfaces is provided in the ESI.† | ||
| Random | Boundary | Waist | Evolution | |
|---|---|---|---|---|
| Dislocations | −1.44 | −4.07 | −1.44 | −7.75 |
| Pleats | −4.07 | −9.78 | −1.44 | −9.41 |
| Scars | −6.25 | −11.35 | −10.89 | −10.44 |
| 5-fold | −9.27 | −11.35 | −11.77 | −10.87 |
| 7-fold | −11.53 | −11.35 | −11.14 | −10.87 |
The appearance and interactions of defects differ for different initializations. While for random initialization defects are already present for the largest value of Ω, scars are mainly accompanied by fivefold disclinations next to the boundary and sevenfold disclinations appear at the waist, the configurations resulting from initialization at the boundary are characterized by migration of dislocations into the surface and the formation of a second row of dislocations, as well as an increase in size of the occurring pleats. For the initialization from the waist, we observe only oriented dislocation for large Ω, with the number increasing with decreasing Ω until the first defects occur also at the boundary. The appearance of pleats comes together with non-oriented dislocations. As the pleats grow, the dislocations become again oriented. For the evolving geometry, the surface remains defect free up to relatively low values for Ω, first defects occur as oriented dislocations at the boundary. Their number stays fixed until pleats are formed after further decreasing Ω. Here pleats do not grow but fall apart, forming an oriented dislocation in the interior and one at the boundary. Scars and sevenfold disclinations are formed at the same time. In contrast with the size dependent exclusive appearance of disclinations or scars reported in ref. 18, we found both defect types at the same time.
We now concentrate on the first appearance of scars, fivefold or sevenfold disclinations and thus a detached topological charge. For random initializations, scars already appear on surfaces with Ω = −6.25. For the initialization at the boundary and the waist the configuration stays without detached topological charge down to Ω = −11.14 and Ω = −11.35, respectively, all in quantitative disagreement with the experimental results in ref. 10. Only the evolving geometry, which resembles the evolution in the experimental setting best, leads to the expected behavior, with no detached topological charge down to −10.44.
To further highlight the quantitative agreement, we compute the detached topological charge qint, as the difference of the number of particles in the interior with seven and five neighbors, the total topological charge qtotal, which in addition considers particles at the boundary, which do not have four neighbors and thus should be zero for Ω ∈ (−12, 0), and the number of defects Ndefect, which we scale by the number of particles N to obtain the ratio ζ = Ndefect/N. This becomes necessary as N is not fixed throughout evolution and can therefore not set to a distinct value. Fig. 4 shows these characteristic quantities as functions of Ω.
 | ||
| Fig. 4 (Left) Detached topological charge qint, (middle) total topological charge qtotal, and (right) scaled number of defects ζ functions of Ω, with green random initialization, black initialization from the boundary, blue initialization from the waist, and purple the evolving surface computation. The left figure shows in addition the experimentally observed linear increase from 0 to 12 for Ω = −10 to Ω = −12 in ref. 10. | ||
The detached topological charge for the evolving surface simulations shows the expected behavior, with qint = 0 down to Ω ≈ −10 and an approximately linear increase up to qint ≈ 12 for Ω ≈ −12. This is in agreement with the experimental results in ref. 10. In agreement with the topological requirement the total charge qtotal remains zero up to the smallest considered value of Ω = −11.86 for all initializations, which is just a consistency check of our postprocessing and the number of defects growth for decreasing Ω. For the evolving surface simulations the configurations stay defect free down to Ω = −7.75, where defects form suddenly. The number of defects stays almost constant afterwards until a second jump can be seen for Ω = −10.44. Below that value more and more defects are introduced. This has a clear influence on the energy, for which we compute again the Coulomb potential 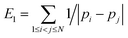 and a power law potential suggested in ref. 20
and a power law potential suggested in ref. 20 with i-th particle position pi and the distance measured in
with i-th particle position pi and the distance measured in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. To eliminate the dependence on N we rescale these energies to obtain Ẽ1 = E1/N2 and Ẽ3 = E3/N2. Fig. 5 shows the computed energies as functions of Ω.
3. To eliminate the dependence on N we rescale these energies to obtain Ẽ1 = E1/N2 and Ẽ3 = E3/N2. Fig. 5 shows the computed energies as functions of Ω.
While the different initializations lead to almost identical results for long-range potential Ẽ1, large differences can be seen for the short range potential Ẽ3. The curve for the evolving surface resembles nicely the characteristic defects. The energy is increasing down to Ω = −7.75 with a defect-free configuration. The sudden drop in the energy results from the occurrence of defects, in the form of dislocations at the boundary. The energy again increases until Ω = −10.44. The small drop here corresponds again to a change in the defect type, which leads to the occurrence of detached topological charge. The energy plots further indicate that the configurations obtained with the evolving surface approach not always lead to the lowest energy. We can assume a highly complex energy landscape, in which all our observed configurations are presumably trapped in local minima. Instead of searching for global minima, as in ref. 19, we concentrate on resampling the experiments in ref. 10, with presumable also only local minima configurations. With the evolving surface approach, which resamples the experimental setting best, quantitative agreement for all considered data qint and ζ can be achieved. The number of defects is thereby lower than in various putative global minima configurations reported in ref. 19.
The goal to chemically functionalize the defects to control self-assembly into supramolecular structures, requires not only the presence of a certain number and type of defects, but also their position and arrangement to be predictable. The configurations obtained with the evolving surface approach here lead to highly symmetric arrangements, see Fig. 3. The number of defects growth until 12 equally spaced oriented dislocations on the boundary are formed. These defects remain and grow into pleats, without changing their position. This highly symmetric arrangement even remains for smaller Ω after the splitting into scars and sevenfold disclinations and only for the lowest values of Ω the symmetry is lost. To identify this symmetric sequence of transitions as the most favorable path requires computation of the energy barriers and minimal energy paths, which is currently under investigation using the string method34 already applied to the phase field crystal model in ref. 35 and 36. The future goal should be to identify similar symmetric defect arrangements at nanoscales and to further explore the complex interplay of topology, geometry and surface evolution for novel materials design. The considered phase field crystal approach, even if computationally more expensive than discrete particle simulations, provides a flexible tool to consider such an evolution and further coupling with other external fields.
This research was supported by DFG within SPP 1296 Grant no. Vo899/7-3 as well as by EU within FP7 Grant no. 247504. We thank S. Praetorius for fruitful discussions and his help with AMDiS.
References
- D. Nelson, Nano Lett., 2002, 2, 1125–1129 CrossRef CAS.
- G. DeVriese, F. Talley, R. Carney and F. Stellacci, Adv. Mater., 2008, 20, 4243–4247 CrossRef.
- V. Vitelli and W. Irvine, Soft Matter, 2013, 9, 8086–8087 RSC.
- H. Seung and D. Nelson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 30, 1005–1018 CrossRef.
- J. Lidmar, L. Mirny and D. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 051910 CrossRef.
- M. Bowick, D. Nelson and A. Travesset, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8738–8751 CrossRef CAS.
- A. Bausch, M. Bowick, A. Cacciuto, A. Dinsmore, M. Hsu, D. Nelson, M. Nikolaides, A. Travesset and D. Weitz, Science, 2003, 299, 1716–1718 CrossRef CAS PubMed.
- M. Bowick, D. Nelson and A. Travesset, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 041102 CrossRef.
- L. Giomi and M. Bowick, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021112 CrossRef.
- W. Irvine, V. Vitteli and P. Chaikin, Nature, 2010, 468, 947–951 CrossRef CAS PubMed.
- W. Irvine and V. Vitelli, Soft Matter, 2012, 8, 10123–10129 RSC.
- A. Travesset, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 036110 CrossRef CAS.
- S. Schneider and G. Gompper, Europhys. Lett., 2005, 70, 136–142 CrossRef CAS.
- D. Wales and S. Ulker, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 212101 CrossRef.
- V. Vitelli, J. Lucks and D. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2007, 103, 12323–12328 CrossRef PubMed.
- R. Backofen, A. Voigt and T. Witkowski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 025701(R) CrossRef.
- M. Bowick and L. Giomi, Adv. Phys., 2009, 58, 449–563 CrossRef CAS.
- M. Bowick and Z. Yao, Europhys. Lett., 2011, 93, 36001 CrossRef.
- H. Kusumaatmaja and D. Wales, Phys. Rev. Lett., 2013, 110, 165502 CrossRef.
- E. Bendito, M. Bowick, A. Medina and Z. Yao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 110, 012405 CrossRef.
- K. Elder, M. Katakowski, M. Haataja and M. Grant, Phys. Rev. Lett., 2002, 88, 245701 CrossRef CAS PubMed.
- J. Thomson, Philos. Mag., 1904, 7, 237–265 CrossRef CAS.
- R. Backofen, M. Gräf, D. Potts, S. Praetorius, A. Voigt and T. Witkowski, Multiscale Model. Simul., 2011, 9, 314–334 Search PubMed.
- S. van Teefelen, R. Backofen, A. Voigt and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051404 CrossRef.
- A. Kuijlaars and E. Saff, Trans. Amer. Math. Soc., 1998, 350, 523–538 CrossRef.
- S. Aland, A. Rätz, M. Röger and A. Voigt, Multiscale Model. Simul., 2012, 10, 82–110 Search PubMed.
- S. Aland, J. Lowengrub and A. Voigt, Phys. Fluids, 2011, 23, 062103 CrossRef PubMed.
- S. Aland, J. Lowengrub and A. Voigt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 046321 CrossRef.
- S. Aland and A. Voigt, Colloids Surf., A, 2012, 413, 298–302 CrossRef CAS PubMed.
- S. Vey and A. Voigt, Comput. Visualization Sci., 2007, 10, 57–66 CrossRef PubMed.
- R. Backofen, A. Rätz and A. Voigt, Philos. Mag. Lett., 2007, 87, 813–820 CrossRef CAS.
- K. Elder and M. Grant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051605 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- W. Ren and W. E. E. Vanden-Eijnden, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 052301 CrossRef.
- R. Backofen and A. Voigt, J. Phys.: Condens. Matter, 2010, 22, 364104 CrossRef CAS PubMed.
- R. Backofen and A. Voigt, Eur. Phys. J.: Spec. Top., 2014, 223, 497–509 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Animation of the evolution of defect motifs on a surface with increasingly negative integrated Gaussian curvature. See DOI: 10.1039/c4sm00228h |
| ‡ The considered particle density ρ is more precisely a non-dimensional density difference with a reference state of an averaged density in the liquid state, see ref. 21. |
| This journal is © The Royal Society of Chemistry 2014 |